Motion Planning for Autonomous Driving in Unsignalized Intersections Using Combined Multi-Modal GNN Predictor and MPC Planner
Abstract
1. Introduction
- (1)
- Multi-modal Trajectory Predictor. A GNN-based multi-modal trajectory predictor is designed, which outputs three deterministic trajectories for each surrounding road user. Each trajectory corresponds to a plausible interaction scenario (e.g., yielding, non-yielding, or aggressively driving). This multi-head predictor is trained on the INTERACTION dataset [20], thereby capturing the multi-modal nature of intersection behavior in a compact form.
- (2)
- Interaction-aware MPC-based Motion Planner. An MPC-based motion planner is devised to incorporate the multiple predicted trajectories of other agents as constraints. In contrast to conventional methods that plan a single forecast trajectory per road user, the proposed planner treats the primary trajectory predicted for each agent as a hard constraint and regards the alternative trajectories as soft constraints via penalty terms, thereby balancing safety and conservatism by not entirely ignoring less likely behaviors of other road users.
- (3)
- Ride Comfort and Feasibility Considerations. The MPC formulation adapts a kinematic bicycle model to represent the ego vehicle and includes penalty terms on acceleration, yaw rate, and jerk to ensure the planned motion is smooth and comfortable for passengers. The online MPC optimization explicitly quantifies comfort by measuring peak acceleration/jerk and an integrated discomfort cost for each maneuver. The MPC-based planner respects vehicle actuator limits and traffic rules.
- (4)
- Evaluation Using INTERACTION Dataset. Two challenging intersection scenarios are extracted from the INTERACTION dataset: (1) an all-way stop intersection, and (2) an unprotected left turn scenario with oncoming traffic. The motion planning algorithm built upon the integrated multi-modal trajectory predictor and the MPC-based planner is evaluated using the two extracted interaction scenarios individually. Using the highly interactive driving scenarios will ensure the testing behaviors (aggressive cross traffic, rolling stops, etc.) are representative and realistic. Our multi-modal trajectory planning will be compared against a baseline for predicting a single trajectory per road user.
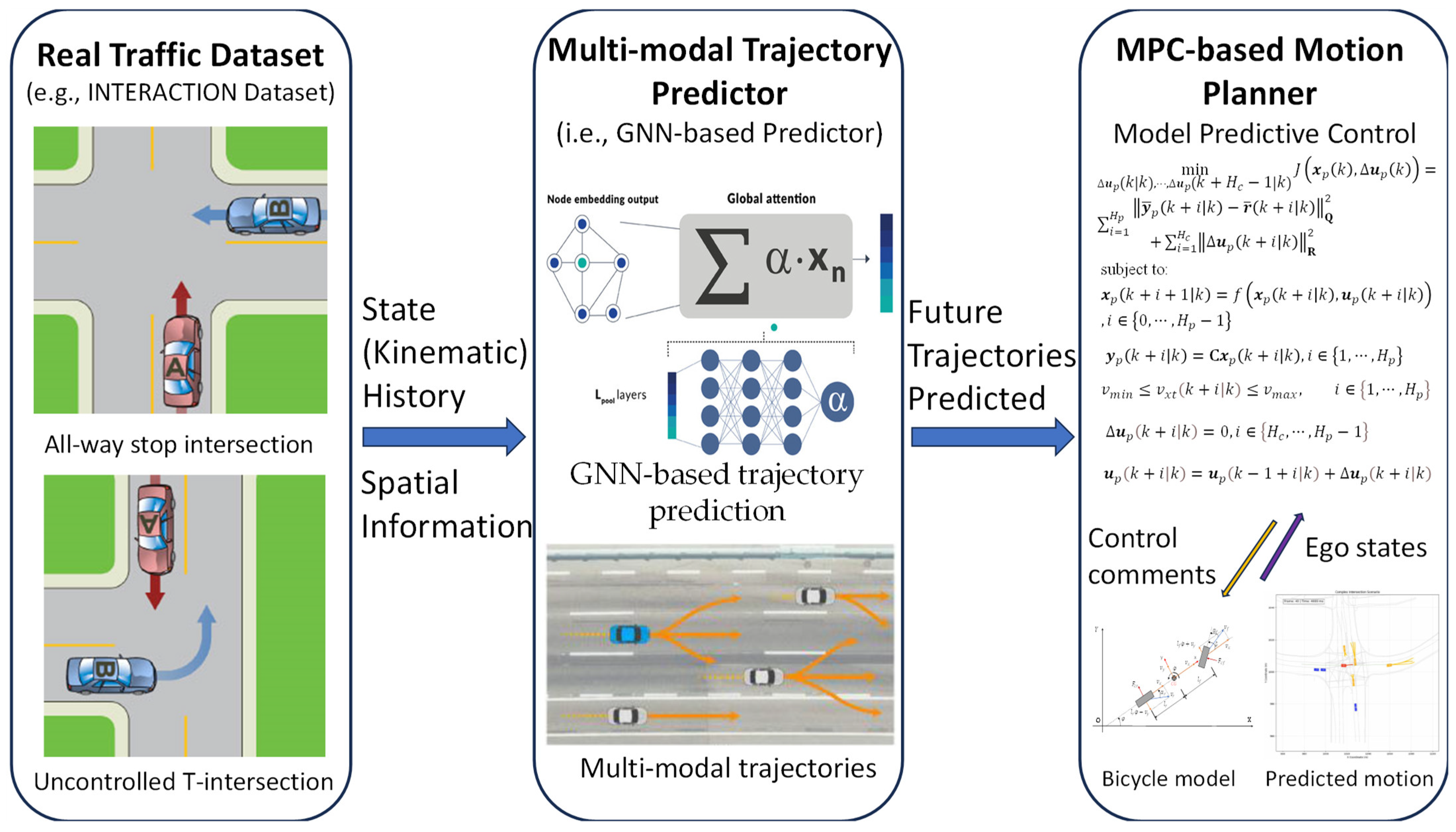
2. Architecture of Integrated Motion Planning Algorithm
3. GNN-Based Multi-Modal Trajectory Predictor
3.1. Input Representation and Encoding
3.2. Graph Neural Network for Modeling Interactions Among Agents
3.3. Training and Validation
4. MPC-Based Motion Planner
4.1. Vehicle Kinematics Model
4.2. Constraints on Collision Avoidance and Traffic Rules
- (1)
- Collision Avoidance Constraints. It is required that for all considered future modes of the other road users, the ego vehicle does not collide with any one of them along the planned trajectory. Thanks to the GNN-based predictor, three possible trajectories are predicted for each agent . Let denote the predicted position of agent at the -th time step in mode m. Each vehicle is modeled as a circle of radius that bounds its dimensions (for a pedestrian, a smaller radius is used). The ego vehicle is similarly bounded by a radius . A simple sufficient condition to avoid collision between the ego vehicle and agent at time step iswhere is the ego vehicle’s position at sampling time , and represent three trajectories of agent under consideration. This constraint enforces that the distance between the ego vehicle center and the agent center at sampling time is larger than the sum of their radii, thus no overlap occurs. In the implementation, (approximating half the vehicle width plus some buffer), and for other vehicles is also set to 1.5 m (slightly less than half the length of a car, since this is a conservative circle bound). Pedestrians, if present, are given Ri approximately 0.5 m.
- (2)
- Lane-Keeping and Road Boundary Constraints. The ego vehicle should stay within drivable boundaries. In an intersection, it is assumed that a reference path (either straight through or a left-turn path) lies within the correct lane. The lateral deviation is constrained by this reference. Specifically, a maximum permitted lateral deviation of 0.5 m is set to either side of the nominal path centerline (ensuring the vehicle remains roughly in its lane). In the straight driving scenario, this means . In the left turn, the path is curving; it is handled by computing the closest point on the reference path to the vehicle and enforcing a similar offset limit. This can be linearized per time step if needed, but since 0.5 m is small, a simple iterative check after solving works (the solver naturally won’t stray far due to large costs if it does).
- (3)
- Kinematic and Actuator Constraints. Bounds on the control inputs are included to respect the vehicle’s physical limits. The acceleration is limited by at all sampling time . Considering ride comfort and hard braking limit, the acceleration bounds are set: (comfortable acceleration) and (hard braking). The front-wheel steering angle is limited to with the bounds , which is consistent with the steering angle range of a car. Moreover, the steering angle rate is implicitly limited by including a jerk penalty. Vehicle forward speed at urban unsignalized intersections is constrained by with .
- (4)
- Traffic Rules. As discussed above, traffic rules like stop sign compliance are largely handled by combining collision avoidance and cost tuning (stopping is strongly encouraged when another agent has right-of-way). However, it is explicitly ensured that the ego vehicle halts at a stop sign before entering the intersection by setting a desired zero speed at the stop line. In the all-way stop scenario, when the ego vehicle’s front bumper reaches the stop line based on the known location from the map, a temporary constraint, , is introduced. This effectively forces the planner to include a stopping maneuver if required. In scenarios where the ego vehicle has clear right-of-way without conflicting road users, this constraint can be lifted. In the unprotected left turn scenario, the ego vehicle can only go while the intersection is clear; the rule is thus simply to yield to oncoming vehicles, which is inherently achieved via collision constraints with those oncoming trajectories.
4.3. Objective Function and Comfort Terms
- Path tracking terms, , penalizes deviation from the reference path. is the target point on the reference path at sampling time . In practice, lateral and longitudinal errors are separated; lateral deviation is heavily penalized (to keep the ego vehicle within the lane), while longitudinal position error is less critical (as long as timing might differ); but for simplicity, they are lumped with weight. penalizes heading error relative to the reference path orientation. These ensure the ego vehicle follows the intended path geometry.
- Speed term, , penalizes speed deviation from a reference . Typically, reference speed, , is set to a desired cruising speed, e.g., 8 m/s for approaching an intersection or 0 m/s if the vehicle is expected to stop. In the stop sign scenario, reference speed, , is set to 0 m/s near the stop line, and then might be set to 5 m/s after the stop line (if proceeding). In the left-turn scenario, reference speed, , could be a comfortable turn speed of 5 m/s.
- Control effort terms, and penalize using high acceleration and large steering angles. These terms indirectly encourage less energy consumption and smooth motions with good ride comfort. Moreover, these terms also serve to avoid extreme inputs if not needed.
- Smoothness (jerk) terms, , penalizes rapid changes in acceleration, i.e., longitudinal jerk, while yaw jerk, , penalizes rapid steering changes. These terms significantly influence passenger comfort by smoothing out the trajectory. They also help produce realistic behavior (no sudden hard braking or abrupt steering unless necessary).
- Soft constraint penalty, , penalizes any slack introduced in the alternative-mode collision constraints. The weighting factor, , is selected to be a very large number for effectively making slack usage highly undesirable. In our experiments, is on the order of , which is much larger than other weights.
4.4. Predictor and Planner Integration and Execution
5. Experimental Results
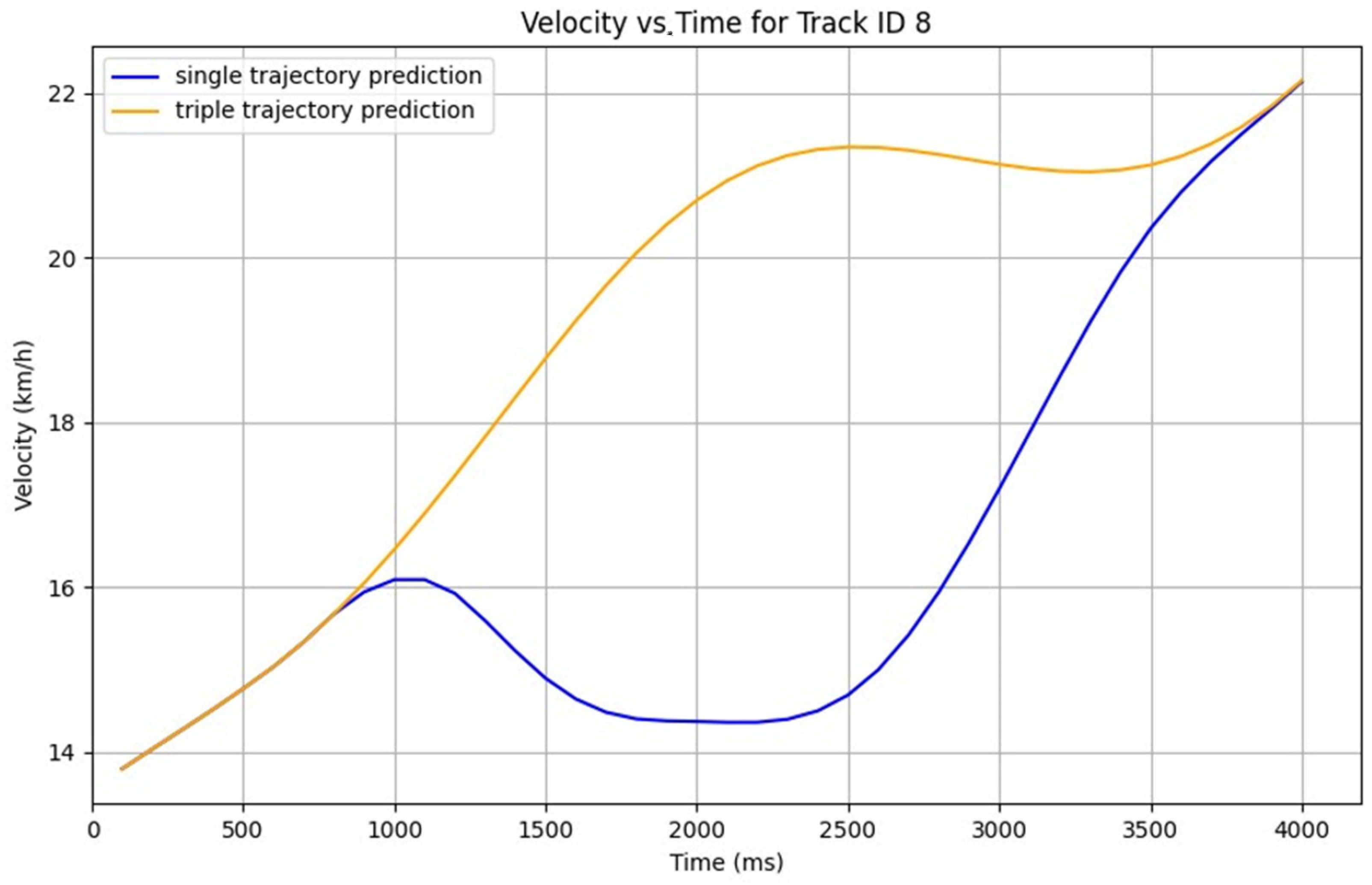
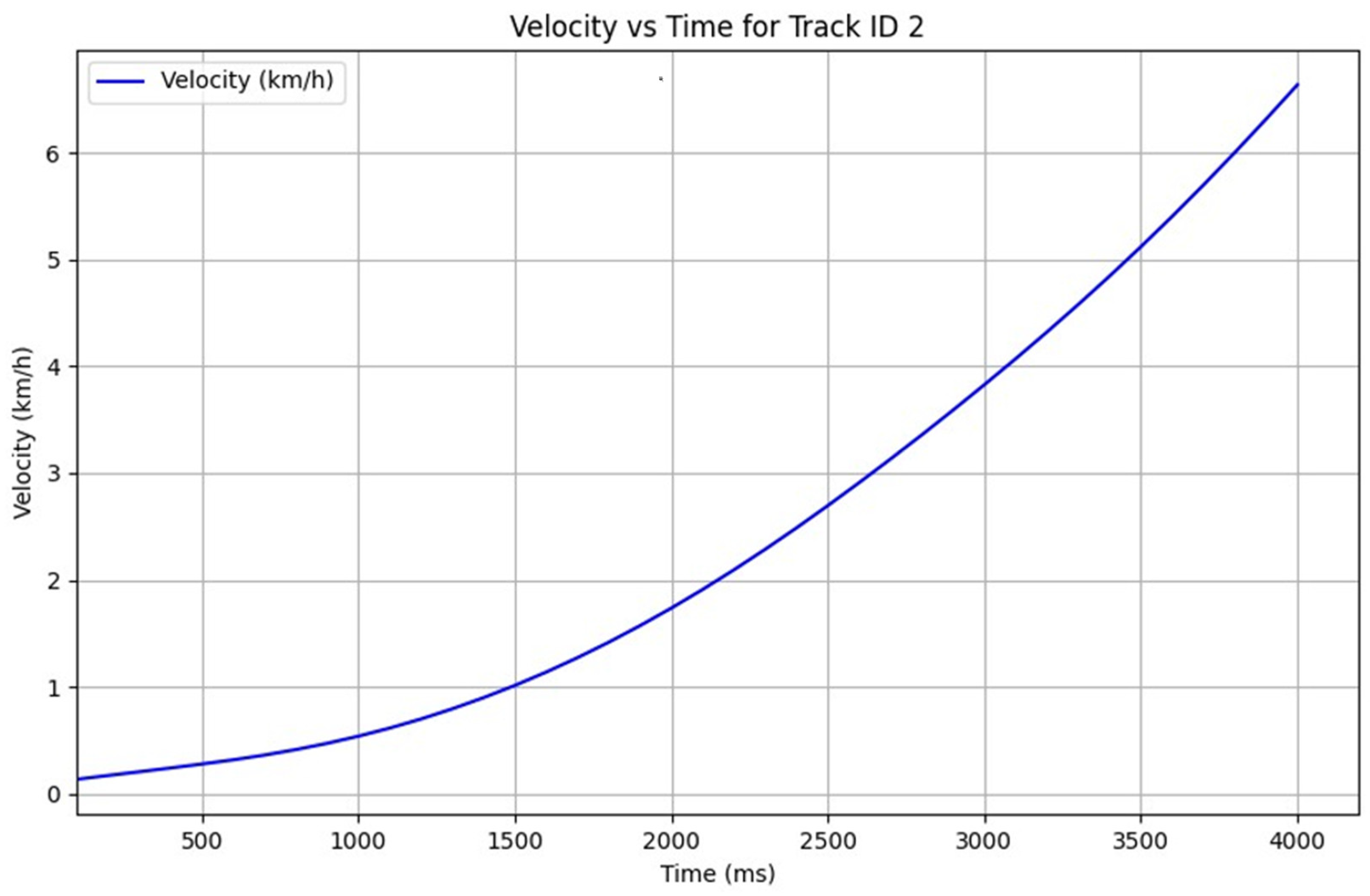
5.1. Trajectory Prediction Performance
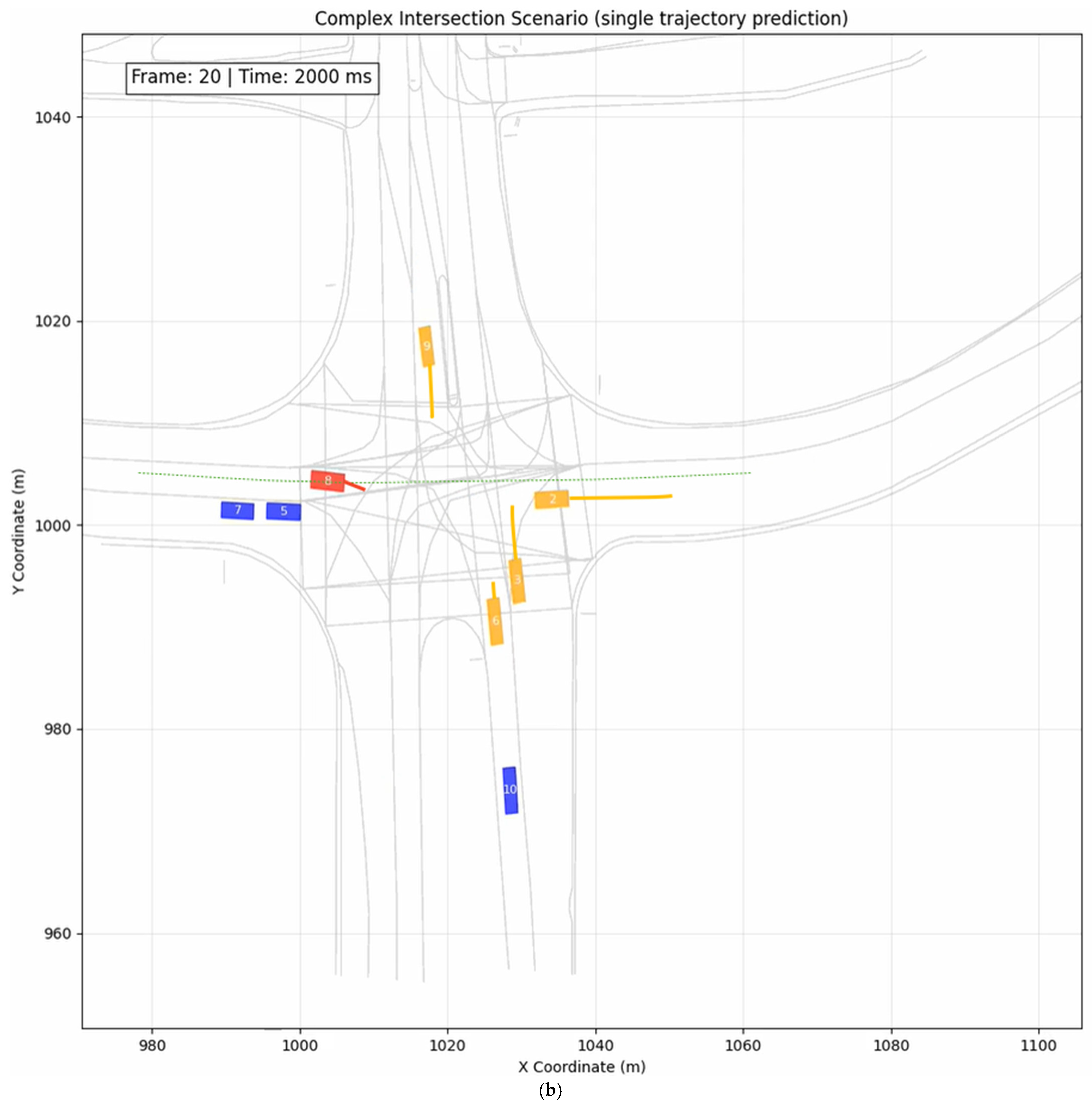
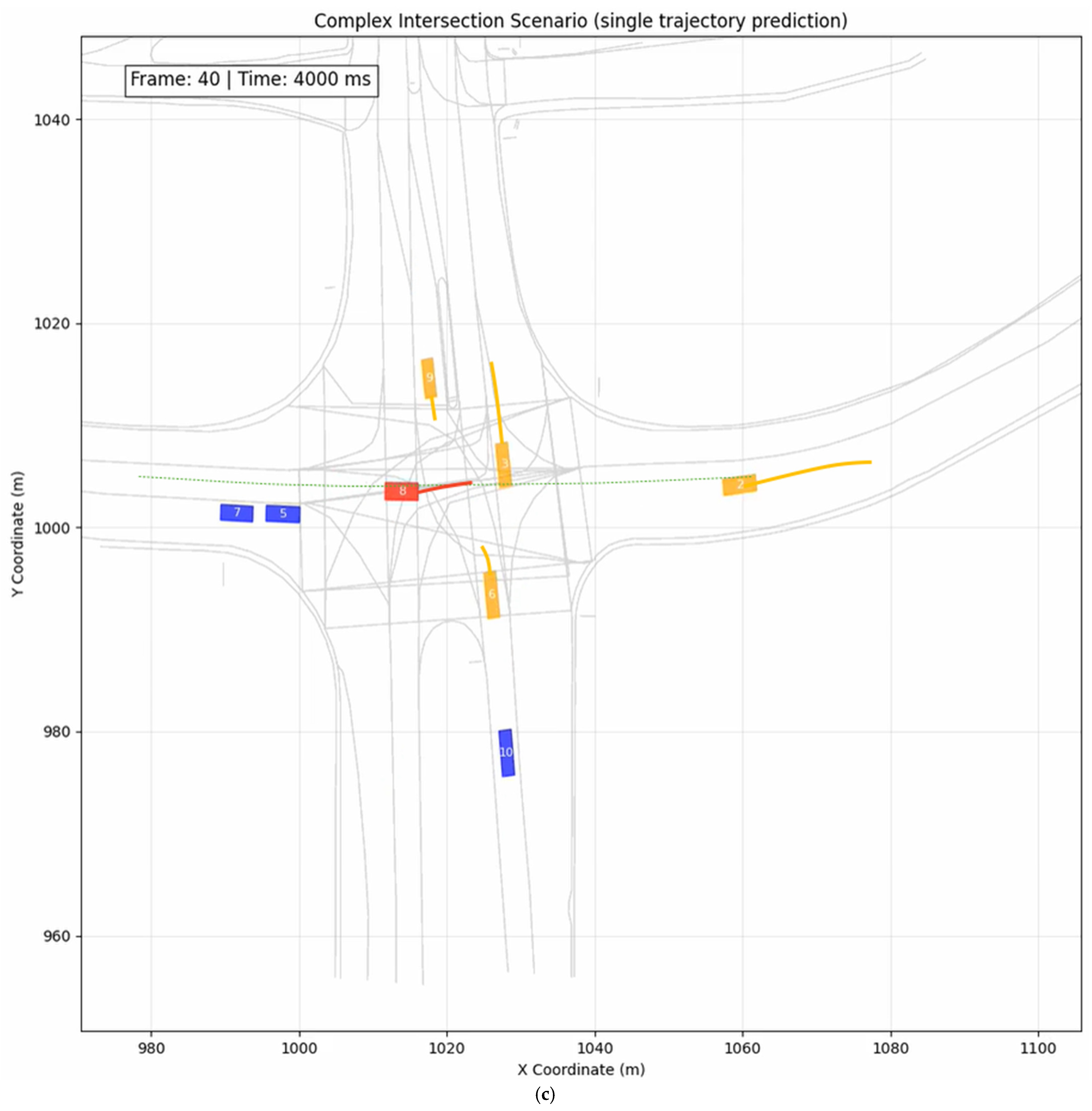
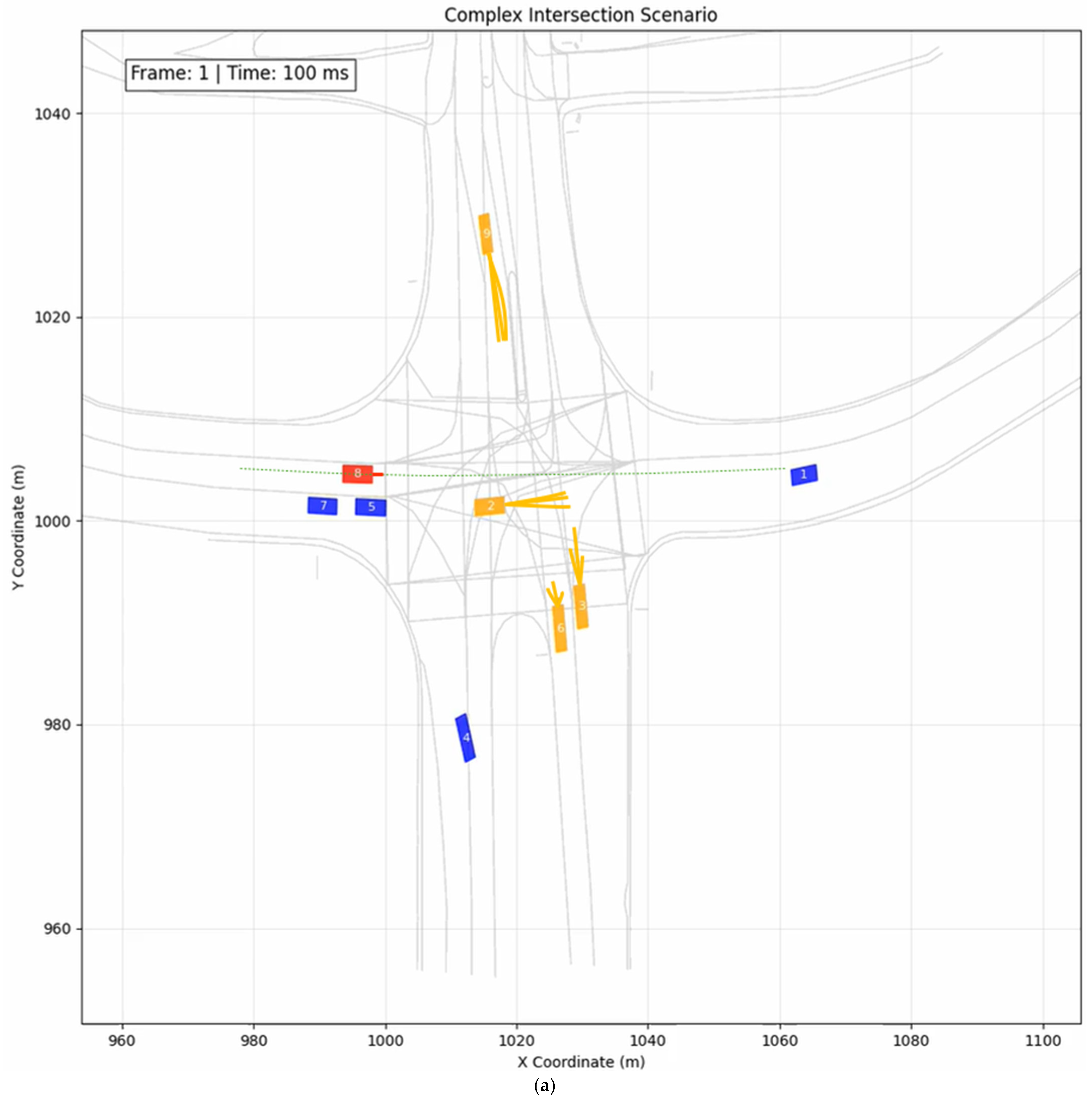
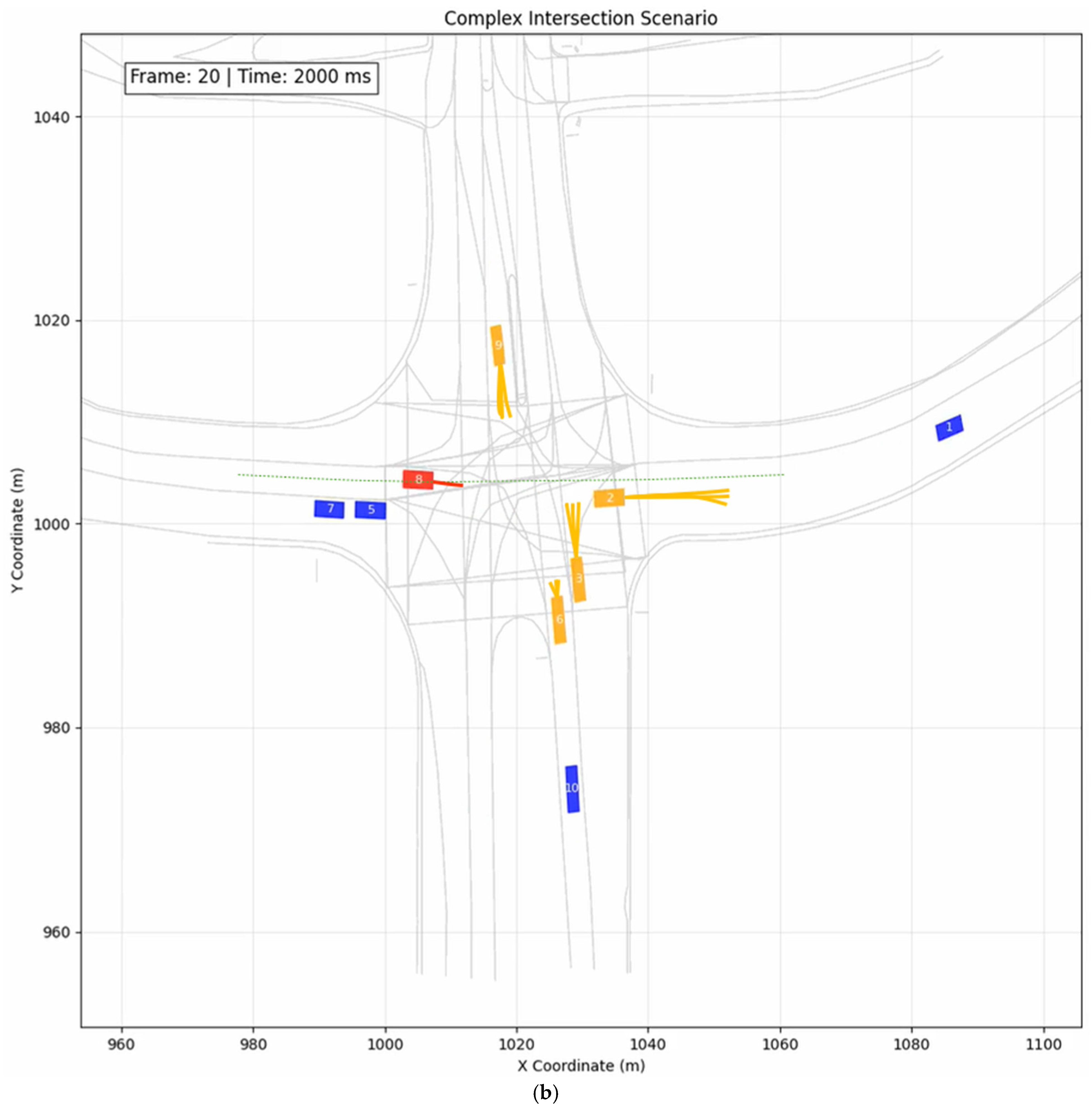
5.2. Case Study 1: All-Way Stop Intersection
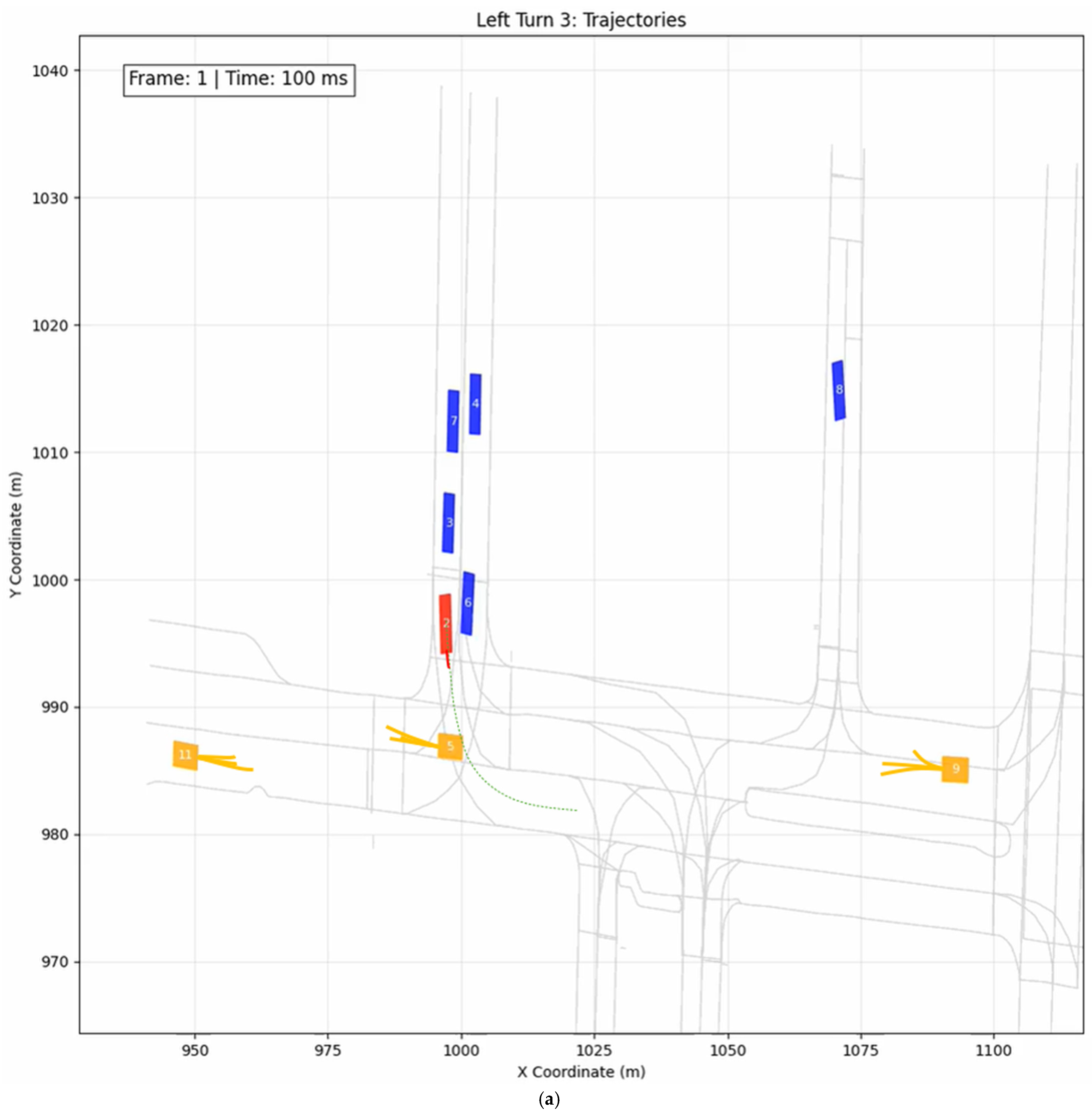
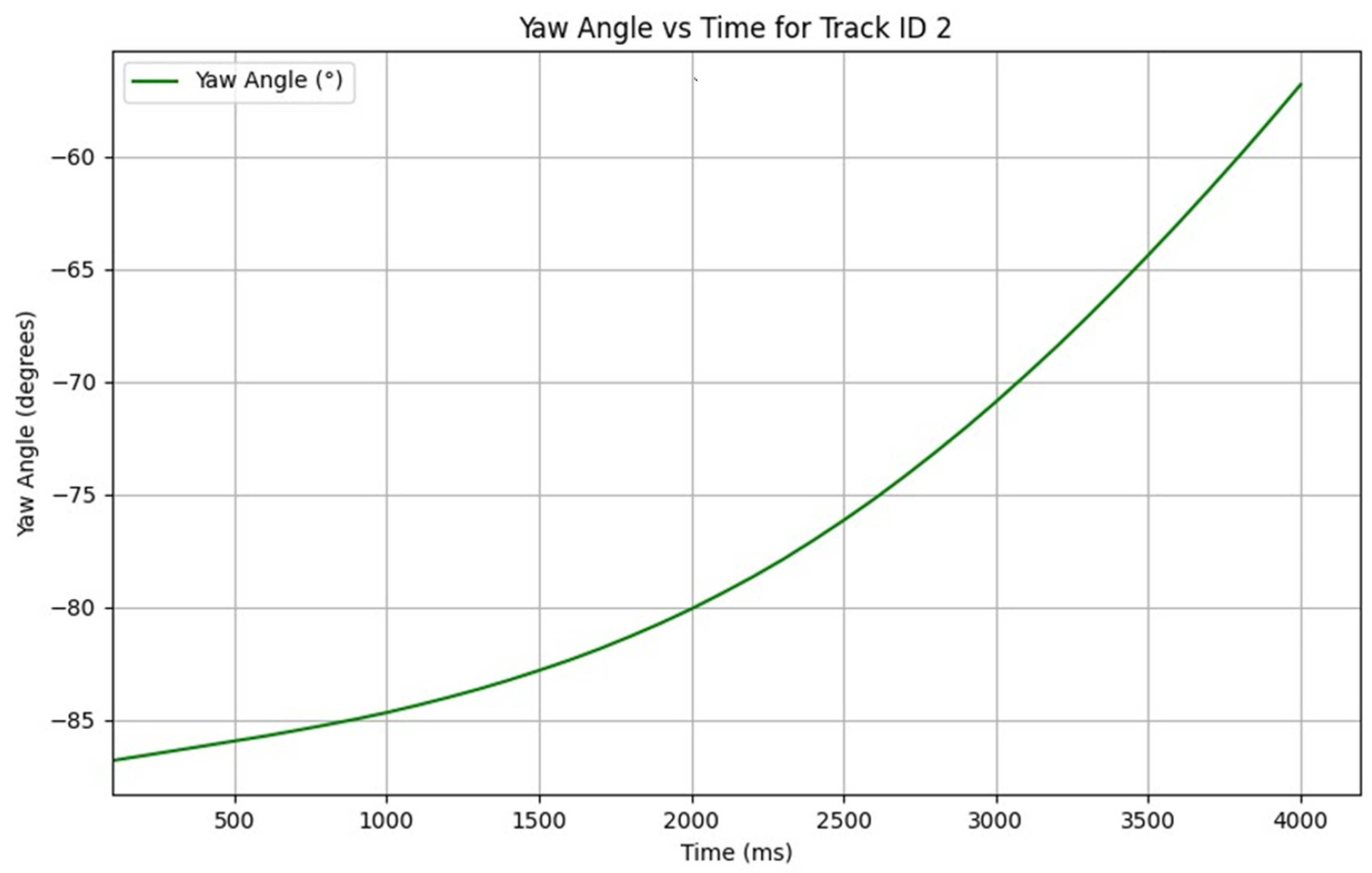
5.3. Case Study 2: Unprotected Left Turn
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
- Trajectory Prediction (GNN-based Multi-Modal Prediction)
- 2.
- Motion Planning (NMPC with IPOPT)
- 3.
- End-to-End Framework Complexity
References
- Yang, K.; Tang, X.; Li, J.; Wang, H.; Zhong, G.; Chen, J. Uncertainties in Onboard Algorithms for Autonomous Vehicles: Challenges, Mitigation, and Perspectives. IEEE Trans. Intell. Transp. Syst. 2023, 24, 8963–8987. [Google Scholar] [CrossRef]
- Sánchez, M.M.; Silvas, E.; Elfring, J.; van de Molengraft, R. Robustness Benchmark of Road User Trajectory Prediction Models for Automated Driving. IFAC-PapersOnLine 2023, 56, 4865–4870. [Google Scholar] [CrossRef]
- Zhang, X.; Zeinali, S.; Schildbach, G. Interaction-aware Traffic Prediction and Scenario-based Model Predictive Control for Autonomous Vehicle on Highways. In Proceedings of the 2024 European Control Conference (ECC), Stockholm, Sweden, 25–28 June 2024; pp. 3344–3350. [Google Scholar]
- Aradi, S. Survey of Deep Reinforcement Learning for Motion Planning of Autonomous Vehicles. IEEE Trans. Intell. Transp. Syst. 2022, 23, 740–759. [Google Scholar] [CrossRef]
- Paden, B.; Čáp, M.; Yong, S.Z.; Yershov, D.; Frazzoli, E. A Survey of Motion Planning and Control Techniques for Self-driving Urban Vehicles. IEEE Trans. Intell. Veh. 2016, 1, 33–55. [Google Scholar] [CrossRef]
- Schwarting, W.; Alonso-Mora, J.; Rus, D. Planning and Decision-making for Autonomous Vehicles. Annu. Rev. Control Robot. Auton. Syst. 2018, 1, 187–210. [Google Scholar] [CrossRef]
- Xin, L.; Wang, P.; Chan, C.Y.; Chen, J.; Li, S.E.; Cheng, B. Intention-aware Long Horizon Trajectory Prediction of Surrounding Vehicles Using Dual LSTM Networks. In Proceedings of the 2018 21st International Conference on Intelligent Transportation Systems (ITSC), Maui, HI, USA, 4–7 November 2018; pp. 1441–1446. [Google Scholar]
- Deo, N.; Trivedi, M.M. Convolutional Social Pooling for Vehicle Trajectory Prediction. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR) Workshops, Salt Lake City, UT, USA, 18–22 June 2018; pp. 1468–1476. [Google Scholar]
- Diehl, F.; Brunner, T.; Le, M.T.; Knoll, A. Graph Neural Networks for Modelling Traffic Participant Interaction. In Proceedings of the 2019 IEEE Intelligent Vehicles Symposium (IV), Paris, France, 9–12 June 2019; pp. 695–701. [Google Scholar]
- Mo, X.; Huang, Z.; Xing, Y.; Lv, C. Multi-agent Trajectory Prediction with Heterogeneous Edge-enhanced Graph Attention Network. IEEE Trans. Intell. Transp. Syst. 2022, 23, 9554–9567. [Google Scholar] [CrossRef]
- Sun, Q.; Huang, X.; Gu, J.; Williams, B.C.; Zhao, H. M2I: From Factored Marginal Trajectory Prediction to Interactive Prediction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; pp. 6533–6542. [Google Scholar]
- Gautam, A.; He, Y.; Lin, X. An Overview of Motion-planning Algorithms for Autonomous Ground Vehicles with Various Applications. SAE Int. J. Veh. Dyn. Stab. NVH 2024, 8, 179–213. [Google Scholar] [CrossRef]
- Qian, X.; Navarro, I.; de La Fortelle, A.; Moutarde, F. Motion Planning for Urban Autonomous Driving Using Bezier Curves and MPC. In Proceedings of the 2016 IEEE 19th International Conference on Intelligent Transportation Systems (ITSC), Rio de Janeiro, Brazil, 1–4 November 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 826–833. [Google Scholar]
- Sharma, T.; He, Y. Design of a Tracking Controller for Autonomous Articulated Heavy Vehicles Using a Nonlinear Model Predictive Control Technique. Proc. Inst. Mech. Eng. Part. K J. Multibody Dyn. 2024, 238, 334–362. [Google Scholar] [CrossRef]
- Rasekhipour, Y.; Khajepour, A.; Chen, S.K.; Litkouhi, B. A Potential Field-based Model Predictive Path-planning Controller for Autonomous Road Vehicles. IEEE Trans. Intell. Transp. Syst. 2016, 18, 1255–1267. [Google Scholar] [CrossRef]
- Testouri, M.; Elghazaly, G.; Frank, R. Towards a Safe Real-Time Motion Planning Framework for Autonomous Driving Systems: A Model Predictive Path Integral Approach. In Proceedings of the 2023 3rd International Conference on Robotics, Automation and Artificial Intelligence (RAAI), Singapore, 14–16 December 2023; pp. 231–238. [Google Scholar]
- Bae, S.; Isele, D.; Nakhaei, A.; Xu, P.; Añon, A.M.; Choi, C. Lane-change in Dense Traffic with Model Predictive Control and Neural Networks. IEEE Trans. Control. Syst. Technol. 2023, 31, 646–659. [Google Scholar] [CrossRef]
- Sheng, Z.; Liu, L.; Xue, S.; Zhao, D.; Jiang, M.; Li, D. A Cooperation-aware Lane Change Method for Automated Vehicles. IEEE Trans. Intell. Transp. Syst. 2023, 24, 3236–3251. [Google Scholar] [CrossRef]
- Gupta, P.; Isele, D.; Lee, D.; Bae, S. Interaction-aware Trajectory Planning for Autonomous Vehicles with Analytic Integration of Neural Networks into Model Predictive Control. In Proceedings of the 2023 IEEE International Conference on Robotics and Automation (ICRA), London, UK, 29 May–2 June 2023; pp. 7794–7800. [Google Scholar]
- INTERACTION Dataset. 2025. Available online: https://interaction-dataset.com/ (accessed on 19 July 2025).
- Zhan, W.; Sun, L.; Wang, D.; Shi, H.; Clausse, A.; Naumann, M.; Kummerle, J.; Konigshof, H.; Stiller, C.; de La Fortelle, A.; et al. INTERACTION Dataset: An International, Adversarial and Cooperative Motion Dataset in Interactive Driving Scenarios with Semantic Maps. arXiv 2019, arXiv:1910.03088. [Google Scholar] [CrossRef]
- The Autoware Foundation. Available online: https://autoware.org/ (accessed on 20 July 2025).
- Pivtoraiko, M.; Kelly, A. Generating Near Minimal Spanning Control Sets for Constrained Motion Planning in Discrete State Spaces. In Proceedings of the 2005 IEEE/RSJ International Conference on Intelligent Robots and Systems, Edmonton, AB, Canada, 2–6 August 2005; IEEE: Piscataway, NJ, USA, 2005; pp. 3231–3237. [Google Scholar]
- Andersson, J.; Gillis, J. CasADi Documentation (PDF version). Release 3.7.1. 23 July 2025. Available online: https://web.casadi.org/docs/ (accessed on 26 July 2024).
- IPOPT Documentation. Available online: https://coin-or.github.io/Ipopt/index.html (accessed on 25 June 2024).
- Bi-Directional Gated Recurrent Unit. Available online: https://www.sciencedirect.com/topics/computer-science/bi-directional-gated-recurrent-unit (accessed on 26 June 2024).
- Gao, J.; Sun, C.; Zhao, H.; Shen, Y.; Anguelov, D.; Li, C.; Schmid, C. VectorNet: Encoding HD Maps and Agent Dynamics from Vectorized Representation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 11525–11533. [Google Scholar]
- Mao, C.; He, Y.; Agelin-Chaab, M. A Design Method for Road Vehicles with Autonomous Driving Control. Actuators 2024, 13, 427. [Google Scholar] [CrossRef]





| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Distance between vehicle CG and its front axle | 1.33 m | Distance between vehicle CG and its front axle | 1.81 m |
| Radius of circle representing ego vehicle | 1.5 m | Radius of circle representing vehicle | 1.5 m |
| Total number of sampling time step | 15 | Duration of one-time step | 0.2 s |
| Maximum acceleration | Maximum deceleration | ||
| Maximum front-wheel steering angle | Maximum vehicle forward-speed | ||
| Maximum permitted lateral deviation | Required ego vehicle speed at stop | 0.0 m/s | |
| Reference ego vehicle speed for different cases * | Prediction horizon | 15 | |
| Control horizon | 15 | Weighting factor for position deviation | 130 |
| Weighting factor for heading angle deviation | 130 | Weighting factor for speed deviation | 4 |
| Weighting factor for acceleration | 6 | Weighting factor for steering angle | 100 |
| Weighting factor for acceleration variation | 50 | Weighting factor for steering angle variation | 10 |
| Weighting factor for slack term |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gautam, A.; He, Y.; Lin, X. Motion Planning for Autonomous Driving in Unsignalized Intersections Using Combined Multi-Modal GNN Predictor and MPC Planner. Machines 2025, 13, 760. https://doi.org/10.3390/machines13090760
Gautam A, He Y, Lin X. Motion Planning for Autonomous Driving in Unsignalized Intersections Using Combined Multi-Modal GNN Predictor and MPC Planner. Machines. 2025; 13(9):760. https://doi.org/10.3390/machines13090760
Chicago/Turabian StyleGautam, Ajitesh, Yuping He, and Xianke Lin. 2025. "Motion Planning for Autonomous Driving in Unsignalized Intersections Using Combined Multi-Modal GNN Predictor and MPC Planner" Machines 13, no. 9: 760. https://doi.org/10.3390/machines13090760
APA StyleGautam, A., He, Y., & Lin, X. (2025). Motion Planning for Autonomous Driving in Unsignalized Intersections Using Combined Multi-Modal GNN Predictor and MPC Planner. Machines, 13(9), 760. https://doi.org/10.3390/machines13090760









