Towards Robust Industrial Control Interpretation Through Comparative Analysis of Vision–Language Models

Abstract

Industrial environments frequently rely on analog control instruments due to their reliability and robustness; however, automating the interpretation of these controls remains challenging due to variability in design, lighting conditions, and scale precision requirements. This research investigates the effectiveness of Vision–Language Models (VLMs) for automated interpretation of industrial controls through analysis of three distinct approaches: general-purpose VLMs, fine-tuned specialized models, and lightweight models optimized for edge computing. Each approach was evaluated using two prompting strategies, Holistic-Thought Protocol (HTP) and sequential Chain-of-Thought (CoT), across a representative dataset of continuous and discrete industrial controls. The results demonstrate that the fine-tuned Generative Pre-trained Transformer 4 omni (GPT-4o) significantly outperformed other approaches, achieving low Mean Absolute Error (MAE) for continuous controls and the highest accuracy and Matthews Correlation Coefficient (MCC) for discrete controls. Fine-tuned models demonstrated less sensitivity to prompt variations, enhancing their reliability. In contrast, although general-purpose VLMs showed acceptable zero-shot performance, edge-optimized models exhibited severe limitations. This work highlights the capability of fine-tuned VLMs for practical deployment in industrial scenarios, balancing precision, computational efficiency, and data annotation requirements.

1. Introduction

Industrial control systems form the backbone of modern manufacturing and automation, where precise interpretation of analog controls is essential to ensure operational integrity and safety. Industrial environments employ diverse instrumentation, ranging from basic pressure gauges to sophisticated multi-parameter monitoring systems [1]. Despite the proliferation of digital instrumentation and Industry 4.0 initiatives, analog controls are prevalent in industrial settings due to their inherent reliability, mechanical robustness, and cost-effectiveness [2]. The persistence of these analog instruments, however, presents significant challenges for automation initiatives, as their manual interpretation remains labor-intensive, susceptible to human error, and poses considerable obstacles to integration with current automated monitoring systems and industrial Internet of Things (IIoT) frameworks [3].

Automated interpretation of analog controls encompasses a complex set of technical challenges that span multiple domains of Computer Vision (CV) and Machine Learning (ML). These challenges include non-uniform illumination, specular reflections that obscure readings, heterogeneous control designs with varying scales and units, and the need for high-precision measurements [4]. Traditional CV methodologies, including techniques such as Hough transforms for circle and gradient-based edge detection, have demonstrated significant limitations in addressing these variations [5]. These approaches particularly struggle with legacy equipment featuring non-standardized designs, varying scales, and degraded visual elements, common in industrial settings with equipment spanning multiple decades of deployment [6]. Even specific Deep Learning (DL) implementations, like Convolutional Neural Networks (CNNs), that have exhibited remarkable capabilities in complex image recognition and interpretation tasks [7], face significant challenges: they often demand high computational resources, struggle with cross-domain generalization across diverse control types, exhibit performance degradation under varying environmental conditions, and necessitate extensive gauge-specific training datasets [8,9]. Beyond technical performance metrics, integrating these solutions into existing industrial infrastructure presents further challenges encompassing system reliability, maintenance requirements, and compatibility with existing industrial communication protocols and control systems, particularly in brownfield installations where legacy systems predominate [10]. A research gap thus persists in developing inclusive solutions for industrial control interpretation that successfully balance robustness, efficiency, and adaptability.

Recent work by Bommasani et al. [11] on foundation models has presented novel opportunities for addressing these challenges in industrial control interpretation, since they can transfer knowledge across different applications without extensive retraining. Pre-trained on diverse domains, Vision–Language Models (VLMs) demonstrate promising capabilities in zero-shot and few-shot learning scenarios that could circumvent the need for control-specific training data [12]. These models exhibit remarkable semantic understanding capabilities, facilitating more robust interpretation across varying control designs and environmental conditions; however, the computational demands of such models present significant implementation challenges in resource-limited industrial environments [13]. The emergence of specialized edge-computing VLMs offers a compelling direction for practical deployment scenarios. Recent advances in model quantization, neural architecture search, and hardware-aware model design have enabled the development of compact yet powerful VLMs suitable for edge deployment [14]. Furthermore, Matryoshka representation enable the extraction of multiple model variants from a single trained model, allowing adaptive computational allocation based on real-time resource constraints without sacrificing performance [15].

This work presents several contributions to the domain of industrial control interpretation. This study advances the field through a global comparative analysis across three distinct methodological approaches: (1) general-purpose VLMs in their base configuration, evaluating their capabilities and limitations in control interpretation tasks; (2) a domain-specialized fine-tuned variant of these models, optimized for industrial control interpretation; and (3) edge-computing solutions. Moreover, this research encompasses two critical dimensions of prompt engineering: Holistic-Thought Protocol (HTP) versus sequential Chain-of-Thought (CoT) approaches, providing insights into optimal interaction strategies. This in-depth analysis yields detailed insights into each approach’s operational characteristics and limitations, concluding in a decision-making methodology for selecting better interpretation strategies based on specific industrial requirements.

2. Related Work

Automating analog gauge reading has evolved from classical CV methods to sophisticated DL-based frameworks. Early approaches relied on hand-crafted feature extraction, e.g., detecting gauge outlines and needles via Hough transforms or edge detection, combined with geometric reasoning to infer readings [16,17]. However, such methods proved fragile under real-world glare, variable lighting, and diverse dial designs [18]. To overcome these limitations, recent works have turned to data-driven DL models. For example, Sun et al. introduced a multi-stage CNN-based framework for robust pointer meter reading under challenging conditions [19]. Their system uses an object detector (YOLOv4) to localize the gauge, then applies semantic segmentation to isolate the pointer, Optical Character Recognition (OCR) to read scale markings, and a custom CNN to regress the needle angle, ultimately calculating the meter value. This approach achieved high accuracy and robustness in industrial scenarios by decomposing the problem into subtasks handled by specialized DL models, outperforming earlier single-stage methods. Similarly, Laroca et al. developed an Automatic Meter Reading (AMR) system that utilizes CNNs to recognize discrete meter displays (e.g., digital or dial counters) with high accuracy [20]. They designed a two-stage pipeline: a Fast-YOLO detector first identifies the meter region, and then a CNN reads the meter digits. A notable contribution of Laroca’s work was the introduction of the UFPR-AMR dataset with 2000 annotated meter images along with data augmentation techniques to expand training examples. This dataset and synthetic augmentation enabled the training of robust models. They demonstrated that state-of-the-art results could be achieved with as few as 200 real training images, mitigating the longstanding issue of limited public data. Data scarcity remains a challenge; as Alcazar et al. observe, analog gauge datasets are still relatively small and costly to annotate compared to standard vision benchmarks [4]. To address this, the authors proposed generating synthetic training data for gauges. They created a realistic synthetic dataset of analog gauge images with ground-truth annotations. They used it to train a two-stage CNN pipeline that detects key gauge components and predicts the needle angle. When evaluated on a real-world dataset of 4813 industrial gauge images, their method significantly outperformed prior methods, reducing average reading error by 4.55° (a 52% relative improvement). This result underlines how simulation-to-real transfer and domain augmentation can overcome data annotation bottlenecks. Other recent efforts emphasize the interpretability and reliability of the reading process. Reitsma et al. developed an interpretable gauge-reading framework for robotics that splits the task into distinct learned steps (gauge detection, scale recognition, needle segmentation, and others) [21]. This modular design allows verification at each step, improving reliability for real-world deployment. Principally, their system does not require prior knowledge of the gauge type or scale range, enabling broad applicability across many instruments. They report a relative reading error under 2% in diverse real-world conditions, demonstrating that a careful combination of DL and geometric reasoning can yield both accuracy and robustness. Despite these advances in CNN-based solutions, challenges remain in generalizing across different gauge styles and reducing the effort of dataset collection and annotation for each new instrument type. These challenges motivate the exploration of more generalizable vision models and few-shot/zero-shot learning approaches.

In parallel with CNN progress, transformer-based architectures and multimodal models have begun to redefine visual recognition tasks, including those in industrial domains. The Vision Transformer (ViT) introduced a self-attention-based network for image classification, dispensing convolution and demonstrating that sufficiently large transformer models can achieve parity with CNNs on vision tasks [22]. Subsequent variants like the Swin Transformer (Swin-ViT) adopted hierarchical feature maps and shifted window attention to improve efficiency and locality, achieving state-of-the-art performance on image benchmarks while reducing computation [23]. The ability of transformers to capture long-range dependencies and global context is especially relevant for complex scenes like control panels, where a model might need to relate the needle position with distant scale markings on a gauge. Gao et al. investigated the application of Large Language Models (LLMs) to spoken language learning, revealing that while LLMs excel at extracting conceptual knowledge, application tasks requiring complex reasoning remain challenging [24]. Their comprehensive evaluation using various prompting strategies (zero-shot, few-shot, and CoT) across 20 distinct models showed that domain-specific fine-tuning significantly improved performance, achieving notable improvements in accuracy when models were fine-tuned with in-domain examples. Wang and Shen evaluated causal reasoning capabilities of LLMs across multiple scenarios, finding that most models encounter challenges in causal cognition despite various prompting schemes [25]. These findings suggest that enhancing cognitive reasoning capabilities remains crucial for complex industrial interpretation tasks. Beyond vision-only architectures, VLMs have emerged that jointly learn from images and text in the shape of captions or labels. Seminal works such as Contrastive Language–Image Pre-training (CLIP) by Radford et al. [26] and by Jia et al. [27] demonstrated that models trained with natural language supervision can learn highly transferable visual representations, enabling zero-shot recognition of new image categories via textual prompts. In CLIP, for instance, an image of a gauge can be associated with text descriptions (e.g., “a pressure gauge reading 50 PSI”), and the model can predict which description matches the image without explicit retraining on gauge data. Such capabilities suggest that pre-trained VLMs might interpret industrial gauges or indicators using their visual knowledge, even if they have never seen those devices during training. Recent contributions reinforce this trend from different angles. Punnaivanam and Velvizhy show that contextual fine-tuning combined with a classifier layer improves reliability in generative tasks [28], a principle that can be extended to industrial VLMs where safety and domain consistency are essential. Trad and Chehab compare prompt engineering against fine-tuning for phishing detection, finding that task-specific fine-tuned LLMs consistently outperform base LLMs [29], suggesting that their results parallel the trade-off between prompt-based strategies and domain-specialized VLMs in other contexts. Yang et al. propose Conditional Cross-Modal Learning (CoCM), a framework that adaptively fuses visual and textual caches, achieving improved accuracy and cross-domain generalization [30], thus aligning with the need for VLMs capable of handling the variability of industrial environments. Bommasani et al. discuss the potential and pitfalls of these foundation models, noting their promise for domains like industrial control where domain-specific data are scarce [11]. The large-scale pre-training imbues them with a general visual understanding that, in principle, could be specialized to gauge reading with minimal additional data. Indeed, recent multimodal models are surprisingly capable: Generative Pre-trained Transformer 4 omni (GPT-4o) and Google’s PaLI can perform image understanding tasks such as reading clock faces, deciphering handwritten notes, or describing the content of diagrams in a zero-shot manner [31]. These models combine an LLM with visual inputs, allowing complex reasoning about images. For example, GPT-4o can answer questions like “What value does this analog gauge show?” by parsing the image and harnessing world knowledge about gauge semantics. Such reasoning was previously rare in traditional vision models. However, applying these models to industrial control interpretation is not straightforward. One challenge is prompt engineering, that is, how to effectively query or instruct the model. A naïve prompt might yield an incorrect or overly general answer. In comparison, a carefully crafted prompt that guides the model (e.g., asking it to identify the scale, and then, the needle position) can significantly improve accuracy. There is active research into multimodal CoT reasoning, where a VLM is prompted to generate step-by-step “explanations” when answering visual questions. This approach can help the model break down complex tasks into intermediate steps, improving the reliability of the final answer [32]. Another challenge is that the knowledge of these models may not perfectly cover specialized industrial visuals; for instance, an unusual gauge might confuse a model that has mostly seen common objects. Fine-tuning the model on a few examples of the new instrument can help, but fine-tuning large transformers is resource-intensive and risks overfitting if data are minimal. In summary, transformers and VLMs bring powerful new capabilities, such as global context, zero-shot recognition, and visual reasoning, so that they could complement or even replace traditional CNN pipelines for control reading, but careful adaptation is required to handle industrial applications’ specificity and precision needs.

Real-time performance and deployability are critical in industrial monitoring scenarios. In many cases, models for gauge reading must run on the edge, like embedded systems or smart cameras on the factory floor, due to latency, bandwidth, or data privacy constraints. There is a growing convergence of edge-computing and Artificial Intelligence (AI), often termed “edge intelligence,” which aims to push complex models closer to the data source. Deng et al. discuss this trend, emphasizing local visual data processing to reduce dependence on cloud infrastructure and improve response times [33]. Edge deployment imposes stringent resource limits: models may need to run on devices with low-power CPUs or small GPUs/TPUs, handle limited memory, and possibly run multiple tasks simultaneously. Stadnicka et al. survey industrial IoT applications and similarly conclude that efficient algorithms are needed to operate within the resource constraints of edge devices. This has driven research into model compression and efficiency optimization for vision tasks. Techniques such as quantization, pruning, and knowledge distillation are frequently applied to reduce the model size and inference time while preserving accuracy [34,35]. For instance, Lu et al. explore quantization-aware neural architecture search to design compact DL models tailored for edge deployment [14]. Such approaches can produce a smaller CNN or transformer that still performs well on gauge reading but can run at higher frame rates on the device. Another strategy is to use efficient backbone architectures, like MobileNet [36] or EfficientNet [37], for the vision model in an edge setting. These architectures are optimized for speed and can transfer effectively to various tasks. Ultimately, achieving inference efficiency is a balancing act with accuracy. In safety-critical industrial systems, it may be unacceptable to sacrifice too much accuracy for speed. Therefore, current research also looks at adaptive techniques, like running a lightweight model on the edge for continuous monitoring and falling back to a heavier model on the cloud for verification on uncertain cases. The need for reliability also means edge models must be robust to operating conditions (e.g., temperature, vibration) and require minimal maintenance. Efforts are underway to validate models under these realistic conditions and ensure real-time performance does not come at the cost of stability. Overall, edge-computing considerations now allow the design of industrial AI solutions, ensuring that even advanced models like VLMs are optimized for deployment without compromising accuracy beyond acceptable limits [38].

Adapting general-purpose models to the specific domain of industrial controls is an active area of research. Fine-tuning a pre-trained model on a smaller target dataset is a common approach to boost performance on domain-specific tasks. Kornblith et al. showed that models with better ImageNet performance tend to transfer more effectively to downstream tasks, implying that using a strong backbone, such as a transformer, is a good starting point for fine-tuning on gauge images [39]. However, fine-tuning still requires some labeled data from the target domain. To minimize this requirement, researchers have explored alternative adaptation methods. Jia et al. proposed visual prompt tuning, which adjusts a pre-trained vision model to new tasks by modifying its inputs rather than updating the model’s weights [40]. This technique can align a model to the industrial domain with minimal training, essentially “teaching” it to pay attention to gauge-relevant features via crafted input patterns. In cases where even a few real images are hard to obtain, synthesizing data or leveraging simulation is valuable, as discussed with Alcazar’s synthetic data approach [4]. Recently, Zeng et al. introduced a framework combining generative modeling and domain adaptation to tackle few-shot industrial meter reading [41]. They employed a diffusion model to generate varied meter images and a simulation-to-real adaptation pipeline to fine-tune an object detector for meter dials using only a handful of real samples. This approach achieved significant performance gains despite minimal ground-truth data, underlining the power of modern generative AI to fill the data gap in industrial applications. On the multimodal front, multimodal CoT prompting is another emerging technique to adapt LLMs for complex visual tasks [31,42]. By guiding a model like GPT-4o to reason stepwise (e.g., first identify what type of control is in the image, then parse its scale, then determine the reading), one can adapt a general model to the particular task of gauge reading without any weight updates, as the adaptation happens in the form of a dialog or reasoning process.

As highlighted in

Table 1. Summary of current approaches for analog and digital control interpretation.

Work	Advantages	Disadvantages	Notes
Classical CV methods
[16,17]	Simple CV with Hough/edges, low compute cost	Fragile to glare, lighting, design variability	Early baselines
[18]	Geometric fitting improves detection robustness	Still limited under real-world variability	Emphasis on geometric reasoning
CNN-based and modular DL approaches
[19]	Multi-stage CNN, high accuracy in industry	Requires multiple models, training data	Strong industrial deployment
[20]	CNN for AMR, public dataset (UFPR-AMR)	Needs annotated data, limited gauge types	Dataset + augmentation contribution
[4]	Synthetic dataset, sim-to-real transfer	Domain gap remains	52% error reduction vs. prior methods
[21]	Modular interpretable pipeline, stepwise reliability	Multi-step complexity, still CNN-dependent	Reliable, error $<2\%$
Transformers, VLMs, and adaptation
[22,23]	ViT/Swin capture global context	Resource-intensive, needs pre-training	Basis for transformers in vision
[26,27]	CLIP-style VLMs, zero-shot recognition	Limited industrial coverage	Strong transfer, prompt-sensitive
[24]	Prompt/fine-tuning improves reasoning accuracy	Application tasks remain difficult	Evidence of domain adaptation benefits
[25]	Systematic evaluation of causal reasoning	Models still weak in causal cognition	Highlights reasoning limits
[28]	Contextual fine-tuning boosts reliability	Extra training needed	Safety-critical relevance
[29]	Fine-tuning vs. prompting comparison	Prompt-only underperforms	Parallel with VLM adaptation trade-offs
[30]	CoCM adaptive fusion improves cross-domain	Complexity in implementation	Better handling of industrial variability
[31,32]	GPT-4o, PaLI multimodal CoT reasoning	Prompt sensitivity, high compute	First multimodal reasoning examples
[41]	Diffusion + sim-to-real few-shot	Compute-heavy, synthetic data quality	Shows generative adaptation potential

, a variety of techniques are being explored to adapt foundation models to industrial control understanding, including fine-tuning, prompting, feature adaptation, and synthetic data augmentation. Each of these strategies poses a different trade-off between the amount of required domain data, computational cost, and attainable performance. The comparative view shows that while classical CV and CNN-based solutions advanced accuracy in specific contexts, they often lacked generalization power. In contrast, transformer-based and multimodal approaches introduced zero-shot reasoning and broader adaptability, but at the cost of high computational demand and prompt sensitivity. The convergence of these research streams now sets the stage for integrated solutions. Yet, studies comparing these approaches in a unified industrial context remain scarce. Addressing this gap, the present work examines vision-based gauge reading, foundation model integration, edge computing, and fine-tuning within a single comparative framework.

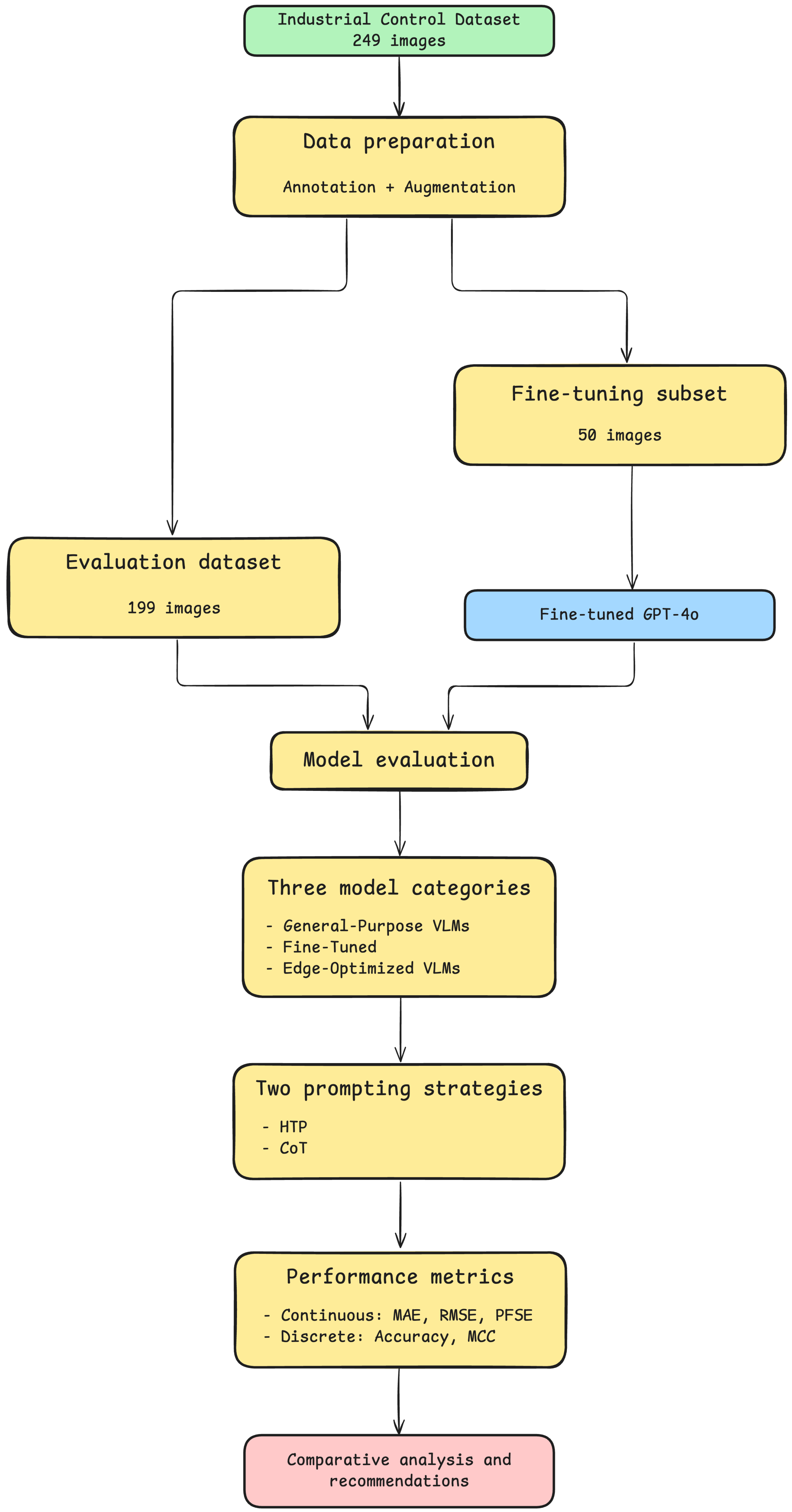
3. Methodology

This section presents the systematic approach to evaluating VLMs for industrial control interpretation across diverse implementation scenarios. The following methodology employs a comparative framework examining three distinct approaches: (1) general-purpose VLMs in their base configuration to assess inherent reasoning capabilities, (2) a fine-tuned variant trained on industrial control images, and (3) IoT models designed for resource-limited environments. Moreover, two prompting strategies are evaluated for each approach: a single prompt with a Holistic-Thought Protocol (HTP) approach, and a sequential CoT strategy. The following subsections detail the experimental setup, implementation specifics, and the evaluation framework used to quantify performance across these dimensions.

3.1. Experimental Setup

A mixed dataset comprising continuous and discrete control types collected from publicly available internet sources [43] facilitates a thorough evaluation of VLM capabilities in industrial control interpretation.

Table 2. Summary of dataset composition and annotation scheme.

Control Type	Samples	Measurement Range/States	Annotation Fields
Continuous	122	(a) Micro-scale [0–0.1] units (b) Industrial-scale [0–800] units (c) Pressure, temperature, flow	(a) annotated_value (b) range_min (c) range_max
Discrete	127	(a) Binary (ON/OFF) (b) Multi-position selectors	(a) annotated_state (b) available_states

summarizes the dataset composition and annotation scheme that underpin the evaluation. The dataset consists of 122 continuous controls, such as pressure gauges and thermometers, and 127 discrete controls, switches with distinct operational states, totaling 249 industrial control samples. Images vary in resolution, quality, lighting conditions, and viewing angles, accurately representing the variability encountered in real-world industrial monitoring scenarios. Continuous controls span diverse measurement ranges, from micro-scale [0–0.1] to industrial-scale [0–800] units, and represent various physical quantities, including pressure, temperature, and flow indicators. Conversely, discrete controls encompass binary, such as ON/OFF, and multi-position selectors. This heterogeneity in image characteristics provides a challenging testbed that reflects actual deployment conditions, where standardized image acquisition is rarely possible, and models must interpret controls across varied visual presentations and environmental conditions. As illustrated in Figure 1, possible industrial controls include both continuous measurement devices (i.e., gauges and dials) and discrete state indicators (i.e., switches and selectors).

A JSON-based methodology to capture each control type’s characteristics has been implemented for annotation and ground truth establishment. Continuous controls were annotated with three key parameters: the precise numerical reading (“annotated_value”) and the scale’s minimum and maximum values (“range_min” and “range_max”) to provide contextual boundaries for measurement interpretation and later evaluation. For example, a pressure gauge reading 0.22 MPa with a scale ranging from 0 to 1 MPa would be annotated accordingly to enable normalized error calculations during evaluation. Discrete controls were annotated with their current state (“annotated_state”) and a list of all possible states (“available_states”), enabling assessment of state classification performance. For instance, a toggle switch would include annotation of its current position (e.g., “OFF”) along with all valid states (e.g., [“OFF”, “ON”]). This annotation structure directly informed the evaluation metrics, enabling quantification of interpretation performance across control types.

To address the variability in industrial control interpretation and enhance model evaluation robustness, image augmentation using the Albumentations Python library [44] has been integrated. The augmentation pipeline was designed to simulate real-world conditions encountered in industrial environments where lighting, viewing angles, and image quality vary considerably. The implementation included multiple transformation categories: noise variants to simulate camera sensor limitations and poor lighting conditions, blur effects to mimic focus issues and camera movement, lighting variations to represent diverse illumination scenarios, and small rotations for different viewing perspectives. This augmentation strategy was essential for increasing the statistical significance of the performance metrics and ensuring that model comparisons reflect real-world deployment conditions where image quality and environmental factors significantly impact interpretation accuracies, such as variable lighting conditions or camera resolution. Figure 2 demonstrates the application of these transformations to a sample control image, simulating common visual challenges encountered in industrial environments, such as poor lighting, camera movement, and sensor noise. Industrial settings present changing conditions. This research evaluates model robustness against temporal lighting changes, equipment vibration, and sensor degradation.

A systematic process is necessary for comparing models and prompting strategies consistently. This research follows a clear pipeline: data preparation, model selection, prompting strategy implementation, and performance evaluation. Figure 3 illustrates this complete methodological framework. The diagram outlines the key components, from the dataset preparation pipeline to the final evaluation that allows for systematic comparison. It shows the three model categories under review, the two implemented prompting strategies, and the framework for analysis.

For domain-specific optimization, fine-tuning on the gpt-4o-2024-08-06 model using a subset of 50 industrial control images was conducted, balanced between 25 continuous and 25 discrete control types, ensuring no overlap with the evaluation dataset. This fine-tuning dataset was deliberately constrained in size to reflect practical limitations in industrial environments, where collecting and annotating large volumes of domain-specific data is often resource-intensive or impractical. Furthermore, according to OpenAI’s official documentation, a dataset comprising 50 images is considered more than adequate for successful fine-tuning outcomes.

The models were chosen to capture current VLM capabilities for industrial control interpretation. General-purpose models provide a benchmark for zero-shot reasoning and broad visual understanding. At the same time, the domain-specialized fine-tuned GPT-4o underscores how minimal but targeted training can substantially enhance performance in specific industrial tasks. On the other hand, including edge-optimized models highlights the practical challenges and constraints associated with deploying these systems in these specific environments. This selection ensures that the evaluation measures peak interpretative accuracy and addresses real-world considerations such as computational efficiency, scalability, and robustness under variable industrial conditions.

3.2. Implementation Details

This study’s implementation framework encompasses three distinct model categories, each representing different deployment scenarios for industrial control interpretation. The first category consists of general-purpose VLMs in their base configuration, including GPT-4o, Claude 3.7 Sonnet, and others, accessed through their provider Application Programming Interfaces (APIs). These models represent the “off-the-shelf” approach requiring no domain adaptation. The second category comprises a domain-specialized fine-tuned variant of the gpt-4o-2024-08-06 model, adapted to industrial control interpretation. The third category features IoT models designed for restricted environments, usually deployed on devices such as Raspberry Pi. Standardized input/output processing protocols have been implemented for each model category to ensure consistent handling of visual inputs and response parsing. This implementation approach enables an overall evaluation across the spectrum from high-capability models to efficient edge deployments, reflecting the diverse computational constraints encountered in real-world industrial monitoring scenarios. All implementations used a uniform Python 3.13.7-based evaluation framework with standardized testing procedures to ensure reproducibility and fair comparison.

For the evaluation of base VLMs, GPT-4o [45], GPT-4o mini, Claude 3.7 Sonnet [46], Molmo 7B [47], and LLaVA v1.6 Vicuna 13B were analyzed [48] as representative general-purpose VLMs. All models were configured with a temperature setting of 0.1 to minimize non-deterministic response variability. The implementation framework established a standardized communication protocol for all API interactions, consisting of specific message formats with text prompts accompanied by base64-encoded image data. GPT-4o and GPT-4o mini models were accessed via the OpenAI client library, while the remaining were accessed through the Replicate API.

A fine-tuned model using the OpenAI API fine-tuning endpoint with the gpt-4o-2024-08-06 base model was created for domain-specialized model development. This approach needs the data to be prepared in JSONL format. Each training example was outlined as a conversation sequence with three components: a system message defining the task scope (e.g., “You are an assistant that identifies industrial control panel values from images, either regression (continuous values) or classification (discrete classes)”), a user message containing the control image encoded as a base64 string or hosted URL with appropriate detail parameters, and an assistant message containing the expected reading (e.g., “off” for a discrete control or “−36.5” for a continuous measurement). The fine-tuning procedure employed supervised learning following OpenAI’s recommended best practices for automatic hyperparameter selection. OpenAI’s fine-tuning API automatically determines optimal hyperparameters based on dataset characteristics, including learning rate multiplier, batch size, and epoch count, without exposing these values to users. This approach ensures that training parameters are optimized for the specific dataset size and complexity rather than using arbitrary fixed values. The training process utilized the default supervised method with automatic hyperparameter selection for the 50-sample dataset.

Fine-tuning process utilized a dataset of 50 industrial control images balanced evenly between continuous and discrete types. The fine-tuning optimization follows a supervised learning approach that minimizes the negative log-likelihood loss function across the training dataset (1):

$$L_{fine-tune}=-{\displaystyle \frac{1}{N}}\sum _{i=1}^{N}logP\left(y_i\right|x_i,I_i,{\theta }_{ft})$$

(1)

where N represents the total number of training samples (50 in this implementation), $x_i$ denotes the textual prompt for sample i, $I_i$ represents the corresponding industrial control image, $y_i$ is the expected interpretation output, and ${\theta }_{ft}$ represents the fine-tuned model parameters. The probability $P\left(y_i\right|x_i,I_i,{\theta }_{ft})$ captures the model’s likelihood of generating the correct interpretation given the multimodal input. The optimization process updates the pre-trained parameters ${\theta }_{base}$ to ${\theta }_{ft}$ through gradient descent (2):

$${\theta }_{ft}={\theta }_{base}-\eta {\nabla }_{\theta }{L}_{fine-tune}$$

(2)

where $\eta$ represents the learning rate multiplier provided by OpenAI’s default hyperparameter configuration.

The fine-tuning resulted in a specialized model (identifier: ft:gpt-4o-2024-08-06:personal:: B4uGYpNL) optimized for industrial control interpretation tasks.

For edge-optimized model evaluation, several VLMs were examined, including Moondream2 [49], SmolVLM-Instruct [50], PaliGemma 3B [51], and Bunny-Phi-2-SigLIP [52]. These models represent different approaches for the efficiency/accuracy trade-off inherent in IoT deployment scenarios. Moondream2 and SmolVLM-Instruct are architected explicitly for IoT applications with minimal computational footprints, while PaliGemma 3B represents Google’s approach to efficient multimodal reasoning with a 3 billion parameter architecture and 224 × 224 pixel input resolution. Bunny-Phi-2-SigLIP offers another efficiency-oriented configuration combining the lightweight Phi-2 language model with the SigLIP vision encoder.

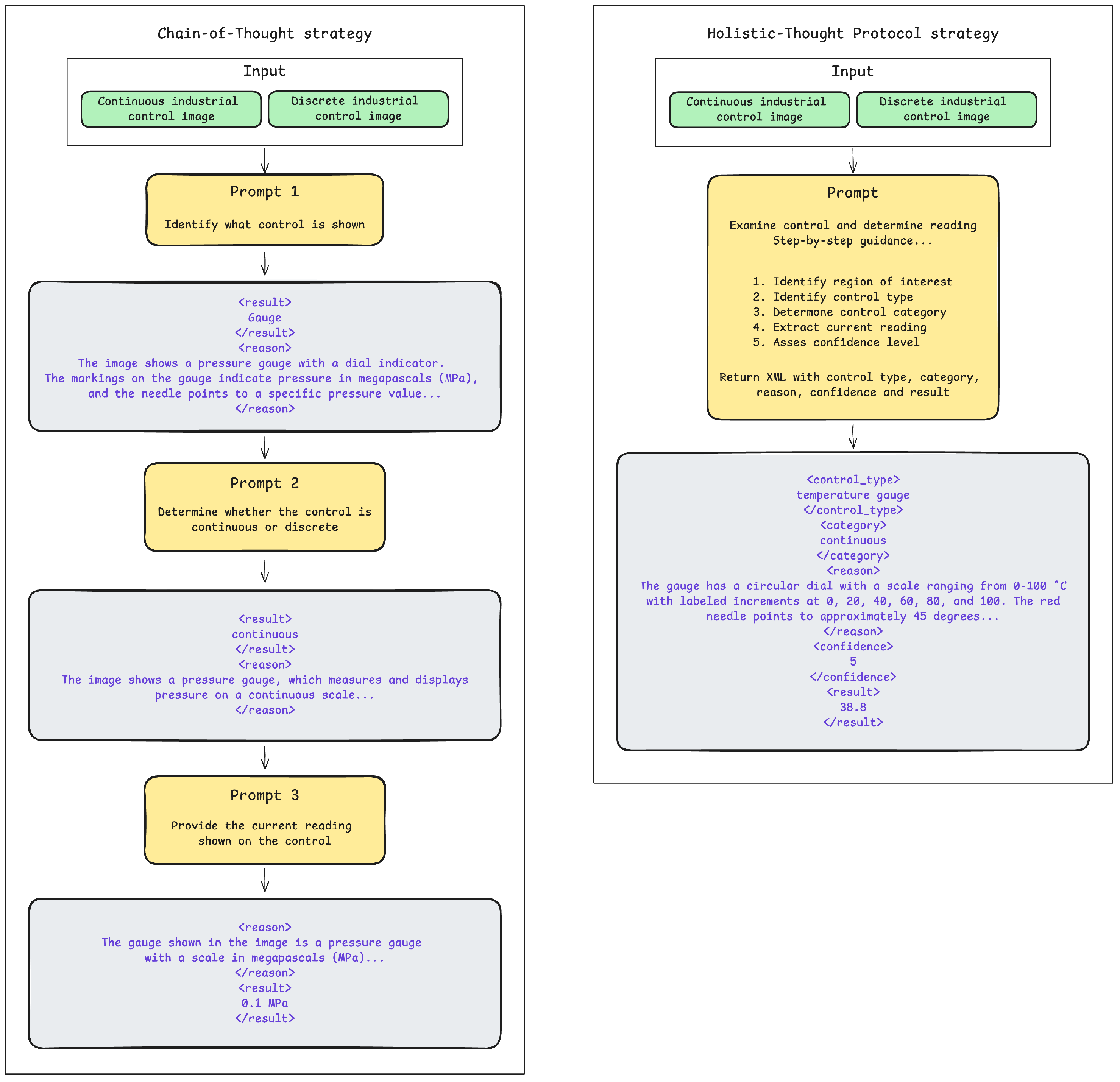
For prompting strategy implementation, two distinct approaches to industrial control interpretation have been applied, as depicted in Figure 4. The HTP strategy implements a single-interaction methodology through an XML-based prompt containing multiple interrelated components: task definition, visual analysis guidelines, step-by-step instructions, format requirements, and examples. This prompting approach explicitly addresses the inherent variability in free-form model responses by enforcing consistency through clearly defined XML tags (e.g., <control_type>, <category>, <reason>, <confidence>, and <result>). Without this framework, extracting consistent and accurate information from model outputs would be challenging due to the inherent unpredictability and variability of unstructured responses. Consequently, the XML-based format facilitates reliable result extraction using regex pattern matching. In contrast, the CoT strategy implements a sequential three-step reasoning process through independent prompts that progressively build contextual understanding. The first prompt focuses on control identification (e.g., “Look at the attached image and identify what control is shown…”), followed by a second prompt for classification determination (e.g., “Determine whether this control is continuous or discrete…”), and ends with a third prompt requesting the specific reading value, based on the previous results. Each CoT step includes XML tag instructions (<result> and <reason>) to standardize response formatting. This sequential implementation simulates a step-by-step reasoning process, allowing explicit intermediate verification while enhancing interpretation accuracy through decomposed problem-solving. This sequential implementation simulates a step-by-step reasoning process, allowing explicit intermediate verification while enhancing interpretation accuracy through decomposed problem-solving. The mathematical formulation of these prompting strategies can be expressed algorithmically as follows. For the HTP approach, the interpretation process is defined as follows (3):

$$R_{HTP}=f_{VLM}(I,P_{comprehensive})$$

(3)

where I represents the input industrial control image, $P_{comprehensive}$ denotes the holistic prompt containing all task components (task definition, visual analysis guidelines, format requirements, and examples), and $f_{VLM}$ represents the VLM’s inference function. The comprehensive prompt structure can be formalized as follows (4):

$$P_{comprehensive}=\{T_{def},G_{visual},S_{steps},F_{format},E_{examples}\}$$

(4)

where each component addresses specific aspects of the interpretation task. In contrast, the CoT strategy implements a sequential reasoning chain, as shown in Equations (5)–(7):

$$R_1=f_{VLM}(I,P_{identify})$$

(5)

$$R_2=f_{VLM}(I,P_{classify},R_1)$$

(6)

$$R_{CoT}=f_{VLM}(I,P_{extract},R_1,R_2)$$

(7)

where $P_{identify}$, $P_{classify}$, and $P_{extract}$ represent the three sequential prompts for control identification, type classification, and value extraction, respectively. Each subsequent step $R_{i+1}$ incorporates the previous responses $\{R_1,\dots ,R_i\}$ as contextual information, enabling progressive refinement of the interpretation process. This decomposition allows for explicit verification at intermediate stages while building comprehensive understanding through stepwise reasoning.

3.3. Evaluation Framework

The evaluation framework implemented in this research follows a hierarchical approach, as illustrated in Figure 5, enabling comparative analysis across model categories and prompting strategies. Each industrial control image traverses a defined pathway through one of three model categories, and is processed using one of the two prompting strategies, generating standardized interpretation results that undergo metric-specific evaluation. The framework processes each control image through the specified model and prompting strategy while handling continuous and discrete control types through specialized processing paths. This approach ensures that performance differences can be directly attributed to the specific model capabilities or prompting strategies rather than evaluation inconsistencies.

The standardized evaluation methodology incorporates an input data processing pipeline that organizes industrial control data according to their classification. Image data and annotations are parsed from JSON files that distinguishes between continuous and discrete control types. Each control image receives appropriate metadata association, and continuous controls are linked with their numerical readings and scale range parameters. Conversely, discrete controls maintain their current state classification and enumeration options. This typology enables validation procedures and normalization techniques, which are particularly critical for continuous controls where scale-aware error calculation significantly impacts evaluation accuracy.

The evaluation framework for continuous control interpretation implements metrics designed to assess numerical prediction accuracy across diverse scales and measurement ranges. All metrics utilize normalized calculations based on each instrument specific ranges to ensure fair comparison across controls with different value ranges.

Mean Absolute Error (MAE) quantifies the average magnitude of prediction errors (8):

$$\mathrm{MAE}={\displaystyle \frac{1}{n}}\sum _{i=1}^n|y_i-{\widehat{y}}_i|$$

(8)

Root Mean Squared Error (RMSE) provides greater sensitivity to large errors (9):

$$\mathrm{RMSE}=\sqrt{{\displaystyle \frac{1}{n}}\sum _{i=1}^n{(y_i-{\widehat{y}}_i)}^2}$$

(9)

The coefficient of determination ($R^2$) measures predictive performance relative to using the mean value, with values closer to 1 indicating superior performance (10):

$$R^2=1-{\displaystyle \frac{{\sum }_i{(y_i-{\widehat{y}}_i)}^2}{{\sum }_i{(y_i-\overline{y})}^2}}$$

(10)

For practical industrial assessment, the percentage Within Tolerance calculates the proportion of predictions falling within a specified tolerance range, typically 5% of the instrument’s full-scale range.

Mean Absolute Percentage Error (MAPE) quantifies error as a percentage of the true value, providing scale-independent comparison but requiring careful handling of values near zero (11):

$$\mathrm{MAPE}={\displaystyle \frac{1}{n}}\sum _{i=1}^n\left|{\displaystyle \frac{y_i-{\widehat{y}}_i}{y_i}}\right|\times 100\%$$

(11)

The coefficient of variation of RMSD (CV-RMSD) offers another scale-independent metric enabling comparison across measurement ranges (12):

$$\mathrm{CV}-\mathrm{RMSD}={\displaystyle \frac{\mathrm{RMSE}}{\overline{y}}}\times 100\%$$

(12)

Finally, the Percentage of Full Scale Error (PFSE) measures error magnitude relative to instrument range rather than measured value (13):

$$\mathrm{PFSE}={\displaystyle \frac{\mathrm{MAE}}{{\mathrm{range}}_{\max }-{\mathrm{range}}_{\min }}}\times 100\%$$

(13)

This multi-dimensional metric approach provides a broad performance assessment balancing absolute accuracy, relative error magnitude, and practical industrial tolerance requirements.

For discrete control evaluation, the framework implements classification metrics designed to assess categorical prediction performance. The foundational measurement is classification accuracy, calculated as the percentage of correctly classified controls within the test set (14):

$$\mathrm{Accuracy}={\displaystyle \frac{TP+TN}{TP+TN+FP+FN}}$$

(14)

where $TP$ represents true positives, $TN$ true negatives, $FP$ false positives, and $FN$ false negatives.

The framework extends beyond simple accuracy with macro-averaged precision and recall metrics to account for class imbalance issues. To avoid false positive classifications, macro-precision quantifies the average ability across all k classes (15):

$${\mathrm{Precision}}_{\mathrm{macro}}={\displaystyle \frac{1}{k}}\sum _{i=1}^k{\displaystyle \frac{T{P}_i}{T{P}_i+F{P}_i}}$$

(15)

Complementarily, macro-recall measures the average ability to identify all instances of each class (16):

$${\mathrm{Recall}}_{\mathrm{macro}}={\displaystyle \frac{1}{k}}\sum _{i=1}^k{\displaystyle \frac{T{P}_i}{T{P}_i+F{N}_i}}$$

(16)

These metrics are synthesized in the macro-F1 score, representing the harmonic mean of precision and recall (17):

$${\mathrm{F}1}_{\mathrm{macro}}={\displaystyle \frac{1}{k}}\sum _{i=1}^k{\displaystyle \frac{2\times {\mathrm{Precision}}_i\times {\mathrm{Recall}}_i}{{\mathrm{Precision}}_i+{\mathrm{Recall}}_i}}$$

(17)

For robust performance assessment, the Matthews Correlation Coefficient (MCC) provides a balanced measure suitable for multiclass settings with class imbalance (18):

$$\mathrm{MCC}={\displaystyle \frac{c·s-{\sum }_k{p}_k·t_k}{\sqrt{(s^2-{\sum }_k{p}_k^2)·(s^2-{\sum }_k{t}_k^2)}}}$$

(18)

where c is the total number of correctly predicted samples, s is the total number of samples, and $p_k$ and $t_k$ are the sums of predicted and actual values for class k, respectively.

A clear and direct performance metric is necessary for evaluating multiclass discrete controls in an industrial context. The Matthews Correlation Coefficient (MCC) was selected because other metrics proved unsuitable for this task. AUC-ROC becomes computationally complex in multiclass scenarios and requires decomposition methods that obscure practical performance assessment. Expected Calibration Error (ECE) was also not applicable, as most evaluated VLMs do not provide probability outputs in a format suitable for calibration analysis.

Additionally, the evaluation tracks class-specific performance through a confusion matrix and per-class metrics, enabling granular analysis of model strengths and weaknesses across different control types.

The cross-model comparison framework implements a standardized evaluation approach that ensures fair assessment across all model categories and prompting strategies. Each model processes the same test images, enabling direct performance comparisons that isolate each model’s specific characteristics from methodology variations. The evaluation pipeline processes each control image through every model/strategy combination. Performance data are stored hierarchically by model category and prompting strategy, facilitating multi-dimensional comparative analysis. This approach captures performance differences attributable specifically to model architecture, parameter count, training methodology, and reasoning approach rather than evaluation inconsistencies. All the calculated metrics allow the identification of model strengths and weaknesses across different industrial control interpretation scenarios, providing insights into optimal model selection based on specific deployment requirements. The evaluation framework establishes a methodology for analyzing error patterns across model predictions, enabling systematic categorization of interpretation failures beyond aggregate performance metrics. For continuous controls, the framework examines metric distributions across value ranges to identify potential biases, whether models systematically underperform on specific measurement scales. The evaluation methodology captures normalized error distributions, distinguishing between small absolute errors on narrow-range instruments versus proportionally significant errors on wide-range instruments through metrics like PFSE and MAPE. The approach utilizes confusion matrices for discrete controls to distinguish between inter-class confusion patterns versus random errors, with particular attention to false-positive and false-negative distributions across control state categories.

4. Results and Discussion

To evaluate the performance of VLMs in interpreting industrial controls, a testing framework that assessed both continuous and discrete control reading capabilities has been developed. The methodology involved presenting models with images of various industrial controls that belong to both categories and comparing their interpretations against ground truth values. The evaluation dataset comprised 122 continuous controls and 127 discrete controls. Two distinct prompting strategies were applied across the selected models: the HTP approach that provided instructions in a single query and a CoT strategy that broke the interpretation task into sequential steps. For each approach, performance using metrics tailored to the control type was measured as explained in Section 3.3. The following sections present detailed evaluation results, examining models’ performance across control types and prompting strategies.

4.1. Continuous Control Interpretation Performance

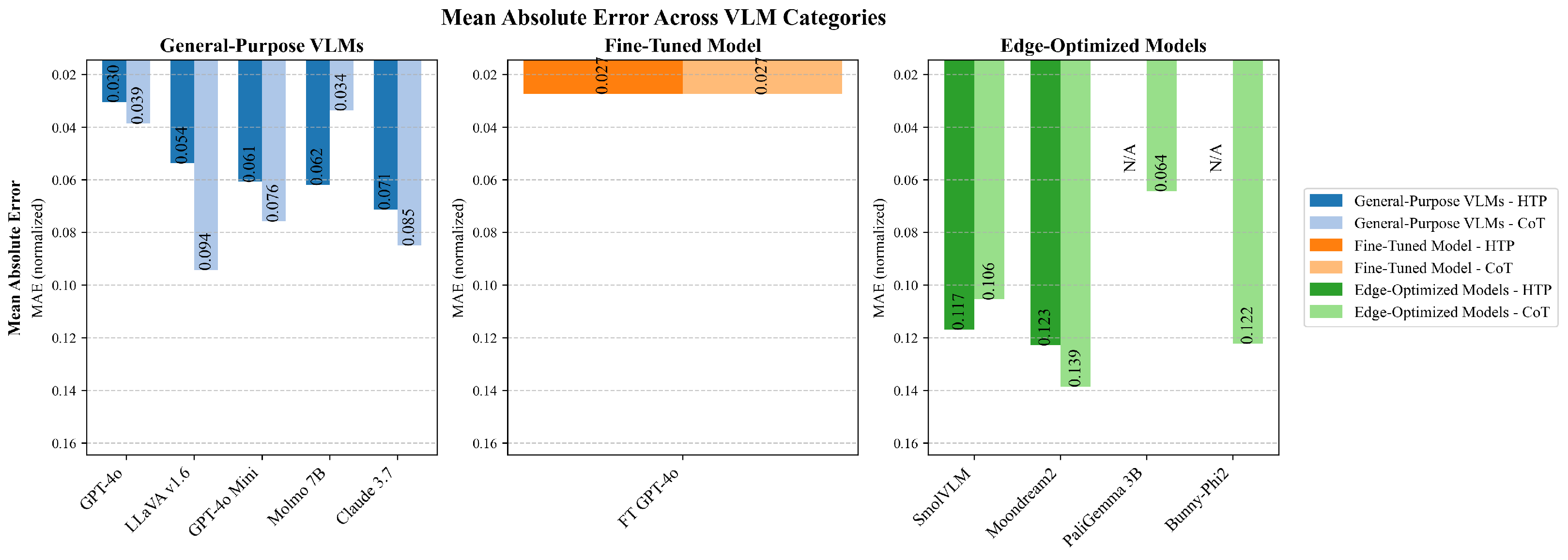
The analysis of continuous control interpretation reveals significant performance variations across the evaluated models and prompting strategies, as shown in Figure 6. Fine-tuned GPT-4o achieved the lowest MAE of 0.027 when employing either prompting strategy, outperforming all other model configurations (see

Table 3. Performance metrics for continuous control interpretation across models and prompting strategies. MAE and Root Mean Squared Error (RMSE) values are normalized, PFSE represents Percentage of Full Scale Error, and Within Tolerance indicates percentage of predictions within ±5% of ground truth.

Model	Strategy	MAE	RMSE	PFSE (%)	Within Tol. (%)
GPT-4o	HTP	0.030	0.084	3.0	87.7
GPT-4o	CoT	0.039	0.098	3.9	83.6
GPT-4o mini	HTP	0.061	0.159	6.1	79.5
GPT-4o mini	CoT	0.076	0.208	7.6	80.3
Claude 3.7	HTP	0.071	0.184	7.1	80.3
Claude 3.7	CoT	0.085	0.216	8.5	77.9
Molmo 7B	HTP	0.062	0.154	6.2	72.1
Molmo 7B	CoT	0.034	0.133	3.4	91.8
LLaVA v1.6	HTP	0.054	0.125	5.4	72.3
LLaVA v1.6	CoT	0.094	0.242	9.4	68.0
Fine-tuned GPT-4o	HTP	0.027	0.093	2.7	91.0
Fine-tuned GPT-4o	CoT	0.027	0.079	2.7	89.3
Moondream2	HTP	0.123	0.173	12.3	24.6
Moondream2	CoT	0.139	0.417	13.9	77.8
SmolVLM	HTP	0.117	0.213	11.7	35.0
SmolVLM	CoT	0.106	0.280	10.6	76.2
PaliGemma 3B	HTP	N/A	N/A	N/A	N/A
PaliGemma 3B	CoT	0.064	0.135	6.4	68.4
Bunny-Phi2	HTP	N/A	N/A	N/A	N/A
Bunny-Phi2	CoT	0.122	0.296	12.2	72.3

). This error level represents an improvement over the baseline performance established by general models like GPT-4o or Molmo 7B, which exhibited MAE values exceeding 0.30 and 0.34, respectively.

MAE is a particularly relevant metric in industrial control reading scenarios as it quantifies the average magnitude of interpretation errors. Even slight deviations in readings can have significant operational implications in practical industrial applications. Interestingly, the performance differential between prompting strategies varied across models, with models such as LLaVA v1.6 showing more improvements when using the HTP approach and models such as Molmo 7B showing more pronounced improvements when using the CoT approach. In contrast, other models exhibited less sensitivity to prompting methodology. This suggests that some models can take advantage of the step-by-step reasoning process to improve their interpretation precision, whereas other models may be limited by their fundamental visual analysis capabilities regardless of prompting technique.

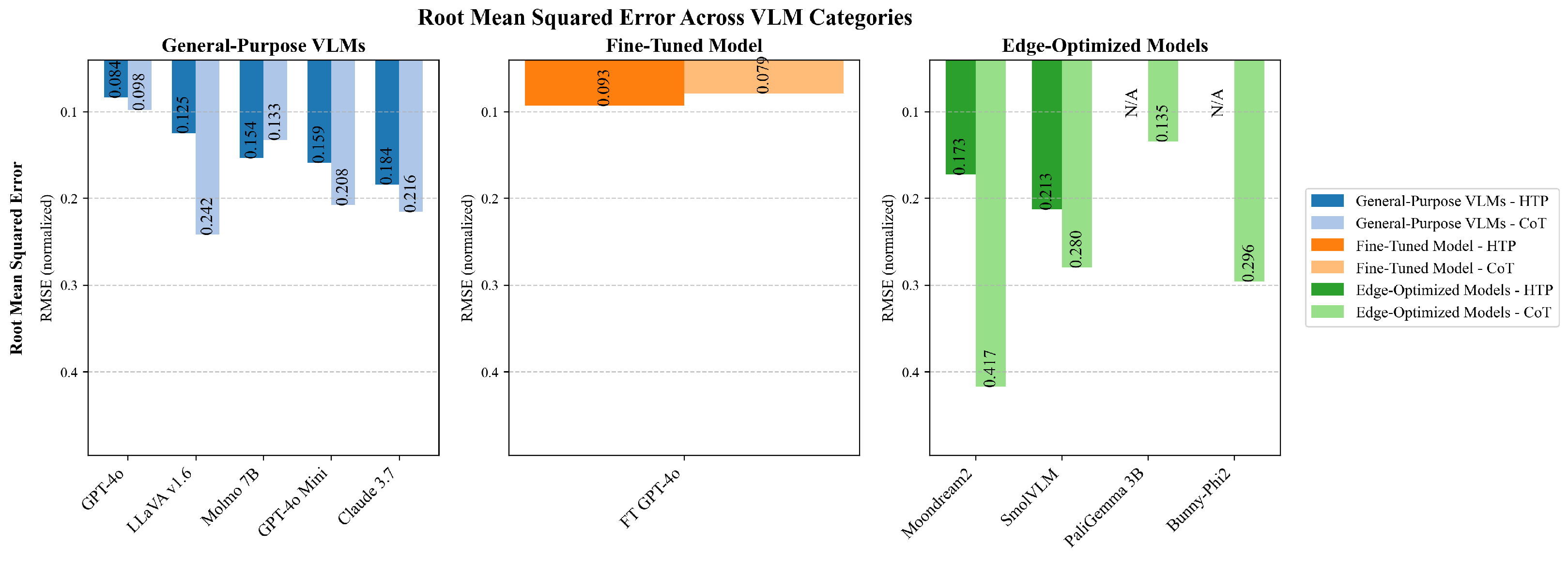
While MAE provides insight into average error magnitude, RMSE offers a complementary perspective by penalizing larger deviations more heavily. As illustrated in Figure 7, the RMSE results follow a pattern similar to MAE across models, with the fine-tuned GPT-4o achieving the lowest RMSE (0.079) when using the CoT strategy.

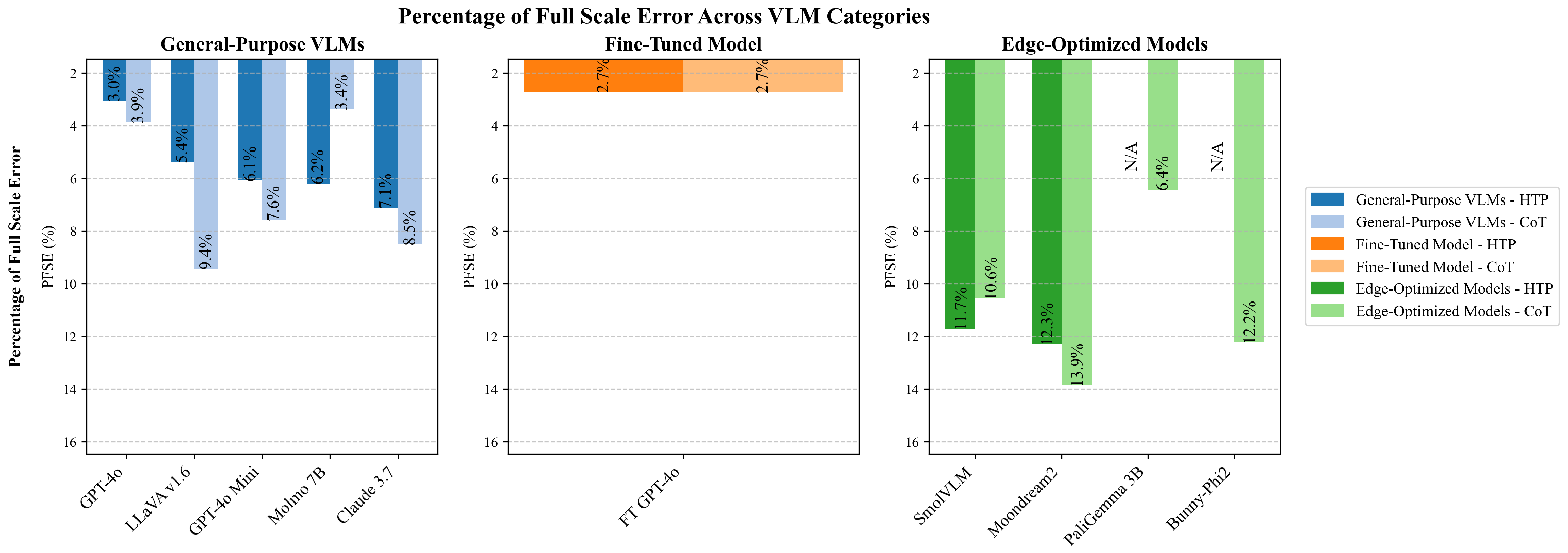
To account for the varying scales of industrial controls, models were additionally evaluated using PFSE, which normalizes errors relative to each instrument’s range. As shown in Figure 8, PFSE results reveal that errors typically represent 5–15% of an instrument’s full scale, with fine-tuned GPT-4o again demonstrating superior performance (2.7% PFSE with either prompting strategy). The PFSE metric provides context for industrial applications, as it translates abstract normalized errors into practical percentage-based deviations that operators can readily interpret. Notably, the GPT-4o model achieved comparable PFSE performance (3.0%) to its fine-tuned counterpart, suggesting that fine-tuning can little optimize for scale-aware interpretation. For instruments with wide operational ranges, such as industrial pressure gauges that might span hundreds of PSI, even models with higher PFSE values could still provide readings with acceptable absolute error for many non-critical applications. However, for precision instruments or safety-critical controls, the lower PFSE values achieved by larger models represent a significant practical advantage. Inspection of the error distribution reveals that misinterpretations are not random but typically stem from recurrent causes:

• Difficulty interpreting controls under strong glare or shadows that obscure pointer edges;
• Scale misalignment in gauges where needles overlap with thick or irregular tick marks;
• Systematic bias in narrow-range instruments where minor pixel-level deviations translate into proportionally large errors.

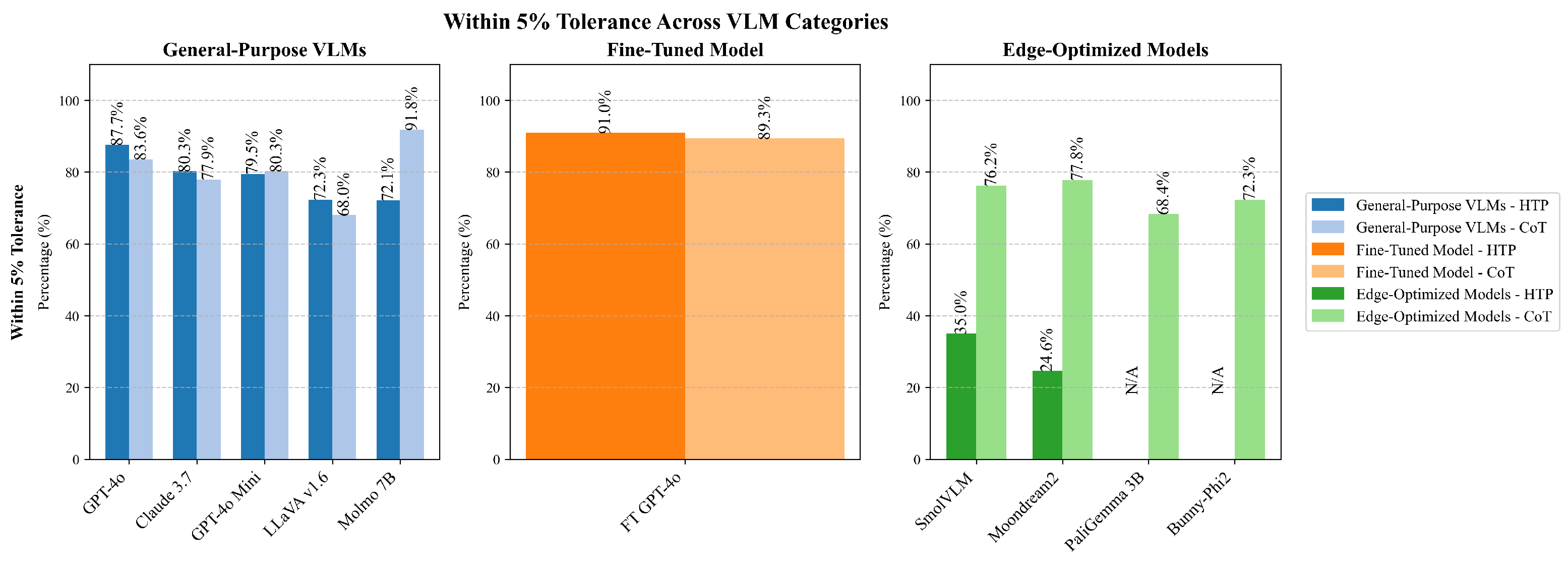
Beyond error metrics, the percentage of readings falling Within Tolerance (±5% of ground truth) provides a pragmatic assessment of model utility in industrial contexts. As depicted in Figure 9, both Molmo 7B with CoT strategy and fine-tuned GPT4-o with HTP strategy achieved the highest within-tolerance rate at 91.0%, followed closely by the fine-tuned GPT4-o with CoT strategy, at 89.3%. This metric effectively translates statistical performance into practical reliability by indicating how frequently a model’s interpretations would meet typical industrial tolerance requirements. Smaller models demonstrated markedly lower performance, with Moondream2 and SmolVLM achieving within-tolerance rates below 50%, thus limiting their suitability for applications requiring consistent accuracy.

Industrial control environments often specify acceptable tolerance bands based on process criticality, with typically tighter tolerances for safety-critical systems (±1–2%) and wider allowances for monitoring-only applications (±5–10%). The within-tolerance metric directly addresses whether a model’s performance satisfies these practical requirements. The left plot of Figure 10 illustrates the relationship between MAE and within-tolerance percentage, revealing an expected negative correlation but with notable outliers. Some models achieved higher within-tolerance rates than their MAE values might suggest, indicating more consistent performance around the mean value rather than exhibiting extreme deviations. This finding highlights the importance of considering multiple performance dimensions when evaluating models for industrial deployment, with GPT-4o, fine-tuned GPT4-o, and Molmo 7B delivering the best overall performance across metrics. These results suggest that model selection should consider both the specific tolerance requirements of the industrial application and the consistency of model performance, not merely average error rates.

4.2. Discrete Control Interpretation Performance

Discrete control interpretation is particularly relevant in industrial contexts for monitoring safety interlocks, operational modes, valve positions, and equipment states. In these scenarios, misclassification can have severe consequences, consequently triggering inappropriate automated responses or providing operators with misleading system status information.

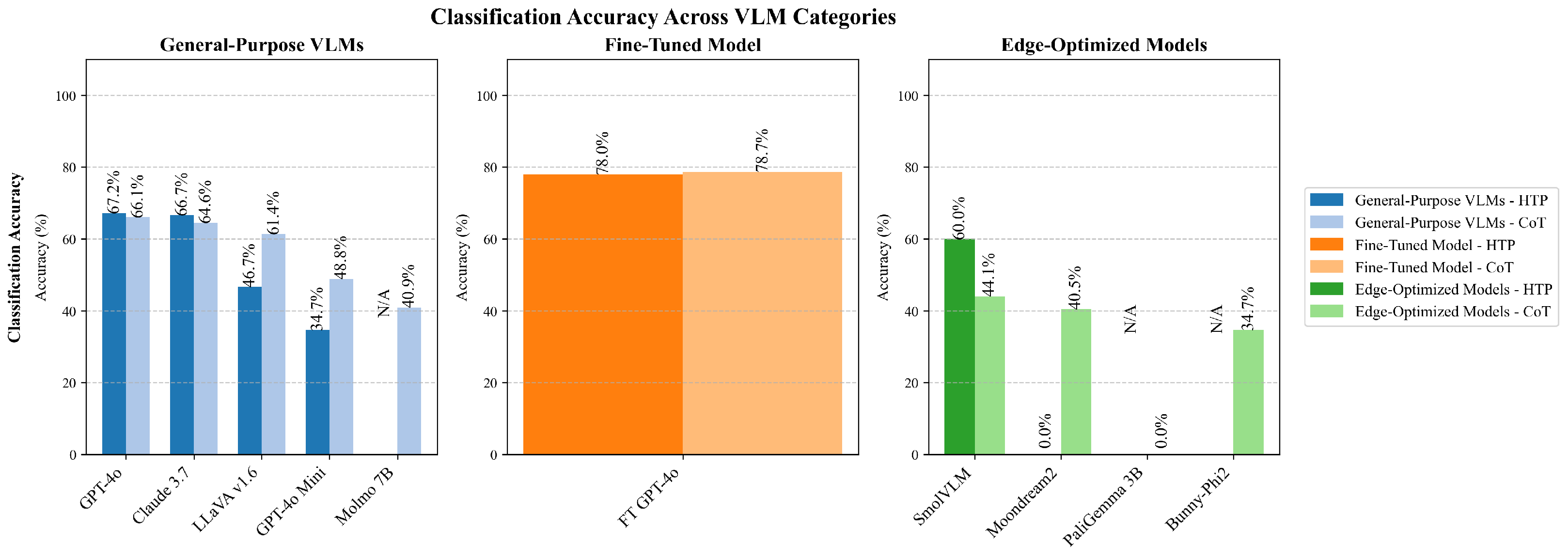
Figure 11 presents the accuracy results for discrete control state classification across the evaluated models and prompt strategies. Fine-tuned GPT-4o again demonstrated superior performance, achieving 78.7% accuracy with the CoT approach, followed by the same model but with the HTP strategy, with 78.0% accuracy (see

Table 4. Classification performance metrics for discrete control interpretation across models and prompting strategies. All precision, recall, and F1-score values represent macro-averaged metrics.

Model	Strategy	Accuracy (%)	MCC
GPT-4o	HTP	67.2	0.61
GPT-4o	CoT	66.1	0.60
GPT-4o mini	HTP	34.7	0.26
GPT-4o mini	CoT	48.8	0.41
Claude 3.7	HTP	66.7	0.59
Claude 3.7	CoT	64.6	0.58
Molmo 7B	HTP	N/A	N/A
Molmo 7B	CoT	40.9	0.31
LLaVA v1.6	HTP	46.7	0.23
LLaVA v1.6	CoT	61.4	0.54
Fine-tuned GPT-4o	HTP	78.0	0.73
Fine-tuned GPT-4o	CoT	78.7	0.74
Moondream2	HTP	0.0	0.0
Moondream2	CoT	40.5	0.29
SmolVLM	HTP	60.0	0.0
SmolVLM	CoT	44.1	0.32
PaliGemma 3B	HTP	N/A	N/A
PaliGemma 3B	CoT	0.0	0.0
Bunny-Phi2	HTP	N/A	N/A
Bunny-Phi2	CoT	34.7	0.21

). The performance gap between the mentioned model and the next with the highest accuracy (GPT4-o with HTP strategy, 67.2% of accuracy) was more pronounced for discrete controls than for continuous readings, with models such as LLaVa v1.6 and GPT-4o mini achieving accuracies below 50%. This widening performance disparity suggests that discrete state classification may require more sophisticated reasoning capabilities.

While accuracy provides an intuitive performance measure, the MCC offers a more integral assessment of classification reliability, particularly for datasets with imbalanced state distributions. As shown in Figure 12, the MCC results reveal significant performance differences across model categories and prompting strategies. Among general-purpose VLMs, GPT-4o achieved the highest MCC value of 0.61 with the HTP prompting approach, with only a slight decrease to 0.60 using CoT. Claude 3.7 followed closely with MCC values of 0.59 (HTP) and 0.58 (CoT), while smaller general-purpose models showed substantially lower performance, with GPT-4o Mini reaching only 0.26 with HTP prompting. The fine-tuned GPT-4o model demonstrated impressive reliability with MCC values of 0.73 (HTP) and 0.74 (CoT), outperforming even the base models. This improvement highlights the value of specialized training for industrial control classification tasks. By contrast, edge-optimized models showed considerably lower reliability, with SmolVLM achieving an MCC of 0.32 using CoT prompting but failing to produce valid predictions with the HTP approach. Similarly, Moondream2 reached 0.29 with CoT while delivering no valid predictions using HTP prompting. Bunny-Phi2 managed an MCC of 0.21 with CoT, while PaliGemma-3B could not produce reliable classifications under either prompting strategy.

The MCC metric, which ranges from −1 to 1 (with 1 indicating perfect prediction), accounts for true and false positives and negatives across all classes, making it especially relevant for industrial applications where misclassifying certain states may have asymmetric consequences. These results demonstrate that while general-purpose VLMs offer reasonable classification reliability, fine-tuned models provide substantially better industrial control state determination performance. The significant gap between larger models and edge-optimized alternatives indicates that effective deployment in industrial settings may require substantial computational resources or specialized training approaches to achieve acceptable reliability levels. Error inspection of discrete tasks shows that most misclassifications occur between visually similar states; for instance, adjacent switch positions or selector dials with degraded labels. Another frequent cause is partial occlusion, which leads the model to confuse discrete positions.

Figure 10 also illustrates the relationship between prediction rate and accuracy for discrete control classification, providing valuable insights into model reliability. The scatter plot reveals distinct performance clusters that align with model capabilities and optimization approaches. Fine-tuned GPT-4o demonstrates the greatest performance, achieving both high prediction rates (near 100%) and higher accuracy (approximately 77–80%), positioning it in the top-right quadrant of the chart. This indicates that the model provides classifications for almost all presented controls and maintains high accuracy in those determinations. The general-purpose VLMs exhibit varied performance patterns. GPT-4o and Claude 3.7 form a high-performance cluster with accuracy between 65–67% and prediction rates near 90%, indicating strong reliability. On the other hand, smaller models show more scattered performance. GPT-4o mini presents an interesting case where the prompting strategy affects the model’s accuracy, but neither surpasses 50% accuracy. Edge-optimized models predominantly occupy the lower regions of the chart, with most achieving accuracies below a practical utility threshold of 50%. Particularly concerning are PaliGemma 3B and Moondream2 with HTP prompting, which could not perform any prediction, indicating fundamental limitations in their ability to interpret industrial controls. SmolVLM presents an interesting exception among edge models, with HTP prompting achieving 60% accuracy despite a low prediction rate (20%), suggesting potential utility in specific constrained scenarios where prediction selectivity is acceptable.

4.3. Prompt Strategy Effectiveness

The evaluation followed in the current study revealed distinct patterns in the effectiveness of different prompting strategies across model categories and control types. The HTP approach generally outperformed the CoT strategy across most metrics and models. As shown in Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12, HTP prompting led to performance improvements in most cases, though with some notable exceptions depending on the model and task type.

For continuous control interpretation, HTP prompting achieved lower error rates across general-purpose VLMs, with GPT-4o showing a normalized MAE of 0.039 with HTP versus 0.030 with CoT. This pattern was consistent across RMSE and PFSE metrics, where HTP generally yielded lower error measurements. Figure 6, Figure 7 and Figure 8 illustrate this trend, with most general-purpose models showing better performance with HTP prompting. The fine-tuned GPT-4o model also performed slightly better under the CoT approach (RMSE of 0.079) compared to HTP (RMSE of 0.093). For discrete control classification, CoT prompting similarly demonstrated advantages. Classification accuracy, as shown in Figure 11, was higher for several models when using HTP, with fine-tuned GPT-4o achieving 78.7% accuracy under CoT. The MCC results (Figure 12) reinforce this finding, with most models showing better-balanced classification performance under CoT prompting. Interestingly, edge-optimized models showed mixed results, with some metrics favoring CoT in specific instances. For example, SmolVLM achieved better within-tolerance percentages with CoT (76.2%) than with HTP (35.0%), as seen in Figure 9. This suggests that while HTP is generally more effective, certain lightweight models may benefit from the designed guidance provided by CoT prompting in some scenarios.

HTP prompting excels in scenarios requiring efficient, direct interpretation, particularly when models have strong inherent reasoning capabilities. Providing instructions in a single query, HTP enables models to make the most out of their internal reasoning processes without the overhead of multiple interactions. This approach is particularly effective for larger models that can process complex instructions. In contrast, CoT may offer advantages for smaller edge-optimized models on specific tasks by providing a framework that compensates for more limited reasoning capabilities. This is demonstrated in models such as Moondream2, which could not make any predictions with HTP prompting while giving a prediction with CoT prompting (see Figure 11).

From an implementation perspective, HTP prompting offers significant practical advantages, requiring only a single API call and reducing both latency and token consumption. For time-sensitive industrial applications, this reduced latency represents a substantial benefit. The token economy also favors HTP. While the initial prompt is larger, the overall token usage is typically lower due to eliminating multiple API calls.

The underlying mechanisms driving these performance differences provide insights for industrial deployment decision-making. Large models like GPT-4o and Claude 3.7 benefit from HTP prompting because their extensive parametric knowledge enables good reasoning within single inference steps. These models can simultaneously process visual information, access domain knowledge, and apply complex reasoning patterns without external scaffolding, explaining their consistent performance across the HTP approach.

Edge-optimized models operate under fundamentally different computational constraints that explain the dramatic performance variations observed in this study. The failure of models like Bunny-Phi2 or PaliGemma 3B under HTP prompting contrasts with their performance using CoT strategies. This pattern indicates that reduced parameter counts limit simultaneous processing of multiple reasoning components. CoT prompting addresses this limitation by decomposing complex interpretation tasks into sequential steps that fit within the computational constraints of smaller models.

The failure patterns provide diagnostic evidence for strategy selection in industrial scenarios. When edge models fail under HTP prompting, they typically produce no output or inconsistent responses, suggesting complete task breakdown rather than gradual performance degradation. CoT prompting prevents this failure mode by establishing clear reasoning checkpoints where models must commit to intermediate conclusions before proceeding. This structured approach explains why Moondream2 achieved 40.5% accuracy with CoT versus minimal functionality with HTP.

These performance patterns translate into actionable deployment strategies for varying industrial scenarios. Safety-critical applications requiring consistent interpretation benefit from HTP prompting with large models, which demonstrated stable performance across both continuous and discrete controls as shown in the presented figures. Resource-constrained environments should employ CoT prompting with edge models, accepting lower peak performance in exchange for reliable operation within computational limits. The diagnostic understanding of failure modes enables practitioners to anticipate model limitations and implement appropriate verification protocols rather than discovering failures during operation, particularly for scenarios involving ambiguous control states or challenging visual conditions where edge models historically demonstrate reduced reliability.

4.4. Fine-Tuning Impact

The fine-tuning of GPT-4o on industrial control images yielded substantial performance improvements across all evaluation metrics. As demonstrated previously, the fine-tuned GPT-4o model consistently outperformed its base version and all other models in the presented evaluation. For continuous control interpretation, the fine-tuned model achieved an MAE of 0.027. Similarly, PFSE (2.7% vs. 3.0%) improvements were observed, indicating that fine-tuning enhanced average accuracy and error consistency. For discrete control classification, the fine-tuned model achieved 78.0% accuracy, a relative improvement over the base model’s 67.2%. This classification improvement was even more pronounced in the MCC, where the fine-tuned model reached 0.73–0.74 compared to the base model’s 0.60–0.61, indicating better-balanced performance across different control states. Perhaps most significantly, the fine-tuned model is less sensitive to prompting strategy variations, maintaining consistent performance across both HTP and CoT approaches. This suggests that specialized training helps the model internalize the interpretation task, reducing reliance on prompt engineering. From a cost–benefit perspective, fine-tuning represents a significant initial investment but offers compelling long-term advantages. The fine-tuning process followed in this research used only 50 annotated control images, with resulting performance improvements that justify the small investment in industrial settings where interpretation errors carry operational or safety implications.

Table 5. Best performance achieved by each model category across continuous and discrete control interpretation.

Model Category	Best Continuous (MAE)	Best Discrete (Accuracy %)	Optimal Strategy
Fine-tuned GPT-4o	0.027	78.7	Both
General-purpose Large	0.030	67.2	HTP
Edge-optimized	0.064	60.0	Both

consolidates the best performance achieved by each model category across both control types.

Reproducibility considerations acknowledge both the strengths and limitations of OpenAI’s fine-tuning approach. While specific hyperparameters remain proprietary, the automatic optimization process does not guarantee identical convergence across different runs because learning rate, batch size, epochs, and optimizer details are not publicly specified. Independent researchers can replicate the methodology using identical training data formatting, the same base model and equivalent dataset size. Token consumption metrics enable transparent cost estimation using known pricing: fine-tuning training costs USD 25 per million training tokens, and inference costs USD 3.75 per million input tokens and USD 15 per million output tokens, applicable to image tokens billed like text.

Economic analysis demonstrates explicit trade-offs based on publicly verifiable pricing. Token accounting, reflecting image tokenization and prompt/response lengths, yields a training cost in the range of low single-dollar to low double-digit USD for 50 images and a few epochs, depending on image resolution and text length. Inference cost per thousand control interpretations similarly ranges from approximately USD 4 to USD 12, depending on image size and output length.

Cost-effectiveness extends beyond initial training to operational deployment. For industrial monitoring applications processing 1000 monthly readings, break-even analysis should be computed using the empirically estimated training cost, based on tokens and model runs, versus per-interpretation inference cost. For example, if training cost is USD 6 and per-reading inference is USD 0.006, break-even occurs after 1000 readings; if inference costs more (e.g., USD 0.012), break-even extends to 500–1000 readings.

5. Conclusions

This investigation presents a comparative analysis of VLMs for industrial control interpretation, evaluating their performance across diverse model categories and prompting strategies. The findings of the presented work demonstrate a clear performance hierarchy: the fine-tuned GPT-4o model consistently outperformed all alternatives, achieving the lowest error rates for continuous controls and the highest classification metrics for discrete controls. General-purpose VLMs, particularly GPT-4o and Claude 3.7 Sonnet, demonstrated strong capabilities even without domain-specific training, while edge-optimized models showed substantially lower performance, particularly in discrete control classification tasks. Regarding prompting strategies, the HTP approach generally yielded better performance for larger models, while CoT occasionally benefited smaller edge-optimized models by providing more guidance. These findings have significant practical implications for industrial monitoring applications, where the selection between model categories involves critical compromises between interpretation accuracy, computational requirements, and deployment constraints.

The traditional CNN-based approaches to industrial control interpretation represent a fundamentally different paradigm than the VLM-based methods evaluated in the presented study. While CNNs have demonstrated effectiveness in specific gauge reading tasks, they typically require extensive control-specific training datasets, often necessitating hundreds or thousands of labeled examples for each gauge type with limited transfer capability between different instrument designs. By contrast, the performed evaluation reveals that general-purpose VLMs offer remarkable zero-shot generalization capabilities, achieving acceptable performance across diverse control types without domain-specific training. This inherent understanding of visual controls substantially reduces the annotation burden characteristic of traditional Computer Vision approaches. Most significantly, fine-tuning results demonstrate that VLMs can achieve substantial performance improvements with minimal training data: the fine-tuned model used only 50 annotated control images yet delivered significant performance gains in both continuous and discrete control interpretation. This data efficiency represents a compelling advantage for industrial applications where collecting and annotating large control-specific datasets is often impractical or prohibitively expensive, suggesting that fine-tuned VLMs offer an optimal balance between implementation effort and interpretation reliability.

Beyond data efficiency, the presented results show that fine-tuned VLMs maintain stable performance across varying lighting conditions, instrument designs, and prompt formulations—scenarios where prior methods in the literature often experienced significant performance degradation. This robustness to domain shifts positions the proposed approach as a more dependable solution for real-world deployments, where variability and environmental factors are unavoidable. In contrast, earlier CNN-based and modular systems typically required retraining or extensive pre-processing to sustain performance under such changes.

Based on the presented analysis, some implementation recommendations tailored to specific industrial requirements are recommended. For safety-critical applications where interpretation accuracy is paramount, fine-tuned VLMs using the HTP prompting strategy represent the optimal solution. Base models like GPT-4o or Claude 3.7 Sonnet offer a compelling balance between performance and implementation simplicity for general monitoring scenarios with moderate accuracy requirements. Resource-restricted environments may leverage edge-optimized models with CoT prompting, though with the understanding that interpretation reliability will be substantially reduced. Deployment considerations must account for operational environments, unstable network connectivity may necessitate edge solutions despite their limitations, while continuous monitoring applications should prioritize HTP prompting to minimize latency and token consumption. Several limitations and promising research directions emerge from this work. The dataset scope, while representative of common industrial control types, represents a foundational evaluation rather than comprehensive coverage of all industrial variants. Real-world industrial environments present additional challenges including chemical corrosion, structural degradation, emergency conditions, and hundreds of specialized gauge configurations that extend beyond the current evaluation scope. The 249 control samples used in this study provide sufficient statistical power for comparative model evaluation while enabling rigorous analysis across multiple architectures and prompting strategies. Industrial deployments typically involve standardized instrumentation within specific facilities, where control types and environmental conditions remain relatively consistent, making the focused approach applicable to many practical scenarios. Future research should investigate transformer distillation techniques to improve edge model performance, explore multimodal retrieval augmentation to enhance interpretation accuracy for specialized instruments, develop hybrid architectures that balance reasoning capabilities with efficiency requirements, and validate performance across larger datasets encompassing extreme environmental conditions. The framework established here provides a systematic methodology for such expanded evaluations while maintaining rigorous comparative analysis standards, enabling incremental scaling to address broader industrial complexity as domain-specific requirements emerge. The analysis of error origins indicates that continuous control deviations arise mainly from visual artefacts such as reflections, blurred needles, or ambiguous scales, whereas discrete errors are concentrated in cases of visual similarity between adjacent states or partial occlusion. These findings emphasize that errors are not arbitrary but traceable to identifiable operational factors, which provides a clear pathway for rectification through better imaging practices, targeted fine-tuning, and redundancy checks in safety-critical systems. Ultimately, this work demonstrates that VLMs present a paradigm shift for industrial control interpretation, offering unprecedented generalization capabilities that can transform monitoring applications across diverse industrial environments.