Optimizing Random Forest with Hybrid Swarm Intelligence Algorithms for Predicting Shear Bond Strength of Cable Bolts
Abstract
1. Introduction
2. Methods
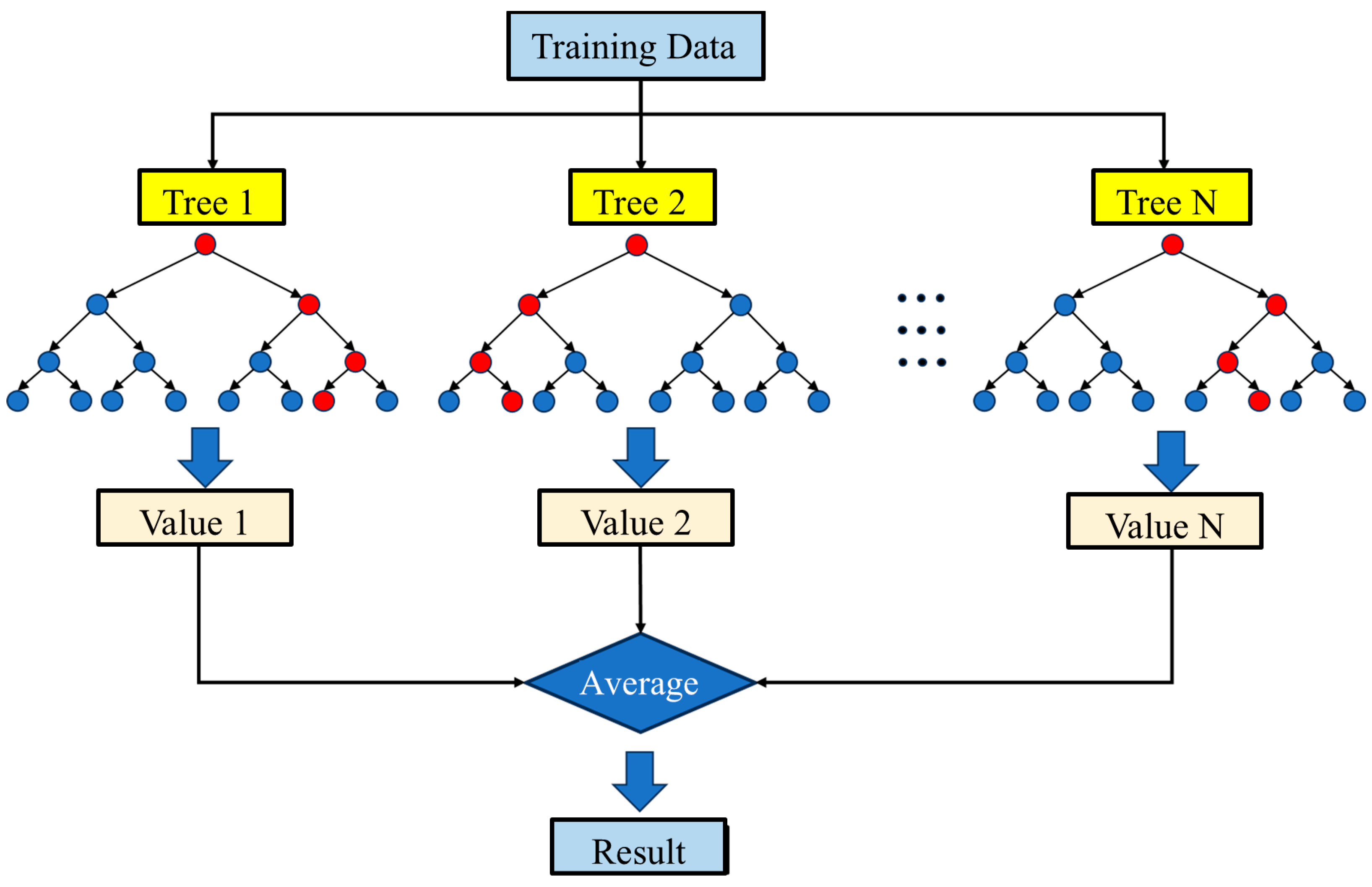
2.1. Random Forest (RF)
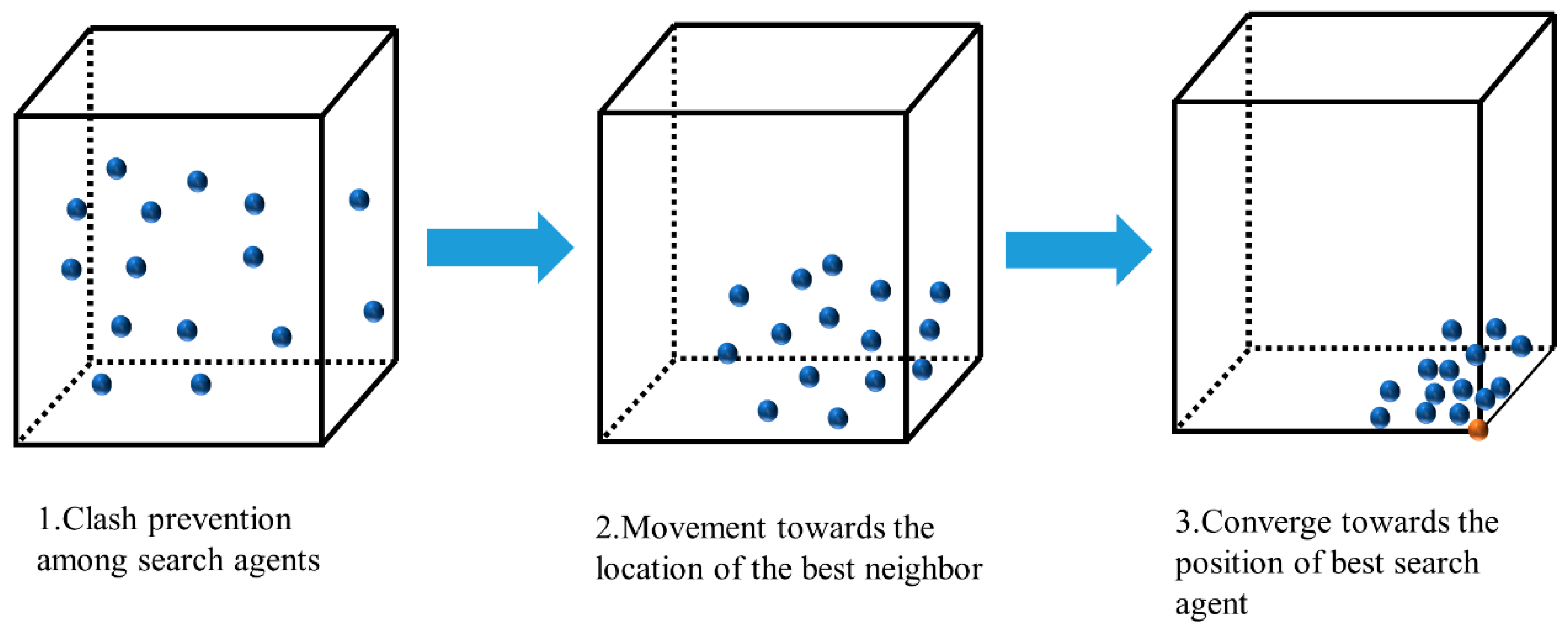
2.2. Tunicate Swarm Algorithm (TSA)
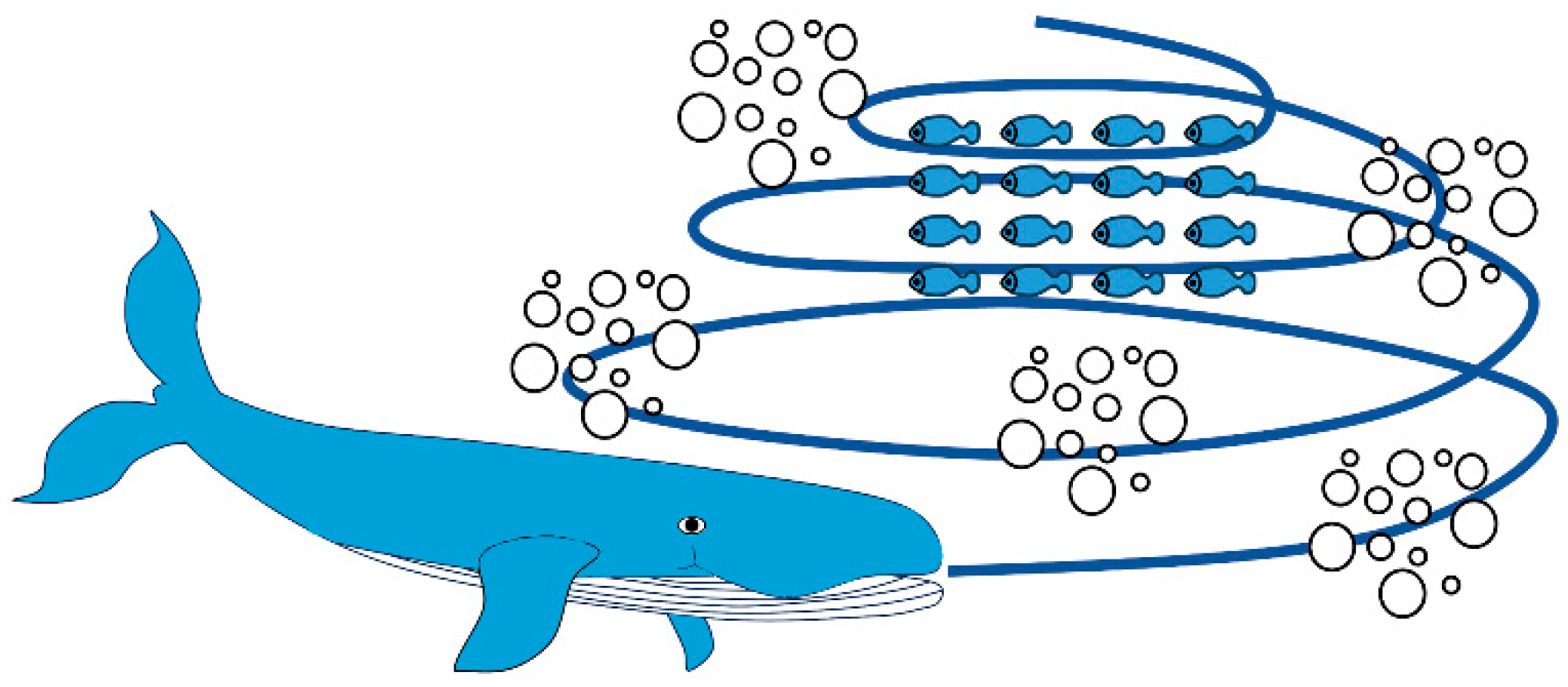
2.3. Whale Optimization Algorithm (WOA)
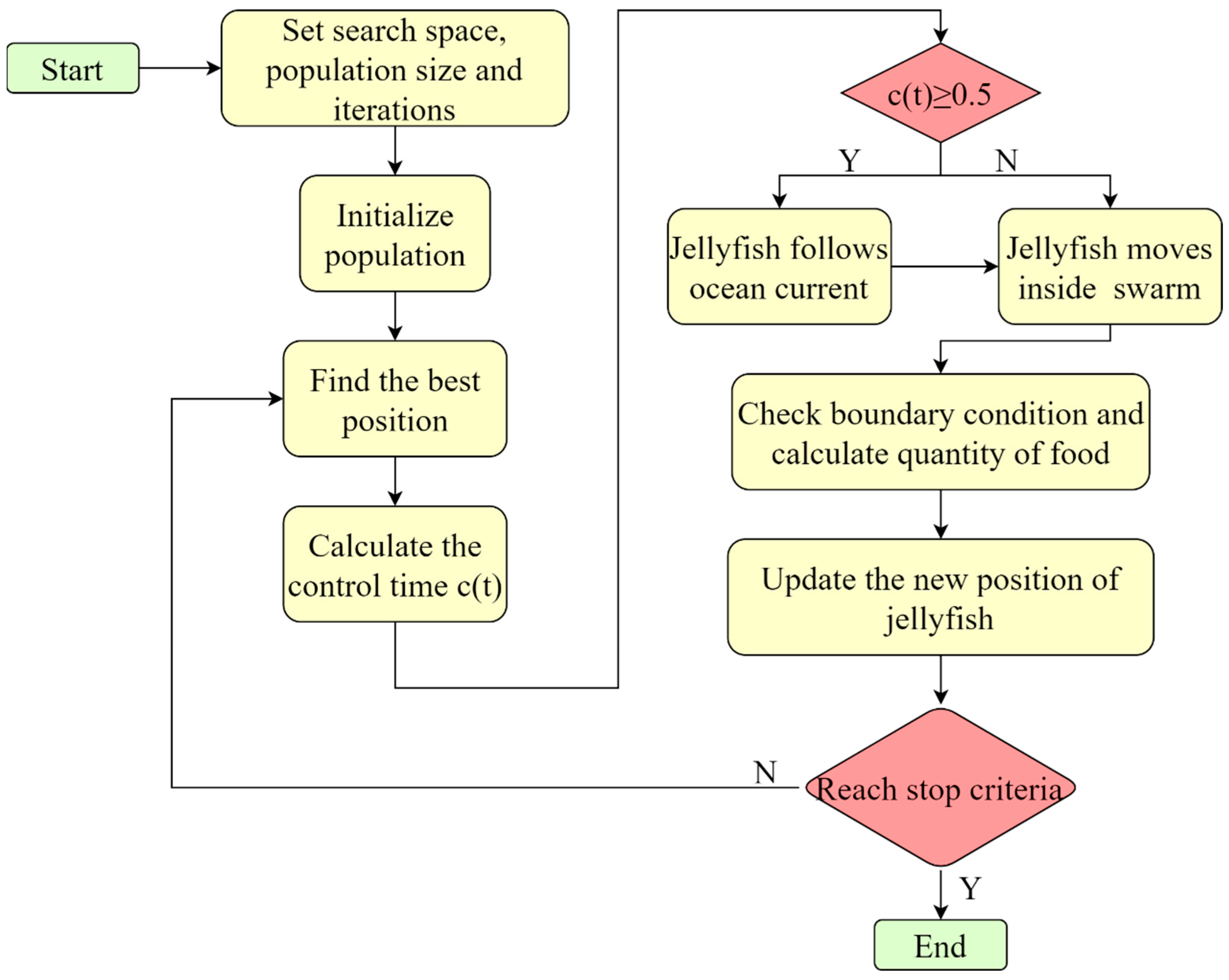
2.4. Jellyfish Search Optimizer (JSO)
3. Data Preparation
3.1. Data Source
3.2. Input Parameter Selection
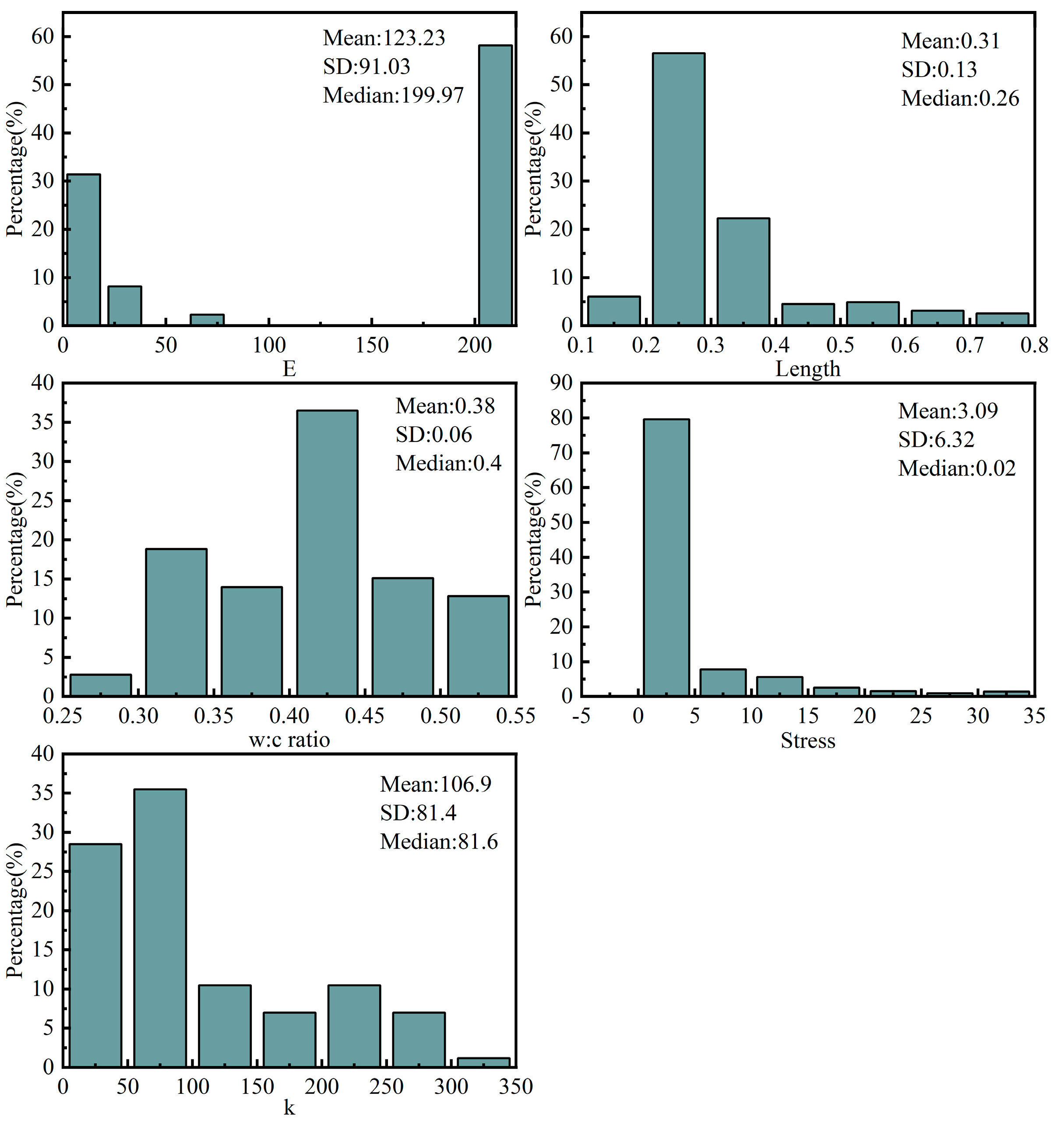
3.3. Data Augmentation
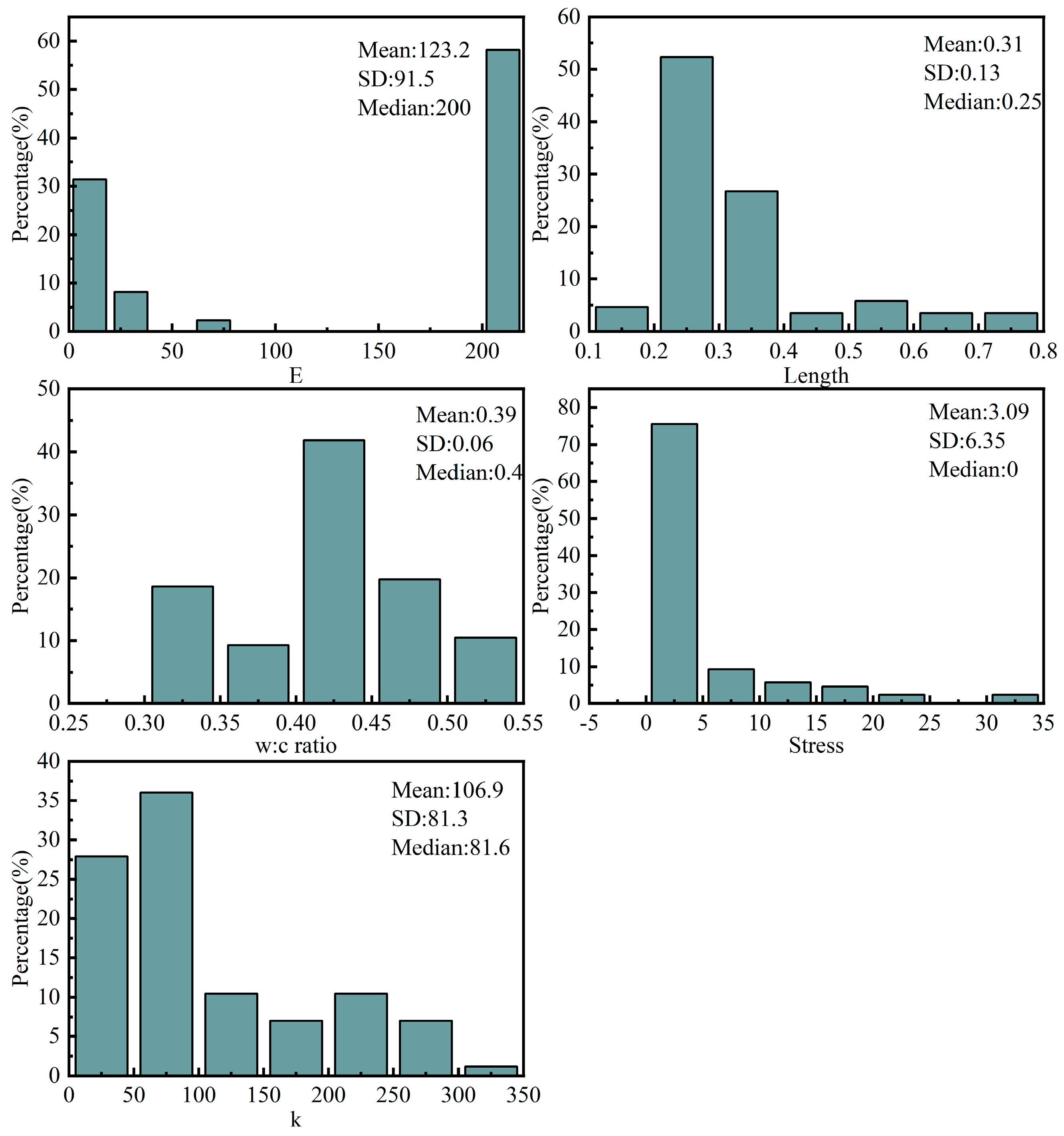
3.4. Data Distribution
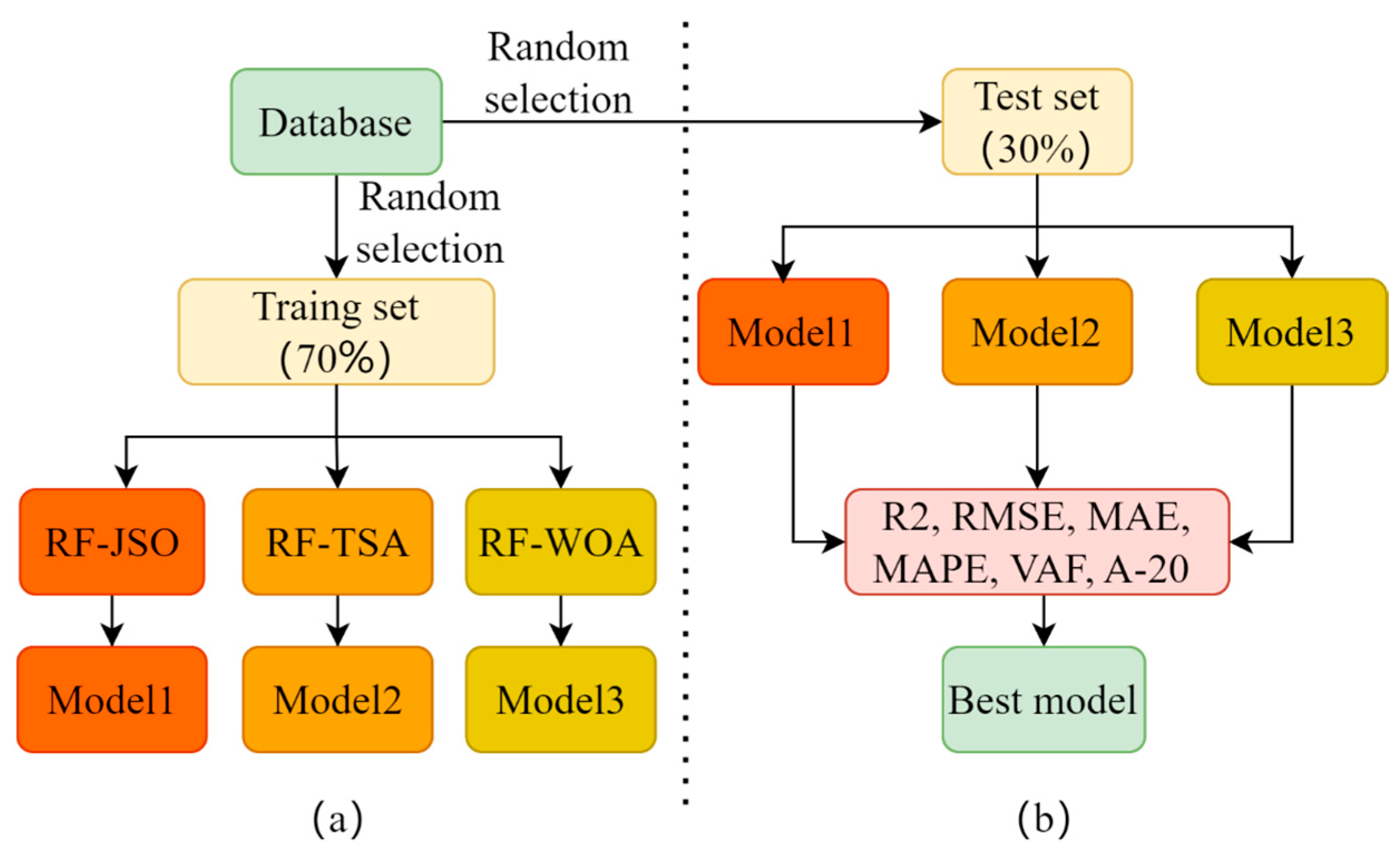
4. Model Development
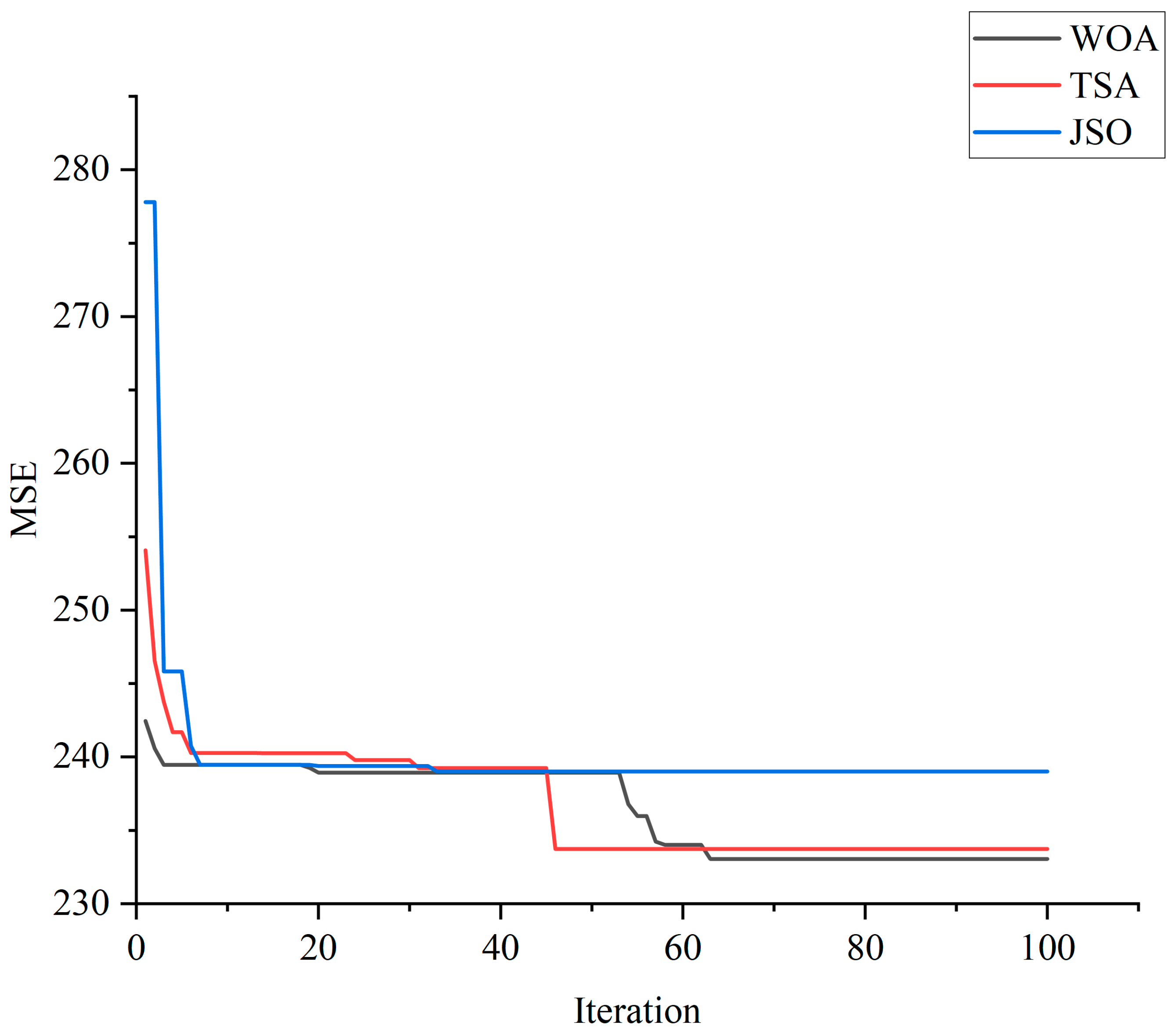
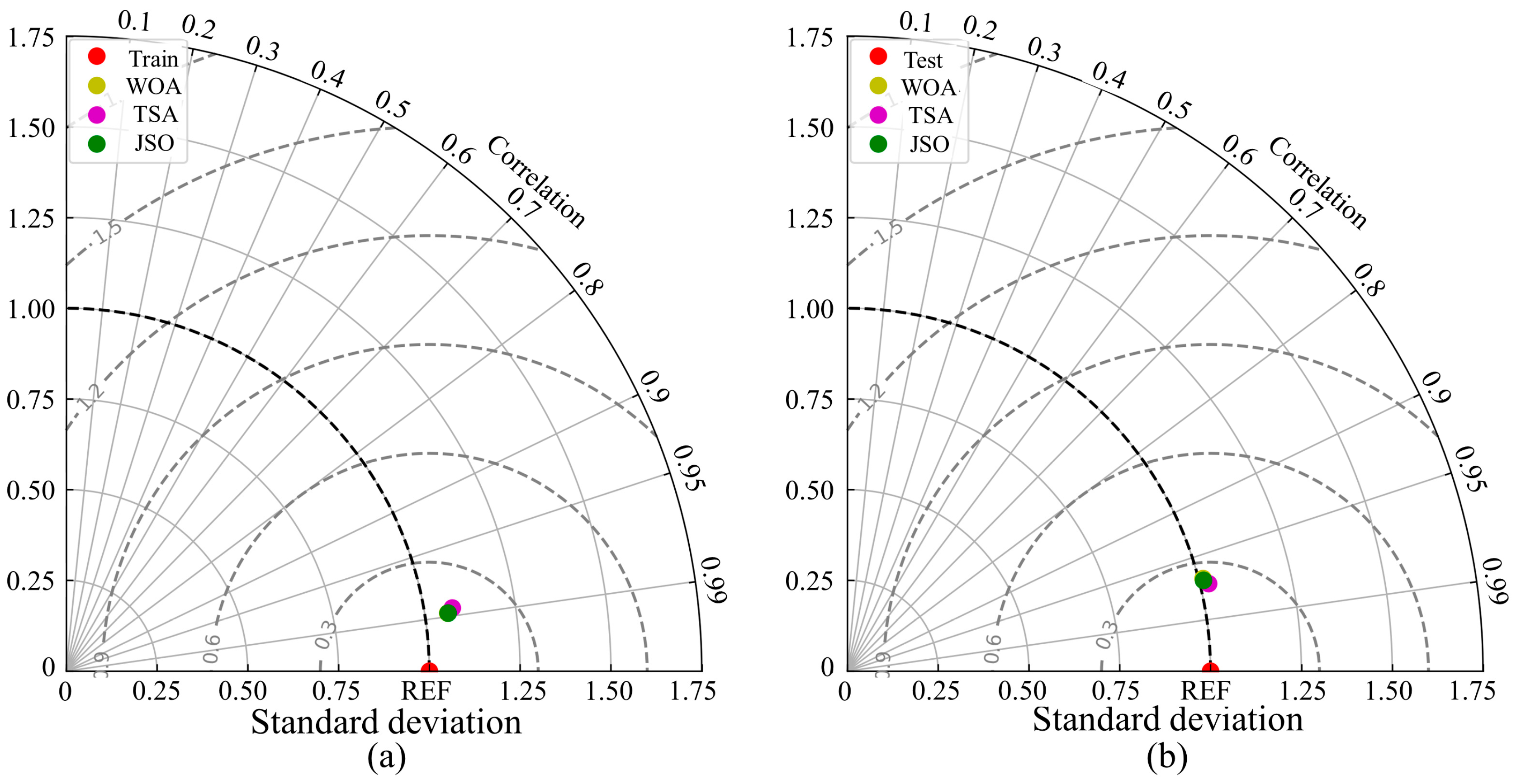
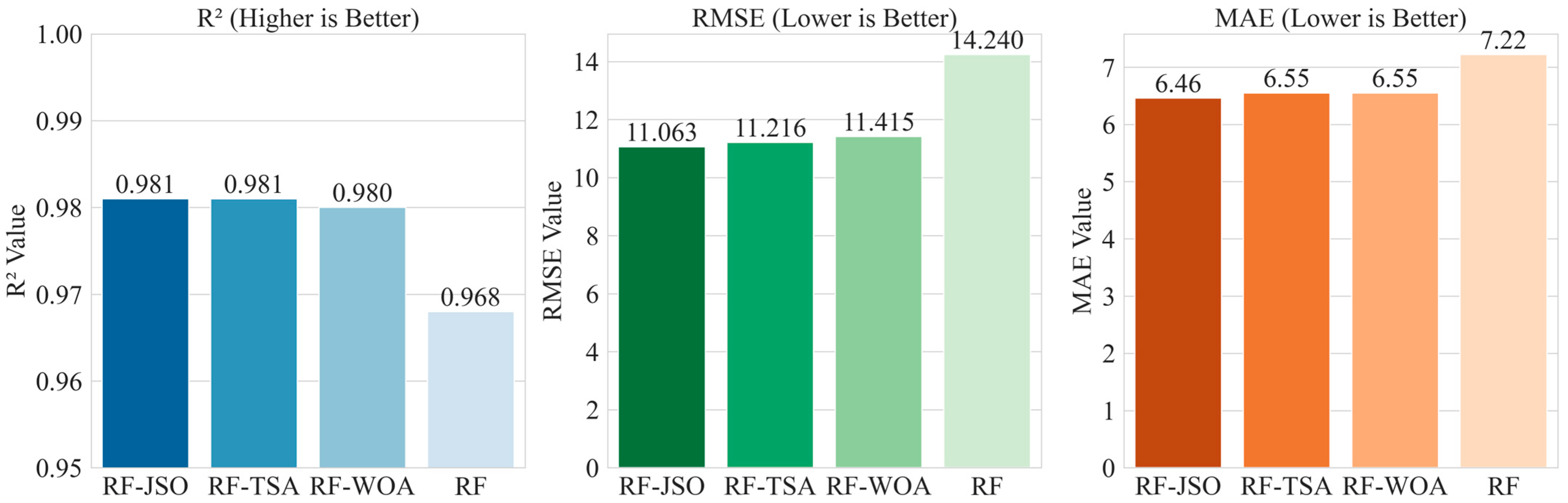
5. Results and Discussion
5.1. Selecting the Best Model
5.2. Model Interpretation
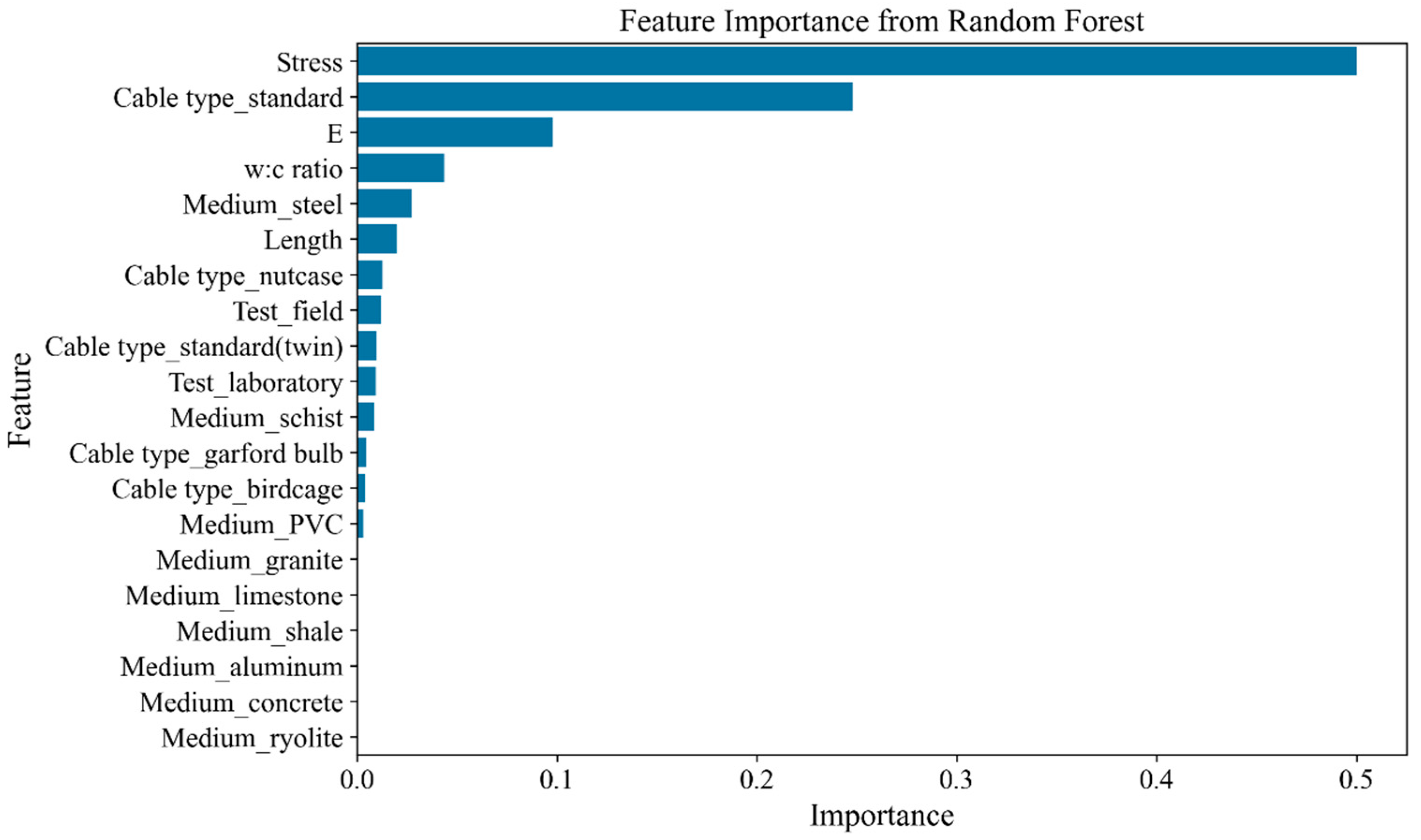
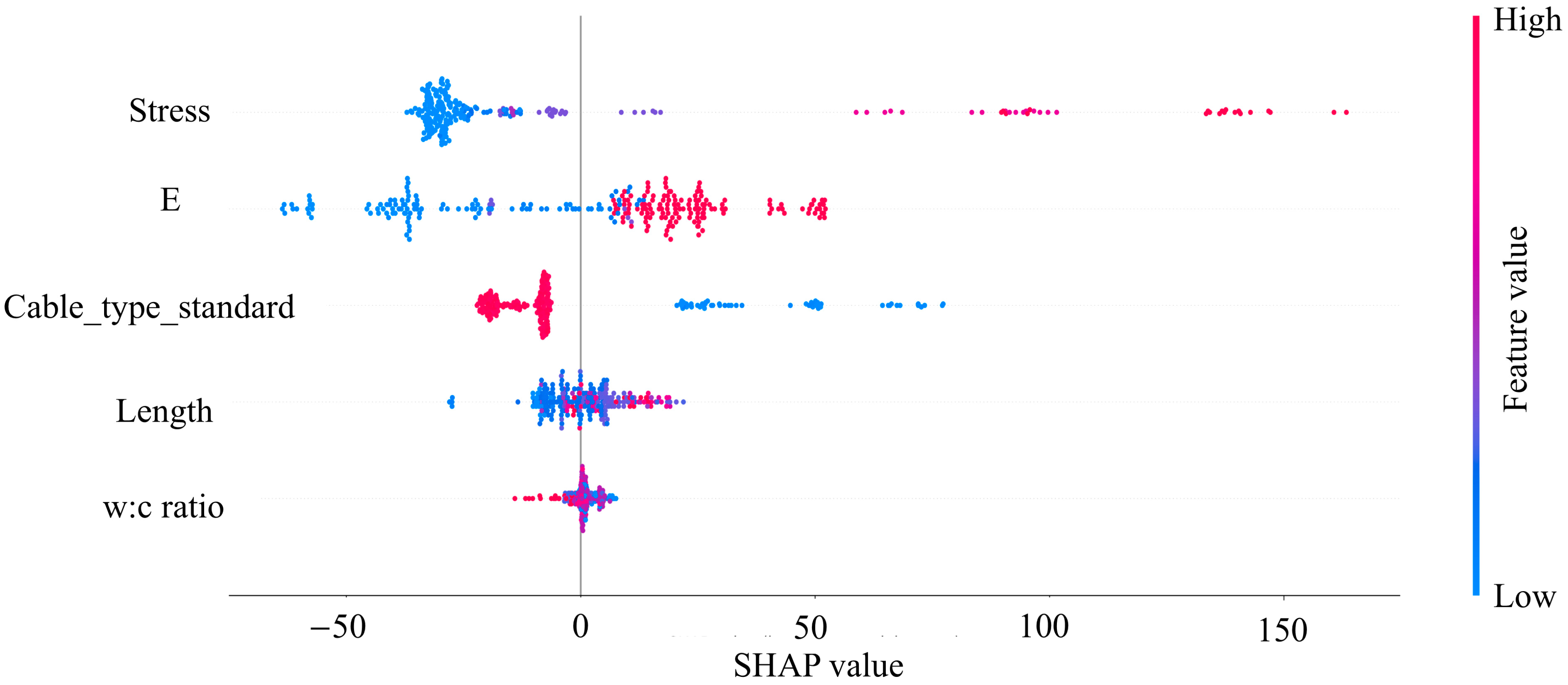
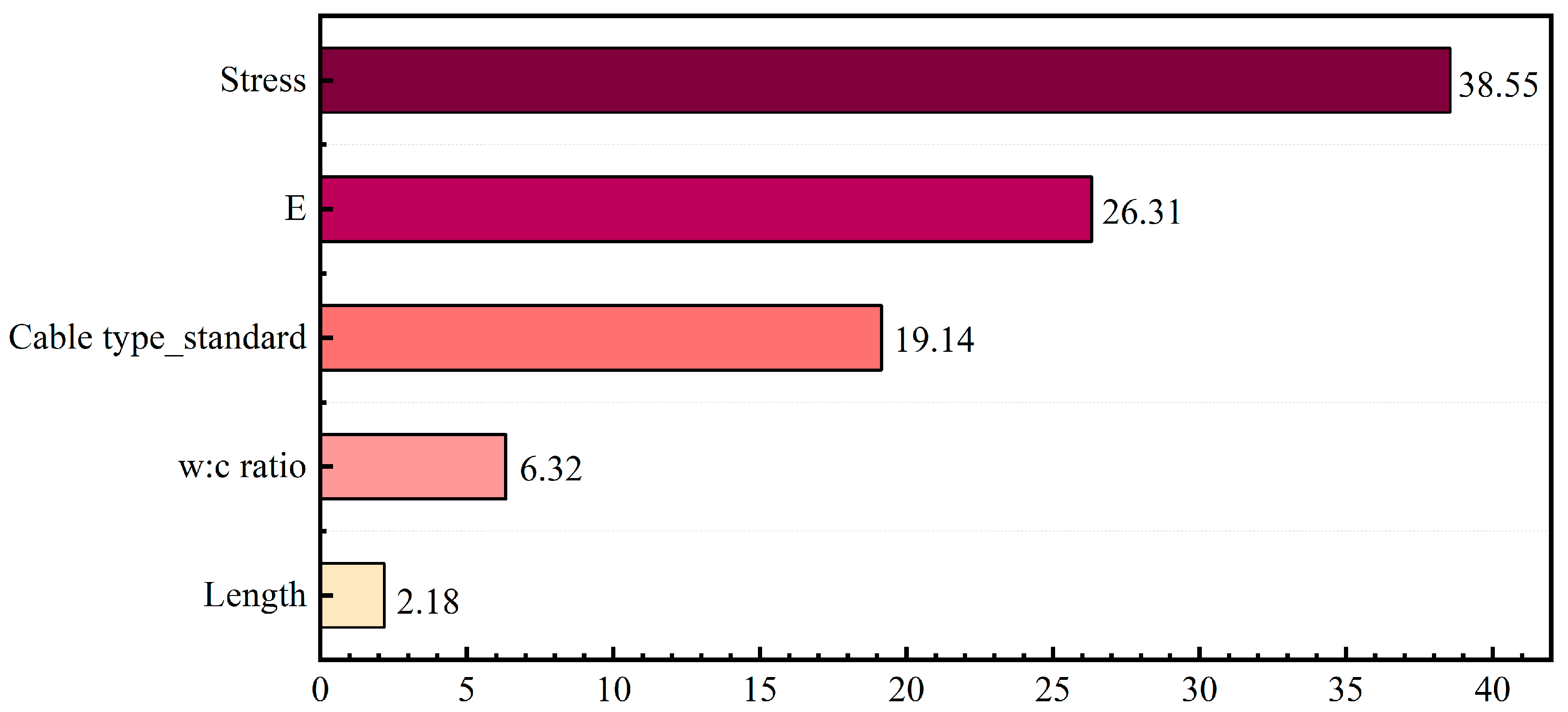
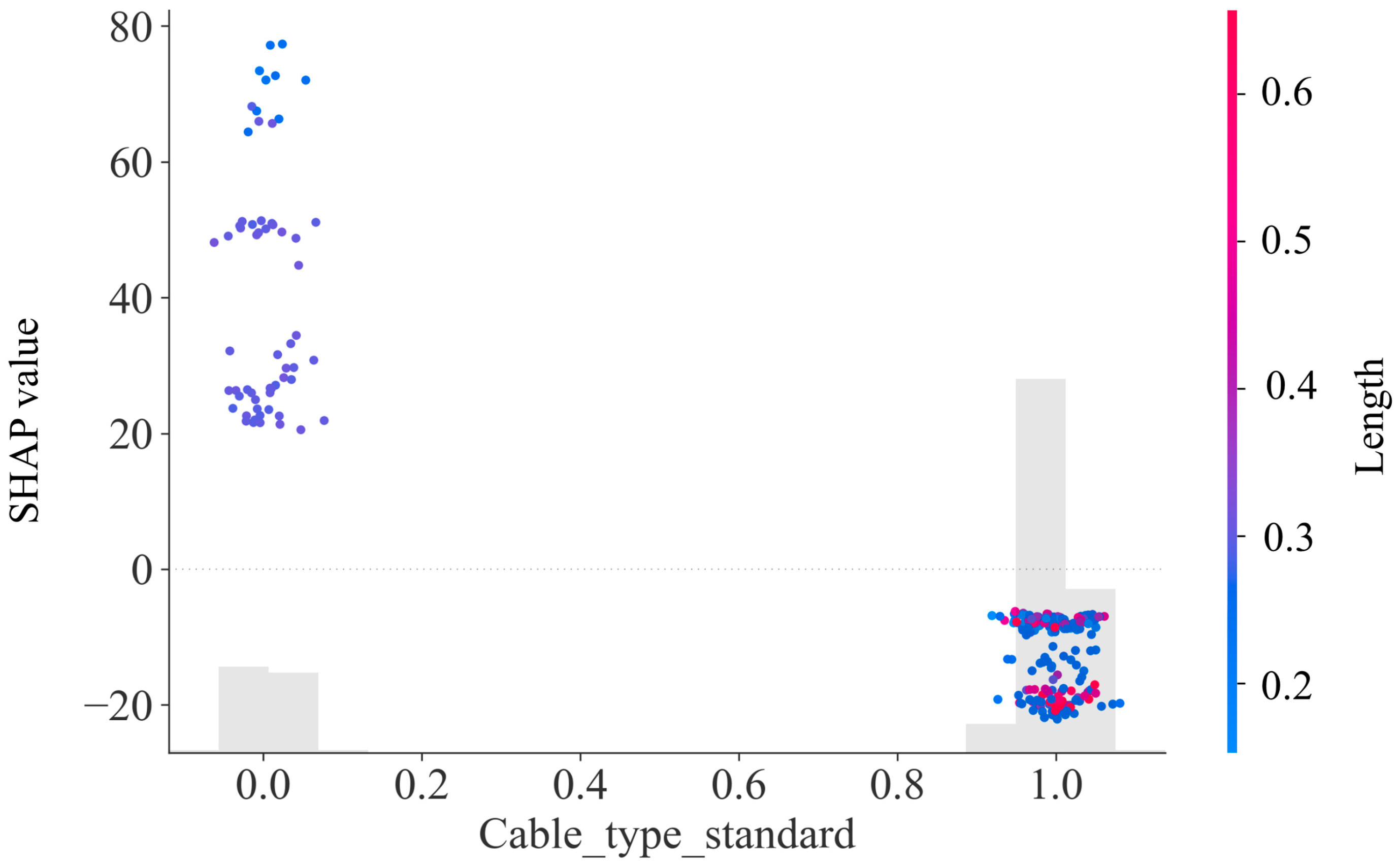
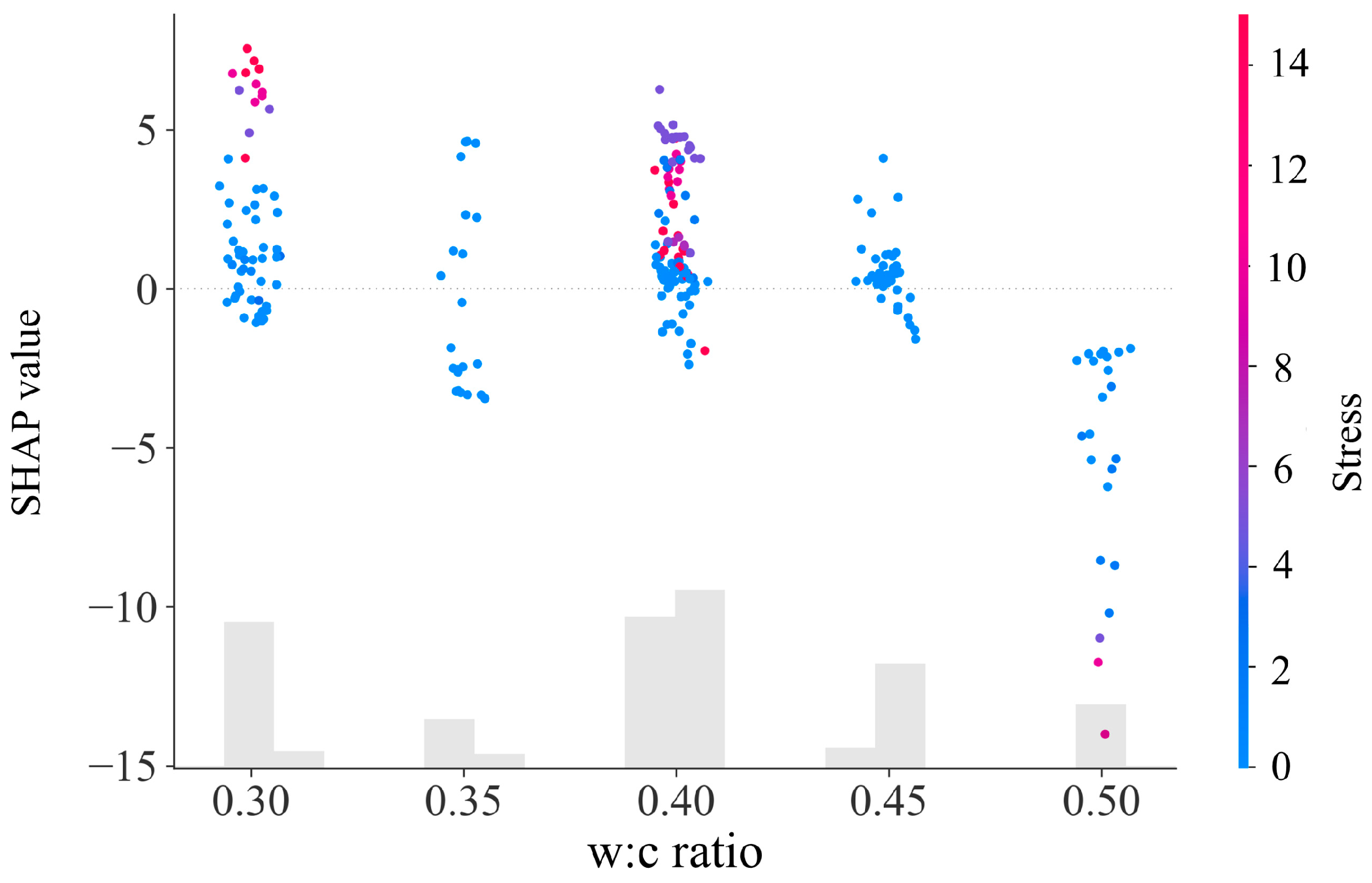
5.2.1. Importance Analysis of Input Variables
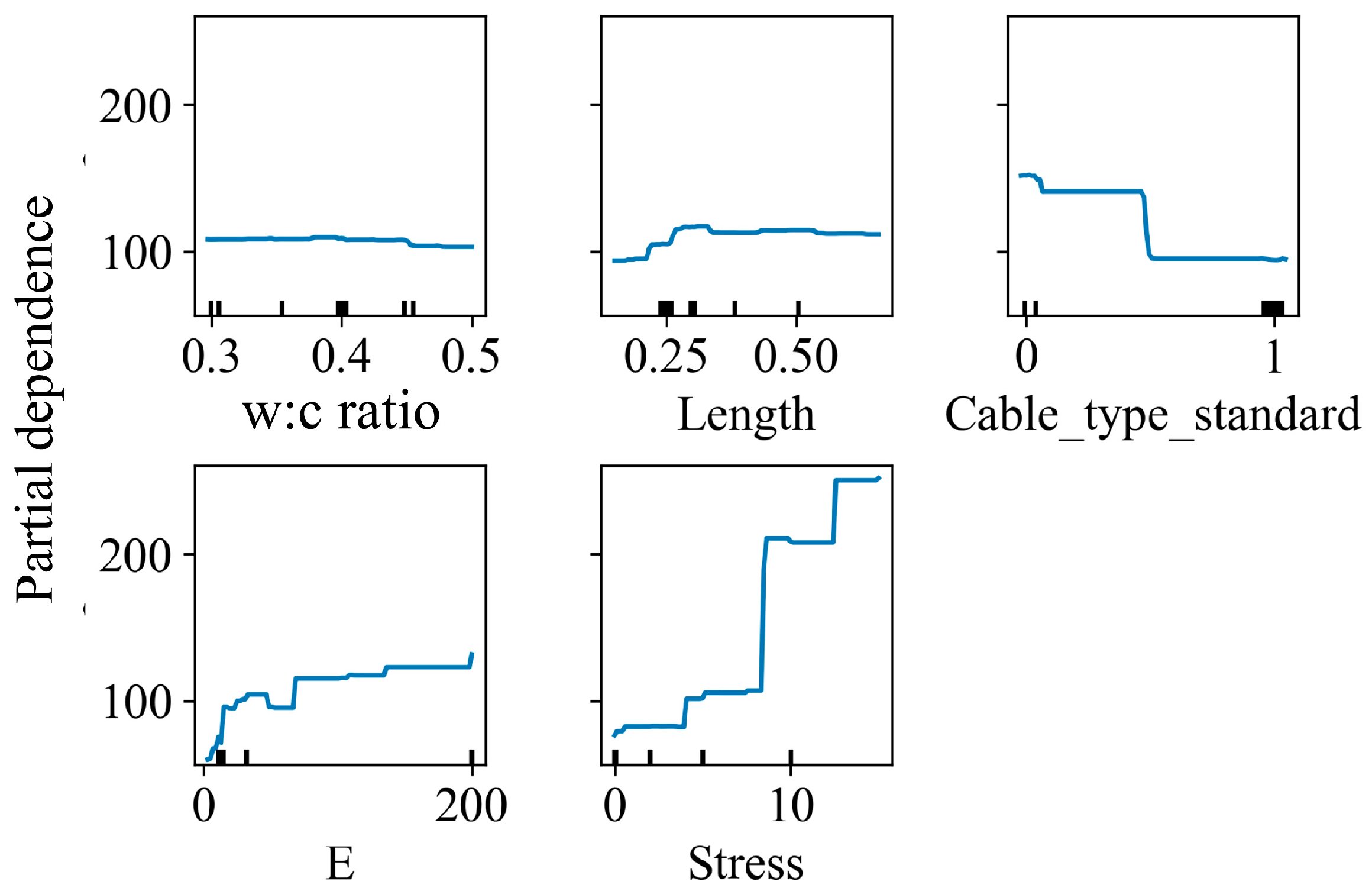
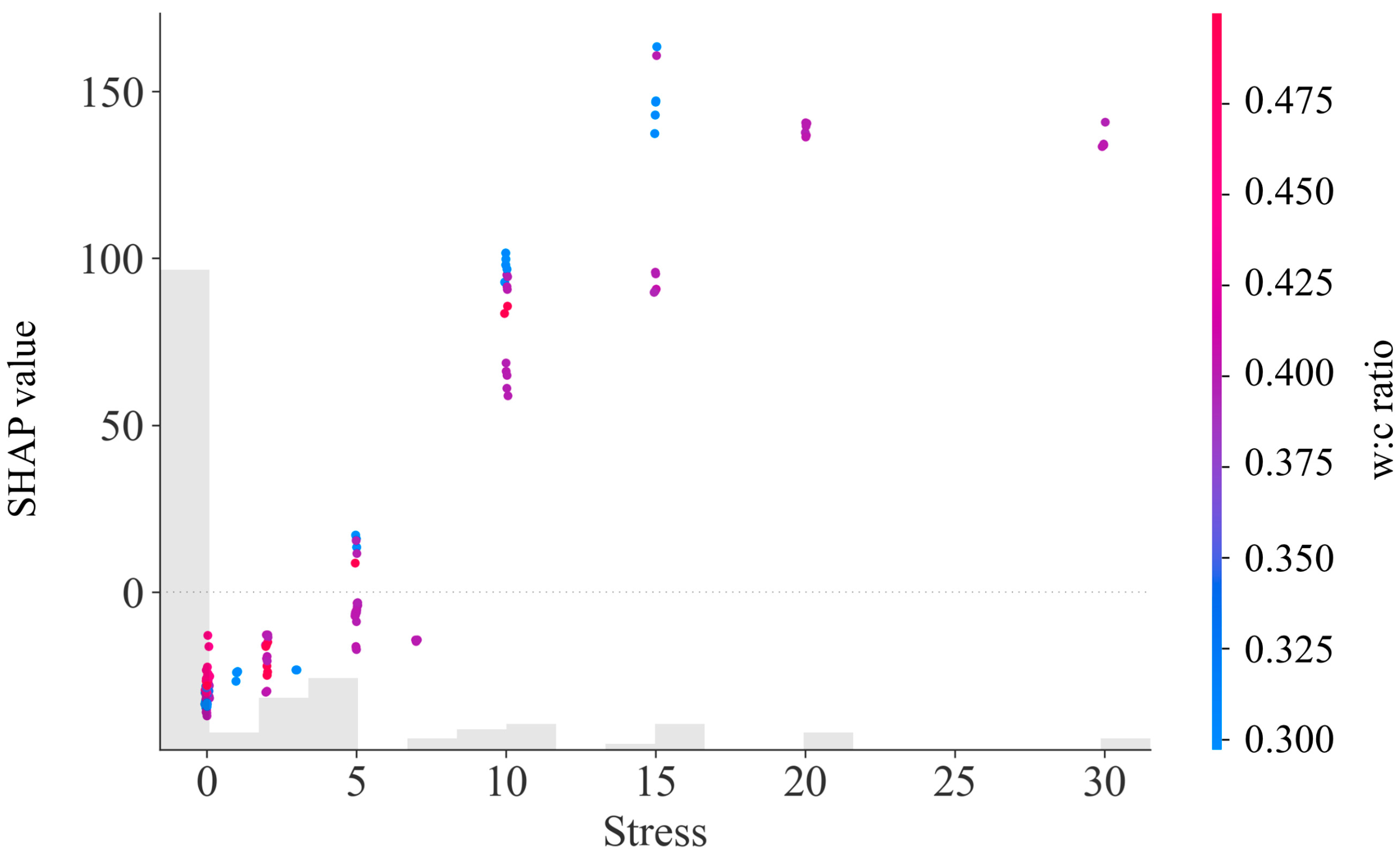
5.2.2. Analysis of the Impact of Changes in Input Variables
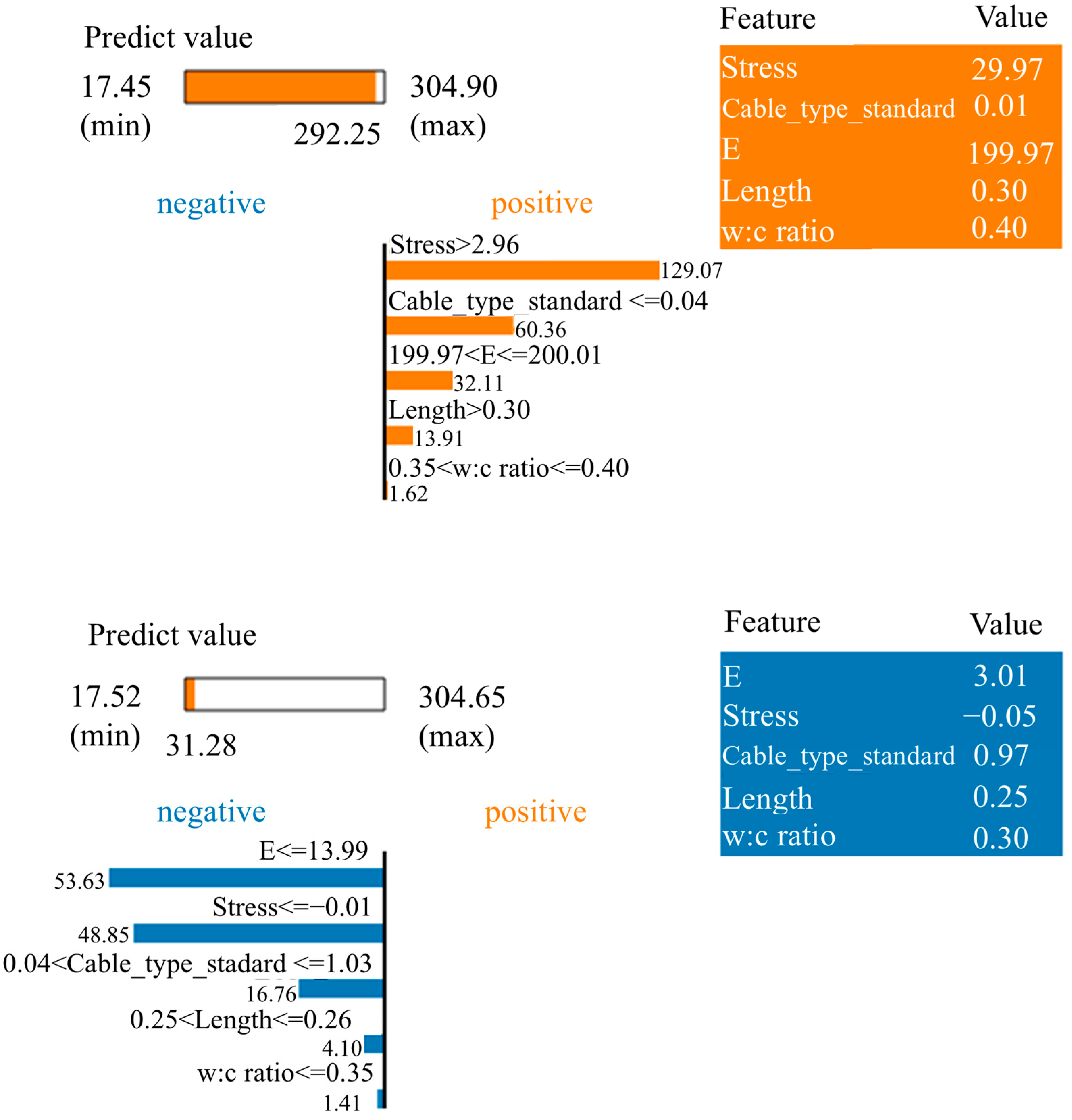
5.2.3. LIME Analysis of Specific Points
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jahangir, E.; Blanco-Martín, L.; Hadj-Hassen, F.; Tijani, M. Development and application of an interface constitutive model for fully grouted rock-bolts and cable-bolts. J. Rock Mech. Geotech. Eng. 2021, 13, 811–819. [Google Scholar] [CrossRef]
- Singh, S.; Srivastava, A.K. Numerical simulation of pull-out test on cable bolts. Mater. Today Proc. 2021, 45, 6332–6340. [Google Scholar] [CrossRef]
- Xu, D.-P.; Jiang, Q.; Li, S.-J.; Qiu, S.-L.; Duan, S.-Q.; Huang, S.-L. Safety assessment of cable bolts subjected to tensile loads. Comput. Geotech. 2020, 128, 103832. [Google Scholar] [CrossRef]
- Salcher, M.; Bertuzzi, R. Results of pull tests of rock bolts and cable bolts in Sydney sandstone and shale. Tunn. Undergr. Space Technol. 2018, 74, 60–70. [Google Scholar] [CrossRef]
- Thenevin, I.; Blanco-Martín, L.; Hadj-Hassen, F.; Schleifer, J.; Lubosik, Z.; Wrana, A. Laboratory pull-out tests on fully grouted rock bolts and cable bolts: Results and lessons learned. J. Rock Mech. Geotech. Eng. 2017, 9, 843–855. [Google Scholar] [CrossRef]
- Fu, M.; Huang, S.; Fan, K.; Liu, S.; He, D.; Jia, H. Study on the relationship between the maximum anchoring force and anchoring length of resin-anchored bolts of hard surrounding rocks based on the main slip interface. Constr. Build. Mater. 2023, 409, 134000. [Google Scholar] [CrossRef]
- Chen, J.; Saydam, S.; Hagan, P.C. Numerical simulation of the pull-out behaviour of fully grouted cable bolts. Constr. Build. Mater. 2018, 191, 1148–1158. [Google Scholar] [CrossRef]
- Chen, J.; Saydam, S.; Hagan, P.C. An analytical model of the load transfer behavior of fully grouted cable bolts. Constr. Build. Mater. 2015, 101, 1006–1015. [Google Scholar] [CrossRef]
- Nourizadeh, H.; Mirzaghorbanali, A.; Serati, M.; Mutaz, E.; McDougall, K.; Aziz, N. Failure characterization of fully grouted rock bolts under triaxial testing. J. Rock Mech. Geotech. Eng. 2024, 16, 778–789. [Google Scholar] [CrossRef]
- Shahani, N.; Kamran, M.; Zheng, X.; Liu, C. Predictive modeling of drilling rate index using machine learning approaches: LSTM, simple RNN, and RFA. Pet. Sci. Technol. 2022, 40, 534–555. [Google Scholar] [CrossRef]
- Kamran, M.; Faizan, M.; Wang, S.; Han, B.; Wang, W.-Y. Generative AI and Prompt Engineering: Transforming Rockburst Prediction in Underground Construction. Buildings 2025, 15, 1281. [Google Scholar] [CrossRef]
- Huang, S.; Zhou, J. An enhanced stability evaluation system for entry-type excavations: Utilizing a hybrid bagging-SVM model, GP and kriging techniques. J. Rock Mech. Geotech. Eng. 2025, 17, 2360–2373. [Google Scholar] [CrossRef]
- Zhang, Y.-l.; Qiu, Y.-g.; Armaghani, D.J.; Monjezi, M.; Zhou, J. Enhancing rock fragmentation prediction in mining operations: A Hybrid GWO-RF model with SHAP interpretability. J. Cent. South Univ. 2024, 31, 2916–2929. [Google Scholar] [CrossRef]
- Ali, F.; Masoud, S.S.; Behnam, F.; Mohamadreza, C. Modeling the load-displacement curve for fully-grouted cable bolts using Artificial Neural Networks. Int. J. Rock Mech. Min. Sci. 2016, 86, 261–268. [Google Scholar] [CrossRef]
- Jodeiri Shokri, B.; Mirzaghorbanali, A.; McDougall, K.; Karunasena, W.; Nourizadeh, H.; Entezam, S.; Hosseini, S.; Aziz, N. Data-Driven Optimised XGBoost for Predicting the Performance of Axial Load Bearing Capacity of Fully Cementitious Grouted Rock Bolting Systems. Appl. Sci. 2024, 14, 9925. [Google Scholar] [CrossRef]
- Soufi, A.; Zerradi, Y.; Bahi, A.; Souissi, M.; Ouadif, L. Machine Learning Models for Cable Bolt Load-Bearing Capacity in Sublevel Open Stope Mining. Min. Metall. Explor. 2025, 42, 1651–1675. [Google Scholar] [CrossRef]
- Bouteldja, M. Design of Cable Bolts Using Numerical Modelling. PhD Dissertation, McGill University, Montreal, QC, Canada, 2000. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- He, B.; Armaghani, D.J.; Lai, S.H. Assessment of tunnel blasting-induced overbreak: A novel metaheuristic-based random forest approach. Tunn. Undergr. Space Technol. 2023, 133, 104979. [Google Scholar] [CrossRef]
- Zhou, J.; Dai, Y.; Khandelwal, M.; Monjezi, M.; Yu, Z.; Qiu, Y. Performance of Hybrid SCA-RF and HHO-RF Models for Predicting Backbreak in Open-Pit Mine Blasting Operations. Nat. Resour. Res. 2021, 30, 4753–4771. [Google Scholar] [CrossRef]
- Kaur, S.; Awasthi, L.K.; Sangal, A.L.; Dhiman, G. Tunicate Swarm Algorithm: A new bio-inspired based metaheuristic paradigm for global optimization. Eng. Appl. Artif. Intell. 2020, 90, 103541. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Watkins, W.A.; Schevill, W.E. Aerial Observation of Feeding Behavior in Four Baleen Whales: Eubalaena glacialis, Balaenoptera borealis, Megaptera novaeangliae, and Balaenoptera physalus. J. Mammal. 1979, 60, 155–163. [Google Scholar] [CrossRef]
- Chou, J.-S.; Truong, D.-N. A novel metaheuristic optimizer inspired by behavior of jellyfish in ocean. Appl. Math. Comput. 2021, 389, 125535. [Google Scholar] [CrossRef]
- Mariottini, G.L.; Pane, L. Mediterranean Jellyfish Venoms: A Review on Scyphomedusae. Mar. Drugs 2010, 8, 1122–1152. [Google Scholar] [CrossRef] [PubMed]
- Medawela, S.; Armaghani, D.J.; Indraratna, B.; Kerry Rowe, R.; Thamwattana, N. Development of an advanced machine learning model to predict the pH of groundwater in permeable reactive barriers (PRBs) located in acidic terrain. Comput. Geotech. 2023, 161, 105557. [Google Scholar] [CrossRef]
- Mei, X.; Li, C.; Sheng, Q.; Cui, Z.; Zhou, J.; Dias, D. Development of a hybrid artificial intelligence model to predict the uniaxial compressive strength of a new aseismic layer made of rubber-sand concrete. Mech. Adv. Mater. Struct. 2023, 30, 2185–2202. [Google Scholar] [CrossRef]
- Gholamy, A.; Kreinovich, V.; Kosheleva, O. Why 70/30 or 80/20 Relation Between Training and Testing Sets: A Pedagogical Explanation. Departmental Technical Reports (CS). 12 March 2018. Available online: https://scholarworks.utep.edu/cs_techrep/1209 (accessed on 12 August 2025).
- Pham, B.T.; Jaafari, A.; Prakash, I.; Bui, D.T. A novel hybrid intelligent model of support vector machines and the MultiBoost ensemble for landslide susceptibility modeling. Bull. Eng. Geol. Environ. 2019, 78, 2865–2886. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. Overview of Supervised Learning. In The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Hastie, T., Tibshirani, R., Friedman, J., Eds.; Springer: New York, NY, USA, 2009; pp. 9–41. [Google Scholar]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Zorlu, K.; Gokceoglu, C.; Ocakoglu, F.; Nefeslioglu, H.A.; Acikalin, S. Prediction of uniaxial compressive strength of sandstones using petrography-based models. Eng. Geol. 2008, 96, 141–158. [Google Scholar] [CrossRef]
- Winter, E. Chapter 53 The shapley value. In Handbook of Game Theory with Economic Applications; Elsevier: Amsterdam, The Netherlands, 2002; Volume 3, pp. 2025–2054. [Google Scholar]
- Koh, P.W.; Liang, P. Understanding black-box predictions via influence functions. In Proceedings of the 34th International Conference on Machine Learning—Volume 70, Sydney, NSW, Australia, 6–11 August 2017; pp. 1885–1894. [Google Scholar]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. “Why Should I Trust You?”: Explaining the Predictions of Any Classifier. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 1135–1144. [Google Scholar]
- Ni, Z.; Yang, J.; Fan, Y.; Hang, Z.; Zeng, B.; Feng, C. Multi-factors effects analysis of nonlinear vibration of FG-GNPRC membrane using machine learning. Mech. Based Des. Struct. Mach. 2024, 52, 8988–9014. [Google Scholar] [CrossRef]
- Kashem, A.; Karim, R.; Malo, S.; Das, P.; Datta, S.; Alharthai, M. Hybrid data-driven approaches to predicting the compressive strength of ultra-high-performance concrete using SHAP and PDP analyses. Case Stud. Constr. Mater. 2024, 20, e02991. [Google Scholar] [CrossRef]
- Zhou, J.; Xu, M.; Li, C. Prediction of dam failure peak outflow using a novel explainable random forest based on metaheuristic algorithms. J. Hydrol. 2025, 662, 133767. [Google Scholar] [CrossRef]
- Nikmah, T.L.; Syafei, R.M.; Muzayanah, R.; Salsabila, A.; Nurdin, A.A. Prediction Of Used Car Prices Using K-Nearest Neighbour, Random Forest and Adaptive Boosting Algorithm. Indones. Community Optim. Comput. Appl. 2023, 1, 17–22. [Google Scholar]
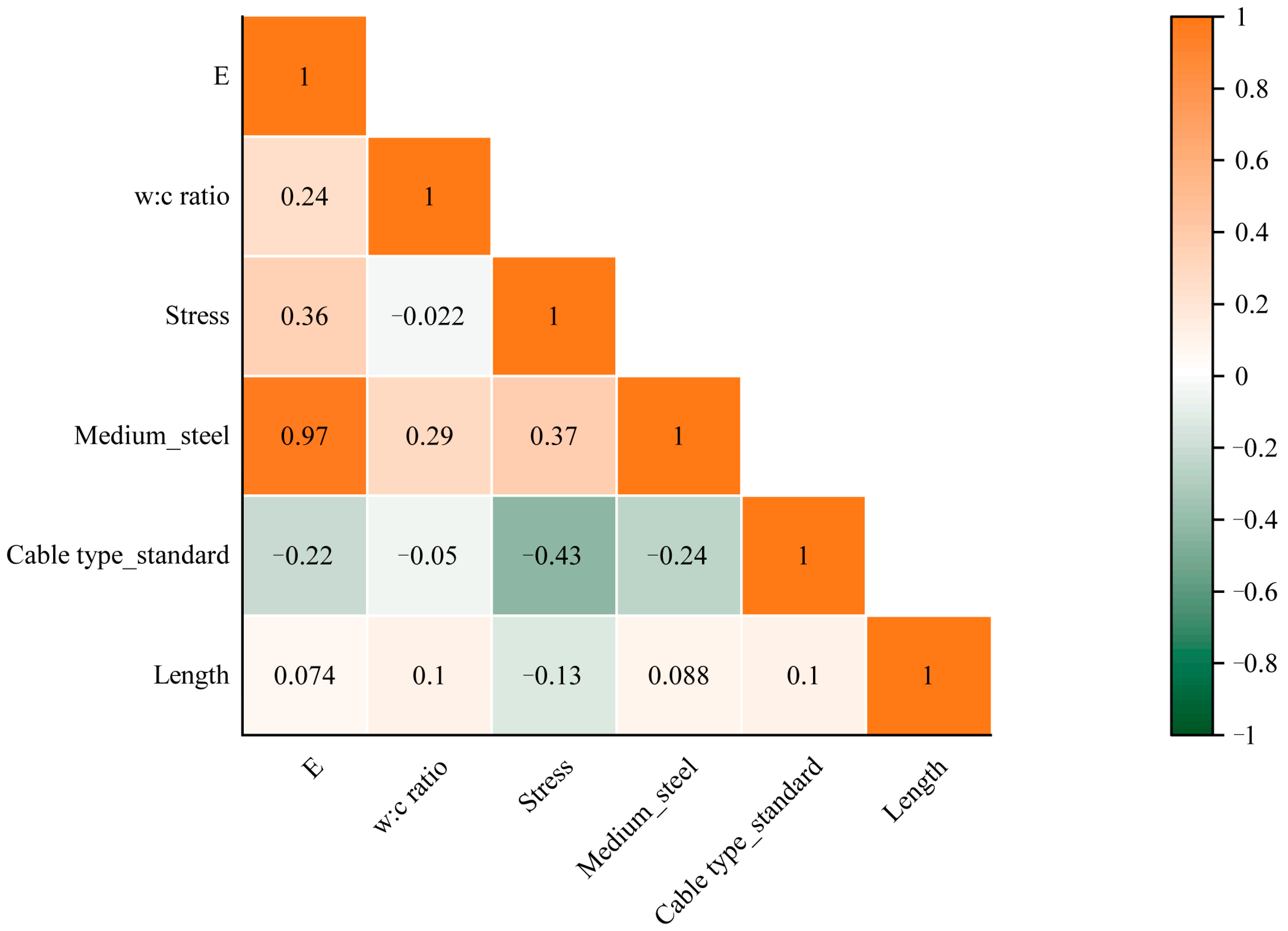


| Feature | VIF Value |
|---|---|
| E | 1.255409 |
| Length | 1.045857 |
| w:c ratio | 1.085248 |
| Stress | 1.385977 |
| Cable_type_standard | 1.235832 |
| Hyper-Parameters | Range | RF | RF-WOA | RF-JSO | RF-TSA |
|---|---|---|---|---|---|
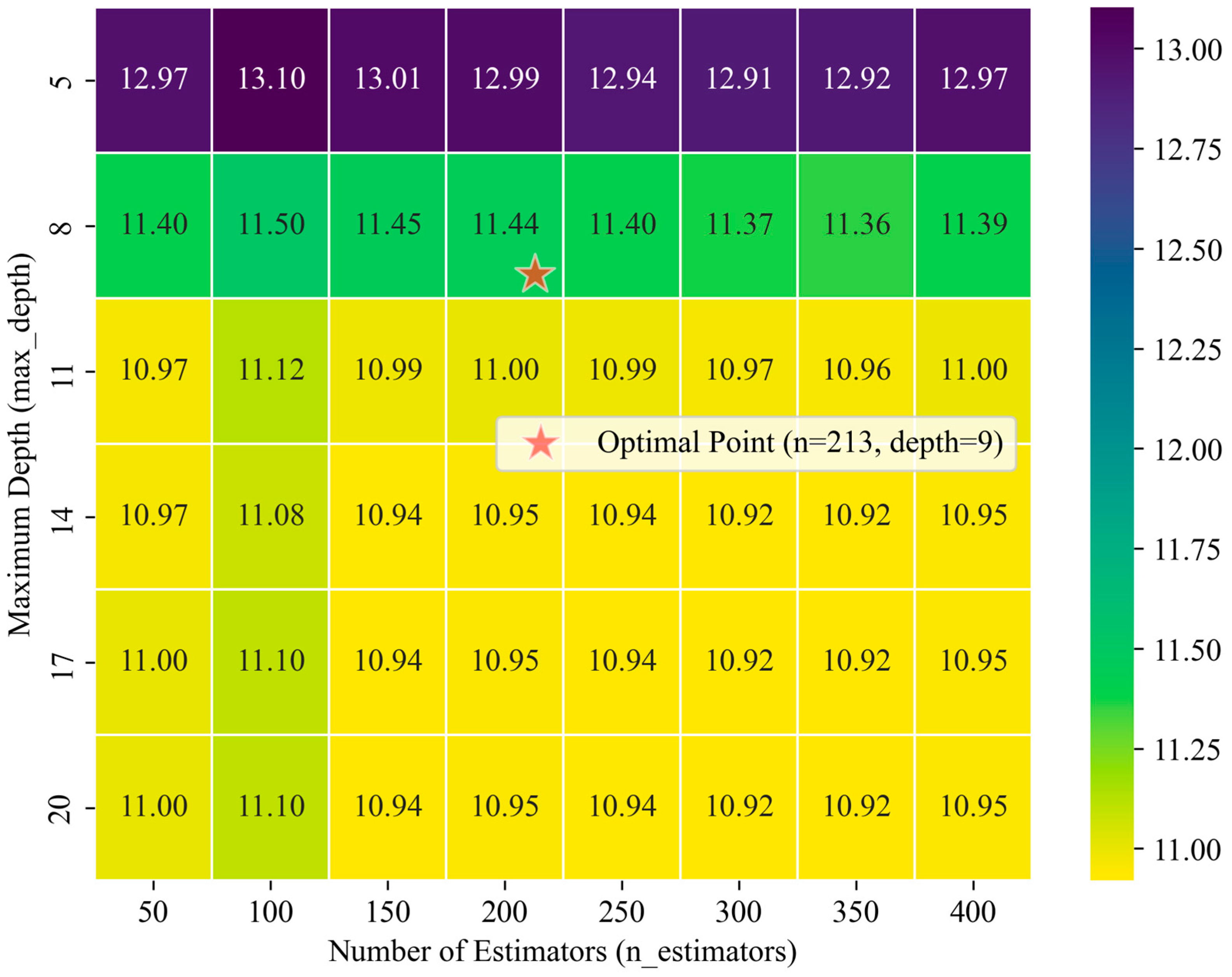
| n_estimators | [50–400] | 100 | 95 | 213 | 73 |
| max_depth | [1–20] | Default | 10 | 9 | 9 |
| min_samples_leaf | [1–50] | Default | 4 | 3 | 3 |
| min_samples_split | [2–50] | Default | 2 | 2 | 2 |
| max_features. | [1–50] | Default | 6 | 6 | 6 |
| Stage | Model | R2 | Score | RMSE | Score | MAE | Score | MAPE | Score | VAF | Score | A-20 | Score | Final Score |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Training set | RF | 0.996 | 4 | 5.367 | 4 | 2.721 | 4 | 4.7 | 4 | 99.572 | 4 | 0.972 | 4 | 24 |
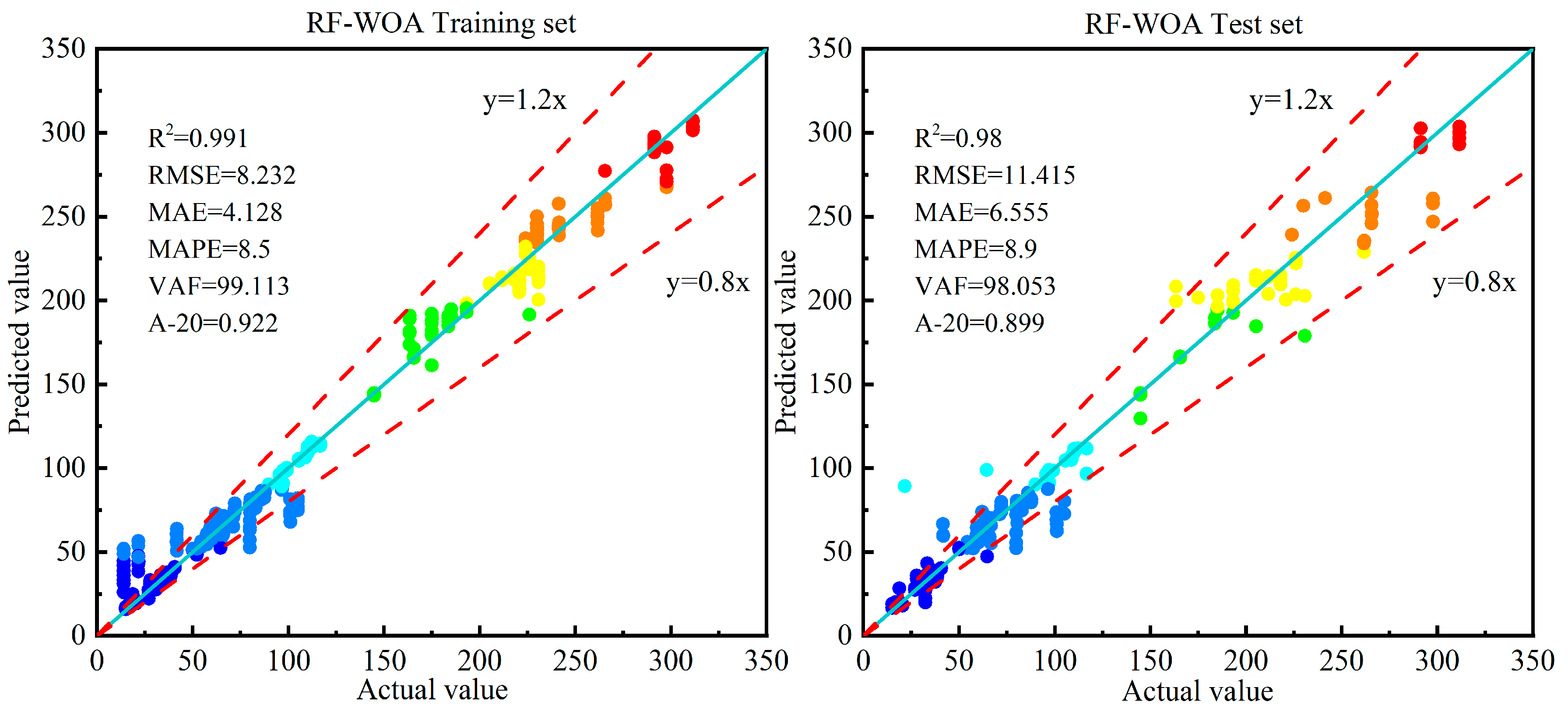
| RF-WOA | 0.991 | 3 | 8.232 | 3 | 4.128 | 3 | 8.5 | 3 | 99.113 | 3 | 0.922 | 3 | 18 | |
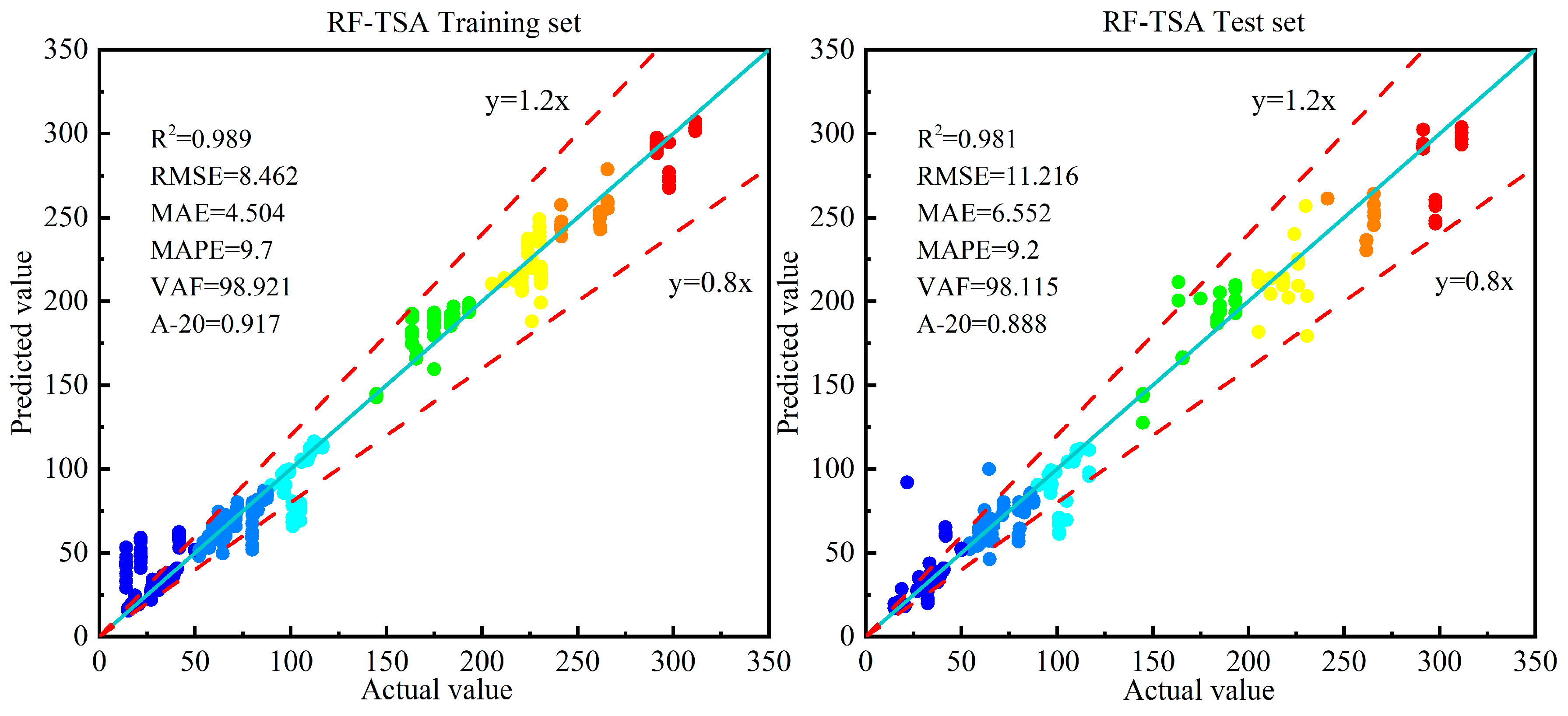
| RF-TSA | 0.989 | 2 | 8.462 | 1 | 4.504 | 1 | 9.7 | 2 | 98.921 | 1 | 0.917 | 2 | 9 | |
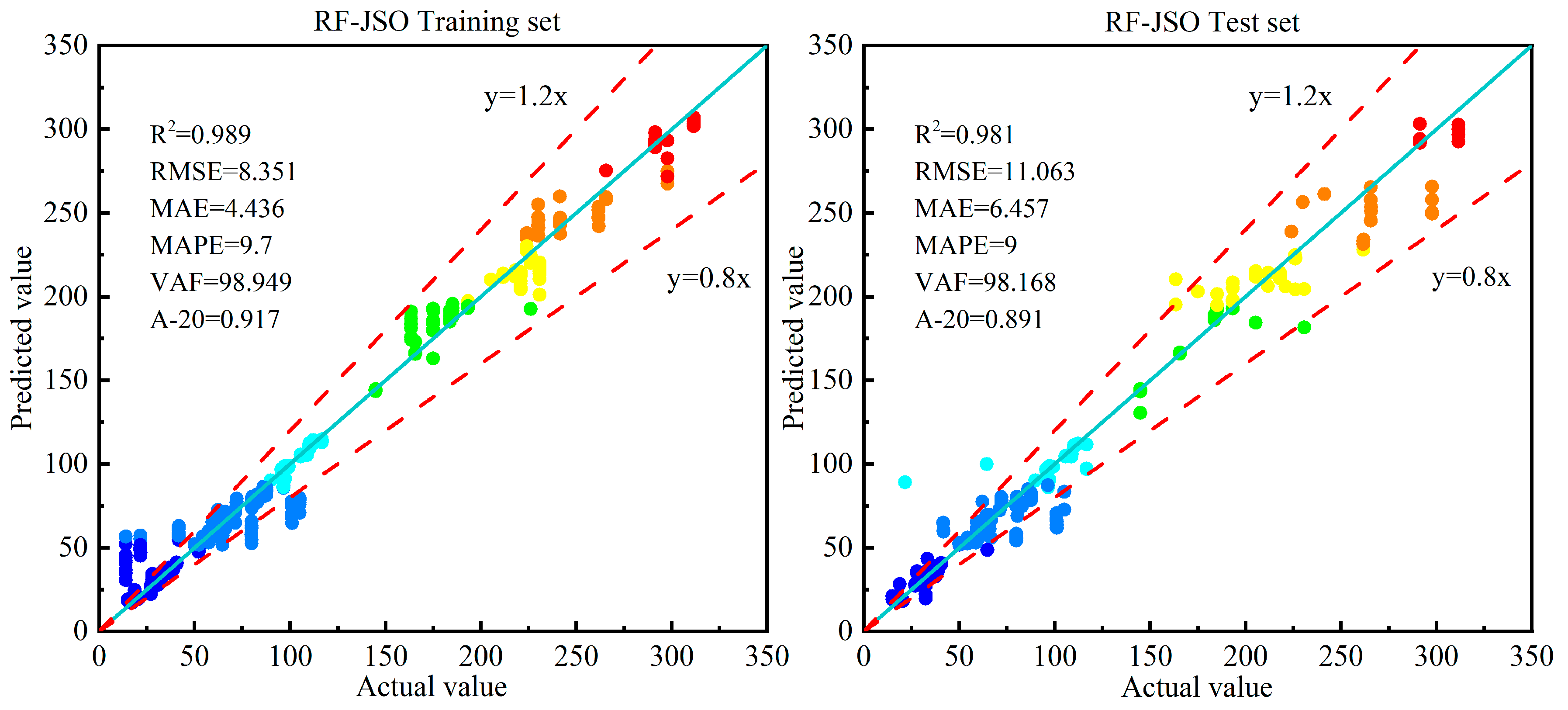
| RF-JSO | 0.989 | 2 | 8.351 | 2 | 4.436 | 2 | 9.7 | 2 | 98.949 | 2 | 0.917 | 2 | 12 | |
| Testing set | RF | 0.968 | 1 | 14.24 | 1 | 7.216 | 1 | 17.5 | 1 | 96.836 | 1 | 0.899 | 4 | 9 |
| RF-WOA | 0.98 | 3 | 11.415 | 2 | 6.555 | 2 | 8.9 | 4 | 98.053 | 2 | 0.899 | 4 | 17 | |
| RF-TSA | 0.981 | 4 | 11.216 | 3 | 6.552 | 3 | 9.2 | 3 | 98.115 | 3 | 0.888 | 2 | 18 | |
| RF-JSO | 0.981 | 4 | 11.063 | 4 | 6.457 | 4 | 9 | 2 | 98.168 | 4 | 0.891 | 3 | 21 |
| Stage | Model | R2 | RMSE | MAE | MAPE | VAF | A-20 |
|---|---|---|---|---|---|---|---|
| Training set | RF-JSO | 0.989 | 8.351 | 4.436 | 9.7 | 98.9 | 0.917 |
| XGBoost | 0.9780 | 12.083 | 8.125 | 18 | 98.9 | 0.814 | |
| LGBM | 0.981 | 9.235 | 6.132 | 11 | 98.1 | 0.845 | |
| Test set | RF-JSO | 0.981 | 11.063 | 6.457 | 9 | 98.1 | 0.891 |
| XGBoost | 0.971 | 13.617 | 9.118 | 14.1 | 97.2 | 0.798 | |
| LGBM | 0.9676 | 14.593 | 9.395 | 13.4 | 96.7 | 0.817 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, M.; Qiu, Y.; Khandelwal, M.; Kadkhodaei, M.H.; Zhou, J. Optimizing Random Forest with Hybrid Swarm Intelligence Algorithms for Predicting Shear Bond Strength of Cable Bolts. Machines 2025, 13, 758. https://doi.org/10.3390/machines13090758
Xu M, Qiu Y, Khandelwal M, Kadkhodaei MH, Zhou J. Optimizing Random Forest with Hybrid Swarm Intelligence Algorithms for Predicting Shear Bond Strength of Cable Bolts. Machines. 2025; 13(9):758. https://doi.org/10.3390/machines13090758
Chicago/Turabian StyleXu, Ming, Yingui Qiu, Manoj Khandelwal, Mohammad Hossein Kadkhodaei, and Jian Zhou. 2025. "Optimizing Random Forest with Hybrid Swarm Intelligence Algorithms for Predicting Shear Bond Strength of Cable Bolts" Machines 13, no. 9: 758. https://doi.org/10.3390/machines13090758
APA StyleXu, M., Qiu, Y., Khandelwal, M., Kadkhodaei, M. H., & Zhou, J. (2025). Optimizing Random Forest with Hybrid Swarm Intelligence Algorithms for Predicting Shear Bond Strength of Cable Bolts. Machines, 13(9), 758. https://doi.org/10.3390/machines13090758









