Lyapunov-Based Adaptive Sliding Mode Control of DC–DC Boost Converters Under Parametric Uncertainties

Abstract

The increasing demand for high-performance power converters for electric vehicle (EV) applications places a significant emphasis on developing effective and robust control strategies for DC-DC converter operation. This paper deals with the development, simulation, and experimental validation of an adaptive Lyapunov-type Nonlinear Sliding Mode Control (L-SMC) strategy for a DC–DC boost converter, addressing significant uncertainties caused by large variations in system parameters (R and L) and ensuring the tracking of a voltage reference. The proposed control strategy employs the Lyapunov stability theory to build an adaptive law to update the parameters of the sliding surface so the system can achieve global asymptotic stability in the presence of uncertainty in inductance, capacitance, load resistance, and input voltage. The nonlinear sliding manifold is also considered, which contributes to a more robust and faster convergence in the controller. In addition, a logic optimization technique was implemented that minimizes switching (chattering) operations significantly, and as a result of this, increases ease of implementation. The proposed L-SMC is validated through both simulation and experimental tests under various conditions, including abrupt increases in input voltage and load disturbances. Simulation results demonstrate that, whether under nominal parameters (R = 320 Ω, L = 2.7 mH) or with parameter variations, the voltage overshoot in all cases remains below 0.5%, while the steady-state error stays under 0.4 V except during the startup, which is a transitional phase lasting a very short time. The current responds smoothly to voltage reference and parameter variations, with very insignificant chattering and overshoot. The current remains stable and constant, with a noticeable presence of a peak with each change in the reference voltage, accompanied by relatively small chattering. The simulation and experimental results demonstrate that adaptive L-SMC achieves accurate voltage regulation, a rapid transient response, and reduces chattering, and the simulation and experimental testing show that the proposed controller has a significantly lower steady-state error, which ensures precise and stable voltage regulation with time. Additionally, the system converges faster for the proposed controller at conversion and is stabilized quickly to the adaptation reference state after the drastic and dynamic change in either the input voltage or load, thus minimizing the settling time. The proposed control approach also contributes to saving energy for the application at hand, all in consideration of minimizing losses.

1. Introduction

The DC-DC converter is a widely used power supply for applications such as DC motor drives and renewable energy systems. In particular, the boost converter is designed to increase the output voltage above the input voltage [1]. To regulate the output of a DC-DC boost converter, the switching mechanism is alternately activated and deactivated to obtain the specified DC voltage [2]. Open-loop control is one of the basic and easier methods for managing a DC-DC boost converter, relying on calculating the Pulse Width Modulation (PWM) pulse based on input and output voltages through duty cycle adjustments [1,3]. On the other hand, this approach is very susceptible to system noise and changes in parameters, which can cause problems like too much capacitor voltage overshoot and too much inductor current [4]. These problems generally make open-loop control less effective, which is why closed-loop control systems are better for DC-DC boost converters.

Despite this, designing an effective closed-loop controller is difficult due to the nonlinear characteristics and inherent phase lag of the boost converter. These factors complicate the control design process, requiring more sophisticated strategies to ensure stable and reliable operation [5]. DC-DC converters are nonlinear and time-invariant systems, characterized by variations in system parameters and signal transitions during startup. Load fluctuations cannot be effectively managed with basic control techniques, necessitating a control method that addresses their intrinsic nonlinearity and wide variations in input voltage and load to ensure stability across all operating conditions [6].

Sliding Mode Control (SMC) is a well-regarded method for managing nonlinear systems, offering robustness and stability in both linear and nonlinear systems. In DC-DC converters, SMC employs a switching control strategy that has been widely researched to enhance the converter’s performance.

Traditional controllers, such as PI and PID controllers, use techniques like Bode plots or Ziegler–Nichols methods. While these approaches are simple to implement, their performance in rejecting disturbances is limited by the nonlinear behavior of DC-DC converters. Moreover, they are highly sensitive to parameter variations, which can significantly affect system performance [7].

To overcome these limitations, more advanced control strategies, such as fuzzy logic control, predictive control, and neural network control, have been developed. Among these, SMC stands out for its robustness in managing disturbed systems, but it operates at high switching frequencies, which can result in undesirable chattering effects. Higher-order Sliding Mode Control techniques provide an alternative, reducing chattering by ensuring the sliding surface and its successive derivatives are zeroed. However, these techniques require knowledge of all time derivatives of the sliding surface, which can be challenging to obtain in practical applications.

Conversely, Sliding Mode Control with the Lyapunov Method (L-SMC) necessitates simply knowledge of the sliding surface, excluding its temporal derivatives. This method strongly guarantees finite-time convergence of the sliding surface and its derivatives, even in the presence of disturbances. Conventional L-SMC incorporates a discontinuous term within its integral action to significantly mitigate, though not fully eliminate, chattering. Additionally, the traditional SMC technique requires knowledge of perturbation gradient limits, which are difficult to determine accurately in practice. This often results in overestimating the perturbation limits, leading to excessively high control gains. Recently, adaptive Sliding Mode Controllers have been proposed to dynamically adjust controller gains in response to perturbations, offering a more effective solution for real-world applications [8,9].

Our work introduces a Lyapunov-based Sliding Mode Controller (L-SMC), offering significant advantages over other contemporary methods in terms of chattering reduction, computational efficiency, and robustness to parameter variations and disturbances.

A common issue with traditional Sliding Mode Controllers, as well as higher-order Sliding Mode Controllers, is the undesirable chattering effect at high switching frequencies. Chattering not only increases the wear on system components but can also lead to instability under certain operating conditions [10]. In comparison to existing methods such as the adaptive Sliding Mode Controller proposed by Zhang et al. in [11], our Lyapunov-based approach significantly reduces chattering by ensuring that the sliding surface and its derivatives converge to zero within a finite time. This is achieved with minimal computational overhead since it does not require knowledge of higher-order time derivatives. As a result, our method offers smoother control action with minimal oscillations, enhancing both system stability and lifespan.

Many modern control methods, such as fuzzy logic-based controllers or neural network controllers, require significant computational resources to process large datasets or to tune parameters for varying operating conditions. These methods can also be computationally expensive during real-time operations. On the other hand, our L-SMC reduces computational complexity by focusing only on the sliding surface itself, without the need for higher-order derivatives or large datasets. This leads to faster convergence and reduced processing time, making our method more suitable for real-time applications, especially in systems with limited computational power. This contrasts with methods like the neural-network-based controller discussed by Patel et al. in [12], which, while offering a good transient performance, demands considerable computational resources.

DC-DC converters are sensitive to variations in parameters, such as load resistance, input voltage, and component tolerances. These variations can significantly affect performance, especially in systems operating under dynamic conditions. Traditional controllers like PI or PID controllers often fail to reject these disturbances effectively, especially when large fluctuations occur [13,14]. In contrast, our Lyapunov-based Sliding Mode Controller is inherently robust to parameter variations and disturbances. It dynamically adjusts control gains in response to changes in system parameters, ensuring a stable performance even in the presence of substantial input voltage fluctuations and load disturbances. This robustness is particularly important for EV applications where operational conditions can vary significantly. Our approach outperforms methods like the fuzzy logic controller proposed by Liu et al. in [15], which, despite being able to handle some parameter variations, still struggles to maintain stability under large and rapid changes in load or input voltage.

While Lyapunov-based adaptive SMC (L-SMC) is robust and well-established for DC–DC boost converters, recent advances involving adaptive SMC (A-SMC) with online gain tuning [1,2], Non-Singular Terminal SMC (NTSMC)/Fast Terminal SMC (FTSMC) [3,4], Observer-based SMC (O-SMC) and Disturbance-Estimation SMC (DE-SMC) [2,4,5], and Higher-Order SMC (HO-SMC) architectures offer further improvements in chattering mitigation [6,7], sensor reduction, and dynamic performance. However, these advanced methods have some drawbacks.

Table 1. Comparative analysis of SMC variants for DC–DC boost converter applications in terms of performance, robustness, and implementation trade-offs.

Method	Robustness and Adaptivity	Chattering Mitigation	Sensor/Observer Use	Tracking and Efficiency	Validation/Applications	Complexity Level	Computational Requirements	Real-Time Feasibility	Key Notes
L-SMC	High (with online parameter adaptation; guaranteed by Lyapunov stability)	Good (adaptive gain tuning reduces chattering)	Can integrate observers to cut sensors	Fast/accurate tracking, energy efficient	Simulation and hardware, especially renewable sources	Moderate/high	Moderate	Yes	Efficient with standard DSP/MCU [16]
A-SMC	Very high (gain updates in real time against disturbances)	Excellent (no over/under estimation, less chattering)	Observer can be integrated [17,18]	Matching or superior to Lyapunov SMC [17]	Real-prototype DC–DC validation	Moderate/high	Moderate	Yes	Real-time gain logic efficient; metaheuristics offline [19,20]
NTSMC/FTSMC	Improved (finite-time, non-singular—avoids infinite control at surface)	Very strong (fast convergence with minimal chatter)	Often used with observers for unmeasured states [21,22]	Strong transient/steady-state accuracy	Hardware/Simulink tested on boost/PV/EV systems [21,22]	Moderate	Moderate	Yes	Needs proper hardware for fractional powers [17,21]
O-SMC/DE-SMC	Strong (estimates/compensates real-time disturbances, lowers parametric dependency)	Reduced (smooth control, less switching)	Sensor reduction—disturbance/state observer [18,22]	High accuracy during uncertainties	Validated under disturbances, load/vin changes [18]	High	Moderate/high	Yes	Observer adds computation; fewer sensors needed [18,21,23]
HO-SMC	Robust (higher disturbance rejection, effective for nonlinearities)	Very high (suppresses chattering via higher derivatives)	May incorporate adaptive observers [24,25]	Excellent, especially for step/disturbances	Proven robust in real wind/PV/boost platforms [24,25]	High	High	Yes (good hardware)	Best chattering suppression, but heaviest calculations [17,25,26]

summarizes a comprehensive comparison of these methods.

This work introduces and applies a proposed methodology utilizing the L-SMC technique, specifically applied to DC-DC boost converters. The suggested technique is intended for high-performance applications. We hope that the proposed technique provides significant robustness, particularly when the converter model is precisely described. The fully nonlinear SMC efficiently manages the output voltage to follow a reference voltage, despite parameter fluctuations. To demonstrate the superiority of the proposed method over conventional control techniques, a comparative analysis was conducted in terms of sensitivity to design parameters and improved robustness against parameter variations.

The structure of this paper is as follows: Section 2 provides a detailed explanation and modeling of the DC-DC boost converter. Section 3 presents the design of the Lyapunov-based Sliding Mode Controller (L-SMC). Section 4 provides details of the simulation results and their discussion in the studied cases. Section 5 presents the laboratory setup. Section 6 presents experimental results, demonstrating the performance of the Lyapunov control approach under varying conditions such as variable inductance and load resistance. Finally, conclusions are drawn in Section 7.

2. Modeling of Boost Converter

The boost converter (illustrated in Figure 1) is a basic DC-DC converter circuit that consists of two main energy-storing elements: a capacitor and an inductor. The inductor and capacitor are coupled with two complementary switches, allowing the boost converter to increase the input voltage to a higher output voltage, as described in [27].

The DC-DC converter operates by the periodic switching of the two components, where the two switches alternately turn ON and OFF at a frequency defined by the PWM control signal. In the ON state of the transistor, the diode is reverse-biased and also closed. Therefore, the input voltage is applied directly to the inductor (L), causing it to take energy in the form of a magnetic field. When the transistor turns OFF, the energy stored in the inductor is released. The load is supplied by both the input source and the energy stored in the LC filter, consequently producing an output voltage greater than the input voltage. Hence, the converter can effectively produce a steady voltage in a regulated manner.

To analyze the boost converter further, we can review the different switching states and how each state allows for voltage regulation. These states of switching allow energy to be transferred from the source to the load as efficiently as possible while allowing for regular operation to be requested of the user/designer during various sets of conditions.

The boost converter is a critical part in many systems, with the converter interfacing the power source and load for energy transfer. The boost converter is able to achieve an increased voltage while transferring renewable energy to the load with electrical efficiency, thus contributing to engineering challenges for applications such as renewable energy systems, battery charging (or developing batteries), and electric vehicles. But the different states supported the application of various control strategies, such as PID control or hysteresis control, to regulate output voltage, as discussed in reference [28]. The operation of the boost converter allows and supports innovative designs regarding physical loads and connected terminals while regulating output voltage for the various possible load conditions.

Figure 1 illustrates the conventional topology of a DC-DC boost converter operating with fixed-frequency switching (FFS). The primary function of this converter is to regulate the output DC voltage (Vout) to a value higher than the input voltage (Vin), ensuring that the reference voltage (Vref) exceeds the input voltage, i.e., Vref > Vin. The system continuously monitors both the inductor current (i_L) and the corresponding capacitor voltage (Vc) to maintain stable operation.

By selecting the state vector as $\mathrm{x}={\left[Vc,i_L\right]}^{\mathrm{T}}$, the system dynamics in continuous conduction mode (CCM) can be described as follows:

$$\dot{X}\left\{\begin{array}{c}{A}_{on}X+B_{on}{V}_{in} ,S=on\\ A_{off}X+B_{off}{V}_{in} ,S=off\end{array}\right.$$

(1)

where $A_{on}=\left[\begin{array}{cc}-{\displaystyle \frac{1}{RC}}& 0\\ 0& 0\end{array}\right]$ $A_{off}=\left[\begin{array}{cc}-{\displaystyle \frac{1}{RC}}& {\displaystyle \frac{1}{C}}\\ -{\displaystyle \frac{1}{L}}& 0\end{array}\right]$

$$B_{ofn}=B_{off}=\left[\begin{array}{c}0\\ {\displaystyle \frac{1}{L}}\end{array}\right]$$

(2)

and S is the switch, C is the filter capacitance, R is the load resistance, and L is the circuit inductance. The time of switch S is on the duty cycle d(t) = {0, 1}, (d = u), and it can be proved that in the DC-DC boost converter, it relates the Vin and Vout through the relation $u(t)={\displaystyle \frac{1-Vin}{Vout}}$, and the state space average equations can be written as follows:

$$\left\{\begin{array}{c}{\displaystyle \frac{d{i}_l}{dt}}=-(1-u){\displaystyle \frac{1}{L}}{V}_o+{\displaystyle \frac{1}{L}}{V}_{in}\\ {\displaystyle \frac{d{V}_0}{dt}}=(1-u){\displaystyle \frac{1}{C}}{i}_L-{\displaystyle \frac{V_{0ut}}{RC}}\end{array}\right.$$

(3)

3. Lyapunov Approach Sliding Mode Control Design

The design of the proposed control strategy, which combines the Lyapunov function approach with a Sliding Mode Control technique, can be divided into two key parts. In the first part, the system’s stability is analyzed using the Lyapunov function. In the second part, the control law for the proposed control method is developed based on this stability analysis [29].

3.1. Lyapunov Stability

The Lyapunov function theory is applied through a series of steps that ensure the analysis remains within the system’s order, preserving mathematical rigor and applicability [30,31]. In the case of DC-DC converters, the system’s stability and control are typically analyzed using an averaged model, which simplifies the switching dynamics of the converter. This model incorporates essential parameters such as inductance (L), resistance (R), and capacitance (C), which directly influence the performance and stability of the converter.

For accurate parameter estimation and stability analysis, the Lyapunov approach incorporates perspectives of various system states, represented by θ₁, θ₂, and θ₃. These perspectives are used to relate the system’s state variables, including the inductor current (i_L), output voltage (Vout), and the inverse of the parameters 1/L, 1/C, and 1/RC. By constructing a Lyapunov function and analyzing its derivatives, we can estimate the optimal values of L, R, and C to ensure system stability.

In this context, the Lyapunov function is employed to assess the stability of the system, ensuring that the system’s energy dissipates over time and converges to a stable equilibrium. The parameters L, R, and C are adjusted to satisfy the Lyapunov stability conditions, ensuring that the derivatives of the Lyapunov function are negative definite. This guarantees that the system remains stable under varying input conditions and disturbances.

The estimation process involves evaluating the system dynamics using the perspectives of θ₁, θ₂, and θ₃, which are functions of the state variables for adjusting these parameters in the Lyapunov function. The system’s behavior can be optimized to reduce sensitivity to load changes, input voltage fluctuations, and other disturbances. This approach provides a robust framework for ensuring the stability and performance of DC-DC converters in practical applications.

The averaged model of the DC-DC converter, incorporating these parameters, is expressed as follows:

$$\left\{\begin{array}{c}{\dot{x}}_1=-\left(1-u\right){\theta }_1{x}_2+{\theta }_1{V}_{in}\hfill \\ \\ {\dot{x}}_2=\left(1-u\right){\theta }_2{x}_1-{\theta }_3{x}_{2 }\hfill \end{array}\right.$$

(4)

where x₁, x₂, ϴ₁, ϴ₃, and ϴ₃ are the perspectives of i_L, V_out, 1/L, 1/C, and 1/RC.

Let us write a Lyapunov function in the following approach:

$$V_1={\displaystyle \frac{1}{2}}(e{)}^2>0$$

(5)

where $e=x_v-x_e$ and

$$V_1={\displaystyle \frac{1}{2}}(x_2-x_{ve}{)}^2>0$$

(6)

where x_ve = Vref, x_v = Vout.

For an analysis of the behavior of the error variable V1, let us estimate its first time derivatives:

$${\dot{V}}_1=e\dot{e}=({\dot{x}}_v-{\dot{x}}_{ve})(x_v-x_{ve})$$

(7)

Substituting Equation (3) into Equation (7) results in the following:

$${\dot{V}}_1=(u_e{\theta }_2{x}_i-{\theta }_3{x}_v-{\dot{x}}_{ve})(x_v-x_{ve})$$

(8)

where u_e = 1 − u, x_i = x_1.

The equation can become negative definite if we define the following control law:

$$x_i={\gamma }_1({\theta }_3{x}_v-{\dot{x}}_{ve})(x_v-x_{ve})$$

(9)

where ${\gamma }_1=u_e{\theta }_2$.

Substituting (9) in (8) gives

$${\dot{V}}_1=(-{\sigma }_1(x_v-x_{ve}\left)\right)(x_v-x_{ve})$$

(10)

$${\dot{V}}_1=-{\sigma }_1(x_v-x_{ve}{)}^2<0$$

(11)

To ensure stability, the condition must be ${\sigma }_1>0$.

Now consider the Lyapunov function V₂:

$$V_2={\displaystyle \frac{1}{2}}(x_i-x_{ie}{)}^2+V_1$$

(12)

For an analysis of the behavior of the error variable V2, let us estimate its first time derivatives:

$${\dot{V}}_2=(x_i-x_{ie})({\dot{x}}_i-{\dot{x}}_{ie})+{\dot{V}}_1$$

(13)

Substituting (3) in (13) gives

$${\dot{V}}_2=(x_i-x_{ie})(-u_e{\theta }_1{x}_v+{\theta }_1{V}_{in}-{\dot{x}}_{ie})+(u_e{\theta }_2{x}_i-{\theta }_3{x}_v-{\dot{x}}_{ve})(x_v-x_{ve})$$

(14)

$$u_c={\gamma }_2(x_i-x_{ie})(-{\theta }_1{V}_{in}-{\dot{x}}_{ie})$$

(15)

where ${\gamma }_2=u_e{\theta }_1$, $u_c=u_e-u$.

$${\dot{V}}_2=(-{\sigma }_2(x_i-x_{ie}\left)\right)(x_i-x_{ie})+{\dot{V}}_1$$

(16)

$${\dot{V}}_2=-{\sigma }_2(x_i-x_{ie}{)}^2+{\dot{V}}_1<0$$

(17)

To ensure stability, the condition must be ${\sigma }_2>0$.

3.2. Lyapunov-Based Sliding Mode Control Design

In order to achieve a control system that appropriately controls for a high level of model uncertainty, e.g., measurement error and variations in parameters, a control system is presented. The steady-state model is similar to the nonlinear dynamics of the system [32,33,34]. This nonlinear system, as noted in Equation (4), is representative of a boost converter, which is sensitive to typical phenomena such as saturation or skin effects as parameters, e.g., resistance and inductance vary. Therefore, the system can be modeled as

$$f_i={\widehat{f}}_i+\mathsf{\Delta }{f}_i,f_i=f_i-{\widehat{f}}_i$$

(18)

The $\mathsf{\Delta }{f}_i$ is the final result of all the parameters and state variations that were mentioned beforehand. Indeed, θ₁, θ₂, and θ₃ are not known with the precision of this fact:

$$\begin{gathered} {\theta }_1\to {\theta }_1\pm \mathsf{\Delta }{\theta }_1 \\ {\theta }_2\to {\theta }_2\pm \mathsf{\Delta }{\theta }_2 \\ {\theta }_3\to {\theta }_3\pm \mathsf{\Delta }{\theta }_3 \end{gathered}$$

(19)

Equation (4) becomes

$$\left\{\begin{array}{c}{\dot{x}}_1=-u_e({\theta }_1\pm \mathsf{\Delta }{\theta }_1)x_2+({\theta }_1\pm \mathsf{\Delta }{\theta }_1)V_{in}\hfill \\ \\ {\dot{x}}_2=u_e({\theta }_2\pm \mathsf{\Delta }{\theta }_2)x_1-{(\theta }_3\pm \mathsf{\Delta }{\theta }_3)x_{2 }\hfill \end{array}\right.$$

(20)

Replacing (17) in (20), we obtain

$${\dot{V}}_2={\dot{V}}_1+(-{\beta }_{2}sign(e)+\mathsf{\Delta }{\theta }_2+\mathsf{\Delta }{\theta }_3)e<0$$

(21)

$$\left(-{\beta }_{2}sign\left(e\right)+\mathsf{\Delta }{\theta }_2+\mathsf{\Delta }{\theta }_{31}\right)e<0 \forall e$$

(22)

$$if:{\beta }_2>\left|\mathsf{\Delta }{\theta }_1+\mathsf{\Delta }{\theta }_2+\mathsf{\Delta }{\theta }_3\right|$$

$$\begin{gathered} \left(-{\beta }_2 sign\left(e\right)+\mathsf{\Delta }{\theta }_2+\mathsf{\Delta }{\theta }_{31}\right)e<0 \forall e \\ {u}_e={\displaystyle \frac{1}{\left({\theta }_2+\mathsf{\Delta }{\theta }_2\right)x_2}}[\left({\theta }_3+\mathsf{\Delta }{\theta }_3\right)x_1+x_{2ref}-{\beta }_1\left(x_2-x_{2ref}\right)-{\beta }_{2}sign\left(x_2-x_{2ref}\right)] \end{gathered}$$

(23)

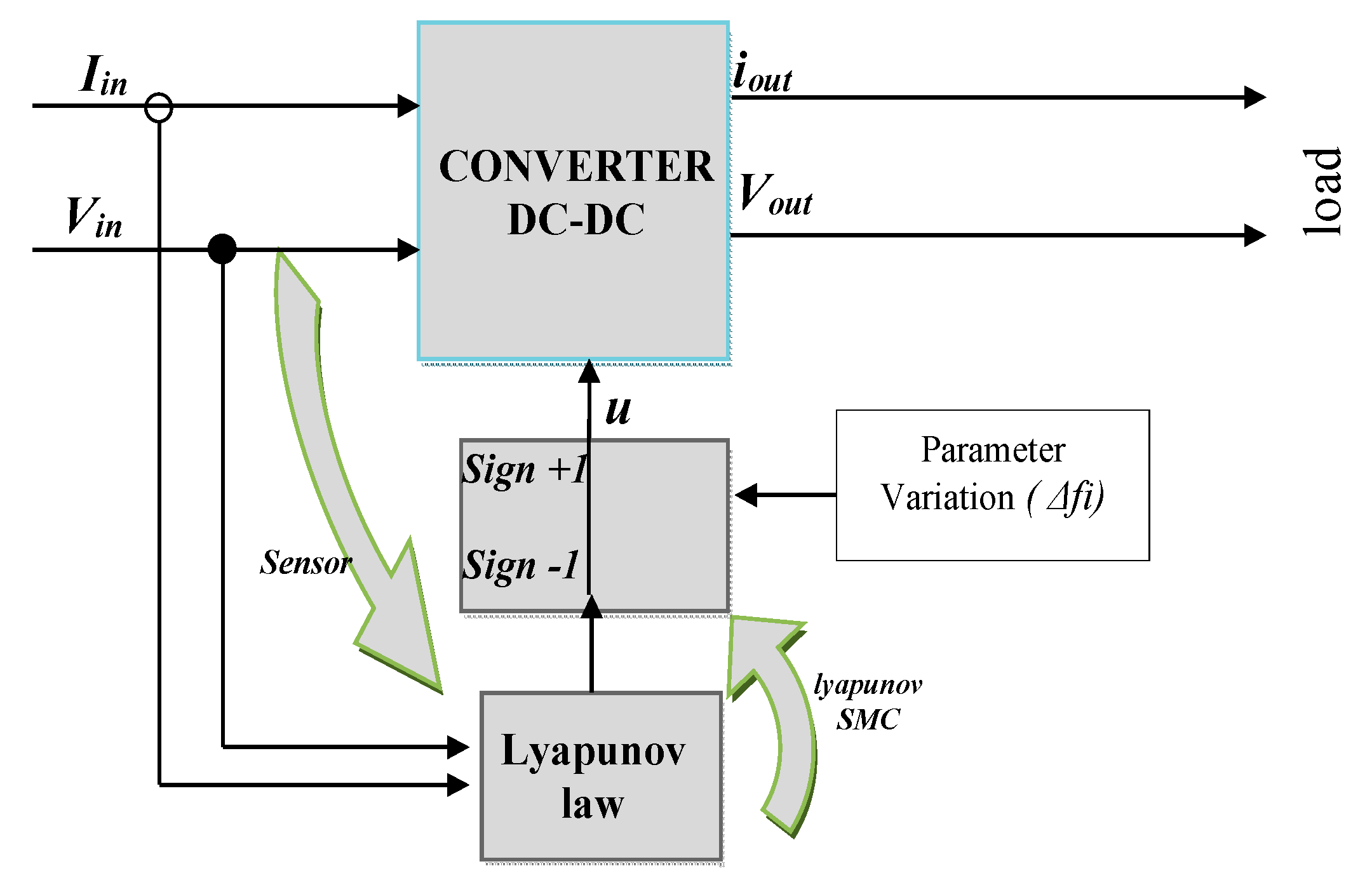
A general schematic of the suggested control scheme is presented in Figure 2.

4. Simulation Results

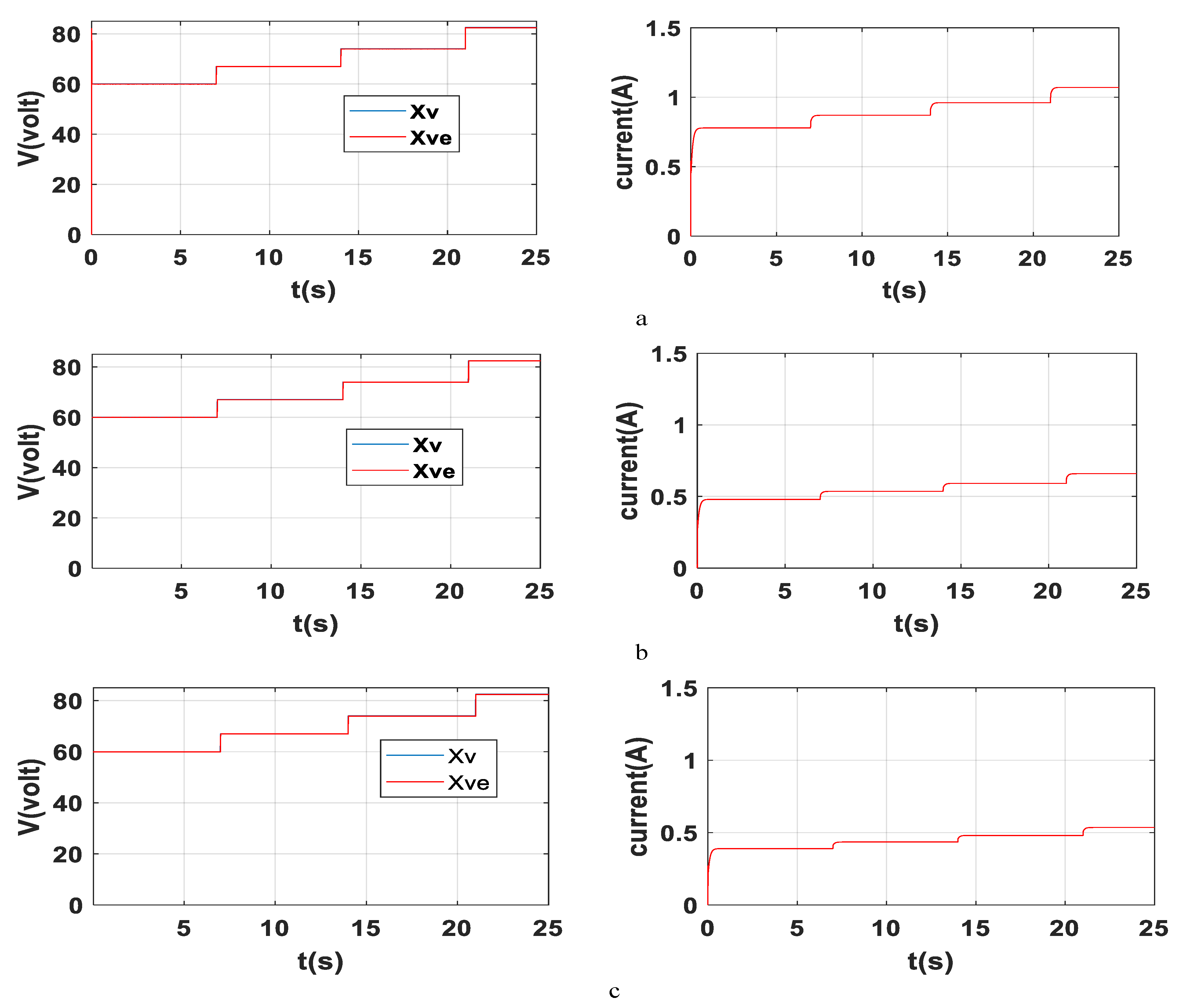
Figure 3 illustrates the dynamic performance of the proposed L-SMC under different operating scenarios. In all cases, the output voltage (Xv) tracks the reference accurately with minimal overshoot and no sustained steady-state error. The inductor current increases proportionally as the load decreases, as illustrated in Figure 3b,c, confirming effective compensation for higher output power demands.

Case a represents nominal conditions, where the output voltage stabilizes rapidly with smooth current evolution.

Case b shows the system response under a 50% reduction in load resistance, causing a higher load current; the controller maintains regulation without increased oscillation.

Case c combines load reduction and a 50% decrease in inductance, simulating significant parameter uncertainty. The controller still achieves convergence with no notable degradation in transient response or stability:

$$\mathrm{Overshoot} (\%) = {\displaystyle \frac{{\mathrm{S}}_{\mathrm{P}\mathrm{e}\mathrm{a}\mathrm{k}\mathrm{V}\mathrm{a}\mathrm{l}\mathrm{u}\mathrm{e}}-{\mathrm{S}}_{\mathrm{f}\mathrm{i}\mathrm{n}\mathrm{a}\mathrm{l}}}{{\mathrm{S}}_{\mathrm{f}\mathrm{i}\mathrm{n}\mathrm{a}\mathrm{l}}}}\times 100$$

(24)

Table 2. Output voltage of proposed L-SMC for the case a: R = 320 Ω, L = 0.0027 H.

Time (s)	Startup	7	14	21
Peak	71.37	66.88	73.8	80.7
Static error	11.37	−0.12	−0.2	−0.3
Overshoot (%)	18.95	−0.1791	−0.2703	−0.3704

,

Table 3. Output voltage of proposed L-SMC for the case b: R = 160 Ω (Δfr = 50%), L = 0.0027 H.

Time (s)	Startup	7	14	21
Peak	59.85	66.87	73.7	80.6
Static error	−0.15	−0.13	−0.3	−0.4
Overshoot (%)	−0.25	−0.1940	−0.4054	−0.4938

and

Table 4. Output voltage of proposed L-SMC for case c: R = 160 Ω (Δfr = 50%), L = 0.0013 H (ΔfL = 50%).

Time (s)	Startup	7	14	21
Peak	59.92	66.89	73.8	80.8
Static error	−0.08	−0.11	−0.2	−0.2
Overshoot (%)	−0.13	−0.1641	−0.2703	−0.2469

summarize the peak, static error, and overshoot percentages for all three test scenarios to assess the robustness and dynamic performance of the proposed L-SMC.

In case a, the nominal conditions are considered. In Figure 3a in the voltage curve, the DC-DC boost converter controlled by L-SMC exhibits a startup overshoot of approximately 18.95% (Table 2), which is expected due to initial energy accumulation in the inductor and capacitor. However, after the initial transient, the overshoot quickly transitions to negligible values despite various changes in the voltage reference at 7 s, 14 s, and 21 s. This attenuation is characterized by smooth convergence without outstanding oscillations.

In case b, where the load resistance is reduced by 50% while the inductance remains unchanged and keeps its value as in case a, the overshoot is effectively suppressed for each change in the reference voltage, as illustrated in Figure 3b. Specifically, the overshoot is limited to −0.25%, −0.1940%, −0.4054%, and −0.4938%, as detailed in Table 3 This outcome demonstrates the adaptive capability of the proposed L-SMC to respond to increased current demand (resistance variation/decreased current demand) while maintaining output voltage almost constant and following the voltage reference.

Similarly, case c introduces simultaneous reductions of 50% in both load resistance and inductance, representing a more severe parameter variation, which is in the goal to further test the robustness. Even under these challenging conditions, the L-SMC forces the DC-DC boost converter to maintain an overshoot of only −0.13%, −0.1641%, −0.2703%, and −0.2469% resulting from the change. In all cases, the voltage steady-state error remains negligible, and the DC-DC boost converter output voltage closely follows the reference voltage.

In all three cases, the output current of the DC-DC boost converter controlled via L-SMC has a stable dynamic behavior with effective damping and rapid convergence in response to each change in the reference voltage or parameters (R and L), as presented in Figure 3. Case a shows a smooth current rise corresponding to the nominal R and L (R = 320 Ω, L = 2.7 mH), without any significant chattering or instability during startup and reference voltage changes.

The current maintains these excellent characteristics even when the load resistance is reduced by 50% and the inductance is constant, as in case b. However, the DC-DC boost converter current increases significantly in amplitude due to the increased current demand. This demonstrates the ability of the proposed L-SMC method to force the DC-DC boost converter to adapt to load resistance changes under various voltage references. Even under more severe disturbances, as in case c, where both resistance and inductance are simultaneously reduced by 50%, the DC-DC boost converter provides a current that maintains stable dynamic behavior without remarkable overshoot or chattering. This later demonstrates the robustness of the proposed L-SMC in the face of severe simultaneous parametric changes.

Overall, the obtained results confirm that the suggested L-SMC for the DC-DC boost converter has a fast settling with excellent disturbance rejection and high precision in the steady state for all cases. The simulation results confirm the theoretical predictions that the L-SMC provides global asymptotic stability and demonstrate that it maintains a stable performance despite large variations in one or both parameters, R and L.

These results demonstrate the robustness of the adaptive L-SMC against both load disturbances and parameter variations. The smooth convergence of output voltage and inductor current confirms the validity of the Lyapunov stability framework implemented in the control design.

5. Laboratory Setup

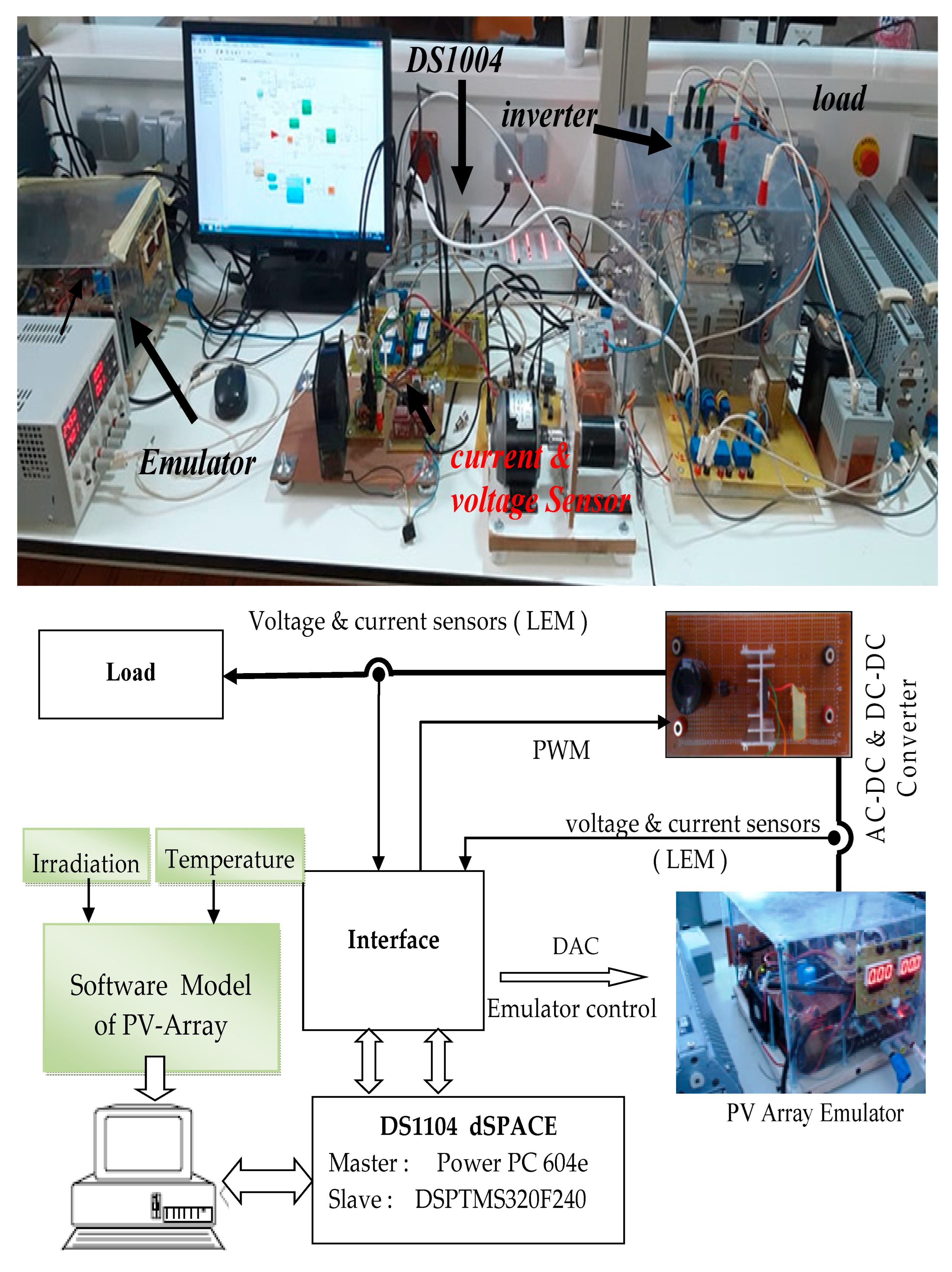
The Lyapunov-based Sliding Mode Control (L-SMC) was validated through experiments in a controlled lab. As illustrated in Figure 4, a boost converter is used in place of a standard voltage source to duplicate real-world power conversion. The measurements of voltage and current are taken with LA-25NP and LV-25P sensors; the LA-25NP is a precise current sensor that measures both the DC and AC current and has a Hall effect sensing component allowing for non-contact measurement with accurate current, with high linearity and low offset, in an industrially specific measurement, high range, and fast measurement frequency. The LA-25NP provides feedback on current dynamics in quick response to the typical frequency of switching that occurs in boost converters. The LV-25P is a voltage-sensing device that minimizes noise and delivers distortion-free voltage measurements. The LV-25P sensor uses capacitive voltage-sensing technology to measure the value of the output voltage while continuously monitoring the voltage dynamics in real time. The LV-25P can measure steady-state and transient voltage and is suitable for DC-DC converter dynamics. The LV-25P has high bandwidth and fast response time, providing the ability to ramp voltage change.

The control algorithm will be executed on the dSPACE DS1104 real-time testing platform (Figure 3), which is a typical and powerful real-time testing platform for the development and testing of control systems in real-time situations. The dSPACE DS1104 is equipped with a real-time processor that will execute the control algorithms with ultra-low latency time periods to give the expected accuracy and response times required when testing high-performance control strategies like L-SMC. The platform allows for rapid prototyping, meaning it is relatively easy to quickly iterate through control models and simulate the system’s dynamics in real time. The dSPACE DS1104 platform is equipped with high-speed I/O interfaces, which allow for smooth transmission between the control system and the hardware. This means that in rapidly changing dynamics, the system can truly capture the parameters of the system, including voltage, current, and switching states with very little lag time, and in the best case, all at once. The dSPACE DS1104’s open interfaces mean that control algorithms can be subjected to practical tests of the true systems to really prove analytical solutions. For the exhaustive evaluation of the L-SMC strategy, the dSPACE DS1104 was an effective platform to assess its effectiveness in stabilizing the boost converter through a wide scope of working scenarios, which included changing the input voltage, disturbance loads, and changing circuit parameters. This provided a comprehensive test bed in which the L-SMC controller could be assessed.

Table 5. Parameters of experimental test.

Parameters	Symbol	Value
Input voltage	Vin	30 V
Switching frequency	fs	10 kHz
Load resistance	R	320 Ω
Inductor	L	0.0027 H
Capacitor	C	0.0022 F
Gain of SMC	${\beta }_2$	0.00125

presents the parameters of the experimental test.

6. The Experimental Results

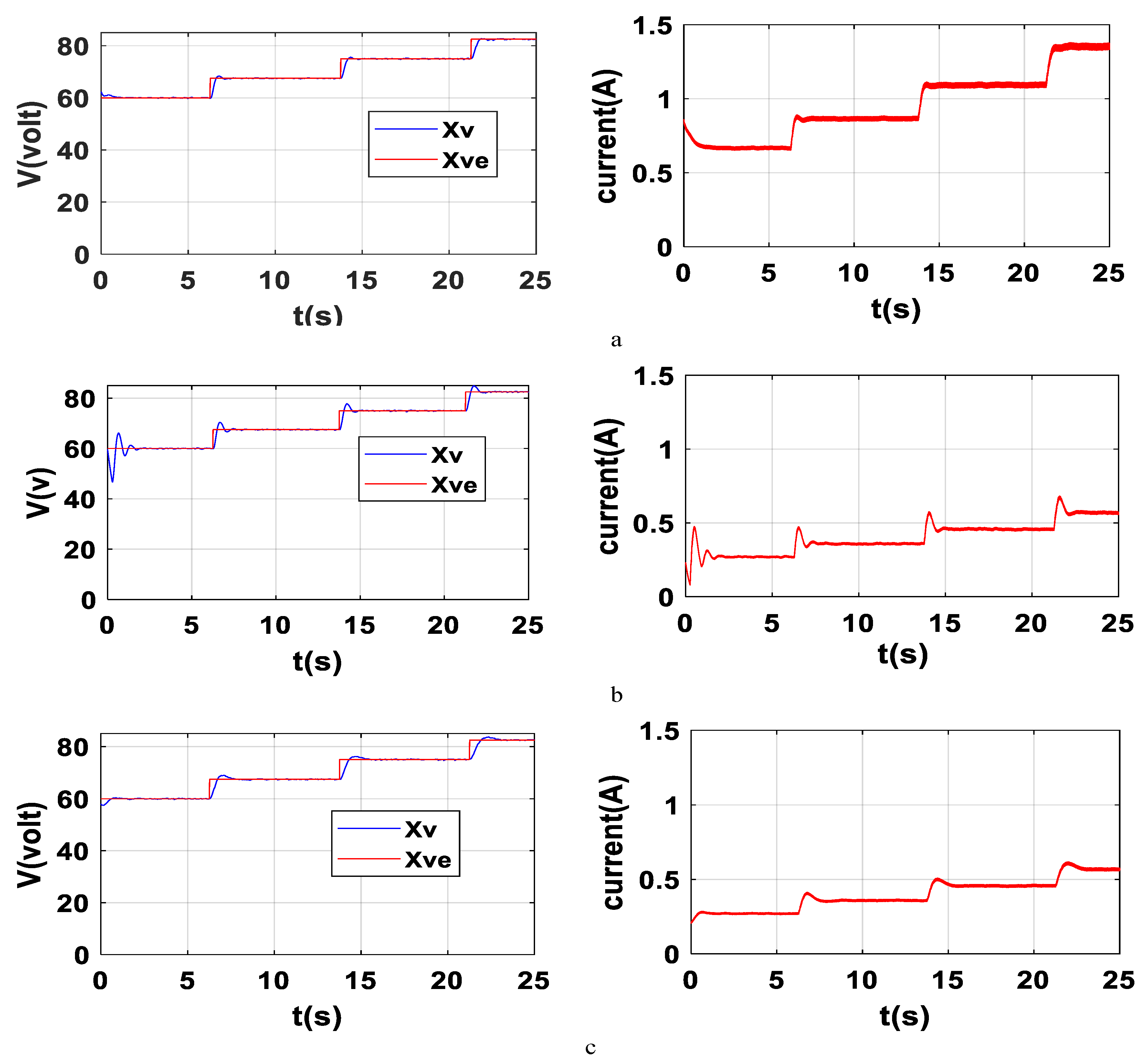
The Lyapunov-based Sliding Mode Control (L-SMC) was tested in the laboratory by subjecting the boost converter to parameter variations—particularly the parameter variation Δf—which is illustrated in the experiment parameters shown in Figure 5. The actual experimental setup will highlight what we want to test. To check the performance of the L-SMC, we monitored the output voltage of the boost converter and compared it to the reference voltage, as described in Equation (22). The focus of the experiment was to check its ability to maintain voltage regulation under input voltage variations and load disturbances, as well as system parameter variations. The reference voltage Vref was modified under different scenarios in order to simulate real-world scenarios while checking how well the system could accurately track the reference voltage under these scenarios. The following key performance variables were checked: Steady-state error: The steady-state error is the difference between the output voltage and the reference voltage in steady-state conditions. The results identified that the steady-state error in each case was significantly decreased with the application of the L-SMC compared to conventional control (PI controller, PID, etc.) [14], and it improved its ability to maintain a stable output voltage because of the reduced steady-state error on account of the L-SMC.

Accuracy in voltage regulation: The capability of the system to control the output voltage accurately despite load and input voltage perturbations. The experimental results showed that the L-SMC was able to control the output voltage very well and maintained it within an acceptable range of the reference voltage value, even when the output was disturbed by a disturbance. Transient response: This refers to the time taken for the system to reach a steady-state condition after a sudden change in load or input voltage. The transient response (t) and the settling time (ts) of the L-SMC were much faster than traditional controllers. That is, the transient response and settling time both reduced regularly due to some disturbance, and the system quickly responded without impulses to the inputs and reduced overshoot and oscillations. Robustness to variations in parameters: The L-SMC was tested under conditions of uncertain and varying values of important parameters of the system, such as resistance and inductance. In addition, the value range of these parameters could cause large differences in behavior.

The L-SMC was observed to be very robust because the output voltage was barely different from either reference values. This fact corroborates an important part of real-world implementations with component tolerance leading to uncertainty and regular external disturbance leading to variation in parameters. Chattering reduction: One of the major advantages of the Lyapunov-based sliding mode construction is the reduction in chattering that is generally experienced with traditional Sliding Mode Controllers. The experimental results showed that for the L-SMC, the high-frequency oscillations were considerably reduced. When evaluated against classical control options, the L-SMC performed better on every measure. Specifically, when exposed to large load disturbances and fluctuations in input voltage, the L-SMC sustained a voltage regulation with tiny errors and quicker stabilization times.

Overall, the experimental data has confirmed a sufficient level of drive behind the conveyed results of the L-SMC controlling the boost converter. The L-SMC outperforms traditional strategies with its robust performance features, rapid convergence, reduced steady-state error, and lower chattering characteristics, which are all characteristics that would lend the most deserving praise in the consideration of recognized control schemes for DC-DC boost converters, especially under normal operating conditions where disturbances and fluctuations in parameters are common.

The results confirm the effectiveness of the proposed Lyapunov-based Sliding Mode Control (L-SMC) method in enhancing the performance of the boost converter. The output voltage Xv (Vout) of the static converter demonstrates exceptional tracking of the reference voltage Xve, achieving various values, specifically within the ranges of 60 V, 75 V, and 85 V. The voltage error remains close to zero, illustrating the L-SMC’s remarkable ability to minimize voltage oscillations and reduce steady-state error, even under varying operating conditions.

Furthermore, the L-SMC efficiently controls the i_L, ensuring that it accurately follows the dynamically changing reference values. This is particularly evident in the results shown in Figure 5, where the inductor current closely aligns with the reference trajectory. The system’s response remains robust despite significant variations in the system’s parameters, with a 50% parameter fluctuation still yielding an excellent performance:

$$\mathrm{Undershoot} (\%) = {\displaystyle \frac{{{\mathrm{S}}_{\mathrm{r}\mathrm{e}\mathrm{f}}-\mathrm{S}}_{\mathrm{P}\mathrm{e}\mathrm{a}\mathrm{k}\mathrm{V}\mathrm{a}\mathrm{l}\mathrm{u}\mathrm{e}}}{{\mathrm{S}}_{\mathrm{r}\mathrm{e}\mathrm{f}}}}\times 100$$

(25)

Table 6. Output voltage of proposed L-SMC for case a: R = 320 Ω, L = 0.0027 H.

Time (s)	Peak	Overshoot	Overshoot (%)	Undershoot	Undershoot (%)	Static Error
Starting	62.27	2.27	3.873	0	0	2.27
7	68.36	1.36	1.274	0	0	0.86
14	75.6	1.6	0.8	0	0	0.6
21	82.76	1.76	0.36	0	0	0.3

,

Table 7. Output voltage of proposed L-SMC for case b; b: R = 160 Ω (Δfr = 50%), L = 0.0027 H.

Time (s)	Peak	Overshoot	Overshoot (%)	Undershoot	Undershoot (%)	Static Error
Starting	66.11	6.11	10.183	13.34	22.23	±0.3
7	70.4	3.4	5.07	7.2	10.74	±0.32
14	77.84	3.84	5.19	7.5	10.14	±0.5
21	84.9	3.9	4.81	6	7.51	±0.4

and

Table 8. Output voltage of proposed L-SMC for case b; c: R = 160 Ω (Δfr = 50%), L = 0.0013 H (ΔfL = 50%).

Time (s)	Peak	Overshoot	Overshoot (%)	Undershoot	Undershoot (%)	Static Error
Starting	60.4	0.4	0.66	2.5	4.17	±0.3
7	69	2	2.99	7	10.45	±0.4
14	76.18	2.18	2.95	7.45	10.07	±0.35
21	83.66	2.66	3.28	6.95	8.85	±0.3

present the output voltage performance of the proposed L-SMC strategy under the same conditions as the simulation test. For case a, the output voltage has a very low overshoot value, rapidly and progressively decreasing over time, starting at 3.87% during startup and dropping to just 0.36% at 21 s. This experiment demonstrates the excellent dynamic behavior of the whole system. The static error is also minimal and declines steadily from 2.27 V to 0.3 V. These results assert that the L-SMC effectively reduces steady-state deviation as the system settles. So, the L-SMC ensures accurate reference tracking and smooth voltage regulation under standard operating conditions.

The results in Table 7 and Table 8 highlight the robustness of the proposed L-SMC under significant parameter variations. In case b (Table 7), the startup overshoot reaches 10.18% and then an undershoot of 22.23%; this shows the fast variation in the transient state. However, both overshoot and undershoot values decrease significantly during subsequent voltage reference changes, with overshoot falling below 4.81% and undershoot below 7.51%, indicating rapid adaptation. The static error remains small (±0.3–0.5 V), confirming accurate voltage tracking despite resistance variation.

The same behavior of the proposed L-SMC occurred regarding simultaneous 50% reductions in both resistance and inductance (case c), as presented in Table 8, where the L-SMC exhibits even lower overshoot values, starting at only 0.66% in the startup and remaining below 3.3% for all reference changes. Undershoot is also reduced compared to case b, with values between 4.17% and 10.45%. The static error remains negligible (±0.3–0.4 V). These results demonstrate that the L-SMC maintains stable voltage regulation and mitigates large transient deviations even under more severe combined parameter changes, confirming its strong robustness and adaptability.

Table 9. Output current of proposed L-SMC for case a: R = 320 Ω, L = 0.0027 H.

	Peak
Time (s)	Case a	Case b	Case c
Starting	0.85	0.47	0.28
7	0.89	0.47	0.41
14	1.15	0.57	0.5
21	1.38	0.68	0.62

shows the peak of DC–DC boost converter output current values controlled via L-SMC for cases a, b, and c at different reference voltage changes. According to the experiment results, across all cases, the L-SMC ensures stable current regulation despite parameter variations. In case a, the peak current rises proportionally with voltage reference changes.

Case b shows consistently higher currents due to the 50% lower load resistance, while case c, despite simultaneous reductions in R and L, maintains currents higher than case a and enables a faster response. Overall, the L-SMC forces the DC–DC boost converter to avoid overshoot and reliably meet load demand under all conditions.

In this context, the output voltage Xv consistently tracks the reference Xve with minimal deviations, even when subjected to considerable disturbances and parameter changes. This underlines the control method’s stability, robustness, and low sensitivity to parameter variations, making it suitable for real-world applications where such variations are common; the overall performance indicates that the L-SMC provides a highly stable and efficient regulation of both output voltage and current, even in the face of substantial external and internal disturbances; this performance enhancement, as observed in the experimental results, highlights the superior robustness of the L-SMC, making it a promising solution for boost converters, particularly in systems where precise control and stability are critical under fluctuating conditions.

7. Conclusions

The experimental results successfully validated the proposed Lyapunov-based Sliding Mode Control (L-SMC). In all tests, the proposed L-SMC method kept the output voltage stable in the boost converter application. We demonstrated the potential of using Lyapunov theory combined with Sliding Mode Control to develop a controlled stimulus that is both robust and reliable to manage system instability and disturbance.

In order to test and demonstrate the suitability of the proposed L-SMC for real-time applications, where parameter variations are inevitable, two critical scenarios involving parameter changes were evaluated. The results confirm the robustness and effectiveness of the proposed method in both cases. In the first case, the inductance was reduced from 2.7 mH to 1.3 mH. In the second case, while maintaining the reduced inductance (a 50% decrease), an additional significant variation was introduced by halving the load resistance from 320 Ω to 160 Ω in order to simulate more critical operating conditions. Despite these significant parameter variations (50%), the suggested L-SMC-controlled boost converter kept working effectively in both cases. In all three cases, the output voltage closely matched the reference, with variances being within ±1 V during the transient state and showing very little inaccuracy in steady-state mode. The output current also remained steady and their DC nature, with only tiny fluctuations, noted when the inductance was decreased. The results show that the proposed L-SMC is robust when it comes to changes in parameters and outside interference, which shows that it can work well in contexts that are uncertain and change over time.

Through testing, we showed that, compared to conventional control methods, the L-SMC provides a better solution than other strategies, with better stability and resilience to changing system parameters. From the results, we infer that the proposed L-SMC is a valid candidate for real-world situations with uncertainty in operational conditions that require consistent and precise regulation of the boost converter at its output voltage.