Energy-Efficient Scheduling in Heat Treatment Workshops Based on Task Clustering and Job Batching
Abstract
1. Introduction
- A dynamic task clustering mechanism is introduced in which tasks are aggregated in real time based on similarities in process characteristics and scheduling flexibility. By exploiting task homogeneity, the adaptability of the scheduling system to production variability is enhanced, and redundant operations are effectively reduced.
- Practical shop floor constraints—transport energy consumption and batch delivery deadlines—are explicitly incorporated into the scheduling model. Unlike idealized formulations, this model is designed to accommodate tight delivery windows and resource limitations, thereby improving its applicability in realistic manufacturing environments.
- To solve the resulting combinatorial scheduling problem, we develop an improved genetic algorithm that integrates a novel reservation-based selection criterion. This mechanism leverages task timeliness, machine workload, and energy metrics to accelerate convergence and improve solution quality.
2. Related Works
3. Methodology
3.1. EJSP Formulation
- All plants, jobs and machines are available at time 0;
- Each machine can process only one job at any given time;
- Transportation time between machines is considered negligible;
- The energy consumption characteristics of each machine are known and deterministic;
- Energy consumption is task-dependent and may vary across machines for the same job;
- Machine breakdowns and stochastic disturbances are not considered in this study.
3.2. Objectives and Constraints
- Workpiece lot indexes are sorted by the time they are sent to the job shop;
- All workpiece batches are in a ready state at the moment of machining start;
- There is no specific limit to the number of original workpiece batches;
- The process information and processing time for each workpiece batch is known and fixed;
- The machining process of the production line cannot be interrupted and will not be terminated before the end of machining;
- The same production line processes up to 3 batches of material from the production cluster at the same time;
- If the original single batch of workpieces exceeds the maximum capacity of the production group, the excess is ignored.
3.3. Mathematical Model
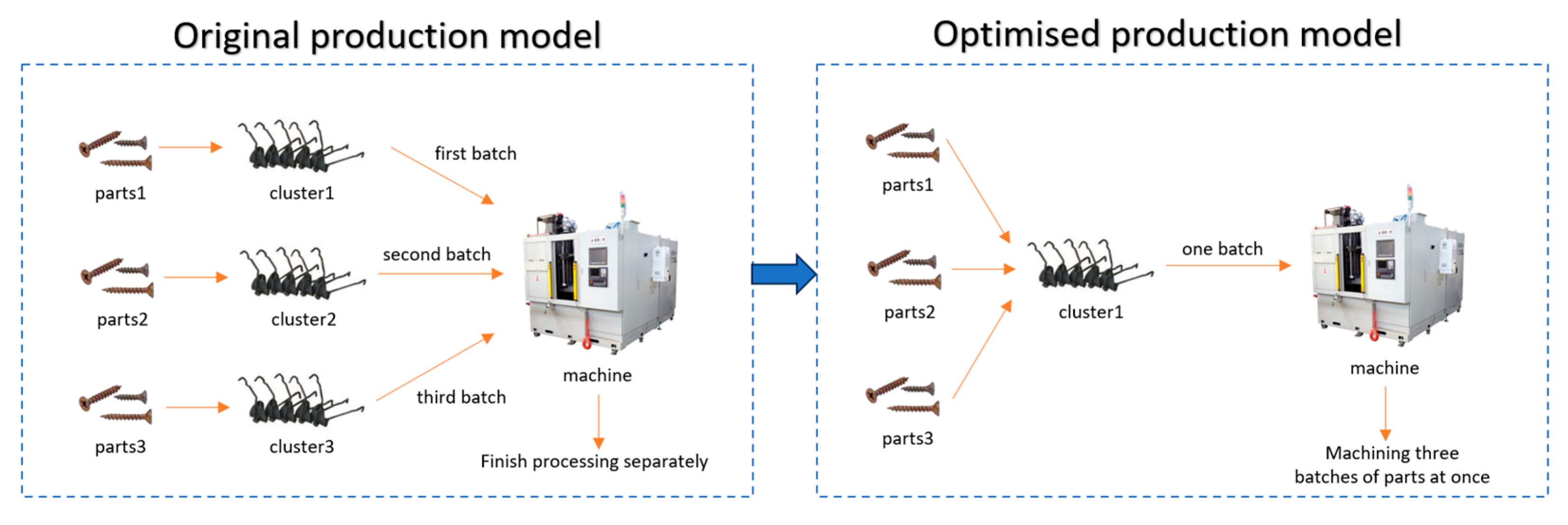
- Only batches of parts that are processed in the same process on the same production line can be consolidated;
- Multiple neighboring batches can be combined;
- Cross-batch consolidation is not allowed;
- The number of parts to be processed in a single lot after consolidation must not exceed the maximum capacity of the production group on the production line;
- The end time of processing after lot consolidation cannot exceed the delivery time of the sub-lot.
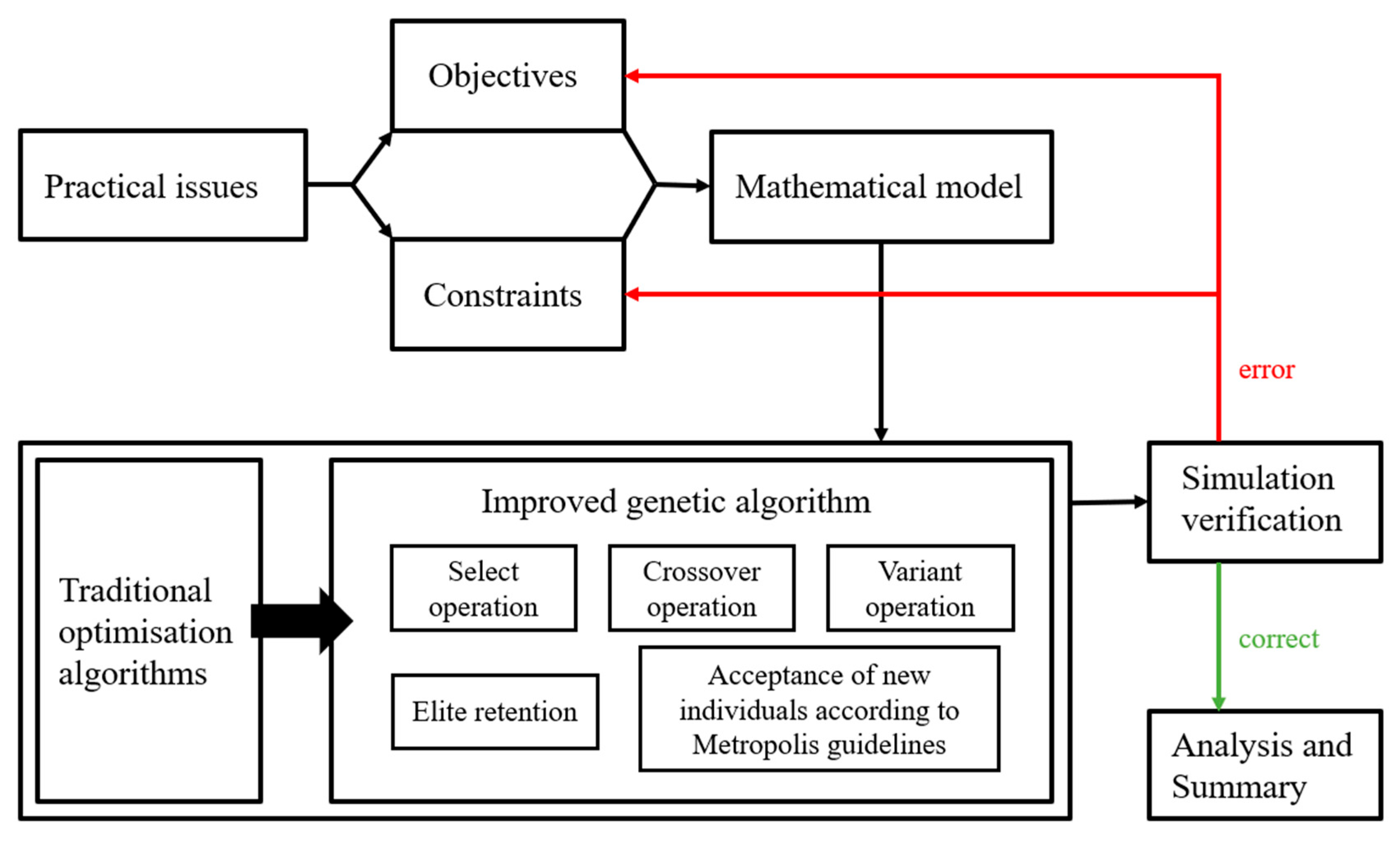
3.4. Improved Algorithm Design
- Initialization: At the beginning of the algorithm, parameter initialization, such as temperature, number of iterations, etc., is carried out, and initial solutions or populations are generated.
- Calculation and selection of solutions: Based on the current temperature, solutions are randomly selected and fitness is calculated. Crossover operation is used to generate new solutions while retaining elite individuals to avoid degradation.
- Judgement and update: Whether to accept the new solution is judged according to the simulated annealing criterion. If the new solution is accepted, the current solution is updated; otherwise, the current solution is kept unchanged.
- Iteration and update: An iteration counter is added and updated according to the set rules.
- Termination and output: Whether the termination condition (e.g., the temperature is lower than a certain threshold) is satisfied is judged; if so, the optimal solution is output and the algorithm is ended.
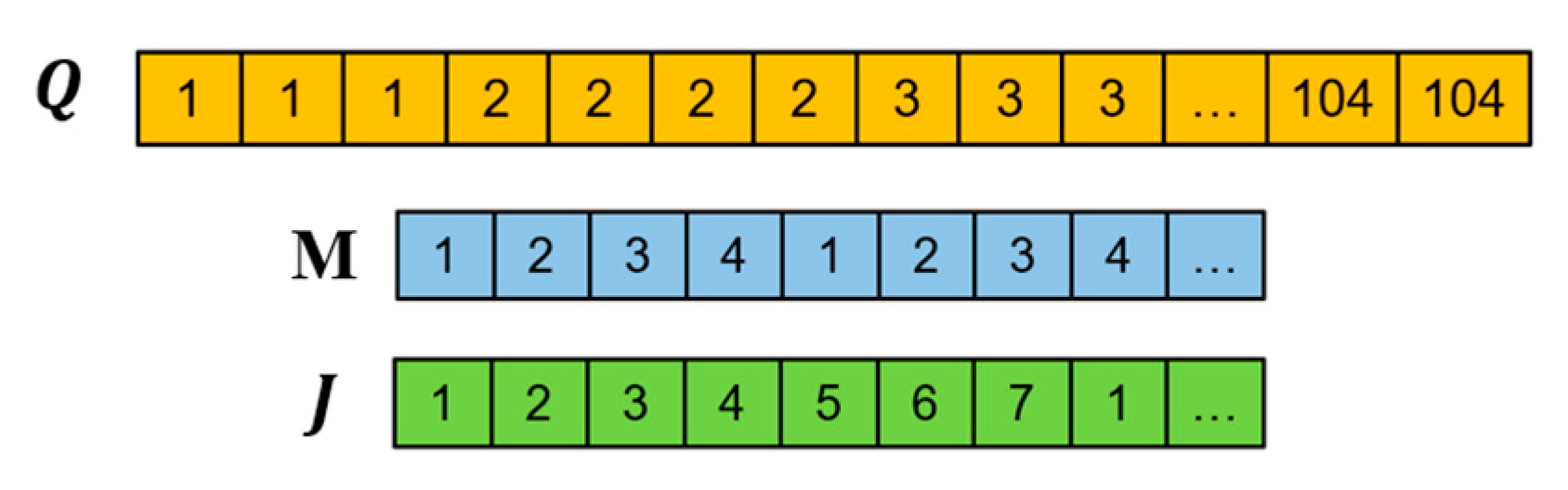
3.4.1. Chromosome Encoding Design
- denotes the task clustering encoding (binary vector), with L representing the total number of tasks; the binary value “1” indicates that two tasks are clustered into the same batch, while “0” indicates they are in separate batches.
- denotes the carrier scheduling encoding (integer vector), where K is the total number of AGVs, M is the number of batches, and the value at each position specifies the AGV assigned to the corresponding batch.
- denotes the equipment assignment encoding (integer vector), with P representing the total number of production clusters; the value at each position indicates the production cluster allocated to the corresponding batch.
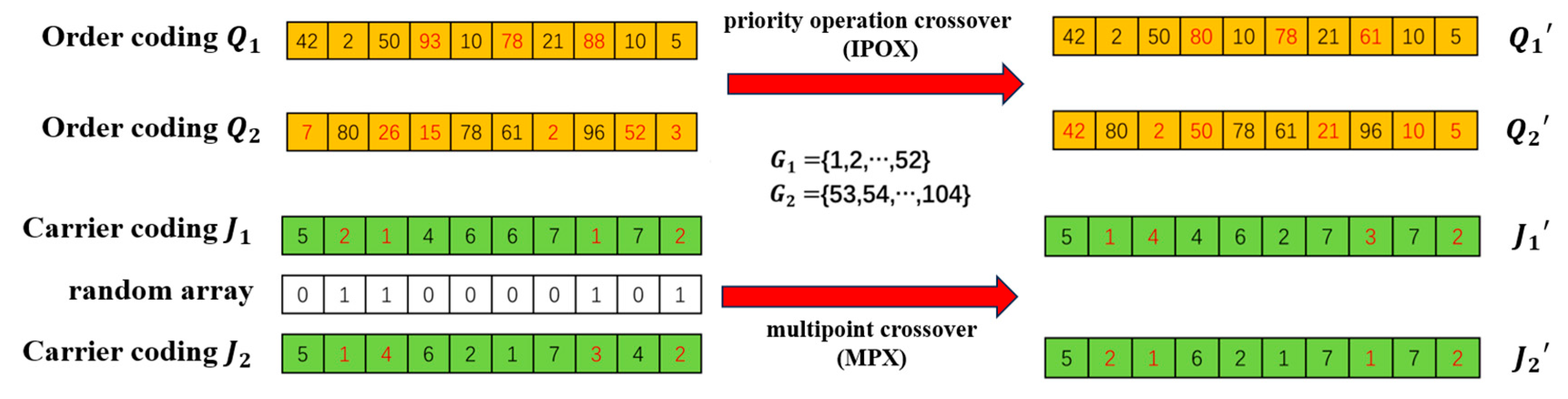
3.4.2. Selection and Crossover Strategies
- Elite retention: The top 5% of individuals with the highest fitness are directly retained into the next generation, forming the elite set, where denotes the fitness function (inversely proportional to total energy consumption , aligning with the optimization goal of minimizing energy use).
- Simulated annealing acceptance criterion: For non-elite individuals, the acceptance probability of a new candidate (generated via crossover/mutation) is defined as:Here, represents the iteratively decaying temperature ( is the initial temperature, is the cooling rate, and t is the current iteration), implementing the Metropolis criterion to avoid trapping in local optima.
4. Implementation and Simulation Results
4.1. Background Description
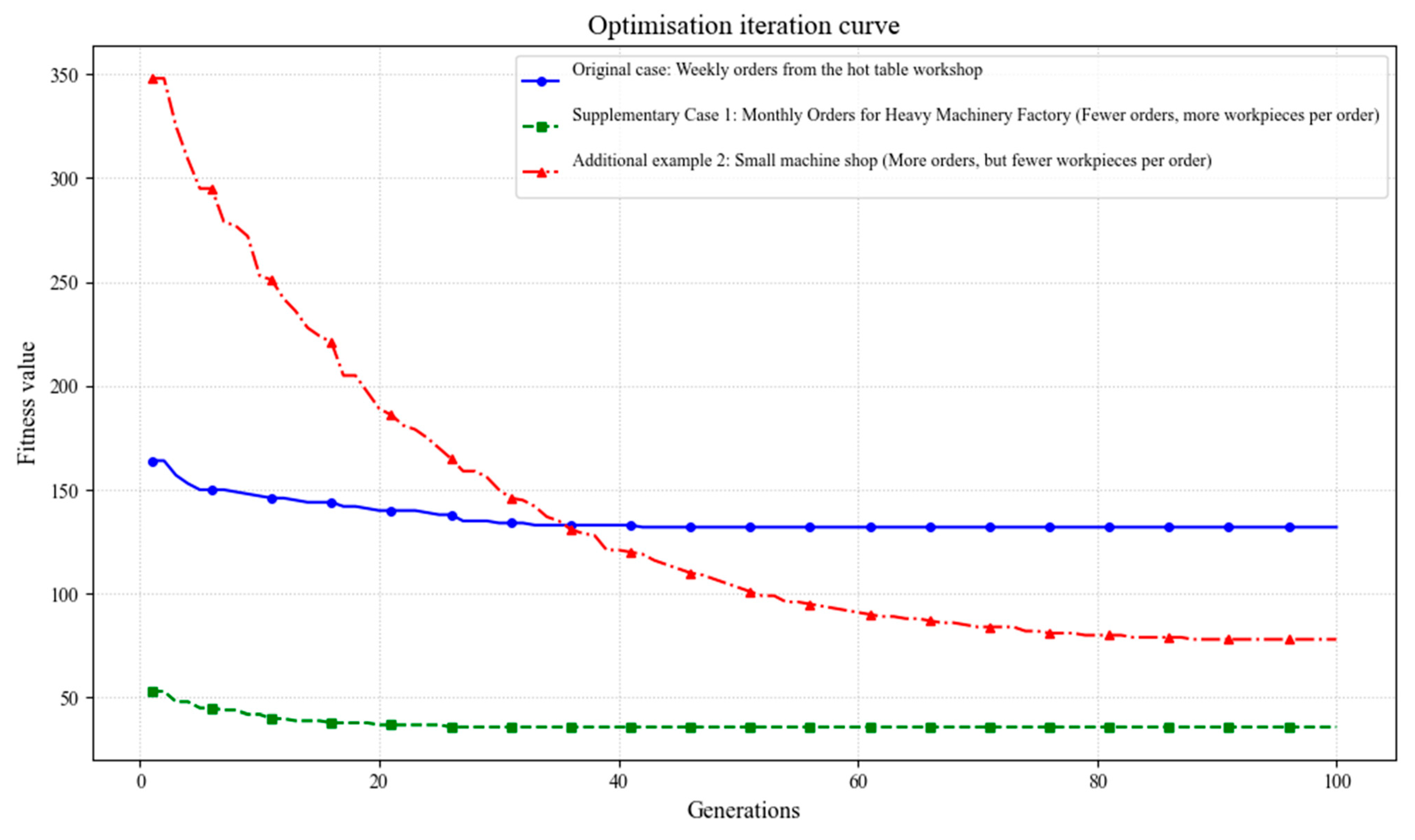
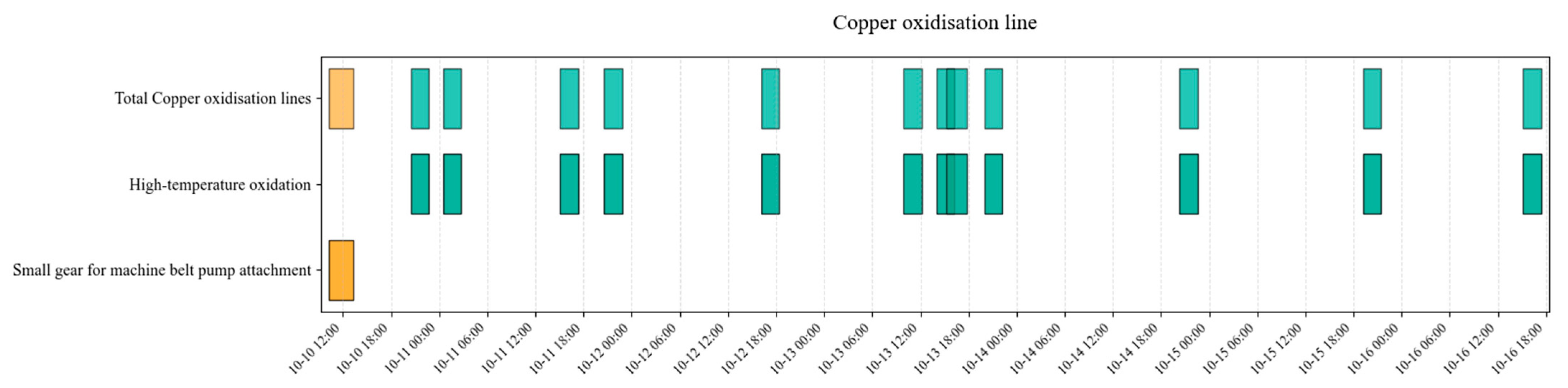
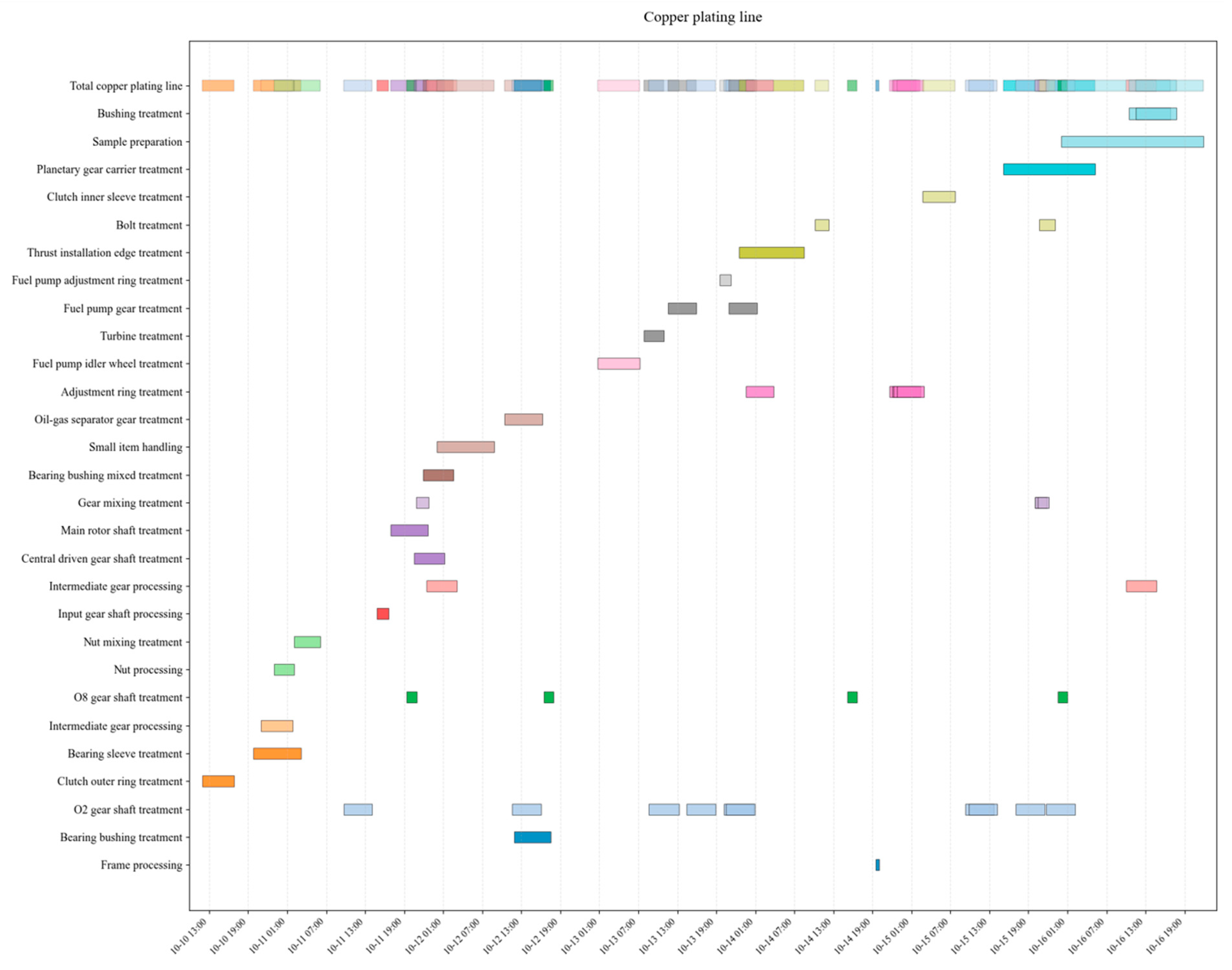
4.2. Experimental and Simulation Validation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kamble, S.; Gawankar, A. Sustainable Industry 4.0 framework: A systematic literature review identifying the current trends and future perspectives. Process Saf. Environ. Prot. 2018, 117, 408–425. [Google Scholar] [CrossRef]
- Xu, L.D.; Xu, E.L.; Li, L. Industry 4.0: State of the art and future trends. Int. J. Prod. Res. 2018, 56, 2941–2962. [Google Scholar] [CrossRef]
- Eduardo, G.; Beatriz, A.; Raul, P. Models and algorithms for production planning, scheduling and sequencing problems: A holistic framework and a systematic review. J. Ind. Inf. Integr. 2022, 27, 100287. [Google Scholar] [CrossRef]
- Wang, Z.; Hu, H.; Gong, J.; Ma, X. Synchronizing production scheduling with resources allocation for precast components in a multi-agent system environment. J. Manuf. Syst. 2018, 49, 131–142. [Google Scholar] [CrossRef]
- Meng, L.; Zhang, C.; Shao, X.; Ren, Y. MILP models for energy-aware flexible job shop scheduling problem. J. Clean. Prod. 2019, 210, 710–723. [Google Scholar] [CrossRef]
- Park, M.-J.; Ham, A. Energy-aware flexible job shop scheduling under time-of-use pricing. Int. J. Prod. Econ. 2022, 248, 108507. [Google Scholar]
- Jiang, X.; Tian, Z.; Liu, W.; Suo, Y.; Chen, K.; Xu, X.; Li, Z. Energy-efficient scheduling of flexible job shops with complex processes: A case study for the aerospace industry complex components in China. J. Ind. Inf. Integr. 2022, 27, 100293. [Google Scholar] [CrossRef]
- Dai, M.; Tang, D.; Adriana, G.; Miguel, A.S. Multi-objective optimization for energy-efficient flexible job shop scheduling problem with transportation constraints. Robot. Comput.-Integr. Manuf. 2019, 59, 143–157. [Google Scholar] [CrossRef]
- Alkayal, E.S.; Jennings, N.R.; Abulkhair, M.F. Efficient Task Scheduling Multi-Objective Particle Swarm Optimization in Cloud Computing. In Proceedings of the 2016 IEEE 41st Conference on Local Computer Networks Workshops (LCN Workshops), Dubai, United Arab Emirates, 7–10 November 2016. [Google Scholar]
- Wang, J.; Qiao, F.; Zhao, F.; Sutherland, J.W. Sutherland. Batch scheduling for minimal energy consumption and tardiness under uncertainties: A heat treatment application. CIRP Ann. 2016, 65, 17–20. [Google Scholar] [CrossRef]
- Qian, S.; Jia, Z.; Li, K. A multi-objective evolutionary algorithm based on adaptive clustering for energy-aware batch scheduling problem. Future Gener. Comput. Syst. 2020, 113, 441–453. [Google Scholar] [CrossRef]
- Hidehiro, K.; Masaki, H.; Hidenori, N. Clustering-Based Task Scheduling in a Large Number of Heterogeneous Processors. Trans. Parallel Distrib. Syst. 2016, 27, 3144–3157. [Google Scholar]
- El-Kholany, M.; Schekotihin, K.; Martin, G. Decomposition-Based Job-Shop Scheduling with Constrained Clustering. In Practical Aspects of Declarative Languages: 24th International Symposium; Springer: Cham, Switzerland, 2022. [Google Scholar]
- Çaliş, B.; Bulkan, S. A research survey: Review of AI solution strategies of job shop scheduling problem. J. Intell. Manuf. 2015, 26, 961–973. [Google Scholar] [CrossRef]
- Karim, T.; Stéphane, D.; Sebastian, K.; Bitar, A.; Yugma, C. Multiobjective optimization for complex flexible job-shop scheduling problems. Eur. J. Oper. Res. 2022, 296, 87–100. [Google Scholar] [CrossRef]
- Amin, J. Robust job shop scheduling problem: Mathematical models, exact and heuristic algorithms. Expert Syst. Appl. 2016, 55, 341–350. [Google Scholar] [CrossRef]
- Zhou, H.; Feng, Y.; Han, L. The hybrid heuristic genetic algorithm for job shop scheduling. Comput. Ind. Eng. 2001, 40, 191–200. [Google Scholar] [CrossRef]
- Wang, Y.; Fu, Y.; Gao, K.; Rahman, H.F.; Huang, M. Open shop scheduling with group and transportation operations by learning-driven hyper-heuristic algorithms. Swarm Evol. Comput. 2024, 91, 101757. [Google Scholar] [CrossRef]
- Huang, L.; Tang, D.; Zhang, Z.; Zhu, H.; Cai, Q.; Zhao, S. An iterated greedy algorithm integrating job insertion strategy for distributed job shop scheduling problems. J. Manuf. Syst. 2024, 77, 746–763. [Google Scholar] [CrossRef]
- Morikawa, K.; Nagasawa, K.; Takahashi, K. Job Shop Scheduling by Branch and Bound Using Genetic Programming. Procedia Manuf. 2019, 39, 1112–1118. [Google Scholar] [CrossRef]
- Oliver, H.; Chandrasekharan, R. Efficient dispatching rules for scheduling in a job shop. Int. J. Prod. Econ. 1997, 48, 87–105. [Google Scholar] [CrossRef]
- Fang, J.; Breada, C.; Andrew, L. Problems and Solution Methods of Machine Scheduling in Semiconductor Manufacturing Operations: A Survey. Sustainability 2023, 15, 13012. [Google Scholar] [CrossRef]
- Gu, W.; Duan, L.; Liu, S.; Guo, Z. A real-time adaptive dynamic scheduling method for manufacturing workshops based on digital twin. Flex. Serv. Manuf. J. 2024, 1–33. [Google Scholar] [CrossRef]
- Hegde, S.N.; Srinivas, D.B.; Rajan, M.A.; Rani, S.; Kataria, A.; Min, H. Multi-objective and multi constrained task scheduling framework for computational grids. Sci. Rep. 2024, 14, 6521. [Google Scholar] [CrossRef]
- Qing-dao-er-ji, R.; Wang, Y. A new hybrid genetic algorithm for job shop scheduling problem. Comput. Oper. Res. 2012, 39, 2291–2299. [Google Scholar] [CrossRef]
- Lin, T.-L.; Horng, S.-J.; Kao, T.-W.; Chen, Y.-H.; Run, R.-S.; Chen, R.-J.; Lai, J.-L.; Kuo, I.-H. An efficient job-shop scheduling algorithm based on particle swarm optimization. Expert Syst. Appl. 2010, 37, 2629–2636. [Google Scholar] [CrossRef]
- Xing, L.; Chen, Y.; Wang, P.; Zhao, Q.-S.; Xiong, J. A Knowledge-Based Ant Colony Optimization for Flexible Job Shop Scheduling Problems. Appl. Soft Comput. 2010, 10, 888–896. [Google Scholar] [CrossRef]
- Mageed, G.; Sharareh, T.; Hossein, Z. Real-time integrated production-scheduling and maintenance-planning in a flexible job shop with machine deterioration and condition-based maintenance. J. Manuf. Syst. 2021, 61, 423–449. [Google Scholar]
- Wu, X.; Yan, X.; Guan, D.; Wei, M. A deep reinforcement learning model for dynamic job-shop scheduling problem with uncertain processing time. Eng. Appl. Artif. Intell. 2024, 131, 7790. [Google Scholar] [CrossRef]
- Ji, S.; Wang, Z.; Yan, J. A Multi-Type data driven framework for solving flexible job shop scheduling problem considering multiple production resource states. Comput. Ind. Eng. 2025, 200, 110835. [Google Scholar] [CrossRef]
- Zhang, L.; Feng, Y.; Xiao, Q.; Xu, Y.; Li, D.; Yang, D.; Yang, Z. Deep reinforcement learning for dynamic flexible job shop scheduling problem considering variable processing times. J. Manuf. Syst. 2023, 71, 257–273. [Google Scholar] [CrossRef]
- Gui, Y.; Tang, D.; Zhu, H.; Zhang, Y.; Zhang, Z. Dynamic scheduling for flexible job shop using a deep reinforcement learning approach. Comput. Ind. Eng. 2023, 180, 109255. [Google Scholar] [CrossRef]
- Fan, C.; Wang, W.; Tian, J. Flexible job shop scheduling with stochastic machine breakdowns by an improved tuna swarm optimization algorithm. J. Manuf. Syst. 2024, 74, 180–197. [Google Scholar] [CrossRef]
- Fadi, S.; Joaquin, O.; Alvaro, G.; Ortega-Mier, M. Optimizing the production scheduling of a single machine to minimize total energy consumption costs. J. Clean. Prod. 2014, 67, 197–207. [Google Scholar] [CrossRef]
- An, Y.; Chen, X.; Zhang, J.; Li, Y. A hybrid multi-objective evolutionary algorithm to integrate optimization of the production scheduling and imperfect cutting tool maintenance considering total energy consumption. J. Clean. Prod. 2020, 268, 121540. [Google Scholar] [CrossRef]
- Adil, B.; Fehmi, B.O. Dynamic scheduling of parallel heat treatment furnaces: A case study at a manufacturing system. J. Manuf. Syst. 2018, 46, 152–162. [Google Scholar] [CrossRef]
- Sivakumar, T.; Sathiya, A.; Saravanan, M.; Uma, G.; Samson, S.A.; Elangovan, A. Dynamic Energy-Efficient Clustering Algorithms Using Advanced Metaheuristics for Prolonged Network Lifetime in Wireless Sensor Networks. In Proceedings of the 2024 4th International Conference on Ubiquitous Computing and Intelligent Information Systems (ICUIS), Gobichettipalayam, India, 12–13 December 2024. [Google Scholar]






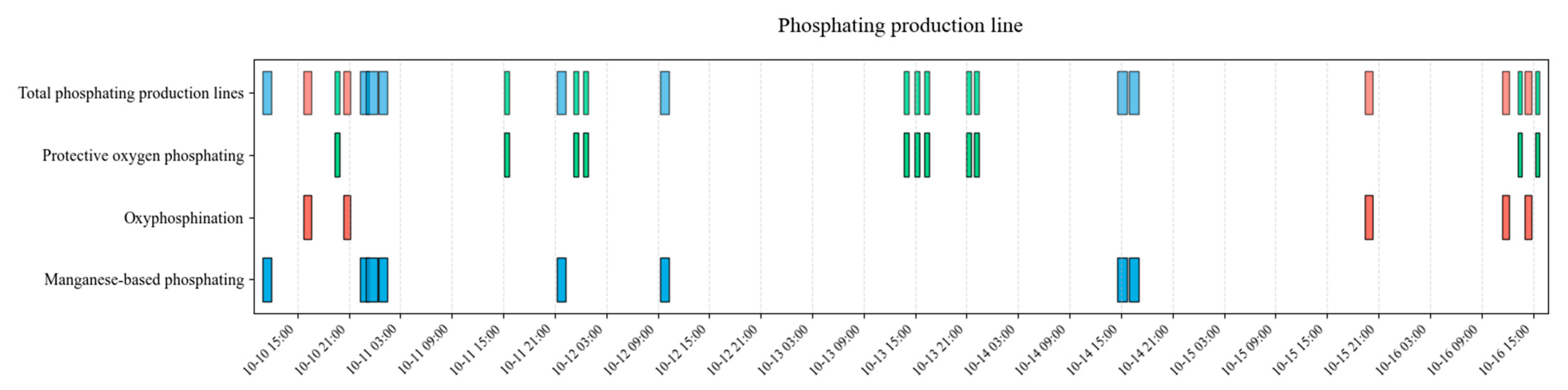
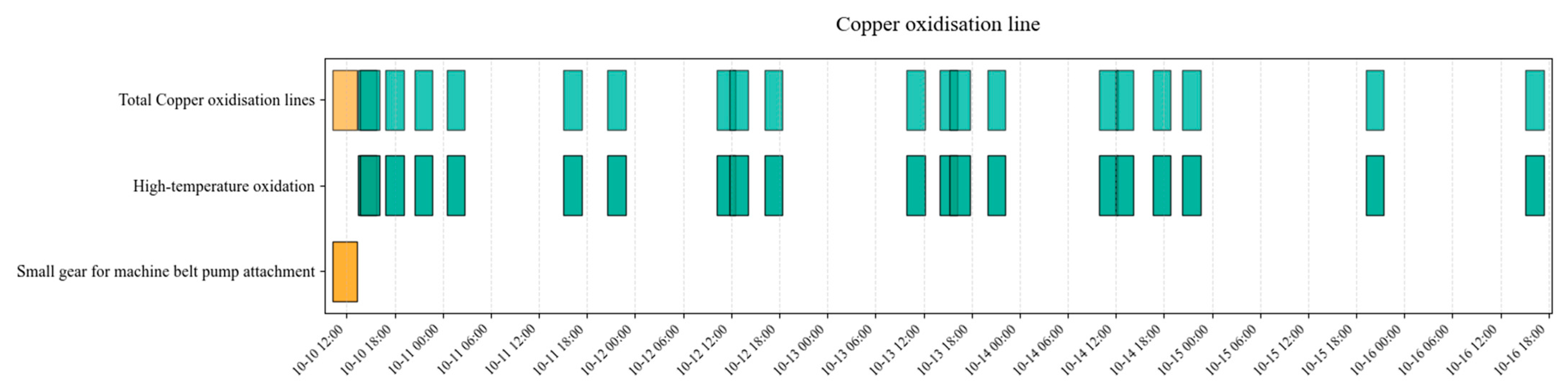
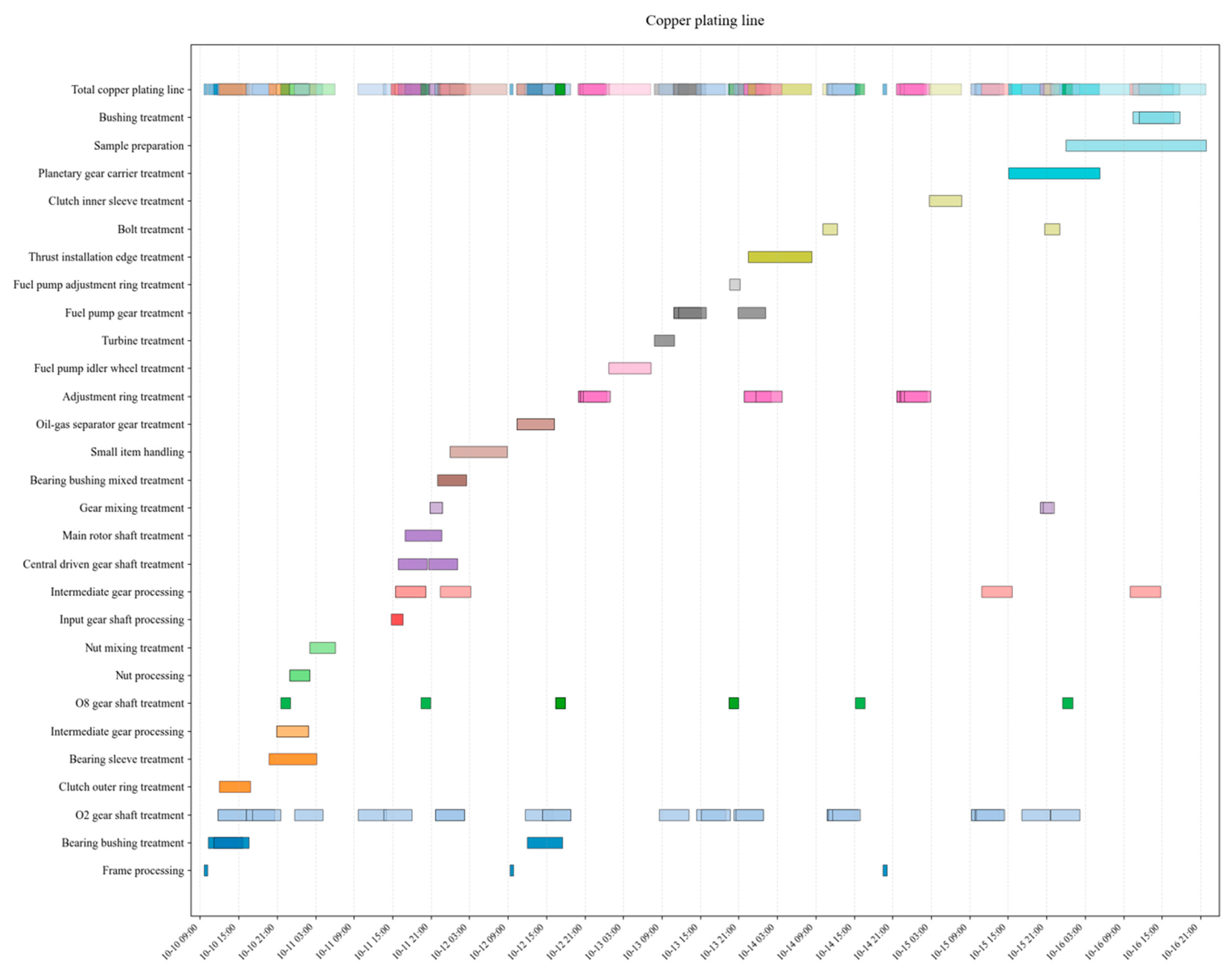
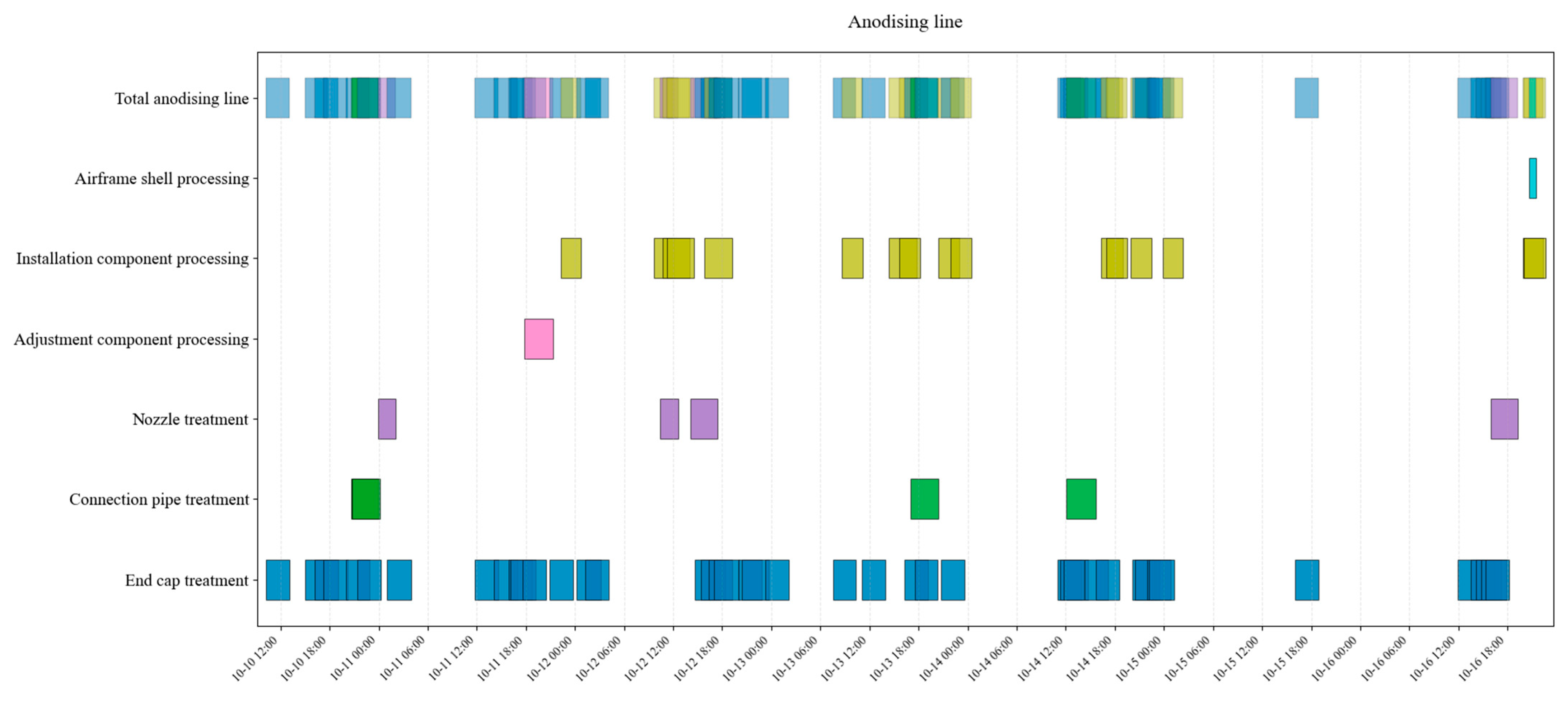


| Parameters | Defination |
|---|---|
| J | Number of production lines |
| M | Number of processes |
| Workpiece batches produced, including merged batches | |
| Indicates that batches a and b are combined | |
| Number of workpieces | |
| F | Total number of production groups |
| Number of production groups on a single production line | |
| s | Index value (=1, 2, …) |
| Workpiece batch index | |
| Production line index | |
| Production group index | |
| Work process index | |
| Process start time of the workpiece | |
| Processing time of the workpiece | |
| Workpiece end time | |
| Workpiece arrival time | |
| Delivery time of workpiece | |
| T | Total time of a production cycle |
| Production group capacity | |
| Production power of the process | |
| Idle power of a process | |
| E | Production energy consumption |
| O(…) | Operation value (=0, 1) An operation value of 1 means operable, 0 means not operable |
| R(…) | Status value (=0, 1) A status value of 1 means ready, 0 means not ready |
| S(…) | Judgement of whether the same (=0, 1) |
| Name of Production Line | Working Power/kW | Idle Power/kW | Utilization Rate of Production Line | Energy Consumption of Each Production Line/kWh | Total Energy Consumption/kWh |
|---|---|---|---|---|---|
| Phosphating line | 150 | 90 | 11.12% | 16,095.888 | 37,555.2738 |
| Copper oxidization line | 110 | 40 | 26.65% | 9766.0575 | |
| Copper plating line | 20 | 6 | 86.73% | 3020.6763 | |
| Anodizing line | 70 | 30 | 55.22% | 8672.652 |
| Genetic Parameters | Population Size | Number of Iterations | Crossover Probability | Variation Probability |
|---|---|---|---|---|
| Setpoint | 500 | 100 | 0.8 | 0.2 |
| Parameter determination method | Preliminary experiments show that within the range of 200–1000, 500 strikes a balance between convergence and computational efficiency. | Based on convergence curves under different parameter trials, it was found that the fitness tends to stabilize after 100 iterations. | Determined through sensitivity analysis, where a ±0.1 fluctuation results in a 5–8% decline in solution quality. | |
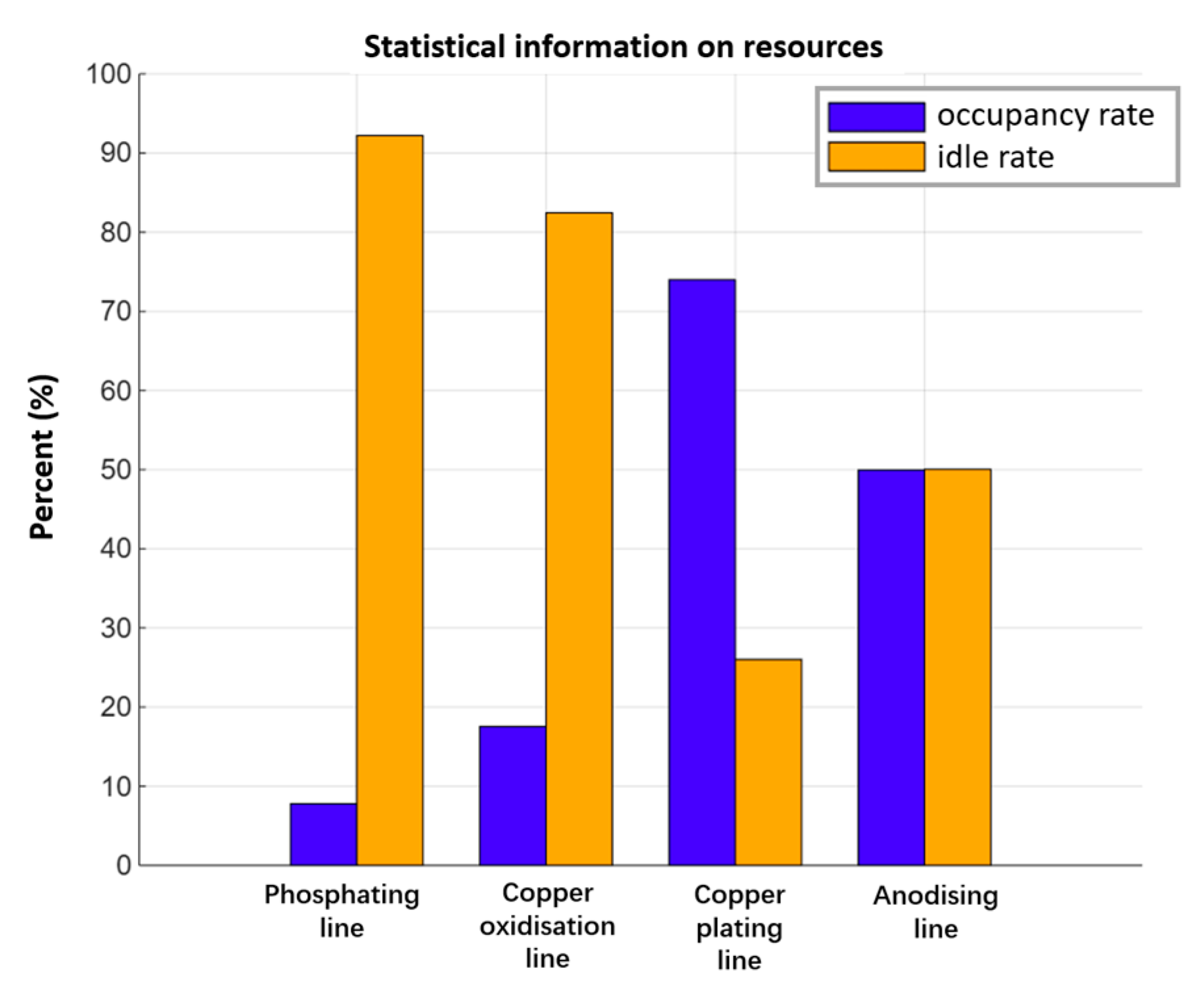
| Name of Production Line | Working Power/kW | Idle Power/kW | Utilization Rate of Production Line | Energy Consumption of Each Production Line/kWh | Total Energy Consumption/kWh |
|---|---|---|---|---|---|
| Phosphating line | 150 | 90 | 7.78% | 15,762.222 | 35,513.7174 |
| Copper oxidization line | 110 | 40 | 17.55% | 8705.4525 | |
| Copper plating line | 20 | 6 | 73.99% | 2723.7069 | |
| Anodizing line | 70 | 30 | 49.96% | 8322.336 | |
| Explanation | Energy consumption decreased by 5.4% (2041.56 kWh/week). Based on an industrial electricity price of CNY 0.8/kWh, this translates to an annual savings of approximately CNY 653,000 and a reduction in carbon emissions of about 12.2 tons. | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, D.; Zhang, T.; Ji, S.; Yan, J. Energy-Efficient Scheduling in Heat Treatment Workshops Based on Task Clustering and Job Batching. Machines 2025, 13, 732. https://doi.org/10.3390/machines13080732
Su D, Zhang T, Ji S, Yan J. Energy-Efficient Scheduling in Heat Treatment Workshops Based on Task Clustering and Job Batching. Machines. 2025; 13(8):732. https://doi.org/10.3390/machines13080732
Chicago/Turabian StyleSu, Dapeng, Tianyi Zhang, Siyang Ji, and Jihong Yan. 2025. "Energy-Efficient Scheduling in Heat Treatment Workshops Based on Task Clustering and Job Batching" Machines 13, no. 8: 732. https://doi.org/10.3390/machines13080732
APA StyleSu, D., Zhang, T., Ji, S., & Yan, J. (2025). Energy-Efficient Scheduling in Heat Treatment Workshops Based on Task Clustering and Job Batching. Machines, 13(8), 732. https://doi.org/10.3390/machines13080732







