An Improved Black-Winged Kite Algorithm for High-Accuracy Parameter Identification of a Photovoltaic Double Diode Model
Abstract
1. Introduction
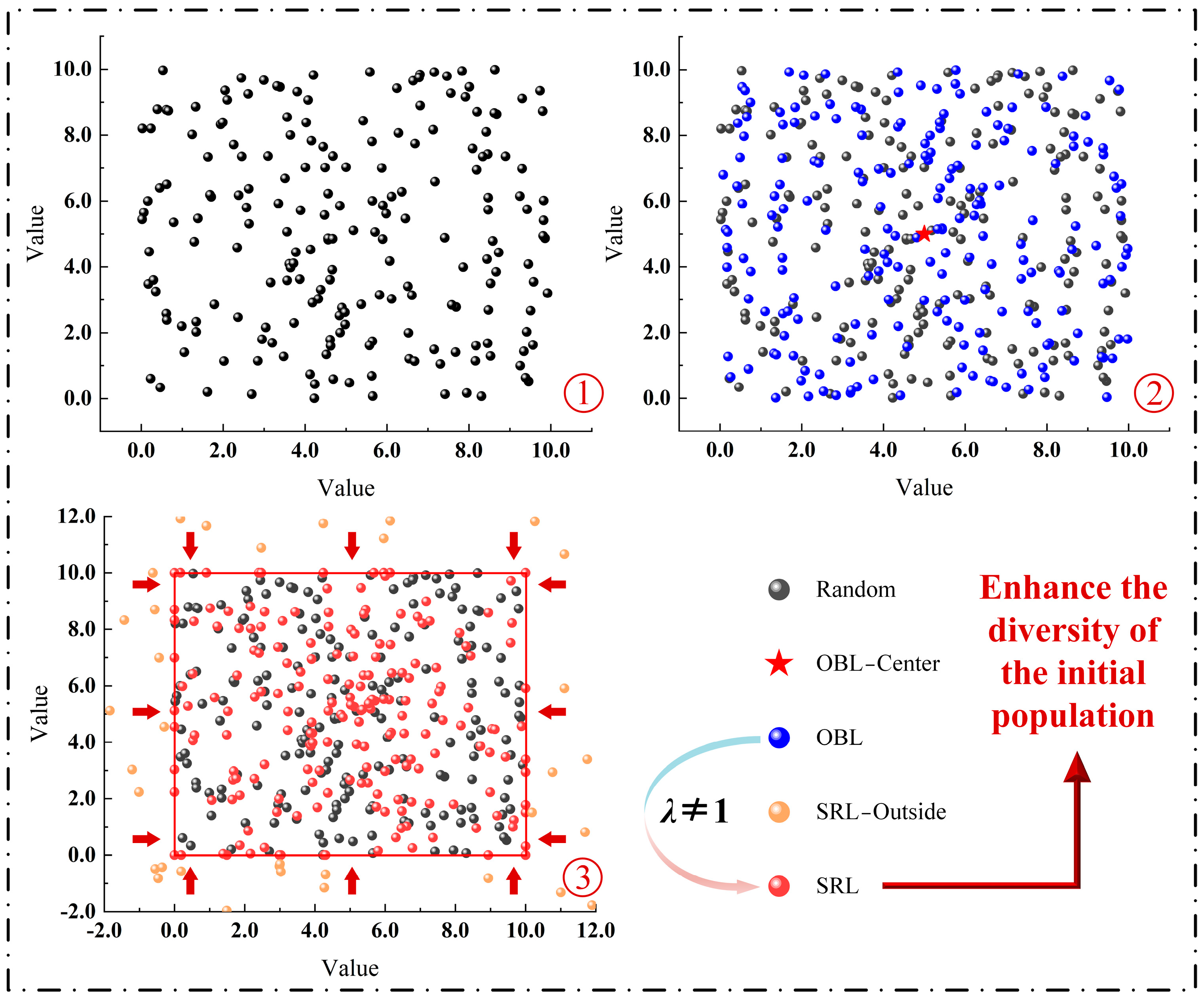
- SRL is introduced into the BKA for the first time to generate high-quality initial solutions via specular reflection, thereby improving population diversity and providing a stronger foundation for accurate and reliable parameter identification.
- A hybrid optimization strategy that combines SRS and QI is proposed to enhance search efficiency. SRS enhances exploration during the early stages and gradually promotes exploitation as iterations progress, whereas QI refines the local search by accelerating convergence toward the optimal parameters.
- A progressive experimental design verifies the SRQ-BKA from theory to application. Benchmark tests confirm its rapid convergence and strong global search capability. Experiments on PV models demonstrate high accuracy, robustness, and practical applicability.
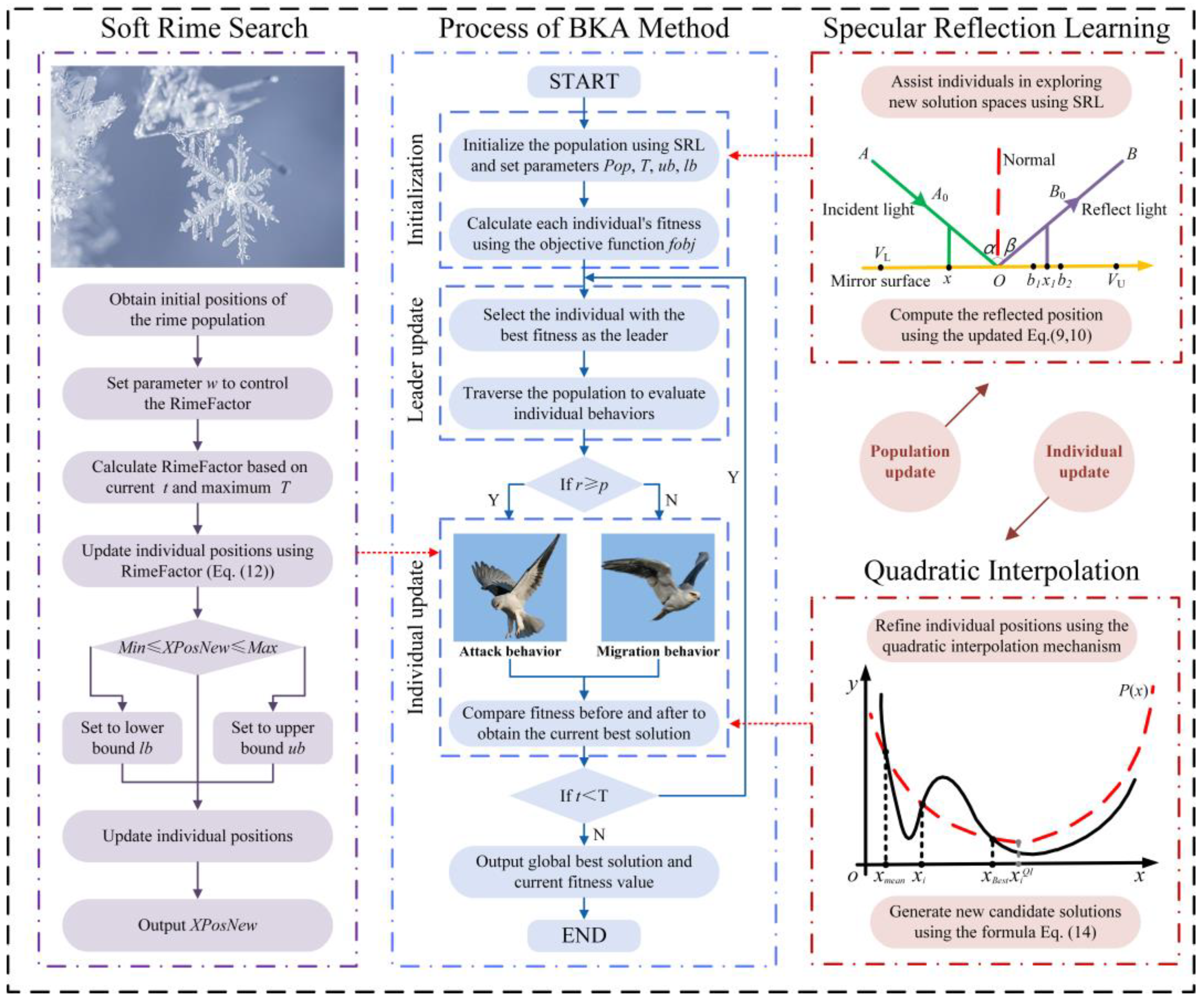
2. Black-Winged Kite Algorithm
2.1. Initialization Stage
2.2. Attacking Stage
2.3. Migratory Stage
3. SRQ-BKA for Model Parameter Identification
3.1. Construction of Fitness Function
3.2. Model Parameter Initialization Method Based on SRL
3.3. Hybrid Optimization with SRS and QI for Efficient Search
3.4. SRQ-BKA
4. Experiments and Verification
- Test PV module (TSM-240). This multicrystalline silicon module has the following key specifications under standard test conditions (STC): short-circuit current Isc = 8.62 A, open-circuit voltage Voc = 37.3 V, and maximum power Pmax = 240 W. Additional parameters and detailed specifications are listed in Table 3.
- I-V acquisition module. A microcontroller governs the relay-based switching to dynamically acquire the I-V characteristics of the tested PV module.
- Environmental monitoring unit. It is equipped with a pyranometer and temperature sensors to continuously record the irradiance (W/m2) and the surface temperature (°C).
- Data processing system. The collected I-V and environmental data are transmitted to an industrial computer through an RS-485 serial interface, where dedicated software displays the real-time I-V curves and extracts key performance parameters.
4.1. Evaluation Methods
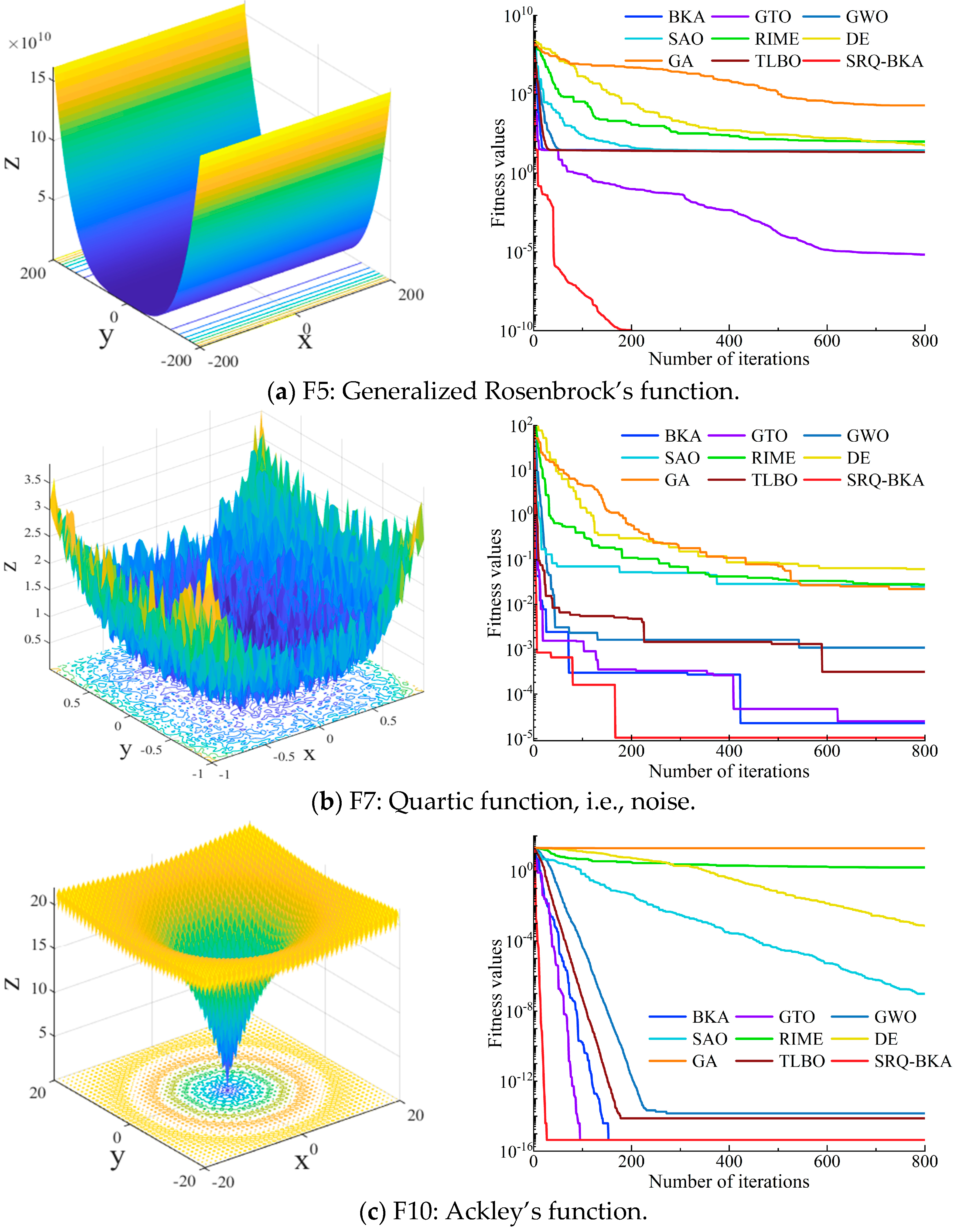
4.2. Experiment 1: Comparison of Optimization Results for Benchmark Test Functions
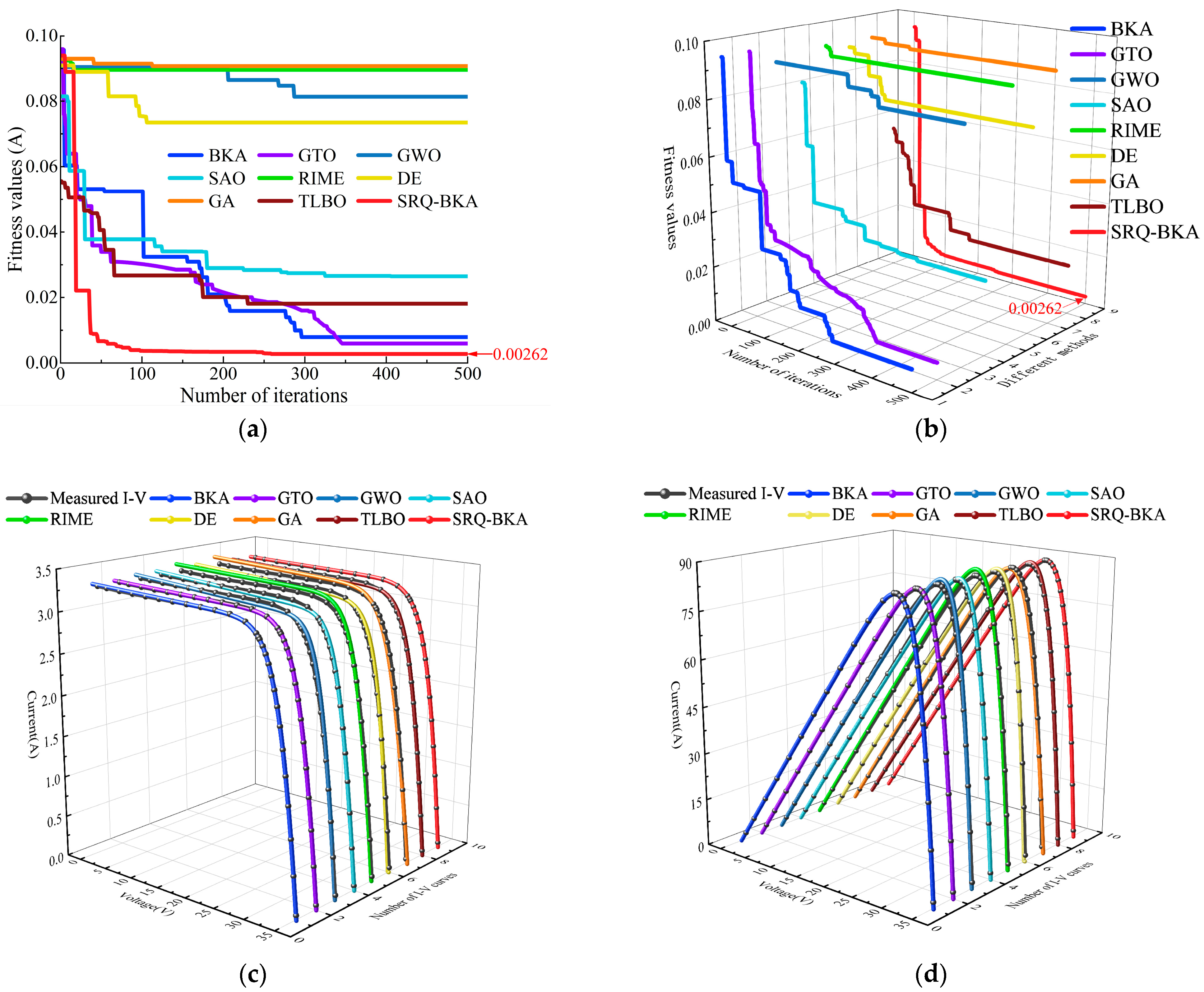
4.3. Experiment 2: Parameter Identification of DDM Based on Measured Data
4.4. Experiment 3: Comparative Study of Parameter Identification for the SDM, DDM, and TDM
4.5. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ABC | Artificial bee colony algorithm | MPA | Marine predators algorithm |
| ASO | Atom search algorithm | MRIME | Modified rime-ice growth optimizer |
| BKA | Black-winged kite algorithm | ||
| CGH-GTO | Combination method based on IGWO, HBA, and GTO | OBL | Opposition-based learning |
| PAs | Physics-based algorithms | ||
| CI | Confidence interval | PDLO | Polynomial differential learning operator |
| CSA | Cooperation search algorithm | ||
| Ctime | Computation time | PSO | Particle swarm optimization |
| DDM | Double diode model | PV | Photovoltaic |
| DE | Differential evolution | QI | Quadratic interpolation |
| EAs | Evolutionary algorithms | R2 | Coefficient of determination |
| EO | Equilibrium optimizer | RIME | Rime optimization algorithm |
| GA | Genetic algorithm | RMSE | Root mean square error |
| GTO | Artificial gorilla troops optimizer | SAO | Snow ablation optimizer |
| GWO | Gray wolf optimizer | SAs | Swarm-intelligence algorithms |
| GWOCS | Combination method based on the GWO and cuckoo search | SD | Standard deviation |
| SDM | Single diode model | ||
| HAs | Human-inspired algorithms | SNO | Social network optimization |
| HBA | Hummingbird algorithm | SRL | Specular reflection learning |
| IFDA | Improved flow direction algorithm | SRQ-BKA | Combination method based on SRL, SRS, QI and BKA |
| IGWO | Improved GWO | SRS | Soft rime search |
| MAE | Mean absolute error | STC | Standard test conditions |
| MAPE | Mean absolute percentage error | TDM | Triple diode model |
| MAs | Metaheuristic algorithms | TLBO | Teaching-learning-based optimization |
| MGA | Material generation algorithm | ||
| MKOA | Multi-strategy fused kepler optimization algorithm | WOA | Whale optimization algorithm |
References
- Hao, D.; Qi, L.; Tairab, A.M.; Ahmed, A.; Azam, A.; Luo, D.; Pan, Y.; Zhang, Z.; Yan, J. Solar Energy Harvesting Technologies for PV Self-Powered Applications: A Comprehensive Review. Renew. Energy 2022, 188, 678–697. [Google Scholar] [CrossRef]
- Amiri, A.F.; Oudira, H.; Chouder, A.; Kichou, S. Faults Detection and Diagnosis of PV Systems Based on Machine Learning Approach Using Random Forest Classifier. Energy Convers. Manag. 2024, 301, 118076. [Google Scholar] [CrossRef]
- Oliva, D.; Elaziz, M.A.; Elsheikh, A.H.; Ewees, A.A. A Review on Meta-Heuristics Methods for Estimating Parameters of Solar Cells. J. Power Sources 2019, 435, 126683. [Google Scholar] [CrossRef]
- Siddiqui, M.U.; Siddiqui, O.K.; Alquaity, A.B.S.; Ali, H.; Arif, A.F.M.; Zubair, S.M. A Comprehensive Review on Multi-Physics Modeling of Photovoltaic Modules. Energy Convers. Manag. 2022, 258, 115414. [Google Scholar] [CrossRef]
- Chenouard, R.; El-Sehiemy, R.A. An Interval Branch and Bound Global Optimization Algorithm for Parameter Estimation of Three Photovoltaic Models. Energy Convers. Manag. 2020, 205, 112400. [Google Scholar] [CrossRef]
- Venkateswari, R.; Rajasekar, N. Review on Parameter Estimation Techniques of Solar Photovoltaic Systems. Int. Trans. Electr. Energ. Syst. 2021, 31, e13113. [Google Scholar] [CrossRef]
- Ridha, H.M.; Hizam, H.; Gomes, C.; Heidari, A.A.; Chen, H.; Ahmadipour, M.; Muhsen, D.H.; Alghrairi, M. Parameters Extraction of Three Diode Photovoltaic Models Using Boosted LSHADE Algorithm and Newton Raphson Method. Energy 2021, 224, 120136. [Google Scholar] [CrossRef]
- Zhou, W.; Wang, P.; Heidari, A.A.; Zhao, X.; Turabieh, H.; Mafarja, M.; Chen, H. Metaphor-Free Dynamic Spherical Evolution for Parameter Estimation of Photovoltaic Modules. Energy Rep. 2021, 7, 5175–5202. [Google Scholar] [CrossRef]
- Restrepo-Cuestas, B.J. Bishop Model Parameter Estimation in Photovoltaic Cells Using Metaheuristic Optimization Techniques. Sol. Energy 2024, 270, 112410. [Google Scholar] [CrossRef]
- Lai, V.; Huang, Y.F.; Koo, C.H.; Ahmed, A.N.; El-Shafie, A. A Review of Reservoir Operation Optimisations: From Traditional Models to Metaheuristic Algorithms. Arch. Comput. Methods Eng. 2022, 29, 3435–3457. [Google Scholar] [CrossRef] [PubMed]
- Song, E.; Yao, Z.; Wang, Z. A Dynamic Multi-Objective Differential Evolution Based on Hierarchical Prediction Strategy. In Proceedings of the 2024 6th International Conference on Data-driven Optimization of Complex Systems (DOCS), Hangzhou, China, 16–18 August 2024; pp. 761–766. [Google Scholar]
- Chun, Y.; Hua, X.; Qi, C.; Yao, Y.X. Improved Marine Predators Algorithm for Engineering Design Optimization Problems. Sci. Rep. 2024, 14, 13000. [Google Scholar] [CrossRef]
- Faramarzi, A.; Heidarinejad, M.; Stephens, B.; Mirjalili, S. Equilibrium Optimizer: A Novel Optimization Algorithm. Knowl. Based Syst. 2020, 191, 105190. [Google Scholar] [CrossRef]
- Hammadi, W.Q.; Qasim, O.S. Hybrid Binary Atom Search Optimization Approaches with Statistical Dependence for Feature Selection. In Proceedings of the 2022 International Conference on Computer Science and Software Engineering (CSASE), Duhok, Iraq, 15–17 March 2022; pp. 218–223. [Google Scholar]
- Deng, L.; Liu, S. Snow Ablation Optimizer: A Novel Metaheuristic Technique for Numerical Optimization and Engineering Design. Expert. Syst. Appl. 2023, 225, 120069. [Google Scholar] [CrossRef]
- Su, H.; Zhao, D.; Heidari, A.A.; Liu, L.; Zhang, X.; Mafarja, M.; Chen, H. RIME: A Physics-Based Optimization. Neurocomputing 2023, 532, 183–214. [Google Scholar] [CrossRef]
- Chen, X.; Yu, K.; Du, W.; Zhao, W.; Liu, G. Parameters Identification of Solar Cell Models Using Generalized Oppositional Teaching Learning Based Optimization. Energy 2016, 99, 170–180. [Google Scholar] [CrossRef]
- Bayzidi, H.; Talatahari, S.; Saraee, M.; Lamarche, C.-P. Social Network Search for Solving Engineering Optimization Problems. Comput. Intell. Neurosci. 2021, 2021, 8548639. [Google Scholar] [CrossRef] [PubMed]
- Feng, Z.; Niu, W.; Liu, S. Cooperation Search Algorithm: A Novel Metaheuristic Evolutionary Intelligence Algorithm for Numerical Optimization and Engineering Optimization Problems. Appl. Soft Comput. 2021, 98, 106734. [Google Scholar] [CrossRef]
- Fan, Y.; Wang, P.; Heidari, A.A.; Chen, H.; HamzaTurabieh; Mafarja, M. Random Reselection Particle Swarm Optimization for Optimal Design of Solar Photovoltaic Modules. Energy 2022, 239, 121865. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Makhadmeh, S.N.; Al-Betar, M.A.; Doush, I.A.; Awadallah, M.A.; Kassaymeh, S.; Mirjalili, S.; Zitar, R.A. Recent Advances in Grey Wolf Optimizer, Its Versions and Applications: Review. IEEE Access 2024, 12, 22991–23028. [Google Scholar] [CrossRef]
- Wang, J.; Wang, W.; Hu, X.; Qiu, L.; Zang, H. Black-Winged Kite Algorithm: A Nature-Inspired Meta-Heuristic for Solving Benchmark Functions and Engineering Problems. Artif. Intell. Rev. 2024, 57, 98. [Google Scholar] [CrossRef]
- Chen, X.; Ding, K.; Zhang, J.; Yang, Z.; Liu, Y.; Yang, H. A Two-Stage Method for Model Parameter Identification Based on the Maximum Power Matching and Improved Flow Direction Algorithm. Energy Convers. Manag. 2023, 278, 116712. [Google Scholar] [CrossRef]
- Jiang, M.; Ding, K.; Chen, X.; Cui, L.; Zhang, J.; Cang, Y.; Yang, H.; Gao, R. CGH-GTO Method for Model Parameter Identification Based on Improved Grey Wolf Optimizer, Honey Badger Algorithm, and Gorilla Troops Optimizer. Energy 2024, 296, 131163. [Google Scholar] [CrossRef]
- Chen, X.; Xu, B.; Mei, C.; Ding, Y.; Li, K. Teaching–Learning–Based Artificial Bee Colony for Solar Photovoltaic Parameter Estimation. Appl. Energy 2018, 212, 1578–1588. [Google Scholar] [CrossRef]
- Long, W.; Cai, S.; Jiao, J.; Xu, M.; Wu, T. A New Hybrid Algorithm Based on Grey Wolf Optimizer and Cuckoo Search for Parameter Extraction of Solar Photovoltaic Models. Energy Convers. Manag. 2020, 203, 112243. [Google Scholar] [CrossRef]
- Alsaggaf, W.; Gafar, M.; Sarhan, S.; Shaheen, A.M.; Ginidi, A.R. Chemical-Inspired Material Generation Algorithm (MGA) of Single- and Double-Diode Model Parameter Determination for Multi-Crystalline Silicon Solar Cells. Appl. Sci. 2024, 14, 8549. [Google Scholar] [CrossRef]
- Hakmi, S.H.; Alnami, H.; Moustafa, G.; Ginidi, A.R.; Shaheen, A.M. Modified Rime-Ice Growth Optimizer with Polynomial Differential Learning Operator for Single- and Double-Diode PV Parameter Estimation Problem. Electronics 2024, 13, 1611. [Google Scholar] [CrossRef]
- Qian, Z.; Zhang, Y.; Pu, D.; Xie, G.; Pu, D.; Ye, M. A New Hybrid Improved Kepler Optimization Algorithm Based on Multi-Strategy Fusion and Its Applications. Mathematics 2025, 13, 405. [Google Scholar] [CrossRef]
- González, I.; Portalo, J.M.; Calderón, A.J. Configurable IoT Open-Source Hardware and Software I-V Curve Tracer for Photovoltaic Generators. Sensors 2021, 21, 7650. [Google Scholar] [CrossRef] [PubMed]
- Ashraf, H.; Draz, A.; Elmoaty, A.M.; El-Fergany, A.A. Precise Modelling of Commercial Photovoltaic Cells/Modules of Different Technologies Using Hippopotamus Optimizer. Energy Convers. Manag. 2025, 325, 119382. [Google Scholar] [CrossRef]
- Oulcaid, M.; El Fadil, H.; Ammeh, L.; Yahya, A.; Giri, F. Parameter Extraction of Photovoltaic Cell and Module: Analysis and Discussion of Various Combinations and Test Cases. Sustain. Energy Technol. Assess. 2020, 40, 100736. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, Y.; Li, Y.; Ding, K.; Feng, L.; Chen, X.; Chen, X.; Wu, J. A Reinforcement Learning Based Approach for On-Line Adaptive Parameter Extraction of Photovoltaic Array Models. Energy Convers. Manag. 2020, 214, 112875. [Google Scholar] [CrossRef]
- Yang, X.; Zeng, G.; Cao, Z.; Huang, X.; Zhao, J. Parameters Estimation of Complex Solar Photovoltaic Models Using Bi-Parameter Coordinated Updating L-SHADE with Parameter Decomposition Method. Case Stud. Therm. Eng. 2024, 61, 104917. [Google Scholar] [CrossRef]
- Zhang, Y. Backtracking Search Algorithm with Specular Reflection Learning for Global Optimization. Knowl. Based Syst. 2021, 212, 106546. [Google Scholar] [CrossRef]
- Qaraad, M.; Amjad, S.; Hussein, N.K.; Farag, M.A.; Mirjalili, S.; Elhosseini, M.A. Quadratic Interpolation and a New Local Search Approach to Improve Particle Swarm Optimization: Solar Photovoltaic Parameter Estimation. Expert. Syst. Appl. 2024, 236, 121417. [Google Scholar] [CrossRef]
- Jiang, M.; Ding, K.; Chen, X.; Cui, L.; Zhang, J.; Yang, Z.; Cang, Y.; Cao, S. Research on Time-Series Based and Similarity Search Based Methods for PV Power Prediction. Energy Convers. Manag. 2024, 308, 118391. [Google Scholar] [CrossRef]







| Aspect | BKA | SRQ-BKA | Improvement |
|---|---|---|---|
| Initialization | Random | SRL | Better diversity |
| Attacking phase | Sinusoidal update | Sinusoidal + SRS | Balanced exploration–exploitation |
| Migration phase | Cauchy peer comparison | Same as original | Retained for global exploration |
| Local refinement | Not included | QI | Improved convergence and accuracy |
| Overall structure | Basic movement strategy | SRL + SRS + QI | More adaptive and stable optimization |
| Application | Moderate accuracy | High accuracy, robust under varying conditions | Better practical use |
| Algorithm: SRQ-BKA |
| Input: |
| N: population size. T: maximum iterations. |
| D: solution dimension. [lb, ub]: search bounds. |
| f(x): objective function. |
| Output: |
| Best_Pos: best solution. Best_Fit: best fitness value. |
| 1: Initialize population X within [lb, ub] |
| 2: Evaluate fitness of X and set Best_Pos, Best_Fit |
| 3: for t = 1 to T do |
| 4: Sort population and update Best_Pos |
| 5: // SRL: Specular Reflection Learning |
| 6: Generate mirrored candidates from elite individuals |
| 7: Replace individuals if mirrored candidates perform better |
| 8: for each X_i in population do |
| 9: // Attacking phase |
| 10: Update X_i via sinusoidal or Soft Rime Search (SRS) |
| 11: // Migration phase |
| 12: Adjust X_i using Cauchy-based peer comparison |
| 13: // QI: Quadratic Interpolation refinement |
| 14: Generate new candidate from X_i, mean(X), and Best_Pos |
| 15: Replace X_i if the new candidate improves fitness |
| 16: end for |
| 17: Record Best_Fit |
| 18: end for |
| 19: Return Best_Pos, Best_Fit |
| Parameter | Symbol | Value |
|---|---|---|
| Maximum power | Pmax,stc | 240 W |
| Voltage at maximum power point | Vmax,stc | 29.7 V |
| Current at maximum power point | Imax,stc | 8.1 A |
| Short-circuit current | Isc,stc | 8.62 A |
| Open-circuit voltage | Voc,stc | 37.3 V |
| Temperature coefficient of Isc | αstc | 0.047%/°C. |
| Temperature coefficient of Voc | βstc | −0.32%/°C. |
| Number of cells in series | Np | 60 |
| Code | Function | Domain |
|---|---|---|
| F5 | [−30, 30] | |
| F7 | [−1.28, 1.28] | |
| F10 | [−32, 32] |
| Voltage (V) | Measured Current (A) | Estimated Current (A) | Absolute Error (A) | Relative Error (%) |
|---|---|---|---|---|
| 0.340 | 3.294 | 3.294 | 0.000 | 0.008 |
| 2.753 | 3.285 | 3.286 | 0.001 | 0.034 |
| 5.165 | 3.278 | 3.279 | 0.001 | 0.016 |
| 7.578 | 3.272 | 3.272 | 0.000 | 0.007 |
| 9.990 | 3.268 | 3.268 | 0.000 | 0.012 |
| 12.403 | 3.266 | 3.267 | 0.001 | 0.023 |
| 14.815 | 3.264 | 3.264 | 0.000 | 0.010 |
| 17.228 | 3.262 | 3.264 | 0.002 | 0.063 |
| 19.640 | 3.259 | 3.261 | 0.002 | 0.075 |
| 22.053 | 3.253 | 3.252 | 0.001 | 0.019 |
| 24.465 | 3.238 | 3.240 | 0.002 | 0.047 |
| 26.878 | 3.185 | 3.185 | 0.000 | 0.005 |
| 28.600 | 3.082 | 3.082 | 0.000 | 0.012 |
| 28.950 | 3.047 | 3.049 | 0.002 | 0.073 |
| 29.140 | 3.025 | 3.023 | 0.002 | 0.074 |
| 29.630 | 2.957 | 2.955 | 0.002 | 0.073 |
| 30.087 | 2.879 | 2.876 | 0.003 | 0.087 |
| 30.543 | 2.781 | 2.783 | 0.002 | 0.063 |
| 31.000 | 2.660 | 2.661 | 0.001 | 0.055 |
| 31.457 | 2.518 | 2.520 | 0.002 | 0.077 |
| 31.913 | 2.345 | 2.348 | 0.003 | 0.107 |
| 32.370 | 2.139 | 2.141 | 0.002 | 0.073 |
| 32.827 | 1.891 | 1.891 | 0.000 | 0.011 |
| 33.283 | 1.607 | 1.608 | 0.001 | 0.092 |
| 33.740 | 1.284 | 1.282 | 0.002 | 0.156 |
| 34.197 | 0.917 | 0.918 | 0.001 | 0.080 |
| 34.653 | 0.506 | 0.504 | 0.002 | 0.369 |
| 35.110 | 0.060 | 0.062 | 0.002 | 3.883 |
| Voltage (V) | Measured Current (A) | Estimated Current (A) | Absolute Error (A) | Relative Error (%) |
|---|---|---|---|---|
| 0.540 | 5.152 | 5.152 | 0.000 | 0.006 |
| 2.777 | 5.139 | 5.138 | 0.001 | 0.022 |
| 5.103 | 5.129 | 5.131 | 0.002 | 0.039 |
| 7.430 | 5.123 | 5.126 | 0.003 | 0.051 |
| 9.757 | 5.120 | 5.120 | 0.000 | 0.001 |
| 12.083 | 5.117 | 5.113 | 0.004 | 0.080 |
| 14.410 | 5.114 | 5.112 | 0.002 | 0.032 |
| 16.737 | 5.110 | 5.112 | 0.002 | 0.036 |
| 19.063 | 5.103 | 5.103 | 0.000 | 0.006 |
| 21.390 | 5.093 | 5.093 | 0.000 | 0.003 |
| 23.717 | 5.072 | 5.074 | 0.002 | 0.033 |
| 26.043 | 4.980 | 4.978 | 0.002 | 0.035 |
| 27.750 | 4.793 | 4.794 | 0.001 | 0.028 |
| 27.920 | 4.765 | 4.766 | 0.001 | 0.011 |
| 27.950 | 4.760 | 4.764 | 0.004 | 0.089 |
| 28.230 | 4.707 | 4.707 | 0.000 | 0.010 |
| 28.787 | 4.581 | 4.581 | 0.000 | 0.005 |
| 29.345 | 4.421 | 4.419 | 0.002 | 0.055 |
| 29.902 | 4.219 | 4.219 | 0.000 | 0.002 |
| 30.460 | 3.983 | 3.981 | 0.002 | 0.039 |
| 31.017 | 3.689 | 3.686 | 0.003 | 0.083 |
| 31.575 | 3.334 | 3.337 | 0.003 | 0.078 |
| 32.132 | 2.915 | 2.915 | 0.000 | 0.003 |
| 32.690 | 2.458 | 2.460 | 0.002 | 0.076 |
| 33.247 | 1.949 | 1.951 | 0.002 | 0.087 |
| 33.805 | 1.365 | 1.362 | 0.003 | 0.221 |
| 34.362 | 0.703 | 0.699 | 0.004 | 0.556 |
| 34.920 | 0.046 | 0.041 | 0.005 | 9.881 |
| Voltage (V) | Measured Current (A) | Estimated Current (A) | Absolute Error (A) | Relative Error (%) |
|---|---|---|---|---|
| 0.900 | 7.883 | 7.886 | 0.003 | 0.032 |
| 2.952 | 7.875 | 7.871 | 0.004 | 0.052 |
| 5.133 | 7.869 | 7.870 | 0.001 | 0.017 |
| 7.315 | 7.864 | 7.867 | 0.003 | 0.037 |
| 9.497 | 7.859 | 7.859 | 0.000 | 0.003 |
| 11.678 | 7.854 | 7.855 | 0.001 | 0.017 |
| 13.860 | 7.848 | 7.846 | 0.002 | 0.032 |
| 16.042 | 7.839 | 7.837 | 0.002 | 0.025 |
| 18.223 | 7.827 | 7.824 | 0.003 | 0.042 |
| 20.405 | 7.807 | 7.806 | 0.001 | 0.009 |
| 22.587 | 7.743 | 7.742 | 0.001 | 0.018 |
| 24.768 | 7.552 | 7.552 | 0.000 | 0.005 |
| 25.970 | 7.315 | 7.317 | 0.002 | 0.027 |
| 26.180 | 7.260 | 7.257 | 0.003 | 0.039 |
| 26.400 | 7.198 | 7.199 | 0.001 | 0.019 |
| 27.000 | 7.001 | 7.001 | 0.000 | 0.001 |
| 27.613 | 6.755 | 6.755 | 0.000 | 0.006 |
| 28.227 | 6.459 | 6.461 | 0.002 | 0.026 |
| 28.840 | 6.109 | 6.110 | 0.001 | 0.010 |
| 29.453 | 5.699 | 5.699 | 0.000 | 0.006 |
| 30.067 | 5.223 | 5.224 | 0.001 | 0.024 |
| 30.680 | 4.666 | 4.667 | 0.001 | 0.013 |
| 31.293 | 4.046 | 4.043 | 0.003 | 0.067 |
| 31.907 | 3.365 | 3.362 | 0.003 | 0.097 |
| 32.520 | 2.625 | 2.622 | 0.003 | 0.111 |
| 33.133 | 1.819 | 1.817 | 0.002 | 0.094 |
| 33.747 | 0.951 | 0.944 | 0.007 | 0.754 |
| 34.360 | 0.053 | 0.056 | 0.003 | 5.978 |
| Method | RMSE (A) | MAE (A) | MAPE (%) | R2 | Ctime (s) |
|---|---|---|---|---|---|
| BKA | 0.00793 | 0.00704 | 0.85622 | 0.99989 | 22.12215 |
| GTO | 0.00596 | 0.00514 | 0.62538 | 0.99996 | 23.65441 |
| GWO | 0.08145 | 0.07193 | 8.23591 | 0.99271 | 22.35456 |
| SAO | 0.02653 | 0.02026 | 2.33716 | 0.99917 | 21.87894 |
| RIME | 0.08961 | 0.07929 | 9.73165 | 0.99165 | 28.54568 |
| DE | 0.07355 | 0.06466 | 6.16545 | 0.99322 | 27.57654 |
| GA | 0.09079 | 0.08038 | 9.85653 | 0.99124 | 54.72315 |
| TLBO | 0.01813 | 0.01357 | 1.07163 | 0.99970 | 31.54447 |
| SRQ-BKA | 0.00262 | 0.00193 | 0.13107 | 0.99999 | 23.33585 |
| Method | RMSE (A) | MAE (A) | MAPE (%) | R2 | Ctime (s) |
|---|---|---|---|---|---|
| BKA | 0.00959 | 0.00757 | 0.73643 | 0.99995 | 19.48948 |
| GTO | 0.00876 | 0.00694 | 0.69541 | 0.99996 | 21.75889 |
| GWO | 0.08854 | 0.07756 | 15.63727 | 0.99624 | 21.08694 |
| SAO | 0.03359 | 0.03081 | 2.56456 | 0.99958 | 17.74258 |
| RIME | 0.09402 | 0.08024 | 12.13256 | 0.99492 | 24.98591 |
| DE | 0.06413 | 0.05613 | 6.65565 | 0.99793 | 23.84567 |
| GA | 0.09113 | 0.07931 | 13.59581 | 0.99587 | 37.46544 |
| TLBO | 0.02722 | 0.02463 | 1.86554 | 0.99967 | 28.15786 |
| SRQ-BKA | 0.00671 | 0.00512 | 0.52945 | 0.99998 | 22.15682 |
| Method | RMSE (A) | MAE (A) | MAPE (%) | R2 | Ctime (s) |
|---|---|---|---|---|---|
| BKA | 0.00963 | 0.00778 | 0.38146 | 0.99998 | 20.67865 |
| GTO | 0.00856 | 0.00690 | 0.32955 | 0.99999 | 21.08977 |
| GWO | 0.09631 | 0.08504 | 8.57161 | 0.99862 | 18.46703 |
| SAO | 0.02742 | 0.02484 | 3.20456 | 0.99983 | 12.54764 |
| RIME | 0.09513 | 0.08405 | 8.54563 | 0.99877 | 23.54232 |
| DE | 0.05355 | 0.04644 | 7.88791 | 0.99959 | 22.45343 |
| GA | 0.09725 | 0.08507 | 15.4655 | 0.99856 | 34.44596 |
| TLBO | 0.03504 | 0.03181 | 4.69872 | 0.99978 | 25.63715 |
| SRQ-BKA | 0.00823 | 0.00673 | 0.32714 | 0.99999 | 22.75781 |
| Parameter | Condition 1 (379 W/m2, 27.9 °C) | Condition 2 (590 W/m2, 36.5 °C) | Condition 3 (900 W/m2, 47.8 °C) |
|---|---|---|---|
| Iph (A) | 3.12 | 4.86 | 7.23 |
| I01 (A) | 2.32 × 10−10 | 3.91 × 10−10 | 5.87 × 10−10 |
| I02 (A) | 1.13 × 10−8 | 2.06 × 10−8 | 3.31 × 10−8 |
| A1 | 1.18 | 1.19 | 1.22 |
| A2 | 1.45 | 1.47 | 1.51 |
| Rs (Ω) | 0.26 | 0.25 | 0.23 |
| Rsh (Ω) | 490.38 | 472.70 | 455.82 |
| Index | BKA | GTO | SAO | TLBO | SRQ-BKA |
|---|---|---|---|---|---|
| RMSE (A) | 0.00824 | 0.00633 | 0.02790 | 0.02031 | 0.00278 |
| Ctime (s) | 20.87567 | 21.15738 | 21.97542 | 28.78677 | 22.44563 |
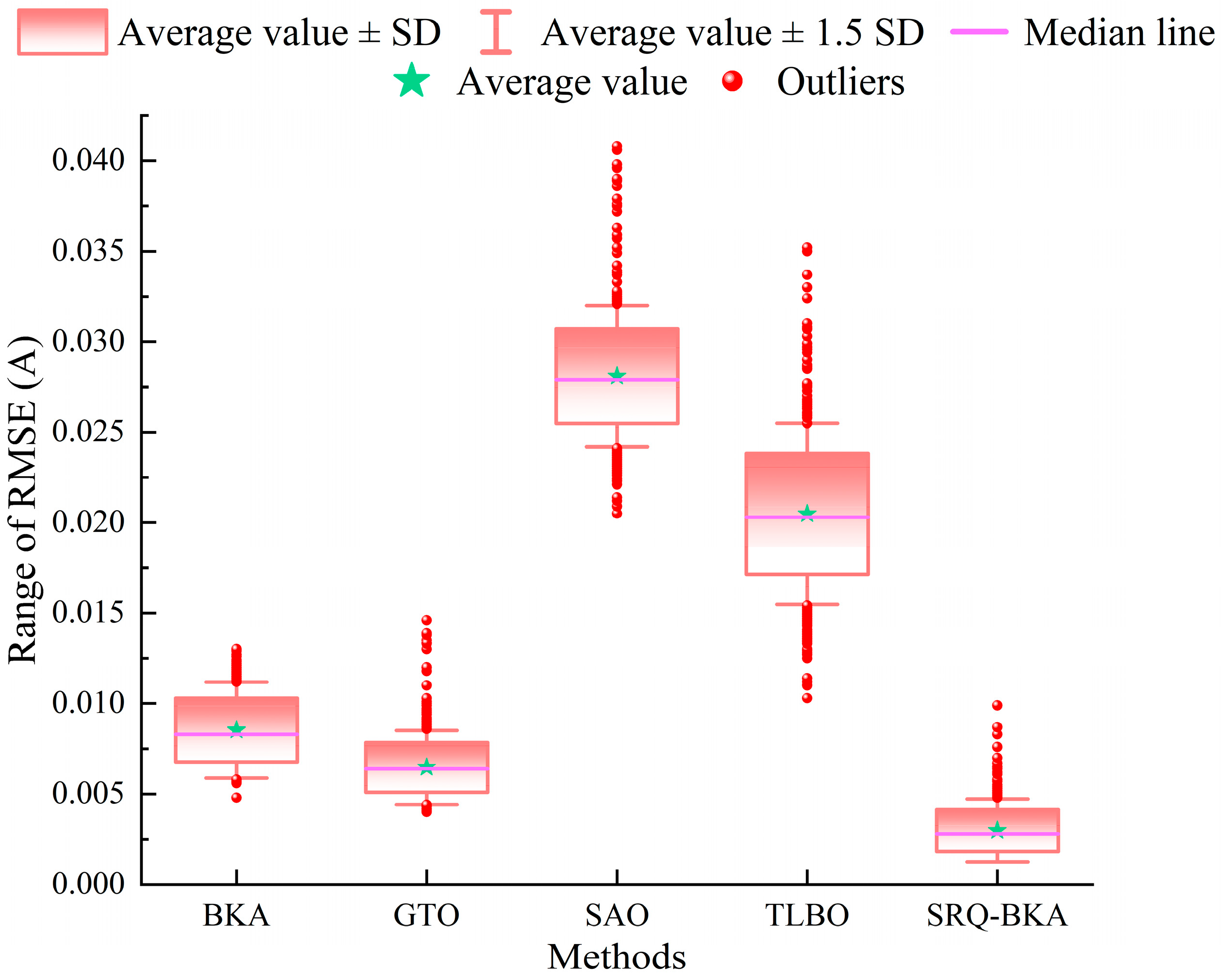
| Method | SD (A) | 95% CI of RMSE (A) | Confidence Interval Width |
|---|---|---|---|
| BKA | 0.00181 | [0.00813, 0.00835] | 0.00022 |
| GTO | 0.00226 | [0.00619, 0.00647] | 0.00028 |
| SAO | 0.00477 | [0.02760, 0.02820] | 0.00060 |
| TLBO | 0.00566 | [0.01996, 0.02067] | 0.00071 |
| SRQ-BKA | 0.00156 | [0.00268, 0.00288] | 0.00020 |
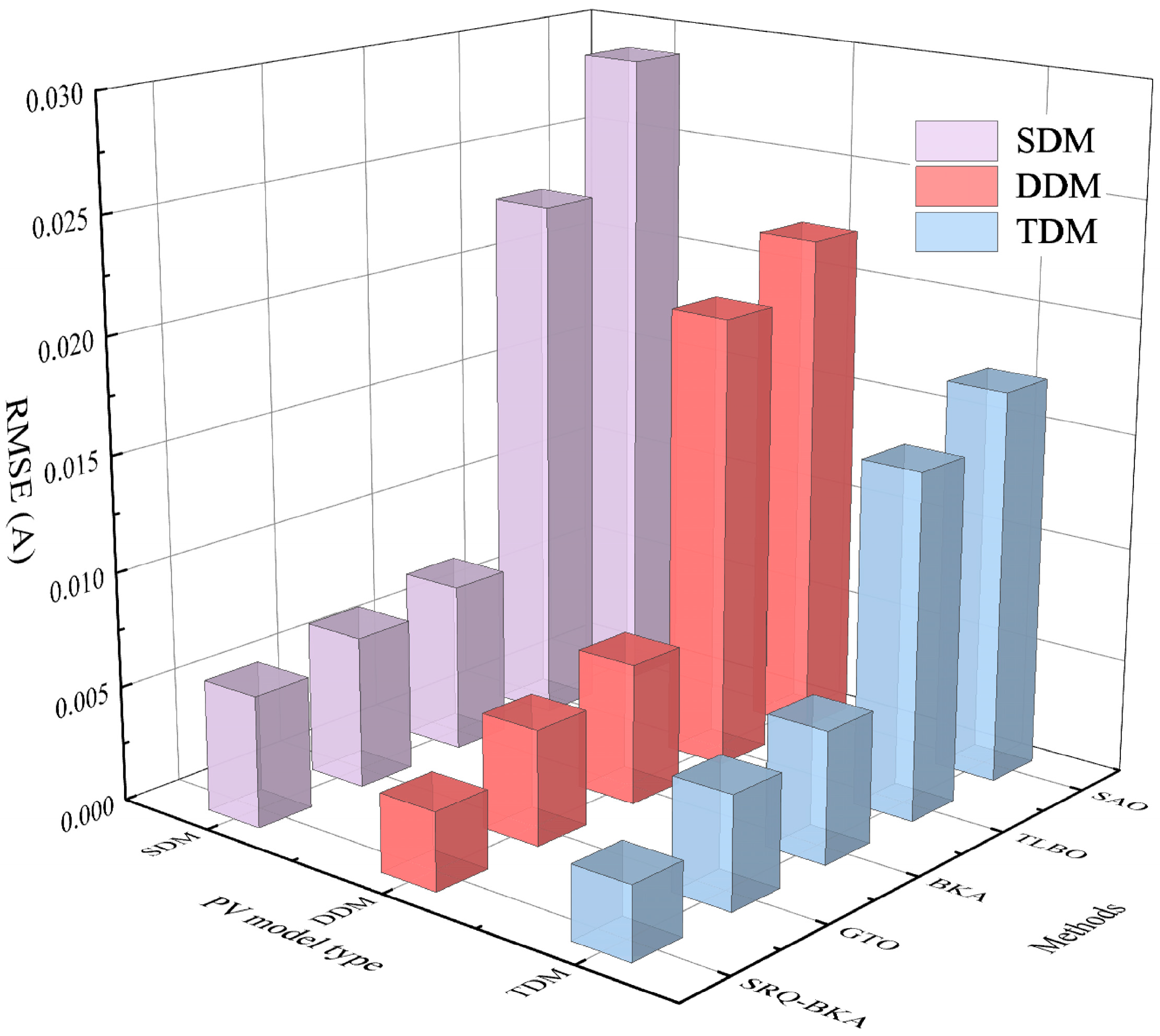
| Method | RMSE (A)—SDM | RMSE (A)—DDM | RMSE (A)—TDM |
|---|---|---|---|
| BKA | 0.00735 | 0.00613 | 0.00571 |
| GTO | 0.00662 | 0.00501 | 0.00487 |
| SAO | 0.02878 | 0.02207 | 0.01712 |
| TLBO | 0.02313 | 0.01975 | 0.01503 |
| SRQ-BKA | 0.00572 | 0.00279 | 0.00266 |
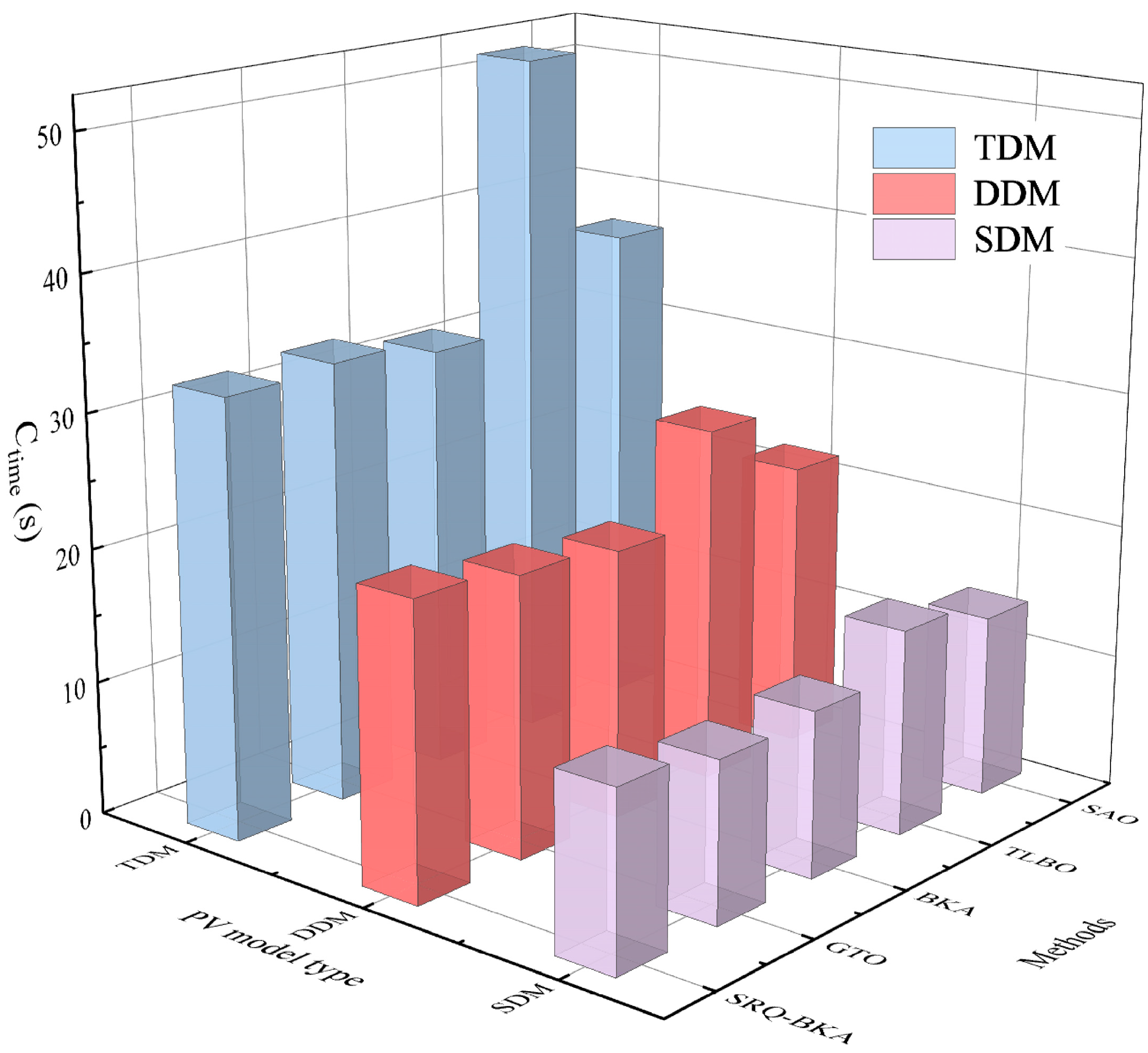
| Method | Ctime (s)—SDM | Ctime (s)—DDM | Ctime (s)—TDM |
|---|---|---|---|
| BKA | 12.31048 | 20.12758 | 31.80107 |
| GTO | 11.90859 | 20.94537 | 32.95732 |
| SAO | 13.58206 | 21.56345 | 36.95821 |
| TLBO | 15.33927 | 26.71751 | 51.96223 |
| SRQ-BKA | 13.15650 | 21.89987 | 32.59736 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Q.; Ding, K.; Chen, X.; Yang, Z.; Xu, M.; Teng, F. An Improved Black-Winged Kite Algorithm for High-Accuracy Parameter Identification of a Photovoltaic Double Diode Model. Machines 2025, 13, 706. https://doi.org/10.3390/machines13080706
Chen Q, Ding K, Chen X, Yang Z, Xu M, Teng F. An Improved Black-Winged Kite Algorithm for High-Accuracy Parameter Identification of a Photovoltaic Double Diode Model. Machines. 2025; 13(8):706. https://doi.org/10.3390/machines13080706
Chicago/Turabian StyleChen, Quanru, Kun Ding, Xiang Chen, Zenan Yang, Mingkang Xu, and Fei Teng. 2025. "An Improved Black-Winged Kite Algorithm for High-Accuracy Parameter Identification of a Photovoltaic Double Diode Model" Machines 13, no. 8: 706. https://doi.org/10.3390/machines13080706
APA StyleChen, Q., Ding, K., Chen, X., Yang, Z., Xu, M., & Teng, F. (2025). An Improved Black-Winged Kite Algorithm for High-Accuracy Parameter Identification of a Photovoltaic Double Diode Model. Machines, 13(8), 706. https://doi.org/10.3390/machines13080706









