Interval Observer for Vehicle Sideslip Angle Estimation Using Extended Kalman Filters
Abstract
1. Introduction
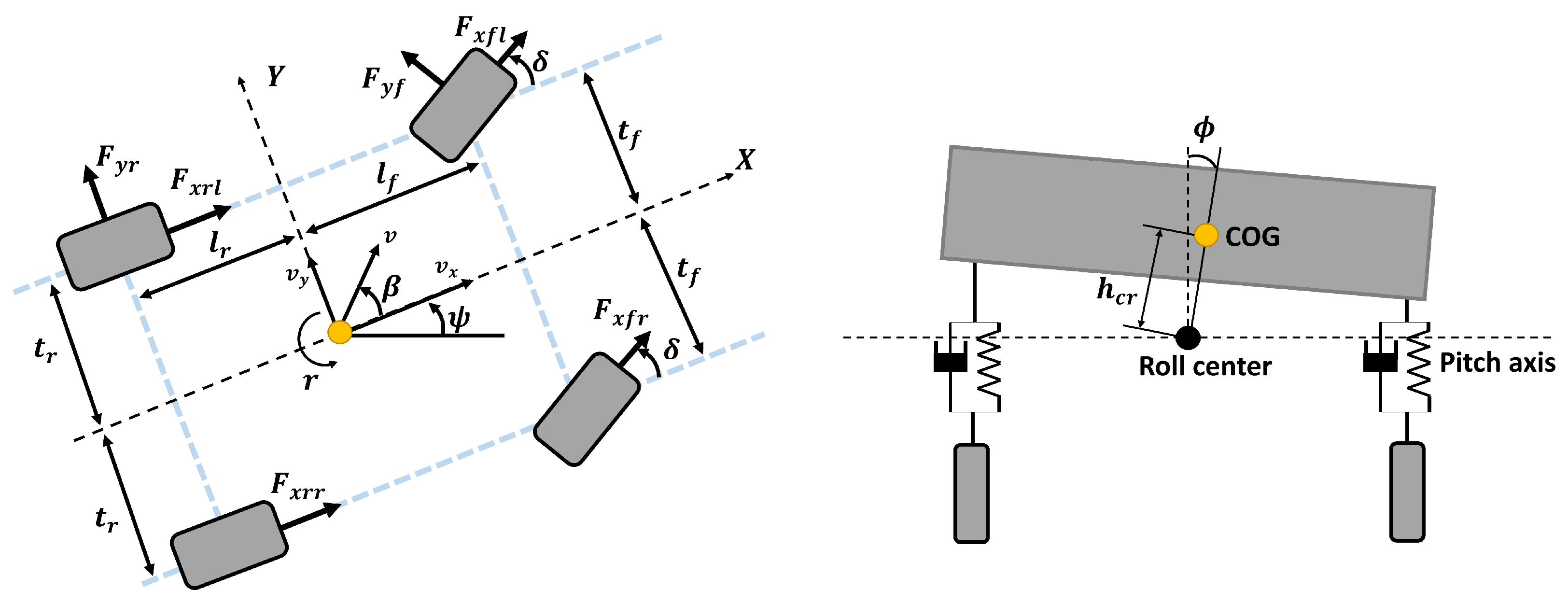
2. Vehicle Model
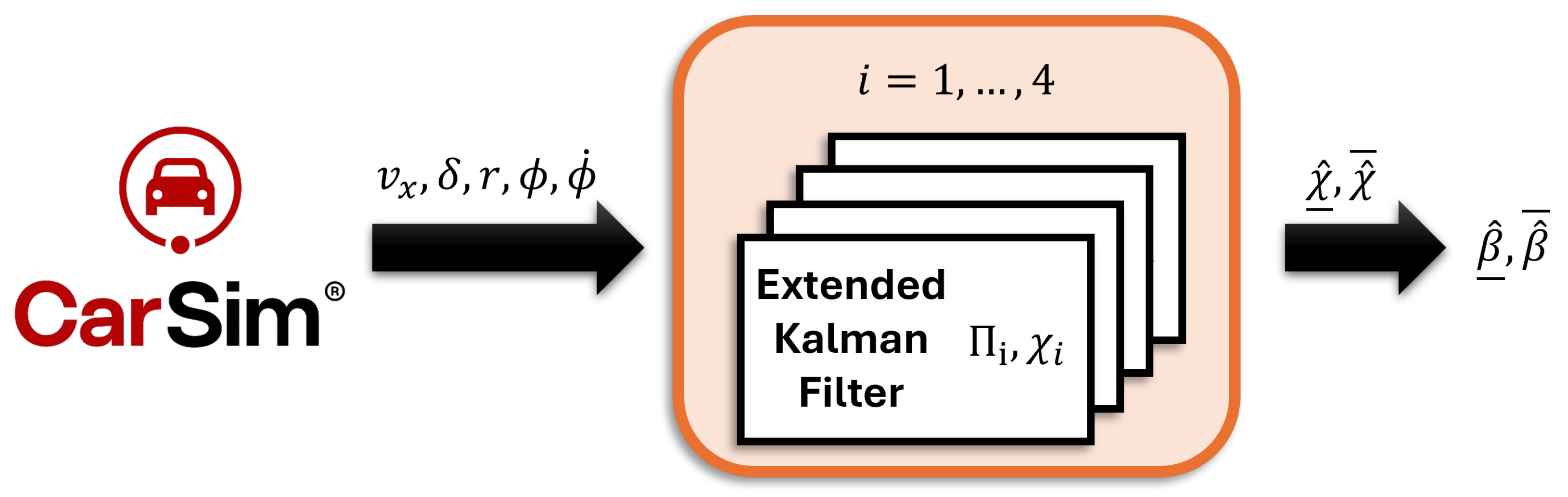
3. Interval Kalman Filter
3.1. Preliminaries
3.2. Extended Kalman Filter
- Predict.
- Update.Matrices P, Q, and R denote the prediction, process noise, and observation noise covariances, respectively. Since Q and R are constant, these do not have time indices.
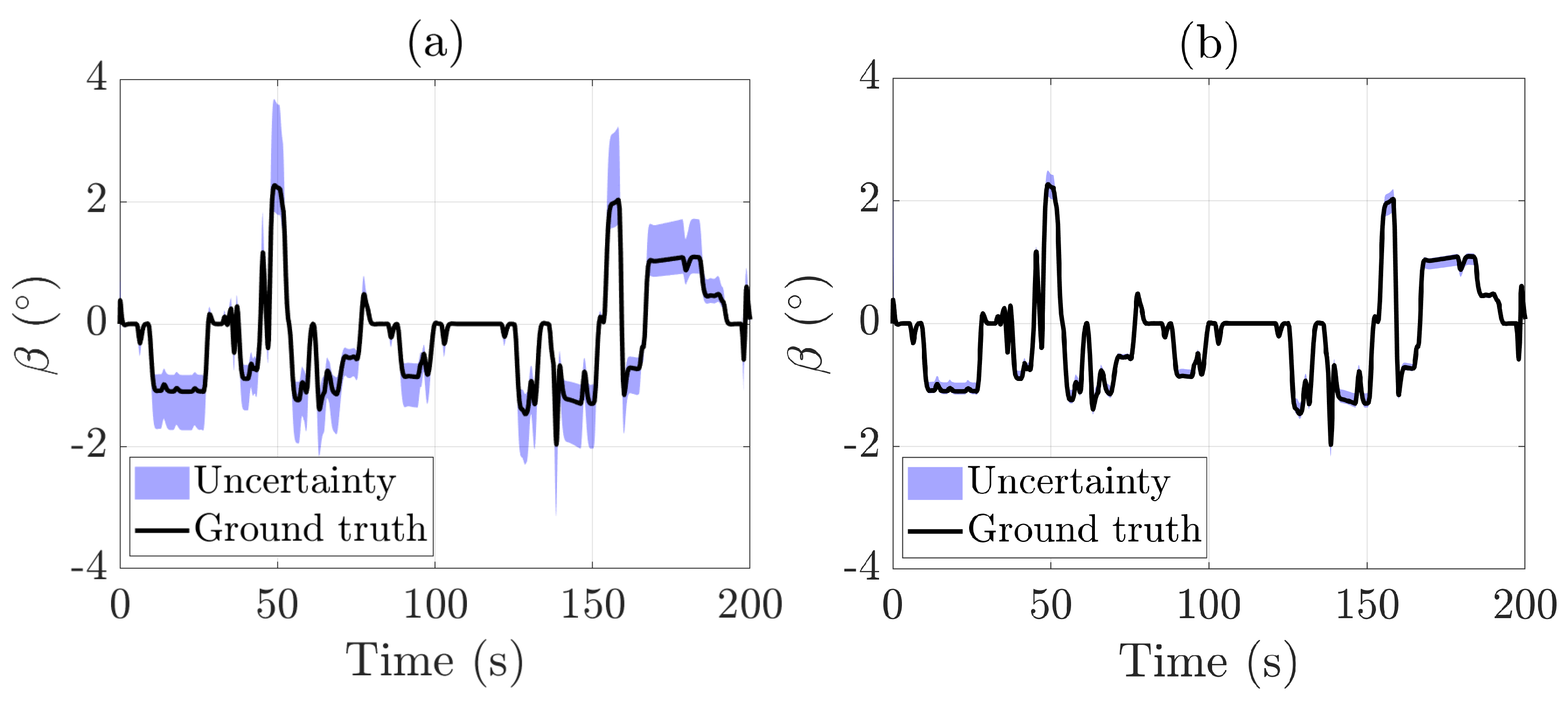
4. Results
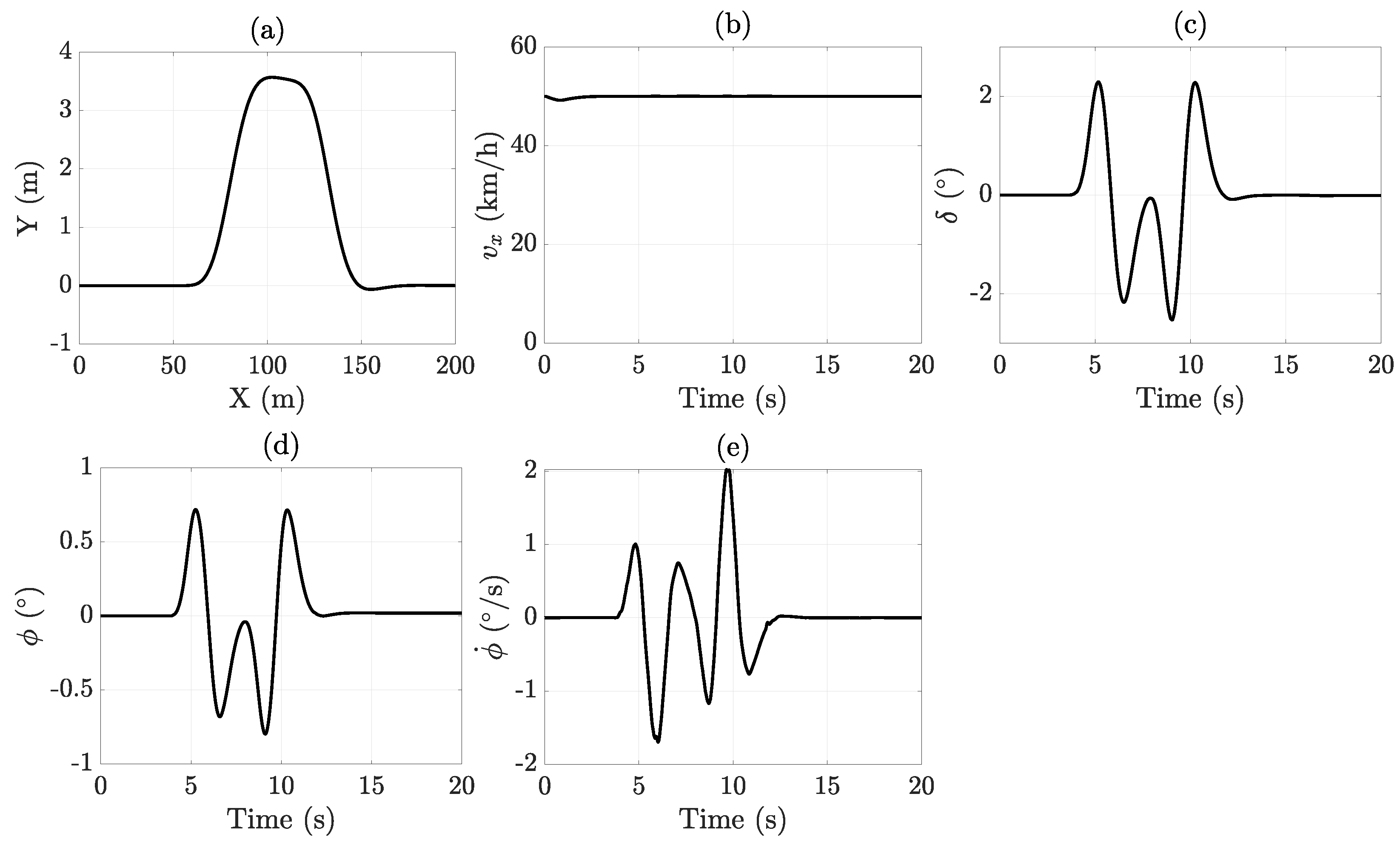
4.1. Double Lane Change Test
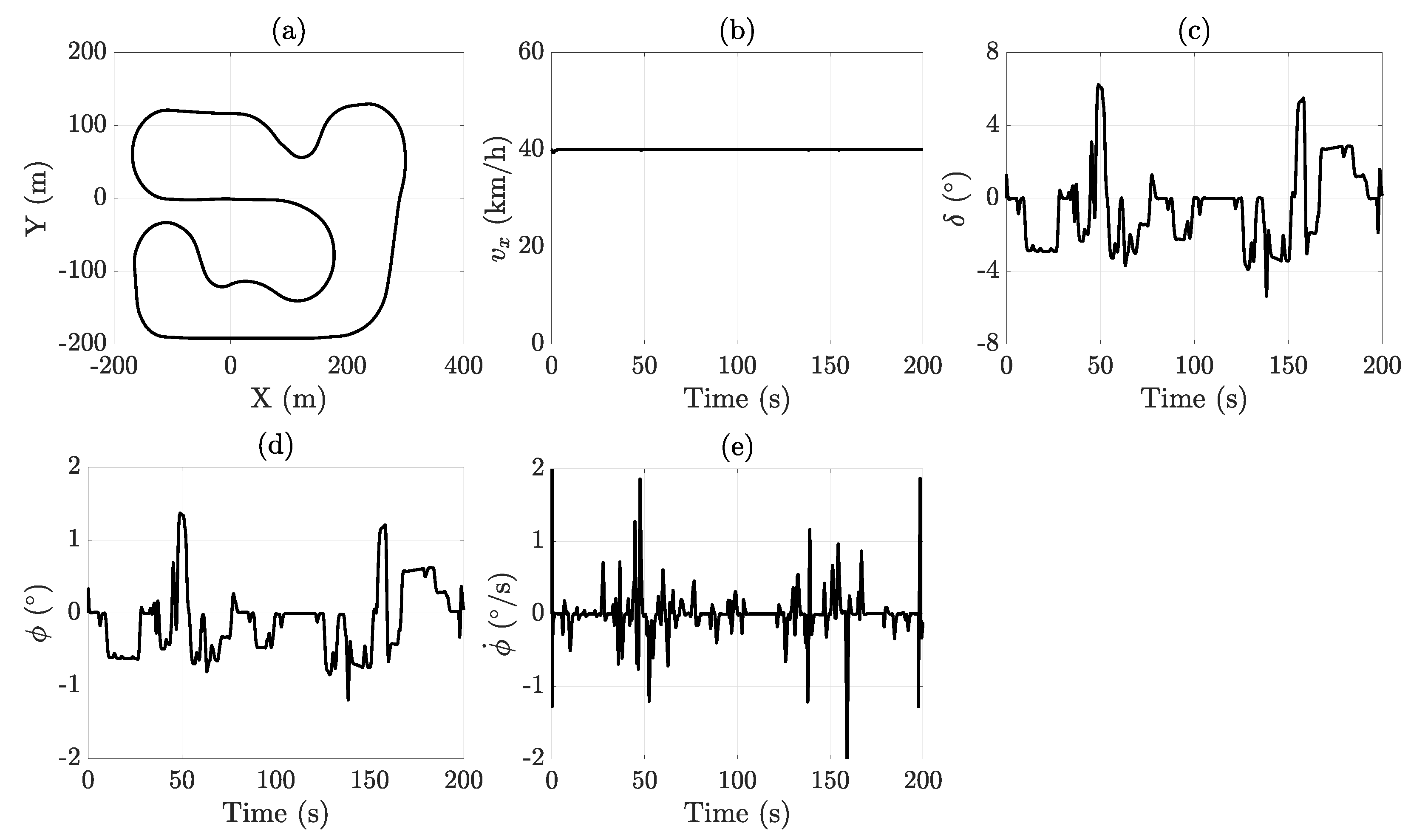
4.2. Racetrack Test
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ESC | Electronic stability control |
| EKF | Extended Kalman Filter |
| IMU | Inertial measurement unit |
| LPV | Linear Parameter-Varying |
| RMS | Root mean square |
References
- Farmer, C.M. Effect of electronic stability control on automobile crash risk. Traffic Inj. Prev. 2004, 5, 317–325. [Google Scholar] [CrossRef]
- Liebemann, E.; Meder, K.; Schuh, J.; Nenninger, G. Safety and Performance Enhancement: The Bosch Electronic Stability Control (ESP); Technical Report, SAE Technical Paper; SAE: Warrendale, PA, USA, 2004. [Google Scholar]
- Chindamo, D.; Lenzo, B.; Gadola, M. On the vehicle sideslip angle estimation: A literature review of methods, models, and innovations. Appl. Sci. 2018, 8, 355. [Google Scholar] [CrossRef]
- Jin, X.; Yin, G.; Chen, N. Advanced estimation techniques for vehicle system dynamic state: A survey. Sensors 2019, 19, 4289. [Google Scholar] [CrossRef] [PubMed]
- Chen, B.C.; Hsieh, F.C. Sideslip angle estimation using extended Kalman filter. Veh. Syst. Dyn. 2008, 46, 353–364. [Google Scholar] [CrossRef]
- Melzi, S.; Sabbioni, E. On the vehicle sideslip angle estimation through neural networks: Numerical and experimental results. Mech. Syst. Signal Process. 2011, 25, 2005–2019. [Google Scholar] [CrossRef]
- Vignati, M.; Sabbioni, E. A cooperative control strategy for yaw rate and sideslip angle control combining torque vectoring with rear wheel steering. Veh. Syst. Dyn. 2022, 60, 1668–1701. [Google Scholar] [CrossRef]
- Sano, S.; Furukawa, Y.; Shiraishi, S. Four wheel steering system with rear wheel steer angle controlled as a function of sterring wheel angle. In SAE Transactions; SAE: Warrendale, PA, USA, 1986; pp. 880–893. [Google Scholar]
- Lin, J.; Zou, T.; Su, L.; Zhang, F.; Zhang, Y. Optimal coordinated control of active front steering and direct yaw moment for distributed drive electric bus. Machines 2023, 11, 640. [Google Scholar] [CrossRef]
- Nagai, M.; Shino, M.; Gao, F. Study on integrated control of active front steer angle and direct yaw moment. JSAE Rev. 2002, 23, 309–315. [Google Scholar] [CrossRef]
- Sun, T.; Wong, P.K.; Wang, X. Back propagation neural network-based fault diagnosis and fault tolerant control of distributed drive electric vehicles based on sliding mode control-based direct Yaw moment control. Vehicles 2023, 6, 93–119. [Google Scholar] [CrossRef]
- Esmailzadeh, E.; Goodarzi, A.; Vossoughi, G. Optimal yaw moment control law for improved vehicle handling. Mechatronics 2003, 13, 659–675. [Google Scholar] [CrossRef]
- Meléndez-Useros, M.; Viadero-Monasterio, F.; Jiménez-Salas, M.; López-Boada, M.J. Static Output-Feedback Path-Tracking Controller Tolerant to Steering Actuator Faults for Distributed Driven Electric Vehicles. World Electr. Veh. J. 2025, 16, 40. [Google Scholar] [CrossRef]
- De Novellis, L.; Sorniotti, A.; Gruber, P. Wheel Torque Distribution Criteria for Electric Vehicles with Torque-Vectoring Differentials. IEEE Trans. Veh. Technol. 2014, 63, 1593–1602. [Google Scholar] [CrossRef]
- Meléndez-Useros, M.; Jiménez-Salas, M.; Viadero-Monasterio, F.; Boada, B.L. Tire slip H∞ control for optimal braking depending on road condition. Sensors 2023, 23, 1417. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.L.P.; Zhou, J.; Zhao, W. A Real-Time Vehicle Navigation Algorithm in Sensor Network Environments. IEEE Trans. Intell. Transp. Syst. 2012, 13, 1657–1666. [Google Scholar] [CrossRef]
- Shahian Jahromi, B.; Tulabandhula, T.; Cetin, S. Real-time hybrid multi-sensor fusion framework for perception in autonomous vehicles. Sensors 2019, 19, 4357. [Google Scholar] [CrossRef]
- Khan, S.M.; Dey, K.C.; Chowdhury, M. Real-Time Traffic State Estimation with Connected Vehicles. IEEE Trans. Intell. Transp. Syst. 2017, 18, 1687–1699. [Google Scholar] [CrossRef]
- Doumiati, M.; Victorino, A.C.; Charara, A.; Lechner, D. Onboard Real-Time Estimation of Vehicle Lateral Tire–Road Forces and Sideslip Angle. IEEE/ASME Trans. Mechatronics 2011, 16, 601–614. [Google Scholar] [CrossRef]
- Viadero-Monasterio, F.; Nguyen, A.T.; Lauber, J.; Boada, M.J.L.; Boada, B.L. Event-Triggered Robust Path Tracking Control Considering Roll Stability Under Network-Induced Delays for Autonomous Vehicles. IEEE Trans. Intell. Transp. Syst. 2023, 24, 14743–14756. [Google Scholar] [CrossRef]
- Zhao, L.; Wang, J.; Hu, Y.; Li, L. Adaptive Unscented Kalman Filter Approach for Accurate Sideslip Angle Estimation via Operating Condition Recognition. Machines 2025, 13, 376. [Google Scholar] [CrossRef]
- Pacejka, H. Tire and Vehicle Dynamics; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Lee, J.; Yim, S. Path tracking control with constraint on tire slip angles under low-friction road conditions. Appl. Sci. 2024, 14, 1066. [Google Scholar] [CrossRef]
- Johnson, D.K.; Botha, T.R.; Els, P.S. Real-time side-slip angle measurements using digital image correlation. J. Terramechanics 2019, 81, 35–42. [Google Scholar] [CrossRef]
- Liu, W.; Xiong, L.; Xia, X.; Yu, Z. Vehicle sideslip angle estimation: A review. In SAE Technical Paper; SAE: Warrendale, PA, USA, 2018. [Google Scholar]
- Tang, Y.; Tao, L.; Li, Y.; Zhang, D.; Zhang, X. Estimation of tire side-slip angles based on the frequency domain lateral acceleration characteristics inside tires. Machines 2024, 12, 229. [Google Scholar] [CrossRef]
- Napolitano Dell’Annunziata, G.; Ruffini, M.; Stefanelli, R.; Adiletta, G.; Fichera, G.; Timpone, F. Four-Wheeled Vehicle Sideslip Angle Estimation: A Machine Learning-Based Technique for Real-Time Virtual Sensor Development. Appl. Sci. 2024, 14, 1036. [Google Scholar] [CrossRef]
- Viadero-Monasterio, F.; García, J.; Meléndez-Useros, M.; Jiménez-Salas, M.; Boada, B.L.; López Boada, M.J. Simultaneous estimation of vehicle sideslip and roll angles using an event-triggered-based iot architecture. Machines 2024, 12, 53. [Google Scholar] [CrossRef]
- Puscul, D.; Lex, C.; Vignati, M.; Shao, L. A Literature Survey on Sideslip Angle Estimation Using Vehicle Dynamics Based Methods. IEEE Access 2024, 12, 70263–70277. [Google Scholar] [CrossRef]
- Hu, J.; Rong, F.; Zhang, P.; Yan, F. Sideslip Angle Estimation for Distributed Drive Electric Vehicles Based on Robust Unscented Particle Filter. Mathematics 2024, 12, 1350. [Google Scholar] [CrossRef]
- Heon Lee, G.; Kim, D.H.; Min Pak, J.; Ahn, C.K. Vehicle Sideslip Angle Estimation Using Finite Memory Estimation and Dynamics/Kinematics Model Fusion Based on Neural Networks. IEEE Trans. Intell. Transp. Syst. 2025, 26, 2157–2168. [Google Scholar] [CrossRef]
- Nguyen, A.T.; Frezzatto, L.; Guerra, T.M.; Delprat, S. Cost-Effective Estimation of Vehicle Lateral Tire-Road Forces and Sideslip Angle via Nonlinear Sampled-Data Observers: Theory and Experiments. IEEE/ASME Trans. Mechatronics 2024, 29, 4606–4617. [Google Scholar] [CrossRef]
- He, B.; Zheng, L.; Jin, Y.; Li, Y. A Robust Adaptive Estimator for Sideslip Angle and Tire-Road Forces Under Time-Varying and Abnormal Noise. IEEE Sensors J. 2025, 25, 15723–15734. [Google Scholar] [CrossRef]
- Li, W.; Xie, Z.; Wong, P.K.; Hu, Y.; Guo, G.; Zhao, J. Event-Triggered Asynchronous Fuzzy Filtering for Vehicle Sideslip Angle Estimation with Data Quantization and Dropouts. IEEE Trans. Fuzzy Syst. 2022, 30, 2822–2836. [Google Scholar] [CrossRef]
- Mazenc, F.; Dinh, T.N.; Niculescu, S.I. Interval observers for discrete-time systems. Int. J. Robust Nonlinear Control 2014, 24, 2867–2890. [Google Scholar] [CrossRef]
- Khan, A.; Xie, W.; Zhang, B.; Liu, L.W. A survey of interval observers design methods and implementation for uncertain systems. J. Frankl. Inst. 2021, 358, 3077–3126. [Google Scholar] [CrossRef]
- Boada, B.L.; Viadero-Monasterio, F.; Zhang, H.; Boada, M.J.L. Simultaneous Estimation of Vehicle Sideslip and Roll Angles Using an Integral-Based Event-Triggered H∞ Observer Considering Intravehicle Communications. IEEE Trans. Veh. Technol. 2023, 72, 4411–4425. [Google Scholar] [CrossRef]
- Nguyen, A.T.; Rath, J.; Guerra, T.M.; Palhares, R.; Zhang, H. Robust Set-Invariance Based Fuzzy Output Tracking Control for Vehicle Autonomous Driving Under Uncertain Lateral Forces and Steering Constraints. IEEE Trans. Intell. Transp. Syst. 2021, 22, 5849–5860. [Google Scholar] [CrossRef]
- Sierra, C.; Tseng, E.; Jain, A.; Peng, H. Cornering stiffness estimation based on vehicle lateral dynamics. Veh. Syst. Dyn. 2006, 44, 24–38. [Google Scholar] [CrossRef]
- Bechtoff, J.; Isermann, R. Cornering stiffness and sideslip angle estimation for integrated vehicle dynamics control. IFAC-PapersOnLine 2016, 49, 297–304. [Google Scholar] [CrossRef]
- Liu, G.; Shao, W. Coordinated Control Strategy for Stability Control and Trajectory Tracking with Wheel-Driven Autonomous Vehicles Under Harsh Situations. World Electr. Veh. J. 2025, 16, 163. [Google Scholar] [CrossRef]
- Viadero-Monasterio, F.; Meléndez-Useros, M.; Jiménez-Salas, M.; Boada, M.J.L. Fault-Tolerant Robust Output-Feedback Control of a Vehicle Platoon Considering Measurement Noise and Road Disturbances. IET Intell. Transp. Syst. 2025, 19, e70007. [Google Scholar] [CrossRef]
- Ribeiro, M.I. Kalman and extended kalman filters: Concept, derivation and properties. Inst. Syst. Robot. 2004, 43, 3736–3741. [Google Scholar]
- Kalman, R.E. A new approach to linear filtering and prediction problems. Trans. ASME—J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Lai, X.; Yang, T.; Wang, Z.; Chen, P. IoT implementation of Kalman filter to improve accuracy of air quality monitoring and prediction. Appl. Sci. 2019, 9, 1831. [Google Scholar] [CrossRef]
- Kim, S.; You, S.H.; Kang, S. A Hybrid Model for Vehicle Sideslip Angle Estimation Based on Attention Regression. IEEE Access 2024, 12, 141335–141343. [Google Scholar] [CrossRef]
- Peng, Y.; Yang, X. Comparison of various double-lane change manoeuvre specifications. Veh. Syst. Dyn. 2012, 50, 1157–1171. [Google Scholar] [CrossRef]
- Arefnezhad, S.; Ghaffari, A.; Khodayari, A.; Nosoudi, S. Modeling of double lane change maneuver of vehicles. Int. J. Automot. Technol. 2018, 19, 271–279. [Google Scholar] [CrossRef]
- Naude, A.F.; Steyn, J.L. Objective Evaluation of the Simulated Handling Characteristics of a Vehicle in a Double Lane Change Manoeuvre; Technical Report, SAE Technical Paper; SAE: Warrendale, PA, USA, 1993. [Google Scholar]
- Li, C.; Jiang, H.; Yang, X.; Wei, Q. Path Tracking Control Strategy Based on Adaptive MPC for Intelligent Vehicles. Appl. Sci. 2025, 15, 5464. [Google Scholar] [CrossRef]
- Hua, L.; Zhu, G. Closed-Loop Transient Longitudinal Trajectory Tracking for Connected Vehicles. Machines 2025, 13, 163. [Google Scholar] [CrossRef]
- Al-bayati, K.Y.; Mahmood, A.; Szabolcsi, R. Robust Path Tracking Control with Lateral Dynamics Optimization: A Focus on Sideslip Reduction and Yaw Rate Stability Using Linear Quadratic Regulator and Genetic Algorithms. Vehicles 2025, 7, 50. [Google Scholar] [CrossRef]
- Zhao, J.; Li, R.; Lv, M.; Li, W.; Xie, Z.; Wong, P.K. Observer-Based Robust Explicit Model Predictive Control for Path Following of Autonomous Electric Vehicles with Communication Delay. Chin. J. Mech. Eng. 2025, 38, 108. [Google Scholar] [CrossRef]
- Viadero-Monasterio, F.; Meléndez-Useros, M.; Zhang, N.; Zhang, H.; Boada, B.L.; Boada, M.J.L. Motion Planning and Robust Output-Feedback Trajectory Tracking Control for Multiple Intelligent and Connected Vehicles in Unsignalized Intersections. IEEE Trans. Veh. Technol. 2025, 1–13, Early Access. [Google Scholar] [CrossRef]

| Symbol | Name | Value |
|---|---|---|
| m | Vehicle mass (total) | 1529.98 kg |
| Distance to the front axle from the center of gravity | 1.139 m | |
| Distance to the rear axle from the center of gravity | 1.637 m | |
| Roll stiffness coefficent | 248,600 Nm/rad | |
| Roll damping coefficient | 15,905 Nms/rad | |
| Cornering stiffness of the front tires (total) | 184,862 ± 15% N/rad | |
| Cornering stiffness of the rear tires (total) | 141,404 ± 15% N/rad | |
| g | Acceleration of gravity | 9.81 m/s2 |
| Distance from the roll center to the center of gravity | 0.22 m | |
| Roll inertia with respect to the center of gravity | 708.22 kg m2 | |
| Yaw inertia with respect to the center of gravity | 4607.47 kg m2 | |
| r | Yaw rate | |
| Sideslip angle | ||
| Longitudinal velocity | ||
| Lateral velocity | ||
| Steering angle |
| Scenario | Bicycle Model | Bicycle + Roll Model | ||
|---|---|---|---|---|
| RMS (°) | (°s) | RMS (°) | (°s) | |
| Double Lane Change (DLC) | 0.1171 | 6.09 | 0.0376 | 0.91 |
| Racetrack | 0.1500 | 106.49 | 0.0500 | 22.65 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Viadero-Monasterio, F.; Meléndez-Useros, M.; Lenzo, B.; Boada, B.L. Interval Observer for Vehicle Sideslip Angle Estimation Using Extended Kalman Filters. Machines 2025, 13, 707. https://doi.org/10.3390/machines13080707
Viadero-Monasterio F, Meléndez-Useros M, Lenzo B, Boada BL. Interval Observer for Vehicle Sideslip Angle Estimation Using Extended Kalman Filters. Machines. 2025; 13(8):707. https://doi.org/10.3390/machines13080707
Chicago/Turabian StyleViadero-Monasterio, Fernando, Miguel Meléndez-Useros, Basilio Lenzo, and Beatriz López Boada. 2025. "Interval Observer for Vehicle Sideslip Angle Estimation Using Extended Kalman Filters" Machines 13, no. 8: 707. https://doi.org/10.3390/machines13080707
APA StyleViadero-Monasterio, F., Meléndez-Useros, M., Lenzo, B., & Boada, B. L. (2025). Interval Observer for Vehicle Sideslip Angle Estimation Using Extended Kalman Filters. Machines, 13(8), 707. https://doi.org/10.3390/machines13080707









