A Study on the Heat Dissipation Effects During the Meshing Process of Involute Gears with Variable Tooth Thickness

Abstract

The involute gear with variable tooth thickness lacks established methods for calculating meshing heat and studying oil-jet lubrication and cooling effects. This study aims to theoretically estimate the meshing heat generated during the engagement process of involute gears with variable tooth thickness. To achieve this, a heat calculation model is derived based on the corresponding tooth surface equations. The impact of oil-jet lubrication parameters—jet velocity, pitch cone angle, face width ratio, and axial displacement—on the gear surface temperature and internal gearbox environment is systematically studied. Numerical simulations of the temperature field are validated through experimental measurements. The results indicate that an oil-jet velocity of 15 m/s combined with a pitch cone angle of 4° significantly reduces both gear surface and internal flow field temperatures. Additionally, smaller face width ratios and axial displacements effectively lower the internal temperature of the gearbox. These findings offer a theoretical basis for calculating meshing heat and designing oil-jet lubrication systems for variable-tooth-thickness involute gears.

1. Introduction

The thermal performance management of gear transmission systems has long been a critical issue in engineering applications [1]. The primary objective is to effectively reduce the frictional heat generated in the gear meshing region [2,3,4] thereby improving operational efficiency and extending gear service life. In addition, it is essential to mitigate wear and thermal scuffing caused by temperature fluctuations [5,6,7,8] ensuring the stability and reliability of the transmission system. This research topic holds significant importance for enhancing the transmission efficiency of mechanical systems and promoting energy conservation and emission reduction.

Early studies investigated thermal behavior using disc and single-gear experiments, leading to numerous empirical formulas [9,10,11,12,13,14]. In recent years, an increasing number of scholars have adopted numerical methods to compensate for the limitations of experimental approaches. Andersson et al. [15] found that spray lubrication enhanced efficiency, while immersion lubrication led to lower gear temperatures in FZG tests. Ambrose et al. [16] showed that XFlow’s results matched those of SPH, and LBM offered greater computational efficiency. Furthermore, Keller et al. [17] found that the single-phase SPH method was more time efficient, and that increasing the spray angle reduced the diffusion effect.

Gradually, researchers have shifted their focus to the influence of jet system layout parameters and configurations on gear lubrication behavior. Akin and Townsend [18,19,20,21] were among the first to establish an analytical model for gear oil-jet impingement depth. They investigated the matching relationship between the oil jet velocity and the gear line speed, laying the groundwork for subsequent studies on gear jet lubrication. Li et al. [22] developed a numerical model and found that increasing the oil film thickness and length could reduce frictional power losses and improve transmission efficiency. Dai et al. [23,24] examined the effect of various nozzle deflection angles on lubrication performance. Their results indicated that deflecting the nozzle toward the driving gear enhances the oil volume fraction within the meshing region. A mathematical model of jet impingement depth was also developed, demonstrating a positive correlation with the oil volume fraction and pressure in the meshing zone [25,26]. Liu et al. [27] developed a single-stage gear oil-jet model, analyzing how jet flow rate, speed, and viscosity affect lubrication, and proposed a CFD modeling approach. Interestingly, research strategies surrounding churning lubrication have also garnered significant attention. Liu et al. [28] investigated oil distribution and churning losses in a single-stage gearbox, with the results aligning closely with experimental data. Another approach employed particle-based flow simulation software to analyze the gear churning process [29].

In addition, gear surface temperature variation serves as a key indicator for evaluating lubrication and heat dissipation performance. Consequently, many researchers have focused on the temperature distribution of gears. Wang et al. [30] extracted convective heat transfer coefficients and performed thermal field simulations, analyzing the influence of jetting parameters on heat transfer. The results indicated that reducing nozzle diameter, increasing nozzle count, and raising oil supply pressure enhance cooling performance. Luo et al. [31] investigated the effect of gear profile modifications on temperature rise, identifying meshing stiffness, equivalent curvature radius, and load distribution as dominant factors. Fatourehchi et al. [32] combined tribological and thermal flow coupling analyses to predict heat generation and dissipation in re-lubricated gearboxes. Deshpande et al. [33] developed a thermo-fluid–solid model, showing lower temperatures on the disengagement side under varying nozzle layouts. Qiao et al. [34] computed the gear surface temperature field by solving for dynamic load and vibration displacement, and subsequently calculating the frictional heat flux.

While conventional gear cooling has been extensively studied, research on oil-jet cooling for variable-tooth-thickness gears remains scarce. Though gearbox thermal fields have been studied, meshing temperatures under varying speeds, pitch angles, face-width ratios, and axial offset remain underexplored. Moreover, the optimization of surface temperature in variable-tooth-thickness gears warrants further investigation. This study introduces a multi-factor framework to assess how pitch angle, jet velocity, face-width ratio, and axial offset collectively affect thermal behavior in variable-tooth-thickness gears. Numerical simulations and experiments jointly evaluate thermal response under coupled conditions, offering insights for advanced gear thermal management.

2. Mathematical Models and Methods

2.1. Mathematical Equations of Involute Variable-Tooth-Thickness Gears

The variable tooth thickness gear was designed based on the instantaneous axial surface. Since the gear defined on the pitch surface cannot satisfy the required center distance between the driving and driven gears, a pitch cone must be adopted for design purposes [35,36,37]. As shown in Figure 1, point M lies on the working pitch cone, with ${\gamma }_{\omega j}$ representing the working pitch cone angle and n denoting the unit normal vector. In Figure 2, $S_f(x_f,y_f,z_f)$ denotes the fixed coordinate system, while $S_1^{\prime }(x_1^{\prime },y_1^{\prime },z_1^{\prime })$ and $S_2^{\prime }(x_2^{\prime },y_2^{\prime },z_2^{\prime })$ represent the coordinate systems of the driving and driven gears, respectively. Although theoretically line contact occurs between the variable tooth thickness gear and the rack cutter, actual transmission involves point contact at point P. Point $E$ denotes the shortest distance between the pitch cones, and $d_1$ is the shortest distance from the cone apex along its axis. Vectors ${\tau }_1$, ${\tau }_2$, ${\gamma }_{\omega 1}$, ${\gamma }_{\omega 2}$, $r_{p\omega 1}$, and $r_{p\omega 2}$ represent the unit direction vectors along the generatrix of the pitch cones for gears 1 and 2, the working pitch cone angles, and the working pitch radii, respectively. The pitch cone equation $R_j(j=1,2)$ in coordinate system $S$ is expressed as:

$$R_j=\left[\begin{array}{c}{x}_j\\ y_j\\ z_j\end{array}\right]=\left[\begin{array}{c}{u}_j\cos {\theta }_j\sin {\gamma }_{\omega j}\\ u_j\sin {\theta }_j\sin {\gamma }_{\omega j}\\ u_j\cos {\gamma }_{\omega j}\end{array}\right]$$

(1)

where point M has coordinates $(x_j,y_j,z_j)$; $u_j$ denotes the distance from point M along the pitch cone generatrix to the cone apex; and ${\theta }_j$ represents the developed angle of point M in the $x-y$ plane. Then, the unit normal vector $n_j$ on the pitch cone generatrix can be expressed as:

$$n_j={\displaystyle \frac{N_j}{\left|N_j\right|}}=\left[\begin{array}{c}\cos {\theta }_j\cos {\gamma }_{\omega j}\\ \sin {\theta }_j\cos {\gamma }_{\omega j}\\ -\sin {\gamma }_{\omega j}\end{array}\right]$$

(2)

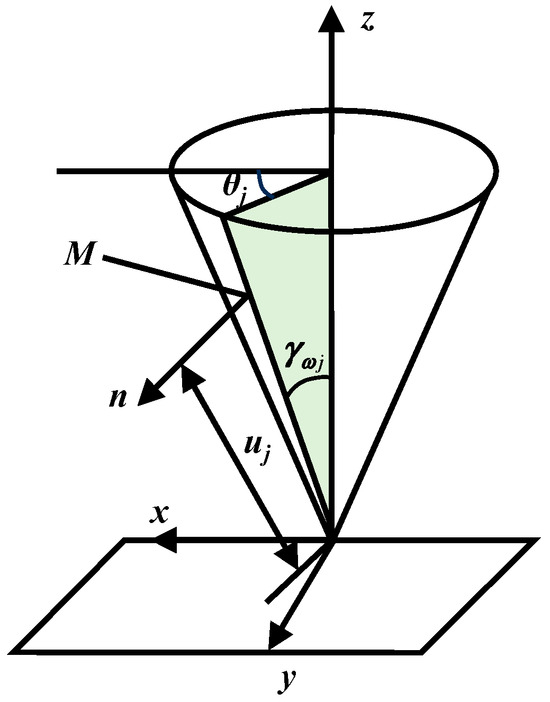
Figure 1. Working pitch cone.

Figure 2. Model of the working pitch cone with variable tooth thickness for parallel axes.

The equation of the contact point is derived through the transformation relationship between coordinate systems.

$$\left\{\begin{array}{c}{R}_{fw}^1=R_{fw}^2\\ n_{fw}^1=-n_{fw}^2\end{array}\right.$$

(3)

In the equation, $R_{fw}^j$ denotes the position vector of the contact point P on gear j; $n_{fw}^j$ represents the unit normal vector at the contact point P on gear j.

Given that $r_{p\omega j}=\sin {\gamma }_{\omega j}{u}_j$, it follows that:

$$\left\{\begin{array}{c}{r}_{p\omega 1}\cos {\theta }_1=r_{p\omega 1}\cos {\theta }_2+E\\ r_{p\omega 1}\sin {\theta }_1=-r_{p\omega 2}\sin {\theta }_2\\ d_1=r_{p\omega 1}\cot {\gamma }_{\omega 1}+r_{p\omega 2}\cot {\gamma }_{\omega 2}\\ \sin {\theta }_1\cos {\gamma }_{\omega 1}=\sin {\theta }_2\cos {\gamma }_{\omega 2}\\ \cos {\theta }_1\cos {\gamma }_{\omega 1}=-\cos {\theta }_2\cos {\gamma }_{\omega 2}\\ \sin {\gamma }_{\omega 1}=\sin {\gamma }_{\omega 2}\end{array}\right.$$

(4)

Furthermore, since $\left|n_{fw}^1\right|=\left|n_{fw}^2\right|$, the relationship between the two pitch cone angles can be expressed as:

$${\gamma }_{\omega 1}={\gamma }_{\omega 2}$$

(5)

By simplification, the mathematical expressions of $E$ and $d_1$ can be obtained as follows:

$$d_1=({\gamma }_{p\omega 1}+{\gamma }_{p\omega 2})\cot {\gamma }_{\omega 1}$$

(6)

$$E={\gamma }_{p\omega 1}+{\gamma }_{p\omega 2}$$

(7)

2.2. Gear Solid Modeling

Due to the non-uniform profile shift along axial sections, a tooth surface-based mathematical model is required instead of standard 3D software features. Based on the pitch cone mathematical model presented in Section 2.1, an accurate tooth surface equation can be derived, enabling the construction of a digital 3D model. Figure 3 shows the MATLAB 2018b-generated tooth surface point cloud of a parallel-axis variable tooth thickness spur gear that was used to construct the 3D solid model.

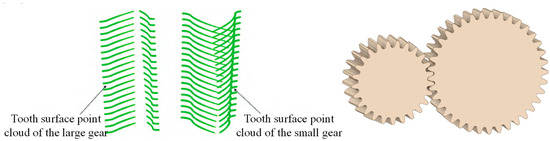
Figure 3. Gear point cloud and geometric model.

Due to the involvement of oil spraying in actual operating conditions, a closed gearbox model is further created based on the generated gear model (see Figure 4). The minimum clearance between the gear tooth tip and the gearbox wall is 10 mm, while the distance between the gear end face and the gearbox wall is 8 mm. Additionally, an oil injection inlet is placed at the top of the gearbox, and an oil outlet is provided on the side. The oil spraying flow rate is set between 0.4 and 0.75 L/min, with the injection nozzle diameter of 1.3 mm and the oil outlet diameter of 10 mm. Basic parameters of the involute gear with variable tooth thickness are shown in Table 1.

Figure 4. Gearbox model.

Table 1. Basic parameters of the involute gear with variable tooth thickness.

Parameter	Driving Wheel	Driven Wheel
Normal module/mm	2.5
Center distance/mm	80
Number of teeth	25	37
Pressure angle/(°)	20
Tooth width/mm	28	26
Pitch angle/(°)	0°, 2°, 4°
Taper coefficient at the small end	0.01	0.0081
Taper coefficient at the large end	1.187	1.101
Pitch circle diameter/mm	62.5	92.5

2.3. Fluid Governing Equations

The jet lubrication process for involute gears with variable tooth thickness constitutes a two-phase flow problem. To establish a gear heat dissipation model within computational fluid dynamics (CFD), the Volume of Fluid (VOF) model is employed. It is assumed that the oil and air phases are homogeneously mixed. In terms of heat transfer, both convective heat exchange and thermal conduction effects are considered. The effects of thermal radiation from the gear, as well as thermal variations induced by changes in fluid kinetic energy, are neglected. The governing equations for fluid flow [35] are as follows:

Continuity equation:

$${\displaystyle \frac{\partial \rho }{\partial t}}+\nabla \left(\rho v\right)=0$$

(8)

where ρ denotes the phase density and v represents the phase velocity.

Momentum equation:

$${\displaystyle \frac{\partial }{\partial t}}\left(r_{\beta }\rho v_i\right)+{\displaystyle \frac{\partial }{\partial x_j}}\left(r_{\beta }\rho v_i{v}_j\right)=-{\displaystyle \frac{\partial p}{\partial x_i}}+{\displaystyle \frac{\partial {\tau }_{ij}}{\partial x_j}}+r_{\beta }\rho g_i+F_i$$

(9)

where P denotes the static pressure, g_i and F_i represent the gravitational force and external body forces, respectively, and τ_ij denotes the stress tensor.

Energy equation:

$${\displaystyle \frac{\partial \left(\rho T\right)}{\partial t}}+\nabla \left(\rho vT\right)=\nabla \left({\displaystyle \frac{k}{c_p}}\mathrm{grad}T\right)+S_T$$

(10)

where c_p is the specific heat capacity, T is the fluid temperature, k is the thermal conductivity, and S_T is the viscous dissipation term.

Additionally, the fluid must satisfy the volume fraction continuity equation, which is expressed as Equation (11) as follows:

$$\sum _{\alpha =1}^N{r}_{\alpha }=1$$

(11)

where N is the number of phases; for this two-phase flow model, N is taken as 2. r_a denotes the volume fraction of fluid phase $\alpha$, which in this case refers to the mixture of lubricating oil and air. To enhance the efficiency of numerical analysis of turbulence within the gearbox, the Renormalization Group (RNG) $k-\epsilon$ model is employed. The RNG k-epsilon model accounts for the stochastic effects of turbulence through time-averaged treatment and is well-suited for simulating flows with high curvature and strong pressure gradients. The governing equations of the RNG k-epsilon model are expressed as follows:

$${\displaystyle \frac{\partial (\rho k)}{\partial t}}+{\displaystyle \frac{\partial (\rho k{u}_i)}{\partial x_i}}={\displaystyle \frac{\partial }{\partial x_j}}\left({\displaystyle \frac{{\mu }_{eff}}{{\sigma }_k}}\cdot {\displaystyle \frac{\partial k}{\partial x_j}}\right)+G_k+G_b-\rho \epsilon -Y_m+S_k$$

(12)

$${\displaystyle \frac{\partial (\rho \epsilon )}{\partial t}}+{\displaystyle \frac{\partial (\rho \epsilon u_i)}{\partial x_i}}={\displaystyle \frac{\partial }{\partial x_j}}\left({\displaystyle \frac{{\mu }_{eff}}{{\sigma }_{\epsilon }}}\cdot {\displaystyle \frac{\partial k}{\partial x_j}}\right)+C_{1\epsilon }{\displaystyle \frac{\epsilon }{k}}(G_k+C_{3\epsilon }{G}_b)-C_{2\epsilon }\rho {\displaystyle \frac{{\epsilon }^2}{k}}+S_{\epsilon }$$

(13)

where k represents the turbulent kinetic energy, and $\epsilon$ is the turbulent dissipation rate. G_k denotes the generation of turbulent kinetic energy due to the mean velocity gradient, while G_b accounts for the generation of turbulent kinetic energy due to buoyancy. Y_m represents the fluctuation-induced expansion in compressible fluids. Constants $C_{1\epsilon }$, $C_{2\epsilon }$ and $C_{3\epsilon }$ are model-specific coefficients, and ${\sigma }_k$ and ${\sigma }_{\epsilon }$ are the turbulent Prandtl numbers for k and $\epsilon$, respectively. The effective viscosity ${\mu }_{eff}$ is given by ${\mu }_{eff}=\mu +{\mu }_t$, where $\mu$ is the dynamic viscosity of the fluid and ${\mu }_t$ is the turbulent viscosity. Finally, $S_k$ and $S_{\epsilon }$ are the source terms for the turbulent kinetic energy and dissipation rate, respectively.

To analyze the gearbox’s transient flow field, the VOF two-phase model is employed for its accuracy in capturing oil–air distribution and lubrication patterns in critical regions. The volume equation for the p-phase fluid across the tracked phase interface is given by:

$${\displaystyle \frac{\partial {\alpha }_p}{\partial t}}+u_i{\displaystyle \frac{\partial {\alpha }_p}{\partial x_i}}=0$$

(14)

where ${\alpha }_p$ denotes the volume fraction of the p-phase fluid; u_i is the velocity component; t represents time; and x_i is the spatial coordinate component.

Additionally, when the fluid flows over the gear surface, heat transfer occurs, which can be addressed using Newton’s law of cooling.

$$q=h\left(t_w-t_f\right)$$

(15)

where q denotes the heat flux density (W·m⁻²), h is the convective heat transfer coefficient (W·m⁻²·K⁻¹), t_w is the temperature of the solid wall surface (K), and t_f is the characteristic temperature of the fluid (K). For internal flow, t_f is the cross-sectional average fluid temperature; for external flow, it is the fluid temperature away from the wall.

2.4. Heat Generation in Gear Meshing

The axial sliding in meshing allows the variable tooth thickness gear to be approximated as a helical gear in terms of load and friction behavior. Therefore, the equivalent helical gear model can be used to approximate the analysis of sliding frictional heat generation. The sliding frictional heat flux can be determined by calculating the work carried out by the friction force during meshing. In this formulation, F_n is the normal load on the tooth surface (N), f is the coefficient of sliding friction [36], and v_t is the relative sliding velocity at the tooth surface (m/s).

$$Q=F_{n}f{\nu }_t$$

(16)

Further, a force analysis of the involute variable tooth thickness gear under steady-state conditions is conducted, as shown in Figure 5. F_ax, F_mt and F_rd represent the axial force, the tangential force, and the radial force, respectively. If the torque is denoted as T and d_m is the pitch diameter at the middle section of the gear, the corresponding calculation formulas are as follows:

$$F_{mt}={\displaystyle \frac{2\times T}{d_m}}$$

(17)

$$F_{ax}={\displaystyle \frac{F_{mt}}{\cos \beta }}(\tan \alpha \sin \gamma +\sin \beta \cos \gamma )$$

(18)

$$F_{rd}={\displaystyle \frac{F_{mt}}{\cos \beta }}(\tan \alpha \cos \gamma +\sin \beta \sin \gamma )$$

(19)

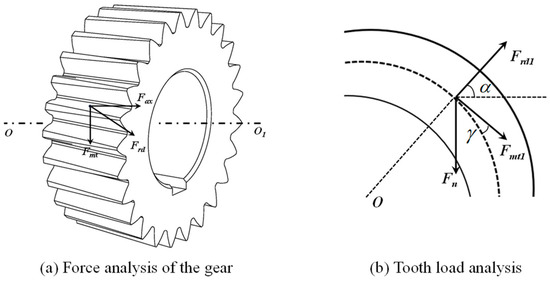
Figure 5. Force analysis of gears under steady-state conditions.

By solving Equations (17)–(19) simultaneously, the expression for F_n can be obtained as follows:

$$F_n=F_{mt}\cos \beta -F_{rd}\sin \beta +F_{ax}\sin \gamma$$

(20)

Finally, the heat of the driving and driven gears is computed using the distribution coefficient (Equation (21)) and applied at meshing points via a User-Defined Function (UDF).

$$\beta \text{'}={\displaystyle \frac{\sqrt{({\lambda }_1{\rho }_1{c}_1{\nu }_{1t})}}{\sqrt{({\lambda }_1{\rho }_1{c}_1{\nu }_{1t})}+\sqrt{({\lambda }_2{\rho }_2{c}_2{\nu }_{2t})}}}$$

(21)

The initial heat flux on the driving gear is shown in Figure 6 below.

Figure 6. Schematic diagram of heat flux on the driving gear.

2.5. Numerical Model and Boundary Conditions

To accurately capture the dynamic behavior and temperature variations during the gear meshing process, a transient time term is incorporated into the simulation [37]. This study utilizes the finite volume method via the commercial software package Ansys Fluent 2019R3 to model the dynamics of a variable tooth thickness gear system. The internal flow within the gearbox is resolved using the VOF two-phase model, coupled with the RNG k-epsilon turbulence model and the energy equation. The working fluid is treated as a mixture of gas and liquid phases: air (primary phase) with a density of 1.225 kg/m³ and dynamic viscosity of 1.7894 × 10⁻⁵ kg/ (m s), and lubricating oil (secondary phase) with a density of 850 kg/m³ and dynamic viscosity of 0.04 kg/ (m·s), both assumed to have the same temperature. The pressure–velocity coupling is handled using the SIMPLE (Semi-Implicit Method for Pressure-Linked Equations) algorithm [38], while convective and diffusive terms are discretized using a second-order upwind scheme. A first-order implicit scheme is employed for time discretization to improve computational efficiency. The simulation is carried out until the residuals for continuity and momentum equations fall below 10⁻⁵, and the result of the energy equation is below 10⁻⁶, satisfying the convergence criteria.

Fluid–gear interactions during rotation lead to a continuously changing interface, complicating numerical model calibration. To address this, dynamic mesh technology is introduced to accommodate the interface deformation. It is important to note that, to minimize numerical errors, the mesh size at the interface should be kept as uniform as possible.

To solve the governing equations, the required boundary conditions are defined as follows [39]: A uniform inlet velocity and constant temperature are applied at the oil injection port, while all variables at the oil outlet are set with Neumann boundary conditions. The far-field boundaries are treated with constant temperature, no-slip, and impermeability conditions, and the gear wall surfaces are also subjected to a no-slip condition. Given the significant temperature differences between the meshing and non-meshing regions of the gear teeth, a UDF is implemented to capture the temperature boundary conditions. The driving and driven gears rotate clockwise and counterclockwise, respectively. Detailed parameters are provided in Table 2.

Table 2. Boundary conditions.

Boundary	Velocity	Temperature	Pressure
Oil injection inlet	12.5 m·s−1	300 K
	15 m·s−1	300 K
	17.5 m·s−1	300 K
	20 m·s−1	313.15 K	---
Oil outlet	---	317.15 K	0 pa
Gears	8000 rpm	udf	---
Gearbox	---	300 K	---

3. Model Validation

To ensure the reliability and applicability of the present results, it is essential to conduct a mesh independence test and validation prior to introducing extensive case studies. This is achieved by comparing theoretical data with numerical results.

After defining the computational domain, the optimal meshing strategy is further evaluated. Mesh refinement is applied to the gear surfaces, meshing region, and areas near the oil injection nozzle, with a mesh size of 0.5 mm, to better capture the heat distribution of the gear teeth and the oil flow phenomena. The remaining areas use a global mesh configuration. The computational mesh is generated using Hypermesh software, with five mesh sizes considered: 2 mm, 3 mm, 4 mm, 5 mm, and 6 mm. A monitoring point is placed 25 mm above the gear meshing location (see Figure 7). Figure 8 presents the corresponding test data. The results show that when the mesh size increases from 4.5 mm to 5.5 mm, the pressure and velocity magnitudes fluctuate by 31.7% and 22.3%, respectively. In contrast, within the 3.5–4.5 mm range, fluctuations remain below 1.6%. Balancing computational cost and accuracy, the 4.5 mm mesh is identified as the optimal configuration (see Figure 9). Furthermore, based on the minimum mesh size (Grid_min = 2.03 × 10⁻⁴) and the Courant number, a time step of 0.001 s is sufficient to meet the demands of large-scale case simulations.

Figure 7. Monitoring point location.

Figure 8. Pressure and velocity data for different grid resolutions.

Figure 9. Overall mesh layout of the gearbox.

Notably, since f is set at constant values (f = 0.06) in this study, the value of Q depends on the normal contact force F_n. Based on the gear structural parameters in Table 1 and Table 2 as well as using Equations (16) and (20), the theoretical normal contact force is calculated to be 2764.117 N. Meanwhile, a dynamic simulation is conducted using specialized software, and the resulting normal contact force is 2546.623 N. By comparing the simulation result with the theoretical value, the error is found to be 7.87%, which falls within the acceptable range. This verifies the rationality and effectiveness of the proposed heat dissipation model.

4. Results and Discussion

An effective approach for monitoring the internal temperature of an involute variable tooth thickness gearbox is the surface-averaging method. Average temperatures at different locations reveal the effects of injection velocity, pitch cone angle, gear width, and axial displacement on temperature distribution. For the placement of internal monitoring sections within the gearbox, monitoring surfaces are positioned 2 mm from both end faces of the driving gear and at the midpoint. The locations of these monitoring surfaces are shown in Figure 10.

Figure 10. Monitoring section locations within the gearbox.

4.1. Effect of Oil Injection Velocity on Thermal Behavior

The magnitude of the oil injection velocity significantly influences the flow field within the gearbox. Therefore, investigating the impact of injection velocity on the internal temperature distribution is of great importance for optimizing and enhancing gear lubrication performance. Figure 11 presents the average temperatures at the monitoring surfaces inside the gearbox for pitch cone angles of 0°, 2°, and 4°, respectively.

Figure 11. Average temperatures at internal monitoring sections of the gearbox under different pitch cone angles.

Based on the analysis in the figure above, it can be observed that when the pitch cone angle is 0°, the temperature variation in the gear at different monitoring sections is relatively small. Overall, as the lubrication oil injection velocity increases, the cooling temperature decreases. Under a 2° pitch cone angle, the average temperature inside the gearbox is the highest compared to the 0° and 4° cases, with a temperature of 322.9 Kelvin. Additionally, the temperature at the thinner side of the gear is significantly lower than at the other two monitoring sections. Under a 4° pitch cone angle, the average temperature at each monitoring section is lower compared to the 0° and 2° cases. This is due to previous studies indicating that the 4° pitch cone angle allows for a higher volume fraction of lubrication oil on the gear surface, which in turn facilitates the removal of more heat. Consequently, the temperature for the 4° pitch cone angle is lower than that of the other two designs. Furthermore, the 4° pitch cone angle maintains the performance characteristics of the 2° pitch cone angle, where the temperature is lower at the thinner edge of the gear. The analysis of the average temperatures at the monitoring sections inside the gearbox for different pitch cone angles shows that the 4° pitch cone angle is more favorable for gear cooling. Figure 12 illustrates the relationship between the oil volume fraction and the gear speed under different pitch cone angle conditions.

Figure 12. The curve depicting the variation in oil volume fraction with gear speed under different cone angle conditions.

4.2. The Effect of Gear Width on Temperature

After prolonged operation, alternating loads and increased tooth wear reduce contact area and enlarge backlash, causing vibration and noise. Involute gears with variable tooth thicknesses (unequal face widths) can alleviate these issues by axial adjustment without changing the center distance. This adjustment decreases backlash and prolongs gear life. For analysis, the gear width ratio ${\psi }_{\mathrm{d}}$ is defined as the face width of the driving gear to that of the driven gear (${\psi }_{\mathrm{d}}=B_2/B_1$, where $B_1$ and $B_2$ are their respective widths). Temperature variations at different width ratios are compared to examine the effect of gear width on flow field temperature during axial adjustment of variable-tooth-thickness gears.

As shown in Figure 13, with a fixed driven gear width of 26 mm and pitch cone angles of 0°, 2°, and 4°, temperature variations across monitoring sections show consistent trends under different gear width ratios. Specifically, as the width of the driving gear increases with the gear width ratio, the average temperature at all three monitoring sections shows an upward trend. This is primarily due to the altered flow direction caused by the increased driving gear width, which leads to a deflection of the oil jet. Consequently, the lubricant fails to fully reach the effective lubrication area, resulting in a slight temperature rise. Therefore, in designing involute gears with variable tooth thicknesses, smaller gear widths and lower width ratios are recommended. This is feasible as long as strength and axial displacement requirements are satisfied, and the ratio ${\psi }_{\mathrm{d}}\ge 1$ ensures a comparable service life for both gears. This approach facilitates better heat dissipation within the gearbox and enhances lubrication performance.

Figure 13. Average temperature in the monitoring section inside the gearbox under different gear width ratios.

4.3. The Effect of Axial Displacement on Temperature

In involute gears with variable tooth thickness (i.e., unequal face widths), axial adjustment can reduce backlash and extend service life without changing the center distance. To assess how axial displacement affects gearbox temperature, three gear pairs with different pitch cone angles are tested under identical conditions, and temperature changes at various displacements are observed.

As shown in Figure 14, with constant gear parameters and pitch cone angles of 0°, 2°, and 4°, temperature variations across monitoring sections show a consistent pattern after axial displacement. Regardless of the offset direction, temperature at all monitoring points rises with axial displacement magnitude. The lowest temperature occurs near zero displacement. This trend is primarily due to changes in the flow direction of the lubricant caused by axial offset, regardless of the direction. Under the influence of air entrainment effects, the oil jet deviates from the meshing zone, leading to a slight temperature rise. Therefore, when gear tooth wear occurs, only minimal axial adjustment should be made—ensuring proper backlash—to avoid temperature increase and potential lubrication failure.

Figure 14. Average temperature at the monitoring section inside the gearbox under different axial displacements.

5. Conclusions

This study investigates the cooling performance of variable-tooth-thickness involute gears under varying oil injection velocities and pitch cone angles. The internal temperature distribution of the gearbox is accurately simulated using the VOF method and UDF-defined heat flux in the mesh region. This provides reliable support for the cooling design of variable-tooth-thickness involute gears. The main conclusions are as follows:

(1)

The simulation results indicate that as the oil injection velocity increases, the cooling performance inside the gearbox decreases, though temperature reduction still occurs. A comparison of the temperature data comparison shows that a 15 m/s injection velocity with a 4° pitch cone angle provides a more economical cooling performance than other configurations. These findings support the selection of cost-effective, eco-friendly lubrication speeds and inform similar practical applications.

(2)

A larger pitch cone angle markedly reduces the maximum and minimum internal temperatures of the gearbox. This analysis provides a reference for the pitch cone angle design of variable-tooth-thickness involute gears. However, it should also be noted that an excessively large pitch cone angle may result in thinner teeth, thereby reducing their bending fatigue strength. Thus, excessively large pitch cone angles should be avoided, and optimal design requires a balanced consideration of multiple factors.

(3)

The influence of gear width on temperature shows that increasing the gear width significantly raises the internal temperature of the gearbox. When the driven wheel tooth width is fixed, selecting a smaller gear width ratio can significantly reduce the internal temperature. This analysis provides a scientific basis for selecting the optimal width for variable-tooth-thickness involute gears.

(4)

The temperature response to axial displacement shows that the gearbox temperature increases with larger positive or negative offsets of variable-tooth-thickness involute gears. The minimum temperature occurs at zero displacement. This analysis provides a theoretical reference for selecting appropriate axial backlash adjustments in variable-tooth-thickness involute gear design.