A Toolpath Planning Method for Optical Freeform Surface Ultra-Precision Turning Based on NURBS Surface Curvature
Abstract
:1. Introduction
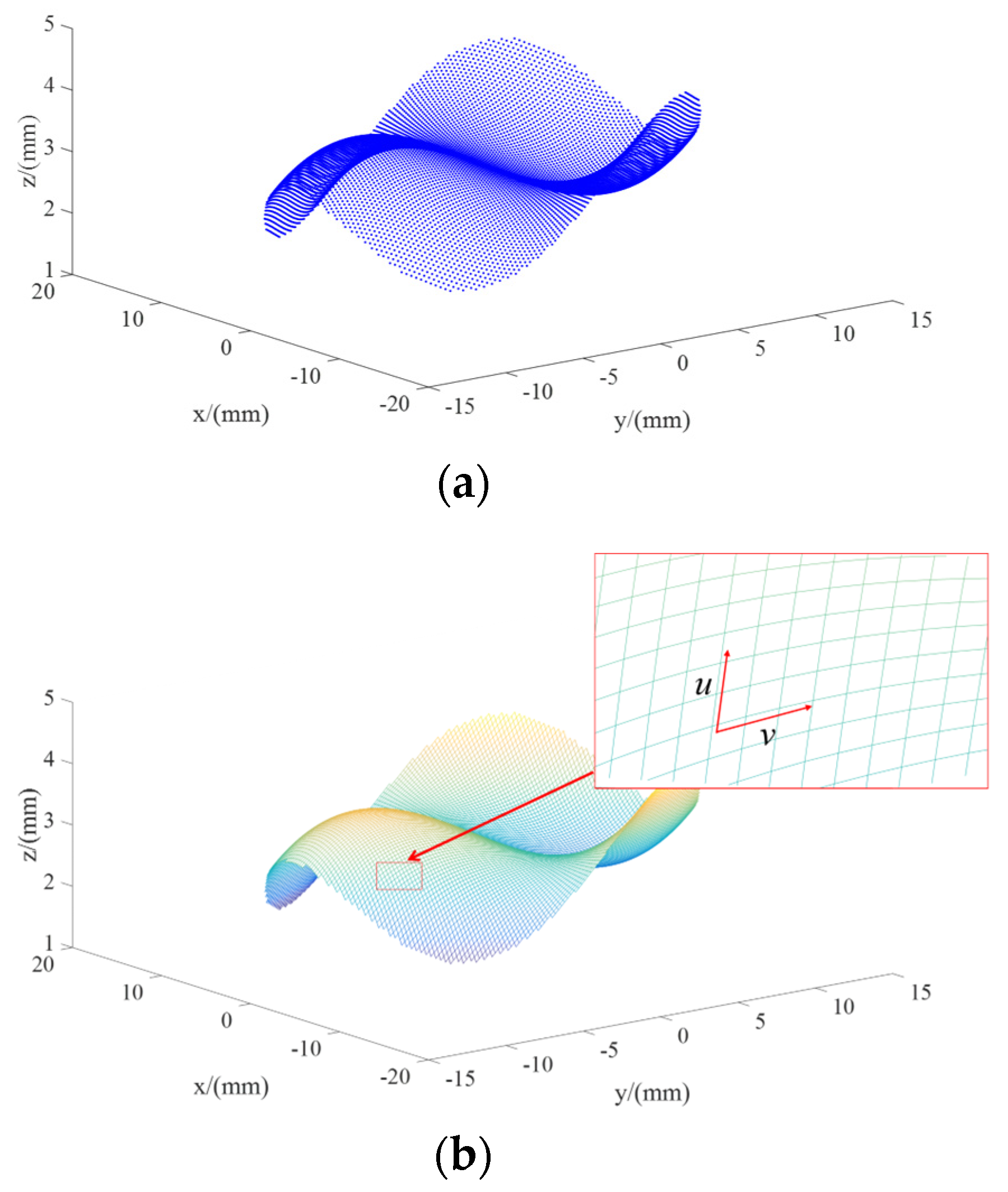
2. Reconstruction of the NURBS Surfaces
3. Toolpath Planning Method for Freeform Surfaces Based on NURBS Surface Curvature
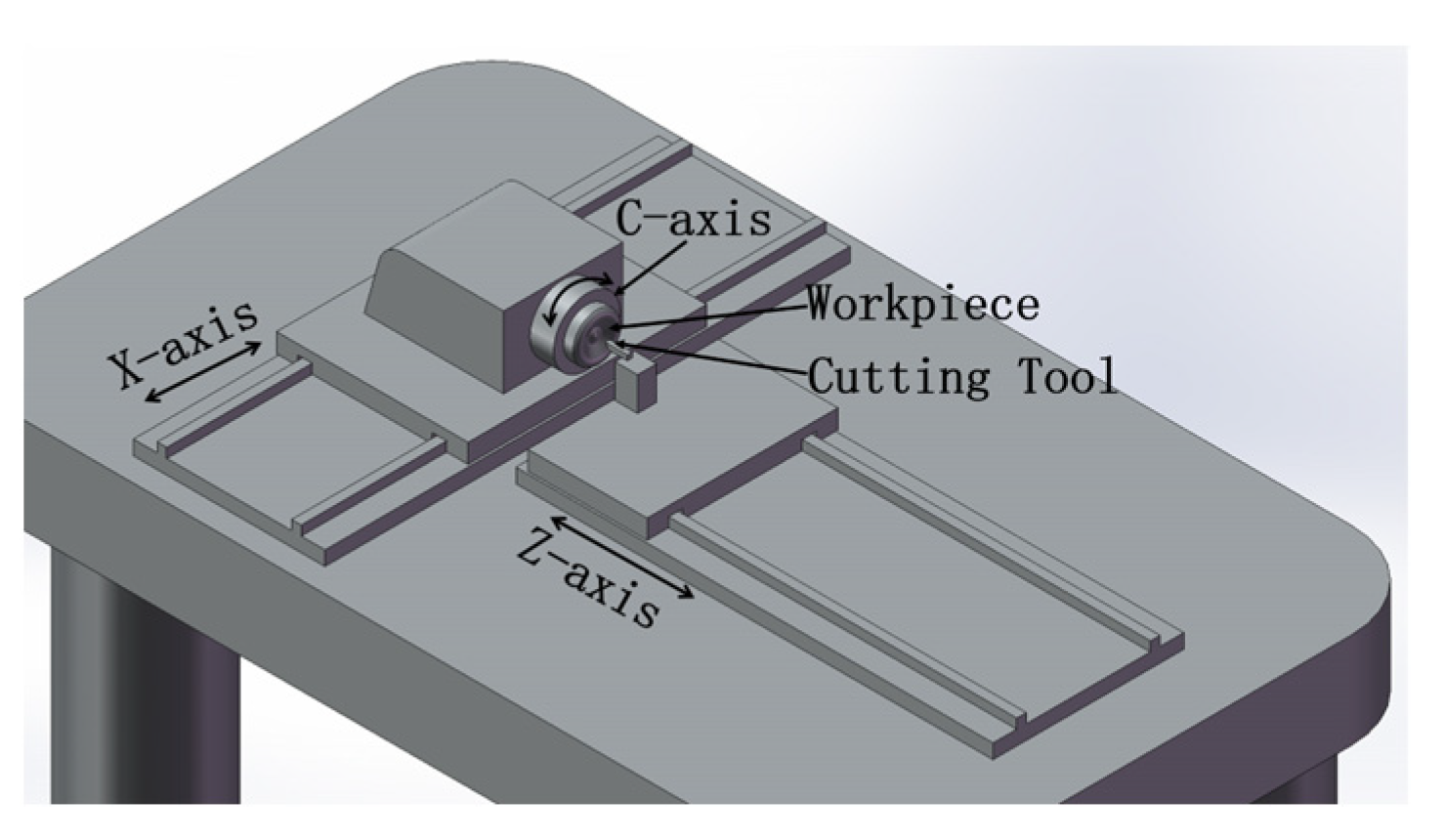
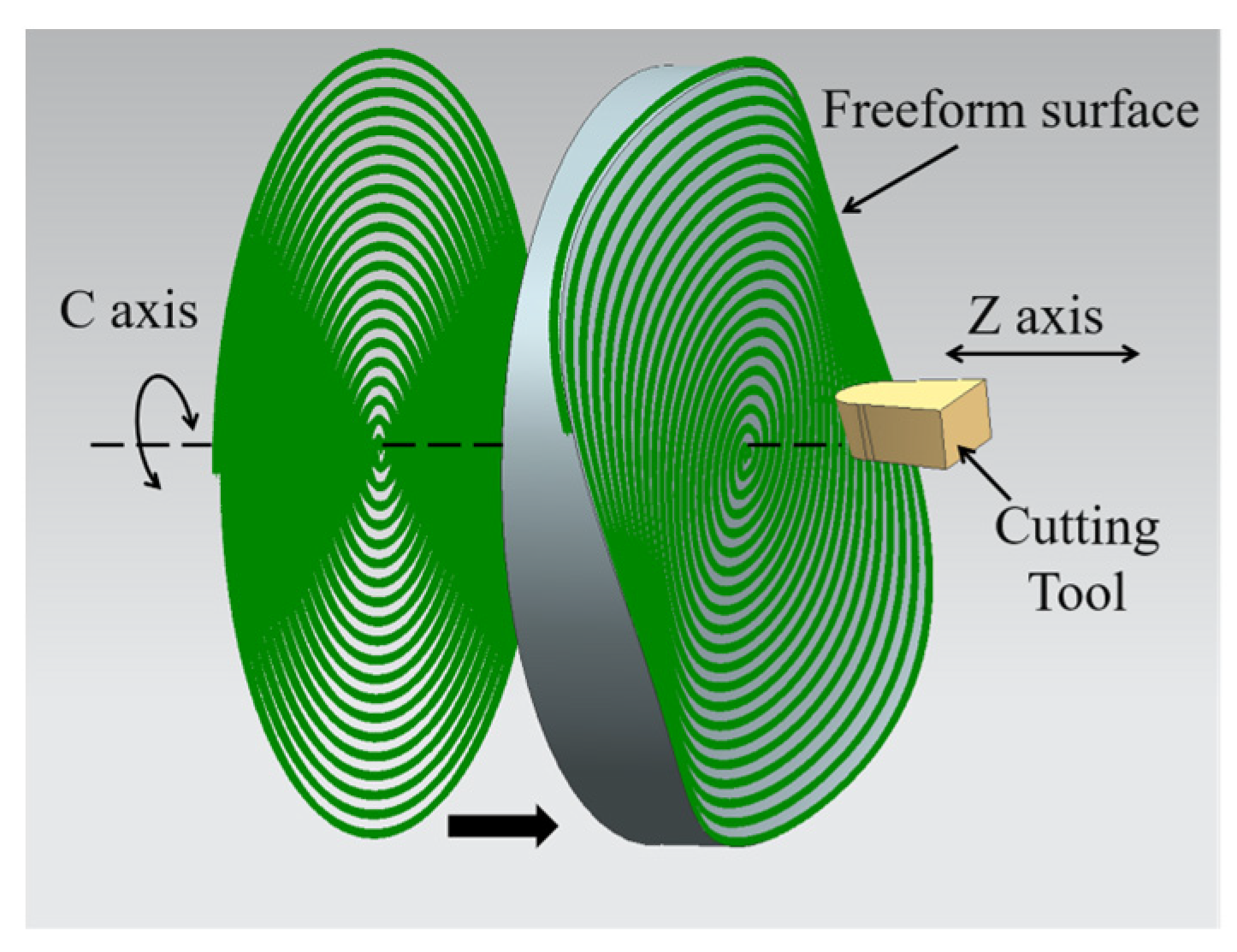
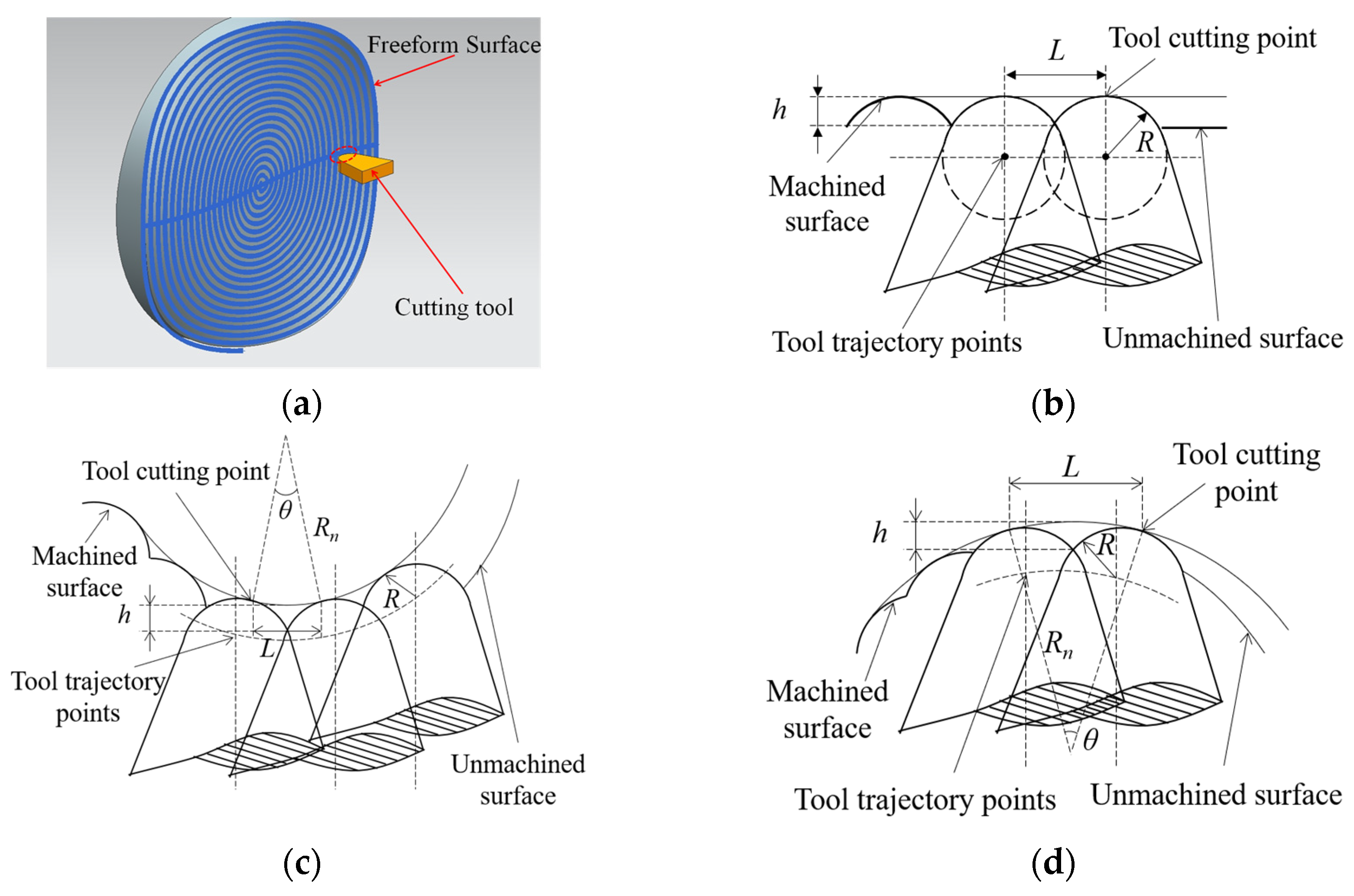
3.1. The Archimedes Spiral Method
3.2. Calculation of Toolpath Parameters Base on Analysis of NURBS Surfaces
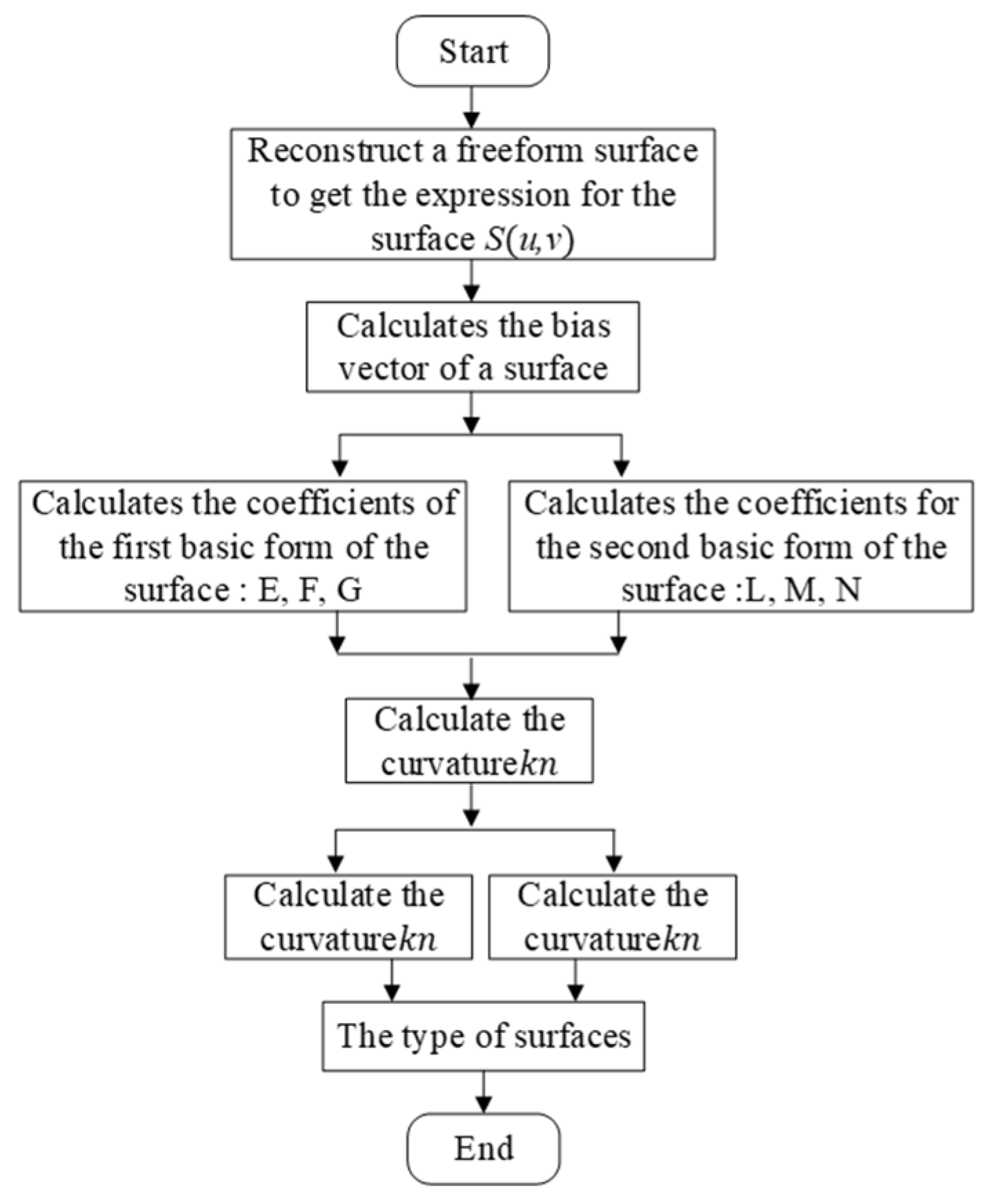
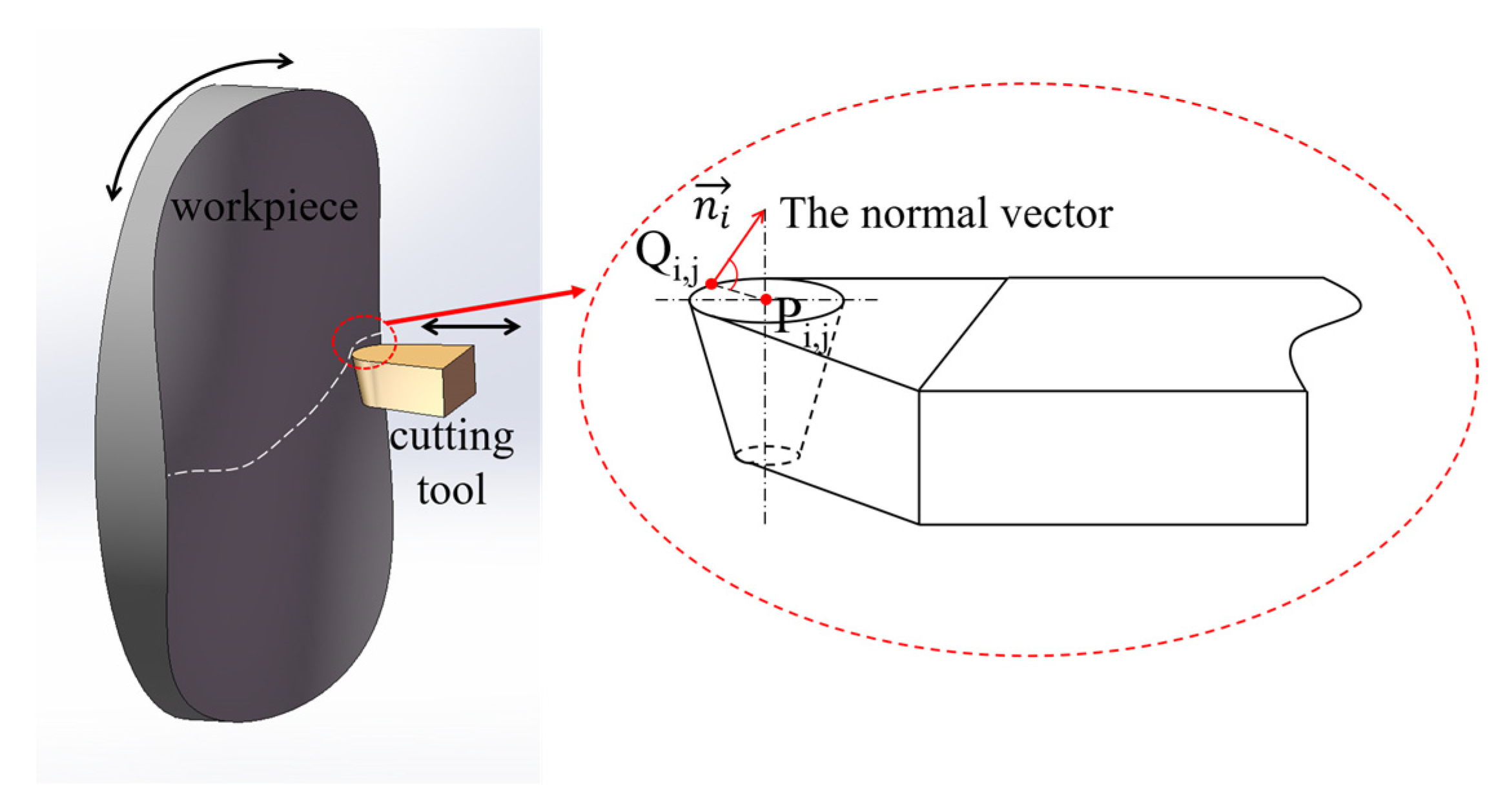
3.2.1. Analysis of NURBS Surfaces
3.2.2. Calculation of Toolpath Parameters
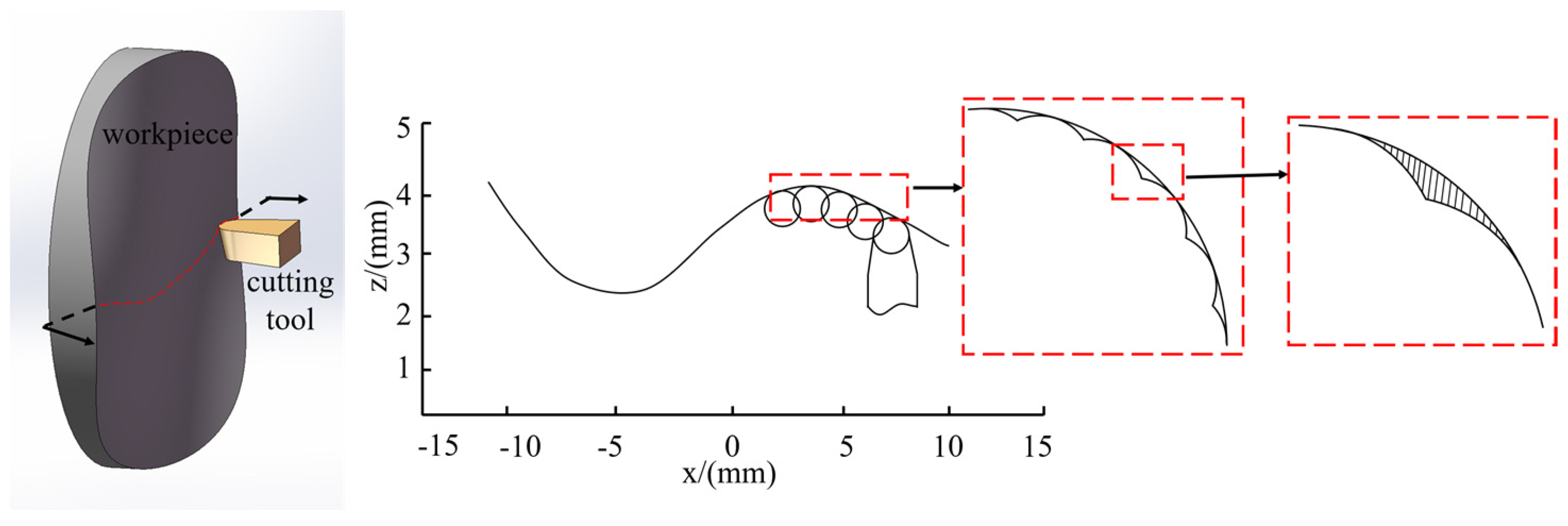
3.3. Toolpath Based on NURBS Surface Curvature
4. Simulation and Analysis
5. Experiment and Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Moein, S.; Suleski, T.J. Freeform optics for variable extended depth of field imaging. Opt. Express 2021, 29, 40524–40537. [Google Scholar] [CrossRef] [PubMed]
- Geyl, R.; Ruch, E.; Bourgois, R.; Mercier-Ythier, R.; Leplan, H.; Riguet, F. Freeform optics design, fabrication and testing technologies for Space applications. In Proceedings of the International Conference on Space Optics—ICSO Location of Conference, Chania, Greece, 9–12 October 2018. [Google Scholar]
- Yang, T.; Wang, Y.; Ni, D.; Cheng, D.; Wang, Y. Design of off-axis reflective imaging systems based on freeform holographic elements. Opt. Express 2022, 30, 20117–20134. [Google Scholar] [CrossRef] [PubMed]
- Zheng, X.; Li, Z.; Zhang, X.; Fang, F. Manufacturing-constrained optical design methodology for cylindrical freeform reflective imaging system. Opt. Express 2018, 26, 22547–22562. [Google Scholar] [CrossRef] [PubMed]
- Duan, Y.; Yang, T.; Cheng, D.; Wang, Y. Design method for nonsymmetric imaging optics consisting of freeform-surface-substrate phase elements. Opt. Express 2020, 28, 1603–1620. [Google Scholar] [CrossRef] [PubMed]
- Ni, J.; Yang, T.; Cheng, D.; Wang, Y. Design method of wide field-of-view imaging systems using Gaussian radial basis functions freeform surfaces. Appl. Opt. 2021, 60, 4491–4501. [Google Scholar] [CrossRef]
- Hu, X.; Hua, H. High-resolution optical see-through multi-focal-plane head-mounted display using freeform optics. Opt. Express 2014, 22, 13896–13903. [Google Scholar] [CrossRef]
- Muslimov, E.; Hugot, E.; Jahn, W.; Vives, S.; Ferrari, M.; Chambion, B.; Henry, D.; Gaschet, C. Combining freeform optics and curved detectors for wide field imaging: A polynomial approach over squared aperture. Opt. Express 2017, 25, 14598–14610. [Google Scholar] [CrossRef]
- Yang, L.; Liu, Y.; Ding, Z.; Zhang, J.; Tao, X.; Zheng, Z.; Wu, R. Design of freeform lenses for illuminating hard-to-reach areas through a light-guiding system. Opt. Express 2020, 28, 38155–38168. [Google Scholar] [CrossRef]
- Shadalou, S.; Gurganus, D.; Cassarly, W.J.; Davies, M.A.; Suleski, T.J. Design, fabrication, and characterization of a tunable LED-based illuminator using refractive freeform arrays. Opt. Express 2022, 30, 42749–42761. [Google Scholar] [CrossRef]
- Zhu, Z.; Wei, S.; Fan, Z.; Ma, D. Freeform illumination optics design for extended LED sources through a localized surface control method. Opt. Express 2022, 30, 11524–11535. [Google Scholar] [CrossRef]
- Sorgato, S.; Mohedano, R.; Chaves, J.; Hernández, M.; Blen, J.; Grabovičkić, D.; Benítez, P.; Miñano, J.C.; Thienpont, H.; Duerr, F. Compact illumination optic with three freeform surfaces for improved beam control. Opt. Express 2017, 25, 29627–29641. [Google Scholar] [CrossRef] [PubMed]
- Yang, T.; Zhu, J.; Wu, X.; Jin, G. Direct design of freeform surfaces and freeform imaging systems with a point-by-point three-dimensional construction-iteration method. Opt. Express 2015, 23, 10233–10246. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Zhou, Y.; Zhang, H.; Xiong, Z.; To, S. Advances in ultra-precision machining of micro-structured functional surfaces and their typical applications. Int. J. Mach. Tools Manuf. 2019, 142, 16–41. [Google Scholar] [CrossRef]
- Zhou, X.; Zuo, C.; Liu, Q.; Lin, J. Surface generation of freeform surfaces in diamond turning by applying double-frequency elliptical vibration cutting. Int. J. Mach. Tools Manuf. 2016, 104, 45–57. [Google Scholar] [CrossRef]
- Zhu, Z.; Tong, Z.; To, S.; Jiang, X. Tuned diamond turning of micro-structured surfaces on brittle materials for the improvement of machining efficiency. CIRP Ann. 2019, 68, 559–562. [Google Scholar] [CrossRef]
- Guo, Y.; Yang, X.; Kang, J.; Zhang, W.; Wang, X.; Li, M.; Wang, Y.; Xie, Q.; Luo, S. Ductile machining of single-crystal germanium for freeform surfaces diamond turning based on a long-stroke fast tool servo. J. Manuf. Process. 2022, 82, 615–627. [Google Scholar] [CrossRef]
- Zhang, S.; Zong, W. A novel surface roughness model for potassium dihydrogen phosphate (KDP) crystal in oblique diamond turning. Int. J. Mech. Sci. 2020, 173, 105462. [Google Scholar] [CrossRef]
- Cheung, C.; Lee, W. A theoretical and experimental investigation of surface roughness formation in ultra-precision diamond turning. Int. J. Mach. Tools Manuf. 2000, 40, 979–1002. [Google Scholar] [CrossRef]
- Brinksmeier, E.; Gläbe, R.; Schönemann, L. Review on Diamond-Machining Processes for the Generation of Functional Surface Structures. CIRP J. Manuf. Sci. Technol. 2012, 5, 1–7. [Google Scholar] [CrossRef]
- Xing, Y.; Li, C.; Liu, Y.; Yang, C.; Xue, C. Fabrication of high-precision freeform surface on die steel by ultrasonic-assisted slow tool servo. Opt. Express 2021, 29, 3708–3723. [Google Scholar] [CrossRef]
- Balabokhin, A.; Tarbutton, J. Iso-scallop tool path building algorithm “based on tool performance metric” for generalized cutter and arbitrary milling zones in 3-axis CNC milling of free-form triangular meshed surfaces. J. Manuf. Process. 2017, 28, 565–572. [Google Scholar] [CrossRef]
- Takasugi, K.; Asakawa, N. Parameter-based spiral tool path generation for free-form surface machining. Precis. Eng. 2018, 52, 370–379. [Google Scholar] [CrossRef]
- Sato, Y.; Yan, J. Tool path generation and optimization for freeform surface diamond turning based on an independently controlled fast tool servo. Int. J. Extreme Manuf. 2022, 4, 025102. [Google Scholar] [CrossRef]
- Wang, D.; Sui, Y.; Yang, H.; Li, D. Adaptive Spiral Tool Path Generation for Diamond Turning of Large Aperture Freeform Optics. Materials 2019, 12, 810. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Li, Z.; Zhang, G. High performance ultra-precision turning of large-aspect-ratio rectangular freeform optics. CIRP Ann. 2018, 67, 543–546. [Google Scholar] [CrossRef]
- Zhang, X.; Gao, H.; Guo, Y.; Zhang, G. Machining of optical freeform prisms by rotating tools turning. CIRP Ann. Manuf. Techn. 2012, 61, 519–522. [Google Scholar] [CrossRef]
- Lang, C.; Li, C.; Fu, H.; Bo, S.; Yang, C.; Xue, C. Ultra-precision turning method efficient for optical freeform surfaces with a hybrid slow–fast tool servo. Appl. Opt. 2022, 61, 818–825. [Google Scholar] [CrossRef]
- Khaghani, A.; Cheng, K. Investigation on multi-body dynamics based approach to the toolpath generation for ultraprecision machining of freeform surfaces. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2019, 234, 571–583. [Google Scholar] [CrossRef]
- Zuo, C.; Meng, G.; Zhou, X.; Liu, Q.; Jiang, S.; Zhang, X.; Xu, P.; Zhang, Y.; Zhang, X.; Yan, G. Diamond turning of freeform surfaces using non-zero rake angle tools. Int. J. Adv. Manuf. Technol. 2021, 118, 2265–2284. [Google Scholar] [CrossRef]
- Zhou, M.; Zhang, H.J.; Chen, S.J. Study on Diamond Cutting of Nonrationally Symmetric Microstructured Surfaces with Fast Tool Servo. Mater. Manuf. Process. 2010, 25, 488–494. [Google Scholar] [CrossRef]
- Yi, A.Y.; Li, L. Design and fabrication of a microlens array by use of a slow tool servo. Opt. Lett. 2005, 30, 1707–1709. [Google Scholar] [CrossRef] [PubMed]
- Fang, F.Z.; Zhang, X.D.; Hu, X.T. Cylindrical coordinate machining of optical freeform surfaces. Opt. Express 2008, 16, 7323–7329. [Google Scholar] [CrossRef] [PubMed]
- Yin, Z.; Dai, Y.; Li, S.; Guan, C.; Tie, G. Fabrication of off-axis aspheric surfaces using a slow tool servo. Int. J. Mach. Tools Manuf. 2011, 51, 404–410. [Google Scholar] [CrossRef]
- Cai, H.B.; Shi, G.Q. Tool Path Generation for Multi-Degree-of-Freedom Fast Tool Servo Diamond Turning of Optical Freeform Surfaces. Exp. Tech. 2019, 43, 561–569. [Google Scholar] [CrossRef]
- Zhang, X.D.; Fang, F.Z.; Wang, H.B.; Wei, G.S.; Hu, X.T. Ultra-precision machining of sinusoidal surfaces using the cylindrical coordinate method. J. Micromechanics Microeng. 2009, 19, 054004. [Google Scholar] [CrossRef]
- Zhu, Z.; To, S. Adaptive tool servo diamond turning for enhancing machining efficiency and surface quality of freeform optics. Opt. Express 2015, 23, 20234–20248. [Google Scholar] [CrossRef]
- Li, Z.; Fang, F.; Chen, J.; Zhang, X. Machining approach of freeform optics on infrared materials via ultra-precision turning. Opt. Express 2017, 25, 2051–2062. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, X.; Fang, F.; Liu, S. Identification and compensation of main machining errors on surface form accuracy in ultra-precision diamond turning. Int. J. Mach. Tools Manuf. 2016, 105, 45–57. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Y.; Lin, J.; Yi, A.; Zhou, X. Effects of Machining Errors on Optical Performance of Optical Aspheric Components in Ultra-Precision Diamond Turning. Micromachines 2020, 11, 331. [Google Scholar] [CrossRef]
- Huang, P.; Wu, X.; To, S.; Zhu, L.; Zhu, Z. Deterioration of form accuracy induced by servo dynamics errors and real-time compensation for slow tool servo diamond turning of complex-shaped optics. Int. J. Mach. Tools Manuf. 2020, 154, 103556. [Google Scholar] [CrossRef]
- He, C.L.; Zong, W.J.; Xue, C.X.; Sun, T. An Accurate 3d Surface Topography Model for Single-Point Diamond Turning. Int. J. Mach. Tools Manuf. 2018, 134, 42–68. [Google Scholar] [CrossRef]
- Piegl, L.; Tiller, W. The Nurbs Book, Monographs in Visual Communication; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Han, Y.; Zhang, L.; Guo, M.; Fan, C.; Liang, F. Tool paths generation strategy for polishing of freeform surface with physically uniform coverage. Int. J. Adv. Manuf. Technol. 2017, 95, 2125–2144. [Google Scholar] [CrossRef]
- Qu, X.; Liu, Q.; Wang, H.; Liu, H.; Sun, H. A spiral path generation method for achieving uniform material removal depth in aspheric surface polishing. Int. J. Adv. Manuf. Technol. 2022, 119, 3247–3263. [Google Scholar] [CrossRef]










| Processing Parameters | Numeric Requirements |
|---|---|
| Spindle speed | 60 rpm |
| Tool arc radius | 1.06 mm |
| Tool material | Diamond |
| Tool rake angle | 0° |
| Tool back angle | 15° |
| Surface radius | 12.5 mm |
| Machining row spacing | 0.012 mm |
| Depth of cut | 0.01 mm |
| Materials | PMMA |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Bai, Q.; Gao, S.; Zhao, L.; Cheng, K. A Toolpath Planning Method for Optical Freeform Surface Ultra-Precision Turning Based on NURBS Surface Curvature. Machines 2023, 11, 1017. https://doi.org/10.3390/machines11111017
Wang X, Bai Q, Gao S, Zhao L, Cheng K. A Toolpath Planning Method for Optical Freeform Surface Ultra-Precision Turning Based on NURBS Surface Curvature. Machines. 2023; 11(11):1017. https://doi.org/10.3390/machines11111017
Chicago/Turabian StyleWang, Xuchu, Qingshun Bai, Siyu Gao, Liang Zhao, and Kai Cheng. 2023. "A Toolpath Planning Method for Optical Freeform Surface Ultra-Precision Turning Based on NURBS Surface Curvature" Machines 11, no. 11: 1017. https://doi.org/10.3390/machines11111017
APA StyleWang, X., Bai, Q., Gao, S., Zhao, L., & Cheng, K. (2023). A Toolpath Planning Method for Optical Freeform Surface Ultra-Precision Turning Based on NURBS Surface Curvature. Machines, 11(11), 1017. https://doi.org/10.3390/machines11111017








