Workspace Analysis and Dynamic Modeling of 6-DoF Multi-Pattern Cable-Driven Hybrid Mobile Robot
Abstract
1. Introduction
2. Methods and Materials
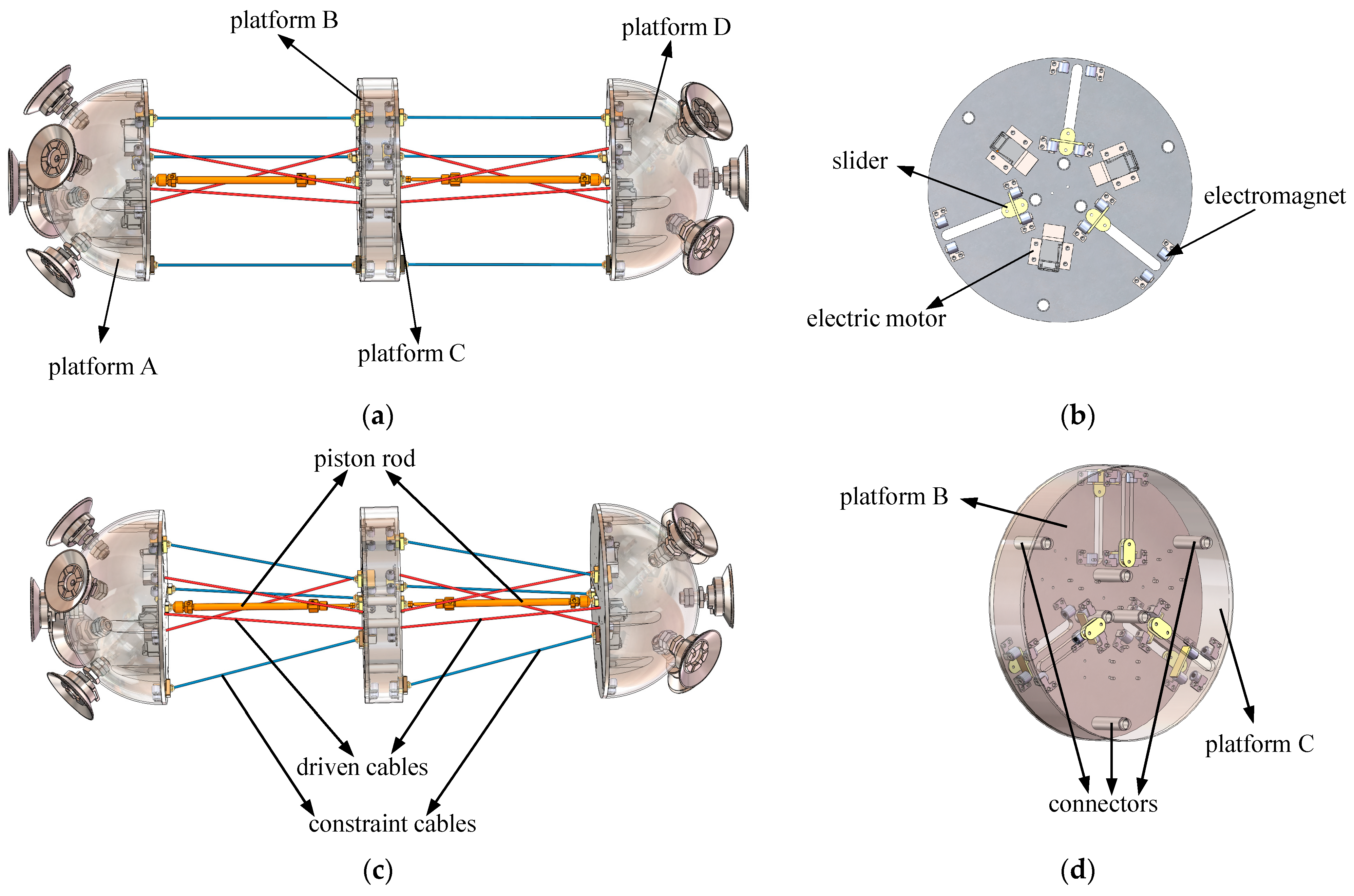
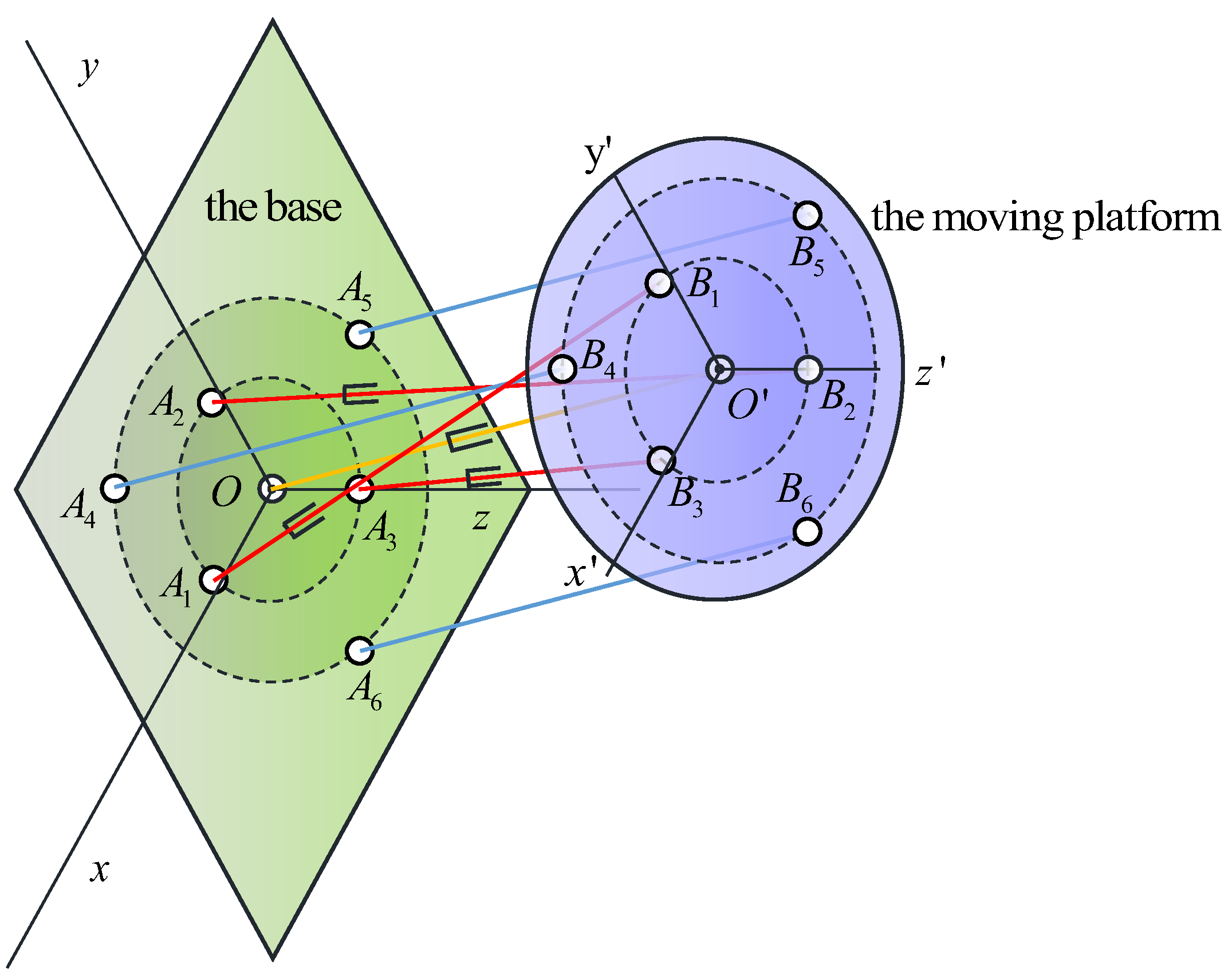
2.1. Robot Architecture
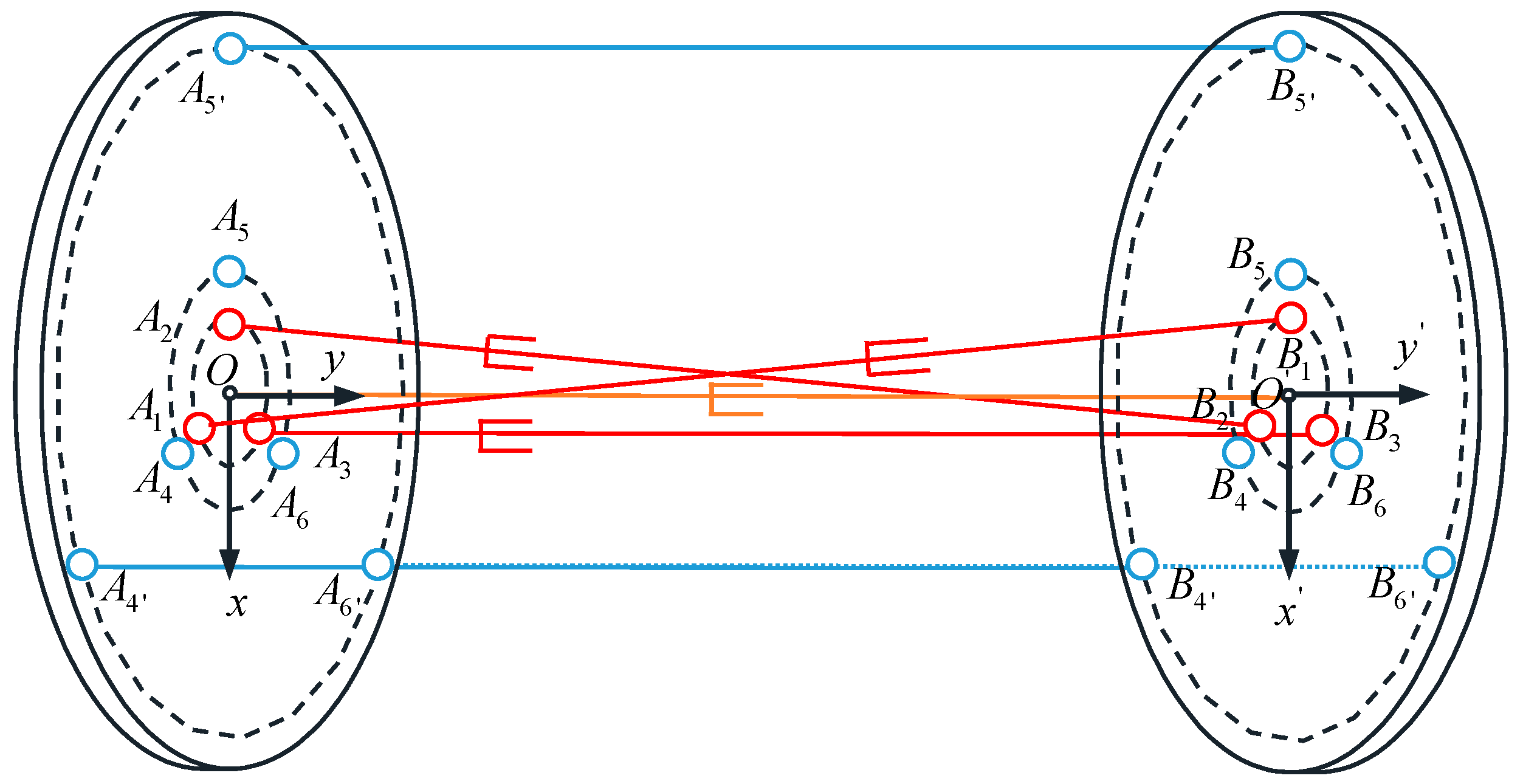
2.2. Workspace Analysis
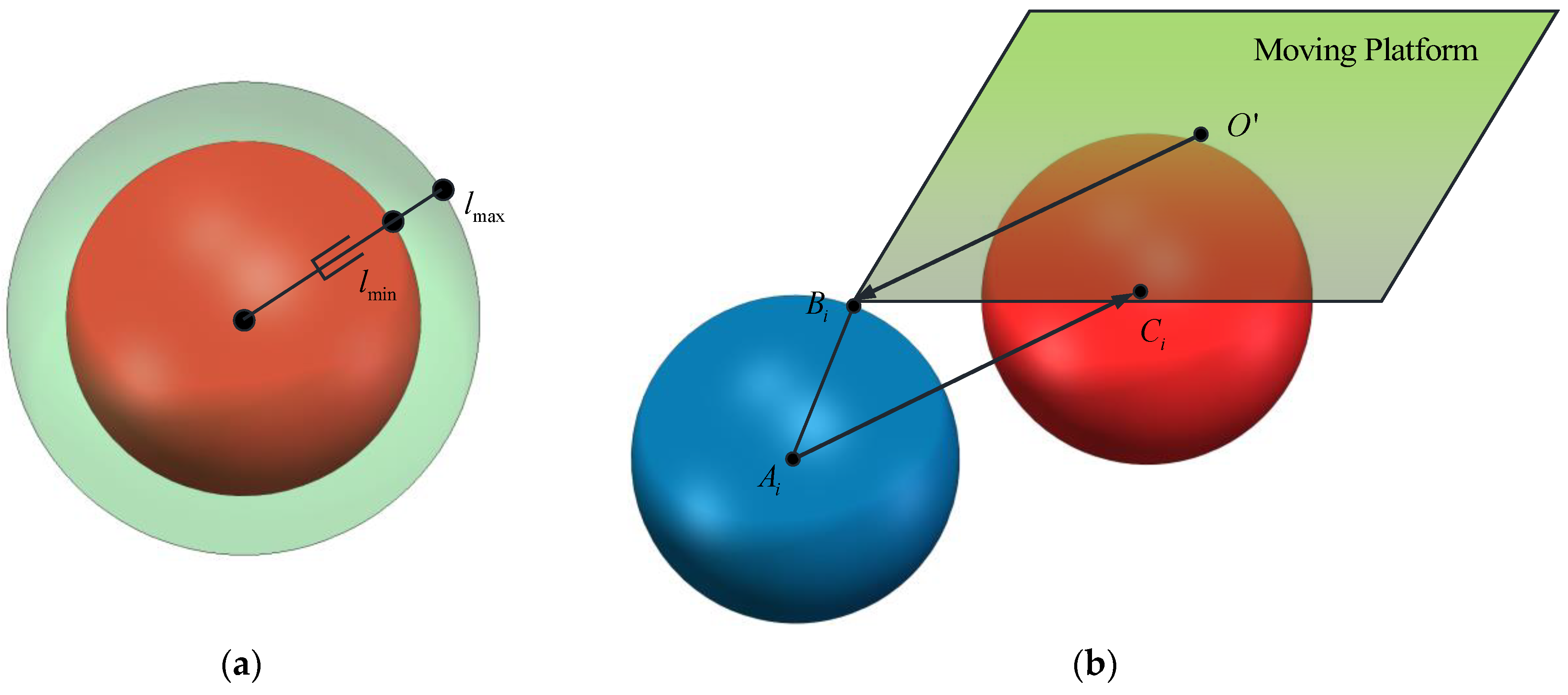
2.2.1. The Intersection of Circles in 2D
2.2.2. The Intersection of Circular Rings in 2D
2.2.3. The Arc Intersection Method for the Workspace
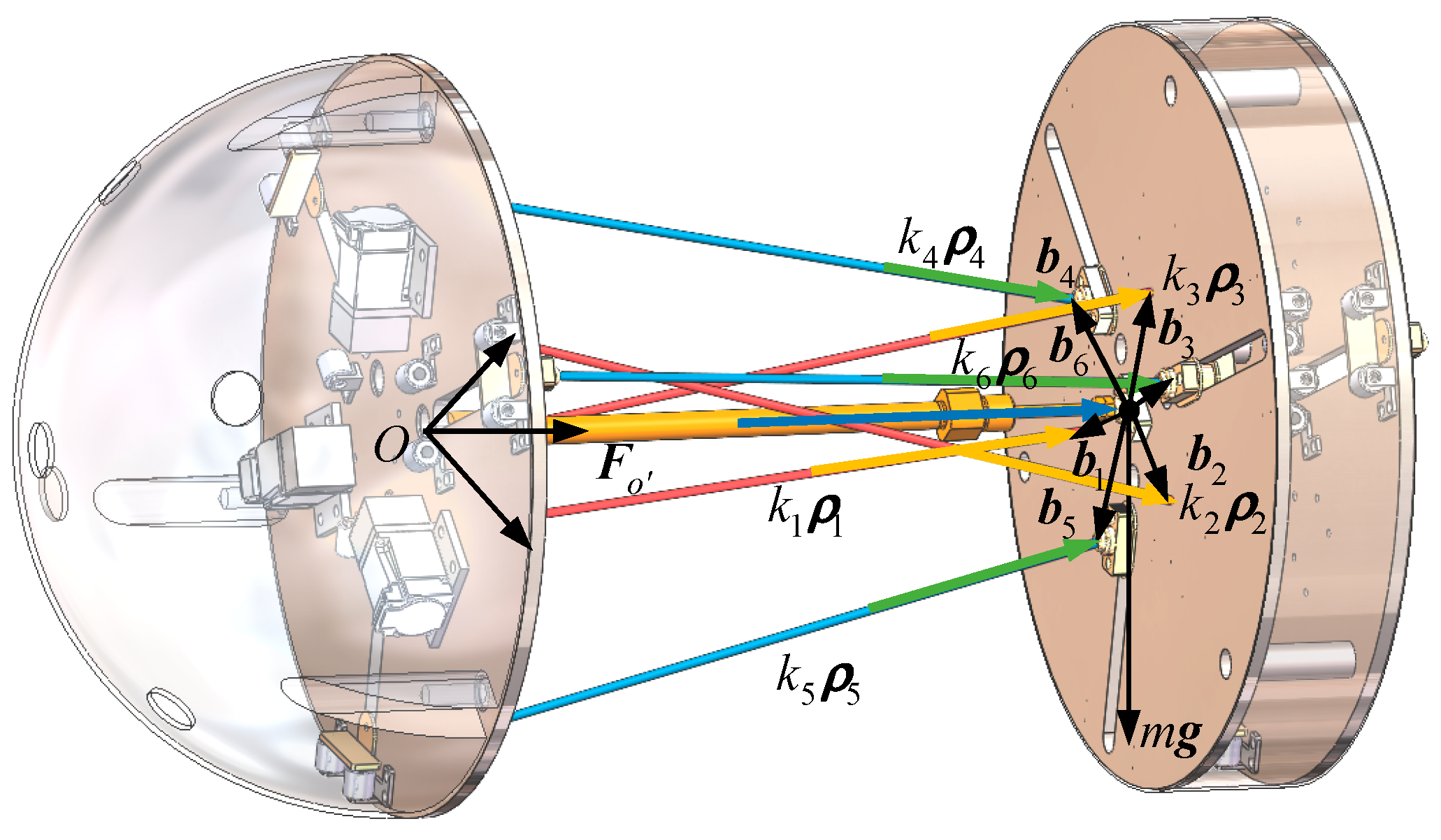
2.3. Dynamic Modeling
3. Results
4. Discussions and Conclusions
- (1)
- The process of the intersection of circles and circular rings in 2D and the corresponding algorithms are reviewed briefly. Then, the arc intersection method based on these algorithms is presented to determine robot workspace. This approach ensures that the workspace analysis accounts for both the constraints imposed by the cables and the geometric limitations introduced by the piston rod. While previous studies on 6-SPS hexapods have focused on cable-driven mechanisms without considering the central piston rod, our work extends the analysis by explicitly incorporating this critical component. This integration allows for a more comprehensive understanding of the robot’s workspace under realistic operational constraints.
- (2)
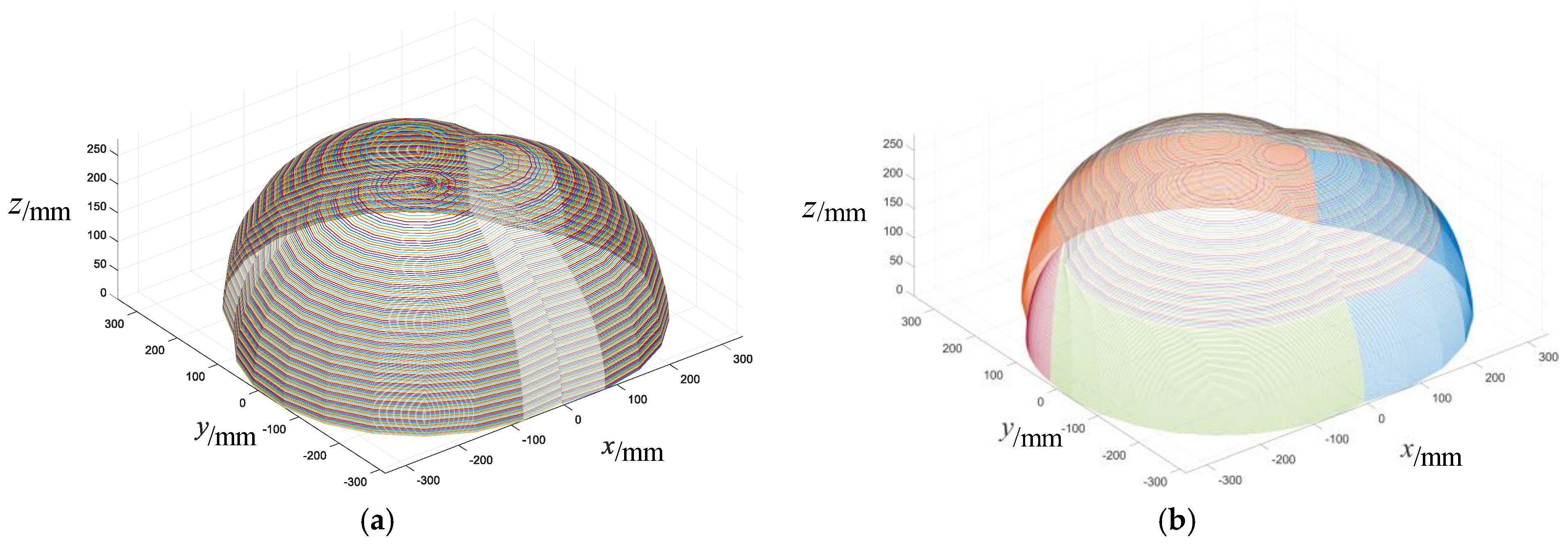
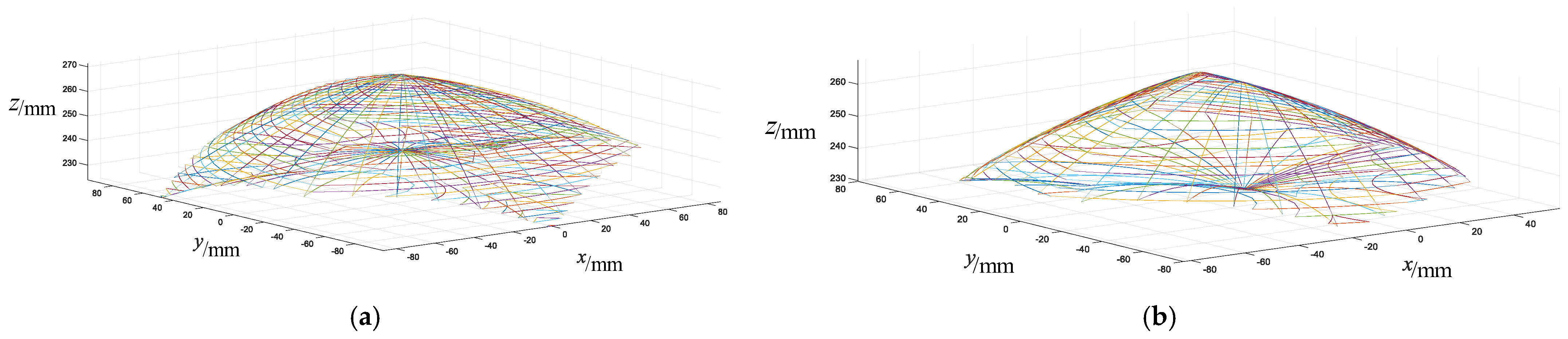
- The workspaces of different motion patterns of the cable-driven mobile robot are determined, and the maximum and minimum areas of the planar region are obtained. The prismatic and pyramidal motion patterns exhibit workspaces that are largest at z = 0 mm and smallest at z = 278 mm, with the shape of the workspace boundaries remaining unchanged as z increases. The arcs no longer intersect at z = 278 mm. For the prismatic motion pattern, the robot’s workspace spans along the z-axis from 0 mm to 278 mm, achieving a maximum planar area of 352,557.7888 mm2 at z = 0 mm and a minimum of 10,518.0522 mm2 at z = 278 mm. Similarly, the pyramidal motion pattern spans the same z-axis range, with a maximum planar area of 325,714.4087 mm2 at z = 0 mm and the same minimum area at z = 278 mm. The workspaces of the cable-driven robot with no constraint cables are presented to illustrate the function of constraint cables on robot workspaces. It is observed that in the prismatic motion pattern, the workspace along the z-axis is restricted to the range of 224 mm to 270 mm. Within this range, the maximum planar area of the workspace reaches 21,200.2824 mm2 at z = 240 mm, while the minimum area is 15.8188 mm2 at z = 224 mm. Similarly, in the pyramidal motion pattern, the workspace along the z-axis is limited to the range of 230 mm to 266 mm. The maximum planar area for this pattern is 14,859.7784 mm2 at z = 240 mm, with the minimum area being 2.7568 mm2 at z = 230 mm.
- (3)
- The dynamic model of the cable-driven mobile robot is formulated, laying the foundation for the following trajectory planning. Indeed, this dynamic model is designed to aid in trajectory planning for the robot. If natural free-motion trajectories can be identified for the dynamic model, it guarantees that these trajectories can be executed by the robot while maintaining cable tension, provided that the actuator’s torque and velocity limits are respected.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Symbols and Abbreviations
| R: O-xyz | The fixed coordinate frame attached to the fixed platform |
| R’: O’-x’y’z’ | The moving coordinate frame attached to the moving platform |
| Ai | The point of the fixed platform A from which cable i extends |
| Bi | The point of the moving platform B where cable i is attached |
| The position vectors of the joints on the base | |
| The position vectors of the joints on the moving platform | |
| Q | The position matrix of the moving platform relative to the base at the initial position |
| The position vector of the moving platform center O’ expressed in the fixed coordinate frame R | |
| is its length | |
| The force provided by the piston rod | |
| The vector of gravitational acceleration | |
| The tension in the ith cable | |
| I | The inertial tensor of the platform around O’ with respect to the moving frame R’ |
| The cable tension-to-length radio |
References
- Albus, J.; Bostelman, R.; Dagalakis, N. The NIST robocrane. J. Robot. Syst. 1993, 10, 709–724. [Google Scholar] [CrossRef]
- Cone, L.L. Skycam: An aerial robotic camera system. Byte 1985, 10, 122–132. [Google Scholar]
- Pott, A. Cable-Driven Parallel Robots: Theory and Application; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Duan, B. A new design project of the line feed structure for large spherical radio telescope and its nonlinear dynamic analysis. Mechatronics 1999, 9, 53–64. [Google Scholar] [CrossRef]
- Zi, B.; Duan, B.; Du, J.; Bao, H. Dynamic modeling and active control of a cable-suspended parallel robot. Mechatronics 2008, 18, 1–12. [Google Scholar] [CrossRef]
- Zi, B.; Qian, S. Design, Analysis and Control of Cable-Suspended Parallel Robots and Its Applications; Springer: Singapore, 2017. [Google Scholar]
- Koh, J.S.; Cho, K.J. Omega-shaped inchworm-inspired crawling robot with large-index-and-pitch (LIP) SMA spring actuators. IEEE/ASME Trans. Mechatron. 2013, 18, 419–429. [Google Scholar] [CrossRef]
- Wang, D.; Dai, J.S. Theoretical foundation of metamorphic Mechanisms and their synthesis. Chin. J. Mech. Eng. 2007, 43, 32–42. [Google Scholar] [CrossRef]
- Wang, R.; Song, Y.; Dai, J.S. Reconfigurability of the origami-inspired integrated 8R kinematotropic metamorphic mechanism and its evolved 6R and 4R mechanisms. Mech. Mach. Theory 2021, 161, 104245. [Google Scholar] [CrossRef]
- Li, P.; Han, H.; Liu, C.; Ren, B.; Wu, Q.; Xu, Z. Workspace analysis of axial offset joint based on parameterization. Robotica 2023, 41, 2882–2906. [Google Scholar] [CrossRef]
- Bibekananda, P.; Anirban, N.; Sandipan, B. Analytical determination of the optimal effective regular workspace of a 6-6 Stewart platform manipulator for a specified orientation workspace. Mech. Mach. Theory 2024, 203, 105791. [Google Scholar] [CrossRef]
- Kolte, A.M.; Ramesh, S.; Bandyopadhyay, S. Analytical derivation of singularity-free tubes in the constant-orientation workspace of 6-6 Stewart platform manipulators. Robotica 2024, 42, 3839–3866. [Google Scholar] [CrossRef]
- Andrea, M.P.; Sergio, J.P.; Antonio, G.R.; Angel Gaspar, G.R.; Alfonso Isidro, L.D.; Guillermo, R.G. A novel design for fully constrained planar Cable-Driven Parallel Robots to increase their wrench-feasible workspace. Mech. Mach. Theory 2023, 180, 105159. [Google Scholar]
- Zhao, X.; Zhao, Z.; Liu, Y.; Su, C.; Meng, J. Analysis of workspace boundary for multi-robot coordinated lifting system with rolling base. Robotica 2024, 42, 3657–3674. [Google Scholar] [CrossRef]
- Edoardo, I.; Marco, C. Static workspace computation for underactuated cable-driven parallel robots. Mech. Mach. Theory 2024, 193, 105551. [Google Scholar]
- Qian, S.; Zhao, Z.; Qian, P.; Wang, Z.; Zi, B. Research on workspace visual-based continuous switching sliding mode control for cable-driven parallel robots. Robotica 2024, 42, 1–20. [Google Scholar] [CrossRef]
- Salemo, M.; Zhang, K.; Menciassi, A.; Dai, J.S. A novel 4-DOFs origami enabled, SMA actuated, robotic end-effector for minimally invasive surgery. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–5 June 2014. [Google Scholar]
- Qin, Y.; Dai, J.S.; Gogu, G. Multi-furcation in a derivative queer-square mechanism. Mech. Mach. Theory 2014, 81, 36–53. [Google Scholar] [CrossRef]
- Yao, L.; Gu, B.; Haung, S.; Wei, G.; Dai, J.S. Mathematical modeling and simulation of the external and internal double circular-arc spiral bevel gears for the nutation drive. ASME J. Mech. Des. 2010, 132, 021008. [Google Scholar] [CrossRef]
- Huo, X.; Song, Z.; Sun, T. A machine learning-based approach for automatic motion/constraint and mobility analysis of parallel robots. Robotica 2024, 42, 2403–2429. [Google Scholar] [CrossRef]
- Gao, C.; Kang, X.; Lei, H.; Xu, P.; Li, B. Design and analysis of a novel large-span two-fold deployable mechanism. Mech. Mach. Theory 2023, 186, 105352. [Google Scholar] [CrossRef]
- Zhang, X.; Kang, X.; Li, B. Origami-inspired design of a single-degree-of-freedom reconfigurable wing with lockable mechanisms. ASME J. Mech. Robot. 2024, 16, 071008. [Google Scholar] [CrossRef]
- Gouttefarde, M.; Daney, D.; Merlet, J.P. Interval-analysis-based determination of the wrench-feasible workspace of parallel cable-driven robots. IEEE Trans. Robot. 2011, 27, 1–13. [Google Scholar] [CrossRef]
- Jaulin, L.; Kieffer, M.; Didrit, O.; Walter, E. Applied Interval Analysis; Springer: London, UK, 2001. [Google Scholar]
- Neumaier, A. Interval Methods for Systems of Equations; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Gosselin, C. Determination of the workspace of 6-DOF parallel manipulators. ASME J. Mech. Des. 1990, 112, 331–336. [Google Scholar] [CrossRef]
- Gosselin, C.; Angeles, J. The optimum kinematic design of a spherical three-degree-of-freedom parallel manipulator. ASME J. Mech. Trans. Autom. 1989, 111, 202–207. [Google Scholar] [CrossRef]
- Spyrakos-Papastavidis, E.; Dai, J.S. Minimally model-based trajectory tracking and variable impedance control of flexible-joint robots. IEEE Trans. Ind. Electron. 2020, 68, 6031–6041. [Google Scholar] [CrossRef]
- Dai, J.S.; Zoppi, M.; Kong, X. Advances in Reconfigurable Mechanisms and Robots I; Springer: London, UK, 2012. [Google Scholar]
- Kang, X.; Lin, Q.; Feng, H.; Li, B. Double-level reconfigurable variation of Bennett-induced 8R mechanism and its evolved metamorphic 7R mechanism family. Mech. Mach. Theory 2025, 205, 105879. [Google Scholar] [CrossRef]
- Zhang, X.; Kang, X.; Li, B. Development and investigation for rigid-flexible coupling dynamic performances of the morphing wing with clearance joints. Mech. Syst. Signal Process. 2025, 223, 111871. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, W.; Kang, X.; Li, B. Design, analysis, and experimentation of deployable multi-closed-loop truss modules for aerospace platforms. Mech. Mach. Theory 2025, 205, 105897. [Google Scholar] [CrossRef]
- Zhang, Y.; Kang, X.; Li, B. A family of folding single-loop metamorphic mechanisms for aerospace manipulators: Synthesis, network, and analysis. Mech. Mach. Theory 2024, 201, 105728. [Google Scholar] [CrossRef]
- Wang, S.; Huang, H.; Jia, G.; Li, B.; Guo, H.; Liu, R. Design of a novel three-limb deployable mechanism with mobility bifurcation. Mech. Mach. Theory 2022, 172, 104789. [Google Scholar] [CrossRef]
- Jia, G.; Huang, H.; Wang, S.; Li, B. Type synthesis of plane-symmetric deployable grasping parallel mechanisms using constraint force parallelogram law. Mech. Mach. Theory 2021, 161, 104330. [Google Scholar] [CrossRef]
- Jia, G.; Li, B.; Huang, H.; Zhang, D. Type synthesis of metamorphic mechanisms with scissor-like linkage based on different kinds of connecting pairs. Mech. Mach. Theory 2020, 151, 103848. [Google Scholar] [CrossRef]
- Feng, H.; Peng, R.; Zang, S.; Ma, J.; Chen, Y. Rigid foldability and mountain-valley crease assignments of square-twist origami pattern. Mech. Mach. Theory 2020, 152, 103947. [Google Scholar] [CrossRef]
- Ma, J.; Zang, S.; Feng, H.; Chen, Y.; You, Z. Theoretical characterization of a non-rigid-foldable square-twist origami for property programmability. Int. J. Mech. Sci. 2021, 189, 105981. [Google Scholar] [CrossRef]
- Ye, S.; Zhao, P.; Zhao, Y.; Kavousi, F.; Feng, H.; Hao, G. A novel radially closable tubular origami structure (RC-ori) for valves. Actuators 2022, 11, 243. [Google Scholar] [CrossRef]
- Huo, X.; Lian, B.; Wang, P.; Song, Y.; Sun, T. Dynamic identification of a tracking parallel mechanism. Mech. Mach. Theory 2020, 155, 104091. [Google Scholar] [CrossRef]
- Huo, X.; Sun, T.; Song, Y. Geometric algebra approach to determine motion/constraint, mobility and dingularity of parallel mechanism. Mech. Mach. Theory 2017, 116, 273–293. [Google Scholar] [CrossRef]
- Song, Y.; Kang, X.; Dai, J.S. Instantaneous mobility analysis using the twist space intersection approach for parallel mechanisms. Mech. Mach. Theory 2020, 151, 103866. [Google Scholar] [CrossRef]
- Qi, J.; Zhang, J.; Yang, F.; Song, Y. Kinematic modeling of 3D clearance in revolute joint and its application in overconstrained linkages. In Proceedings of the Advances in Mechanism, Machine Science and Engineering in China, Yantai, China, 30 July–1 August 2022. [Google Scholar]
- Chen, Z.; An, K.; Wang, Z.; Miao, T.; Song, Y.; Shangguan, Q. Dynamic optimization of mechanism parameters of bipedal robot considering full-range walking energy efficiency. Appl. Sci. 2023, 13, 10791. [Google Scholar] [CrossRef]
- Song, J.; Yang, S.; Zhang, Y.; Fang, Z.; Zou, T. Type synthesis of closed-loop robots for machining and manufacturing of complex quadric surfaces. Robotica 2025, 1–29. [Google Scholar] [CrossRef]
- Song, J.; Zou, T.; Liu, Q.; Wu, J.; Yang, S.; Zhang, Y. The conceptual design of multi-pattern cable-driven hybrid robot. In Proceedings of the 2025 International Conference on Mechanical Design (ICMD), Hangzhou, China, 9–11 May 2025; in press. [Google Scholar]
- Xue, F.; Fang, Z.; Song, J.; Liu, Q.; Yang, S. A new method for displacement modelling of serial robots using finite screw. Machines 2024, 12, 658. [Google Scholar] [CrossRef]

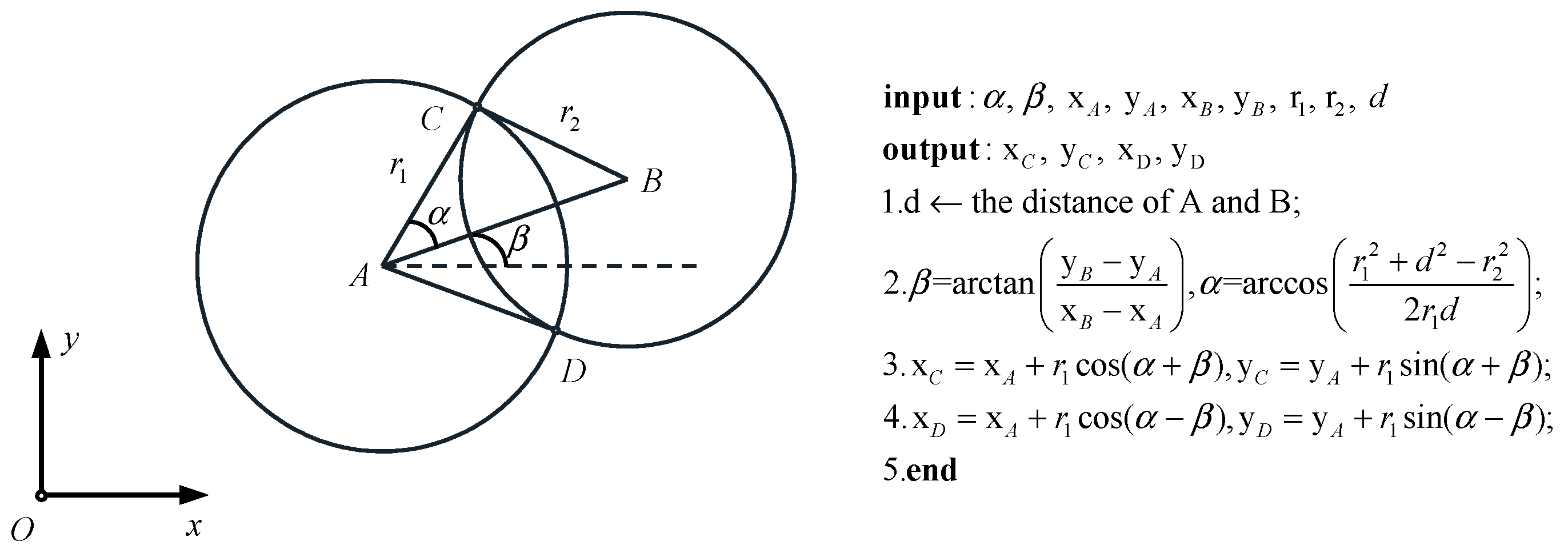

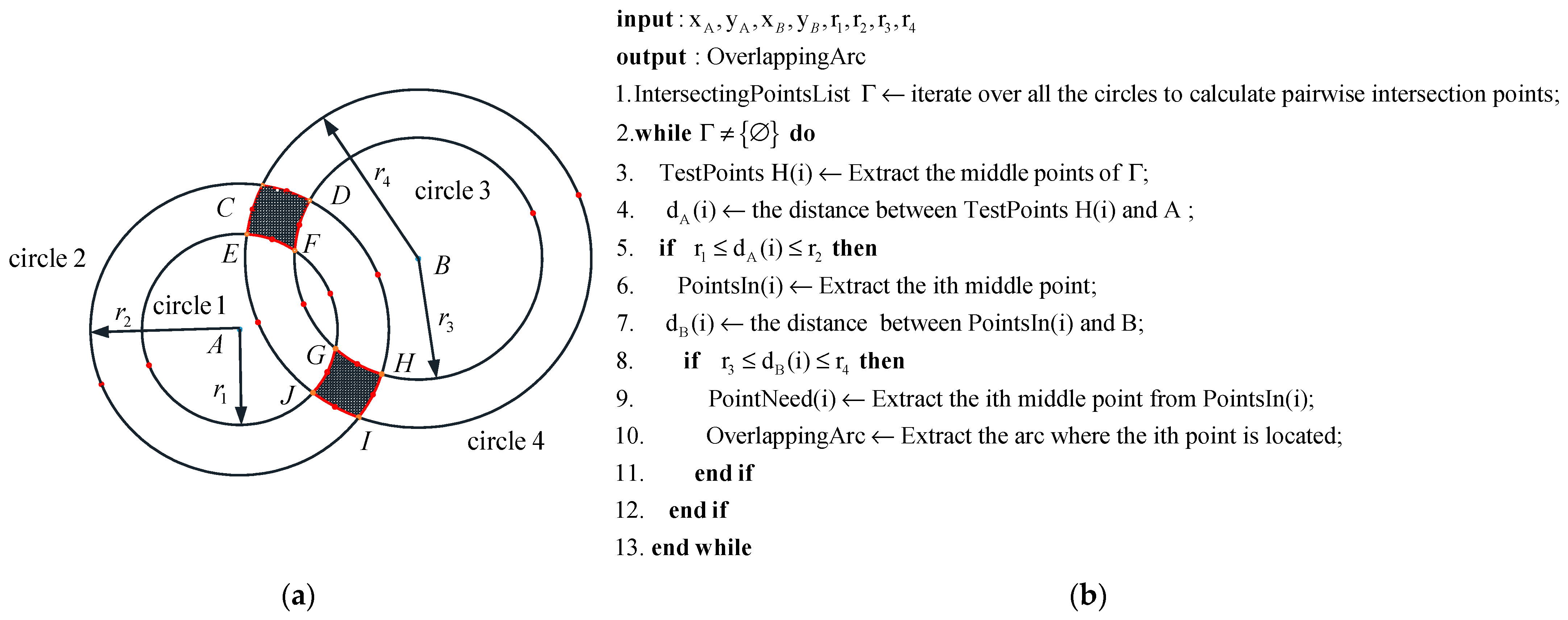

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, J.; Wang, M.; Wu, J.; Liu, Q.; Yang, S. Workspace Analysis and Dynamic Modeling of 6-DoF Multi-Pattern Cable-Driven Hybrid Mobile Robot. Machines 2025, 13, 659. https://doi.org/10.3390/machines13080659
Song J, Wang M, Wu J, Liu Q, Yang S. Workspace Analysis and Dynamic Modeling of 6-DoF Multi-Pattern Cable-Driven Hybrid Mobile Robot. Machines. 2025; 13(8):659. https://doi.org/10.3390/machines13080659
Chicago/Turabian StyleSong, Jiahao, Meiqi Wang, Jiabao Wu, Qing Liu, and Shuofei Yang. 2025. "Workspace Analysis and Dynamic Modeling of 6-DoF Multi-Pattern Cable-Driven Hybrid Mobile Robot" Machines 13, no. 8: 659. https://doi.org/10.3390/machines13080659
APA StyleSong, J., Wang, M., Wu, J., Liu, Q., & Yang, S. (2025). Workspace Analysis and Dynamic Modeling of 6-DoF Multi-Pattern Cable-Driven Hybrid Mobile Robot. Machines, 13(8), 659. https://doi.org/10.3390/machines13080659





