A Novel Flow Characteristic Regulation Method for Two-Stage Proportional Valves Based on Variable-Gain Feedback Grooves
Abstract
1. Introduction
- (1)
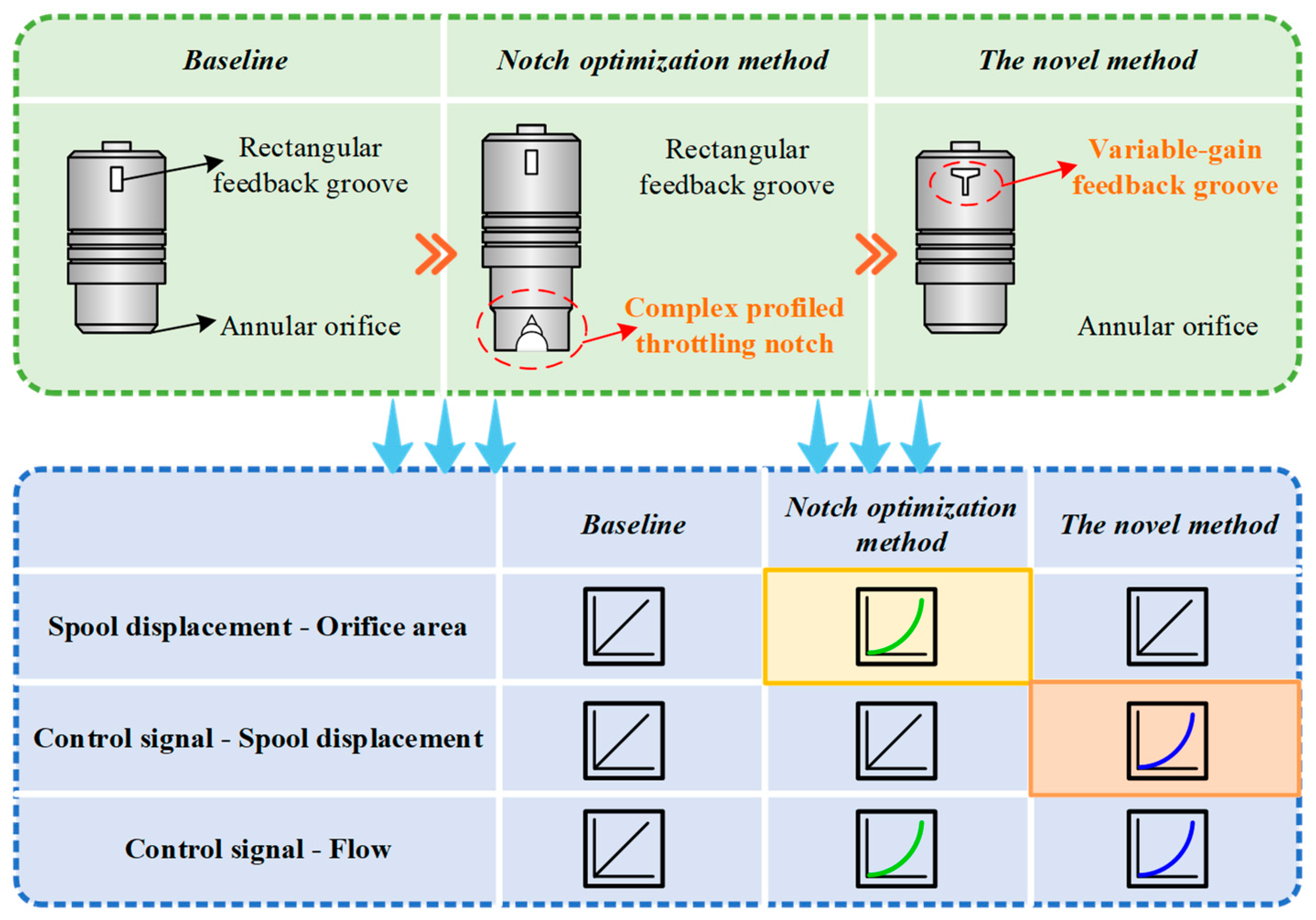
- Insufficient research on flow characteristic regulation based on pilot–main valve mapping: Existing studies rarely optimize flow characteristics by leveraging this core mapping relationship in two-stage proportional valves.
- (2)
- Limitations of notch optimization methods: Although complex-shaped throttling notches improve micro-motion performance, they are limited by their high manufacturing cost and difficulty. These designs increase pressure loss, energy consumption, and cavitation risks. In particular, for Valvistor valves with cone structures, machining complex notches is more challenging than for spool valves and increases the main valve stroke, thereby degrading dynamic response.
- (3)
- Cost and complexity of active pressure difference regulation: This approach necessitates additional electromechanical components, which significantly increases system cost and structural complexity.
2. Working Mechanism
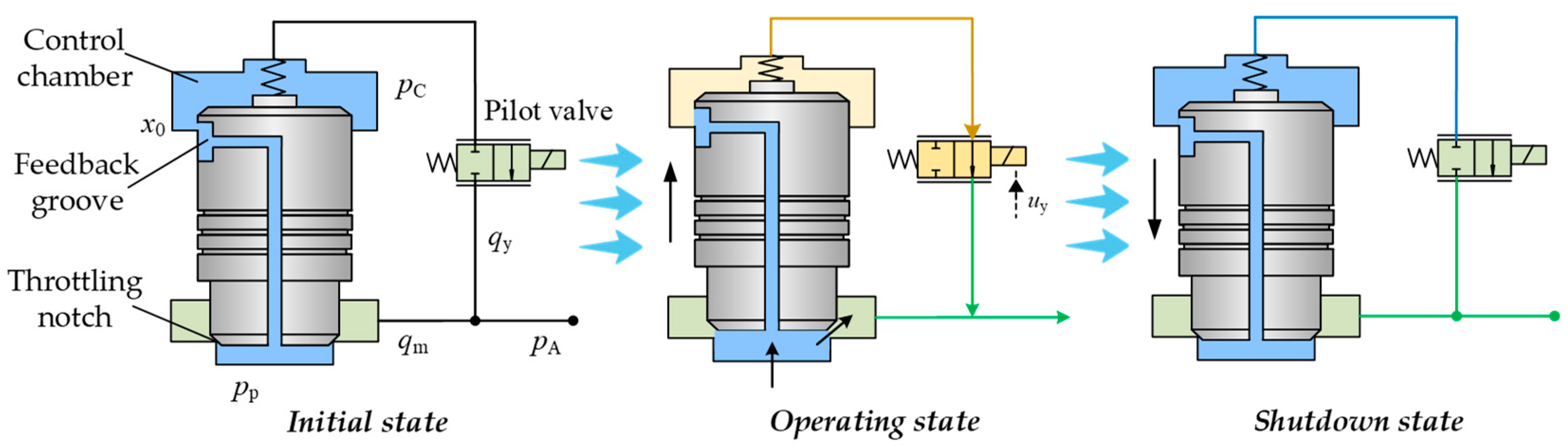
2.1. Working Principle of the Two-Stage Proportional Valve
- (1)
- Initial state:
- (2)
- Operating state:
- (3)
- Shutdown state:
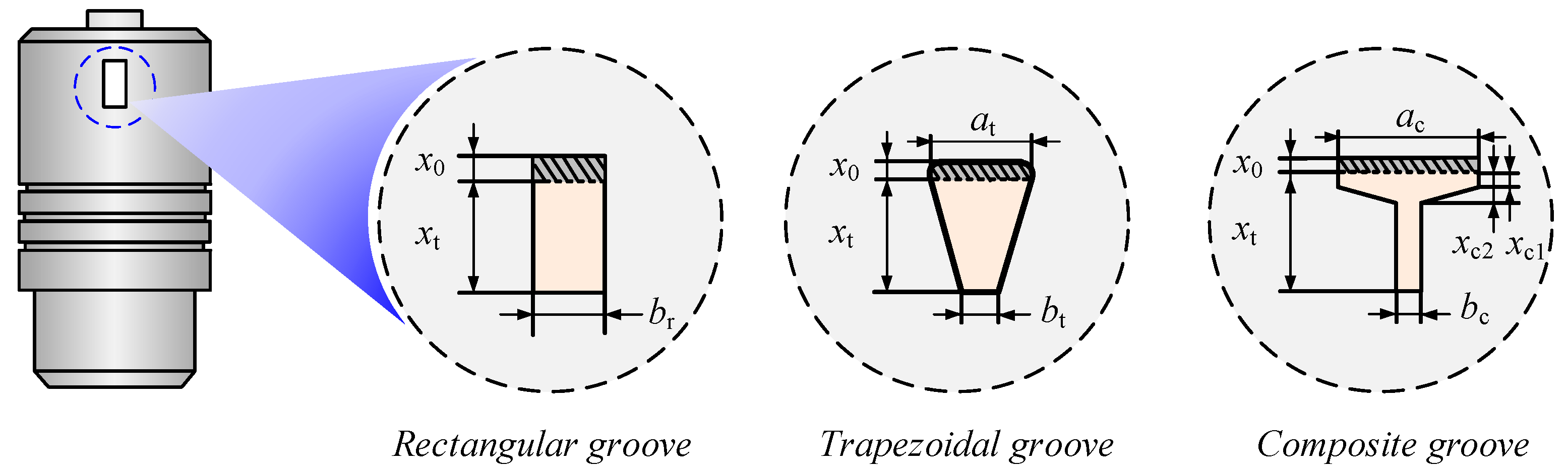
2.2. Design of the Variable-Gain Feedback Groove
- (1)
- Trapezoidal groove: Features pre-opening length x0 (shaded area). Initial area gain exceeds terminal gain bt, with height xt. High initial gain promotes smooth actuator starting. As spool displacement increases, area gain decreases while displacement gain rises.
- (2)
- Composite groove: Combines two rectangles with different widths connected by a trapezoidal transition. The pre-opening of the composite groove is represented by x0, and the region from xc1 to xc2 serves as the transition zone. Pre-transition area gain ac exceeds post-transition gain bc. This configuration enables segmented flow control: the pre-transition zone optimizes fine control, while the post-transition zone provides rapid actuation with high flow gains.
3. Mechanism of Feedback Groove Flow Regulation
3.1. Static Mathematical Model of the Two-Stage Proportional Valve
3.2. Mathematical Model of Variable-Gain Feedback Grooves
3.2.1. Trapezoidal Feedback Groove
3.2.2. Composite Feedback Groove
3.3. Dynamic Mathematical Model of the Two-Stage Proportional Valve
4. Simulation
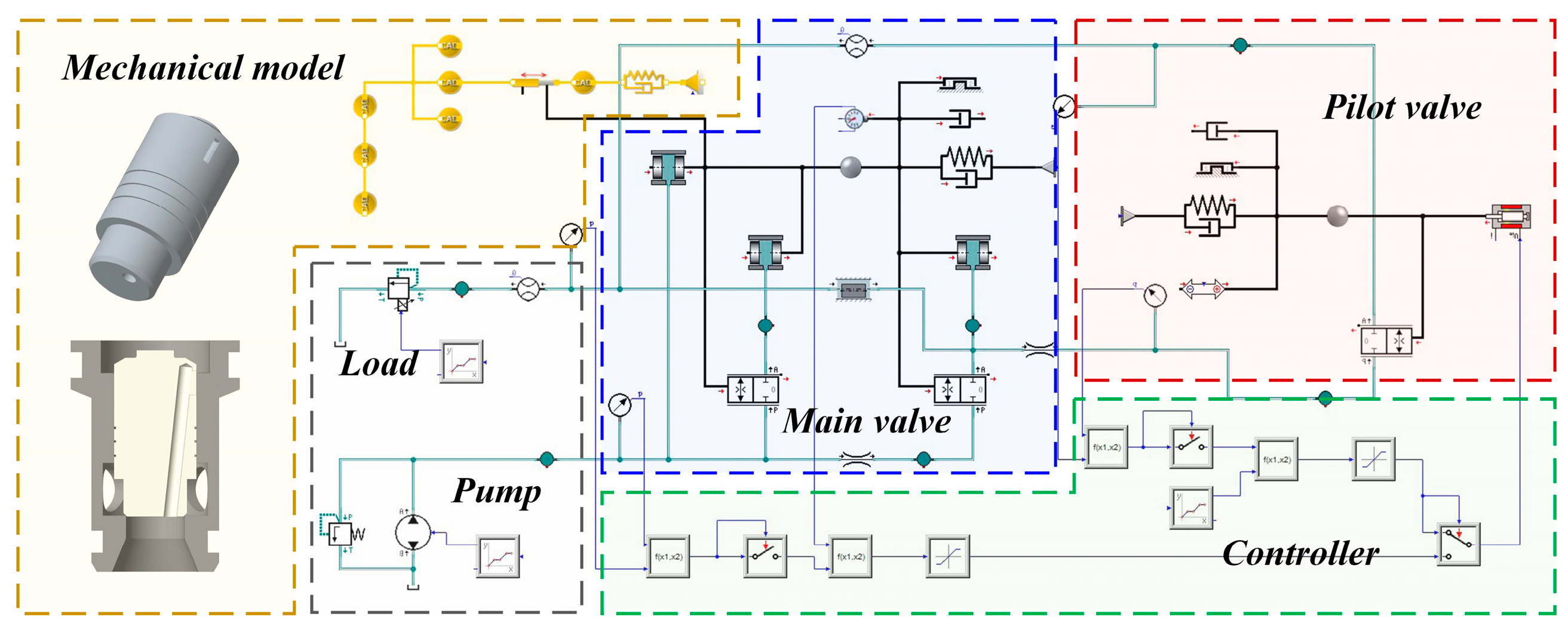
4.1. Modeling
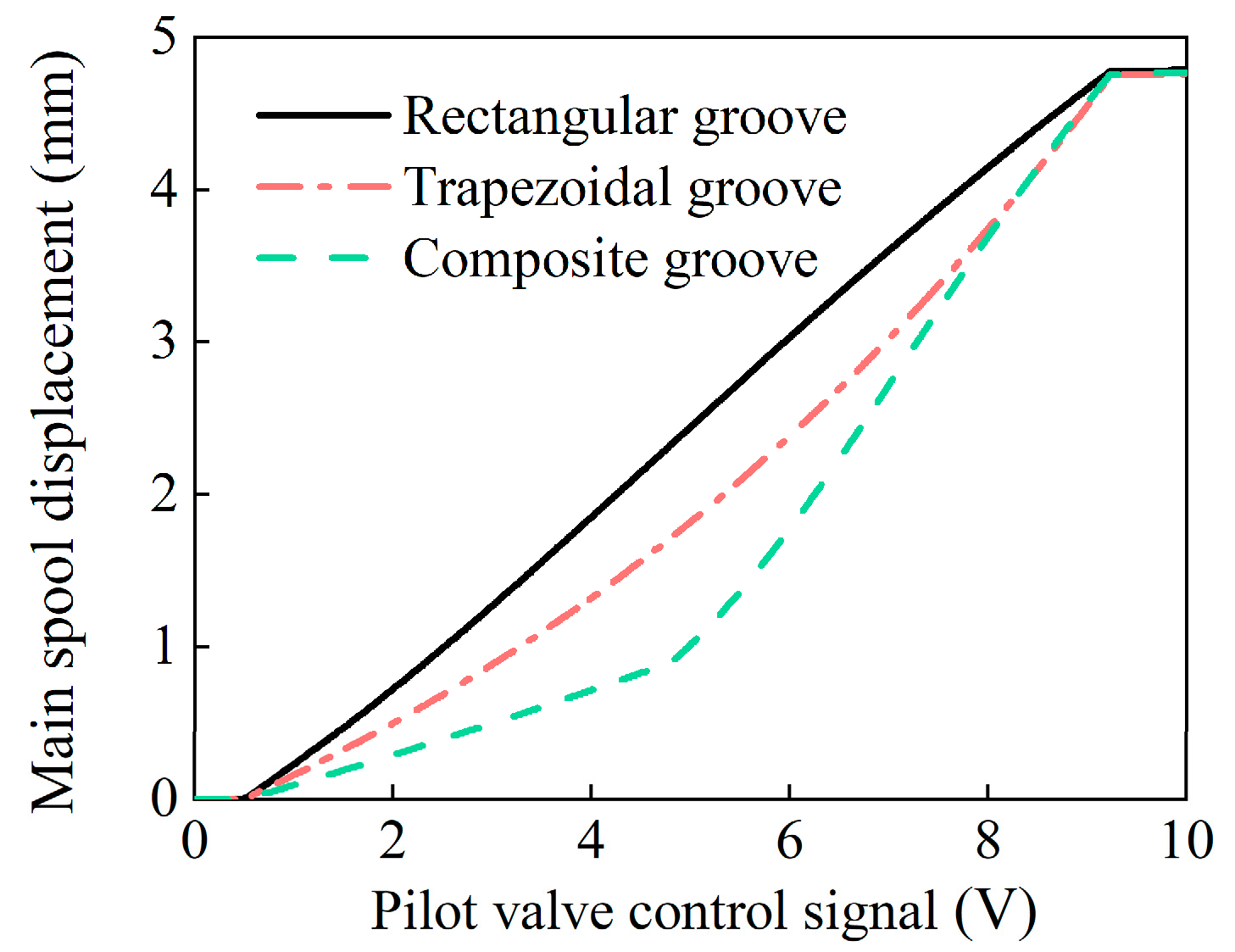
4.2. Displacement Characteristics of Variable-Gain Feedback Groove Valves
4.3. Flow Characteristics of Variable-Gain Feedback Groove Valves
4.4. Dynamic Characteristics of Variable-Gain Feedback Groove Valves
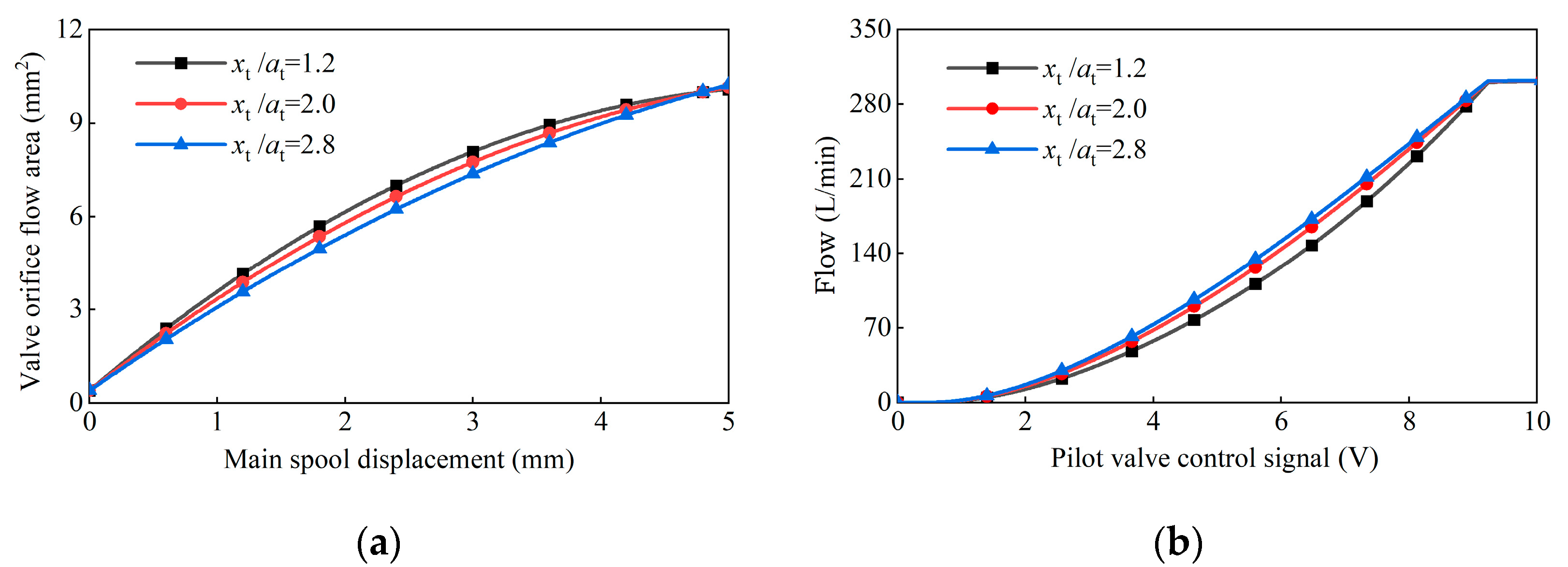
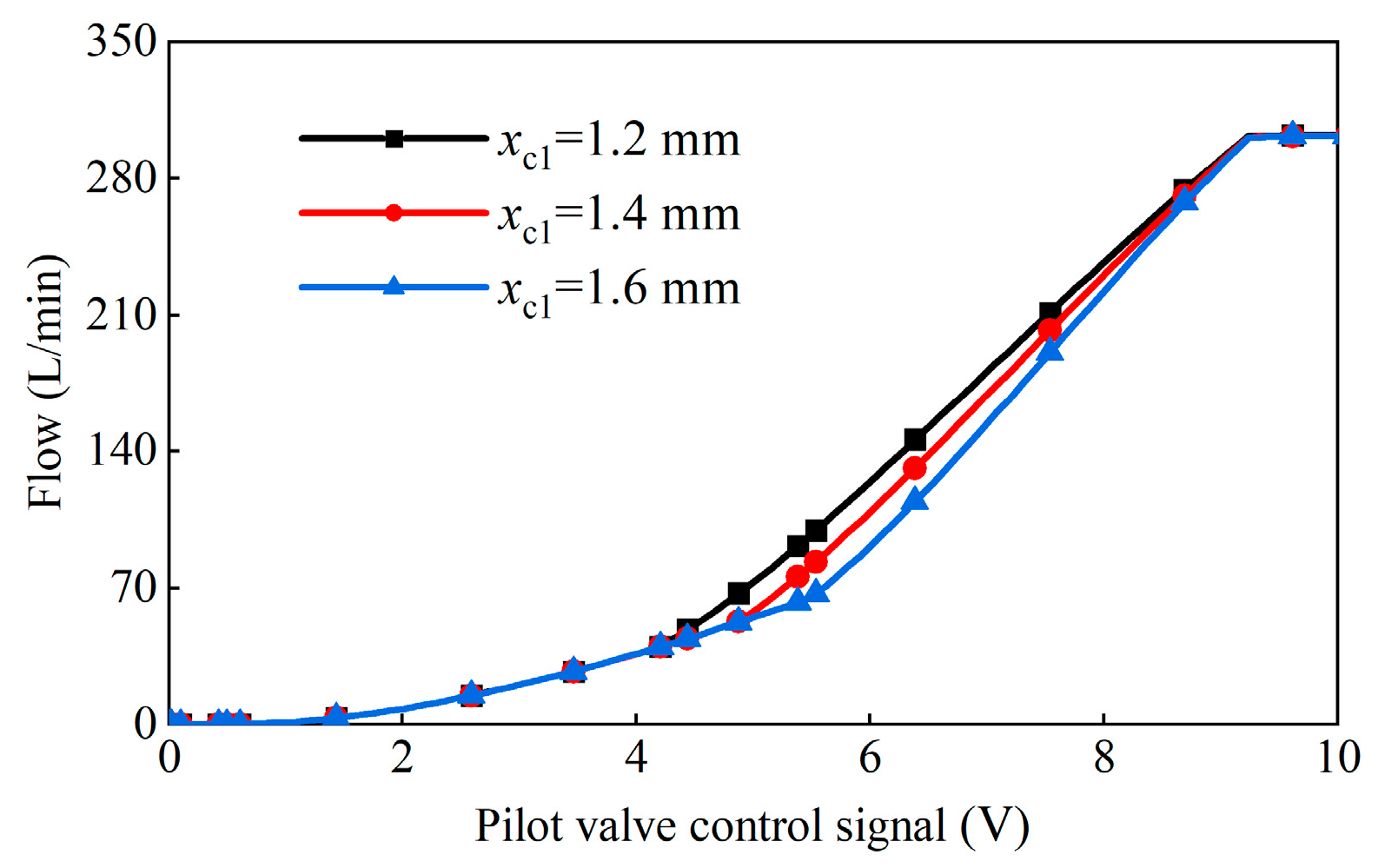
4.5. Influence of Feedback Groove Parameters on Flow Characteristics
4.5.1. Trapezoidal Feedback Groove Parameters
4.5.2. Composite Feedback Groove Parameters
5. Experiment
5.1. Developed Variable-Gain Feedback Groove Spools
5.2. Experimental Platform Setup
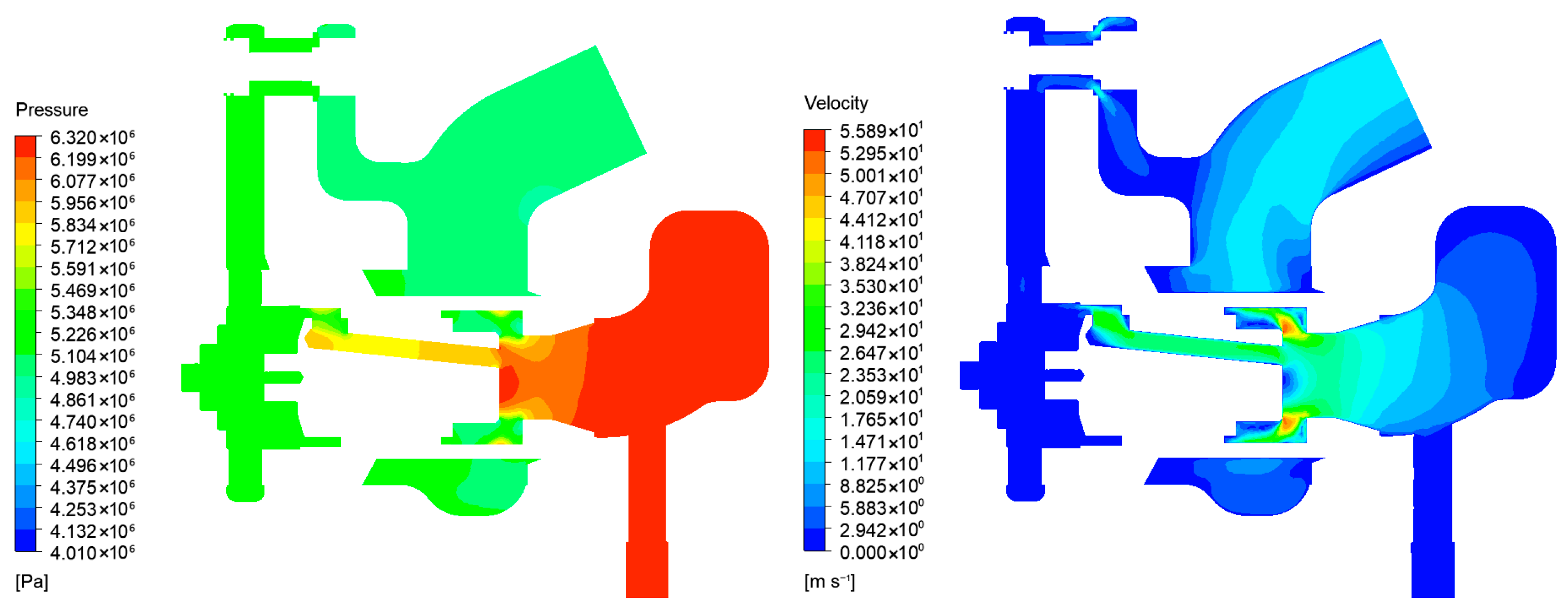
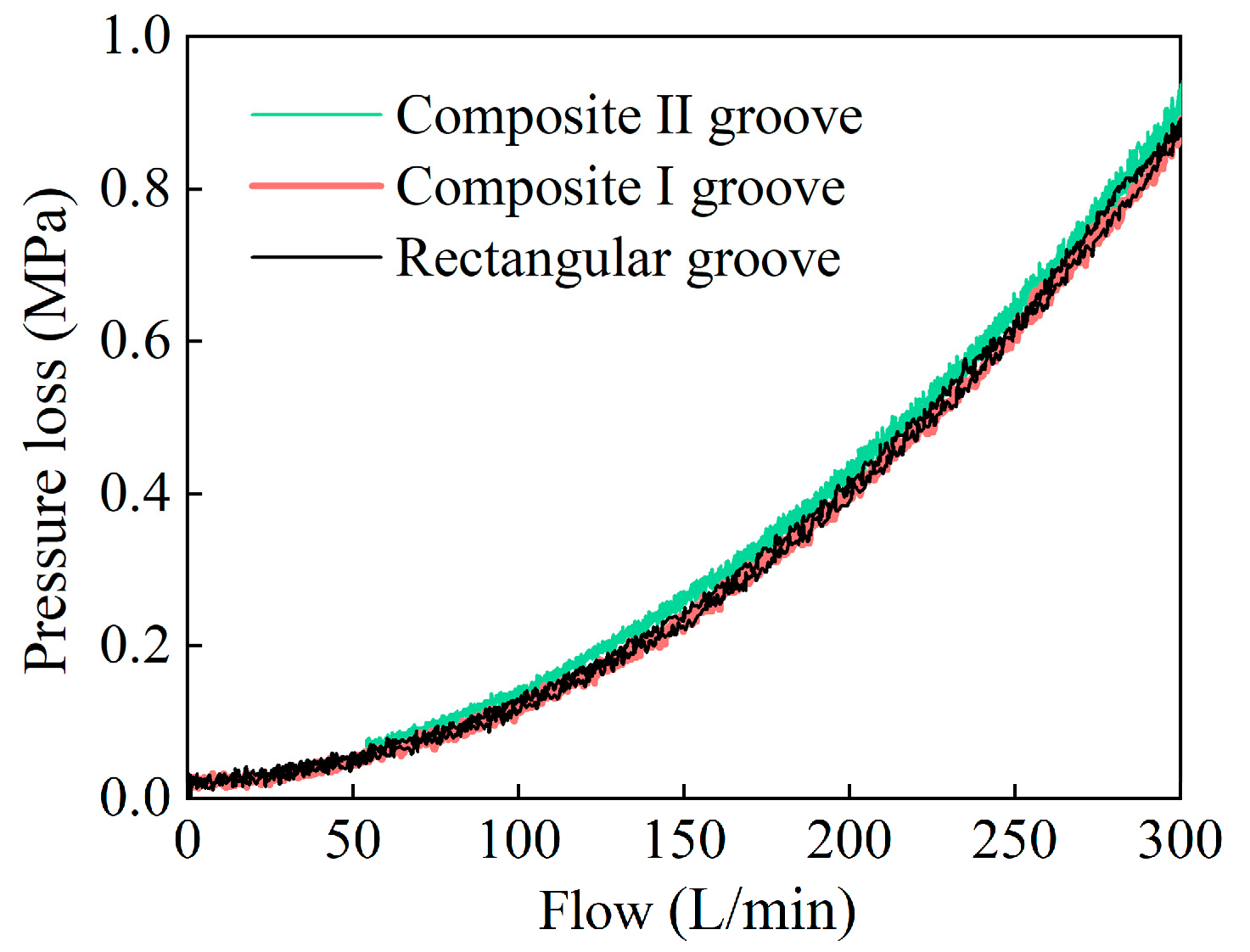
5.3. Pressure Loss Characteristics
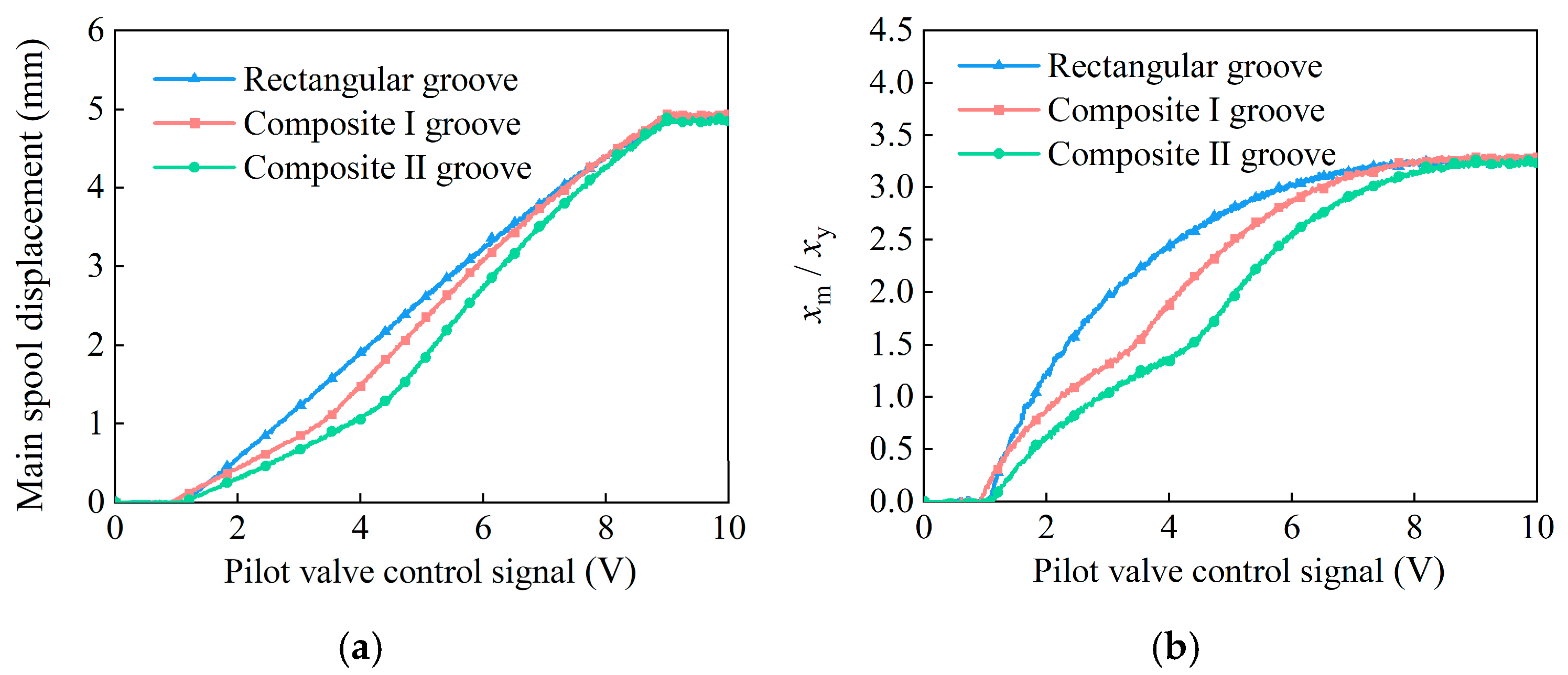
5.4. Experimental Study on Main Spool Displacement Characteristics
5.5. Experimental Study on Flow Characteristics
- Composite I feedback groove: Micro-motion: 1.1–3.5 V; rapid actuation: 3.5–8.9 V.
- Composite II feedback groove: Micro-motion: 1.1–4.4 V; rapid actuation: 4.4–8.9 V.
6. Discussion
6.1. Uncertainty Evaluation
6.2. Benchmarking Against Commercially Available Products
7. Conclusions
- (1)
- Mathematical modeling reveals the core mechanism: variable-gain feedback grooves dynamically adjust the pilot-to-main valve mapping relationship. By modifying groove geometry and area gain characteristics, spool displacement mapping is reconfigured to achieve target signal-flow characteristic curves.
- (2)
- Two groove profiles are designed: trapezoidal and composite. Simulations show that conventional rectangular grooves produce near-linear flow rate vs. signal relationships; trapezoidal grooves exhibit monotonically increasing flow rate gain; composite grooves generate dual-regime curves with distinct linear regions before/after transition points. Moreover, larger feedback groove area gains improve main spool response speed.
- (3)
- Prototypes with composite grooves are developed for construction machinery applications. Experiments confirm that the feedback groove effectively regulates flow characteristics. The pilot–main mapping relationship is inversely proportional to the groove area gain: higher gain enhances micro-motion control for minute flows; lower gain increases main valve flow gain, enabling rapid actuation.
- (4)
- Comparative experiments show the composite-groove spool achieves segmented flow characteristics (micro-motion and rapid actuation regions). Its flow gain in the micro-motion region (2.04 L/(min·0.1 V)) is 61.9% lower than that of conventional rectangular grooves, effectively improving micro-motion performance.
- (5)
- Parametric studies confirm that adjusting the groove’s area gain and transition point flexibly tunes flow gain magnitude and micro-motion region length. Additionally, the variable-gain feedback groove method does not significantly increase the valve’s pressure loss or energy consumption; the pressure loss of the developed two-stage proportional valve is only 0.88 MPa (at 300 L/min rated flow).
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jiao, Z.; Wu, S.; Li, Y.; Zhang, C.; Jin, H.; Shu, S.; Wei, R.; Li, R.; Wang, Y.; Zhang, H. Development Status and Trends of the Intelligence of Hydraulic Components and Systems. J. Mech. Eng. 2023, 59, 357–384. [Google Scholar]
- Zhong, Q.; Wang, J.; Xu, E.; Yu, C.; Li, Y. Multi-objective optimization of a high speed on/off valve for dynamic performance improvement and volume minimization. Chin. J. Aeronaut. 2024, 37, 435–444. [Google Scholar] [CrossRef]
- Tamburrano, P.; Plummer, A.; Distaso, E.; Amirante, R. A review of direct drive proportional electrohydraulic spool valves: Industrial state-of-the-art and research advancements. J. Dyn. Syst. Meas. Control 2019, 141, 020801. [Google Scholar] [CrossRef]
- Li, Y.; Li, R.; Yang, J.; Yu, X.; Xu, J. Review of Recent Advances in the Drive Method of Hydraulic Control Valve. Processes 2023, 11, 2537. [Google Scholar] [CrossRef]
- Xie, H.; Wang, C.; Yang, H. Research on back-pressure compensation characteristics of a pilot-assisted load control valve applied in overrunning load hydraulic systems. Flow Meas. Instrum. 2021, 82, 102048. [Google Scholar] [CrossRef]
- Suzuki, K.; Urata, E. Development of a water hydraulic pressure-compensated flow control valve. Int. J. Fluid Power 2008, 9, 25–33. [Google Scholar] [CrossRef]
- Park, Y.; Kim, B.; Jeon, J.; Jung, D.; Choi, S. The Effect of Spool Displacement Control to the Flow Rate in the Piezoelectric Stack-Based Valve System Subjected to High Operating Temperature. Actuators 2021, 10, 239. [Google Scholar] [CrossRef]
- Liu, J.; Sitte, A.; Weber, J. Investigation of temperature influence on flow mapping of electrohydraulic valves and corresponding application. Fluid Power Syst. Technol. ASME 2022, 86335, V001T01A022. [Google Scholar]
- Liu, H.; Quan, L.; Zhao, X.; Ge, L.; Xia, L. Research on Displacement and Flow Control Characteristics of the Proportional Directional Valve Based on a Flow Feedback Mechanism. IEEE/ASME Trans. Mechatron. 2025. [Google Scholar] [CrossRef]
- Zhao, R.; Chai, W.; Zhang, Y.; Yuan, X.; Lian, Z.; Shi, H. Dynamics and experimental study of a novel proportional directional valve with displacement feedback groove controlled by high-speed switching valves. Flow Meas. Instrum. 2024, 100, 102711. [Google Scholar] [CrossRef]
- Huang, J.; Wang, X.; Wang, H.; Hao, H. Development of a flow control valve with digital flow compensator. Flow. Meas. Instrum. 2019, 66, 157–169. [Google Scholar] [CrossRef]
- Hao, Y.; Quan, L.; Huang, J. Research on the performance of electro-hydraulic proportional flow valve controlled by active pilot pump. Proc. Inst. Mech. Eng. E J. Process Mech. Eng. 2017, 231, 720–731. [Google Scholar] [CrossRef]
- Xu, B.; Shen, J.; Liu, S.; Qi, S.; Zhang, J. Research and development of electro-hydraulic control valves oriented to industry 4.0: A review. Chin. J. Mech. Eng. 2020, 33, 1–20. [Google Scholar] [CrossRef]
- Ding, R.; Yan, P.; Cheng, M.; Xu, B. A flow inferential measurement of the independent metering multi-way valve based on an improved RBF neural network. Measurement 2023, 223, 113750. [Google Scholar] [CrossRef]
- Lu, L.; Yao, B. Energy-saving adaptive robust control of a hydraulic manipulator using five cartridge valves with an accumulator. IEEE Trans. Ind. Electron. 2014, 61, 7046–7054. [Google Scholar] [CrossRef]
- Muniak, D. Sizing the radiator control valve taking account of inner authority. Procedia Eng. 2016, 157, 98–105. [Google Scholar] [CrossRef]
- Hucko, S.; Krampe, H.; Schmitz, K. Evaluation of a soft sensor concept for indirect flow rate estimation in solenoid-operated spool valves. Actuators 2023, 12, 148. [Google Scholar] [CrossRef]
- Jian, H.; Du, M.; Gu, H. Modeling and bifurcation analysis of a hydraulic actuator system with different valve spool geometry. Adv. Mech. Eng. 2022, 14, 16878132221118439. [Google Scholar] [CrossRef]
- Ye, Y.; Yin, C.; Li, X.; Zhou, W.; Yuan, F. Effects of groove shape of notch on the flow characteristics of spool valve. Energy Convers. Manag. 2014, 86, 1091–1101. [Google Scholar] [CrossRef]
- Ye, Y.; Yin, C.; Liu, H.; Zou, G.; Jiang, X. Stationary Flow Characteristics of Notches on Throttling Grooves. Trans. Chin. Soc. Agric. Mach. 2014, 45, 308–316. [Google Scholar]
- Pan, X.; Wang, G.; Lu, Z. Flow field simulation and a flow model of servo-valve spool valve orifice. Energy Convers. Manag. 2011, 52, 3249–3256. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, A.; Chen, W.; Kuang, L.; Jiang, T. Methodology for expressing the flow coefficients of coupled throttling grooves in a proportional—Directional valve. J. Zhejiang Univ.-Sci. A 2020, 21, 799–816. [Google Scholar] [CrossRef]
- Muniak, D. Control valve with a constant inner authority value. J. Therm. Sci. 2018, 27, 487–495. [Google Scholar] [CrossRef]
- Muniak, D. A new methodology to determine the pre-setting of the control valve in a heating installation. Appl. Energy 2014, 135, 35–42. [Google Scholar] [CrossRef]
- Borghi, M.; Milani, M.; Paoluzzi, R. Influence of Notch Shape and Number of Notches on the Metering Characteristics of Hydraulic Spool Valves. Int. J. Fluid Power 2005, 6, 5–18. [Google Scholar] [CrossRef]
- Li, S.; Du, J.; Shi, Z.; Xu, K.; Shi, W. Characteristics Analysis of the Pilot-Operated Proportional Directional Valve by Experimental and Numerical Investigation. Energies 2022, 15, 9418. [Google Scholar] [CrossRef]
- Qian, J.; Hou, C.; Mu, J.; Gao, Z.; Jin, Z. Valve core shapes analysis on flux through control valves innuclear power plants. Nucl. Eng. Technol. 2020, 52, 2173–2182. [Google Scholar] [CrossRef]
- Yuan, S.; Yin, C.; Ye, Y.; Liu, S. Studies on the Throttling Performance of Non-circumferential Throttling Port. Trans. Chin. Soc. Agric. Mach. 2014, 45, 321–327. [Google Scholar]
- Kong, X.; Song, Y.; Ai, C.; Hu, J.; Xia, Q. Visualization Experiment of Flow Characteristics of Special Shaped Valve Port in Proportional Valve Using PIV Technology. Trans. Chin. Soc. Agric. Mach. 2015, 46, 328–335. [Google Scholar]
- Qiu, T.; Yang, L.; Zhang, J.; Wang, Z.; Song, Y.; Ai, C. Investigation of Valve Seat Cone Angle on Small Opening Direct-Acting Relief Valve Cavitation Noise. Machines 2024, 12, 434. [Google Scholar] [CrossRef]
- Ji, H.; Fu, X.; Yang, H. Study on steady flow force of non-circular opening spool valve. J. Mech. Eng. 2003, 6, 13–17. [Google Scholar] [CrossRef]
- Simic, M.; Herakovic, N. Reduction of the flow forces in a small hydraulic seat valve as alternative approach to improve the valve characteristics. Energy Convers. Manag. 2015, 89, 708–718. [Google Scholar] [CrossRef]
- Shangguan, S.; Duan, H.; Li, R.; Yuan, W.; Chen, L.; Wang, Z.; Chen, H. Study on the flow field and steady-state hydrodynamics of a sliding valve with a sloping U-shaped throttle groove. Flow Meas. Instrum. 2025, 104, 102886. [Google Scholar] [CrossRef]
- Yuan, C.; Zhu, L.; Du, Z.; Liu, S. Numerical investigation into the cavitating jet inside water poppet valves with varied valve seat structures. Eng. Appl. Comput. Fluid Mech. 2021, 15, 391–412. [Google Scholar] [CrossRef]
- Frosina, E.; Marinaro, G.; Amoresano, A.; Senatore, A. A numerical and experimental methodology to characterize the gaseous cavitation in spool valves with U-notches. J. Fluids Eng. 2021, 143, 101401. [Google Scholar] [CrossRef]
- Zou, J.; Fu, X.; Du, X.; Ruan, X.; Ji, H.; Ryu, S.; Ochiai, M. Cavitation in a non-circular opening spool valve with U-grooves. Proc. Instn. Mech. Eng. A J. Power Energy 2008, 222, 413–420. [Google Scholar] [CrossRef]
- Jia, W.; Liu, Y.; Yin, C.; Li, G.; Zhu, D.; Ding, S. Effects of U-shaped two-step throttling groove parameters on cavitation erosion characteristics. J. Theor. Appl. Mech. 2021, 59, 529–538. [Google Scholar] [CrossRef]
- Du, X.; Fu, X.; Tang, H. Effects of Gas nucleus on Cavitation Inception and Bubble characteristics inside V-throttling groove. Adv. Mater. Res. 2014, 1006, 147–151. [Google Scholar] [CrossRef]
- Li, Y.; Bai, Y.; Zhang, J.; Jiang, J. Flow Field Simulation and Experimental Research on the Triangle Groove Cone Throttle Valve. Appl. Mech. Mater. 2015, 779, 42–49. [Google Scholar] [CrossRef]
- Zhao, X.; Wang, B.; Quan, L.; Ge, L.; Zou, X. Design and Characteristics of Independent Metering Control Multi-way Valve with Spool in Series. J. Mech. Eng. 2024, 60, 113–125. [Google Scholar]
- Zhao, X.; Wang, B.; Zhao, B.; Li, Y.; Quan, L. Research on characteristics of differential pressure controllable multi-way valve driven by electro-mechanical actuator. Mach. Tool Hydraul. 2022, 50, 73–78. [Google Scholar]
- Wang, B.; Zhao, X.; Quan, L.; Li, Y.; Hao, Y.; Ge, L. A method for improving flow control valve performance based on active differential pressure regulation. Measurement 2023, 219, 113271. [Google Scholar] [CrossRef]
- Stosiak, M.; Karpenko, M.; Skačkauskas, P.; Deptuła, A. Identification of pressure pulsation spectrum in a hydraulic system with a vibrating proportional valve. J. Vib. Control 2024, 30, 4917–4930. [Google Scholar] [CrossRef]
- Stosiak, M.; Skačkauskas, P.; Towarnicki, K.; Deptuła, A.; Deptuła, A.; Praznowski, K.; Grzywacz, Z.; Karpenko, M.; Urbanowicz, K.; Lapka, M. Analysis of the impact of vibrations on a micro-hydraulic valve using a modified induction algorithm. Machines 2023, 11, 184. [Google Scholar] [CrossRef]
- Lu, L.; Wang, J.; Li, M.; Ryu, S. Experimental and numerical analysis on vortex cavitation morphological characteristics in u-shape notch spool valve and the vortex cavitation coupled choked flow conditions. Int. J. Heat Mass Transf. 2022, 189, 122707. [Google Scholar] [CrossRef]
- Liu, H.; Geng, H.; Yang, G.; Huang, W.; Wang, X.; Quan, L. Research on flow measurement and control integrated strategy based on a flow sensor with active regulation. Measurement 2025, 249, 117055. [Google Scholar] [CrossRef]



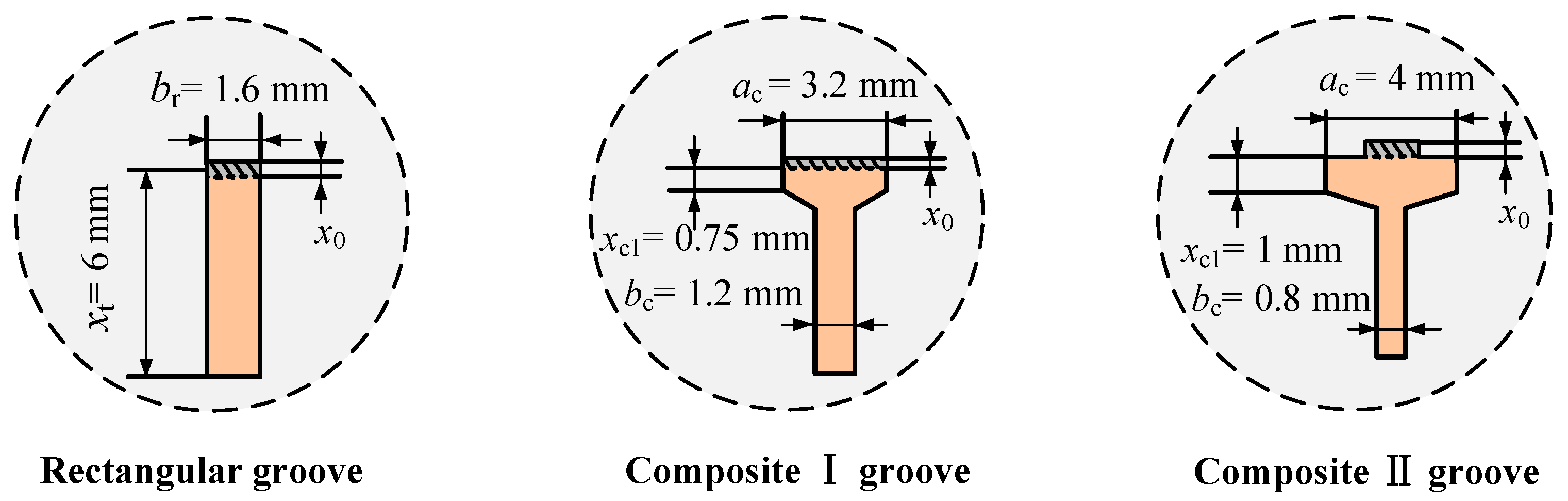

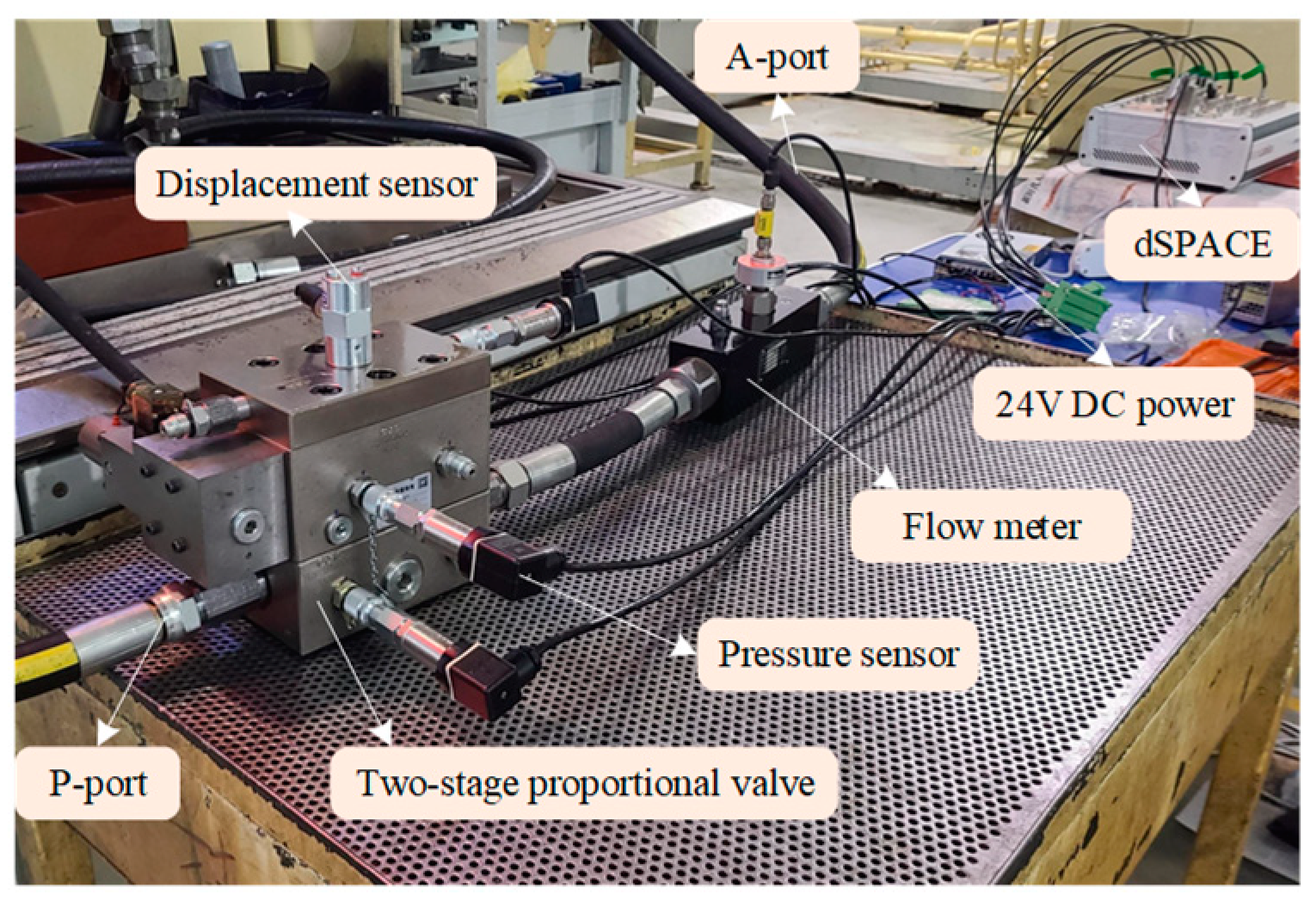

| Element | Supplier/Modle | Specification |
|---|---|---|
| Flow meter | Parker (Mineral Wells, TX, USA)/SCFT 300 | Range: 8–300 L/min; Accuracy: ±1% FS |
| Pressure sensor | Parker/SCP01 | Range: 0–40 MPa; Accuracy: ±0.2% FS |
| LVDT | Schramme (Hamburg, Germany) | Range: ±5 mm; Accuracy: ±0.25% FS |
| Proportional solenoid | Schramme/GP8045A59 | Rated force: 85 N; Working stroke: 3 mm |
| Performance | EATON NG25 | Valve from This Paper |
|---|---|---|
| Pressure loss (rated flow) | 9 bar (400 L/min) | 8.8 bar (300 L/min) |
| Step response time | 85 ms | 50 ms |
| Feedback groove profile | Rectangular | Composite |
| Segmented control | Not Supported | Enabled |
| Flow resolution under consistent pilot conditions | 8.54 L/(min·0.1 V) | 2.04 L/(min·0.1 V) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, X.; Geng, H.; Quan, L.; Xu, C.; Wang, B.; Ge, L. A Novel Flow Characteristic Regulation Method for Two-Stage Proportional Valves Based on Variable-Gain Feedback Grooves. Machines 2025, 13, 648. https://doi.org/10.3390/machines13080648
Zhao X, Geng H, Quan L, Xu C, Wang B, Ge L. A Novel Flow Characteristic Regulation Method for Two-Stage Proportional Valves Based on Variable-Gain Feedback Grooves. Machines. 2025; 13(8):648. https://doi.org/10.3390/machines13080648
Chicago/Turabian StyleZhao, Xingyu, Huaide Geng, Long Quan, Chengdu Xu, Bo Wang, and Lei Ge. 2025. "A Novel Flow Characteristic Regulation Method for Two-Stage Proportional Valves Based on Variable-Gain Feedback Grooves" Machines 13, no. 8: 648. https://doi.org/10.3390/machines13080648
APA StyleZhao, X., Geng, H., Quan, L., Xu, C., Wang, B., & Ge, L. (2025). A Novel Flow Characteristic Regulation Method for Two-Stage Proportional Valves Based on Variable-Gain Feedback Grooves. Machines, 13(8), 648. https://doi.org/10.3390/machines13080648





