Abstract
This research introduces an innovative passive vibration control methodology employing acoustic black hole (ABH) structures to mitigate vibration transmission in electric automotive steering machines—a prevalent issue adversely affecting driving comfort and vehicle safety. Leveraging the inherent bending wave manipulation properties of ABH configurations, we conceive an integrated vibration suppression framework synergizing advanced computational modeling with intelligent optimization algorithms. A high-fidelity finite element (FEM) model integrating ABH-attached steering machine system was developed and subjected to experimental validation via rigorous modal testing. To address computational challenges in design optimization, a hybrid modeling strategy integrating parametric design (using Latin Hypercube Sampling, LHS) with Kriging surrogate modeling is proposed. Systematic parameterization of ABH geometry and damping layer dimensions generated 40 training datasets and 12 validation datasets. Surrogate model verification confirms the model’s precise mapping of vibration characteristics across the design space. Subsequent multi-objective genetic algorithm optimization targeting RMS velocity suppression achieved substantial vibration attenuation (29.2%) compared to baseline parameters. The developed methodology provides automotive researchers and engineers with an efficient suitable design tool for vibration-sensitive automotive component design.
1. Introduction
The steering machine, as a crucial component of electric automobiles, is directly related to the personal comfort and safety of the driver and passengers. When vibration and noise occur in the steering machine, the driver’s control stability can be easily affected. Therefore, reducing vibration and noise in the steering machine is an important measure to ensure driving safety. Most existing studies have shown that the causes of vibration and noise in the steering machine are complex and involve numerous influencing factors. An [1] established a vibration control model for the motor-driven power steering (MDPS) system, providing a solution for high-frequency noise control in electric vehicles. Pietrusiak [2] established a model of the electric power steering assembly, concluding that nonlinearity and damping contact stiffness models can more accurately simulate dynamic responses. Chen [3] established an X-EPS steering machine model, with experimental verification showing an error of less than 5%, meeting design standards. Lin [4] established a variable transmission ratio model for steer-by-wire (SBW) systems, improving vehicle handling stability and safety. In terms of control effectiveness, active vibration control has good application prospects in automotive steering machines. However, active vibration control systems are complex, costly, and difficult to maintain. Haas [5] has employed a combination of virtual passive absorber technology and a damping connection joint (DCJ) compensation method. The integration of these two approaches significantly improves the control accuracy and stability of the steering test bench, providing an effective solution for testing and validation in automotive development. However, passive vibration control has limitations in its control range, and usually causes an increase in the weight of the machine, which is not conducive to the lightweight design of the structure. The acoustic black hole (ABH) structures, as an emerging wave manipulation technology, feature lightweight design, high integration, and strong constructability, making them a promising passive vibration and noise reduction technique. At the structural design, ABHs can be categorized as one-dimensional [6] or two-dimensional [7]. In 1D structures, gradient attenuation of bending wave speed is achieved through power-law thickness tapering. 2D structures are extended to planar waveguide manipulation, with their energy-focusing capability being enhanced. Regarding the vibration characteristic analysis methods for ABH structures, three primary approaches are typically employed: the semi-analytical method [8,9], the transfer matrix method [10], and numerical methods [11,12]. At present, ABH technology has not been widely applied in engineering practice by researchers, and is mostly at the level of theoretical research. Ma [13] optimized the thickness distribution of an ABH using a genetic algorithm and a Daubechies wavelet model, reducing vibration and acoustic radiation. Xu [14] employed the finite element method to establish an ABH-embedded viscoelastic damping material (ABH-VDM) model, which extended the vibration reduction bandwidth (by 900 Hz) and lowered vibration levels by 1.4 dB. Fu [15] applied neural networks and simulated annealing to optimize a segmented ABH beam, improving vibration suppression by reducing reflection coefficients. Jia [16] investigated a thin-walled structure combining embedded ABH with distributed dynamic vibration absorbers (DVAs), demonstrating significant vibration attenuation across the entire frequency spectrum. Sheng [17] used the transfer matrix method (TMM) to establish a dynamic model of a double-power-law ABH (DP-ABH) beam; comparison with the finite element method (FEM) validated the DP-ABH’s ultra-low-frequency broadband gap performance. Some researchers [18,19] use the NSGA-II algorithm to optimize the ABH structure in order to achieve maximum vibration reduction effect. Huang [20] optimized the geometry and topology of the damping layer, proposing the upper bound of kinetic energy as the objective function. The optimized damping significantly improved the broadband energy dissipation performance of the ABH plate. Xiao [21] adopted the Rayleigh–Ritz method and 3D FEM to construct a rail-mounted P-ABH vibration absorber model; this design achieved a broader vibration reduction bandwidth compared to traditional methods. Han [22] proposed a metamaterial double-beam (MDB) structure combining ABH with local resonators (LR). By analyzing a periodically arranged double-beam unit-cell model, they demonstrated excellent low-frequency broadband vibration reduction characteristics. Besse [23] established the motion equation model for a three-layer sandwich plate using Hamilton’s principle and zigzag theory. Experimental results confirmed that ABH can effectively achieve passive vibration control in sandwich plates. Zhang [24] established a multilayer composite sandwich panel structure incorporating filled imperfect acoustic black holes (F-IABH), which outperformed conventional ABH structures in broadband vibration and noise reduction. Zhao [25] created a partitioned ABH (PABH) dynamic vibration absorber (PABH-DVA) model using the PABH design method. Comparative experiments revealed the superior vibration reduction performance of PABH-DVA. Bu designed four novel fluid-conveying pipeline configurations [26] and a drill-string pipeline structure [27] by integrating phononic crystal and ABH techniques. Theoretical and numerical analyses demonstrated that these four pipeline configurations effectively suppress vibrations under rotational operating conditions. The drill-string pipeline structure creates low-frequency broadband band gaps for autonomous vibration suppression. Furthermore, the engineered periodic ABH wedge configuration [28] enables effective vibration energy absorption at the wedge edges. These findings provide new perspectives for vibration mitigation in engineering pipeline systems.
To optimize vibration reduction in steering machines with attached ABH plates, the geometric parameter ranges for both the ABH and damping components must first be determined. However, the combinations formed within these ranges are infinite, making it impossible to obtain all results through finite element methods alone. The function values corresponding to all design variables across their value ranges can be accurately fitted by the surrogate model using limited sample training data, providing a new approach for solving such problems. Extensive research on structural optimization using surrogate models has been conducted by scholars across various fields. Several researchers have employed Kriging models for optimization, achieving significant improvements in prediction accuracy, training efficiency [29], vibration reduction performance [30], and bandgap characteristics of elastic metamaterials [31]. Yang [32] adopted a parallel adaptive enhancement (PAE)-based surrogate modeling approach, which substantially enhanced both prediction precision and training efficiency. Cheng [33] utilized an integrated surrogate model combining SDAE, SA, and GRU with the D-MOHOCD-ELS algorithm to optimize the safety and vibration reduction properties of rail transit structures. Song [34] applied the KSM-CPSO method to optimize suspension parameters for high-speed electric multiple units (EMUs), resulting in improved critical speed, running indexes, safety indexes, and overall dynamic performance. Other researchers have implemented multi-objective genetic algorithms (MOGA) to enhance vibration transmissibility [35] and structural performance [36].
To address the steering machine vibration issue, a vibration reduction scheme assisted by a surrogate model with ABHs is proposed in this paper. This scheme combines the surrogate model with the FEM to construct a vibration characteristics database of a steering machine attached with an ABH plate. The database is then used to optimize the key parameters of the ABH and damping, aiming to achieve the best performance in vibration control for the steering machine. The proposed methodology provides automotive researchers and engineers with an efficient suitable design tool for vibration-sensitive vehicular systems. The structure of this paper is as follows. Section 2 describes the optimization flowchart for the ABH and damping parameters, as well as the modeling of the steering machine attached with an ABH plate. Section 3 presents the FEM model and analyzes the vibration response. Section 4 validates the accuracy of the model through experimental test. Section 5 focuses on constructing the surrogate model for the vibration characteristics of the steering machine attached with an ABH plate. Section 6 optimizes the key parameters of the ABHs and damping layers using the MOGA method based on the established surrogate model and compares the results with the unoptimized combination. Conclusions close the paper in Section 7.
2. Optimization Process Flowchart and Modeling of the Steering Machine Attached with 2D ABH
2.1. Flowchart of Modeling and Optimization Design
Figure 1 illustrates the optimization design process for ABH parameters and damping materials in the steering machine with attached ABH plates. First, a dynamic model of the steering machine with attached ABH plates is established to analyze its vibration characteristics, with the model’s accuracy being verified through modal testing. The geometric parameters of the ABH and damping materials requiring optimization are then determined, along with their upper/lower limits and optimization objectives. These parameters are sampled algorithmically to obtain different combinations of ABHs and damping materials. Modeling and finite element analyses are subsequently performed to construct a high-precision surrogate model, thereby establishing a vibration characteristics database. Finally, the MOGA is employed to obtain the optimal combination of ABH plates and damping materials, achieving maximum vibration reduction for the steering machine model. The subsequent sections of this paper follow this workflow.
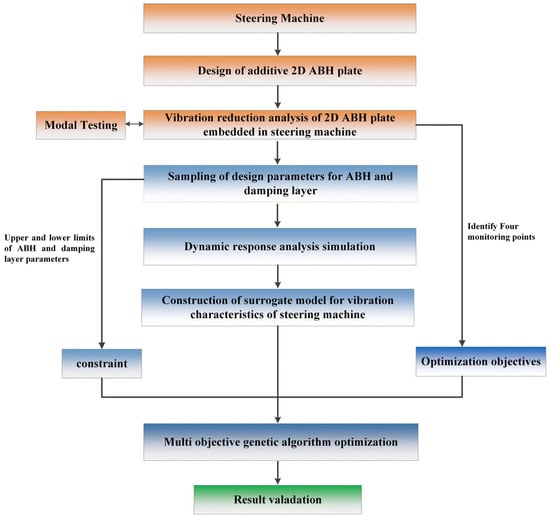
Figure 1.
The process of multi-objective optimization of acoustic black hole based on surrogate model.
2.2. Geometric Modeling of Steering Machine Attached with ABH Plate
A specific automotive steering machine was selected as the research object, as shown in Figure 2a. 3D modeling and necessary geometric simplification were performed using Creo software 8.0. During the modeling process, the following specific operations were conducted: the structural features with minor influence were removed, including fillets, chamfers, small ribs, minor protrusions, and small-diameter holes. For more complex components, reconstruction was performed to ensure high accuracy of critical geometric dimensions such as inner/outer diameters, lengths, offset angles, and mounting platform positions. The reconstructed main housing model was then assembled with other simplified component models to obtain the complete 3D steering machine model (Figure 2b). The final assembly consists of 21 internal components with a total length of 846 mm.

Figure 2.
Steering machine model: (a) Physical picture of steering machine; (b) Simplified diagram of the steering machine model.
If the ABH structure is formed on the steering machine by removing materials, it will seriously weaken the strength of the steering machine. Therefore, an externally attached ABH structural design is proposed. A semi-circular ABH plate is designed, with its geometric configuration illustrated in Figure 3. Considering the actual dimensional constraints of the steering machine, the maximum side length and uniform thickness of the ABH plate are restricted to 130 mm and 4 mm, respectively. The geometric parameters of the ABH region satisfy Equation (1), where the key parameters are set as follows:
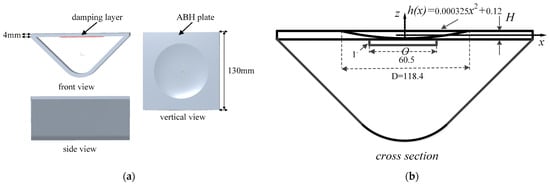
Figure 3.
The proposed semi-circular ABH plate: (a) three-view diagram; (b) Sectional schematic diagram.
The parameter ε in the equation is a constant, and the maximum diameter of ABH can be achieved by changing ε. m is a power exponent and must satisfy m ≥ 2, h0 is the truncation thickness, and R is the radius of the ABH.
The semi-circular ABH plate was assembled to the right side of the steering machine outer shell using the 3D modeling software Creo 8.0, with the ABH plate surface perpendicular to the Z-direction, as shown in Figure 4.
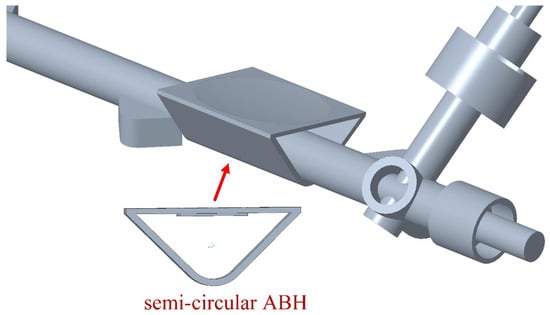
Figure 4.
The 3D model of the steering machine attached with the designed ABH plate.
3. Establishment of FEM Model and Vibration Characteristics Analysis
3.1. Establishment of FEM Model
Preprocessing was performed on the simplified steering machine model attached with the ABH plate. For complex geometric features such as intersecting cylinders in the shell structure, second-order tetrahedral elements (C3D10M) were used for meshing: A mesh size of 2 mm was adopted in the intersecting regions, with local refinement to 0.4 mm in high-curvature areas. A base size of 5 mm was applied to the remaining regions, with local refinement to 0.8 mm. All transition zones were assigned a feature angle of 30° to ensure mesh quality. The FEM models of the original steering machine and the steering machine attached with ABH are shown in Figure 5. Critical components such as the lead screw and steering wheel were defined as steel. The shell structure and ABH plate were set as aluminum. The properties of all materials are presented in Table 1.

Figure 5.
The established FEM models: (a) FEM model of the original steering machine; (b) FEM model of the steering machine attached with ABH plate.

Table 1.
Material Properties.
3.2. Modal Simulation of the Steering Machine
A constrained modal analysis was performed on the established FEM model. The boundary conditions were applied to three installation holes, with fixed constraints in the x, y, and z directions as illustrated in Figure 6. The analysis step was configured to extract the first six modes. The natural frequency values are shown in the Table 2, with the first order frequency being 83.202 Hz and the sixth order frequency being 269.22 Hz. The vibration modes of the steering machine are shown in the Figure 7, with dominant bending and torsional deformation observed. Significant deformation was identified in the steering housing at the 1st, 3rd, and 6th modes, while the motor exhibited noticeable deformation at the 2nd, 3rd, 4th, 5th, and 6th modes.
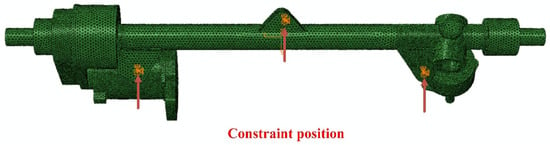
Figure 6.
Schematic diagram of boundary conditions for the FEM simulation.

Table 2.
Computed natural frequencies of the original steering machine.
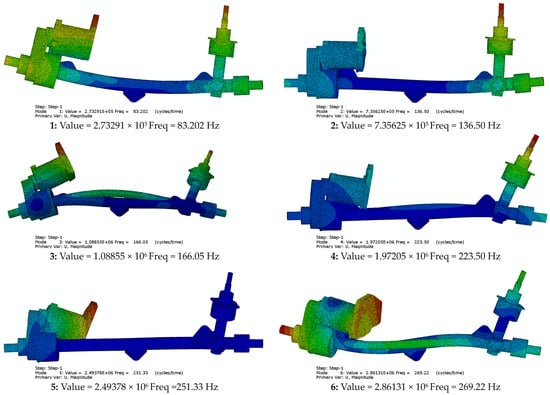
Figure 7.
Natural frequency and vibration mode of steering machine.
3.3. Vibration Response Analysis of the Steering Machine Attached with ABH Plate
This section presents the vibration response analysis, in which the ABH and damping parameters are set as follows: the radius of the ABH is 59.2 mm, the m is 2.3, the h0 is 0.12 mm, and the damping layer dimensions are 60.5 × 60.5 × 1 mm. The 1N harmonic excitation in the Z-direction was applied to the left end of the screw, and a frequency sweep analysis from 1 to 1000 Hz was conducted, as illustrated Figure 8a. Finally, the harmonic response characteristics of the structure were computed using the Lanczos solver in Abaqus. Five monitoring points were distributed across the entire range of the steering machine, with their locations shown in Figure 8b.

Figure 8.
Schematic diagram of exciting and monitoring point locations: (a) the exciting point; (b) the monitoring points.
Figure 9 shows the vibration response of five monitoring points. Figure 9 exhibits multiple peaks, with the vibration velocity being significantly higher in the 0–250 Hz frequency range and less pronounced in other frequency bands. Among the measured points, RP1 demonstrates the lowest vibration velocity, whereas RP4 shows the highest. At the first peak, the vibration velocity of RP4 reaches up to 20 mm/s. All peak vibration velocity magnitude at this location is taken as the optimized comparison group to verify the optimization effect. In this study, the effectiveness of the ABH and damping parameters for vibration reduction in the steering machine will be evaluated from the perspective of kinetic energy. To characterize the effects of the ABH and damping, the average velocity at the frequency of interest will be calculated based on the results of the monitoring points, and the equation is as follows: the average of the sum of the squares of all velocity peaks will be used for parameter optimization design.
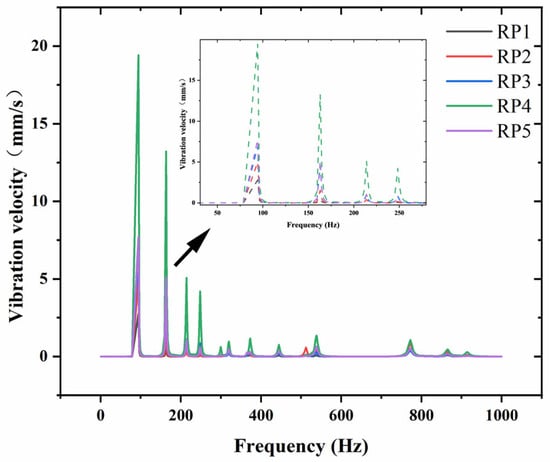
Figure 9.
Vibration velocity of five monitoring points.
4. Accuracy Validation Experiment of FEM Model of Steering Machine
To verify the computational accuracy of the established FEM model, vibration modal testing of the original steering machine was conducted in this paper. Firstly, the total of 42 measurement points were designed and arranged for the tested steering machine. The spatial coordinates of all measuring points are referenced to the center of the steering machine, which is set as the coordinate origin. Furthermore, in the modal analysis module of the M + P Smartoffice Analyzer software 4.0, the spatial coordinates of 42 measurement points were entered, and each measurement point was connected to form a 3D rough configuration for steering machine modal testing, as shown in Figure 10.
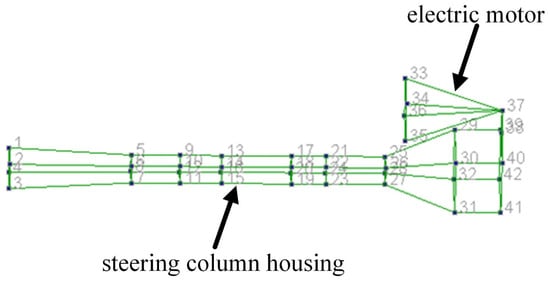
Figure 10.
3D composition diagram for modal testing of steering machine.
The experiment was conducted using the modal testing module in the M + P vibration testing and analysis system. The modal test used a fixed force hammer excitation point position and a moving accelerometer (ICP type) method to obtain the steering machine modal array. The actual test is shown in Figure 11a. We collected vibration acceleration response signals of the structure through parameter settings, with a sampling rate of 12,800 Hz and an effective bandwidth of 5000 Hz, as shown in Figure 11b.
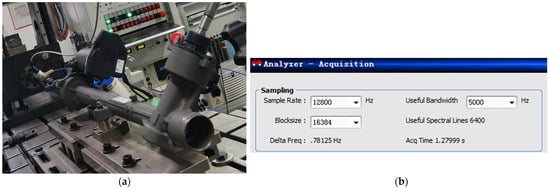
Figure 11.
Modal testing setting conditions: (a) Physical image of the original steering machine vibration mode test. (b) Acceleration response signal acquisition parameter setting diagram.
Through the acquisition of test signals from 42 measurement points, the acceleration response signals across the full frequency range can be observed in the software. Based on the modal simulation results obtained from the preceding finite element analysis, the signal within the 0–300 Hz frequency range was chosen to analyze the low-frequency modal characteristics of the steering machine. According to the settings, the data were subjected to feature extraction by the SO Analyzer software 4.0, and six modal orders were identified within the specified interval.
A comparison between the simulation and experimental modal results is presented in the Table 3. It can be observed that good agreement was achieved across all six modal orders, with the minimum deviation being 0.1% and the maximum deviation not exceeding 3.7%. The modal test results have verified that the FEM models of the steering machine vibration characteristics established in this paper have high computational accuracy, which can provide support for the subsequent construction of surrogate models and multi-objective optimization design.

Table 3.
Comparison of natural frequencies between simulation and experiment results.
5. Construction of Surrogate Model for Vibration Characteristics
5.1. Design Variables and Optimization Objectives
To optimize the vibration reduction performance of the ABH and damping material on the steering machine model, four key geometric parameters of the ABH and damping layer were selected as design variables: the side length of the damping layer, the ABH radius, the truncation thickness, and the power-law exponent. The value ranges for these parameters are listed in Table 4. The design objective was defined as the mean square velocity at the nodal points, as specified in Table 5.

Table 4.
Geometric Parameters of ABH and Damping Layers.

Table 5.
Optimization Objectives.
The Latin Hypercube Sampling (LHS) method was employed to conduct spatial sampling of the four design variables (X1, X2, X3, X4), resulting in the construction of a design space comprising 40 parameter combinations. As illustrated in Figure 12, all initial sampling values were parametrically configured. Based on these training samples, 40 FEM models of the steering machine attached with ABH plates were established, each with distinct parameter combinations. All models were simulated following the vibration characteristic analysis procedure described in Section 3, where the meshing criteria, excitation force parameters (location and amplitude), and monitoring point arrangements were maintained consistently. Through systematic finite element analysis, the mean square velocity response values at five monitoring points were ultimately obtained and used to construct the surrogate model.
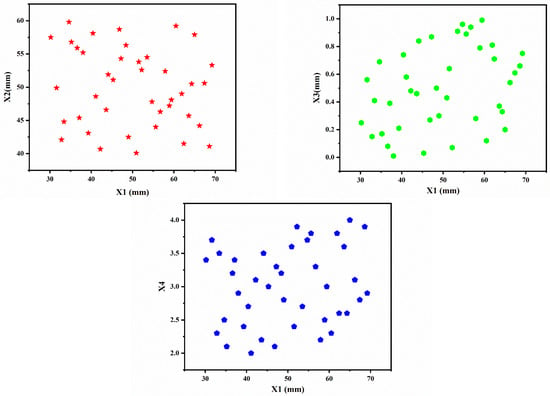
Figure 12.
Distribution of points obtained through sampling in space.
5.2. Construction of Surrogate Model Based on Kriging Method
The Kriging surrogate model is used to establish a mathematical model between design variables and output responses using numerical simulation results from 40 sampling points. The Kriging surrogate model assumes that the input variable x and the output variable y satisfy the following equation:
where is the basis function, is the coefficient of the basis function, and is the Gaussian process. Let the following:
Then Equation (3) can be written as:
where , then from the linear unbiased condition , we can get:
From , we can get , so the following equation can be got:
Calculating the mean square deviation of regression function , the following optimization problem can be established:
Then constructing the following Lagrange function:
Calculating the partial derivative of Equation (11), and the predictive value of x is:
From , the optimal prediction of can be obtained:
Thus, the output values of the samples to be predicted are as follows:
5.3. Fitting Accuracy Validation of Surrogate Model
Five surrogate models were constructed using the Kriging method to predict the mean square velocity responses at five monitoring points on both the steering machine model and the ABH plate. To evaluate the prediction accuracy of the surrogate models, 12 validation samples were generated through the LHS method, and the coefficient of determination (R2) was employed to analyze the fitting precision of the models. The parameter combinations are also ensured not to duplicate those of the training group.
In the Equation (13), is the true value of the i test sample, is the predicted value of the polynomial regression model, is the mean of the true values of the test samples, and n is the number of n test samples. The closer R2 is to 1, the higher the model accuracy.
The validation results are presented in Figure 13, where the X-axis and Y-axis represent the FEM simulation results and surrogate model prediction results, respectively. Data points closer to the 1:1 reference line (red dashed line in the Figure) indicate higher prediction accuracy of the surrogate models. As shown in Figure 13, all test sample points were observed to be tightly distributed near the reference line, demonstrating that all five surrogate models possess excellent predictive performance. Furthermore, R2 values listed in Table 6 were all found to exceed 0.8, which further verifies that the established surrogate models for the dynamic characteristics of the ABH- attached steering machine exhibit high accuracy and can meet the requirements for subsequent optimization analysis.
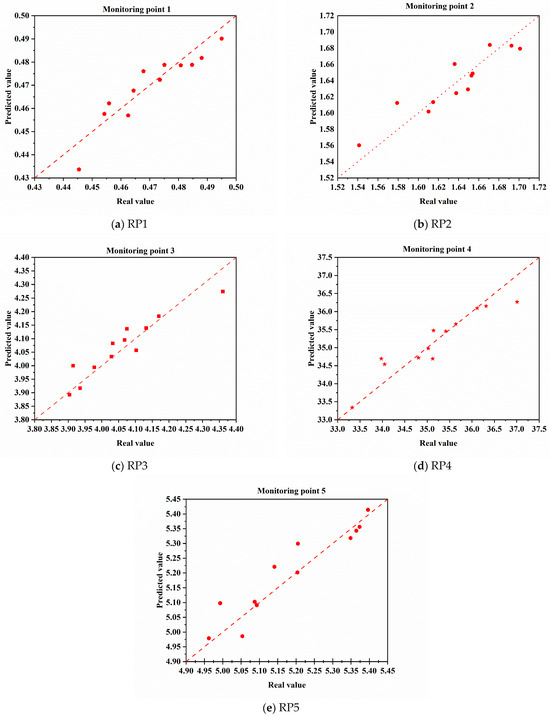
Figure 13.
Comparison between actual output and predicted output of test points.

Table 6.
Determination coefficient R2 values.
6. Design Optimization of ABH Plate Based on MOGA
Based on the high-accuracy surrogate models established in Section 5, the key parameters of the ABH and damping were optimized. First, the geometric parameters and their ranges were determined. The optimization objective was specifically defined by the following equation.
Complex relationships were identified between the four design variables of the ABH and damping parameters and the optimization objectives, necessitating multi-objective collaborative optimization. Based on the high-accuracy surrogate models developed in Section 5, the MOGA was employed to optimize the ABH and damping layer parameters. The multi-objective optimization problem is transformed into a single-objective optimization problem in this study, where all five optimization objectives are multiplied by a weight coefficient of 0.2 and summed to obtain a new optimization objective Y. Thus, the optimal design parameters for the ABH and damping materials can be obtained. Through this multi-objective optimization process, the optimal parameter combination was ultimately obtained, as presented in Table 7.

Table 7.
Optimal Combination Geometric Parameters.
To validate the multi-objective optimization results obtained through MOGA, a FEM model incorporating the optimized ABH and damping parameters was reconstructed, and vibration response analysis was conducted. Figure 14 shows the comparison of vibration velocities at five monitoring points and the average velocity difference in Table 8. A comparative analysis of vibration velocities across the five monitoring points reveals that all measured values remain below the unoptimized vibration velocity curve shown in Figure 9. The maximum reduction in vibration velocity (2.28 mm/s) was observed at Monitoring Point 4, while the minimum vibration velocity (0.38 mm/s) was achieved at Monitoring Point 5. At the same time, it also corresponds to a maximum reduction of 29.2% and a minimum reduction of 11% in the average speed of each monitoring point. These results demonstrate that the optimized geometric parameters of the ABH and damping layer can significantly suppress the vibration velocity response of the steering machine.
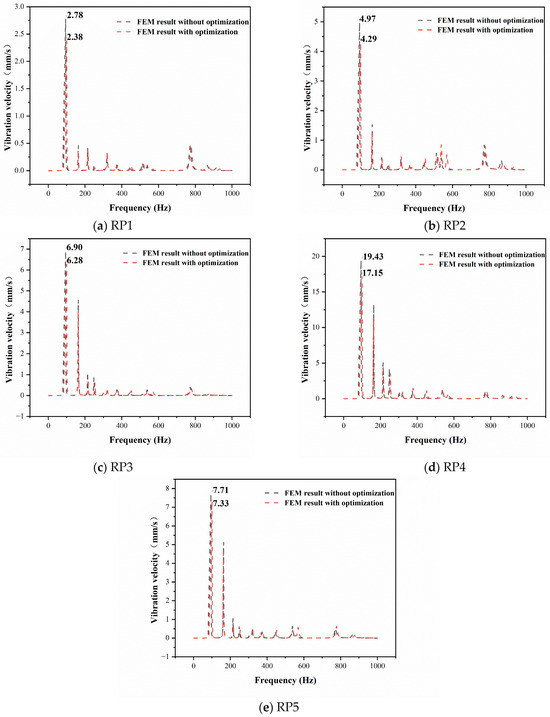
Figure 14.
Comparison of vibration velocity at 5 monitoring points before and after optimization.

Table 8.
Comparison between optimized finite element results and unoptimized results.
7. Conclusions
To address the vibration optimization issue in the steering machine, an embedded ABH structure was introduced. The ABH structure is characterized by its lightweight nature, high integration, and enabling effective vibration reduction in the low-frequency range. This study proposed a vibration reduction optimization design method combining a high-precision surrogate model with the FEM. First, a FEM model of the steering machine attached with an ABH plate is established, and its vibration characteristics are analyzed to obtain the dynamic model. The accuracy of the FEM modeling processing is further verified through modal testing experiments. Then, the LHS method is employed to generate sample points in the parameter space. FEM models with different parameter combinations are constructed, and vibration response analyses are performed to obtain vibration characteristic data for building a high-precision surrogate model. Subsequently, the accuracy of the surrogate model is evaluated using validation data, and a MOGA is applied to optimize four key parameters: the side length of the damping plate, the radius of the ABH, the truncation thickness, and the power-law exponent. Finally, the optimized results are compared with the non-optimized results to verify the accuracy of the MOGA algorithm. The research conclusions are as follows:
1. FEM model accuracy verification: The FEM simulation results are compared with experimental data, showing a minimum deviation of 0.1% and a maximum deviation not exceeding 3.7%. The established FEM model of the steering machine’s vibration characteristics is verified to possess high computational accuracy, which can provide support for subsequent surrogate model construction and multi-objective optimization design.
2. Surrogate modelling accuracy: R2 for the validation dataset is greater than 0.8, and the predicted values closely match the simulated values, with data points distributed near the 1:1 reference line. This indicates that the established surrogate model for the dynamic characteristics of the ABH- attached steering machine has high accuracy and can effectively support subsequent optimization analysis.
3. Vibration reduction optimization effectiveness of the steering machine: The optimal parameter combination obtained through MOGA optimization is 42.8 mm, 51.8 mm, 0.86 mm, and 3.5. Finite element simulations confirm that, compared to the unoptimized structure, the optimized steering machine achieves a maximum reduction of 29.2% and a minimum reduction of 11% in vibration mean square velocity of monitoring points. The results demonstrate that the optimization method based on the finite element method and high-precision surrogate model significantly improves the vibration reduction performance of the steering machine.
Author Contributions
Conceptualization, X.D. and W.L.; software, W.L.; validation, X.D. and W.L.; formal analysis, X.D.; investigation, W.L. and F.H.; writing—original draft preparation, W.L. and X.D.; writing—review and editing, X.D. and Q.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (grant number 52405275), the Natural Science Foundation of the Higher Education Institutions of Jiangsu Province, China (grant number 24KJB460017) and Scientific Research Foundation for High-level Talents of Nanjing Institute of Technology (grant number YKJ202102).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- An, K.; Back, J.; Lee, S.-K.; Shin, S.; Jang, D. Active vibration control for reduction of interior noise caused by R-MDPS of electric power steering in electric vehicle. Appl. Acoust. 2023, 211, 109544. [Google Scholar] [CrossRef]
- Pietrusiak, D.; Wróbel, J.; Czechowski, M.; Fiebig, W. Dynamic NVH Numerical Analysis of Power Steering in the Presence of Lubricant in the System. Materials 2022, 15, 2406. [Google Scholar] [CrossRef] [PubMed]
- Chen, F.; Fu, Z.; Qiu, B.; Si, C.; Zhu, Q.; Feng, C.; Sun, X.; Liang, H.; Yang, L. Predicting the Fatigue Life of a Commercial Vehicle X-EPS Steering Gear with a Rigid–Flexible Coupling Dynamics Method. Machines 2025, 13, 218. [Google Scholar] [CrossRef]
- Lin, J.; Zhang, F.; Su, L.; Song, G.; Liu, Z.; Zhang, Y. Research on Variable Transmission Ratio Control Method to Improve Vehicle Handling Comfort Based on Steer-by-Wire System. Actuators 2024, 13, 48. [Google Scholar] [CrossRef]
- Haas, A.; Schrage, B.; Menze, G.; Sieberg, P.M.; Schramm, D. Oscillation and Vibration Reduction Approaches on a HiL-Steering-Test-Bench. IEEE ASME Trans. Mechatron. 2023, 29, 1295–1305. [Google Scholar] [CrossRef]
- McCormick, C.A.; Shepherd, M.R. Design optimization and performance comparison of three styles of one-dimensional acoustic black hole vibration absorbers. J. Sound Vib. 2020, 470, 115164. [Google Scholar] [CrossRef]
- Lyu, X.; Ding, Q.; Ma, Z.; Yang, T. Ultra-Wide Bandgap in Two-Dimensional Metamaterial Embedded with Acoustic Black Hole Structures. Appl. Sci. 2021, 11, 11788. [Google Scholar] [CrossRef]
- Tang, L.; Cheng, L.; Ji, H.; Qiu, J. Characterization of acoustic black hole effect using a one-dimensional fully-coupled and wavelet-decomposed semi-analytical model. J. Sound Vib. 2016, 374, 172–184. [Google Scholar] [CrossRef]
- Deng, J.; Zheng, L.; Guasch, O.; Wu, H.; Zeng, P.; Zuo, Y. Gaussian expansion for the vibration analysis of plates with multiple acoustic black holes indentations. Mech. Syst. Signal Process. 2019, 131, 317–334. [Google Scholar] [CrossRef]
- Leng, J.; Romero-García, V.; Pelat, A.; Picó, R.; Groby, J.-P.; Gautier, F. Interpretation of the Acoustic Black Hole effect based on the concept of critical coupling. J. Sound Vib. 2020, 471, 115199. [Google Scholar] [CrossRef]
- Conlon, S.C.; Fahnline, J.B.; Semperlotti, F. Numerical analysis of the vibroacoustic properties of plates with embedded grids of acoustic black holes. J. Acoust. Soc. Am. 2015, 137, 447–457. [Google Scholar] [CrossRef] [PubMed]
- Zhou, T.; Tang, L.; Ji, H.; Qiu, J.; Cheng, L. Dynamic and Static Properties of Double-Layered Compound Acoustic Black Hole Structures. Int. J. Appl. Mech. 2017, 9, 1750074. [Google Scholar] [CrossRef]
- Ma, L.; Dong, H.-W.; Cheng, L. An alternative and optimized thickness profile of an acoustic black hole plate. J. Sound Vib. 2020, 486, 115619. [Google Scholar] [CrossRef]
- Xu, L.; Zhang, J.; Li, J.; Tian, H.; Zheng, C.; Guo, S. Design of a lightweight broadband vibration reduction structure with embedded acoustic black holes in viscoelastic damping materials. Mater. Des. 2024, 248, 113450. [Google Scholar] [CrossRef]
- Fu, Q.; Wu, J.; Yu, C.; Du, X.; Zhang, N.; Zhang, J. Parametric studies and optimal design of the exponents collocation of a segmented acoustic black hole beam. Appl. Acoust. 2022, 200, 109086. [Google Scholar] [CrossRef]
- Jia, X.-X.; Yu, Y.; Du, Y. Embedded periodically ABHs and distributed DVAs for passive low-frequency broadband vibration attenuation in thin-walled structures. Sci. Rep. 2024, 14, 18496. [Google Scholar] [CrossRef] [PubMed]
- Sheng, H.; He, M.-X.; Lyu, X.-F.; Ding, Q. Ultra-low frequency broadband gap optimization of 1D periodic structure with dual power-law acoustic black holes. J. Intell. Mater. Syst. Struct. 2022, 33, 532–546. [Google Scholar] [CrossRef]
- Bao, Y.; Yao, Z.; Zhang, Y.; Hu, X.; Liu, X.; Shan, Y.; He, T. Ultra-broadband gaps of a triple-gradient phononic acoustic black hole beam. Int. J. Mech. Sci. 2024, 265, 108888. [Google Scholar] [CrossRef]
- Wang, J.; Huang, W.; Ji, H.; Qiu, J. Multi-Objective Collaborative Optimization of Stiffness and Damping Performance of Acoustic Black Hole Plate. Int. J. Acoust. Vib. 2024, 29, 39–47. [Google Scholar] [CrossRef]
- Huang, W.; Tao, C.; Ji, H.; Qiu, J. Optimization of profile and damping layer of plates embedded with acoustic black hole indentations for broadband energy dissipation. J. Intell. Mater. Syst. Struct. 2022, 33, 1947–1959. [Google Scholar] [CrossRef]
- Xiao, Y.; Zhu, H.; Ye, K.; Weng, S.; Luo, H.; Du, Y. A piezoelectric acoustic black hole absorber for rail vibration reduction and energy harvesting: Semi-analytical model. Eng. Struct. 2025, 322, 119028. [Google Scholar] [CrossRef]
- Han, Y.; Chen, X.; Wei, Y.; Jiang, S.; Du, C.; Jiang, G.; Zhang, H. Vibration attenuation of metamaterial dual-beam with simultaneous acoustic black hole and local resonator. Eur. J. Mech. A Solids 2025, 111, 105535. [Google Scholar] [CrossRef]
- Besse, A.; O’Donoughue, P.; Aklouche, O.; Ablitzer, F.; Pelat, A.; Gautier, F. Wave propagation in a honeycomb sandwich panel of variable thickness: Model and characterisation of the Black Hole Acoustic effect. J. Phys. Conf. Ser. 2024, 2647, 172011. [Google Scholar] [CrossRef]
- Zhang, S.; Ding, L.; Wu, X.; Ma, Y.; Deng, Z. Vibroacoustic suppression of sandwich plates with imperfect acoustic black hole. Int. J. Mech. Sci. 2024, 283, 109690. [Google Scholar] [CrossRef]
- Zhao, X.; Wang, C.; Ji, H.; Qiu, J.; Cheng, L. Vibration Reduction by a Partitioned Dynamic Vibration Absorber with Acoustic Black Hole Features. Chin. J. Mech. Eng. 2024, 37, 75. [Google Scholar] [CrossRef]
- Bu, Y.; Tang, Y.; Wu, J.; Yang, T.; Ding, Q.; Li, Y. Novel vibration suppression of spinning periodically acoustic black hole pipes based on the band-gap mechanism. Thin-Walled Struct. 2025, 212, 113198. [Google Scholar] [CrossRef]
- Bu, Y.; Tang, Y.; Chen, D.; Yang, T.; Ding, Q. Novel vibration self-attenuation design of drill-string-like pipes transporting fluid with the enhancement of acoustic black hole effect. Ocean Eng. 2025, 335, 121694. [Google Scholar] [CrossRef]
- Bu, Y.; Tang, Y.; Ding, Q. Novel vibration self-suppression of periodic pipes conveying fluid based on acoustic black hole effect. J. Sound Vib. 2023, 567, 118077. [Google Scholar] [CrossRef]
- Cheng, C.; Zhang, S.; Wang, Z.; Qiu, L.; Tu, L.; Zhu, L.; Yao, R. Surrogate-model-based dynamic-sensing optimization method for high-speed elevator car horizontal vibration reduction. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2024, 238, 5498–5514. [Google Scholar] [CrossRef]
- Du, X.; Fu, Q. Surrogate model-based multi-objective design optimization of vibration suppression effect of acoustic black holes and damping materials on a rectangular plate. Appl. Acoust. 2024, 217, 109837. [Google Scholar] [CrossRef]
- Cao, L.; Wu, J.; Zhang, Z.; Zhang, C.; Wan, W.; Bao, J.; Gao, Y. Design optimization of elastic metamaterials with multilayered honeycomb structure by Kriging surrogate model and genetic algorithm. Struct. Multidiscip. Optim. 2024, 67, 82. [Google Scholar] [CrossRef]
- Yang, F.; Zhang, X.; Han, Y.; Yang, L.; Wang, L. Random Vibration Analysis of Train–Bridge System Based on Parallel Adaptive Enhanced-Surrogate Model. Int. J. Struct. Stab. Dyn. 2025, 2650164. [Google Scholar] [CrossRef]
- Cheng, F.; Liu, H. Surrogate model-based multi-objective optimization algorithm for train-ballast turnout system: Balancing safety and vibration damping in parameter design. Eng. Struct. 2024, 304, 117685. [Google Scholar] [CrossRef]
- Song, Y.; Qi, Y.; Dai, H. Multi-parameter optimization based on a surrogate model for improving vehicle dynamics and reducing wheel wear in high-speed EMUs. Veh. Syst. Dyn. 2024, 1–24. [Google Scholar] [CrossRef]
- Lim, J.; Jang, Y.S.; Chang, H.S.; Park, J.C.; Lee, J. Multi-objective genetic algorithm in reliability-based design optimization with sequential statistical modeling: An application to design of engine mounting. Struct. Multidiscip. Optim. 2020, 61, 1253–1271. [Google Scholar] [CrossRef]
- Beylergil, B. Multi-objective optimal design of hybrid composite laminates under eccentric loading. Alex. Eng. J. 2020, 59, 4969–4983. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).