The Research on Multi-Objective Maintenance Optimization Strategy Based on Stochastic Modeling
Abstract
1. Introduction
2. Construction of the Prognostic Model
2.1. Multi-Sensor Data Fusion Method
2.2. Linear Wiener Process Model
2.3. Parameter Estimation
3. Maintenance Strategy Optimization
3.1. Maintenance Strategy Based on Cost Objective
3.2. Maintenance Strategy Based on Availability Objective
3.3. Bi-Objective Coordinated Optimization
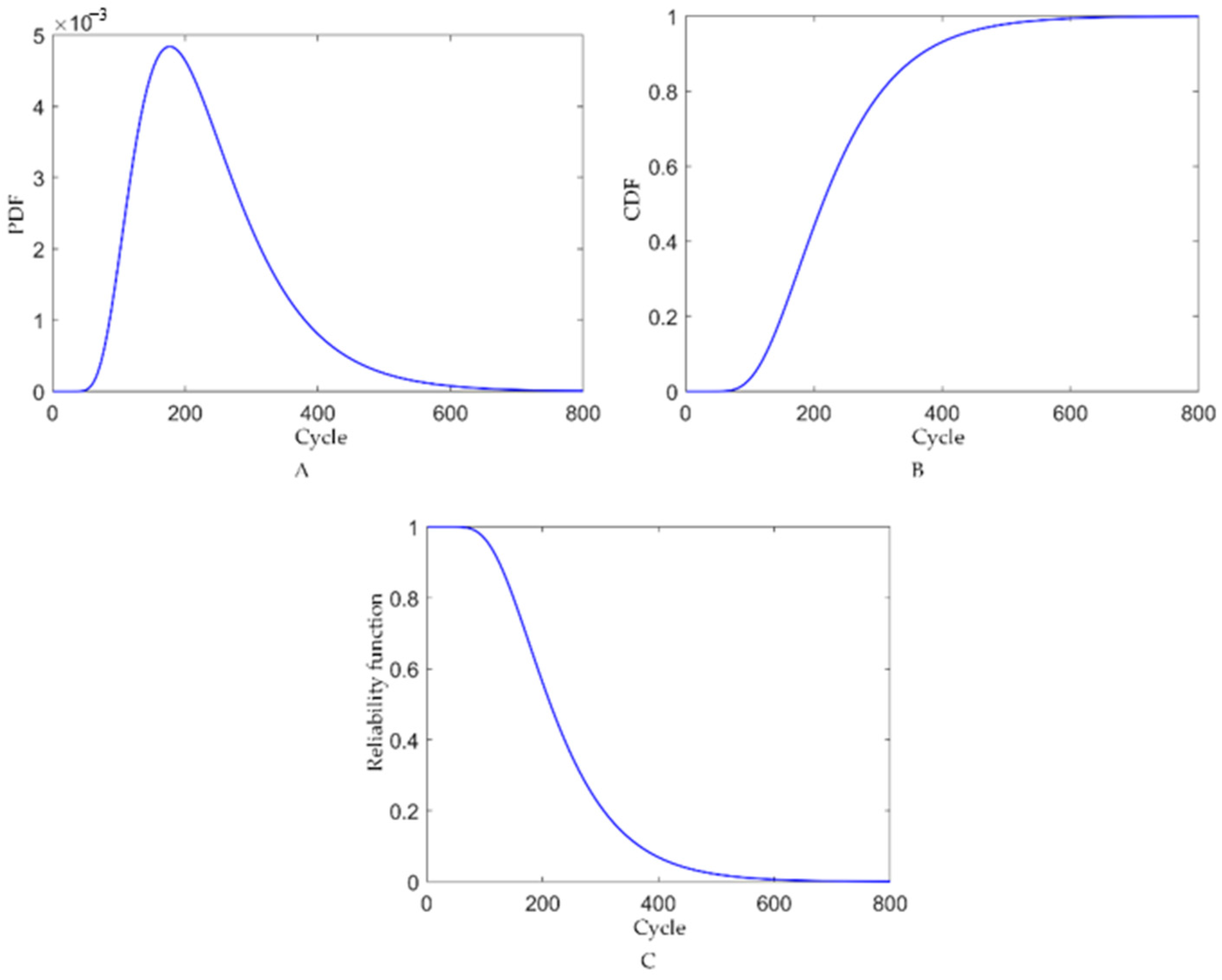
4. Results
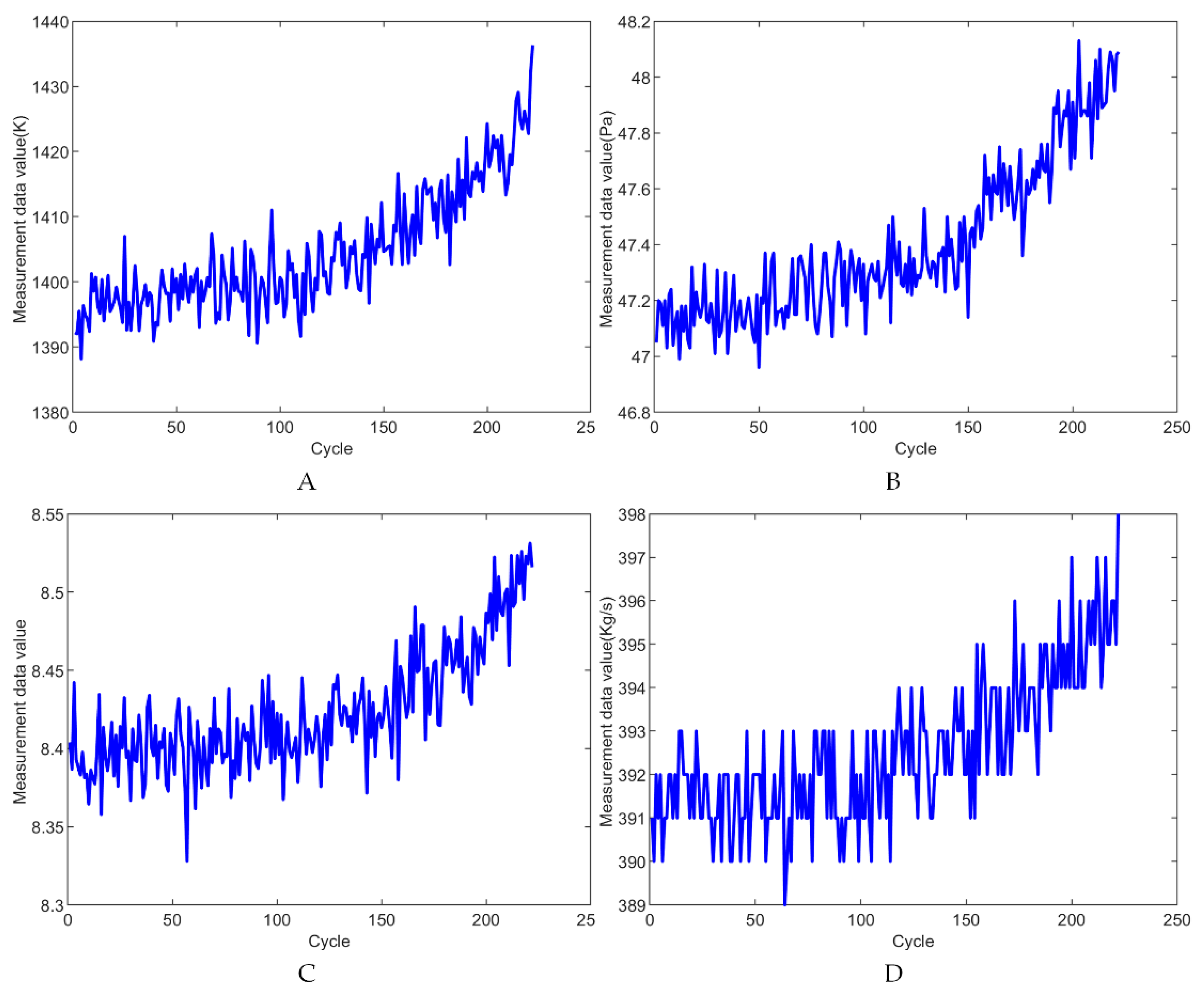
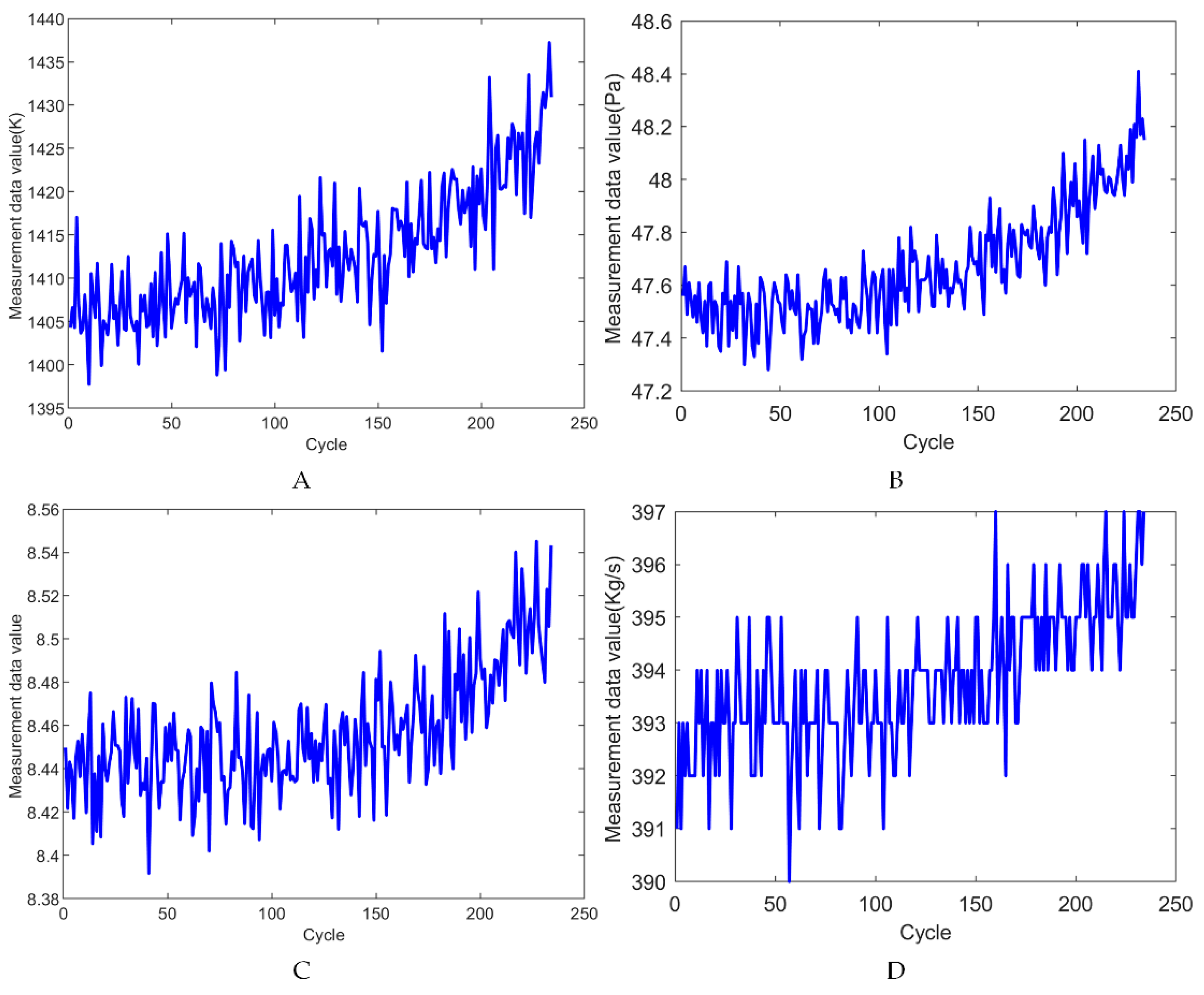
4.1. Dataset Description
4.2. Evaluation Index
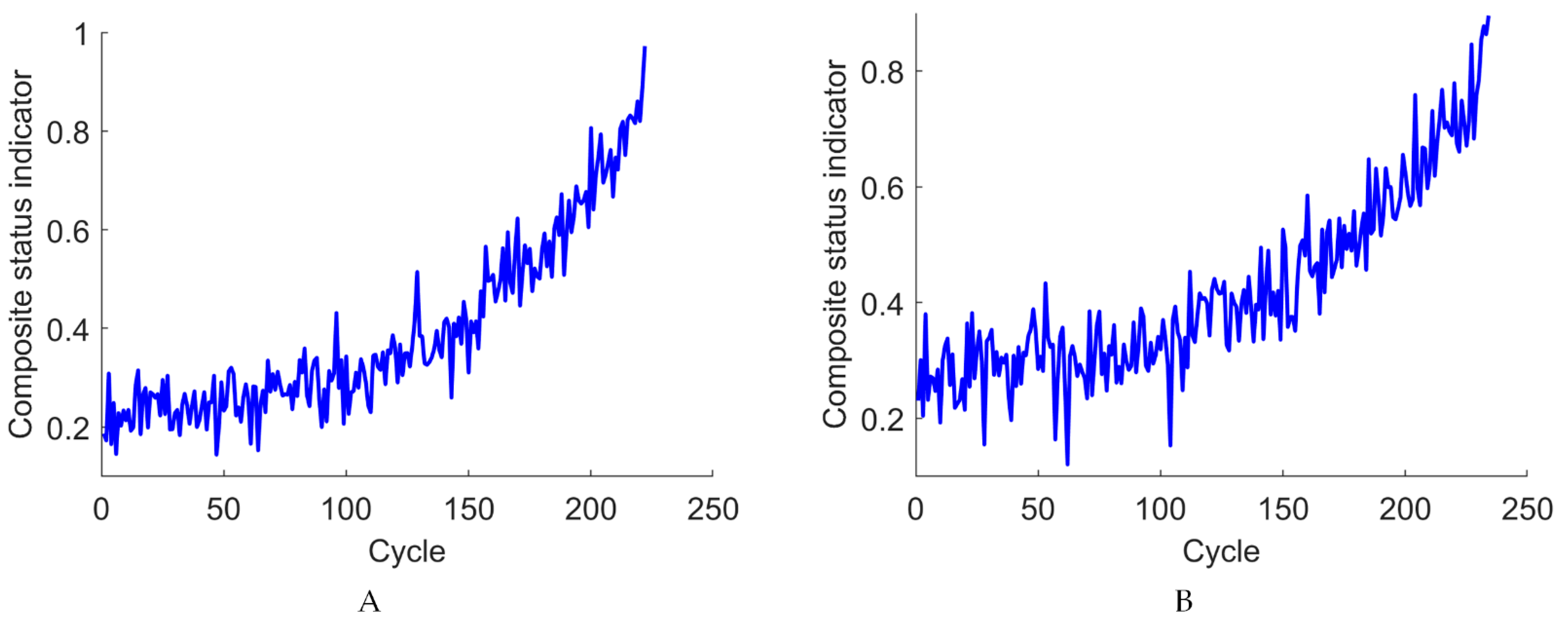
4.3. Construction of Predictive Models
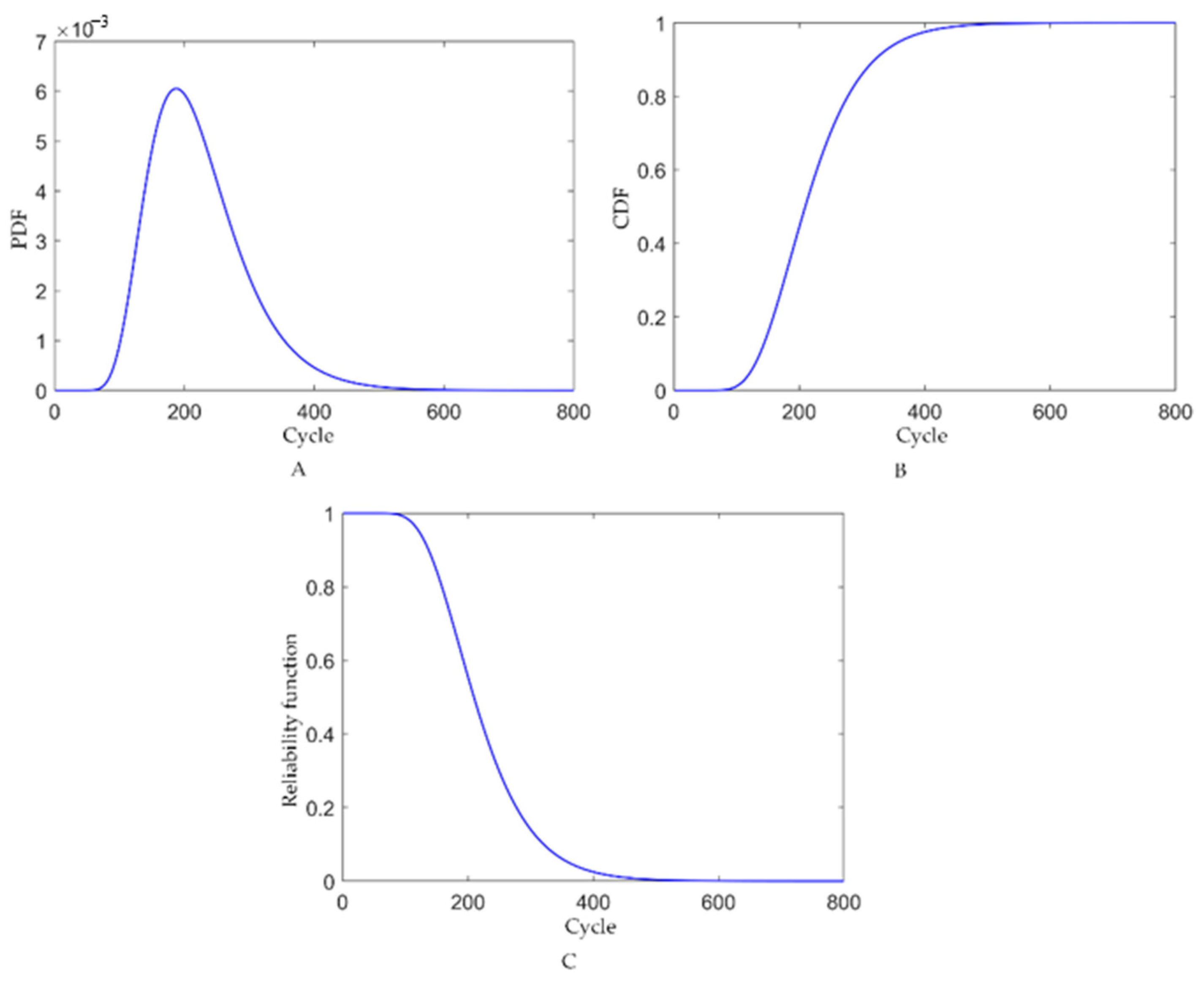
4.4. Optimization of Maintenance Strategies
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ren, W.; Wang, Z.; Chen, Z.; Zhao, S.; Dong, L.; Li, Y.; Fan, X. Multi-fault Feature Wasserstein Generative Adversarial Networks for Fault Diagnosis in Unbalanced Data. IEEE Trans. Instrum. Meas. 2025, 74, 3544909. [Google Scholar] [CrossRef]
- Li, H.; Zhang, Z.; Li, T.; Si, X. A review on physics-informed data-driven remaining useful life prediction: Challenges and opportunities. Mech. Syst. Signal Process. 2024, 209, 111120. [Google Scholar] [CrossRef]
- Broek, M.A.U.H.; Teunter, R.H.; de Jonge, B.; Veldman, J. Joint condition-based maintenance and condition-based production optimization. Reliab. Eng. Syst. Saf. 2021, 214, 107743. [Google Scholar] [CrossRef]
- Jiménez, J.J.M.; Vingerhoeds, R.; Grabot, B.; Schwartz, S. An ontology model for maintenance strategy selection and assessment. J. Intell. Manuf. 2023, 34, 1369–1387. [Google Scholar] [CrossRef]
- Lei, Y.; Li, N.; Guo, L.; Li, N.; Yan, T.; Lin, J. Machinery health prognostics: A systematic review from data acquisition to RUL prediction. Mech. Syst. Signal Process. 2018, 104, 799–834. [Google Scholar] [CrossRef]
- Ali, A.; Abdelhadi, A. Condition-Based Monitoring and Maintenance: State of the Art Review. Appl. Sci. 2022, 12, 688. [Google Scholar] [CrossRef]
- Ma, H.-G.; Wu, J.-P.; Li, X.-Y.; Kang, R. Condition-Based Maintenance Optimization for Multicomponent Systems Under Imperfect Repair—Based on RFAD Model. IEEE Trans. Fuzzy Syst. 2019, 27, 917–927. [Google Scholar] [CrossRef]
- West, J.; Siddhpura, M.; Evangelista, A.; Haddad, A. Improving Equipment Maintenance—Switching from Corrective to Preventative Maintenance Strategies. Buildings 2024, 14, 3581. [Google Scholar] [CrossRef]
- Cao, Y.; Luo, J.; Dong, W. Optimization of condition-based maintenance for multi-state deterioration systems under random shock. Appl. Math. Model. 2023, 115, 80–99. [Google Scholar] [CrossRef]
- Chen, N.; Ye, Z.-S.; Xiang, Y.; Zhang, L. Condition-based maintenance using the inverse Gaussian degradation model. Eur. J. Oper. Res. 2015, 243, 190–199. [Google Scholar] [CrossRef]
- Zhao, X.; Fouladirad, M.; Bérenguer, C.; Bordes, L. Condition-based inspection/replacement policies for non-monotone deteriorating systems with environmental covariates. Reliab. Eng. Syst. Saf. 2010, 95, 921–934. [Google Scholar] [CrossRef]
- You, M.Y. A generalized three-type lifetime probabilistic models-based hybrid maintenance policy with a practical switcher for time-based preventive maintenance and condition-based maintenance. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2019, 233, 1231–1244. [Google Scholar] [CrossRef]
- Arts, J.; Basten, R. Design of multi-component periodic maintenance programs with single-component models. IISE Trans. 2018, 50, 606–615. [Google Scholar] [CrossRef]
- Ding, S.H.; Kamaruddin, S.; Azid, I.A. Development of a model for optimal maintenance policy selection. Eur. J. Ind. Eng. 2014, 8, 50–68. [Google Scholar] [CrossRef]
- Zhu, Z.; Xiang, Y.; Li, M.; Zhu, W.; Schneider, K. Preventive maintenance subject to equipment unavailability. IEEE Trans. Reliab. 2019, 68, 1009–1020. [Google Scholar] [CrossRef]
- Wang, Z.; Jiang, P.; Chen, Z.; Li, Y.; Ren, W.; Dong, L.; Du, W.; Wang, J.; Zhang, X.; Shi, H. Remaining useful life prediction method based on two-phase adaptive drift Wiener process. Reliab. Eng. Syst. Saf. 2025, 258, 110908. [Google Scholar] [CrossRef]
- Jiang, P.; Ren, W.; Chen, Z.; Wang, Z.; Li, Y.; Dong, L. A nonlinear dynamic ensemble remaining useful life prediction method considering multi-source data uncertainty. Mech. Syst. Signal Process. 2025, 230, 112607. [Google Scholar] [CrossRef]
- Wang, F.; Ni, X.; Zhang, Q.; Guo, S.; Zhou, J.; Chen, D. Estimation of combine harvester throughput using multisensor data fusion. Comput. Electron. Agric. 2025, 237, 110713. [Google Scholar] [CrossRef]
- Gu, M. Improved kalman filtering and adaptive weighted fusion algorithms for enhanced multi-sensor data fusion in precision measurement. Informatica 2025, 49, 85–100. [Google Scholar] [CrossRef]
- Khemani, K. AI-Driven Predictive Maintenance with Real-Time Contextual Data Fusion for Connected Vehicles. Res. Sq. 2025; in press. [Google Scholar] [CrossRef]
- Orošnjak, M. Enhancing sustainability in tyre manufacturing with machine learning and knowledge graphs: An energy-based maintenance solution. J. Clean. Prod. 2025, 520, 146090. [Google Scholar] [CrossRef]
- Zhang, J.-X.; Hu, C.-H.; He, X.; Si, X.-S.; Liu, Y.; Zhou, D.-H. A Novel Lifetime Estimation Method for Two-Phase Degrading Systems. IEEE Trans. Reliab. 2019, 68, 689–709. [Google Scholar] [CrossRef]

| Symbol | Meaning | Symbol | Meaning |
|---|---|---|---|
| H | Flight altitude | EPR | Engine compression ratio |
| Ma | Mach number | PS30 | High-pressure compressor outlet static pressure |
| TRA | Throttle lever angle | PHI | Fuel flow and P30 ratio |
| T2 | Fan inlet temperature | NRF | Corrected fan speed |
| T24 | Low-pressure compressor outlet temperature | NRC | Core engine corrected speed |
| T30 | High-pressure compressor outlet temperature | BPR | Bypass ratio |
| T50 | Low-pressure turbine outlet temperature | FARB | Combustion chamber gas ratio |
| P2 | Fan inlet pressure | HT_BLEED | Bleed air enthalpy |
| P15 | Total bypass pressure | NF_DMD | Fan speed command value |
| P30 | High-pressure compressor outlet total pressure | PCNFR_DMD | Fan correction speed command value |
| NF | Uncorrected fan speed | W31 | High-pressure turbine cooling air flow |
| NC | Uncorrected core speed | W32 | Low-pressure turbine cooling air flow |
| Dataset | Evaluation Index | C1 | C2 | C3 |
|---|---|---|---|---|
| Engine 10 | RMSE | 36.6931 | 21.7358 | 2.2693 |
| MAE | 36.6931 | 21.7358 | 2.2693 | |
| CRA | −0.3724 | 0.0356 | 0.9897 | |
| Engine 20 | RMSE | 46.7134 | 35.2351 | 12.7846 |
| MAE | 46.7134 | 35.2351 | 12.7846 | |
| CRA | −0.2445 | 0.3925 | 0.9422 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, G.; Jiang, P.; Ren, W.; Li, Y.; Chen, Z. The Research on Multi-Objective Maintenance Optimization Strategy Based on Stochastic Modeling. Machines 2025, 13, 633. https://doi.org/10.3390/machines13080633
Xu G, Jiang P, Ren W, Li Y, Chen Z. The Research on Multi-Objective Maintenance Optimization Strategy Based on Stochastic Modeling. Machines. 2025; 13(8):633. https://doi.org/10.3390/machines13080633
Chicago/Turabian StyleXu, Guixu, Pengwei Jiang, Weibo Ren, Yanfeng Li, and Zhongxin Chen. 2025. "The Research on Multi-Objective Maintenance Optimization Strategy Based on Stochastic Modeling" Machines 13, no. 8: 633. https://doi.org/10.3390/machines13080633
APA StyleXu, G., Jiang, P., Ren, W., Li, Y., & Chen, Z. (2025). The Research on Multi-Objective Maintenance Optimization Strategy Based on Stochastic Modeling. Machines, 13(8), 633. https://doi.org/10.3390/machines13080633






