Abstract
In this study, the combined influence of vibration direction, feature selection strategy, and the support vector machine (SVM) kernel on the classification accuracy of unbalance faults was investigated. Experiments were carried out on a Jeffcott rotor test rig at a constant speed and under three operating conditions. The overlapping sliding window method was used for raw sample expansion. Features extracted from time domain signals and from the order and power spectra obtained in the frequency domain were ranked using the Kruskal–Wallis algorithm. Based on the feature-ranking results, the three most discriminative features for each domain–axis combination, as well as all nine most discriminative features for each axis in a hybrid manner, were fed into SVM classifiers with different kernels, and their performance was evaluated using ten-fold cross-validation. Classification using vibration signals in the vertical direction had higher accuracy rates than those using signals in the horizontal direction for the feature sets obtained in the same domains. According to the statistical results, feature set selection had a much greater impact on classification accuracy than SVM kernel choice. Power spectrum-based features allowed higher classification accuracies in all SVM algorithms compared to both the time domain features and the order spectrum-based features for detecting unbalance faults. Increasing the number of features or employing hybrid feature selection did not result in a consistent or significant enhancement in overall classification performance. Selecting the right SVM kernel shapes both the model’s flexibility and its fit to the chosen feature space; when this fit is inadequate, classification accuracy may decrease. Consequently, by selecting the appropriate vibration direction, feature set, and SVM kernel, an improvement of up to 67% in unbalance fault classification accuracy was achieved.
1. Introduction
Rotating machines are widely used in industry. To prevent significant financial losses and potentially catastrophic failures that can result from undetected rotor failures, it is very important that such failures are detected correctly and in a timely manner so that reliable and efficient operations can be achieved. Continuous monitoring is essential for identifying and classifying faults in rotating machinery. Rotating machinery’s optimal performance depends on the early and reliable identification of rotor faults [1].
Common rotor faults include unbalance, misalignment, rubbing, bending, oil whirl, and pedestal looseness [2]. Vibration in a rotating machine is caused by unbalance, which happens when the mass center and the geometric center do not align. Unbalanced rotors can produce damaging vibrations that may harm the machine’s components. To prolong the machine’s lifespan, it is important to reduce the vibration caused by unbalance to a safe level. Misalignment refers to the improper alignment of the shaft and bearings, causing excessive forces and wear. Rubbing can occur when two rotor parts come into contact, leading to friction and potential damage. Bending can result from excessive loads or operating conditions, leading to deformation of the rotor. Oil whirl happens when the rotor and oil film oscillate in response to forces, potentially causing instability. Finally, pedestal looseness can occur due to improper mounting or wear, leading to excessive vibrations and potential failure.
Traditional frequency-based vibration analysis methods are often ineffective in identifying rotor faults, particularly unbalance and misalignment, as these faults can exhibit similar frequency patterns [3]. The use of intelligent fault classification methods, such as machine learning (ML), in rotor systems has grown rapidly in recent years [4]. Supervised and unsupervised learning are the two main subcategories of ML. In supervised learning, models are trained using data obtained from normal and faulty operations to distinguish between normal and faulty operations. Unsupervised learning, on the other hand, automatically learns patterns from data collected during normal and faulty operations [5].
ML has been proven to be effective in a wide range of predictive maintenance (PdM) applications [6]. Vibration-based PdM is a highly effective method for monitoring machinery conditions. PdM uses data analysis, ML, and sensor technology to predict when equipment is likely to fail. System availability and reliability can be increased, while overall maintenance costs can be reduced through a successful PdM program. With the continued growth of big data and advances in big data technologies, the attractiveness of data-driven PdM has increased significantly. With the vast amount of data available, the use of ML methods has become a powerful solution. ML algorithms, such as support vector machines (SVMs), artificial neural networks and k-nearest neighbors, provide a unique approach to data processing and analysis, contributing to the efficiency and accuracy of PdM strategies [7].
SVM algorithms have gained widespread popularity in the field of diagnostic applications due to their robust optimization and generalization capabilities, along with their efficient training process. This makes them well-suited for addressing the non-linear and high-dimensional datasets commonly encountered in real-world scenarios. In the context of rotor fault diagnosis, where the signals from the rotor system exhibit non-linear and non-stationary characteristics, the SVM’s ability to effectively handle non-linear data and perform multi-class classification becomes particularly crucial. This adaptability positions the SVM as a valuable tool for accurately diagnosing rotor faults by effectively processing complex and dynamic data patterns [8].
The performance of SVM is significantly influenced by the selection of hyperparameters and the method used for evaluation, just like any other ML model. One particularly important hyperparameter for SVM is the kernel function. The kernel function choice significantly impacts SVM model accuracy and generalization capabilities [9,10]. Zhang et al. conducted a comprehensive investigation of the effectiveness of polynomial, Gaussian radial basis function, and sigmoid SVM kernels in detecting unbalance faults and, remarkably, achieved 100% classification accuracy using each of these kernels [9]. In another study, Hübner et al. achieved an 84.8% accuracy in unbalance detection using a linear SVM, and 83.3% with polynomial and Gaussian radial basis function kernels [10]. It is crucial to choose the appropriate evaluation method in addition to tuning hyperparameters. In k-fold cross-validation, a technique for training and testing in ML, the choice of k significantly impacts model performance. Choosing an appropriate k value can improve accuracy. In general, the values of five (5) or ten (10) are preferred in the literature as they are believed to provide estimates of the test error rate with acceptable variance [11].
When analyzing vibration to detect unbalance, it is crucial to consider the impact of the chosen measurement axis on the accuracy of detection. Unbalance results in radial vibration, which comprises both vertical and horizontal components. In the ideal scenario, axial measurements should indicate minimal vibration, as the majority of forces are generated perpendicular to the shaft [3,12]. When analyzing the radial vibrations during unbalance detection, Alsaleh et al. noted that vibrations in the vertical direction consistently had higher amplitudes than vibrations in the horizontal direction since the stiffness along the horizontal direction is higher than that in the vertical direction [13].
Fault detection accuracy can be enhanced by using the most discriminative features [14]. In the feature ranking process, one-way analysis of variance (ANOVA) is applied to data with a normal distribution, whereas the Kruskal–Wallis test is designed for datasets that do not follow a normal distribution [15].
This study addresses a remaining gap in rotor fault-diagnosis research. Previous works have typically examined either the influence of the measurement axis on unbalance detection, or the role of feature selection strategies and SVM kernel tuning. However, the combined impact of all three factors has not been investigated in a single experimental framework. To address this, the impact of these three factors on the accuracy of unbalance fault classification was investigated as follows: (i) vibration direction (vertical vs. horizontal) was considered; (ii) the most discriminative features were drawn from time domain signals and from the order and power spectra obtained in the frequency domain; (iii) six different SVM kernels were examined. Radial vibration signals were obtained from a Jeffcott rotor test rig designed to simulate a gas turbine rotor. Experiments were carried out at 1000 rpm under the following three operating conditions: normal operation without an added mass, and faulty operations with 3.6 g and 5.2 g unbalance masses. The overlapping sliding window method with a 25% overlap rate was used for raw sample expansion. Extracted features were ranked using the Kruskal–Wallis ranking test, and then the three most discriminative features in each domain–axis combination, in addition to all nine most discriminative features for each axis in a hybrid manner, were fed to the classifiers and evaluated using ten-fold cross-validation.
2. Materials and Methods
The flowchart representing all the processes carried out within the framework of this study is given in Figure 1.
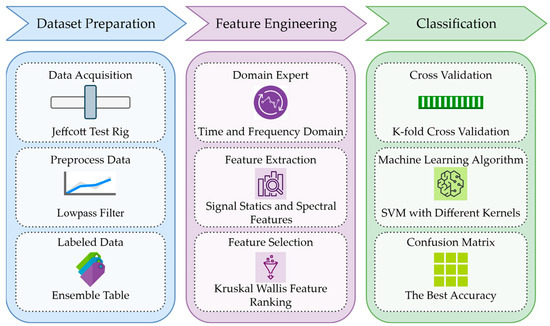
Figure 1.
The flowchart of the whole process.
2.1. Experimental Setup
The Jeffcott rotor test rig was designed at the engine dynamics laboratory of TUSAS Engine Industries Inc. (TEI) to simulate a gas turbine rotor, particularly in terms of unbalance faults. The rotor test rig consists of an Inconel 718 shaft (TEI Alloys Inc., Eskişehir, Turkey) with a length of 455 millimetres and a diameter of 6 millimetres. The shaft is supported by two GRW6001 ball bearings (GRW Gebr. Reinfurt GmbH & Co. KG, Rimpar, Germany) mounted on relatively rigid pedestals. A plastic disc with an outer diameter of 70 mm and a thickness of 40 mm in the middle of the shaft. The disc has two holes located 10 mm from the centreline of the shaft. An unbalance mass, also known as an eccentric mass, can be attached to the disc using a bolt and nut. The 455-millimetre-long shaft is connected to adjustable compressed air through an air wheel. The motor operation is controlled by adjustable compressed air for variable or constant speed rotation of the shaft. Two PCB 352A24 accelerometers (PCB Piezotronics, Depew, NY, USA) near the bearings on the shaft support measure radial rotor vibrations in the horizontal and vertical directions. The test rig’s rotational speed is measured using a BAUMER CH-8501 laser sensor CH-8501 laser tachometer (Baumer Electric AG, Frauenfeld, Switzerland) and a shaft-mounted reflector. The main components found in the rotor test rig are shown in Figure 2.
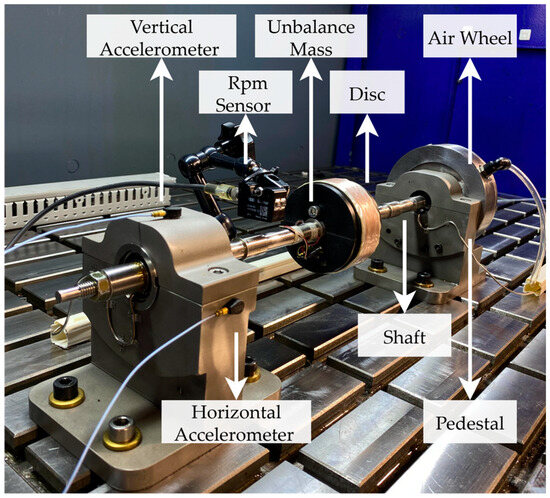
Figure 2.
The Jeffcott rotor test rig.
Detecting unbalance at speeds well below the first critical speed can make it possible to implement predictive maintenance practices by identifying, in advance, the more severe unbalances that may arise in the critical-speed region. The rotation speed was maintained at 1000 rpm, corresponding to a frequency of 16.66 Hz for all tests. The rotor was modelled using DyRoBes software (version 22.00) and its critical speeds were analysed. The first and second critical speeds were found to be 8936 rpm and 41,192 rpm, respectively. The selected test speed of 1000 rpm is well below these values, and according to ISO 21940-11 [16], the rotor is, therefore, considered rigid. As stated in ISO 21940-11, experimental tests at low speeds for rigid rotors are considered safe and allow the effects of unbalance to be observed in a linear and predictable manner. With the same unbalance mass, the vibration amplitude at test speed is lower than at higher speeds, making fault detection most challenging; hence, the classifier is evaluated under the lowest SNR conditions. The fast Fourier transform (FFT) will indicate a dominant vibration frequency at 1× rpm for all forms of unbalance [17]. The amplitude of the vibration at the 1× rpm frequency will vary directly with the square of the rotational speed [18].
In practical engineering applications, the quality of the fault samples obtained is often low due to high-frequency electrical noise, leading to lower fault diagnosis accuracy [19]. Although proper grounding and shielding were implemented, the signals acquired from the test rig still exhibited high noise levels. This electrical noise results from capacitive and inductive coupling, common-mode voltages, ground loop currents, conductive coupling, and electromagnetic radiation within the measurement chain. The key contributors are the switch-mode DC supply powering the BAUMER CH-8501 laser tachometer, the PCB 352A24 accelerometer cables, and the battery-powered LMS SCADAS XS data acquisition unit, which is connected to a PC via a USB port. In addition to electrical noise, raw vibration signals also contain high-frequency nutation vibrations [20], which occur in any rotating system with constant torque [21]. Therefore, in the signal pre-processing phase, the raw vibration signals were filtered with a low-pass filter, designed to suppress electrical noise and nutation vibrations and to remove aliasing. The low-pass filter’s cut-off frequency was set at 200 Hz, higher than the 1× rpm frequency and below half the sampling frequency [22].
Aliasing is a phenomenon that causes distortion of a signal by improperly sampling its frequency content with a low sampling rate. It results in high frequency data appearing at a lower frequency than its actual value, so the sampling rate must be high enough to ensure an accurate signal representation. According to the Nyquist theorem, a periodic signal must be sampled at a minimum of twice the frequency of its highest frequency component [23]. A sampling frequency of 4.096 kHz, which is high enough to exceed both the 1× rpm frequency and the low-pass filter’s 200 Hz cut-off frequency, was chosen to satisfy the Nyquist criterion. The data collected were transferred to a personal computer using the Simcenter Testlab software (version 2019.1) and the LMS SCADAS XS portable data acquisition hardware (Siemens Industry Software NV, Leuven, Belgium).
As the depth structure of the ML model required more training observations [24], the overlapping sliding window method was used for sample expansion. In this method, the dataset is divided using a specific size, which is then moved by a certain step interval with overlapping. The overlapping sliding window method with a 25% overlap rate was used. Thus, 300 sliding windows and a series of observations with 4096 samples in each window were created at each load condition to extract the features. The summary of the acquired dataset is presented in Table 1.

Table 1.
The summary of dataset.
Feature extraction, ranking, k-fold cross-validation, and classification were carried out using MATLAB R2023a, specifically employing the Diagnostic Feature Designer and the Classification Learner applications. All analyses were conducted on a computer equipped with an Intel Core i7-4702MQ processor and 32 GB of RAM. The random seed values were managed internally by the software, and the Classification Learner app was used with its default settings.
2.2. Feature Extraction
Feature extraction transforms the dataset into information suitable for ML algorithms, thereby aiding generalisation during the learning phase. Generalisation is essential to avoid overfitting the model to specific examples. ML model performance is highly dependent on selected features and data size [25]. In this study, feature extraction was performed separately in the time and frequency domains using filtered and overlapped vibration data in the vertical and horizontal directions to detect the unbalance faults.
2.2.1. Time Domain Analysis and Temporal Features
In vibration analysis, signals are obtained as a series of values, and these values represent physical quantities, such as acceleration in the time domain. The measurement signals, which are generally sampled repeatedly at predetermined time intervals, are in the time domain. A fault in the mechanical structure may cause the vibration waveform to change [26]. Time domain statistical features can be extracted from waveforms to identify faults. Thirteen different time domain features, known as temporal features, were used in this study.
2.2.2. Frequency Domain Analysis and Spectral Features
Frequency domain features, known as spectral features, are commonly used for the vibration analysis of rotating machines. Frequency domain features are generally more effective than time domain features for fault detection in rotating machines [27]. Machine faults cause some component(s) to be observed at abnormal frequencies in the frequency spectrum of the vibration signal [26].
Both power spectrum (PS) and order spectrum (OS) characterize the frequency content of a system and provide valuable information for feature generation. In this study, five different features were extracted using the PS and OS based frequency domain vibration analysis techniques.
The summary of temporal and spectral features is presented in Table 2, and the equations for the features are provided in Table 3 [28,29].

Table 2.
Temporal and spectral features.

Table 3.
Temporal and spectral features equations.
2.3. Feature Ranking
Feature ranking is important to identify the most informative features of the unbalance faults. The feature histograms showing the ability of the features to discriminate the operating conditions were generally non-normally distributed, and, therefore, the features were ranked using the Kruskal–Wallis ranking test. For non-normally distributed datasets with more than two groups, the Kruskal–Wallis feature ranking technique is used [30]. This method assesses whether data groups originate from the same or different populations by comparing their medians. Test statistics are calculated using ranks. Observations are ordered from smallest to largest across all groups, with each assigned a rank according to its position. For observations with identical values, the rank is determined by averaging the ranks of the tied observations.
The Kruskal–Wallis test uses the chi-square statistic, with the probability value (p-value) determining the significance of the test [14]. According to the Kruskal–Wallis test, if the p-value is less than a certain value, usually 0.01, it is concluded that the medians of the groups are statistically significantly different, i.e., the median of at least one group is different from the others [30].
2.4. K-Fold Cross-Validation
Cross-validation is used to prevent the overfitting and underfitting of classification models [31,32]. In this technique, the dataset is divided into k equal folds. During each iteration, k-1 folds are used to train the model and the kth fold is reserved for testing to validate the accuracy of the model. The whole procedure is repeated k times. In this study, to investigate the effects of different unbalance masses on fault severity, three operating conditions were used as three classes. The 10-fold cross-validation method was used to train and test the classification models. After the feature extraction process, each feature dataset used in the 10-fold cross-validation consisted of a total of 300 observations, with 100 observations per class, and each observation had 4096 samples. In each iteration of the 10-fold cross-validation, 30 observations obtained under normal and faulty operating conditions were used for testing, and the remaining 270 observations obtained under normal and faulty operating conditions were used to train the classification model. This process was repeated 10 times so that the model was tested and trained on all observations.
2.5. Classification
SVM, a type of supervised ML algorithm, is widely used for solving both classification and regression problems [33]. The SVM classifies data into two or more classes using hyperplanes, as presented in Figure 3. The support vectors are the data points closest to the hyperplane that separates the classes and lie along the plane’s boundaries. The SVM algorithm seeks to identify a hyperplane that most effectively distinguishes data points of one class from those of another [32]. The margin represents the maximum width of the plane parallel to the hyperplane that contains no data points. When the margin between classes is larger, the classification error tends to be lower [34]. The simplest form of SVM is the linear SVM algorithm, which can be used when the samples associated with the labels can be separated linearly. SVM algorithms can also handle non-linear classification problems through kernel tricks when the set of samples cannot be separated linearly [26].
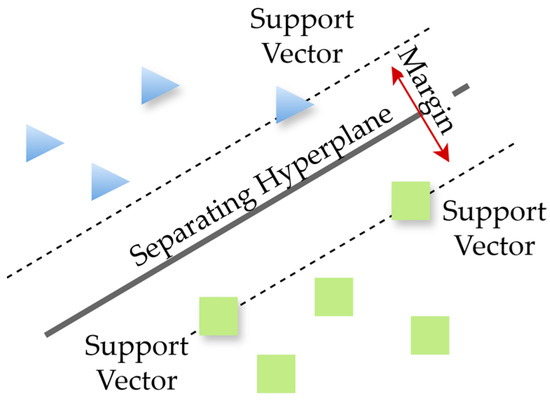
Figure 3.
Classification of two classes using SVM.
The decision functions of linear SVM and non-linear SVM can be expressed as the following Equations (1) and (2), respectively [26]:
where is the number of observation, are the input vectors, each of which has a number of component features, s are the labels also known as classes associated with the input vectors, s are the coefficients, b is a scalar representing the offset of the hyperplane from the origin in the input space, and is the kernel function.
The kernel functions used in SVM algorithms and kernel scales are shown in Table 4 [30,35], where P represents the number of predictors, also known as the number of features, which was three in this study. The kernel scale was set to ‘auto’ for the linear, quadratic, and cubic SVM models, whereas it was set to 0.43 for fine Gaussian SVM, 1.7 for medium Gaussian SVM, and 6.9 for coarse Gaussian SVM.

Table 4.
Used SVM algorithms with different kernels.
A confusion matrix is used to display the performance of a classification model. The correctly classified fault types are indicated by the diagonal entries of the matrix, while the misclassified fault types correspond to the off-diagonal entries. Various performance metrics are employed to evaluate classification algorithms, including accuracy, precision, recall, and F1 score [36]. These metrics are derived from the confusion matrix. After training and testing different classification algorithms, the model with the highest performance metrics is chosen. A typical confusion matrix for multi-class classification as in this study is shown in Figure 4, where, , and Class 1 is the normal operation without mass (Fault Code 1); Class 2 is a faulty operation with a 3.6g unbalance mass (Fault Code 2) and Class 3 is a faulty operation with a 5.2g unbalance mass (Fault Code 3), s are the Class i samples that were correctly classified, while s are the Class i samples that were incorrectly classified as Class j.
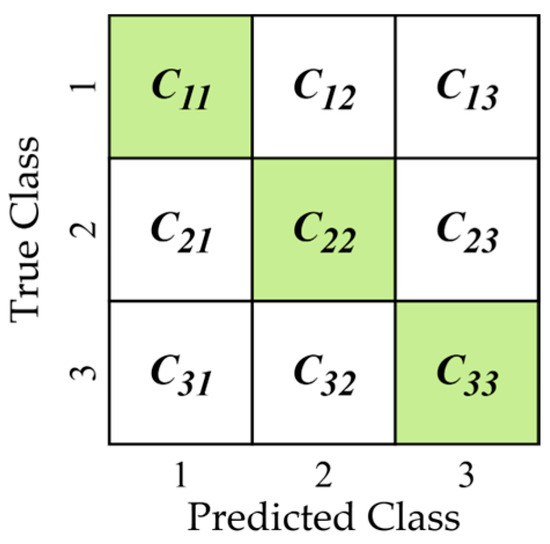
Figure 4.
A typical confusion matrix. Green diagonal cells (s) denote correctly classified instances, whereas white cells (s ) indicate misclassifications.
Classification algorithms are rated according to their accuracy, recall, precision, and F1 score. Accuracy measures the overall correctness of the model, recall measures how many instances of a particular class have been correctly identified, precision measures how many instances predicted to be a particular class are actually that class, and the F1 score is the harmonic mean of precision and recall for each class. The value of the F1 score ranges from zero to one, with high F1 scores indicating high classification performance [35]. The expressions for accuracy, recall, precision and F1 score are given in Equations (3)–(6), as follows [37]:
A scatter plot is a graphical representation of data that is used to evaluate the relationship between two variables. It is commonly used to determine which features distinguish between different fault classes. The best features are the ones that have the highest difference between classes. This means that the means of both classes are located farthest from each other on the scatter plot, while the same feature’s intra-class difference is minimal [38].
3. Results and Discussion
Ensemble views of the raw and low-pass-filtered vibration signals under the three load conditions are presented in Figure 5 and Figure 6, respectively. Because the rotor–bearing system exhibited greater stiffness along the horizontal axis than along the vertical axis, the vertical channel consistently registered larger vibration amplitudes. In addition, the low-pass filter effectively attenuated the broadband high-frequency noise present in the raw data. Consequently, classification models trained on the vertical signals attained superior accuracy compared with the models trained on horizontal signals.
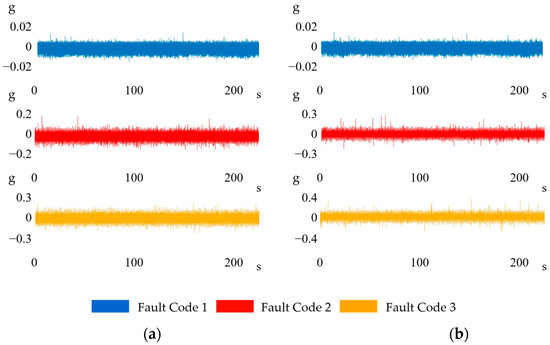
Figure 5.
Ensemble views of raw vibration signals in (a) horizontal and (b) vertical directions.
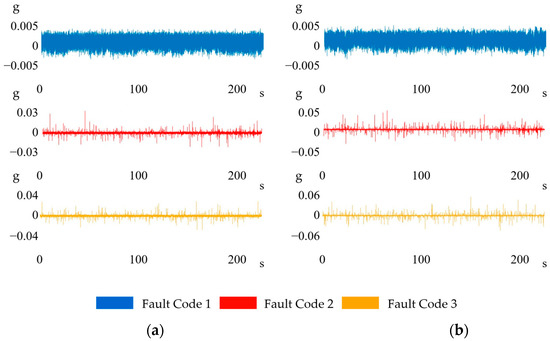
Figure 6.
Ensemble views of filtered vibration signals in (a) horizontal and (b) vertical directions.
The feature histograms for feature set F7 with normalised probability values showing the concentration of data points within certain intervals, where it can be observed that the features do not have a normal distribution, are shown in Figure 7. The feature ranking results obtained by the Kruskal–Wallis ranking algorithm are given in Figure 8, and, according to the feature ranking results, the features used for classification are given in Table 5.
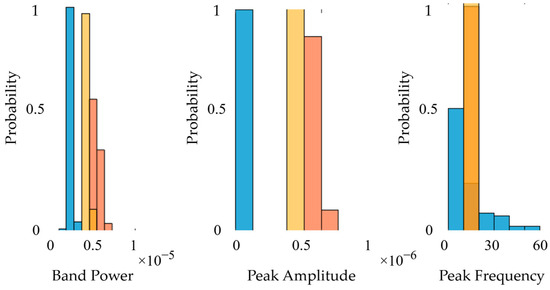
Figure 7.
Feature histograms for feature set F7.
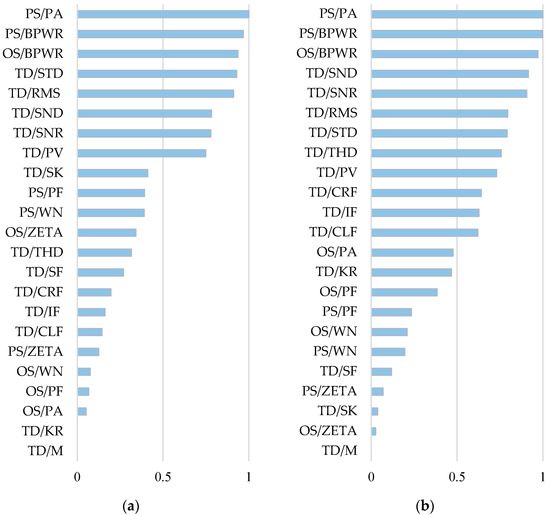
Figure 8.
Feature ranking results for (a) horizontal and (b) vertical directions.

Table 5.
Selected features.
The classification performances of SVM algorithms with different kernels for different feature sets are shown as a heat map in Table 6.

Table 6.
Classification performances.
The effects of kernel and feature set selection on classification accuracy were statistically analysed separately using average classification accuracies at a significance level of α = 0.05. The non-parametric Friedman test was applied, followed by paired Wilcoxon signed-rank tests with Holm correction for post hoc comparisons, and Kendall’s W was reported as the effect-size measure. The statistical analysis results are given in Table 7. According to the results, feature set selection had a much greater impact on the classification accuracy than the SVM kernel choice.

Table 7.
Statistical analysis results.
Classification using vibration signals in the vertical direction has higher accuracy rates than methods using signals in the horizontal direction for the feature sets obtained in the same domains. In other words, the classification accuracies obtained with the feature sets of F5, F6, F7, and F8 are higher than F1, F2, F3, and F4, respectively.
The highest average classification accuracy of 99.9% was obtained with feature set F7 (PA, BPWR, and PF) based on the PS of the vertical vibration signal, whereas the lowest average accuracy of 74.1% was achieved with feature set F2 (BPWR, ZETA, and WN) based on the OS of the horizontal vibration signal (Figure 9a). As the PS focuses on the energy distribution of the signal and can better express the energy density, especially at constant speed, the PS-based features allowed higher classification accuracies in all SVM algorithms compared to both the time domain features and the OS-based features for detecting unbalance faults. On the other hand, an analysis of the average classification accuracies for feature sets F4 and F8, which incorporate the nine most discriminative features in the time and frequency domains, revealed that neither hybrid feature selection nor increasing the number of features led to a notable and consistent improvement in overall classification performance.
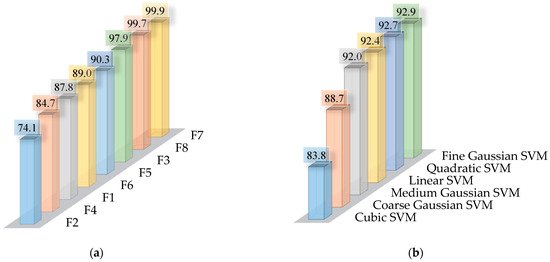
Figure 9.
The average classification accuracies for different (a) feature sets and (b) SVM kernels.
Among the kernels tested, the fine Gaussian SVM provided the best overall performance with an average accuracy of 92.9%, while on the other hand, the Cubic SVM provided the worst overall performance, with an average accuracy of 83.8% (Figure 9b). The highest classification accuracy of 100% was achieved with the linear SVM, cubic SVM, medium Gaussian SVM, and coarse Gaussian SVM using feature set F7, and with the linear SVM using feature set F8; on the other hand, the lowest classification accuracy of 60% was obtained with the cubic SVM using the F2 feature set. To further elucidate the performance differences among kernels, in the fine Gaussian SVM, the fine Gaussian kernel, with its smaller kernel width, effectively adapted to both clearly separable (F7) and complex feature distributions (F2). Although it did not achieve the highest single-set accuracy (100%), it consistently demonstrated strong performance and flexibility across diverse feature sets, resulting in the highest overall mean accuracy (92.9%). The quadratic SVM, employing a second-degree polynomial kernel, achieved a relatively high average accuracy of 92.7%. It successfully modeled moderate non-linearities but lacked optimal adaptability for highly intricate distributions. The Linear kernel achieved perfect classification accuracy (100%) on the linearly well-structured feature sets F7 and F8. However, its inherently simpler structure resulted in reduced adaptability to more complex, overlapping feature distributions, thereby producing comparatively lower accuracy on challenging sets, such as F2. The medium Gaussian kernel balanced kernel locality and smoothness effectively, reaching perfect accuracy (100%) for clearly separable features in F7. Although its broader kernel width resulted in slightly lower accuracy on more complex distributions (e.g., F2) compared to the fine Gaussian kernel, it still provided stable and reliable performance. On the other hand, with its larger kernel width producing smoother decision boundaries, the coarse Gaussian kernel excellently handled distinct feature clusters (F7), achieving perfect accuracy (100%). Nevertheless, this kernel exhibited limited flexibility for distinguishing closely spaced features in more complex sets, resulting in slightly reduced overall performance relative to the fine and medium Gaussian kernels. As for the cubic SVM, Despite being able to model moderate non-linearities due to its third-degree polynomial structure, the cubic kernel significantly struggled with complex, overlapping distributions, especially evident with feature set F2. This limitation resulted in the lowest overall average accuracy (83.8%). Consequently, if the chosen kernel function does not align sufficiently well with the feature-space geometry, classification accuracy may decrease.
The scatter plots and confusion matrix obtained with the linear SVM, cubic SVM, medium Gaussian SVM, and coarse Gaussian SVM classifiers using feature set F7 are given in Figure 10. The Kruskal–Wallis ranking results showed that PA was the most discriminative feature, followed by BPWR and finally PF. This can also be clearly seen in the scatter plots. According to the confusion matrix, the recall and precision values are 100%, and the F1 score is 1 for each class. Thus, all three different operating conditions were classified with 100% accuracy.
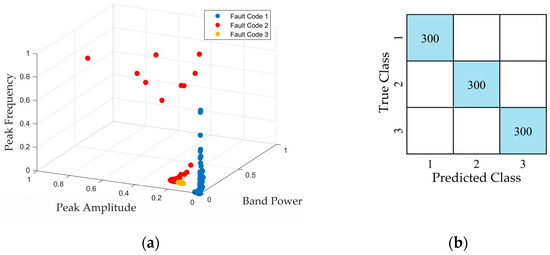
Figure 10.
The (a) scatter plots and (b) confusion matrix (light-blue diagonal cells represent correctly classified instances, while white cells denote misclassifications.) for feature set F7 with the linear SVM, cubic SVM, medium Gaussian SVM, and coarse Gaussian SVM classifiers.
A summary of the training results analysis for feature set F7 can be found in Table 8. These results demonstrate that the trained models are highly accurate and computationally efficient. Prediction speeds of over 9000 observations per second (obs/s) for the linear and medium Gaussian support vector machines indicate their suitability for future real-time applications. Their compact model sizes (16–25 kB) also make them appropriate for embedded systems.

Table 8.
Training results analysis for feature set F7.
Additional analyses were also conducted with the F7 feature set, which had previously yielded the highest mean classification accuracy (99.9%). Four factors influencing the classification performance were examined individually, as follows: (i) Classifier type—perfect accuracy (100%) was obtained with the decision tree, k-nearest neighbor, and neural network classifiers, indicating that F7 maintains strong discriminative power across diverse algorithms; (ii) sliding-window overlap ratio—windows with no overlap and those with 50% overlap produced identical mean accuracies (99.8%), suggesting that overlap has little effect when the dataset is sufficiently large; (iii) dataset size—when the data were down sampled by 50% and 90%, mean accuracies declined only to 99.4% and 99.1%, respectively, demonstrating the feature set’s robustness to reduced sample counts; (iv) noise filtering—when classification was performed on raw (unfiltered) signals, the mean accuracy dropped to 74.5%, and this finding confirms that effectively attenuating all frequency components other than the unbalance-related 1 × rpm component is critical for classification performance.
4. Conclusions
This study systematically quantified how vibration direction, feature selection strategy, and the SVM kernel choice interact to influence unbalance fault classification in a Jeffcott-rotor test rig. Statistical analyses showed that feature set selection had a much greater impact on classification accuracy than SVM kernel choice. Features extracted from vertical vibration signals consistently outperformed those from the horizontal axis, whereas power spectrum features delivered markedly higher accuracies than either order spectrum or time domain features. The higher energy concentration and clearer spectral peaks present in vertical vibration signals at constant speed make power spectrum-based features more separable in the SVM feature space. Overall classification performance was not consistently or noticeably improved by either hybrid feature selection or the inclusion of more features. Selecting the right SVM kernel shapes both the model’s flexibility and its fit to the chosen feature space; when this fit is inadequate, classification accuracy may decrease. Accordingly, this study offers a novel, integrated benchmark that quantifies the interplay among measurement axis, feature domain, and kernel choice, providing practitioners with concrete guidelines for sensor placement, feature engineering, and SVM hyperparameter tuning in real-world unbalance-monitoring systems. To detect unbalance faults, experiments were performed at a constant rotational speed in a controlled laboratory environment. In future, this work will be extended to include variable rotor speeds and different fault types, both on a laboratory test rig and on an operational gas turbine engine. The ultimate goal is to develop a real-time warning system for rotor faults in gas turbine engines using machine learning techniques.
Author Contributions
Conceptualization, B.E.; methodology, B.E.; software, M.A.; validation, B.E.; formal analysis, B.E.; investigation, M.A. and B.E.; resources, M.A.; data curation, M.A.; writing—original draft preparation, B.E.; writing—review and editing, M.A. and B.E.; visualization, M.A.; supervision, B.E.; project administration, B.E.; funding acquisition, B.E. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by The Scientific and Technological Research Council of Türkiye—TUBITAK (Grant No. 118C103) under the “Development of Gas Turbine Engine Technologies” project as part of the TÜBİTAK 2244 industrial Ph.D. programme.
Data Availability Statement
The data presented in this study are available from the corresponding author upon reasonable request, with restrictions due to company security policies as the datasets were generated as part of company operations. Access will be limited to what is permissible under the company’s security protocols.
Conflicts of Interest
Author Mine Ateş was employed by the company R&D Department, Tusaş Engine Industries Inc. (TEI), 26210 Eskişehir, Turkey. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| c | Damping coefficient |
| D | Distortion power |
| k | Stiffness |
| m | Mass |
| N | Noise power |
| S | Signal power |
References
- Almutairi, K.; Sinha, J.K.; Wen, H. Fault detection of rotating machines using poly-coherent composite spectrum of measured vibration responses with machine learning. Machines 2024, 12, 573. [Google Scholar] [CrossRef]
- Singh, S.; Kumar, N. Rotor faults diagnosis using artificial neural networks and support vector machines. Int. J. Acoust. Vib. 2015, 20, 153–159. [Google Scholar] [CrossRef]
- Tahir, M.M.; Hussain, A.; Badshah, S.; Khan, A.Q.; Iqbal, N. Classification of unbalance and misalignment faults in rotor using multi-axis time domain features. In Proceedings of the 2016 International Conference on Emerging Technologies (ICET), Islamabad, Pakistan, 16 January 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Bechiri, M.B.; Allal, A.; Naoui, M.; Khechekhouche, A.; Alsaif, H.; Boudjemline, A. Effective diagnosis approach for broken rotor bar fault using bayesian-based optimization of machine learning hyperparameters. IEEE Access 2024, 12, 3464108. [Google Scholar] [CrossRef]
- Ozkat, E.C. Vibration data-driven anomaly detection in UAVs: A deep learning approach. Eng. Sci. Technol. Int. J. 2024, 54, 101702. [Google Scholar] [CrossRef]
- Akyaz, T.; Engın, D. Machine learning-based predictive maintenance system for artificial yarn machines. IEEE Access 2024, 12, 125446–125461. [Google Scholar] [CrossRef]
- Zhu, T.; Ran, Y.; Zhou, X.; Wen, Y. A survey of predictive maintenance: Systems, purposes and approaches. arXiv 2019, arXiv:1912.07383. [Google Scholar] [CrossRef]
- Lan, L.; Liu, X.; Wang, Q. Fault detection and classification of the rotor unbalance based on dynamics features and support vector machine. Meas. Control 2023, 56, 1075–1086. [Google Scholar] [CrossRef]
- Zhang, J.; Ma, W.; Lin, J.; Ma, L.; Jia, X. Fault diagnosis approach for rotating machinery based on dynamic model and computational intelligence. Measurement 2015, 59, 73–87. [Google Scholar] [CrossRef]
- Hübner, G.R.; Pinheiro, H.; de Souza, C.E.; Franchi, C.M.; da Rosa, L.D.; Dias, J.P. Detection of mass imbalance in the rotor of wind turbines using Support Vector Machine. Renew. Energy 2021, 170, 49–59. [Google Scholar] [CrossRef]
- Nti, I.K.; Nyarko-Boateng, O.; Aning, J. Performance of machine learning algorithms with different k values in k-fold cross validation. Int. J. Inf. Technol. Comput. Sci. 2021, 13, 61–71. [Google Scholar] [CrossRef]
- Nath, A.G.; Udmale, S.S.; Singh, S.K. Role of artificial intelligence in rotor fault diagnosis: A comprehensive review. Artif. Intell. Rev. 2021, 54, 2609–2668. [Google Scholar] [CrossRef]
- Alsaleh, A.; Sedighi, H.M.; Ouakad, H.M. Experimental and theoretical investigations of the lateral vibrations of an unbalanced Jeffcott rotor. Front. Struct. Civ. Eng. 2020, 14, 1024–1032. [Google Scholar] [CrossRef]
- Jamil, M.A.; Khanam, S. Influence of One-Way ANOVA and Kruskal–Wallis based feature ranking on the performance of ML classifiers for bearing fault diagnosis. J. Vib. Eng. Technol. 2024, 12, 3101–3132. [Google Scholar] [CrossRef]
- McKight, P.E.; Najab, J. Kruskal-wallis test. In The Corsini Encyclopedia of Psychology; Wiley Online Library: Hoboken, NJ, USA, 2010; p. 1. [Google Scholar] [CrossRef]
- ISO 21940-11; Mechanical vibration—Rotor balancing—Part 11: Procedures and tolerances for rotors with rigid behaviour. International Organization for Standardization (ISO): Geneva, Switzerland, 2016.
- Choudhury, T.; Viitala, R.; Kurvinen, E.; Viitala, R.; Sopanen, J. Unbalance estimation for a large flexible rotor using force and displacement minimization. Machines 2020, 8, 39. [Google Scholar] [CrossRef]
- Girdhar, P.; Scheffer, C. Practical Machinery Vibration Analysis and Predictive Maintenance, 1st ed.; Elsevier: Oxford, England, 2004; p. 90. [Google Scholar] [CrossRef]
- Wang, C.; Sun, H.; Cao, X. Construction of the efficient attention prototypical net based on the time–frequency characterization of vibration signals under noisy small sample. Measurement 2021, 179, 109412. [Google Scholar] [CrossRef]
- Xiang, B.; Xu, J.; Liu, Z.; Wong, W.; Zheng, L. Vibration characteristics and cross-feedback control of magnetically suspended blower based on complex-factor model. J. Sound Vib. 2023, 556, 117729. [Google Scholar] [CrossRef]
- Kasdin, N.J.; Paley, D.A. Engineering Dynamics: A Comprehensive Introduction, 1st ed.; Princeton University Press: Princeton, NJ, USA, 2011; p. 489. [Google Scholar]
- El Badaoui, M.; Bonnardot, F. Impact of the non-uniform angular sampling on mechanical signals. Mech. Syst. Signal Process. 2014, 44, 199–210. [Google Scholar] [CrossRef]
- Leis, J.W. Digital Signal Processing Using MATLAB for Students and Researchers, 1st ed.; Wiley: Hoboken, NJ, USA, 2011; pp. 81–82. [Google Scholar] [CrossRef]
- Hendrickx, K.; Meert, W.; Mollet, Y.; Gyselinck, J.; Cornelis, B.; Gryllias, K.; Davis, J. A general anomaly detection framework for fleet-based condition monitoring of machines. Mech. Syst. Signal Process. 2020, 139, 106585. [Google Scholar] [CrossRef]
- Domingos, P. A few useful things to know about machine learning. Commun. ACM. 2012, 55, 78–87. [Google Scholar] [CrossRef]
- Lei, Y. Intelligent Fault Diagnosis and Remaining Useful Life Prediction of Rotating Machinery, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2017; pp. 30–38, 121–124. [Google Scholar] [CrossRef]
- Vishwakarma, M.; Purohit, R.; Harshlata, V.; Rajput, P. Vibration analysis & condition monitoring for rotating machines: A review. Mater. Today Proc. 2017, 4, 2659–2664. [Google Scholar] [CrossRef]
- MathWorks. Predictive Maintenance Toolbox™ User’s Guide, R2021b; MathWorks Inc.: Natick, MA, USA, 2021; Available online: https://www.mathworks.com/help/predmaint/ (accessed on 21 July 2025).
- Kester, W. MT-003 TUTORIAL Understand SINAD, ENOB, SNR, THD, THD + N, and SFDR so You Don’t Get Lost in the Noise Floor; Analog Devices: Norwood, MA, USA, 2009. [Google Scholar]
- Vargas-Lopez, O.; Perez-Ramirez, C.A.; Valtierra-Rodriguez, M.; Yanez-Borjas, J.J.; Amezquita-Sanchez, J.P. An explainable machine learning approach based on statistical indexes and svm for stress detection in automobile drivers using electromyographic signals. Sensors 2021, 21, 3155. [Google Scholar] [CrossRef] [PubMed]
- Hassan, S.; Li, Q.; Zubair, M.; Alsowail, R.A.; Qureshi, M.A. Unveiling the correlation between nonfunctional requirements and sustainable environmental factors using a machine learning model. Sustainability 2024, 16, 5901. [Google Scholar] [CrossRef]
- Pule, M.; Matsebe, O.; Samikannu, R. Application of PCA and SVM in fault detection and diagnosis of bearings with varying speed. Math. Probl. Eng. 2022, 2022, 5266054. [Google Scholar] [CrossRef]
- Vamsi, I.; Sabareesh, G.R.; Penumakala, P.K. Comparison of condition monitoring techniques in assessing fault severity for a wind turbine gearbox under non-stationary loading. Mech. Syst. Signal Process. 2019, 124, 1–20. [Google Scholar] [CrossRef]
- Hasan, M.M.; Chowdhury, D.; Hasan, A.S.M.K. Statistical features extraction and performance analysis of supervised classifiers for non-intrusive load monitoring. Eng. Lett. 2019, 27, 776–782. [Google Scholar]
- MathWorks. Statistics and Machine Learning Toolbox™ User’s Guide, R2016b; MathWorks Inc.: Natick, MA, USA, 2016; Available online: https://www.mathworks.com/help/stats/ (accessed on 21 July 2025).
- Al-Haddad, L.A.; Jaber, A.A.; Hamzah, M.N.; Fayad, M.A. Vibration-current data fusion and gradient boosting classifier for enhanced stator fault diagnosis in three-phase permanent magnet synchronous motors. Electr. Eng. 2023, 106, 3253–3268. [Google Scholar] [CrossRef]
- Tharwat, A. Classification assessment methods. Appl. Comput. Inform. 2020, 17, 168–192. [Google Scholar] [CrossRef]
- Kafeel, A.; Aziz, S.; Awais, M.; Khan, M.A.; Afaq, K.; Idris, S.A.; Alshazly, H.; Mostafa, S.M. An expert system for rotating machine fault detection using vibration signal analysis. Sensors 2021, 21, 7587. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).