Advanced Control Strategy for Induction Motors Using Dual SVM-PWM Inverters and MVT-Based Observer
Abstract
1. Introduction
2. Model of Induction Motor and Power Driver
- The switching frequency;
- The voltage slew rate ();
- The layout and grounding of the power stage;
- The common mode voltage (CMV);
- The cable lengths and shielding;
- The parasitic components.
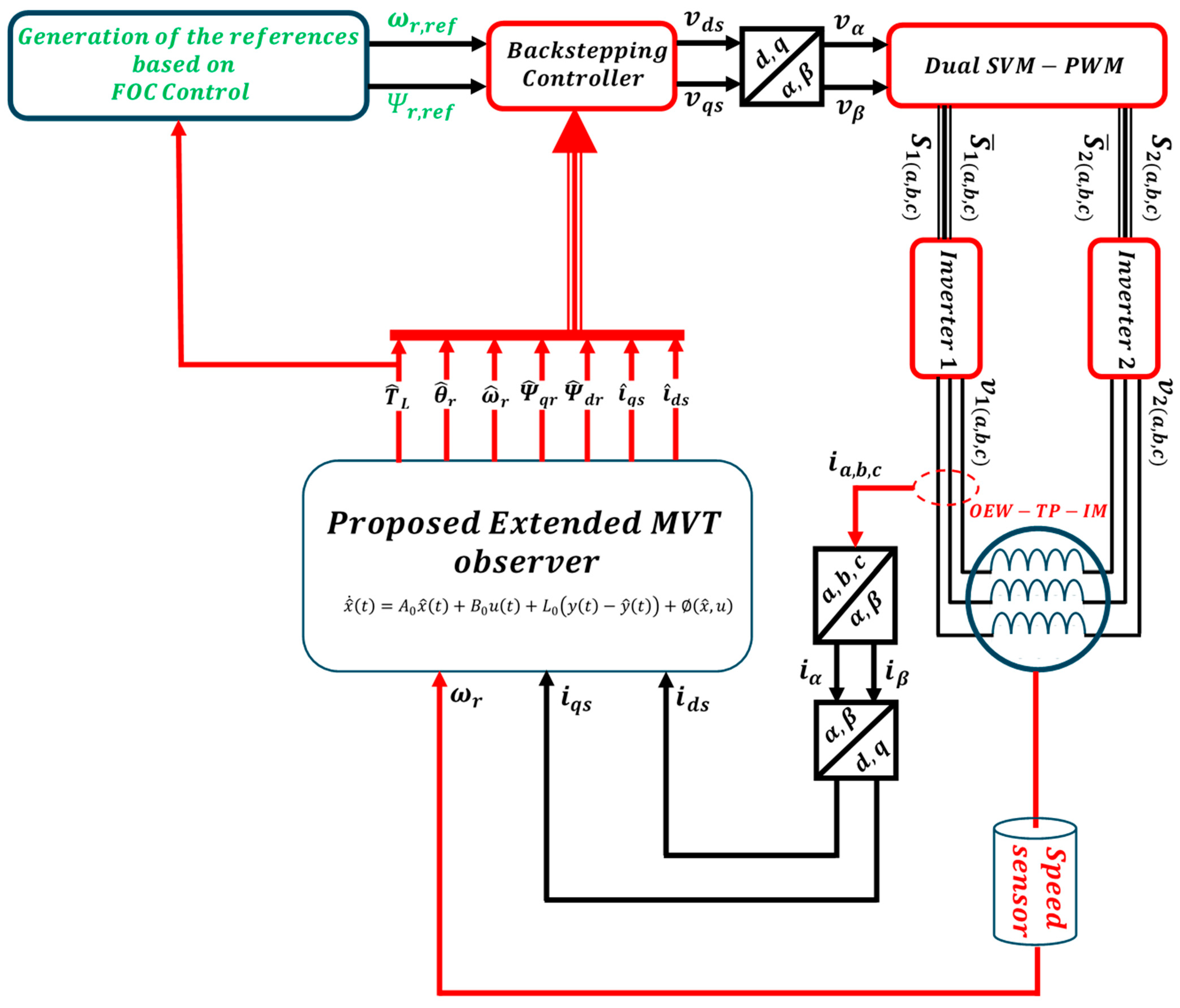
3. Backstepping Control Design Based on a MVT Observer
3.1. Backstepping Control of OEW-IM Machine
3.2. Speed and Flux Control
4. Mean Value Theorem Observer Design
4.1. Mean Value Theorem
4.2. Nonlinear Sector Concept
4.3. Stability Design
5. Simulation Results
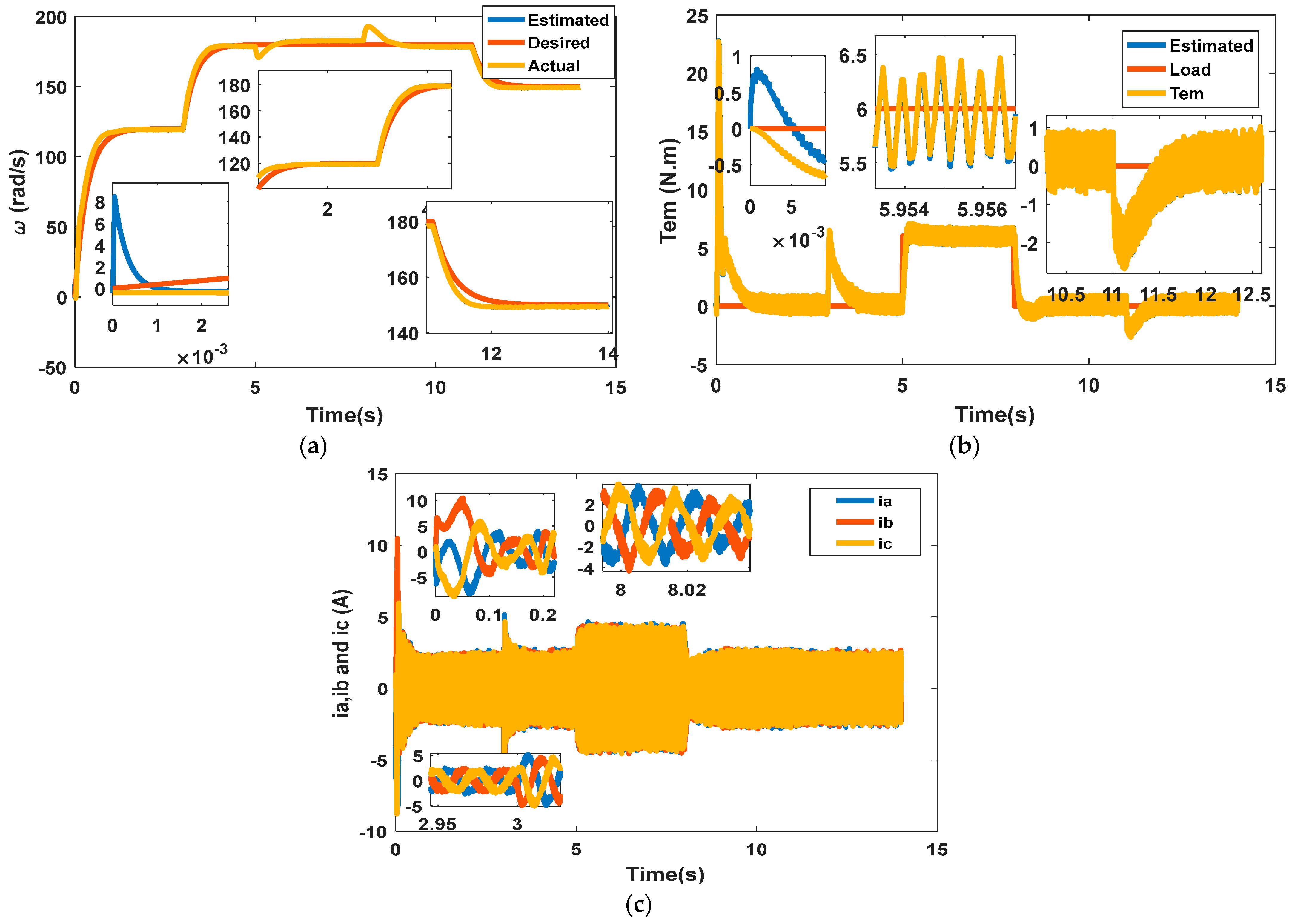
5.1. Assessment of Performance Under Normal Operating Conditions
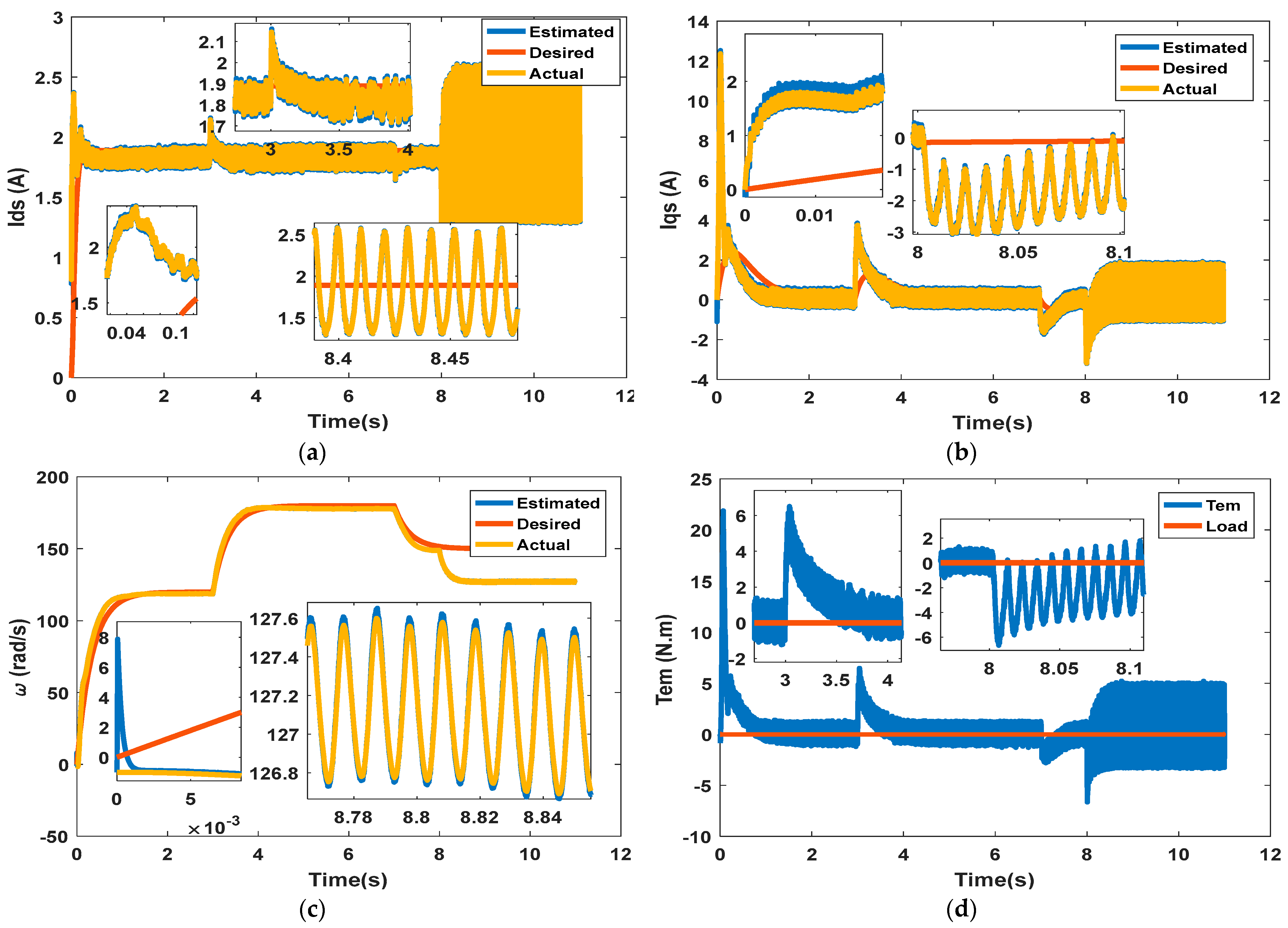
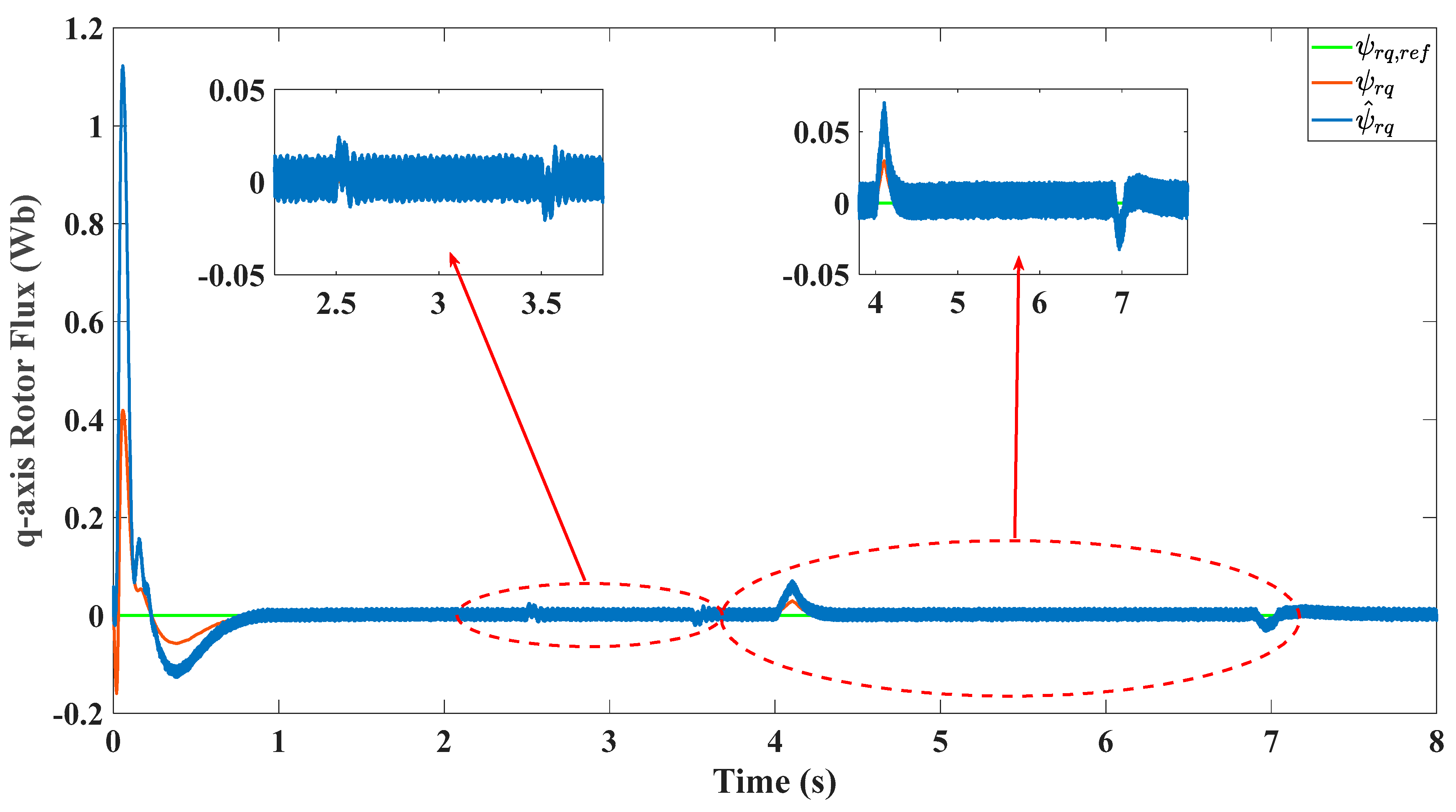
5.2. Performance Under Short Circuit and Parameter Variations
5.3. Performance Metrics Evaluation of the Proposed Extended MVT Observer
- Variation of by 30% of its initial value, which is considered an internal parameter uncertainty;
- Load torque variation, which is considered an external perturbation.
- RMSE: root mean square error;
- IAE: integral of absolute error;
- ITAE: integral of time-weighted absolute error;
- ISE: integral of squared error.
5.4. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mavila, P.C.; Rajeevan, P.P. A New Direct Torque Control Scheme for Five Phase Open-end Winding Induction Motor Drives with Reduced DC Voltage Requirement. In Proceedings of the IEEE International Conference on Power Electronics, Smart Grid and Renewable Energy, Cochin, India, 2–4 January 2020. [Google Scholar]
- Levi, E.; Nyoman, I.; Wahyu, N.; Nandor, B.; Martin, J. A Space-Vector Modulation Scheme for Multilevel Open-End Winding Five-Phase Drives. IEEE Trans. Energy Convers. 2012, 27, 1–10. [Google Scholar]
- Trabelsi, R.; Khedher, A.; Mimouni, F.M.; M’Sahli, F. An Adaptive Backstepping Observer for On-Line Rotor Resistance Adaptation. Int. J. Sci. Tech. Autom. Control Comput. Eng. 2010, 4, 1246–1267. [Google Scholar]
- Moutchou, M.; Abbou, A.; Mahmoudi, H. MRAS-Based Sensorless Speed Backstepping Control for Induction Machine, Using a Flux Sliding Mode Observer. Turk. J. Electr. Eng. Comput. Sci. 2015, 23, 187–200. [Google Scholar] [CrossRef]
- Regaya, C.B.; Farhani, F.; Zaafouri, A.; Chaari, A. An Adaptive Sliding-Mode Speed Observer for Induction Motor under Backstepping Control. ICIC Express Lett. 2017, 11, 763–771. [Google Scholar]
- Zhonggang, Y.; Guoyin, L.; Yanqing, Z.; Jing, L.; Xiangdong, S.; Yanru, Z. A Speed and Flux Observer of Induction Motor Based on Extended Kalman Filter and Markov Chain. IEEE Trans. Power Electron. 2017, 32, 7096–7117. [Google Scholar]
- Khadar, S.; Kouzou, A.; Hafaifa, A.; Iqbal, A. Investigation on SVM Backstepping Sensorless Control of Five-Phase Open-End Winding Induction Motor Based on Model Reference Adaptive System and Parameter Estimation. Eng. Sci. Technol. Int. J. 2019, 22, 1013–1026. [Google Scholar]
- Khadar, S.; Kouzou, A.; Rezaoui, M.M.; Hafaifa, A. Fault Tolerant Sensorless Sliding Mode Control by Parameters Estimation of an Open-End Winding Five-Phase Induction Motor. Model. Meas. Control A 2019, 92, 6–15. [Google Scholar] [CrossRef]
- Khadar, S.; Abu-Rub, H.; Kouzou, A. Sensorless Field-Oriented Control for Open-End Winding Five-Phase Induction Motor with Parameters Estimation. IEEE Open J. Ind. Electron. Soc. 2021, 2, 266–279. [Google Scholar] [CrossRef]
- Meziane, S.; Toufouti, R.; Benalla, H. Nonlinear Control of Induction Machines Using an Extended Kalman Filter. Acta Polytech. Hung. 2008, 5, 41–58. [Google Scholar]
- Pourgholi, M.; Majd, V.J. A Nonlinear Adaptive Resilient Observer Design for a Class of Lipschitz Systems Using LMI. Circ. Syst. Signal Process 2011, 30, 1401–1415. [Google Scholar] [CrossRef]
- Zemouche, A.; Boutayeb, M.; Bara, G.I. Observer Design for Nonlinear Systems: An Approach Based on the Differential Mean Value Theorem. In Proceedings of the IEEE Conference on Decision and Control, Cancun, Mexico, 9–11 December 2008; pp. 6353–6358. [Google Scholar]
- Hammoudi, M.Y.; Allag, A.; Becherif, M.; Benbouzid, M.; Alloui, H. Observer Design for Induction Motor: An Approach Based on the Mean Value Theorem. Front. Energy 2014, 8, 426–433. [Google Scholar] [CrossRef]
- Imen, H.B.; Hajji, S.; Chaari, A. Backstepping Controller Design Using a High Gain Observer for Induction Motor. Int. J. Comput. Appl. 2011, 23, 1–6. [Google Scholar]
- Regaya, C.B.; Farhani, F.; Zaafouri, A.; Chaari, A. A Novel Adaptive Control Method for Induction Motor Based on Backstepping Approach Using dSpace DS1104 Control Board. Mech. Syst. Signal Process 2018, 100, 466–481. [Google Scholar]
- Bennassar, A.; Abbou, A.; Akherraz, M.; Barara, M. Sensorless Backstepping Control Using an Adaptive Luenberger Observer with Three Levels NPC Inverter. Int. J. Comput. Electr. Autom. Control Inf. Eng. 2013, 7, 1171–1177. [Google Scholar]
- Aziz, A.G.M.A.; Rez, H.; Diab, A.A.Z. Robust Sensorless Model-Predictive Torque Flux Control for High-Performance Induction Motor Drives. Mathematics 2021, 9, 403. [Google Scholar] [CrossRef]
- Zeghib, O.; Allag, A.; Allag, M.; Hamidani, B. A Robust Extended H∞ Observer Based on the Mean Value Theorem Designed for Induction Motor Drives. Int. J. Syst. Assur. Eng. Manag. 2019, 10, 533–542. [Google Scholar] [CrossRef]
- Allag, M.; Allag, A.; Zeghib, O.; Hamidani, B. Robust H∞ Control Based on the Mean Value Theorem for Induction Motor Drive. J. Control Autom. Electr. Syst. 2019, 30, 657–665. [Google Scholar] [CrossRef]
- Hamidatou, T.; Kouzou, A.; Kaddouri, A.M.; Mida, A. Fuzzy logic based speed control of indirect field oriented controlled doubly star open-end winding induction motor. In Proceedings of the 2023 Second International Conference on Energy Transition and Security (ICETS), Adrar, Algeria, 12–14 December 2023; pp. 1–6. [Google Scholar]
- Guzmán, J.; Silva, C.A.; Carvajal, G.; Agüero, J.C. Model Predictive Control for Suppression of Zero-Sequence Current in Open-End Winding Induction Motors. In Proceedings of the 2023 IEEE International Future Energy Electronics Conference (IFEEC), Sydney, Australia, 20–23 November 2023; pp. 251–256. [Google Scholar]
- Lee, K.; Han, Y. Discontinuous PWM Scheme for an Open-end Winding Induction Motor Drives Fed by Dual Inverter. In Proceedings of the 2022 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 9–13 October 2022; pp. 1–6. [Google Scholar]
- Khadar, S.; Kouzou, A.; Mohamed-Seghir, M. “Stability Analysis of Adaptive Full-Order Observer for Open-End Winding Five-Phase Induction Motor. In Proceedings of the 2021 IEEE Southern Power Electronics Conference (SPEC), Kigali, Rwanda, 6–9 December 2021; pp. 1–5. [Google Scholar]
- Khadar, S.; Abu-Rub, H.; Kouzou, A. MRAS-Based Sensorless Control Scheme for Open- End Stator Winding Six-Phase Induction Motor with Fuzzy Logic Speed Controller: Real-Time Simulation. In Proceedings of the 2021 IEEE 30th International Symposium on Industrial Electronics (ISIE), Kyoto, Japan, 20–23 June 2021; pp. 1–6. [Google Scholar]
- Khadar, S.; Abu-Rub, H.; Kouzou, A. Sensorless Sliding Mode Control of Open-End Dual-Stator Induction Motor using Extended Kalman Filter. In Proceedings of the 2021 18th International Multi-Conference on Systems, Signals Devices (SSD), Monastir, Tunisia, 22–25 March 2021; pp. 1136–1141. [Google Scholar]
- Mohan, L.; Pant, K.; Rajeevan, P.P. A Speed Range Extension Scheme for Scalar-Controlled Open-End Winding Induction Motor Drives. IEEE Trans. Ind. Appl. 2022, 58, 2055–2062. [Google Scholar] [CrossRef]
- Jia, Y.F.; Xu, N.; Chu, L.; Zhang, Y.; Xu, Z.; Li, Y.K.; Yang, Z.H. Control Strategy for an Open-End Winding Induction Motor Drive System for Dual-Power Electric Vehicles. IEEE Access 2020, 8, 8844–8860. [Google Scholar] [CrossRef]
- Younes, D.; El Mehdi, A.S.A.; Houcine, C.; Mouloud, D. Sensorless Torque Control of an Electric Vehicle Driven by an Open End Winding Induction Motor: An Experimental Study. In Proceedings of the 2023 Second International Conference on Energy Transition and Security (ICETS), Adrar, Algeria, 12–14 December 2023. [Google Scholar]
- Lodi, K.A.; Beig, A.R.; Al Jaafari, K.A.; Aung, Z. ANN-Based Improved Direct Torque Control of Open-End Winding Induction Motor. IEEE Trans. Ind. Electron. 2024, 71, 12030–12040. [Google Scholar] [CrossRef]
- Reddy, K.S.; Baskar, S. A Literature Review on Open End Windings Induction Motor Drives. In Proceedings of the 2021 5th International Conference on Electrical, Electronics, Communication, Computer Technologies and Optimization Techniques (ICEECCOT), Mysuru, India, 10–11 December 2021; pp. 395–398. [Google Scholar]
- Hamdi, W.; Hammoudi, M.Y.; Boukhlouf, A. Observer Design for Takagi–Sugeno Fuzzy Systems with Unmeasurable Premise Variables Based on Differential Mean Value Theorem. Eng. Proc. 2023, 58, 28. [Google Scholar] [CrossRef]
- Houili, R.; Hammoudi, M.Y.; Benbouzid, M.; Titaouine, A. Observer-Based Controller Using Line Integral Lyapunov Fuzzy Function for TS Fuzzy Systems: Application to Induction Motors. Machines 2023, 11, 374. [Google Scholar] [CrossRef]
- Krzemiński, Z. Nonlinear Control of Induction Motor. IFAC Proc. Vol. 1987, 20, 357–362. [Google Scholar] [CrossRef]
- Ranjit, M.; Reddy, T.B.; Suryakalavathi, M. Performance Improvements in Open End Winding Induction Motor Drive Using Decoupled PWM Techniques. Energy Procedia 2017, 117, 810–817. [Google Scholar] [CrossRef]
- Zerdani, M.; Chafouk, H.; Ardjoun, S.A.E.M. Performance Analysis of a Dual-Inverter-Fed Open-End Winding Induction Machine under Asymmetrical Control: Theoretical Approach and Experimental Validation. Symmetry 2024, 16, 395. [Google Scholar] [CrossRef]
- Kiadehi, A.D.; Drissi, K.E.K.; Pasquier, C. Voltage THD Reduction for Dual-Inverter Fed Open-End Load With Isolated DC Sources. IEEE Trans. Ind. Electron. 2017, 64, 2102–2111. [Google Scholar] [CrossRef]
- Kalaiselvi, J.; Srinivas, S. Bearing Currents and Shaft Voltage Reduction in Dual-Inverter-Fed Open-End Winding Induction Motor with Reduced CMV PWM Methods. IEEE Trans. Ind. Electron. 2015, 62, 144–152. [Google Scholar] [CrossRef]
- Hang, J.; Wang, X.; Li, W.; Ding, S. Interturn Short-Circuit Fault Diagnosis and Fault-Tolerant Control of DTP-PMSM Based on Subspace Current Residuals. IEEE Trans. Power Electron. 2025, 40, 3395–3404. [Google Scholar] [CrossRef]
- Hang, J.; Qiu, G.; Hao, M.; Ding, S. Improved Fault Diagnosis Method for Permanent Magnet Synchronous Machine System Based on Lightweight Multisource Information Data Layer Fusion. IEEE Trans. Power Electron. 2024, 39, 13808–13817. [Google Scholar] [CrossRef]
- He, W.; Hang, J.; Ding, S.; Sun, L.; Hua, W. Robust Diagnosis of Partial Demagnetization Fault in PMSMs Using Radial Air-Gap Flux Density Under Complex Working Conditions. IEEE Trans. Ind. Electron. 2024, 71, 12001–12010. [Google Scholar] [CrossRef]
- Zeng, Z.; Zhu, C.; Goetz, S.M. Fault-Tolerant Multiparallel Three-Phase Two-Level Converters with Adaptive Hardware Reconfiguration. IEEE Trans. Power Electron. 2024, 39, 3925–3930. [Google Scholar] [CrossRef]
- Zhang, R.; Wang, S.; Ma, J.; Jiang, Y.; Wang, P.; Liu, T.; Yang, Y. An Asymmetric Hybrid Phase-Leg Modular Multilevel Converter with Small Volume, Low Cost, and DC Fault-Blocking Capability. IEEE Trans. Power Electron. 2025, 40, 5336–5351. [Google Scholar] [CrossRef]
- Li, S.; Zhou, J.; Zhou, F.; Niu, F.; Deng, W. A Reduced Current Ripple Overmodulation Strategy for Indirect Matrix Converter. IEEE Trans. Ind. Electron. 2025, 72, 3768–3777. [Google Scholar] [CrossRef]





| Parameters | Symbol | Values | Unit |
|---|---|---|---|
| Pole pair number | np | 2 | - |
| Rotor inductance | Lr | 0.4718 | H |
| Stator inductance | Ls | 0.4718 | H |
| Rotor resistance | Rr | 4.30 | Ω |
| Stator resistance | Rs | 10.5 | Ω |
| Mutual inductance | M | 0.4475 | H |
| Moment of inertia | J | 0.0293 | Kg·m−2 |
| Rise Time (s) | 0.2461 | 0.2698 |
| Settling Time (s) | 2.5164 | 2.6271 |
| Overshoot (%) | 7.5142 | 7.4145 |
| Interval | Parameter | |||||
|---|---|---|---|---|---|---|
| 2.5–3.5 s | variation | 1.1033 | 1.0173 | 3.0567 | 1.2172 | |
| 3.8–7.8 s | variation | 2.2925 | 6.3448 | 37.431 | 21.242 | |
| 2.5–3.5 s | variation | 1.3061 | 1.2398 | 3.7241 | 1.7059 | |
| 3.8–7.8 s | variation | 2.3142 | 6.9483 | 41.247 | 21.423 |
| Interval | Parameter | |||||
|---|---|---|---|---|---|---|
| 2.5–3.5 s | variation | 0.00096 | 0.0008 | 0.0024 | 9.19 × 10−7 | |
| 3.8–7.8 s | variation | 0.0045 | 0.0082 | 0.0444 | 0.00008 | |
| 2.5–3.5 s | variation | 0.006 | 0.005 | 0.0149 | 3.56 × 10−5 | |
| 3.8–7.8 s | variation | 0.0105 | 0.02669 | 0.1476 | 0.00043 |
| 1.086 | 1.001 | 5.5137 | 1.1794 | |
| 1.2879 | 1.2225 | 6.7322 | 1.1794 | |
| 0.00092 | 0.00077 | 0.0044 | 3.04 × 10−5 | |
| 0.0055 | 0.0047 | 0.026 | 8.4 × 10−7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Allag, O.; Kouzou, A.; Allag, M.; Hafaifa, A.; Rodriguez, J.; Abdelrahem, M. Advanced Control Strategy for Induction Motors Using Dual SVM-PWM Inverters and MVT-Based Observer. Machines 2025, 13, 520. https://doi.org/10.3390/machines13060520
Allag O, Kouzou A, Allag M, Hafaifa A, Rodriguez J, Abdelrahem M. Advanced Control Strategy for Induction Motors Using Dual SVM-PWM Inverters and MVT-Based Observer. Machines. 2025; 13(6):520. https://doi.org/10.3390/machines13060520
Chicago/Turabian StyleAllag, Omar, Abdellah Kouzou, Meriem Allag, Ahmed Hafaifa, Jose Rodriguez, and Mohamed Abdelrahem. 2025. "Advanced Control Strategy for Induction Motors Using Dual SVM-PWM Inverters and MVT-Based Observer" Machines 13, no. 6: 520. https://doi.org/10.3390/machines13060520
APA StyleAllag, O., Kouzou, A., Allag, M., Hafaifa, A., Rodriguez, J., & Abdelrahem, M. (2025). Advanced Control Strategy for Induction Motors Using Dual SVM-PWM Inverters and MVT-Based Observer. Machines, 13(6), 520. https://doi.org/10.3390/machines13060520










