Avoiding Lyapunov-Krasovskii Functionals: Simple Nonlinear Sampled–Data Control of a Semi-Active Suspension with Magnetorheological Dampers

Abstract

This paper presents a novel control design methodology for a magnetorheological (MR) damper-based semi-active suspension system operating under communication-induced time delays, which introduce nonlinear sampled-data dynamics. To address these challenges, a linear matrix inequality (LMI) framework is developed for synthesizing the current controller, with the dual goals of enhancing ride comfort and safety while ensuring system stability and robustness against road disturbances. The proposed approach deliberately avoids the use of Lyapunov-Krasovskii functionals, offering a more practical and computationally efficient alternative. Experimental results confirm that the proposed MR damper model outperforms traditional Lyapunov-Krasovskii-based methods. Additionally, two simulated road profiles are used to evaluate the suspension system’s behavior, further demonstrating the effectiveness of the proposed control strategy.

1. Introduction

Vehicle suspension systems play a vital role in automotive engineering, significantly influencing both ride comfort and handling [1,2,3,4]. These systems can be categorized into three types: passive, semi-active, and active [5]. Passive suspension systems typically employ mechanical elements like springs and dampers to absorb shocks and regulate oscillations [6]. While simple and cost-effective, passive suspensions lack adaptability to changing road and driving conditions. In contrast, semi-active and active suspension systems incorporate mechanisms that allow external control over the system’s behavior [7,8,9]. Active suspensions are equipped with actuators capable of exerting force, either lifting or compressing the vehicle body, to counteract vibrations caused by uneven road surfaces [10]. Semi-active suspensions, on the other hand, do not introduce additional energy into the system. Instead, they dynamically adjust parameters such as the damping coefficient in real time, in order to adapt the vehicle dynamics to the road conditions [11,12,13]. Achieving an optimal balance between ride comfort and road holding is inherently challenging with passive suspensions, as the performance of these two factors is inherently contradictory. To address this, a range of control strategies has been developed for active and semi-active suspensions, with an emphasis on robustness and adaptability under varying road conditions [14,15,16].

Many conventional control strategies assume instantaneous communication between sensors, actuators, and controllers. However, in real-world applications, this assumption is inaccurate. Delays are an inherent part of modern control systems, as sensor data must be processed and transmitted to controllers, which then compute control signals to be sent to actuators [17]. Each stage in this loop introduces a certain amount of latency, which can negatively impact system performance and stability [18,19,20]. These delays may originate from several sources, including signal processing time, communication lags, and actuator response time [21,22,23]. As systems grow more complex and distributed, communication delays become increasingly significant, particularly in high-frequency data exchange. Insufficient bandwidth or inefficient data handling can exacerbate these delays, leading to outdated information influencing real-time decisions. This has the potential to compromise control accuracy or lead to instability, as controllers may rely on outdated sensor data. Such mismatches can induce oscillations, amplify disturbances, or result in loss of control. Managing these delays is therefore critical, and ongoing research is being conducted into control algorithms that can adapt to timing uncertainties and maintain stable, precise performance [24].

As a direct consequence of the aforementioned system delays, sensors may no longer be able to acquire vehicle data at consistent, regular intervals [25,26,27]. This leads to non-periodic or nonlinear data sampling, further complicating control design and reducing the reliability of time-dependent feedback mechanisms. Historically, Lyapunov-Krasovskii functionals have been traditionally employed as a mathematical tool for analyzing delayed systems [28,29,30]. However, this method introduces a significant degree of conservativeness (low dissipative capacity). As a result, the solutions derived may technically satisfy stability requirements but could be suboptimal for practical control applications. For instance, the computed control or observer gains may be insufficient to ensure rapid system response or robustness under uncertainty. The application of Lyapunov-Krasovskii theory typically leads to the formulation of the control or estimation problem as a linear matrix inequality (LMI) [31,32,33]. The inclusion of delay-dependent terms in the Lyapunov–Krasovskii functional leads to a complex quadratic form, which is then evaluated under an LMI [34]. A serious limitation of this approach is that the resulting quadratic form treats inherently related terms, such as the current system state and its delayed counterpart, as independent. This false characterization leads to the inclusion of spurious state terms, which artificially inflate the dimensionality of the problem and further deteriorate its conservativeness [35]. Given these drawbacks, the use of Lyapunov-Krasovskii functionals may not be the most appropriate method for dealing with the control challenges posed by non-periodic sampling and communication delays. Alternative approaches that better capture the structure and interdependence of delayed state variables are warranted to achieve more efficient and less conservative control solutions.

In light of the aforementioned challenges, this paper proposes a novel control strategy for semi-active suspension systems utilizing magnetorheological (MR) dampers. The proposed approach explicitly accounts for the effects of nonlinear and non-periodic data sampling arising from sensor delays in the measurement of the system’s dynamic state. Unlike conventional approaches that rely on Lyapunov–Krasovskii functionals, which imply increased conservativeness, this method avoids their use entirely. Instead, the method employs a Linear Parameter-Varying (LPV) modeling approach, wherein system stability is analyzed as a function of the time interval between successive data samples. This formulation significantly relaxes the controller design constraints, enabling a more practical and less conservative solution that allows for real-time implementation.

The remainder of this paper is organized as follows. Section 2 presents the semi-active suspension model. Section 3 describes the methodology used for the controller design. Section 4 provides several simulation results to demonstrate the feasibility of the proposed approach. Finally, the conclusions of this work are summarized in Section 5.

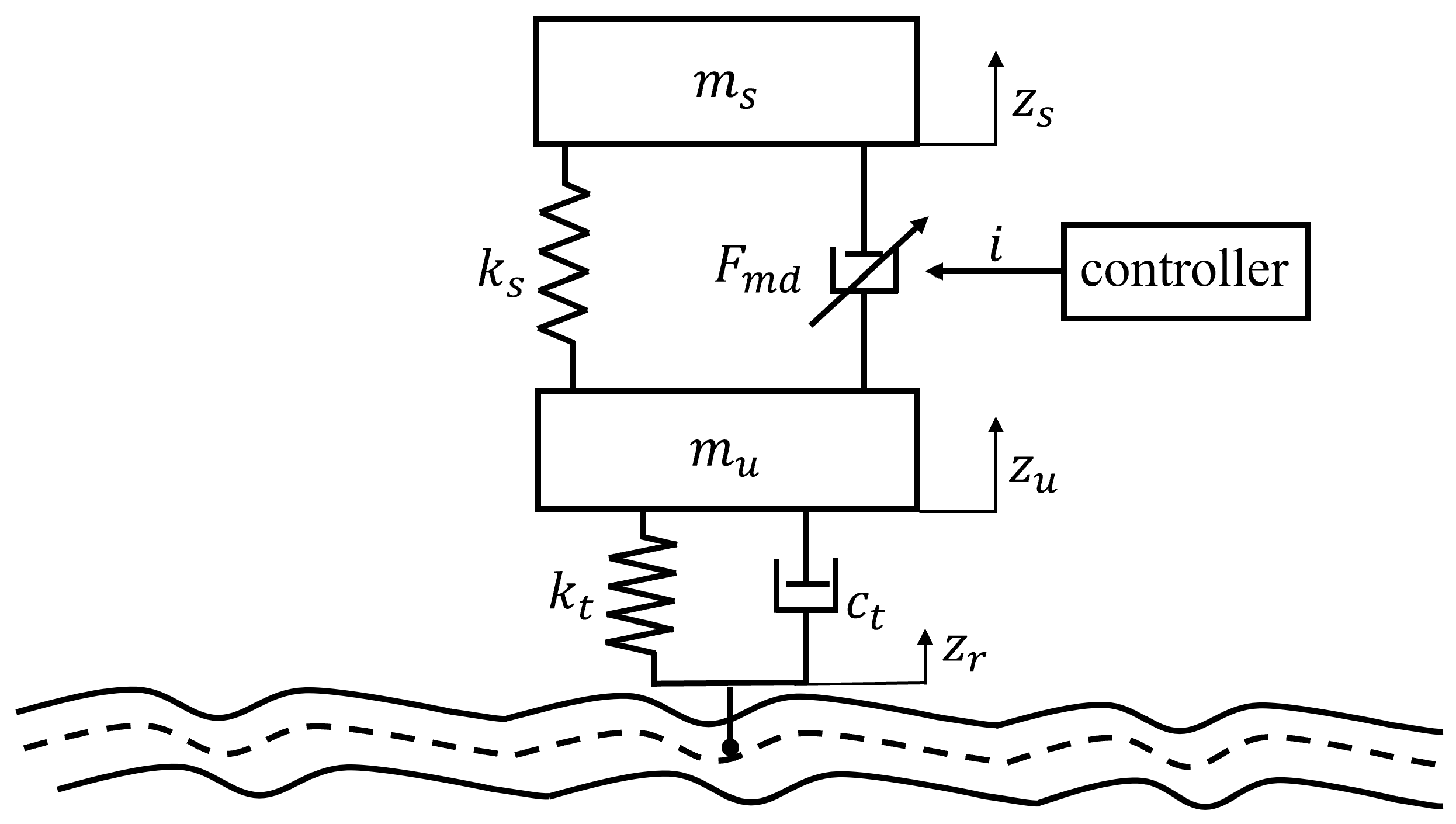
2. Semi-Active Suspension Model

A quarter-car vehicle model (see Figure 1) is chosen for this study due to its widespread application in analyzing suspension performance [36,37,38]. The vehicle body is assumed to be rigid, with motion restricted solely to the vertical direction, allowing for a focused examination of ride dynamics and suspension behavior.

The equations of motion governing the quarter-car model, incorporating the semi-active suspension dynamics influenced by a MR damper, are formulated as follows:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & m_s{\ddot{z}}_s\left(t\right)+k_s\left(z_s\left(t\right)-z_u\left(t\right)\right)+F_{md}\left(t\right)=0\hfill \\ \hfill & m_u{\ddot{z}}_u\left(t\right)+k_s\left(z_u\left(t\right)-z_s\left(t\right)\right)-F_{md}\left(t\right)\hfill \\ \hfill & +k_t\left(z_u\left(t\right)-z_r\left(t\right)\right)+c_t\left({\dot{z}}_u\left(t\right)-{\dot{z}}_r\left(t\right)\right)=0\hfill \end{array}\end{array}$$

(1)

Here, $z_s$, $z_u$ and $z_r$ represent the displacements of the sprung mass, unsprung mass, and road profile, respectively. The key parameters of the quarter-car model are summarized in

Table 1. Key parameters of the quarter-car model employed for this work.

Parameter	Name	Value
$m_s$	Vehicle sprung mass	243.2 kg
$m_u$	Vehicle unsprung mass	28.5 kg
$k_s$	Spring stiffness	10,680 N/m
$k_t$	Tire stiffness	25,278 N/m
$c_t$	Tire damping	3.65 N s/m
$z_{max}$	Maximum suspension deflection	0.05 m

.

The force generated by the MR damper $F_{md}$ is characterized by the following empirically derived formula [39]:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill F_{md}\left(t\right)=& (a_0+a_{1}i\left(t\right))\tanh \left(a_2\left({\dot{z}}_{def}\left(t\right)+{\displaystyle \frac{V_0}{X_0}}{z}_{def}\left(t\right)\right)\right)\hfill \\ \hfill & +a_3\left({\dot{z}}_{def}\left(t\right)+{\displaystyle \frac{V_0}{X_0}}{z}_{def}\left(t\right)\right)\hfill \end{array}\end{array}$$

(2)

where $a_j$, $j\in 0,\dots ,3$ are experimentally determined parameters, described in

Table 2. Experimental MR damper parameters [39].

Parameter	Value
$a_0$	236.3 N
$a_1$	655.8 N/A
$a_2$	4.67 s/m
$a_3$	343.1 N s/m
$V_0/X_0$	6.05 s−1

. The current applied to the MR damper is denoted by i. The damper deflection is defined as $z_{def}=z_s-z_u$. The ratio $V_0/X_0$ is a function of the absolute values of the hysteretic critical velocity $V_0$ and the hysteretic critical displacement $X_0$, which represent the velocity and displacement values at which the damper force is zero. From Equation (2), the stiffness ($k_{mr}$) and damping ($c_{mr}$) coefficients of the MR damper are expressed as follows:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill k_{mr}& =a_3{\displaystyle \frac{V_0}{X_0}}\hfill \\ \hfill c_{mr}& =a_3\hfill \end{array}\end{array}$$

(3)

Following the Equation (2), Figure 2 presents the interaction between damper force, control current, and suspension deflection, highlighting how the damper’s behavior varies under different actuation levels and mechanical displacements.

In order to design a suspension system that ensures optimal performance, the following factors must be carefully considered during the design phase [40,41,42]:

(1)

To improve ride comfort, it is essential to minimize the vertical acceleration ${\ddot{z}}_s$

$$\min {\ddot{z}}_s\left(t\right)=-{\displaystyle \frac{k_s\left(z_s\left(t\right)-z_u\left(t\right)\right)+F_{md}\left(t\right)}{m_s}}$$

(4)

(2)

The suspension deflection is constrained by the mechanical structure and must not exceed a specified maximum value $z_{max}$

$$\left|\begin{array}{c}{z}_s\left(t\right)-z_u\left(t\right)\end{array}\right|\le z_{max}$$

(5)

(3)

To ensure consistent and uninterrupted contact between the wheels and the road, it is essential for the dynamic tire load to remain below the static tire load

$$k_t\left(z_u\left(t\right)-z_r\left(t\right)\right)<(m_s+m_u)g$$

(6)

Based on Equations (1)–(6), the continuous-time state-space representation of the quarter-car semi-active suspension model is formulated as follows:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \dot{x}\left(t\right)& =\mathcal{A}x\left(t\right)+\mathcal{B}u\left(t\right)+{\mathcal{B}}_{\omega }\omega \left(t\right)\hfill \\ \hfill z\left(t\right)& =C_{z}x\left(t\right)+D_{z}u\left(t\right)\hfill \end{array}\end{array}$$

(7)

where x is the state vector, u represents the control input, and $\omega$ is the road disturbance. The performance vector z serves as a quantitative metric used to evaluate whether the suspension deflection, vertical acceleration, and dynamic tire load are maintained within acceptable limits.

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & x\left(t\right)=\left[\begin{array}{c}{z}_s\left(t\right)-z_u\left(t\right)\\ z_u\left(t\right)-z_r\left(t\right)\\ {\dot{z}}_s\left(t\right)\\ {\dot{z}}_u\left(t\right)\end{array}\right],\omega \left(t\right)={\dot{z}}_r\left(t\right),z_{def}\left(t\right)=z_s\left(t\right)-z_u\left(t\right),\hfill \\ \hfill & u\left(t\right)=(a_0+a_{1}i\left(t\right))\tanh \left(a_2\left({\dot{z}}_{def}\left(t\right)+{\displaystyle \frac{V_0}{X_0}}{z}_{def}\left(t\right)\right)\right)\hfill \end{array}\end{array}$$

(8)

The state-space matrices of the system (7) are defined as follows:

$$\mathcal{A}=\left[\begin{array}{cccc}0& 0& 1& -1\\ 0& 0& 0& 1\\ -{\displaystyle \frac{k_s+k_{mr}}{m_s}}& 0& -{\displaystyle \frac{c_{mr}}{m_s}}& {\displaystyle \frac{c_{mr}}{m_s}}\\ {\displaystyle \frac{k_s+k_{mr}}{m_u}}& {\displaystyle \frac{k_t}{m_u}}& {\displaystyle \frac{c_{mr}}{m_u}}& -{\displaystyle \frac{c_{mr}+c_t}{m_u}}\end{array}\right],\mathcal{B}=\left[\begin{array}{c}0\\ 0\\ -{\displaystyle \frac{1}{m_s}}\\ {\displaystyle \frac{1}{m_u}}\end{array}\right],{\mathcal{B}}_{\omega }=\left[\begin{array}{c}0\\ -1\\ 0\\ {\displaystyle \frac{c_t}{m_u}}\end{array}\right],$$

$$C_z=\left[\begin{array}{cccc}-{\displaystyle \frac{k_s+k_{mr}}{m_s}}& 0& -{\displaystyle \frac{c_{mr}}{m_s}}& {\displaystyle \frac{c_{mr}}{m_s}}\\ {\displaystyle \frac{1}{z_{max}}}& 0& 0& 0\\ 0& {\displaystyle \frac{k_t}{(m_s+m_u)g}}& 0& 0\end{array}\right],D_z=\left[\begin{array}{c}-{\displaystyle \frac{1}{m_s}}\\ 0\\ 0\end{array}\right]$$

Having formulated the suspension system model, the next section describes a procedure for designing a controller for the semi-active suspension. This system will dynamically adjust the MR damper current based on the vehicle state.

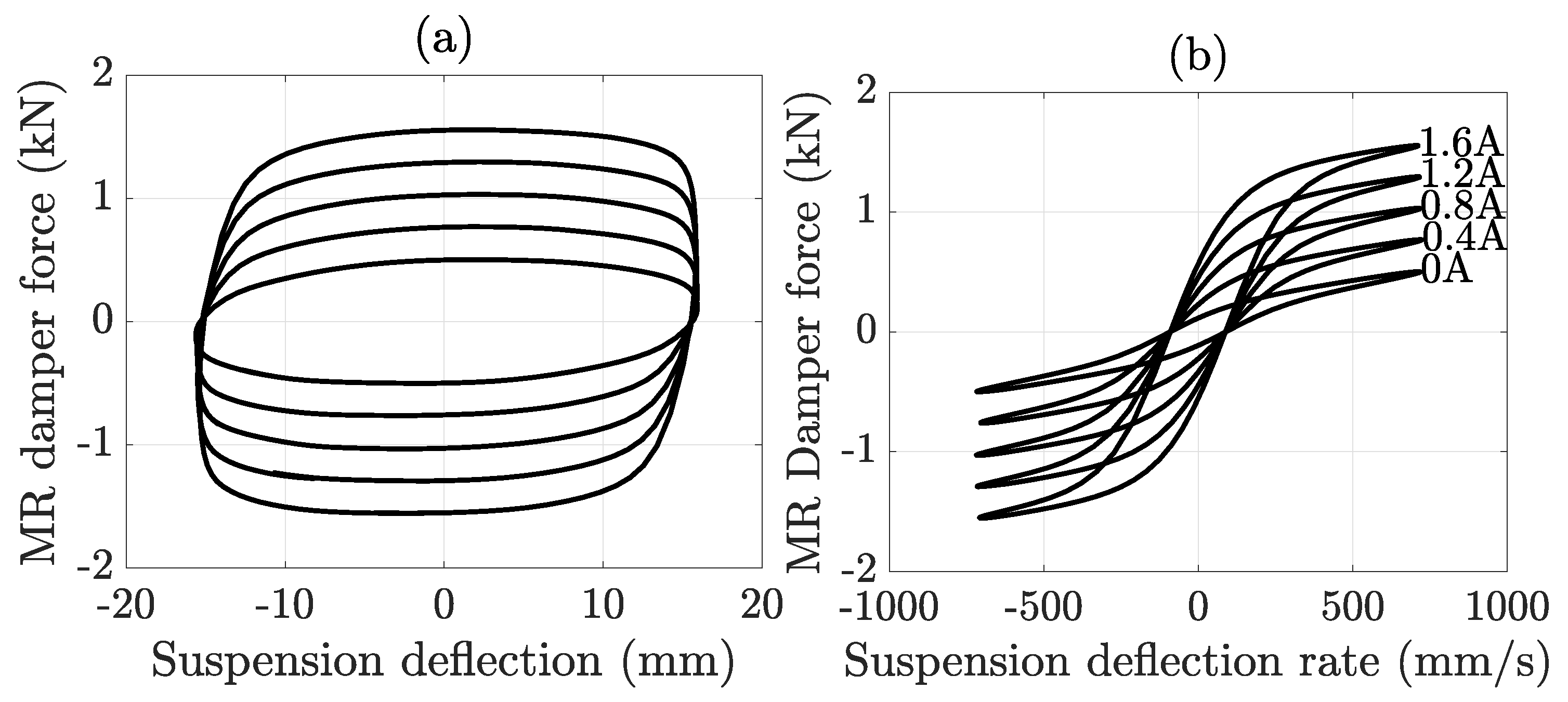
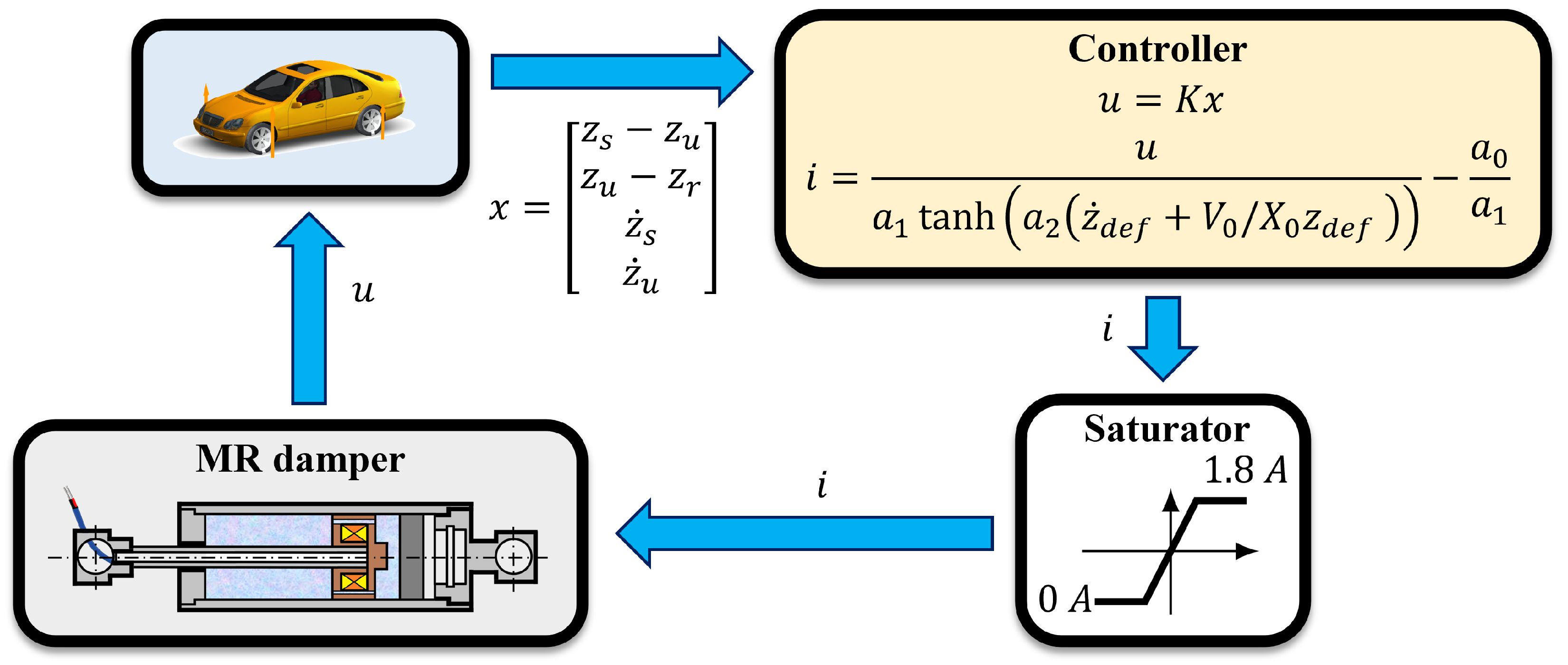
3. MR Damper Controller with Robustness to Nonlinear Sampled-Data

This section presents a state-feedback controller designed to adjust the current of an MR damper, allowing the vehicle to adapt to changing road conditions. Given that data sampling in real systems may not always occur at regular intervals, nonlinear data sampling introduces irregularities or non-uniformity in the timing of data collection [43]. As such, the controller must be robust to these nonlinear sampling effects, ensuring reliable performance even when the data is acquired at varying time intervals. Additionally, the controller is designed to attenuate the effect of external disturbances, further enhancing the system’s robustness and adaptability.

To enable real-time implementation, the continuous-time system described by Equation (7) is discretized using Euler’s method [44]

$$\dot{x}\left(t\right)\simeq {\displaystyle \frac{x(k+1)-x\left(k\right)}{T_d}},\forall k\in {\mathbb{Z}}_{+}$$

(9)

where $T_d\in [{\underline{T}}_d,{\overline{T}}_d]$ is used to denote the unknown time interval between consecutive data samplings. The minimum and maximum durations of the sampling period are denoted by ${\underline{T}}_d$ and ${\overline{T}}_d$, respectively. The application of (9) leads to the discrete-time state-space model

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill x(k+1)& =A\left(T_d\right)x\left(k\right)+B\left(T_d\right)u\left(k\right)+B_{\omega }\left(T_d\right)\omega \left(k\right)\hfill \\ \hfill z\left(k\right)& =C_{z}x\left(k\right)+D_{z}u\left(k\right)\hfill \end{array}\end{array}$$

(10)

with the state-space matrices

$$A=I+T_d\mathcal{A},B=T_d\mathcal{B},B_{\omega }=T_d{\mathcal{B}}_{\omega }$$

(11)

The measurement of system states can be achieved through the use of a linear variable differential transformer (LVDT), which is capable of measuring suspension deflection. Tire deflection can be measured using laser displacement sensors. The velocities of the sprung and unsprung masses can be estimated through the processing of data obtained from an inertial measurement unit (IMU).

The control signal u is generated according to the state-feedback law

$$u\left(k\right)=Kx\left(k\right)$$

(12)

where K is a control gain matrix to be designed.

The current i to be applied to the MR damper is obtained by substituting the values of u, $z_{def}$ and ${\dot{z}}_{def}$ in (8), such that

$$i\left(k\right)={\displaystyle \frac{u\left(k\right)}{a_1\tanh \left(a_2\left({\dot{z}}_{def}\left(k\right)+\frac{V_0}{X_0}{z}_{def}\left(k\right)\right)\right)}}-{\displaystyle \frac{a_0}{a_1}}$$

(13)

The following theorem establishes a sufficient set of conditions for designing an MR damper current controller for the semi-active suspension system (10). This theorem is specifically designed to account for the potential occurrence of nonlinear sampling intervals, ensuring robust performance under varying data acquisition rates.

Theorem 1. 

The state-feedback controller (12) guarantees stability and presents an ${\mathcal{H}}_{\infty }$ performance index $\gamma >0$ for the semi-active suspension system (10), if there exist matrices $Q=Q^{\top }>0$ and M of appropriate dimensions, such that the following linear matrix inequality (LMI) convex optimization problem yields a feasible solution:

$$\min \gamma \mathrm{s}.\mathrm{t}.\left(14\right)$$

where

$$\Xi \left(T_d\right)=\left[\begin{array}{cccc}-Q& \star & \star & \star \\ 0& -{\gamma }^{2}I& \star & \star \\ A\left(T_d\right)Q+B\left(T_d\right)M& B_{\omega }\left(T_d\right)& -Q& \star \\ C_{z}Q+D_{z}M& 0& 0& -I\end{array}\right]<0$$

(14)

Proof. 

In order to evaluate the closed-loop stability of the system (10), select the Lyapunov function

$$V\left(k\right)=x^{\top }\left(k\right)Px\left(k\right)>0,P>0$$

(15)

where P is the Lyapunov matrix. To guarantee system stability, the variation of the Lyapunov function between two successive discrete-time instants must be negative. This condition is formally expressed as:

$$\Delta V\left(k\right)=V(k+1)-V\left(k\right)<0$$

(16)

Furthermore, to evaluate the system’s robustness in mitigating the impact of external disturbances; specifically, variations in the road profile, the ${\mathcal{H}}_{\infty }$ performance criterion is employed. This evaluates the influence of external disturbances on the control output z, and is formally defined as follows:

$$z^{\top }\left(k\right)z\left(k\right)-{\gamma }^2{\omega }^{\top }\left(k\right)\omega \left(k\right)<0$$

(17)

To evaluate both stability and robustness, inequalities (16) and (17) bust be addressed together, such that

$$V(k+1)-V\left(k\right)+z^{\top }\left(k\right)z\left(k\right)-{\gamma }^2{\omega }^{\top }\left(k\right)\omega \left(k\right)<0$$

(18)

Following (10) and (12), (18) can be expressed as the quadratic form

$${\left[\begin{array}{c}x\left(k\right)\\ \omega \left(k\right)\end{array}\right]}^{\top }\left(\left[\begin{array}{cc}-P+{(C_z+D_{z}K)}^{\top }(C_z+D_{z}K)& \star \\ 0& -{\gamma }^{2}I\end{array}\right]+{\mathcal{W}}^{\top }P\mathcal{W}\right)\left[\begin{array}{c}x\left(k\right)\\ \omega \left(k\right)\end{array}\right]<0$$

(19)

where

$$\mathcal{W}=\left[\begin{array}{cc}A\left(T_d\right)+B\left(T_d\right)K& B_{\omega }\left(T_d\right)\end{array}\right]$$

(20)

Using the Schur complement, the quadratic form (19) is equivalent to

$$\left[\begin{array}{ccc}-P+{(C_z+D_{z}K)}^{\top }(C_z+D_{z}K)& \star & \star \\ 0& -{\gamma }^{2}I& \star \\ A\left(T_d\right)+B\left(T_d\right)K& B_{\omega }\left(T_d\right)& -P^{-1}\end{array}\right]<0$$

(21)

Next, applying the congruent transformation $\mathrm{diag}(P^{-1},I,I)$ to (21) yields

$$\left[\begin{array}{ccc}-P^{-1}+P^{-1}{(C_z+D_{z}K)}^{\top }(C_z+D_{z}K)P^{-1}& \star & \star \\ 0& -{\gamma }^{2}I& \star \\ A\left(T_d\right)P^{-1}+B\left(T_d\right)K{P}^{-1}& B_{\omega }\left(T_d\right)& -P^{-1}\end{array}\right]<0$$

(22)

Now, applying the Schur complement once more leads to

$$\left[\begin{array}{cccc}-P^{-1}& \star & \star & \star \\ 0& -{\gamma }^{2}I& \star & \star \\ A\left(T_d\right)P^{-1}+B\left(T_d\right)K{P}^{-1}& B_{\omega }\left(T_d\right)& -P^{-1}& \star \\ (C_z+D_{z}K)P^{-1}& 0& 0& -I\end{array}\right]<0$$

(23)

Finally, applying the transformations $P=Q^{-1}$ and $M=K{P}^{-1}$ leads to the LMI (14), thus completing the proof. □

It is important to note that Theorem 1 relies on knowledge of the time interval between the current and the subsequent sampling period, which limits the practical application. Therefore, it is necessary to adapt the theorem to ensure system stability and robustness in the event of the next sampling interval being unknown.

Theorem 2. 

The state-feedback controller (12) guarantees stability and presents an ${\mathcal{H}}_{\infty }$ performance index $\gamma >0$ for the semi-active suspension system (10), if there exist matrices $Q=Q^{\top }>0$ and M of appropriate dimensions, for $j=1,2$, such that the following linear matrix inequality (LMI) convex optimization problem yields a feasible solution:

$$\min \gamma \mathrm{s}.\mathrm{t}.\left(24\right)$$

where

$${\Xi }_j=\left[\begin{array}{cccc}-Q& \star & \star & \star \\ 0& -{\gamma }^{2}I& \star & \star \\ A_{j}Q+B_{j}M& B_{\omega ,j}& -Q& \star \\ C_{z}Q+D_{z}M& 0& 0& -I\end{array}\right]<0$$

(24)

Proof. 

System matrices that depend on $T_d$ can be expressed as

$$\left[\begin{array}{ccc}A\left(T_d\right)& B\left(T_d\right)& B_{\omega }\left(T_d\right)\end{array}\right]=\sum _{j=1}^2{\alpha }_j\left(T_d\right)\left[\begin{array}{ccc}{A}_j& B_j& B_{\omega ,j}\end{array}\right]$$

(25)

with

$$\begin{array}{ccc}\hfill \left[A_1\hspace{1em}{B}_1\hspace{1em}{B}_{\omega ,1}\right]& =& \left[A\left({\underline{T}}_d\right)\hspace{1em}B\left({\underline{T}}_d\right)\hspace{1em}{B}_{\omega }\left({\underline{T}}_d\right)\right]\\ \hfill \left[A_2\hspace{1em}{B}_2\hspace{1em}{B}_{\omega ,2}\right]& =& \left[A\left({\overline{T}}_d\right)\hspace{1em}B\left({\overline{T}}_d\right)\hspace{1em}{B}_{\omega }\left({\overline{T}}_d\right)\right]\end{array}$$

(26)

The weighting functions ${\alpha }_1$ and ${\alpha }_2$ are defined as

$${\alpha }_1\left(T_d\right)={\displaystyle \frac{T_d-{\underline{T}}_d}{{\overline{T}}_d-{\underline{T}}_d}},{\alpha }_2\left(T_d\right)={\displaystyle \frac{{\overline{T}}_d-T_d}{{\overline{T}}_d-{\underline{T}}_d}}$$

(27)

By examining (14) and (24), it becomes evident that

$$\Xi \left(T_d\right)=\sum _{j=1}^2{\alpha }_j\left(T_d\right){\Xi }_j$$

(28)

given that ${\alpha }_j>0$ by definition, it can be concluded that

$${\Xi }_j<0\forall j\Rightarrow \Xi \left(T_d\right)<0$$

(29)

which proves that Theorem 2 is an improved version of Theorem 1, as it eliminates the need know $T_d$. □

Theorem 1 assumes that the exact time interval between successive samplings is known, which is an unrealistic requirement in most practical applications due to the unpredictable nature of sensor and communication delays. To address this issue, Theorem 2 has provided a more practical and robust solution by designing a control gain $K=MP$ that guarantees stability for any sampling interval within predefined bounds. This makes Theorem 2 particularly suitable for real-world implementations where delay variability must be accounted for.

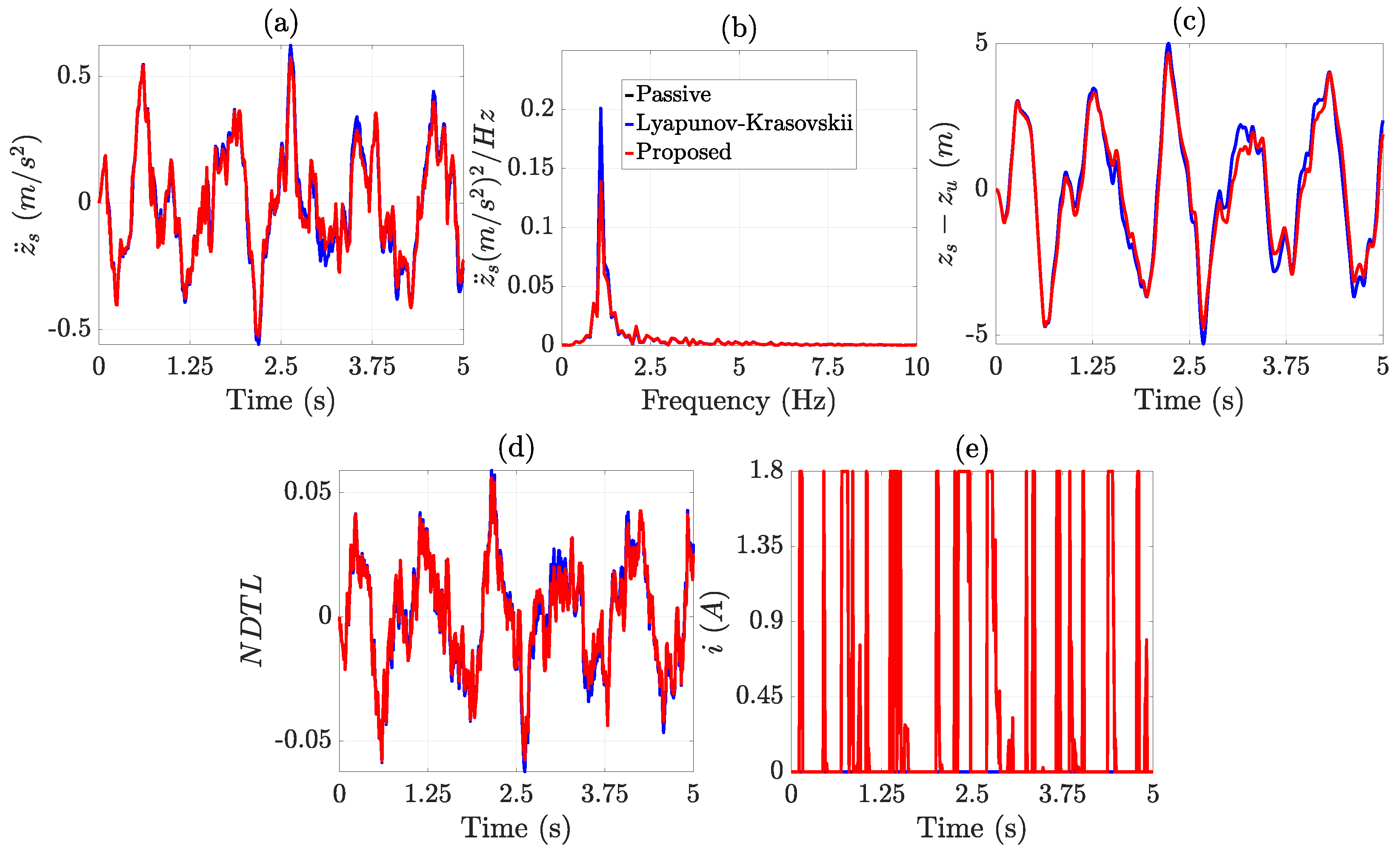
4. Results

This section presents simulation results conducted to validate the effectiveness of the proposed MR damper current controller. Multiple simulations were performed using Matlab 2024a to evaluate the performance of the MR damper-based semi-active suspension system in a vehicle. The quarter-car vehicle model (7) was simulated using the parameters introduced in Table 1, while the MR damper (2) was modeled based on the experimental parameters provided in Table 2. Figure 3 shows the architectural framework of the simulation setup. The controller adjusts the current supplied to the MR damper in order to modify its stiffness. To ensure proper operation, the current applied to the damper is constrained within the range of 0–1.8 A.

A feasible solution for the MR damper current controller was found by solving the proposed Theorem 2, assuming the time interval between consecutive data samplings as $T_d\in [10,20]$ ms. The LMIs were solved by the Matlab robust control toolbox, which retrieved the controller gain (12)

$$K_{proposed}=\left[\begin{array}{cccc}-12531.31& -24987.65& 1634.60& -1675.15\end{array}\right]$$

(30)

For comparison, the performance of the proposed controller is evaluated against two benchmarks: (i) the same suspension system operating in passive mode, represented by a zero control gain ($K_{passive}=\left[0\right]$), and (ii) a semi-active suspension employing a controller designed using the Lyapunov-Krasovskii method [45,46,47], which yields a different control gain matrix

$$K_{Lyapunov-Krasovskii}=\left[\begin{array}{cccc}-48.01& -214.88& 80.75& -14.84\end{array}\right]$$

(31)

It is important to note that the elements of the proposed gain matrix are significantly larger than those obtained via the Lyapunov-Krasovskii approach. This indicates that the solution obtained through Lyapunov-Krasovskii functionals is more conservative, resulting in lower control inputs over time. The impact of this conservatism on the vehicle’s dynamic performance will be examined in subsequent analysis.

The time interval between consecutive data samplings is generated randomly in the range $T_d\in [10,20]$ ms. To evaluate the vertical dynamics of the vehicle, two commonly used road disturbance profiles are considered:

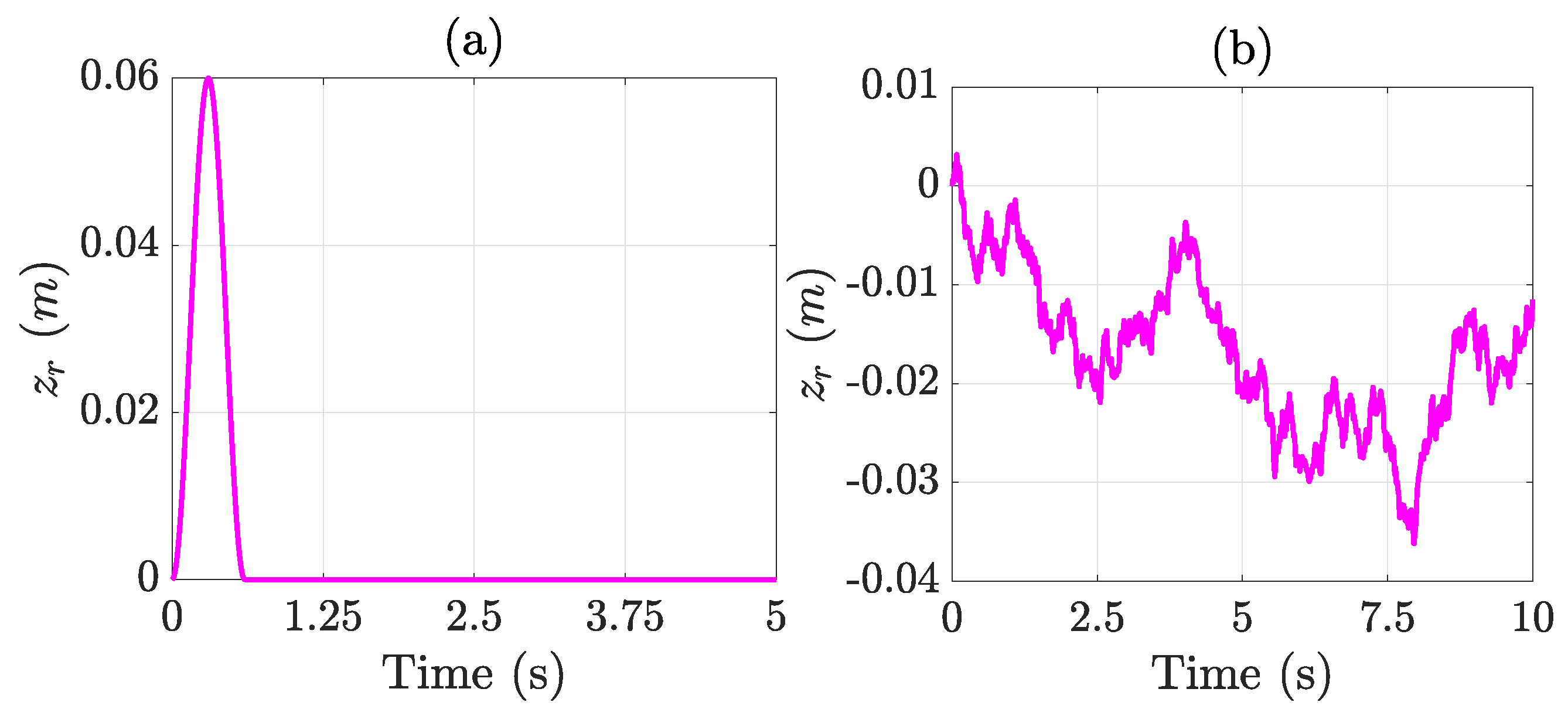
• A road bump with a height of $H=6$ cm and a length of $L=5$ m at a vehicle speed of $V=30$ km/h. The road bump profile as a function of time is described by the following equation:

  $$z_r\left(t\right)=\left\{\begin{array}{cc}{\displaystyle \frac{H}{2}}\left(1-\cos \left({\displaystyle \frac{2\pi V}{L}}t\right)\right),& 0\le t\le {\displaystyle \frac{L}{V}}\\ 0,& t>{\displaystyle \frac{L}{V}}\end{array}\right.$$

  (32)
  Conducting a bump test is a straightforward but revealing way to evaluate how well the suspension handles sharp, high-energy disturbances.
• A Class A random road profile, according to ISO 8608 [48], under a vehicle speed of $V=80$ km/h. The purpose of evaluating the suspension system under this profile is to ensure that its performance remains consistent under typical highway conditions; that is, to verify that the semi-active control does not intervene unnecessarily when it is not required to.

The road profiles described above are illustrated in Figure 4.

The bump road simulation results can be found in Figure 5. It is evident that the proposed controller outperforms the alternatives in terms of reducing body acceleration over time, thereby ensuring improved ride comfort. In terms of root mean square (RMS), the RMS values for the vertical acceleration were $1.083$, $1.081$ and 0.99 m/s² for the passive, Lyapunov-Krasovskii, and proposed controllers, respectively. This indicates that the Lyapunov-Krasovskii solution has a minimal impact on enhancing the suspension performance, yielding only a $0.21\%$ improvement. In contrast, the proposed method achieves a more substantial $8.27\%$ improve in the RMS of the vertical acceleration, therefore improving ride comfort. By analyzing the frequency components of the vehicle’s vertical acceleration through the power spectral density (PSD) of the signal, it is observed that the maximum frequency component decreases from 2.27 ${(\mathrm{m}/{\mathrm{s}}^2)}^2$/Hz in the passive suspension to 1.65 ${(\mathrm{m}/{\mathrm{s}}^2)}^2$/Hz for the proposed semi-active suspension, what demonstrates that the proposed controller leads to improved ride comfort. The suspension deflection remains within the maximum allowable limit of the mechanical structure $z_{max}$ = 0.05 m, demonstrating that the proposed method can be effectively implemented without compromising the structural integrity of the suspension system. Additionally, the normalized dynamic tire load (NDTL) consistently remains below 1, thereby ensuring that each vehicle wheel maintains continuous contact with the road surface, which guarantees driving safety. Further simulation tests for the bump scenario, conducted at various vehicle speeds, are summarized in

Table 3. RMS results for the vertical acceleration of the vehicle under different bump simulations.

Vehicle Speed	Passive	Lyapunov-Krasovskii	Proposed
15 km/h	0.775 m/s2	0.772 m/s2	0.721 m/s2
20 km/h	1.059 m/s2	1.055 m/s2	0.977 m/s2
25 km/h	1.113 m/s2	1.109 m/s2	1.017 m/s2

.

The Class A road simulation results can be found in Figure 6. The results once again confirm that the proposed control design offers a marked improvement in vehicle performance compared to its Lyapunov-Krasovskii. This is particularly evident in the lower PSD of the vertical acceleration, which reflects a smoother and more comfortable ride. The findings from this test indicate that the vehicle maintains safe operating conditions under standard highway scenarios. Moreover, the observed reduction in vertical acceleration contributes to improved ride comfort, highlighting the effectiveness of the proposed suspension system in mitigating road-induced vibrations. To further validate the effectiveness of the proposed methodology, additional simulation tests were conducted at various driving speeds. The results, summarized in

Table 4. RMS results for the vertical acceleration of the vehicle under different Class-A road simulations.

Vehicle Speed	Passive	Lyapunov-Krasovskii	Proposed
50 km/h	0.200 m/s2	0.199 m/s2	0.187 m/s2
60 km/h	0.211 m/s2	0.211 m/s2	0.196 m/s2
70 km/h	0.240 m/s2	0.240 m/s2	0.227 m/s2
80 km/h	0.255 m/s2	0.255 m/s2	0.241 m/s2

, consistently demonstrate superior ride performance and comfort across all scenarios, since the RMS of the vertical acceleration is reduced with the proposed method.

5. Conclusions

This paper has presented a robust control design method for a semi-active suspension system based on an MR damper, taking into account potential variations in sensor data sampling that may introduce delays in signal transmission.

Convex LMI conditions were derived for the design of practical, robust controllers for MR damper-based systems. Unlike traditional approaches that rely on Lyapunov-Krasovskii functionals to handle time-delay effects, this work adopts an LPV framework to represent the system dynamics as a function of the delays, significantly reducing both computational complexity and conservatism.

The effectiveness of the proposed system was analyzed under two representative driving conditions: a road bump and a Class A road profile, as defined by the ISO 8608 standard. The results clearly demonstrate that replacing the traditional Lyapunov-Krasovskii-based control approach with the proposed controller for a semi-active suspension system yields substantial gains in both ride comfort and safety. Notably, in the most demanding scenario, the proposed method achieves an 8.27% reduction in vehicle vertical acceleration, whereas the Lyapunov-Krasovskii solution offers only a marginal improvement of 0.21% relative to the passive suspension.

Future work will evaluate the feasibility of using the proposed controller design method for other vehicle control purposes, such as path tracking. Furthermore, it is our intention to extended this research to agricultural machinery, and to incorporate driver preferences [49,50,51,52].