Vibration Attenuation in Particle Mixer Using Magnetorheological Damping Technology to Mitigate the Brazil Nut Effect
Abstract
1. Introduction
2. Materials and Methods
2.1. MR Damper and Control System
2.2. Vibration Experiment of Drum Mixer with MR Damper
2.3. DEM Modeling and Simulation
3. Results and Discussion
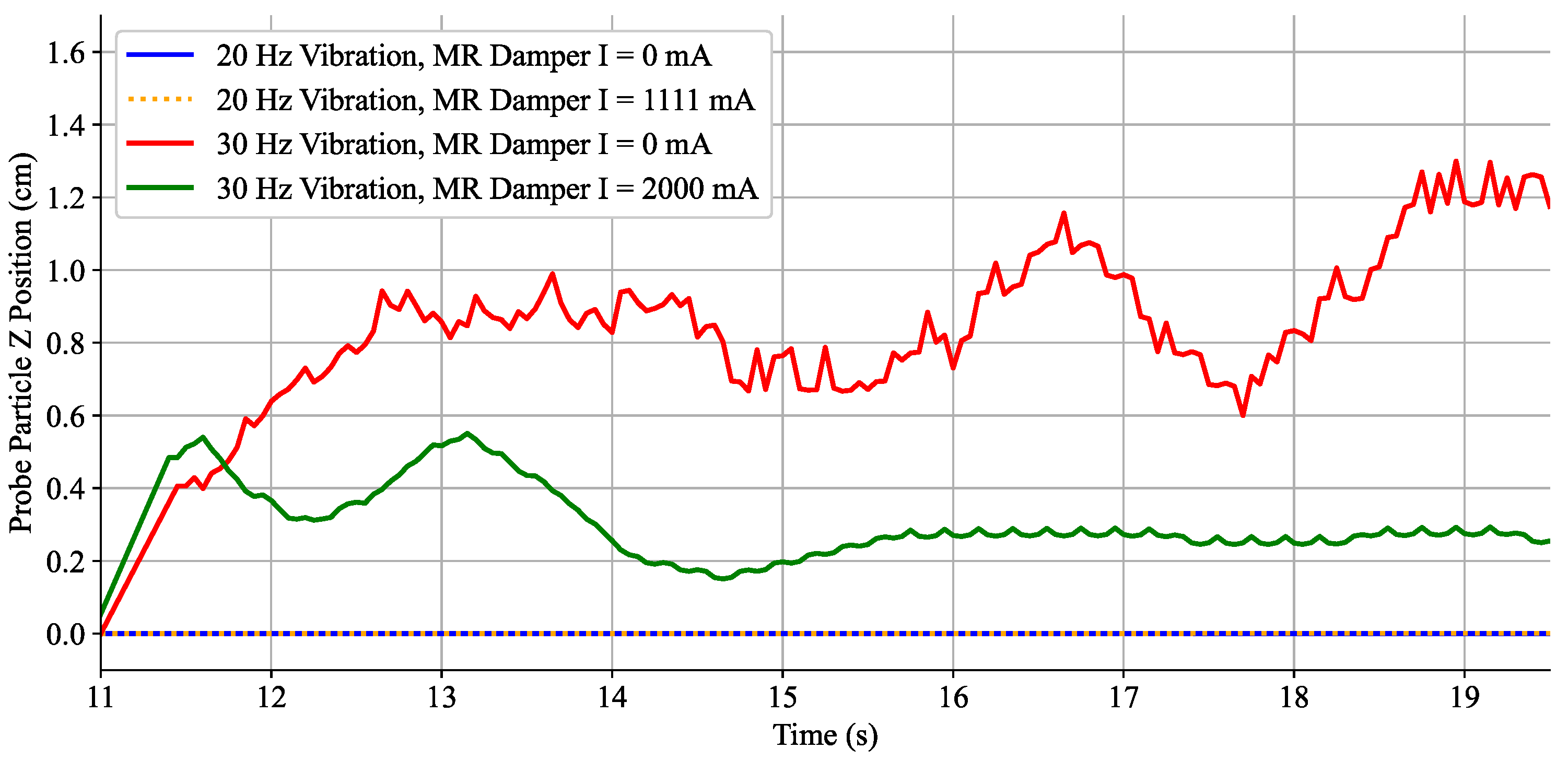
3.1. Experimental Results and Discussion
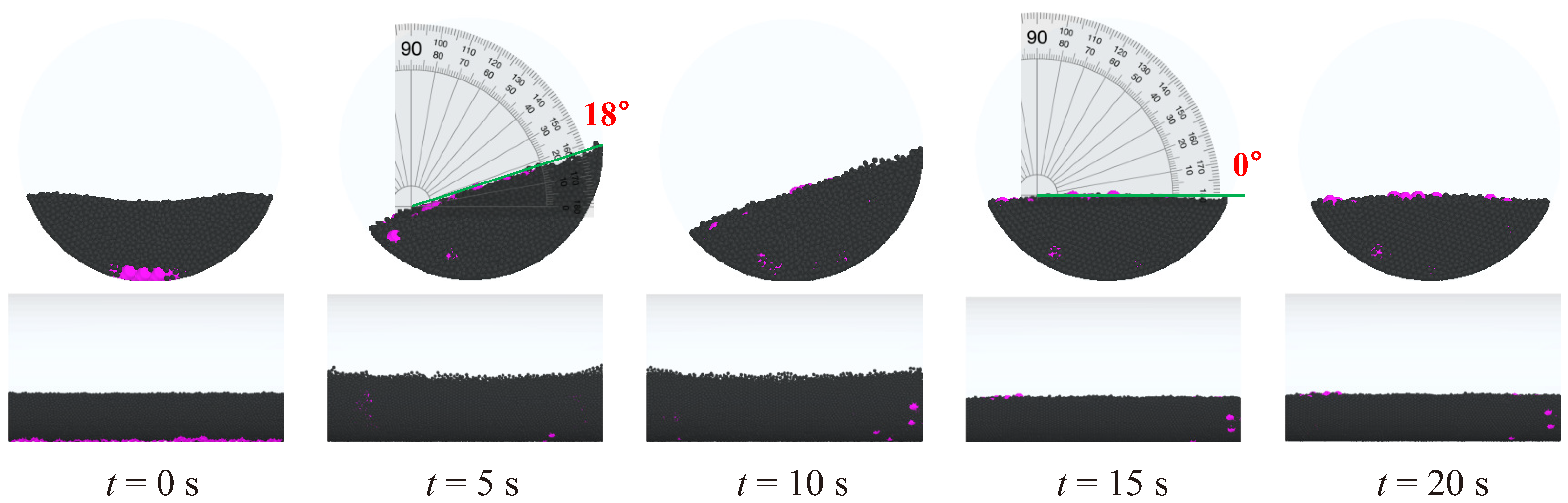
3.2. Simulation Results and Discussion
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Harnby, N. An Engineering View of Pharmaceutical Powder Mixing. Pharm. Sci. Technol. Today 2000, 3, 303–309. [Google Scholar] [CrossRef]
- Pernenkil, L.; Cooney, C.L. A Review on the Continuous Blending of Powders. Chem. Eng. Sci. 2006, 61, 720–742. [Google Scholar] [CrossRef]
- Bauman, I.; Ćurić, D.; Boban, M. Mixing of Solids in Different Mixing Devices. Sadhana 2008, 33, 721–731. [Google Scholar] [CrossRef]
- Bridgwater, J. Mixing of Powders and Granular Materials by Mechanical Means—A Perspective. Particuology 2012, 10, 397–427. [Google Scholar] [CrossRef]
- Huang, A.N.; Kuo, H.P. Developments in the Tools for the Investigation of Mixing in Particulate Systems—A Review. Adv. Powder Technol. 2014, 25, 163–173. [Google Scholar] [CrossRef]
- Asachi, M.; Nourafkan, E.; Hassanpour, A. A Review of Current Techniques for the Evaluation of Powder Mixing. Adv. Powder Technol. 2018, 29, 1525–1549. [Google Scholar] [CrossRef]
- Kuo, H.; Hsu, R.; Hsiao, Y. Investigation of Axial Segregation in a Rotating Drum. Powder Technol. 2005, 153, 196–203. [Google Scholar] [CrossRef]
- He, Y.; Chen, H.; Ding, Y.; Lickiss, B. Solids Motion and Segregation of Binary Mixtures in a Rotating Drum Mixer. Chem. Eng. Res. Des. 2007, 85, 963–973. [Google Scholar] [CrossRef]
- Jiang, M.; Zhao, Y.; Liu, G.; Zheng, J. Enhancing Mixing of Particles by Baffles in a Rotating Drum Mixer. Particuology 2011, 9, 270–278. [Google Scholar] [CrossRef]
- Alizadeh, E.; Dubé, O.; Bertrand, F.; Chaouki, J. Characterization of Mixing and Size Segregation in a Rotating Drum by a Particle Tracking Method. AIChE J. 2013, 59, 1894–1905. [Google Scholar] [CrossRef]
- Yamamoto, M.; Ishihara, S.; Kano, J. Evaluation of Particle Density Effect for Mixing Behavior in a Rotating Drum Mixer by DEM Simulation. Adv. Powder Technol. 2016, 27, 864–870. [Google Scholar] [CrossRef]
- Deng, R.; Tan, Y.; Zhang, H.; Xiao, X.; Jiang, S. Experimental and DEM Studies on the Transition of Axial Segregation in a Truck Mixer. Powder Technol. 2017, 314, 148–163. [Google Scholar] [CrossRef]
- Yang, S.; Sun, Y.; Zhang, L.; Chew, J.W. Segregation Dynamics of a Binary-Size Mixture in a Three-Dimensional Rotating Drum. Chem. Eng. Sci. 2017, 172, 652–666. [Google Scholar] [CrossRef]
- He, S.; Gan, J.; Pinson, D.; Zhou, Z. Particle Shape-Induced Radial Segregation of Binary Mixtures in a Rotating Drum. Powder Technol. 2019, 341, 157–166. [Google Scholar] [CrossRef]
- Huang, P.; Miao, Q.; Ding, Y.; Sang, G.; Jia, M. Research on Surface Segregation and Overall Segregation of Particles in a Rotating Drum Based on Stacked Image. Powder Technol. 2021, 382, 162–172. [Google Scholar] [CrossRef]
- Huang, A.; Cheng, T.; Hsu, W.; Huang, C.; Kuo, H. DEM Study of Particle Segregation in a Rotating Drum with Internal Diameter Variations. Powder Technol. 2021, 378, 430–440. [Google Scholar] [CrossRef]
- Miao, Q.; Huang, P.; Ding, Y.; Guo, J.; Jia, M. Particle Mixing and Segregation Behaviors in the Rotating Drums with Adjacent Axial Segmentations in Different Speed Directions. Powder Technol. 2022, 405, 117534. [Google Scholar] [CrossRef]
- Kuo, H.; Hsiao, Y.; Shih, P. A Study of the Axial Segregation in a Rotating Drum Using Deformable Particles. Powder Technol. 2006, 166, 161–166. [Google Scholar] [CrossRef]
- Lin, L.; Zhang, X.; Yu, M.; Mujtaba, I.M.; Chen, X. Optimized Structure Design for Binary Particle Mixing in Rotating Drums Using a Combined DEM and Gaussian Process-Based Model. Digit. Chem. Eng. 2024, 12, 100175. [Google Scholar] [CrossRef]
- Miao, Q.; Zhu, W.; Ding, Y.; Huang, P.; Hu, C.; Ge, Y. Impact of Axial Segregation Characteristics on the Particle Collision Energy in Rotating Drums. Miner. Eng. 2024, 218, 109015. [Google Scholar] [CrossRef]
- Liao, C.C.; Zhang, Z.H. Experimental Investigate the Influences of Particle Shape on Density-Induced Segregation and Dynamic Properties in Binary Granular Mixture in a Rotating Drum. Powder Technol. 2025, 454, 120696. [Google Scholar] [CrossRef]
- He, J.; Wang, Y.; Yang, L.; Zheng, Q.; Xu, J.; Liu, S.; Zhou, Z. Similarity Analysis of Size-Induced Segregation and Flow Behavior during the Scaling up Process of Rotating Drums. Powder Technol. 2024, 448, 120252. [Google Scholar] [CrossRef]
- Kumar, S.; Garg, Y.; Khatoon, S.; Dubey, P.; Kumari, K.; Anand, A. Predicting Mixing: A Strategy for Integrating Machine Learning and Discrete Element Method. Ind. Eng. Chem. Res. 2024, 63, 19640–19661. [Google Scholar] [CrossRef]
- Dai, S.; Zhang, S.; Gao, F.; He, X.; Sheng, D. Investigation of Particle Segregation in a Vertically Vibrated Binary Mixture: Segregation Process and Mechanism. Comput. Geotech. 2024, 169, 106236. [Google Scholar] [CrossRef]
- Dai, S.; Shan, F.; Xiong, H.; Zhang, S.; He, X.; Sheng, D. Evolution of Pore Structure and Flow Properties in Particle Segregation. J. Hydrol. 2025, 652, 132651. [Google Scholar] [CrossRef]
- Schröter, M.; Ulrich, S.; Kreft, J.; Swift, J.B.; Swinney, H.L. Mechanisms in the Size Segregation of a Binary Granular Mixture. Phys. Rev. E 2006, 74, 011307. [Google Scholar] [CrossRef]
- Gajjar, P.; Johnson, C.G.; Carr, J.; Chrispeels, K.; Gray, J.M.N.T.; Withers, P.J. Size Segregation of Irregular Granular Materials Captured by Time-Resolved 3D Imaging. Sci. Rep. 2021, 11, 8352. [Google Scholar] [CrossRef]
- van der Linden, M.N.; Everts, J.C.; van Roij, R.; van Blaaderen, A. Realization of the Brazil-nut Effect in Charged Colloids without External Driving. Proc. Natl. Acad. Sci. USA 2023, 120, e2213044120. [Google Scholar] [CrossRef] [PubMed]
- Maurel, C.; Ballouz, R.L.; Richardson, D.C.; Michel, P.; Schwartz, S.R. Numerical Simulations of Oscillation-Driven Regolith Motion: Brazil-nut Effect. Mon. Not. R. Astron. Soc. 2017, 464, 2866–2881. [Google Scholar] [CrossRef]
- Kruppa, T.; Neuhaus, T.; Messina, R.; Löwen, H. Soft Repulsive Mixtures under Gravity: Brazil-nut Effect, Depletion Bubbles, Boundary Layering, Nonequilibrium Shaking. J. Chem. Phys. 2012, 136, 134106. [Google Scholar] [CrossRef]
- Liao, C.C.; Hsiau, S.S. Transport Properties and Segregation Phenomena in Vibrating Granular Beds. KONA Powder Part. J. 2016, 33, 109–126. [Google Scholar] [CrossRef]
- Qiao, J.; Duan, C.; Dong, K.; Wang, W.; Jiang, H.; Zhu, H.; Zhao, Y. DEM Study of Segregation Degree and Velocity of Binary Granular Mixtures Subject to Vibration. Powder Technol. 2021, 382, 107–117. [Google Scholar] [CrossRef]
- Choi, S.B.; Li, W.; Yu, M.; Du, H.; Fu, J.; Do, P.X. State of the Art of Control Schemes for Smart Systems Featuring Magneto-Rheological Materials. Smart Mater. Struct. 2016, 25, 043001. [Google Scholar] [CrossRef]
- Gopinath, B.; Sathishkumar, G.; Karthik, P.; Martin Charles, M.; Ashok, K.; Ibrahim, M.; Mohamed Akheel, M. A Systematic Study of the Impact of Additives on Structural and Mechanical Properties of Magnetorheological Fluids. Mater. Today Proc. 2021, 37, 1721–1728. [Google Scholar] [CrossRef]
- Huang, X.; Yang, B. Towards Novel Energy Shunt Inspired Vibration Suppression Techniques: Principles, Designs and Applications. Mech. Syst. Signal Process. 2023, 182, 109496. [Google Scholar] [CrossRef]
- Sharma, S.K.; Sharma, R.C.; Upadhyay, R.K.; Lee, J. Enhanced Ship Engine Vibration Reduction Using Magnetorheological Dampers and Adaptive Neuro-Fuzzy Control System. Ships Offshore Struct. 2025, 20, 143–159. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, C.; Zheng, X.; Zhao, L.; Qiu, Y. Advancements in Semi-Active Automotive Suspension Systems with Magnetorheological Dampers: A Review. Appl. Sci. 2024, 14, 7866. [Google Scholar] [CrossRef]
- Kumbhar, M.B.; Desavale, R.G.; Jagadeesha, T. Experimentation and Damping Performance Analysis of a MR Damper for Resonance Control in a Quarter Car Suspension System. J. Vib. Eng. Technol. 2024, 12, 5973–5983. [Google Scholar] [CrossRef]
- Zhang, Y.; Guo, J.; Yang, J.; Li, X. Recent Structural Developments and Applications of Magnetorheological Dampers (MRD): A Review. Magnetochemistry 2023, 9, 90. [Google Scholar] [CrossRef]
- Xu, Z.D.; Chen, Z.H.; Huang, X.H.; Zhou, C.Y.; Hu, Z.W.; Yang, Q.H.; Gai, P.P. Recent Advances in Multi-Dimensional Vibration Mitigation Materials and Devices. Front. Mater. 2019, 6, 143. [Google Scholar] [CrossRef]
- Garg, D.P.; Anderson, G.L. Structural Damping and Vibration Control via Smart Sensors and Actuators. J. Vib. Control. 2003, 9, 1421–1452. [Google Scholar] [CrossRef]
- Yu, Y.; Royel, S.; Li, Y.; Li, J.; Yousefi, A.M.; Gu, X.; Li, S.; Li, H. Dynamic Modelling and Control of Shear-Mode Rotational MR Damper for Mitigating Hazard Vibration of Building Structures. Smart Mater. Struct. 2020, 29, 114006. [Google Scholar] [CrossRef]
- Son, K.J.; Fahrenthold, E.P. Evaluation of Magnetorheological Fluid Augmented Fabric as a Fragment Barrier Material. Smart Mater. Struct. 2012, 21, 075012. [Google Scholar] [CrossRef]
- Son, K.J.; Fahrenthold, E.P. Magnetorheological Damping of Fragment Barrier Suspension Systems. J. Dyn. Syst. Meas. Control. 2018, 140, 091002. [Google Scholar] [CrossRef]
- Son, K.J.; Fahrenthold, E.P. Impact Dynamics Simulation for Magnetorheological Fluid Saturated Fabric Barriers. J. Comput. Nonlinear Dyn. 2024, 19, 061002. [Google Scholar] [CrossRef]
- Son, K.J. A Discrete Element Model for the Influence of Surfactants on Sedimentation Characteristics of Magnetorheological Fluids. Korea-Aust. Rheol. J. 2018, 30, 29–39. [Google Scholar] [CrossRef]
- Kumar, V.; Kumar, R.; Kumar, H. Rheological Characterization and Performance Evaluation of Magnetorheological Finishing Fluid. J. Appl. Fluid Mech. 2020, 13, 185–197. [Google Scholar] [CrossRef]
- Saha, P.; Mukherjee, S.; Mandal, K. Rheological Response of Magnetic Fluid Containing Fe3O4 Nano Structures. J. Magn. Magn. Mater. 2019, 484, 324–328. [Google Scholar] [CrossRef]
- Pei, P.; Peng, Y. Constitutive Modeling of Magnetorheological Fluids: A Review. J. Magn. Magn. Mater. 2022, 550, 169076. [Google Scholar] [CrossRef]
- Genç, S.; Phulé, P.P. Rheological Properties of Magnetorheological Fluids. Smart Mater. Struct. 2002, 11, 140. [Google Scholar] [CrossRef]
- Upadhyay, R.V.; Choi, S.B. Modeling, Measurements and Validation of Magnetic Field Dependent Flow Behavior of Magnetorheological Fluids; Static and Dynamic Yield Stress. Smart Mater. Struct. 2021, 30, 117002. [Google Scholar] [CrossRef]
- Zhu, X.; Jing, X.; Cheng, L. Magnetorheological Fluid Dampers: A Review on Structure Design and Analysis. J. Intell. Mater. Syst. Struct. 2012, 23, 839–873. [Google Scholar] [CrossRef]
- Cruze, D.; Hemalatha, G.; Jebadurai, S.V.S.; Sarala, L.; Tensing, D.; Christy, S.S.J.E. A Review on the Magnetorheological Fluid, Damper and Its Applications for Seismic Mitigation. Civ. Eng. J. 2018, 4, 3058–3074. [Google Scholar] [CrossRef]
- Masa’id, A.; Lenggana, B.W.; Ubaidillah, U.; Susilo, D.D.; Choi, S.B. A Review on Vibration Control Strategies Using Magnetorheological Materials Actuators: Application Perspective. Actuators 2023, 12, 113. [Google Scholar] [CrossRef]
- Desai, R.M.; Jamadar, M.E.H.; Kumar, H.; Joladarashi, S.; Rajasekaran, S.C.; Amarnath, G. Evaluation of a Commercial MR Damper for Application in Semi-Active Suspension. SN Appl. Sci. 2019, 1, 993. [Google Scholar] [CrossRef]
- Jamadar, M.e.H.; Desai, R.M.; Saini, R.S.T.; Kumar, H.; Joladarashi, S. Dynamic Analysis of a Quarter Car Model with Semi-Active Seat Suspension Using a Novel Model for Magneto-Rheological (MR) Damper. J. Vib. Eng. Technol. 2021, 9, 161–176. [Google Scholar] [CrossRef]
- Alchikh-Sulaiman, B.; Alian, M.; Ein-Mozaffari, F.; Lohi, A.; Upreti, S.R. Using the Discrete Element Method to Assess the Mixing of Polydisperse Solid Particles in a Rotary Drum. Particuology 2016, 25, 133–142. [Google Scholar] [CrossRef]
- Son, K.J. A Numerical Study of the Influence of Rheology of Cohesive Particles on Blade Free Planetary Mixing. Korea-Aust. Rheol. J. 2018, 30, 199–209. [Google Scholar] [CrossRef]
- Son, K.J. A Numerical Study of the Influence of Operating Conditions of a Blade Free Planetary Mixer on Blending of Cohesive Powders. Korea-Aust. Rheol. J. 2019, 31, 15–23. [Google Scholar] [CrossRef]
- Byun, J.; Son, K.J. Experimental and Numerical Study of Computer Vision-Based Real-Time Monitoring of Polymeric Particle Mixing Process in Rotary Drum. Polymers 2024, 16, 1524. [Google Scholar] [CrossRef]
- Son, K.J. Discrete Element Method Analysis of Soil Penetration Depth Affected by Spreading Speed in Drone-Seeded Rice. Agriculture 2025, 15, 422. [Google Scholar] [CrossRef]
- Fleissner, F.; Gaugele, T.; Eberhard, P. Applications of the Discrete Element Method in Mechanical Engineering. Multibody Syst. Dyn. 2007, 18, 81–94. [Google Scholar] [CrossRef]
- Tavarez, F.A.; Plesha, M.E. Discrete element method for modelling solid and particulate materials. Int. J. Numer. Methods Eng. 2007, 70, 379–404. [Google Scholar] [CrossRef]
- Hlosta, J.; Jezerská, L.; Rozbroj, J.; Žurovec, D.; Nečas, J.; Zegzulka, J. DEM Investigation of the Influence of Particulate Properties and Operating Conditions on the Mixing Process in Rotary Drums: Part 1—Determination of the DEM Parameters and Calibration Process. Processes 2020, 8, 222. [Google Scholar] [CrossRef]
- Höhner, D.; Wirtz, S.; Scherer, V. Experimental and Numerical Investigation on the Influence of Particle Shape and Shape Approximation on Hopper Discharge Using the Discrete Element Method. Powder Technol. 2013, 235, 614–627. [Google Scholar] [CrossRef]
- Wen, Y.; Liu, M.; Liu, B.; Shao, Y. Comparative Study on the Characterization Method of Particle Mixing Index Using DEM Method. Procedia Eng. 2015, 102, 1630–1642. [Google Scholar] [CrossRef]
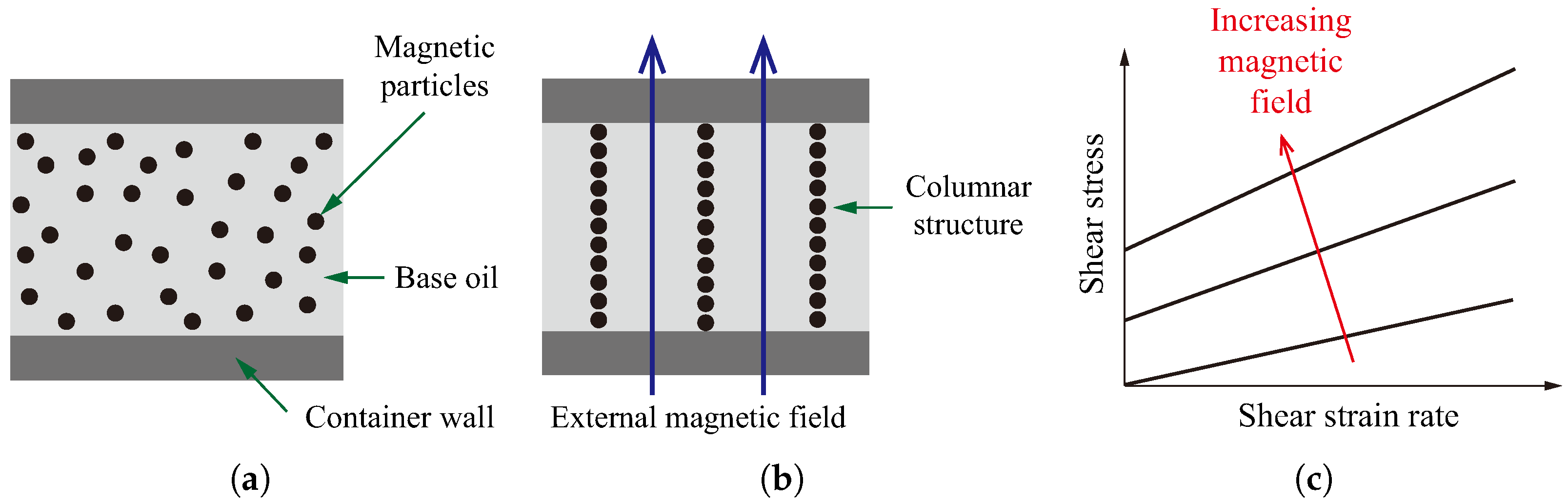





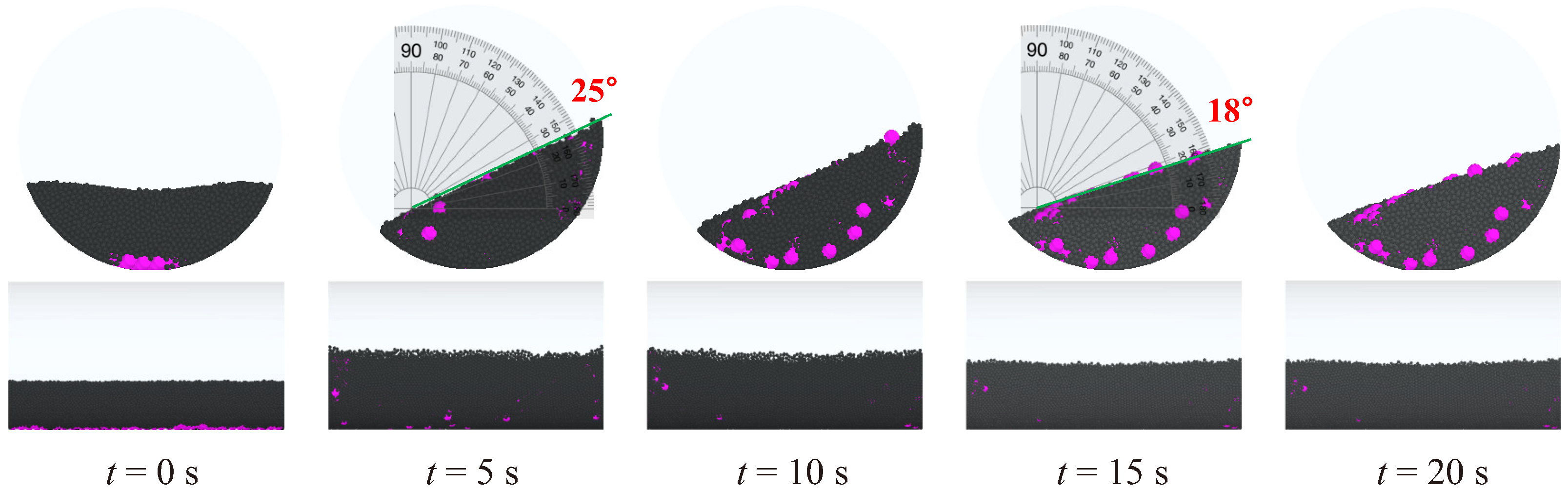
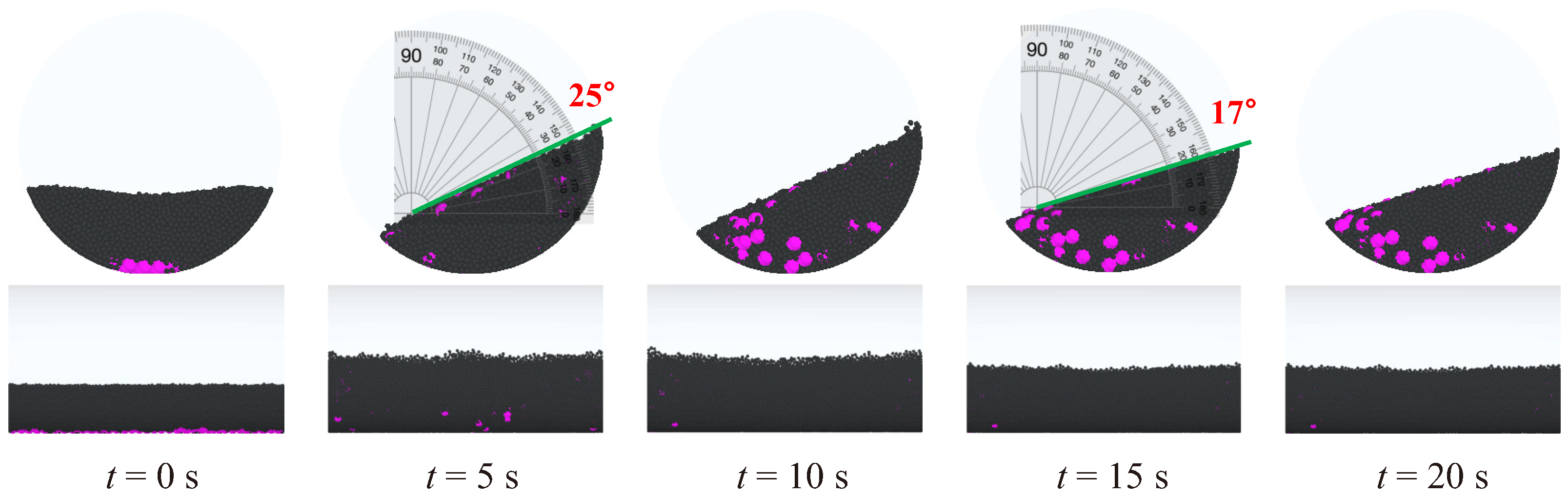
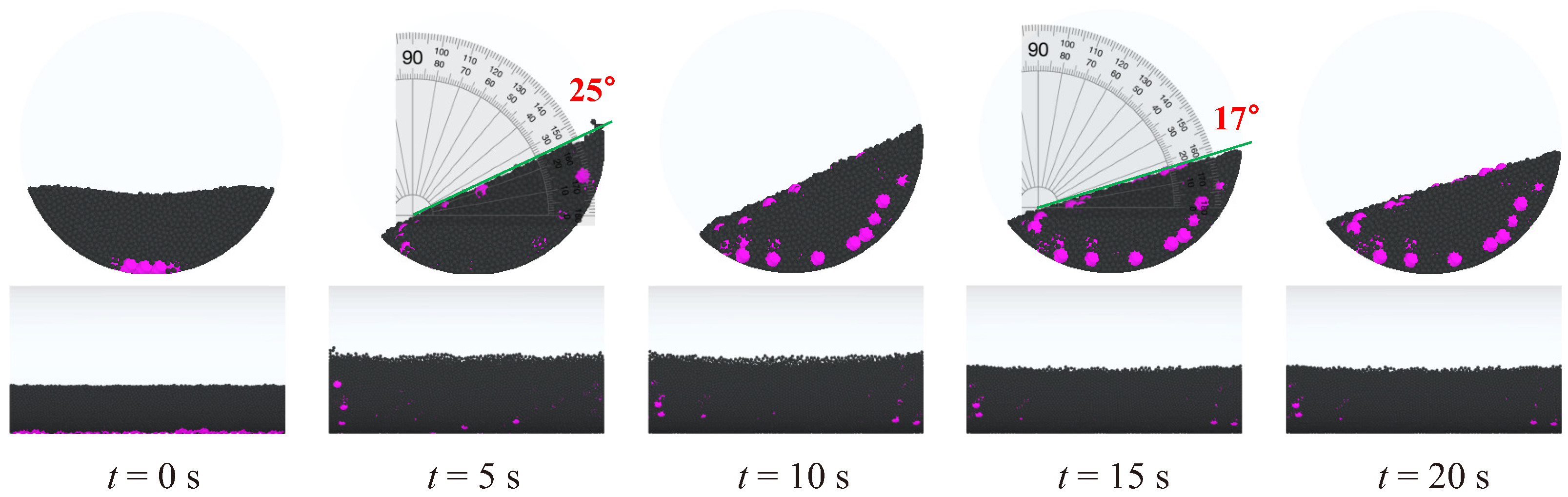

| Specification 1 | Unit | Value |
|---|---|---|
| Stroke distance | mm | 74.0 |
| Max tensile strength | N | 8896 |
| Max continuous current (30 s max) | A | 1 |
| Max intermittent current (short bursts) | A | 2 |
| Magnetized damping force (5 cm/s @ 1 A) | N | 2447 |
| Non-magnetized damping force (20 cm/s) | N | 667 |
| Property | Unit | Value |
|---|---|---|
| Density | 1250 | |
| Modulus of elasticity | MPa | 300 |
| Poisson’s ratio | - | 0.4 |
| Coefficient of lateral friction | - | 0.39 |
| Coefficient of rolling friction | - | 0.000271 |
| Coefficient of restitution | - | 0.55 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Son, K.J. Vibration Attenuation in Particle Mixer Using Magnetorheological Damping Technology to Mitigate the Brazil Nut Effect. Machines 2025, 13, 487. https://doi.org/10.3390/machines13060487
Son KJ. Vibration Attenuation in Particle Mixer Using Magnetorheological Damping Technology to Mitigate the Brazil Nut Effect. Machines. 2025; 13(6):487. https://doi.org/10.3390/machines13060487
Chicago/Turabian StyleSon, Kwon Joong. 2025. "Vibration Attenuation in Particle Mixer Using Magnetorheological Damping Technology to Mitigate the Brazil Nut Effect" Machines 13, no. 6: 487. https://doi.org/10.3390/machines13060487
APA StyleSon, K. J. (2025). Vibration Attenuation in Particle Mixer Using Magnetorheological Damping Technology to Mitigate the Brazil Nut Effect. Machines, 13(6), 487. https://doi.org/10.3390/machines13060487







