Parameter Stress Response Prediction for Vehicle Dust Extraction Fan Impeller Based on Feedback Neural Network
Abstract
1. Introduction
2. Finite Element Analysis and Parametric Modeling of Impeller Blades in Dust Extraction Fans
2.1. Establishment of Finite Element Model
2.1.1. Geometric Model
2.1.2. Mesh Generation
2.1.3. Boundary Conditions
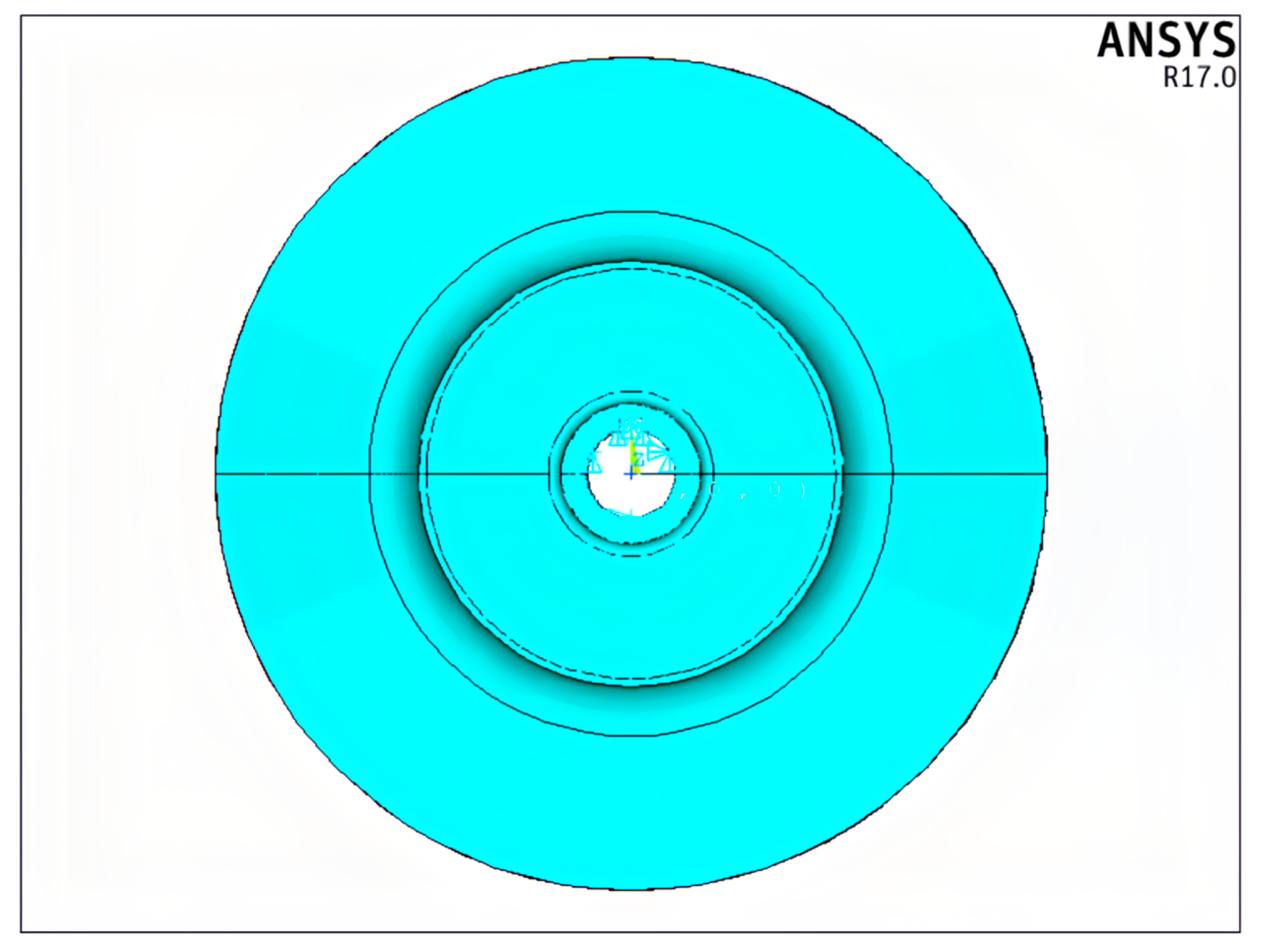
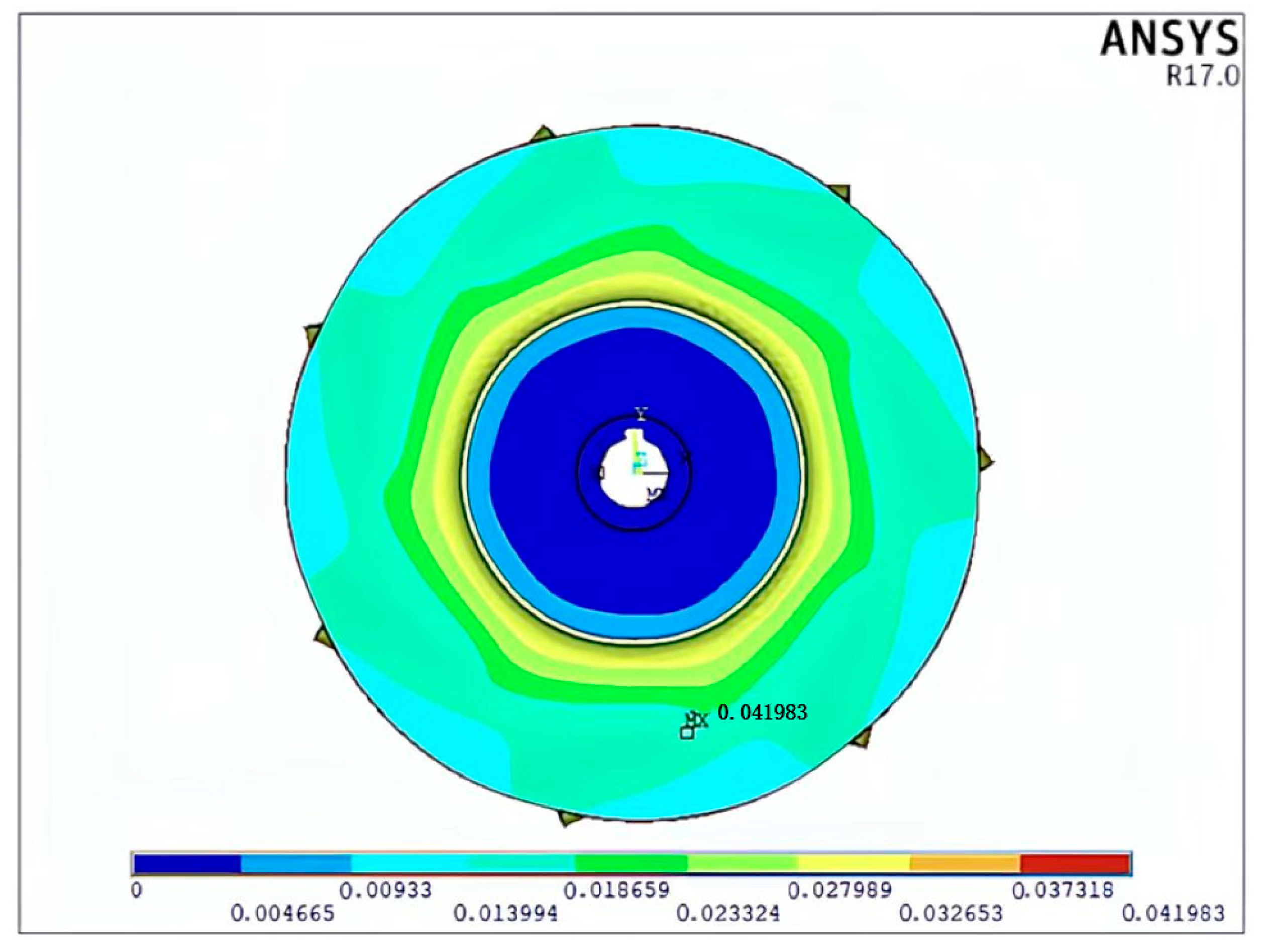
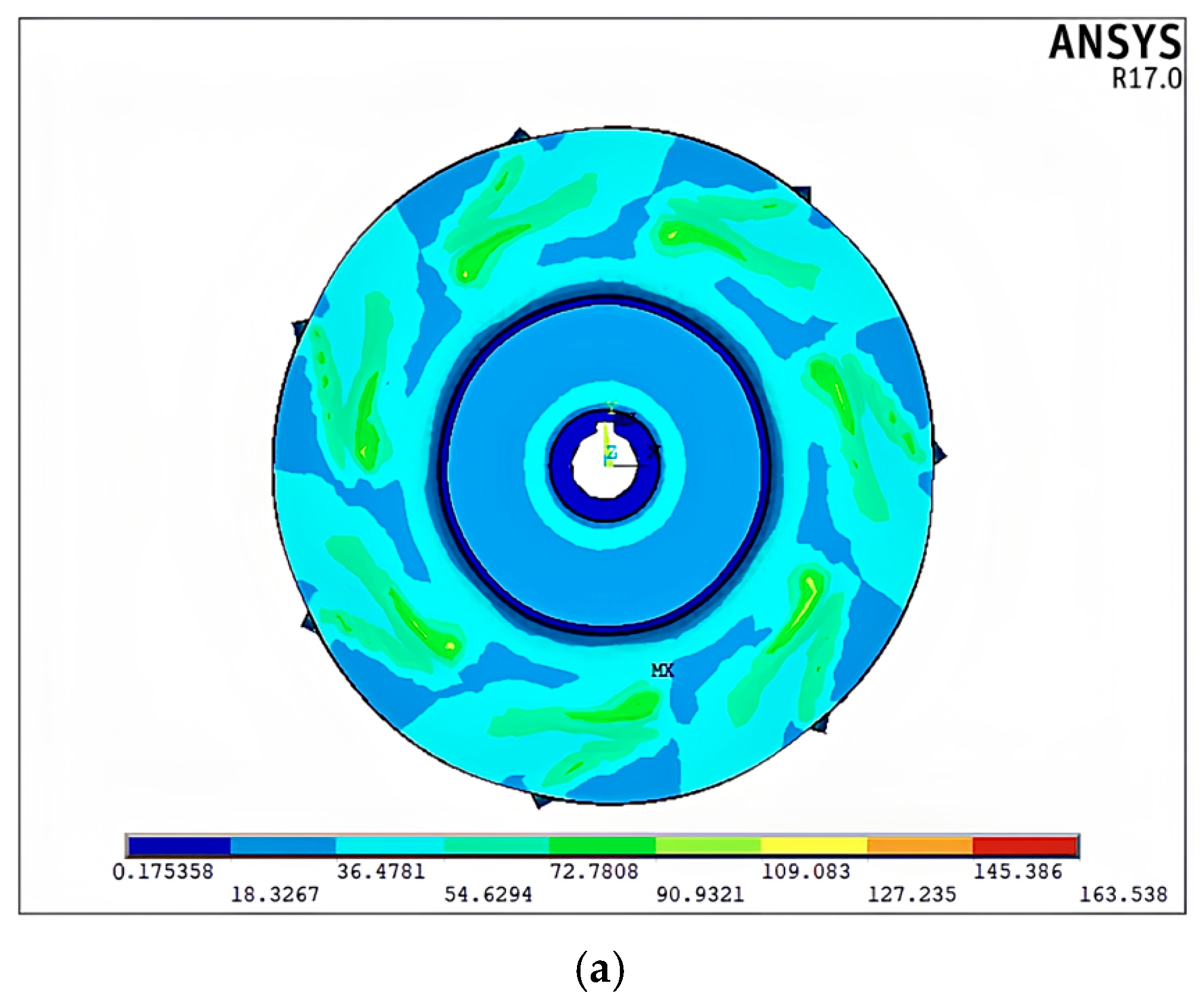
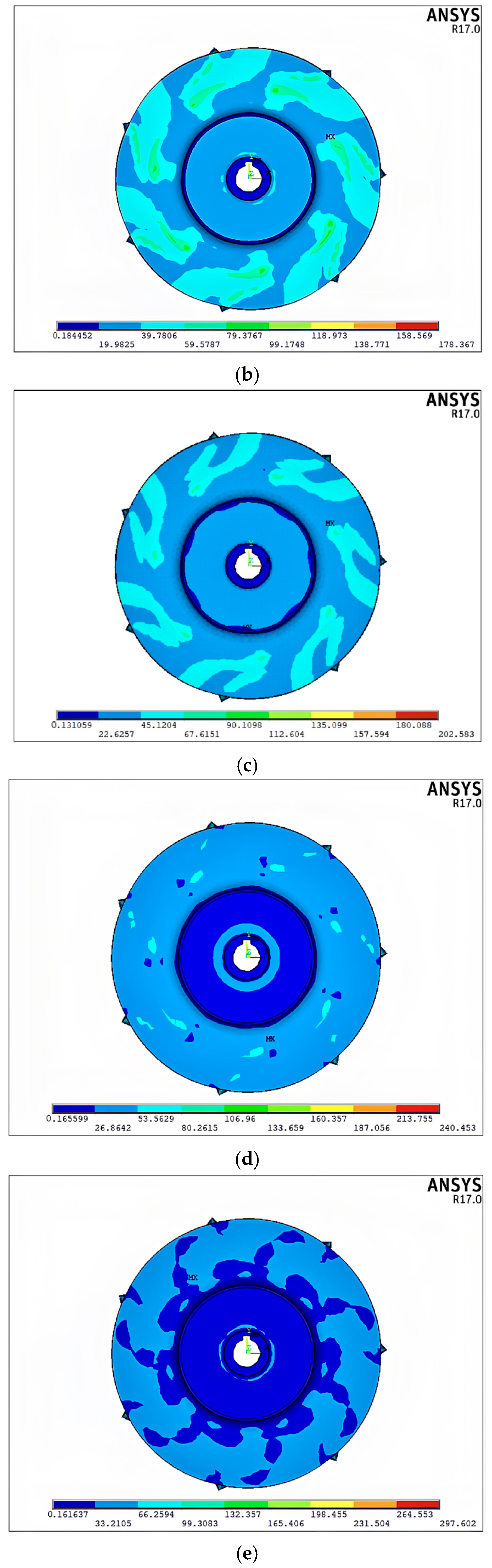
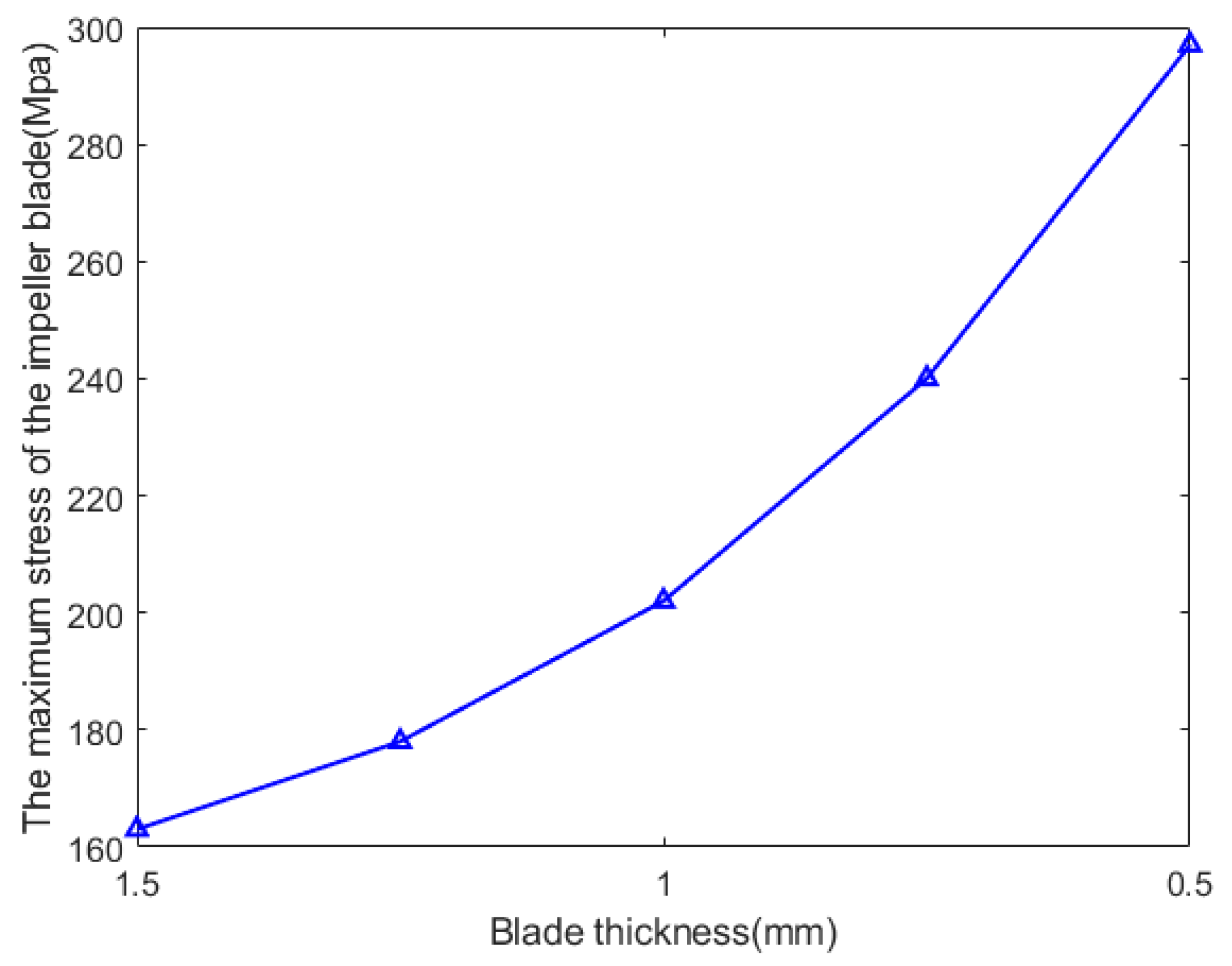
2.1.4. Finite Element Simulation Results
2.2. Parametric Modeling of Impeller Blades
2.2.1. Selection of Design Parameters
2.2.2. Parametric Modeling
3. Parameter Response Prediction for Impeller Blades Using Surrogate Models
3.1. Impeller Blade Stress Prediction Based on Feedback Neural Network
3.1.1. Principle of Feedback Neural Network
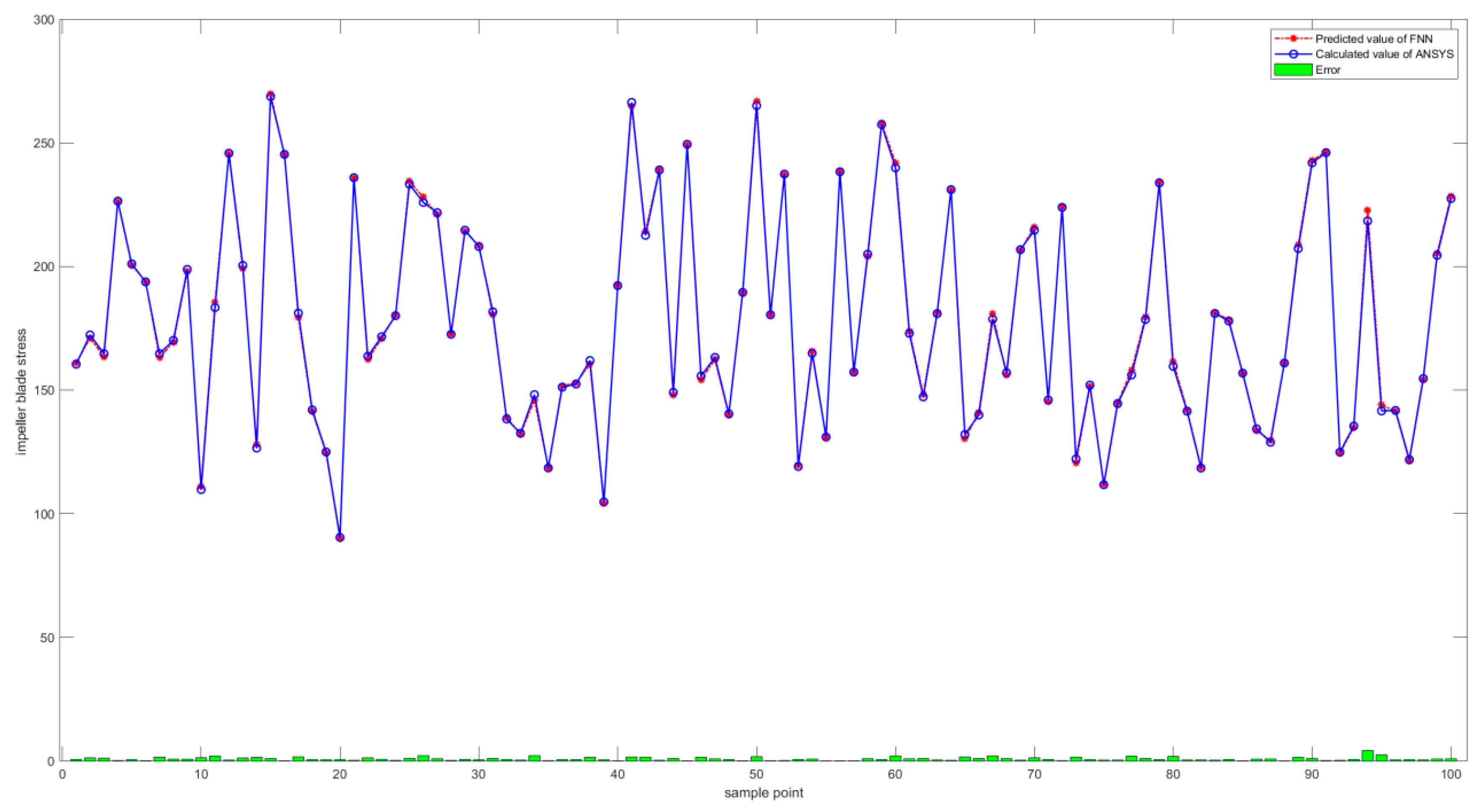
3.1.2. FNN Stress Predictions
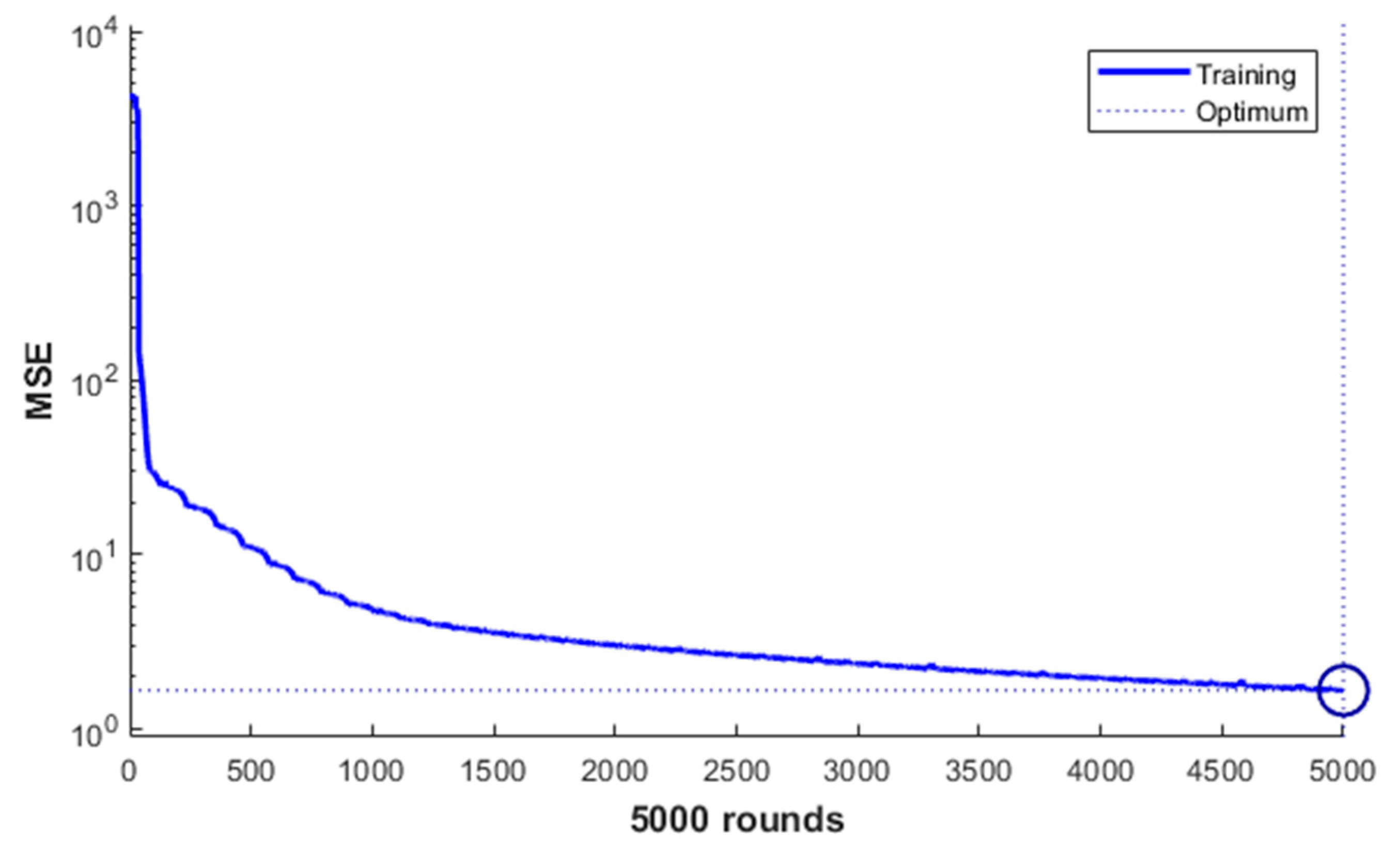
3.2. Impeller Blade Stress Prediction Based on Backpropagation Neural Network
3.2.1. Principle of Backpropagation Neural Network
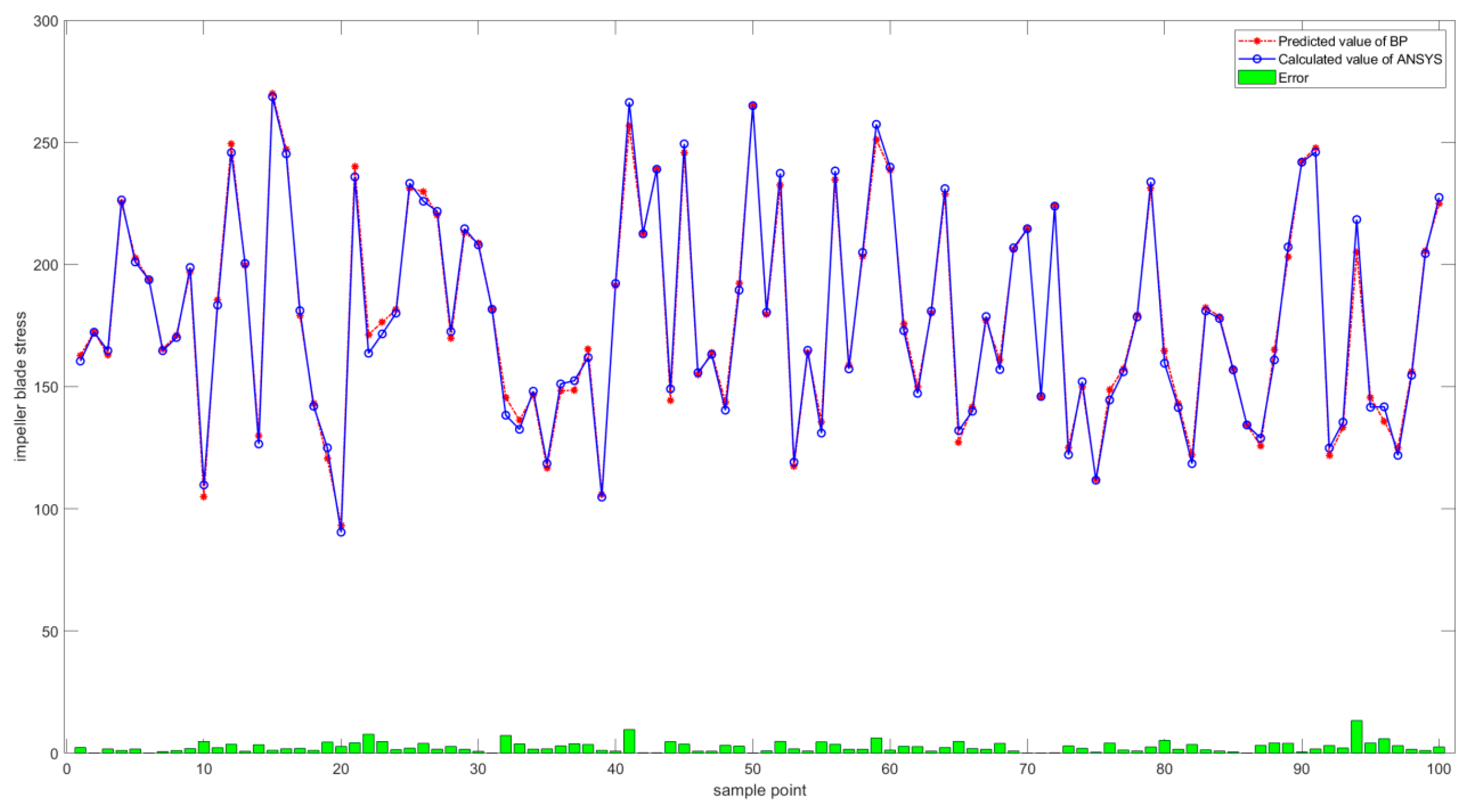
3.2.2. BPNN Stress Predictions
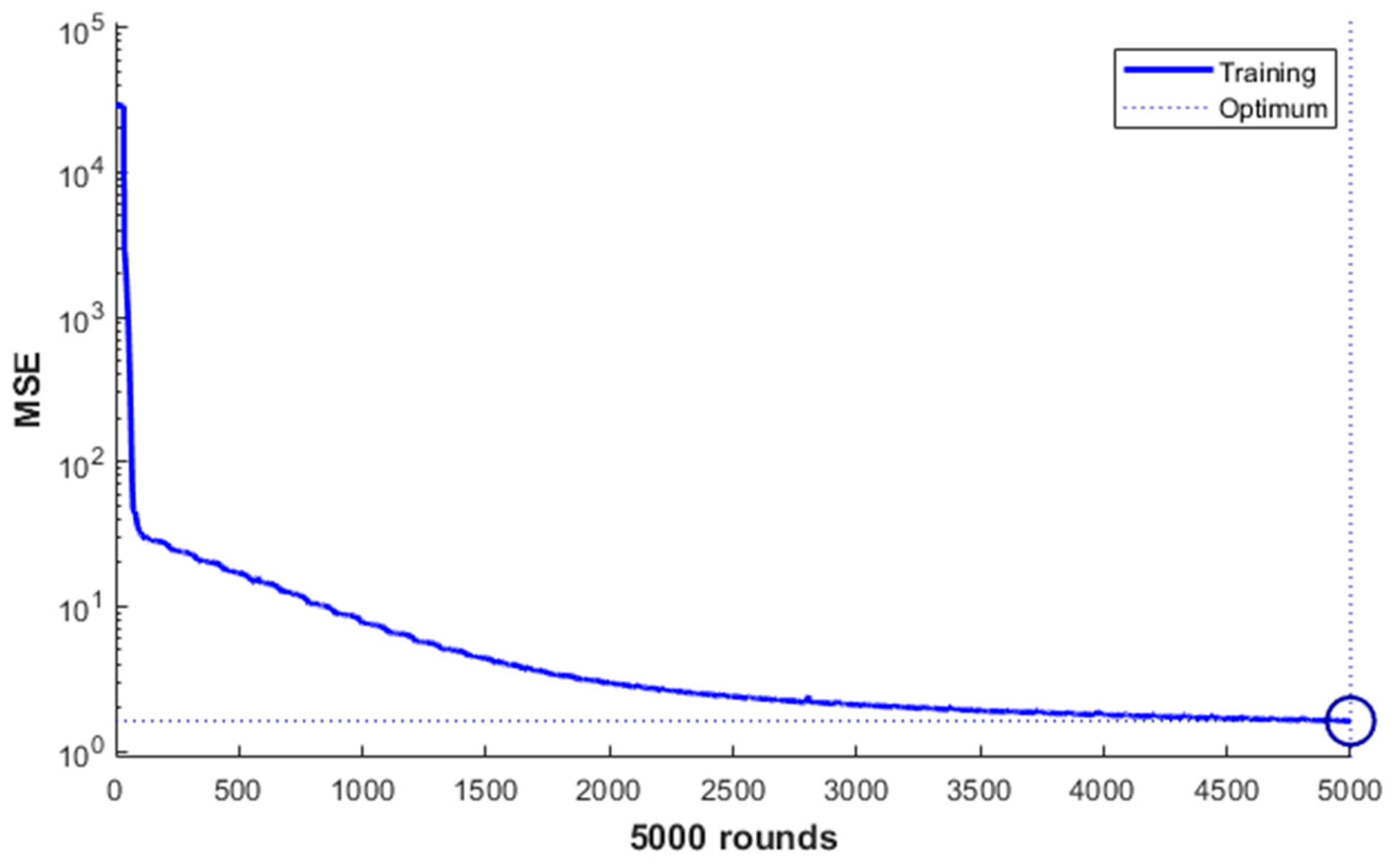
3.3. Impeller Blade Stress Prediction Based on Quadratic Polynomial Response Surface Method
3.3.1. Principle of Quadratic Polynomial Response Surface Method
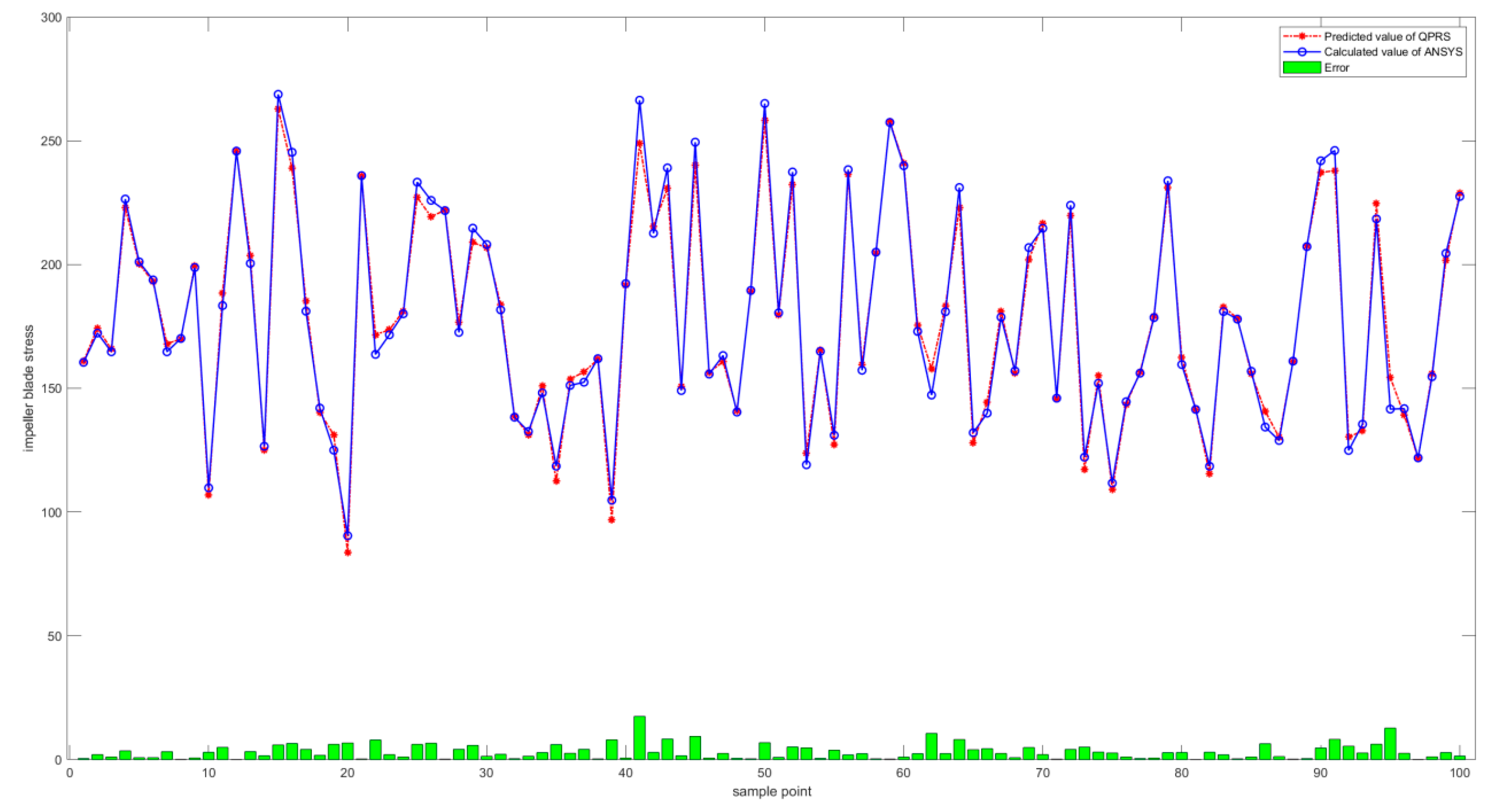
3.3.2. QPRS Stress Predictions
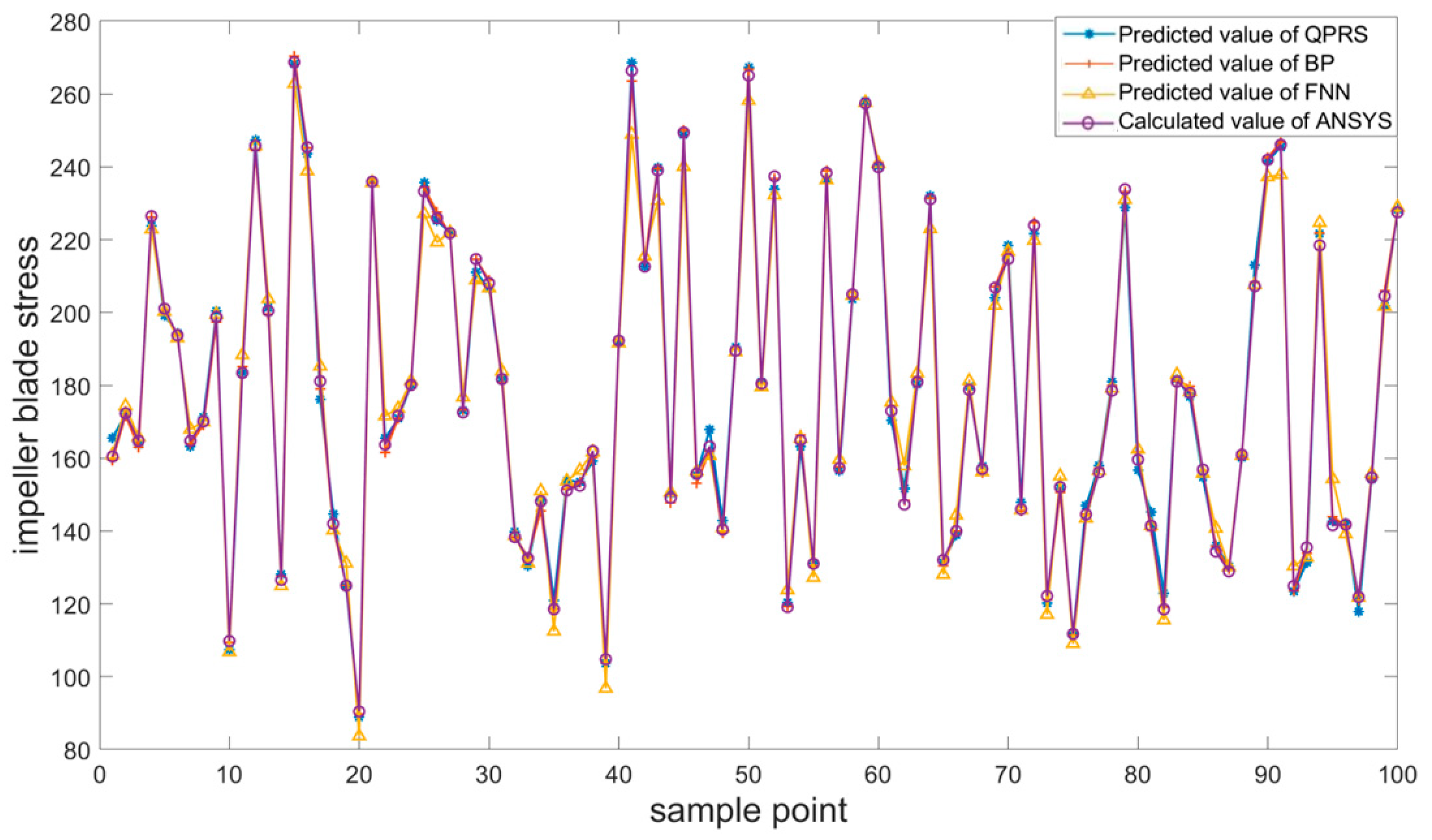
3.4. Comparison of Surrogate Model Performance
4. Conclusions
- (1)
- The structural characteristics and load conditions of the impeller were analyzed in detail to clarify the constraints and loads it experiences during service. The stress and displacement distributions in impeller blades with different thicknesses were determined through a series of finite element analyses considering the appropriate material property definitions, mesh generation, constraint conditions, and load application. The most critical location on the impeller blade was determined to be the midpoint of the blade tip, where the maximum displacement was observed.
- (2)
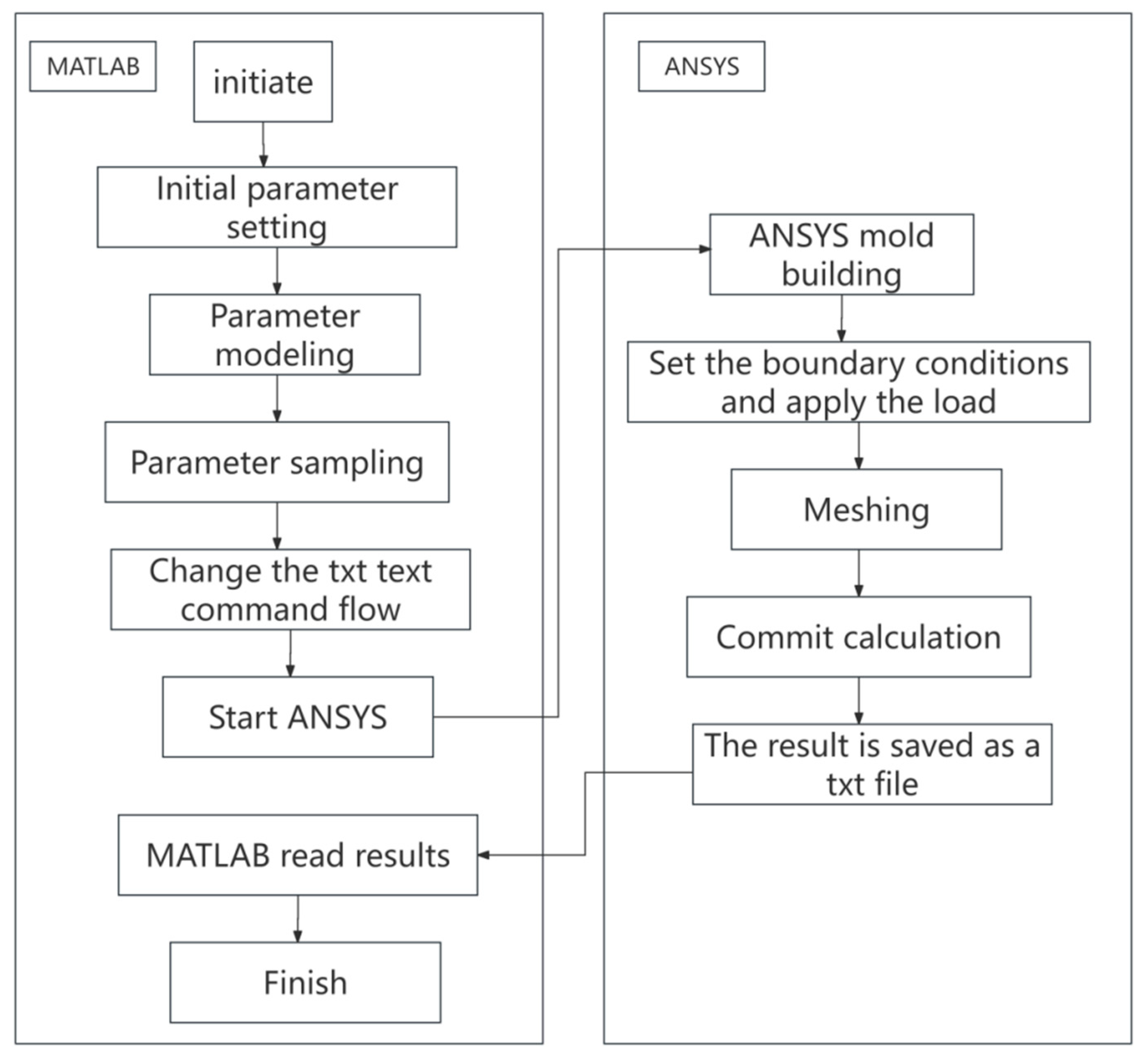
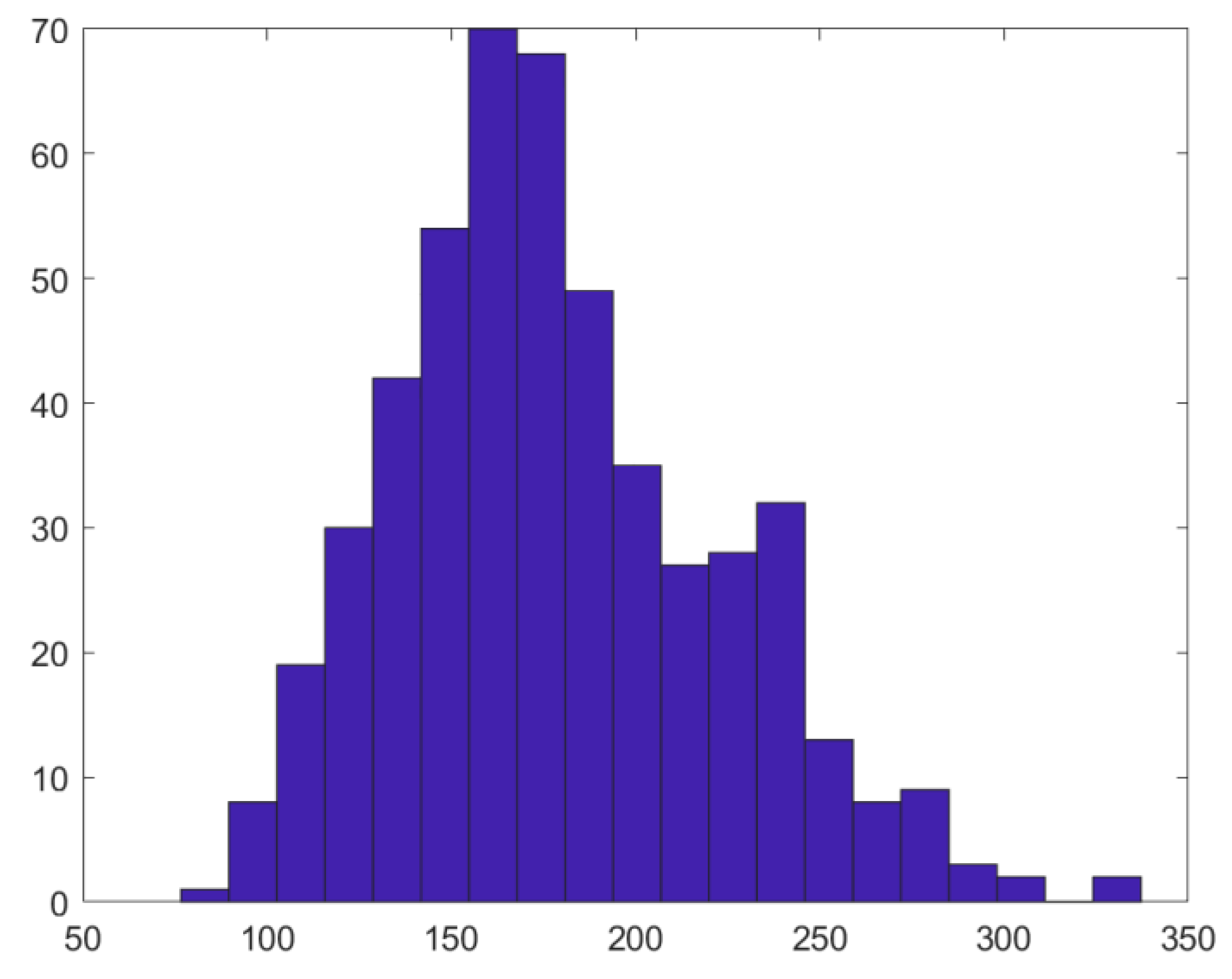
- The FNN, BPNN, and QPRS surrogate models were constructed to predict the impeller blade stress based on the input parameters. Six random variables were selected as the inputs to each model, and the maximum stress in the impeller blades was considered the output. MATLAB R2023a software was used to construct training samples based on the distribution of each parameter, and a parametric model was established using APDL to conduct batch calculations. After these calculations were completed, the parameter values and corresponding stresses were combined into a training set to train each surrogate model. Among the three considered surrogate models, the FNN exhibited the smallest prediction error of 0.0043.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, Y.; Cai, Y.; Yang, G.; Zhou, H.; Liu, J. Neural adaptive pointing control of a moving tank gun with lumped uncertainties based on dynamic simulation. J. Mech. Sci. Technol. 2022, 36, 2709–2720. [Google Scholar] [CrossRef]
- Lu, J.; Xie, D.; Wang, J.; Sun, Y.; Qiao, M.; Li, J.; Li, W.; Chen, K. Experimental Study on the Air Filter of a Heavy Vehicle in Desert Areas. Veh. Power Technol. 2016, 3, 16–20. [Google Scholar]
- Rivera, B.H.; Rodriguez, M.G. Characterization of Airborne Particles Collected from Car Engine Air Filters Using SEM and EDX Techniques. Int. J. Environ. Res. Public Health 2016, 13, 985. [Google Scholar] [CrossRef] [PubMed]
- Song, X. Performance Analysis and Structural Optimization of the Air Filter of a Heavy Truck Based on Fluid-Structure Interaction. Master’s Thesis, Qilu University of Technology, Jinan, China, 2023. [Google Scholar]
- Zhang, J.; Guo, Z.; Zhang, H.; Wang, X. Flow Field Analysis and Structural Optimization of the Air Filter of a Vehicle Diesel Engine. Intern. Combust. Engines 2023, 39, 26–32. [Google Scholar]
- Hu, T. Discussion on the Performance Testing Method of Motorcycle Air Filters. Motorcycle Technol. 2005, 7, 25–26+48. [Google Scholar]
- Lu, J.; Sun, Y.; Qiao, M.; Wang, J.; Chen, K. Simulation and Experimental Study on the Performance of Air Filter Filter Materials. Veh. Power Technol. 2019, 1, 38–42+49. [Google Scholar]
- Sun, Y.; Wang, J.; Lu, J.; Qiao, M.; Chen, K.; Li, W.; Li, J. Research on a Simulation Analysis Method of Air Filters. Veh. Power Technol. 2014, 3, 32–34+49. [Google Scholar]
- Hao, Y. Analysis of the Force-Thermal Coupling Response of Turbine Blades. Master’s Thesis, Beijing University of Chemical Technology, Beijing, China, 2023. [Google Scholar]
- Tang, Y. Point Cloud Denoising and Surface Reconstruction in the Preparation of Turbine Blades Based on Deep Learning. Master’s Thesis, Southwest University of Science and Technology, Langfang, China, 2023. [Google Scholar]
- Li, Y.; Qin, Q.; Wang, Y.; Hu, M. Welded Joint Fatigue Reliability Analysis on Bogie Frame of High-Speed Electric Multiple Unit. J. Shanghai Jiaotong Univ. (Sci.) 2017, 22, 365–370. [Google Scholar] [CrossRef]
- Gao, W.; Mo, X.; Fu, R.; Sun, G. 6σ Robust Optimization Design of the Crashworthiness of Foam-Filled Conical Thin-Walled Structures Based on Kriging. Acta Mech. Solida Sin. 2012, 33, 370–378. [Google Scholar]
- Gupta, S.; Manohar, C.S. Improved response surface method for time-variant reliability analysis of nonlinear random structures under non-stationary excitations. Nonlinear Dyn. 2004, 36, 267–280. [Google Scholar] [CrossRef]
- Zhang, C.; Bai, G.; Xiang, J. Reliability Optimization Design of Flexible Mechanisms Based on the Extreme Value Response Surface Method. J. Harbin Eng. Univ. 2010, 31, 1503–1508. [Google Scholar]
- Kang, Z.; Luo, Y. Reliability-based structural optimization with probability and convex set hybrid models. Struct. Multidiscip. Optim. 2010, 42, 89–102. [Google Scholar] [CrossRef]
- Ling, J.; Kurzawski, A.; Templeton, J. Reynolds averaged turbulence modelling using deep neural networks with embedded invariance. J. Fluid Mech. 2016, 807, 155–166. [Google Scholar] [CrossRef]
- Ladický, L.U.; Jeong, S.; Solenthaler, B.; Pollefeys, M.; Gross, M. Data-driven fluid simulations using regression forests. ACM Trans. Graph. 2015, 34, 1–9. [Google Scholar] [CrossRef]
- Milani, P.M.; Ling, J.; Eaton, J.K. Physical interpretation of machine learning models applied to film cooling flows. J. Turbomach. 2019, 141, 011004. [Google Scholar] [CrossRef]
- Maral, H.; Şenel, C.B.; Deveci, K.; Alpman, E.; Kavurmacıoğlu, L.; Camci, C. A genetic algorithm based multi-objective optimization of squealer tip geometry in axial flow turbines: A constant tip gap approach. J. Fluids Eng. 2020, 142, 021402. [Google Scholar] [CrossRef]
- Zhang, L.; Sun, X.; Chen, J.; Sun, Y.; Guo, J.; Zheng, J. Research Progress in Reliability Analysis and Optimal Design of Automobile Structures. China Mech. Eng. 2024, 35, 1948–1962. [Google Scholar]
- Roccia, B.A.; Ruiz, M.; Gebhardt, C.G. On the use of feed-forward neural networks in the context of surrogate aeroelastic simulations. Acta Mech. 2025, 236, 673–705. [Google Scholar] [CrossRef]
- Awad, A.N.; Jarad, T.S. Hybrid Particle Swarm Optimization and Feedforward Neural Network Model for Enhanced Prediction of Gas Turbine Emissions. Int. J. Energy Prod. Manag. 2024, 9, 97–105. [Google Scholar] [CrossRef]
- Ma, C.; Wang, N.; Guo, S.; Wang, R. Numerical Simulation of the Performance Deterioration of a Radial Flow Turbine Caused by Particle Erosion. Trans. CSICE 2024, 42, 358–366. [Google Scholar] [CrossRef]
- Singh, G. Effect of suspended particles on erosion characteristics of impeller steels utilizing combined CFD and DOE approach. Ind. Lubr. Tribol. 2025, 77, 202–210. [Google Scholar] [CrossRef]
- Wang, L.-F.; Zhou, X.-P. A field-enriched finite element method for simulating the failure process of rocks with different defects. Comput. Struct. 2021, 250, 106539. [Google Scholar] [CrossRef]
- Fan, Z. Research on the Distribution Law of NC Machining Precision. Ph.D. Thesis, Northeastern University, Shenyang, China, 2013. [Google Scholar]
- Liu, L.; Zhong, L. Research on the Thermal Shock Resistance of the Fuselage Coating Based on the Feedback Neural Network. Ordnance Mater. Sci. Eng. 2023, 46, 106–111. [Google Scholar]
- Yan, H. Coal gangue image classification model based on the improved feedback neural network. Ind. Mine Autom. 2022, 48, 50–55+113. [Google Scholar]
- Mohamad, E.T.; Faradonbeh, R.S.; Armaghani, D.J.; Monjezi, M.; Majid, M.Z.A. An optimized ANN model based on genetic algorithm for predicting ripping production. Neural Comput. Appl. 2017, 28, 393–406. [Google Scholar] [CrossRef]
- Shan, D.; Li, Q.; Khan, I.; Zhou, X. A novel finite element model updating method based on substructure and response surface model. Eng. Struct. 2015, 103, 147–156. [Google Scholar] [CrossRef]
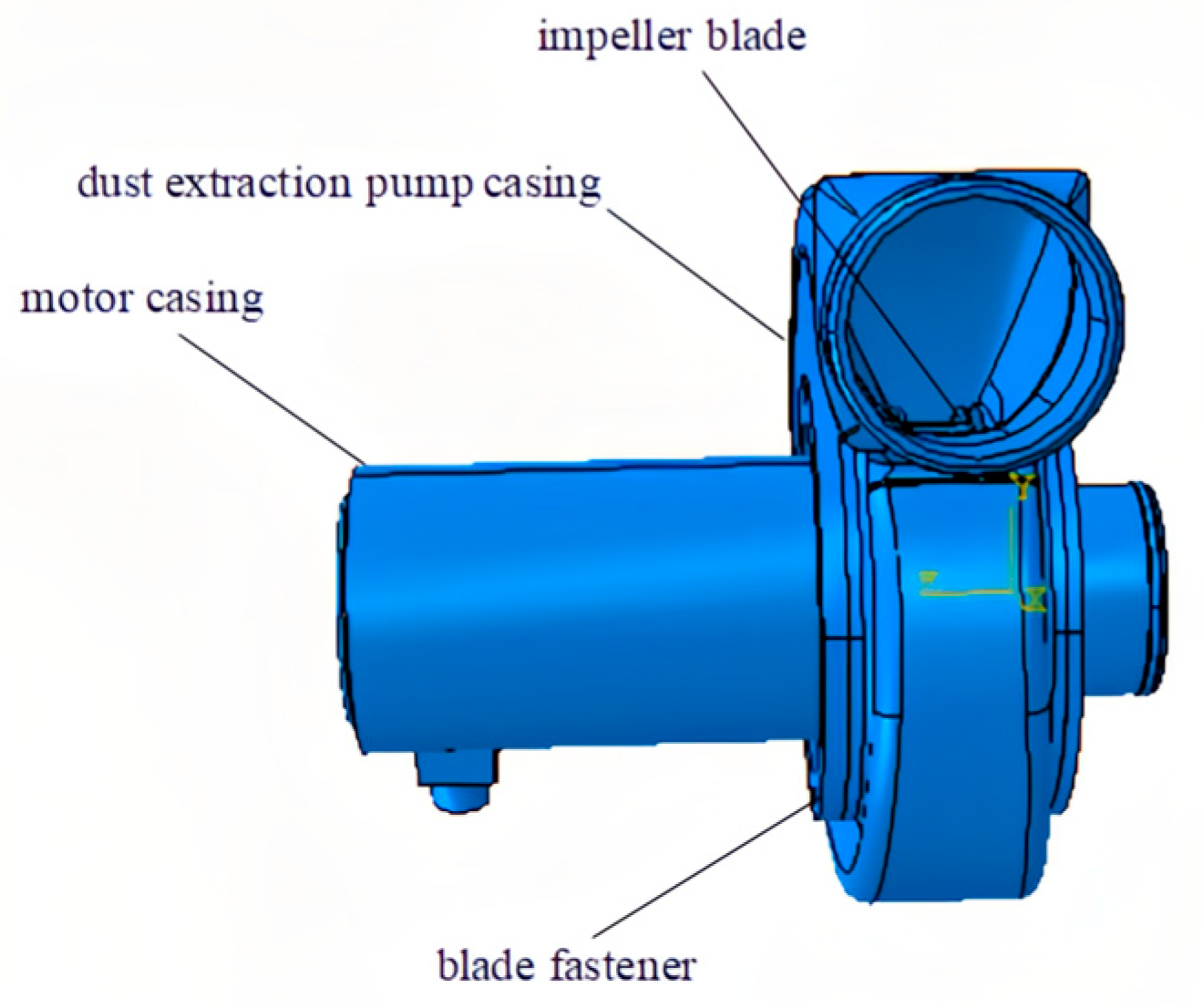
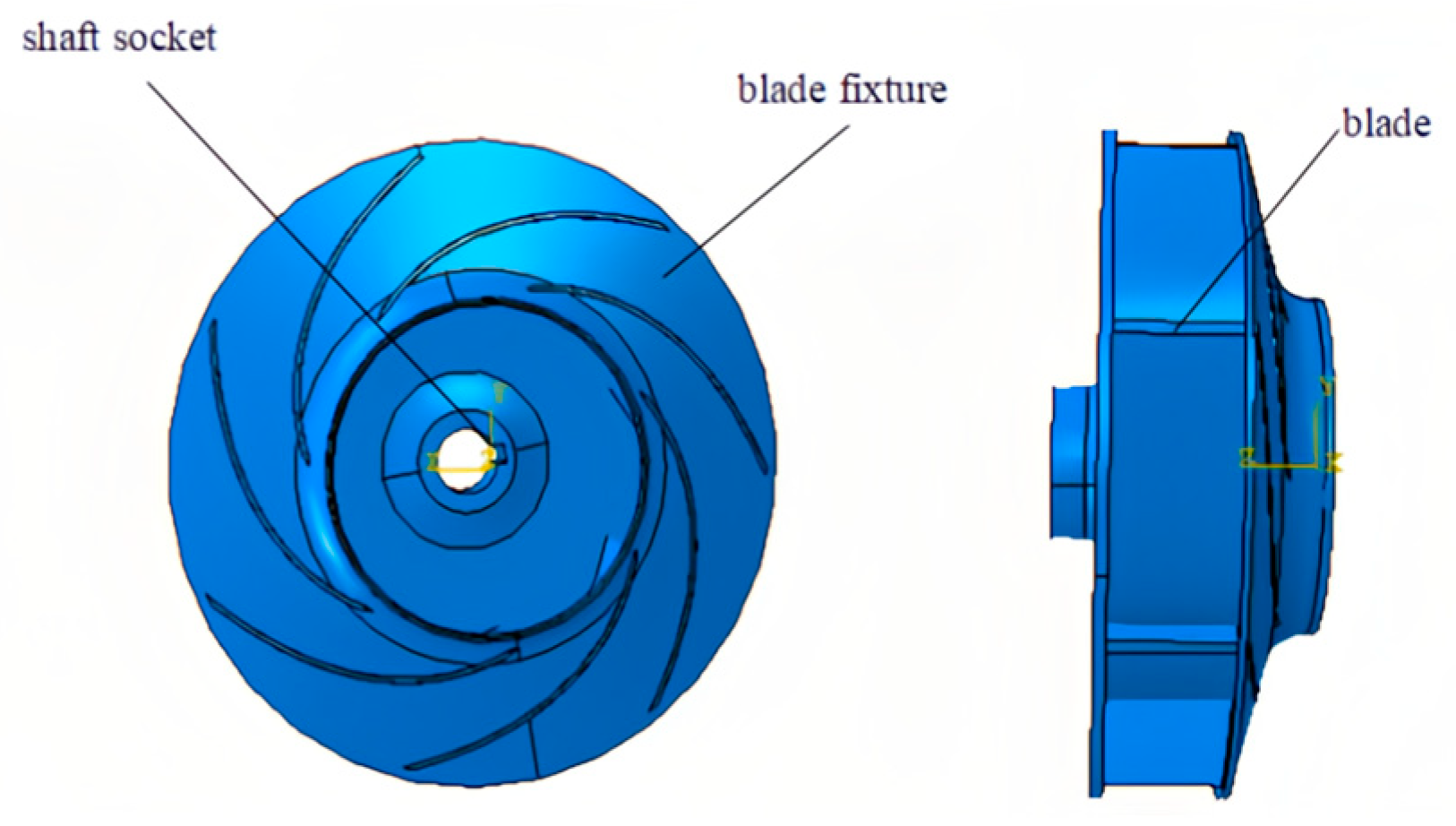
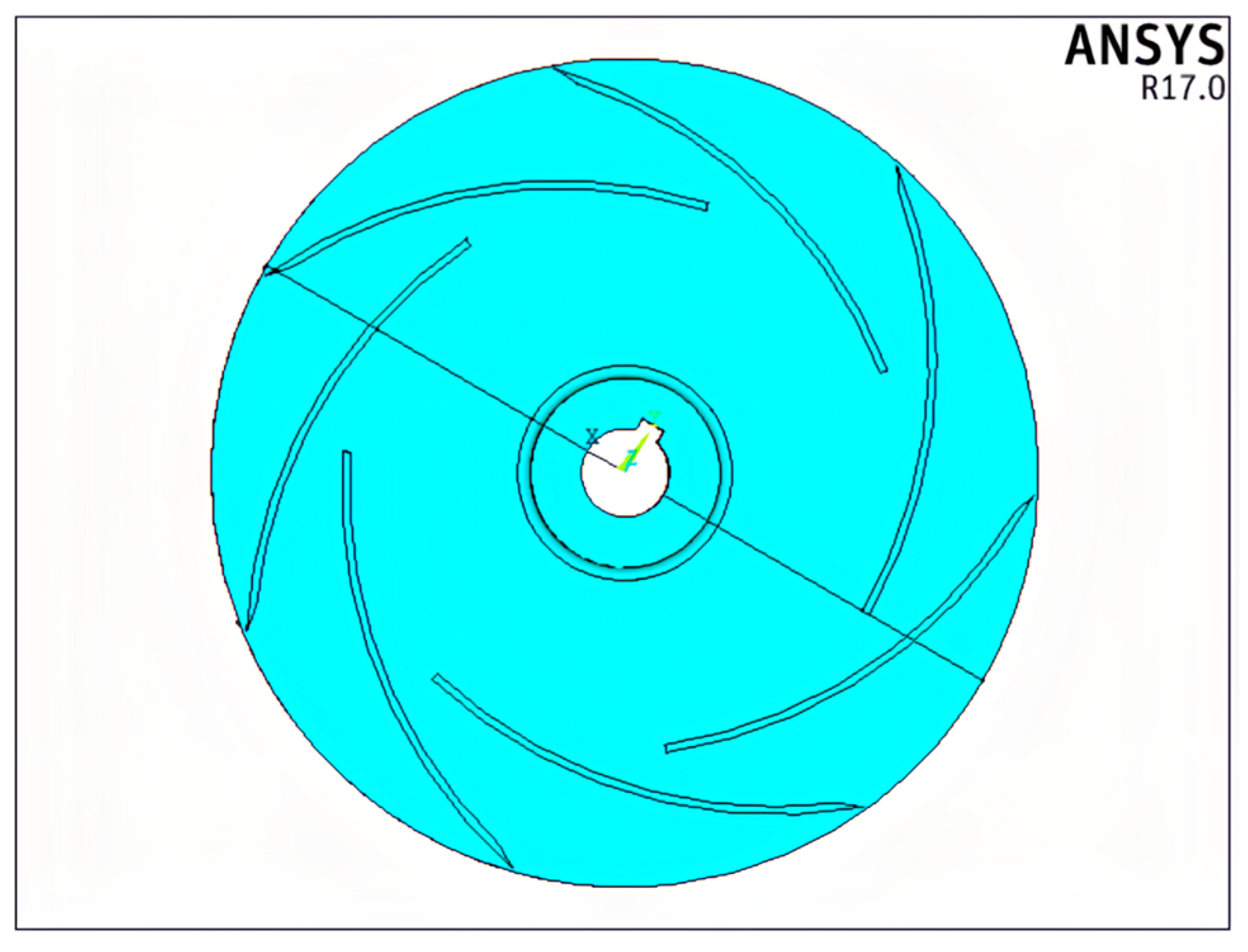

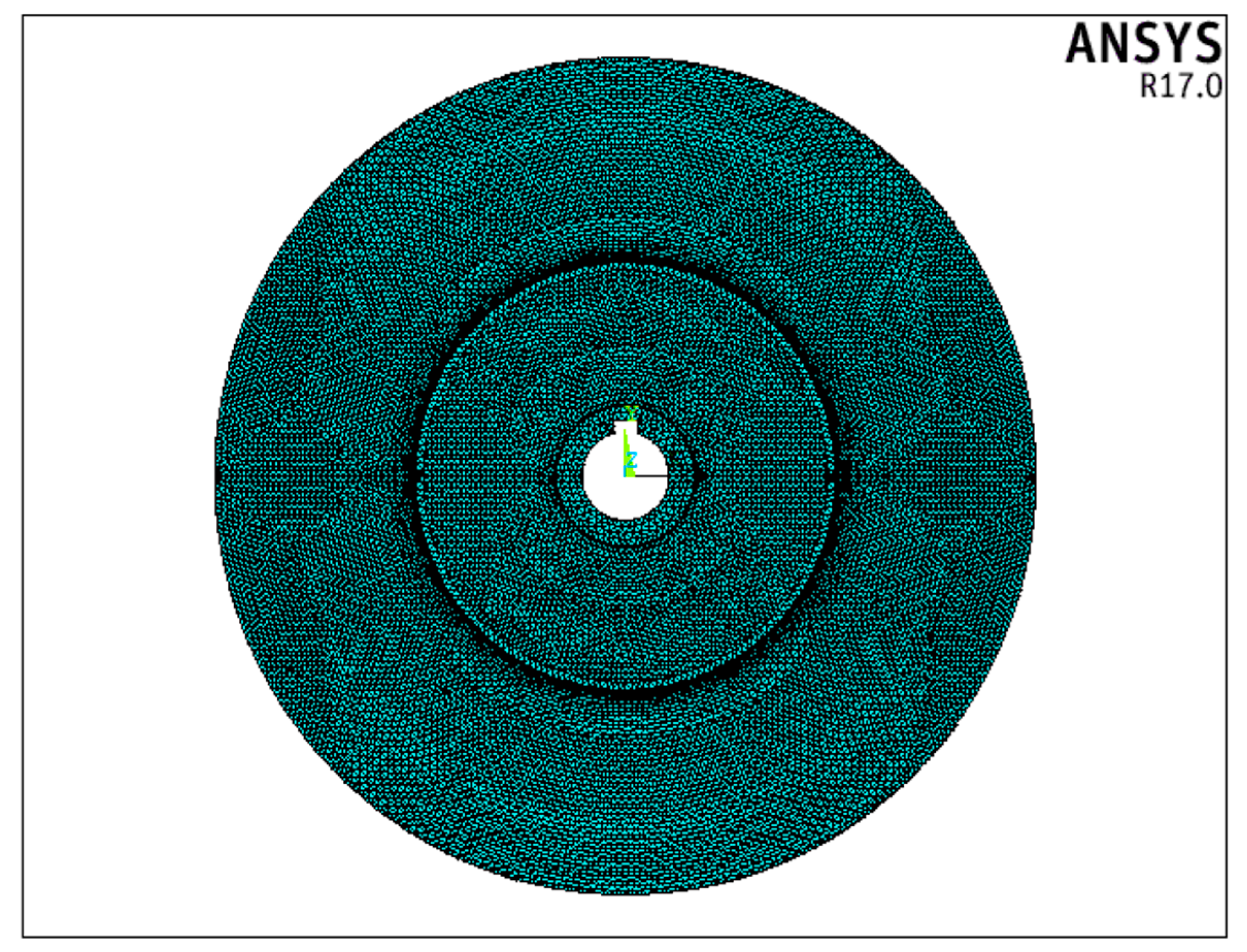

| Parameter | Value |
|---|---|
| Elastic modulus | 210 GPa |
| Poisson’s ratio | 0.3 |
| Density | 7.85 t/m3 |
| Yield strength | 235 MPa |
| Impeller outer diameter | 130 mm |
| Lower impeller fixture inner hole diameter | 14 mm |
| Upper impeller fixture hole diameter | 64 mm |
| Blade thickness | 1 mm |
| Upper impeller fixture thickness | 2 mm |
| Lower impeller fixture thickness | 2 mm |
| Blade spline width | 4 mm |
| Blade spline depth | 2 mm |
| Blade spline length | 12 mm |
| Parameter | Distribution | Mean | Coefficient of Variation |
|---|---|---|---|
| Fixture thickness N | Normal | 7 | 0.1 |
| Poisson’s ratio P | Normal | 0.3 | 0.1 |
| Elastic modulus E | Normal | 210,000,000,000 | 0.1 |
| Blade thickness T | Normal | 1 | 0.1 |
| Density D | Normal | 7.85 × 10−9 | 0.1 |
| Rotational speed R | Normal | 12,500 | 0.1 |
| Sequence | N (mm) | P | E (GPa) | T (mm) | D (t/mm3) | R (r/min) |
|---|---|---|---|---|---|---|
| 1 | 6.838 | 0.3140 | 187 | 0.894 | 7.025 × 10−9 | 1290 |
| 2 | 6.647 | 0.2593 | 185 | 1.098 | 7.330 × 10−9 | 1364 |
| 3 | 7.735 | 0.3484 | 178 | 0.899 | 7.143 × 10−9 | 1600 |
| 4 | 7.601 | 0.2933 | 196 | 0.928 | 7.596 × 10−9 | 1248 |
| 5 | 7.610 | 0.2952 | 237 | 1.006 | 8.024 × 10−9 | 1319 |
| 6 | 5.928 | 0.3379 | 212 | 0.918 | 8.719 × 10−9 | 1647 |
| 7 | 7.610 | 0.2908 | 223 | 1.044 | 7.676 × 10−9 | 1173 |
| 8 | 6.462 | 0.3177 | 223 | 1.080 | 7.493 × 10−9 | 1340 |
| 9 | 5.885 | 0.2819 | 189 | 1.156 | 8.053 × 10−9 | 1273 |
| 10 | 6.908 | 0.3229 | 242 | 0.930 | 8.148 | 1364 |
| 11 | 6.462 | 0.2366 | 196 | 0.916 | 8.976 | 1600 |
| 12 | 8.673 | 0.2973 | 189 | 0.934 | 8.477 | 1248 |
| Model | Training Set Fit | Maximum Stress Error in Test Set | Average Stress Error in Test Set | Training Speed |
|---|---|---|---|---|
| BPNN | 0.99997 | 0.1483 | 0.0179 | 14 s |
| FNN | 0.99973 | 0.0125 | 0.0043 | 9 s |
| QPRS | 0.9378 | 0.09 | 0.0189 | 1 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, F.; Tian, Y.; Du, R.; Xu, Y.; Gao, Y.; Li, X. Parameter Stress Response Prediction for Vehicle Dust Extraction Fan Impeller Based on Feedback Neural Network. Machines 2025, 13, 496. https://doi.org/10.3390/machines13060496
Zhang F, Tian Y, Du R, Xu Y, Gao Y, Li X. Parameter Stress Response Prediction for Vehicle Dust Extraction Fan Impeller Based on Feedback Neural Network. Machines. 2025; 13(6):496. https://doi.org/10.3390/machines13060496
Chicago/Turabian StyleZhang, Feng, Yuxiang Tian, Ruijie Du, Yuxiao Xu, Yang Gao, and Xin Li. 2025. "Parameter Stress Response Prediction for Vehicle Dust Extraction Fan Impeller Based on Feedback Neural Network" Machines 13, no. 6: 496. https://doi.org/10.3390/machines13060496
APA StyleZhang, F., Tian, Y., Du, R., Xu, Y., Gao, Y., & Li, X. (2025). Parameter Stress Response Prediction for Vehicle Dust Extraction Fan Impeller Based on Feedback Neural Network. Machines, 13(6), 496. https://doi.org/10.3390/machines13060496







