Vision-Guided Fuzzy Adaptive Impedance-Based Control for Polishing Robots Under Time-Varying Stiffness
Abstract
1. Introduction
2. Toolpath Generation and Force Analysis
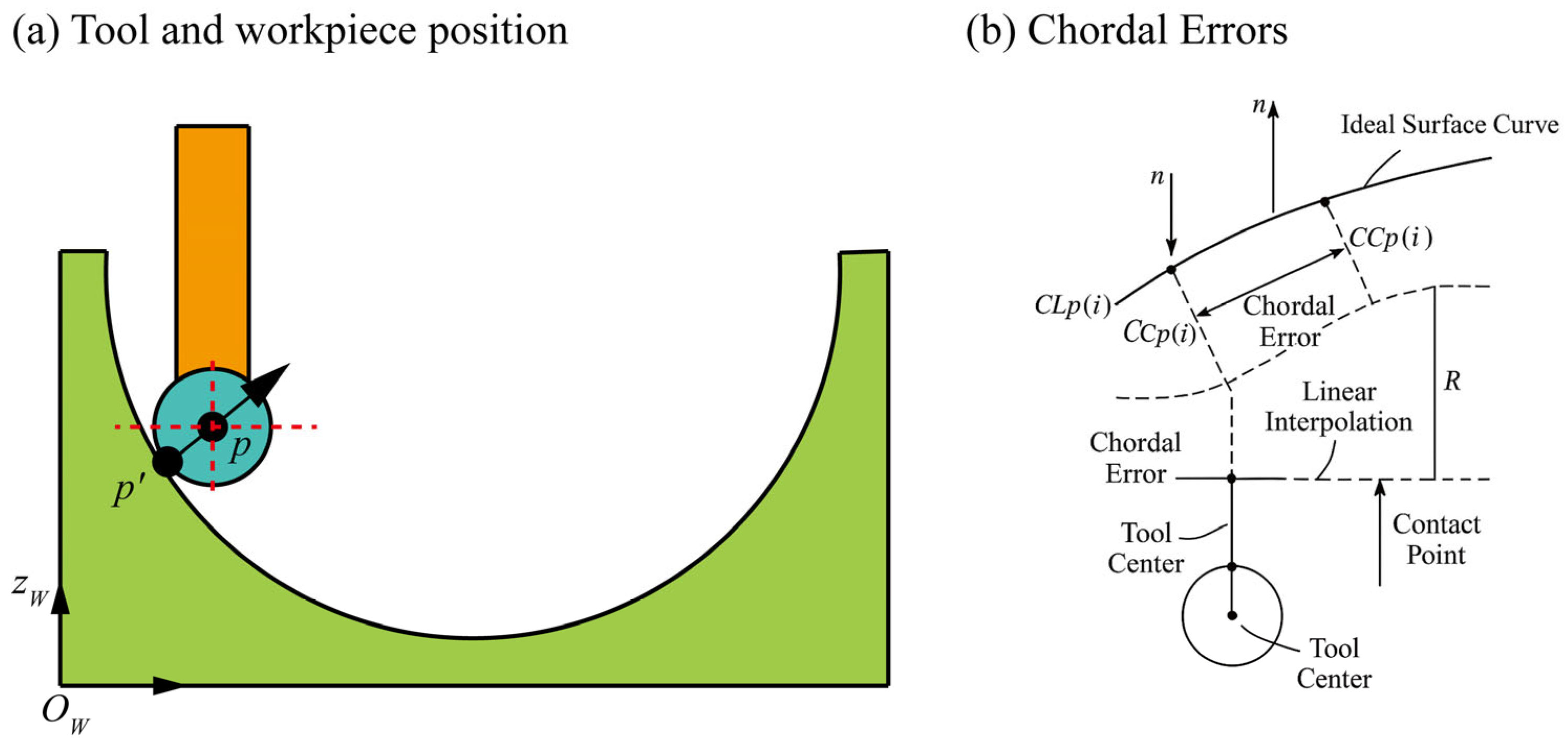
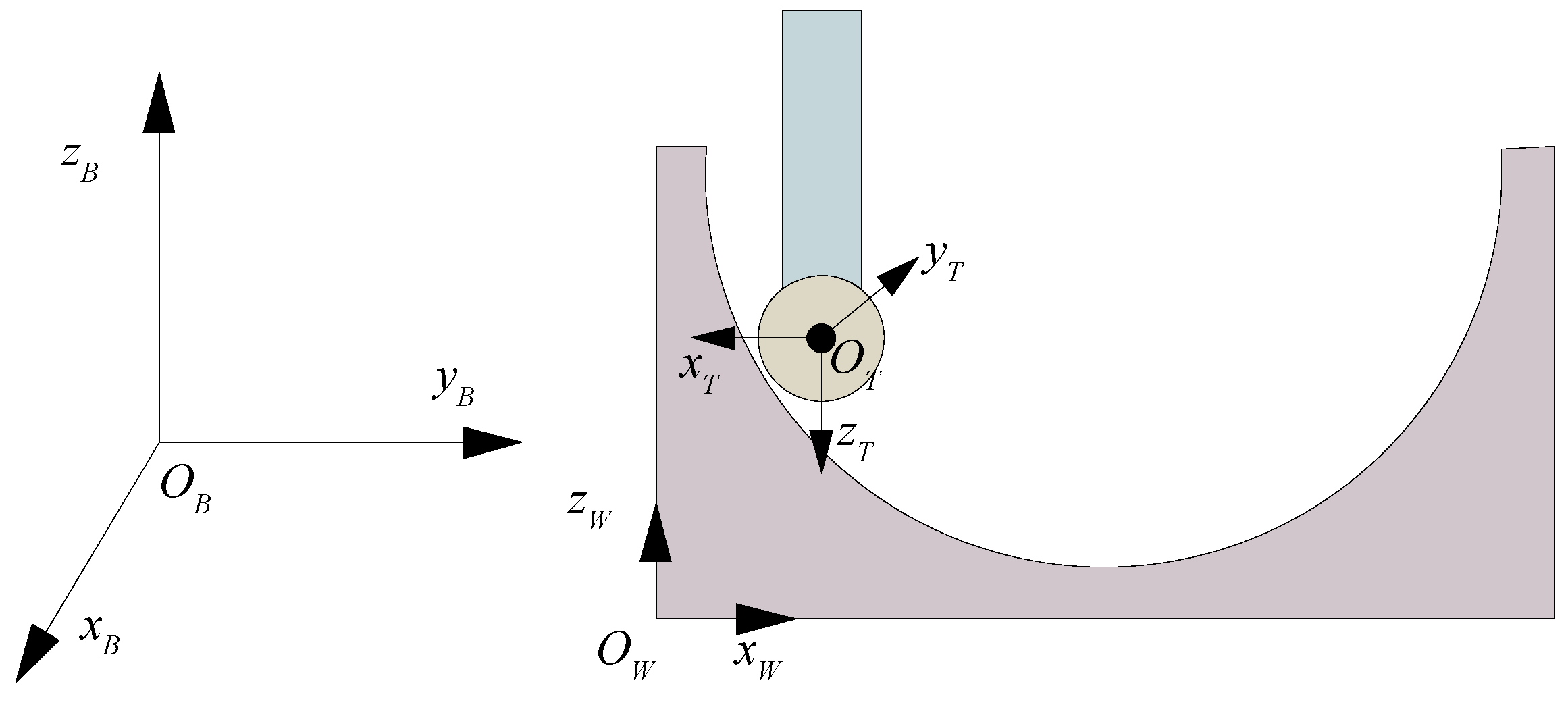
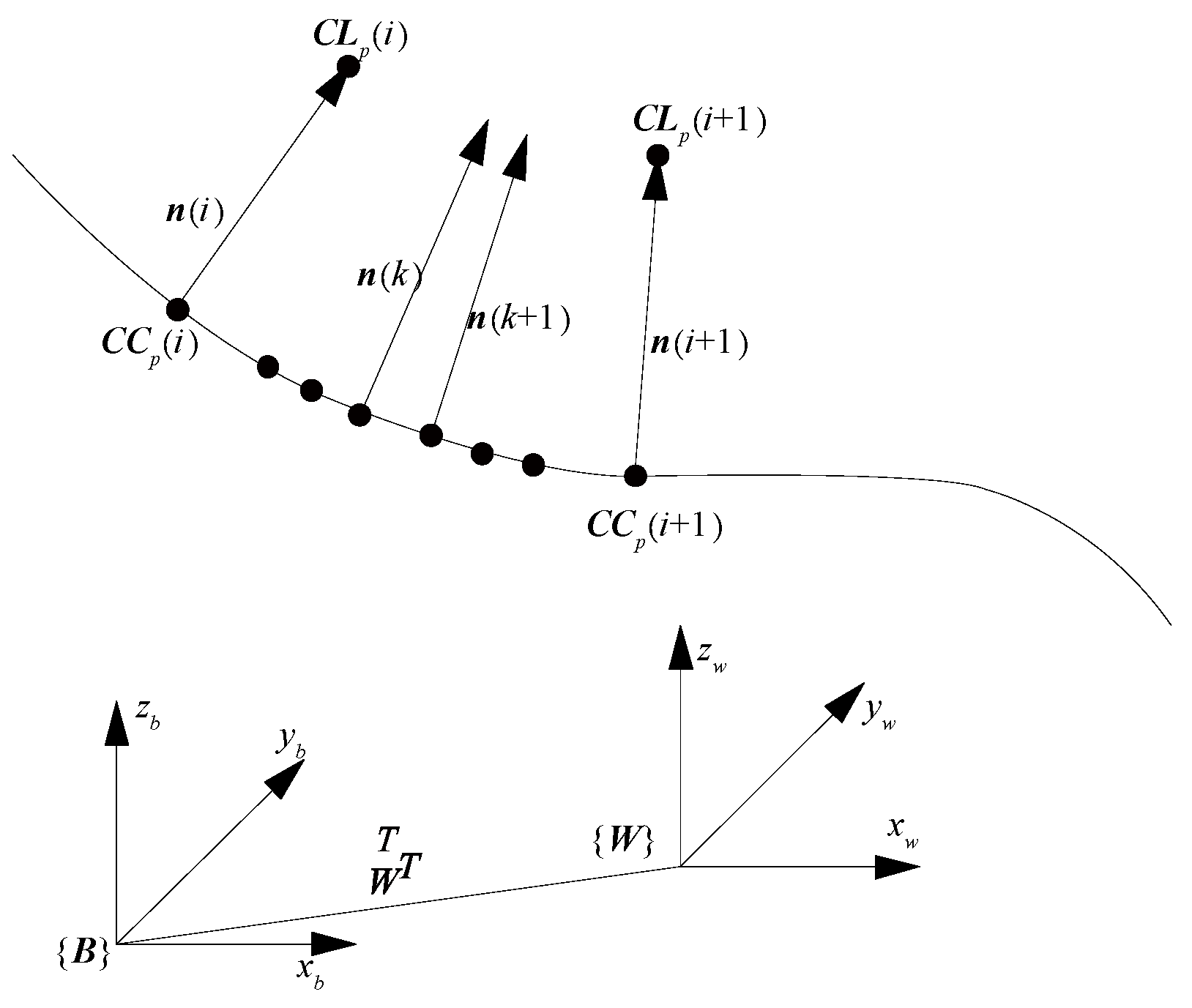
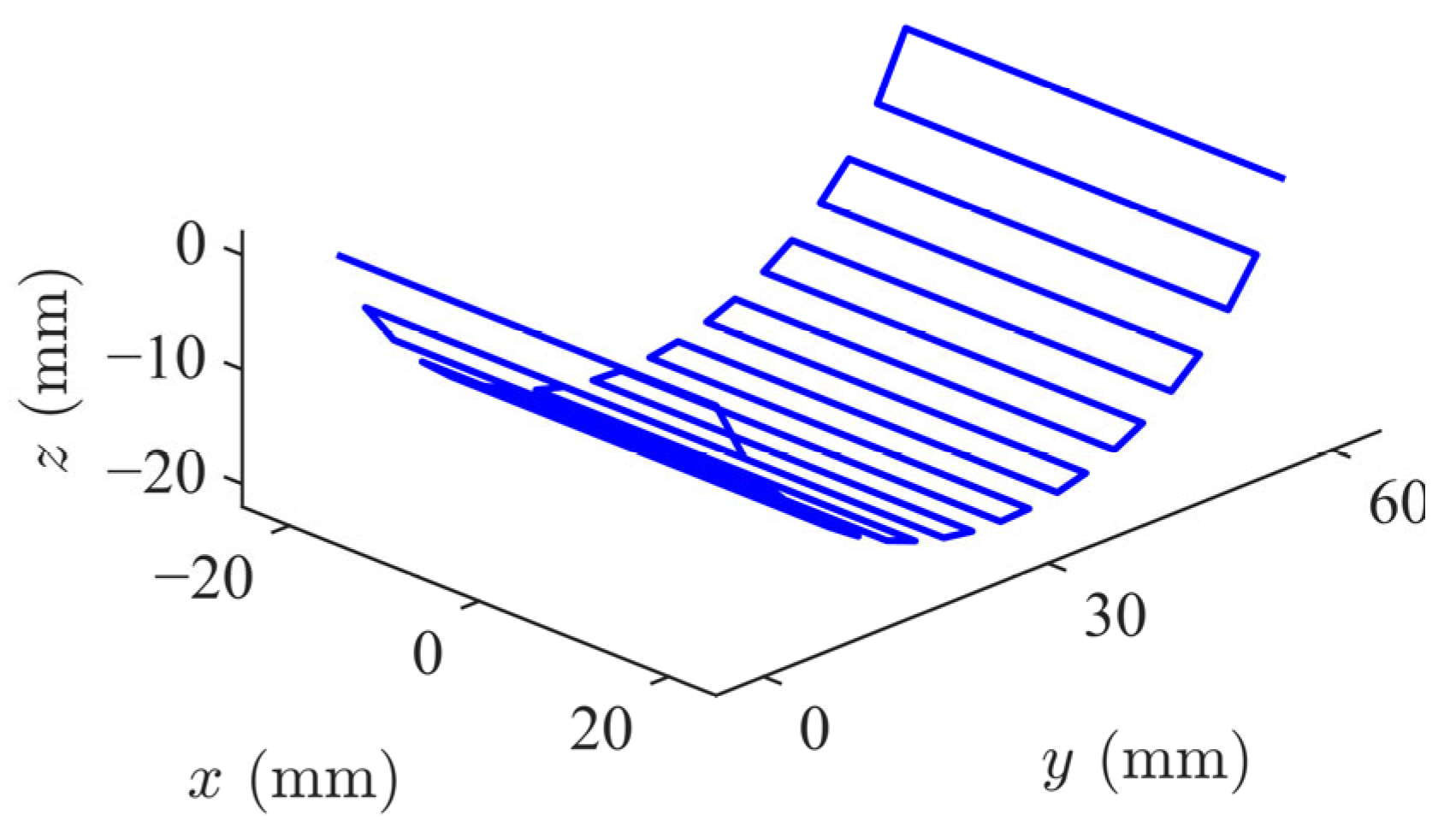
2.1. Generation of the Toolpath
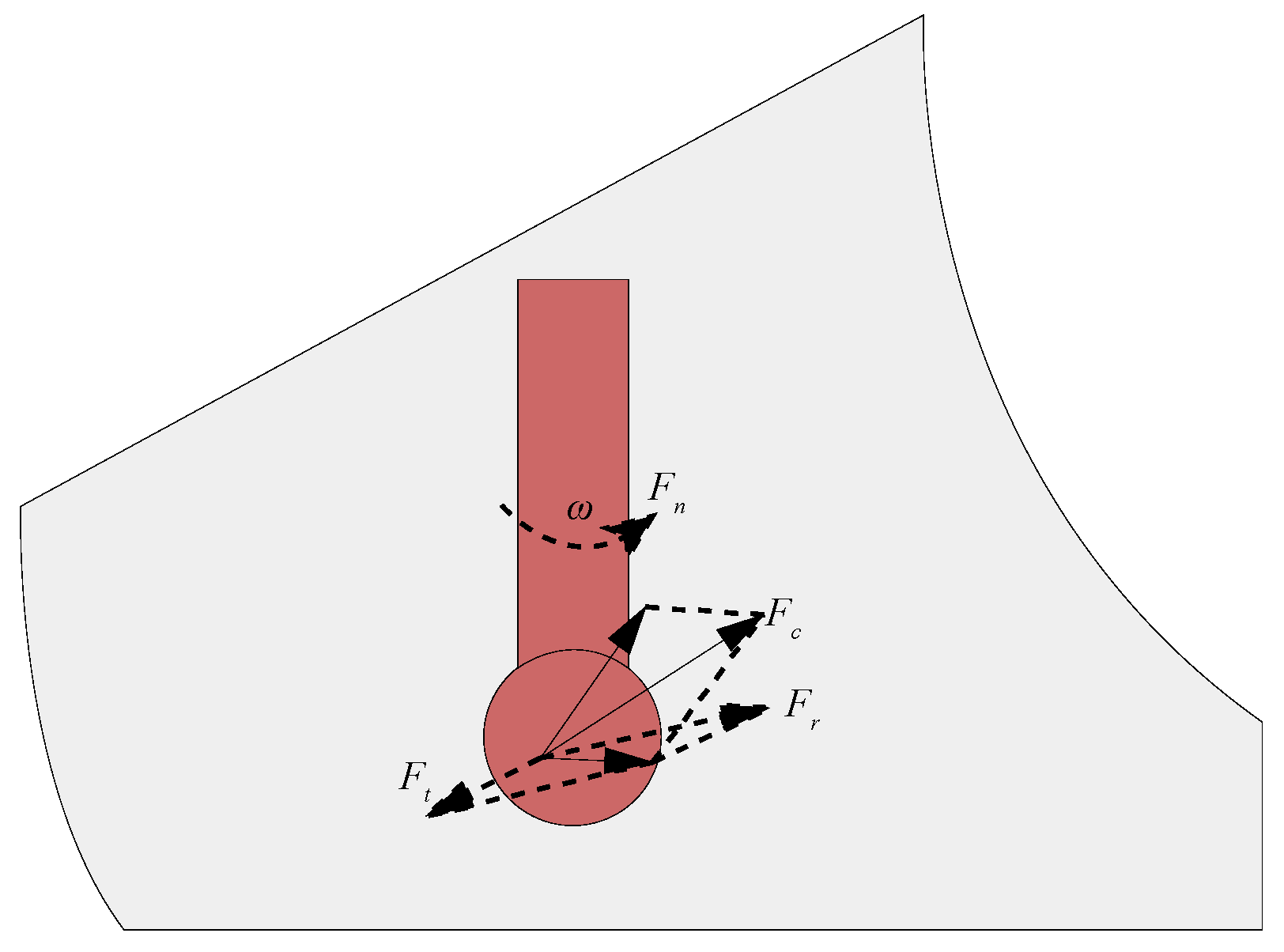
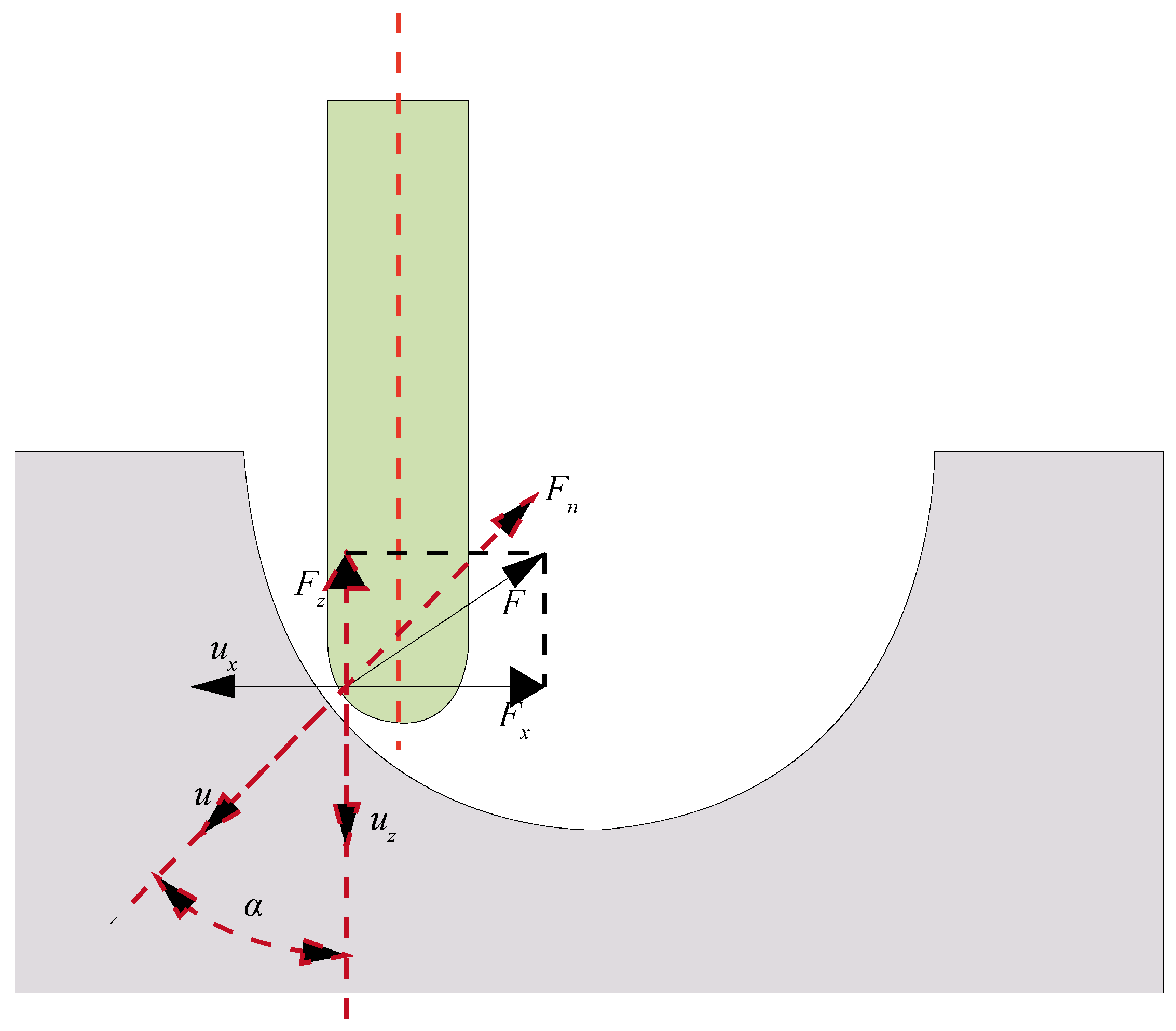
2.2. Force Analysis and Compensation
3. Control Design for Polishing Robotic Systems
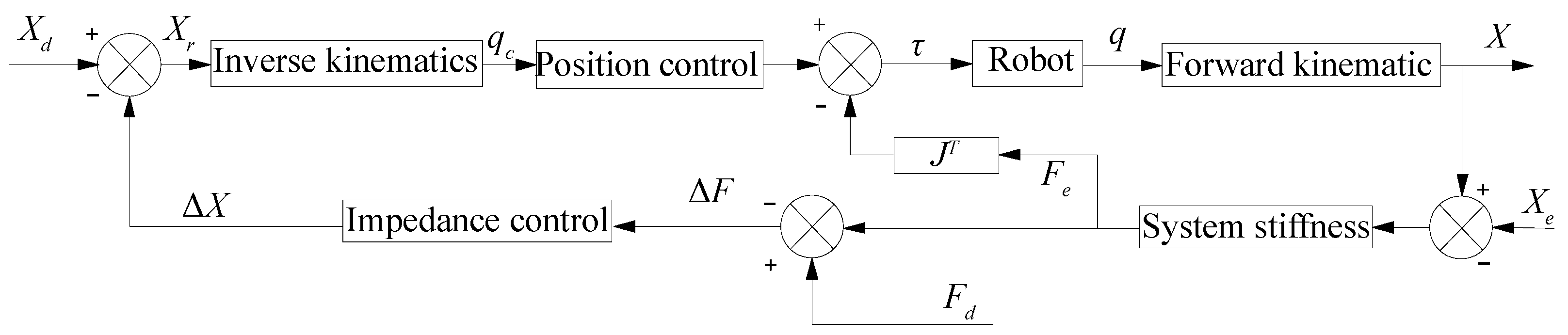
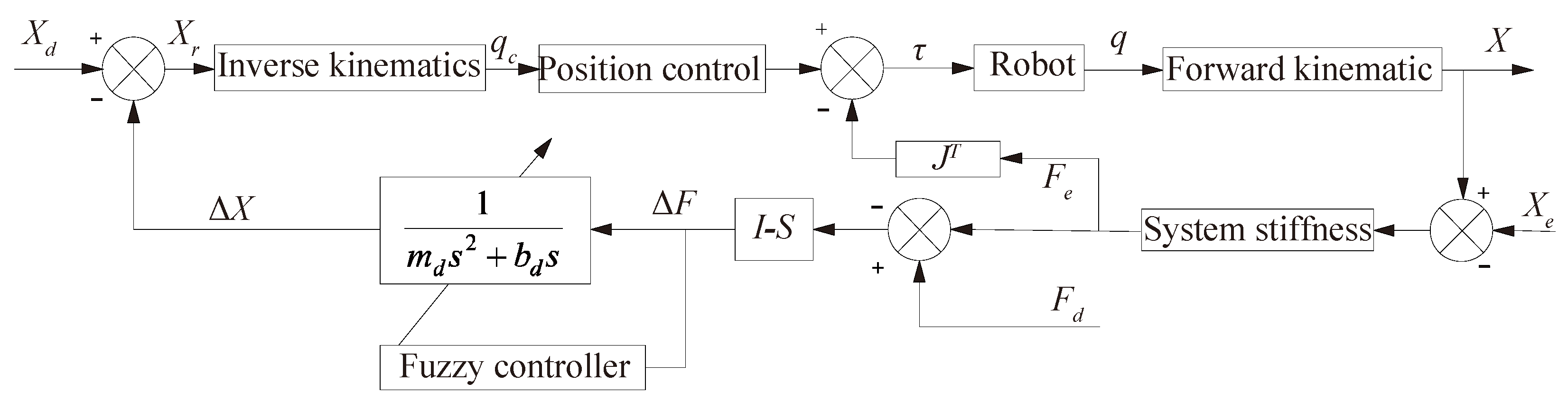
3.1. Impedance Control
3.2. Fuzzy Adaptive Impedance Control
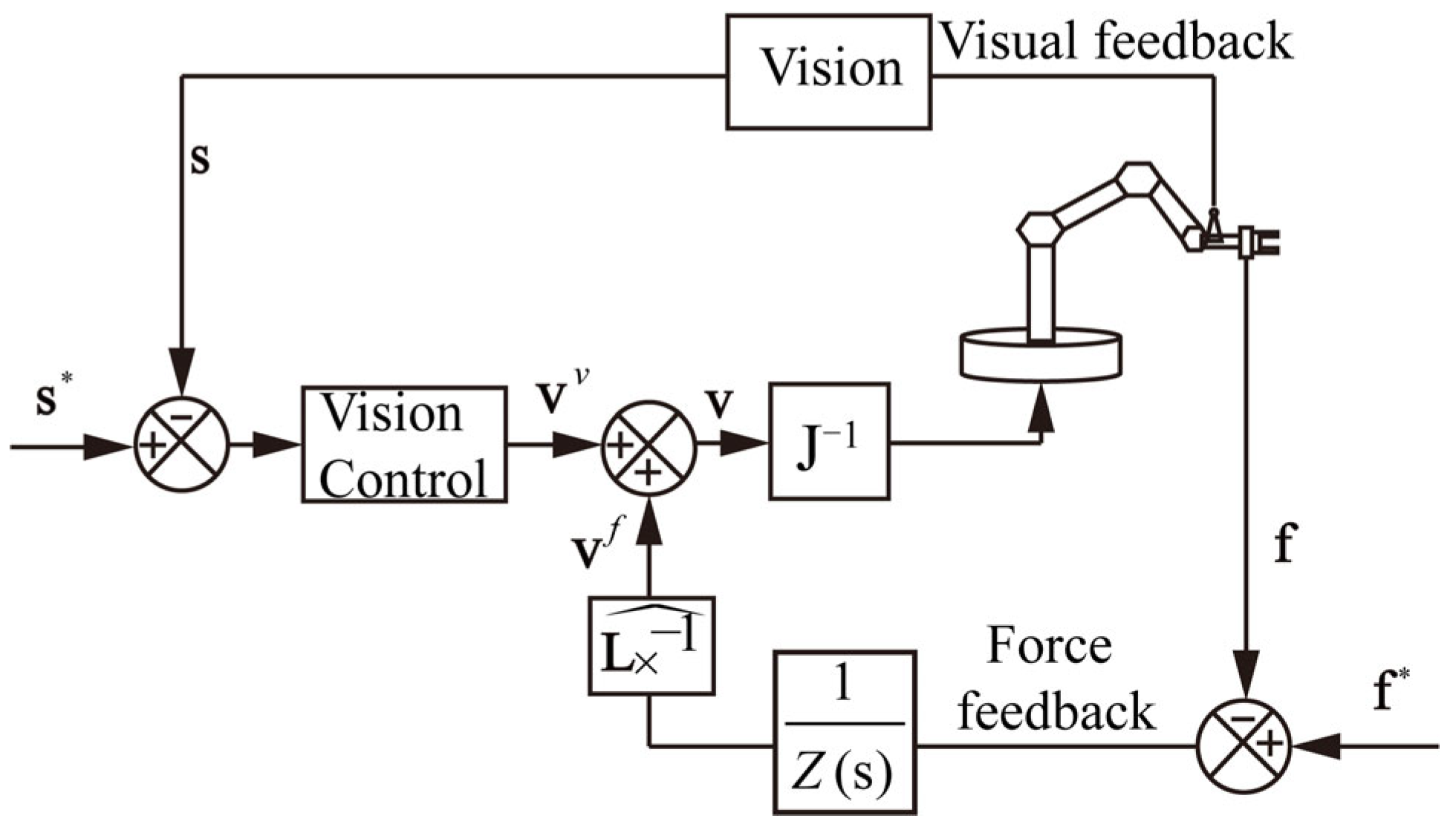
3.3. Vision-Guided Fuzzy Adaptive Impedance Control
3.3.1. Description of the Impedance Vision-Force Control Approach
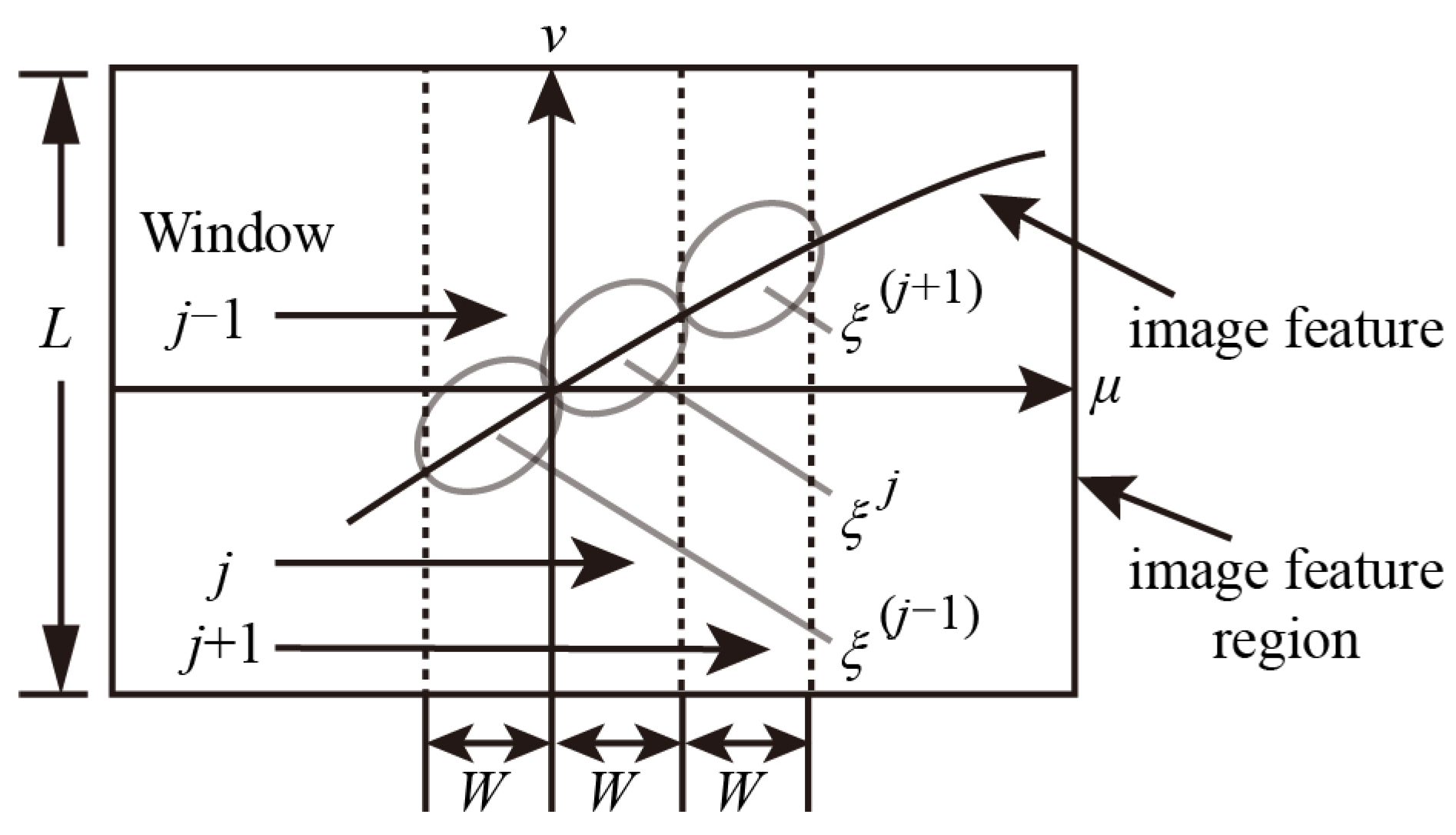
3.3.2. SVR-Based Jacobi Mapping Method
3.3.3. Fuzzy Adaptive Impedance Control with Vision Guidance
4. Simulation and Experiment Results and Discussion of Polishing Robotic Systems
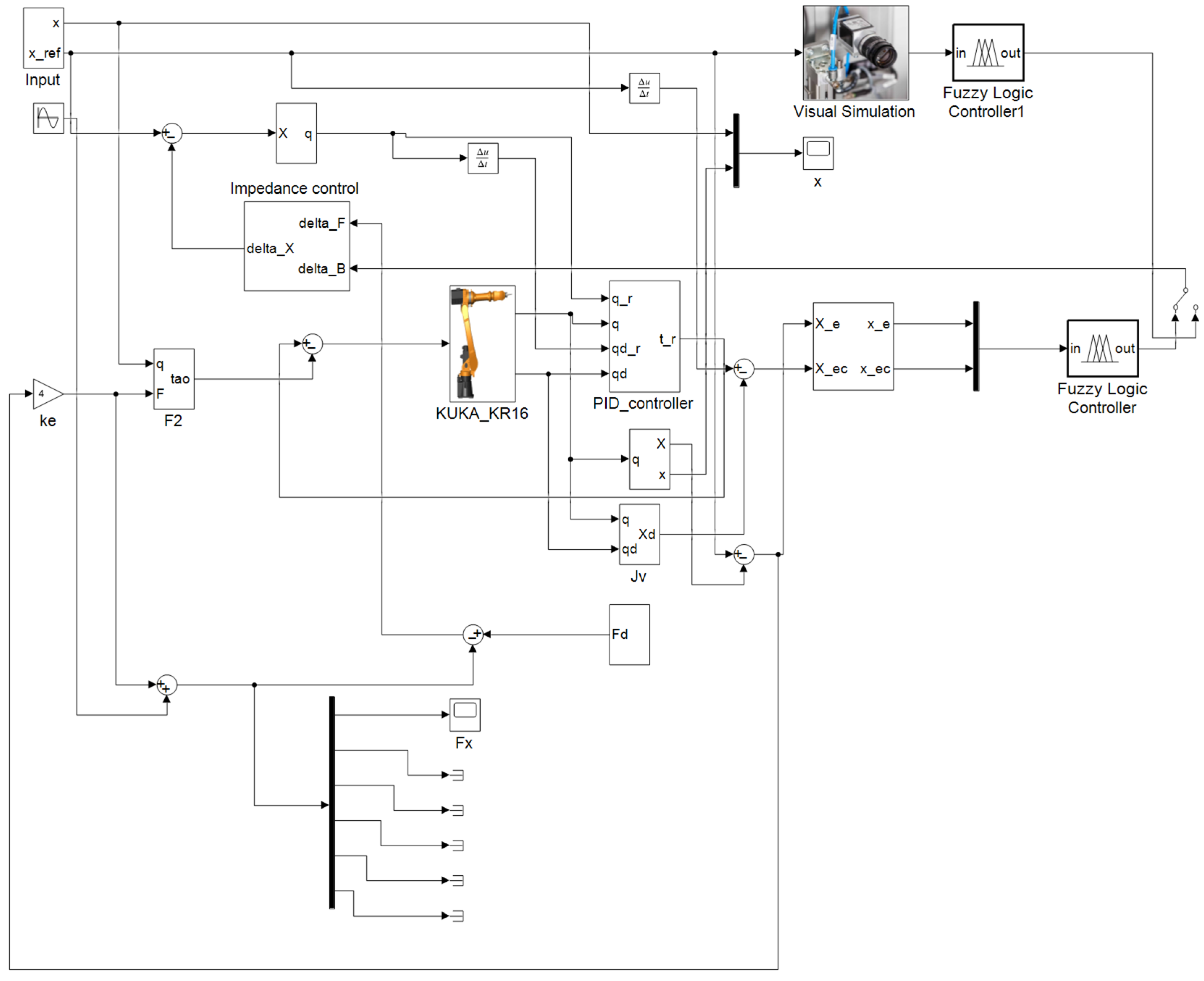
4.1. Simulation Design
4.2. Experimental Design
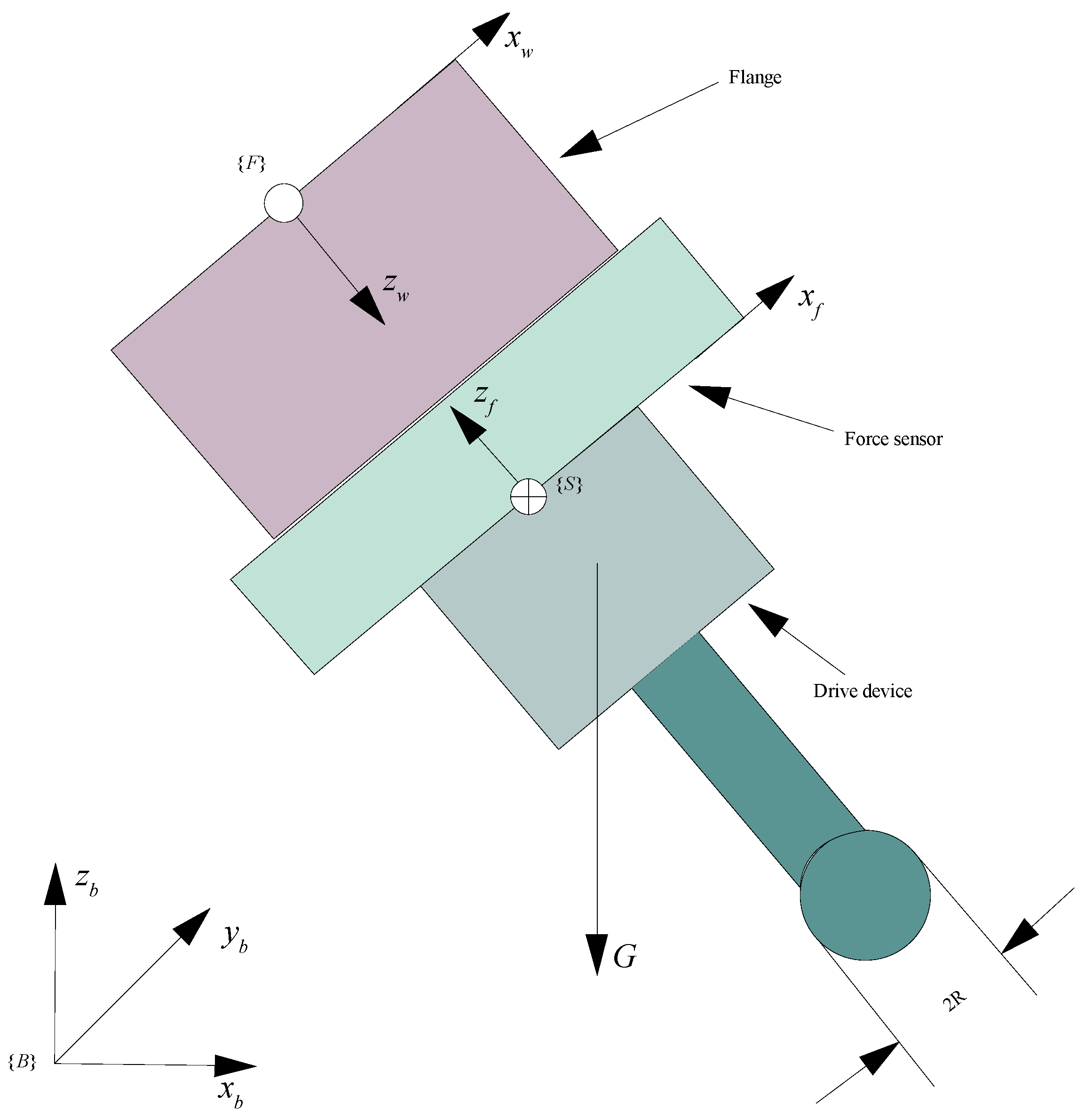
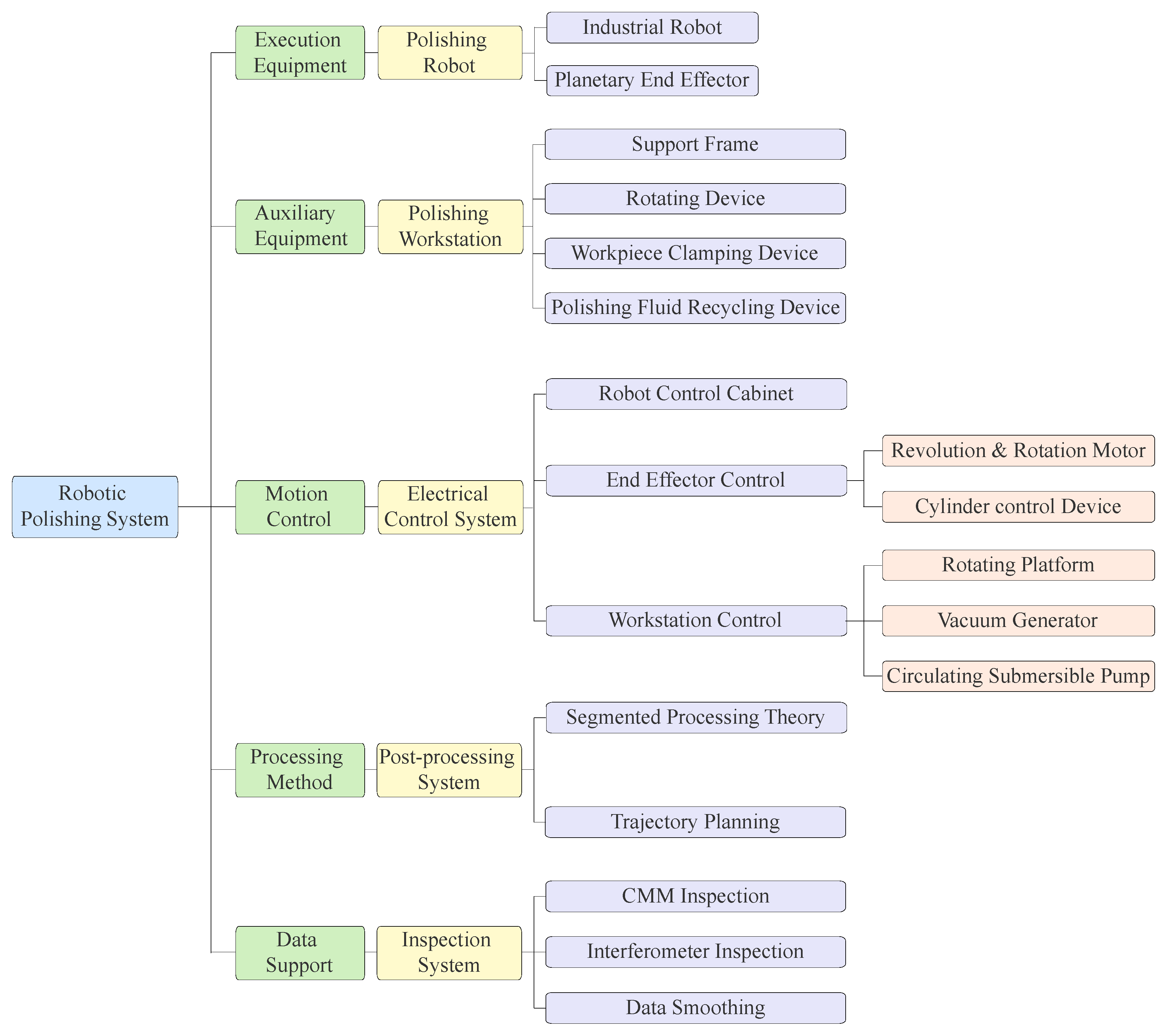
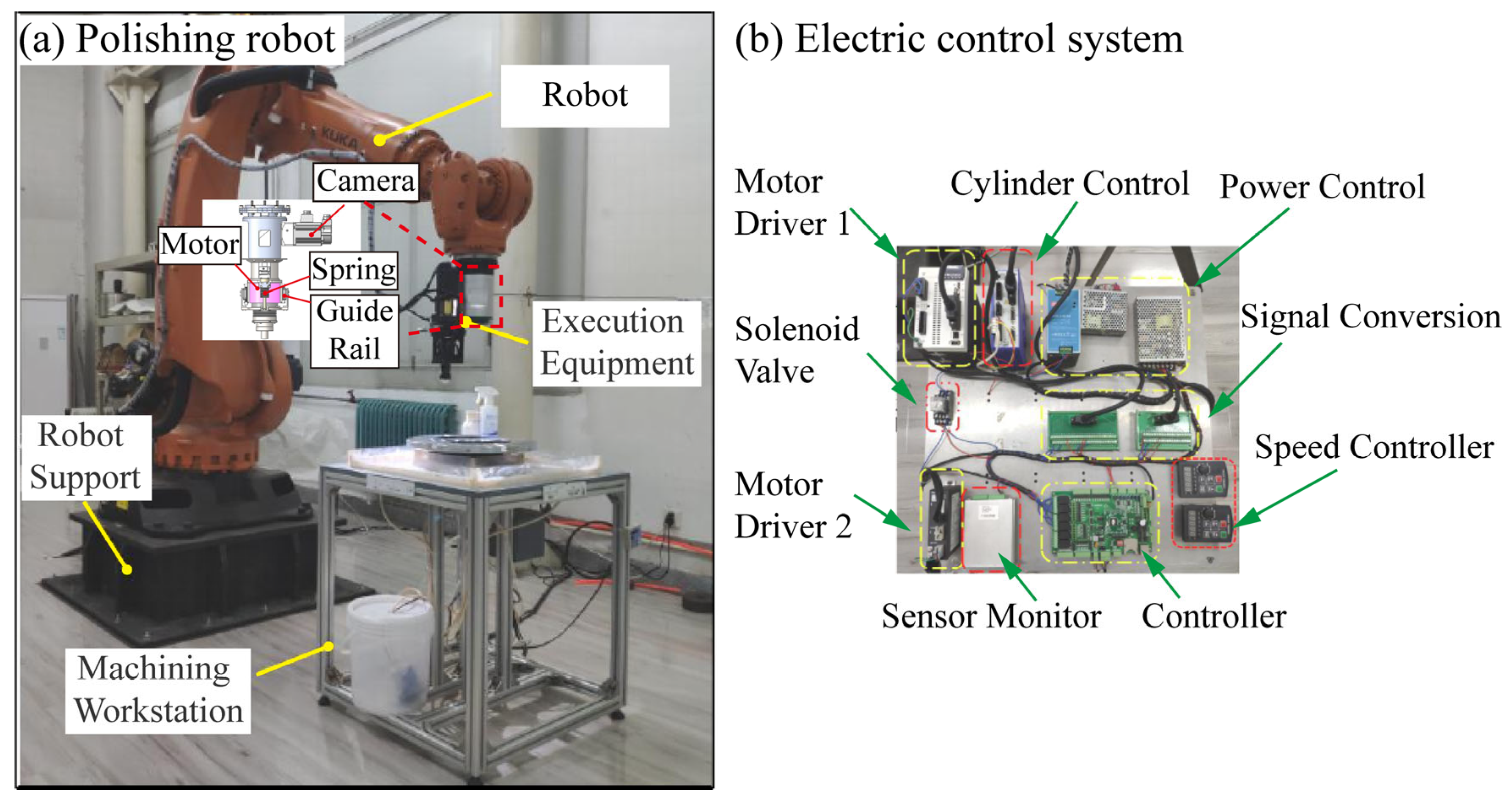
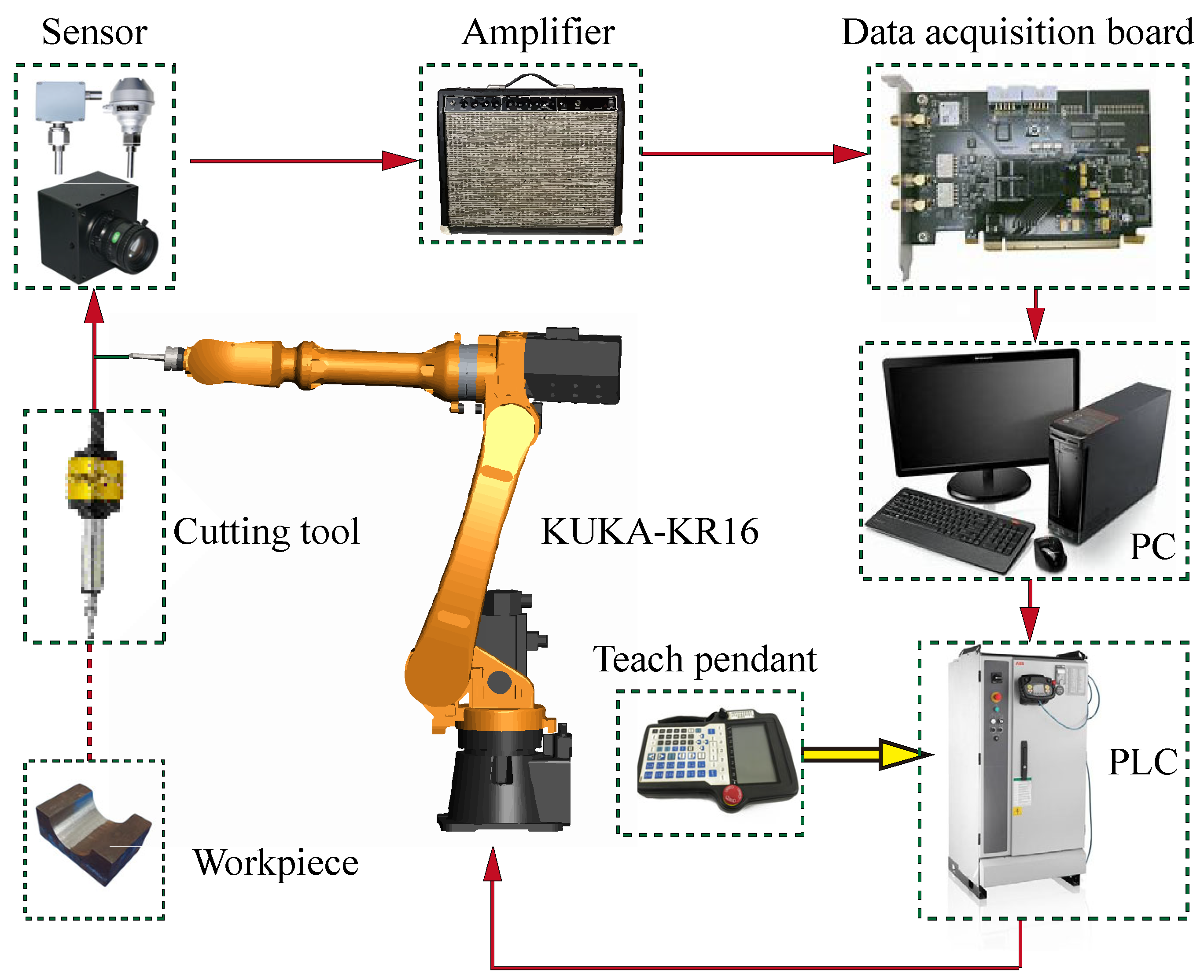
4.2.1. Robotic Polishing Platform
4.2.2. Experimental Parameters and Control Strategy
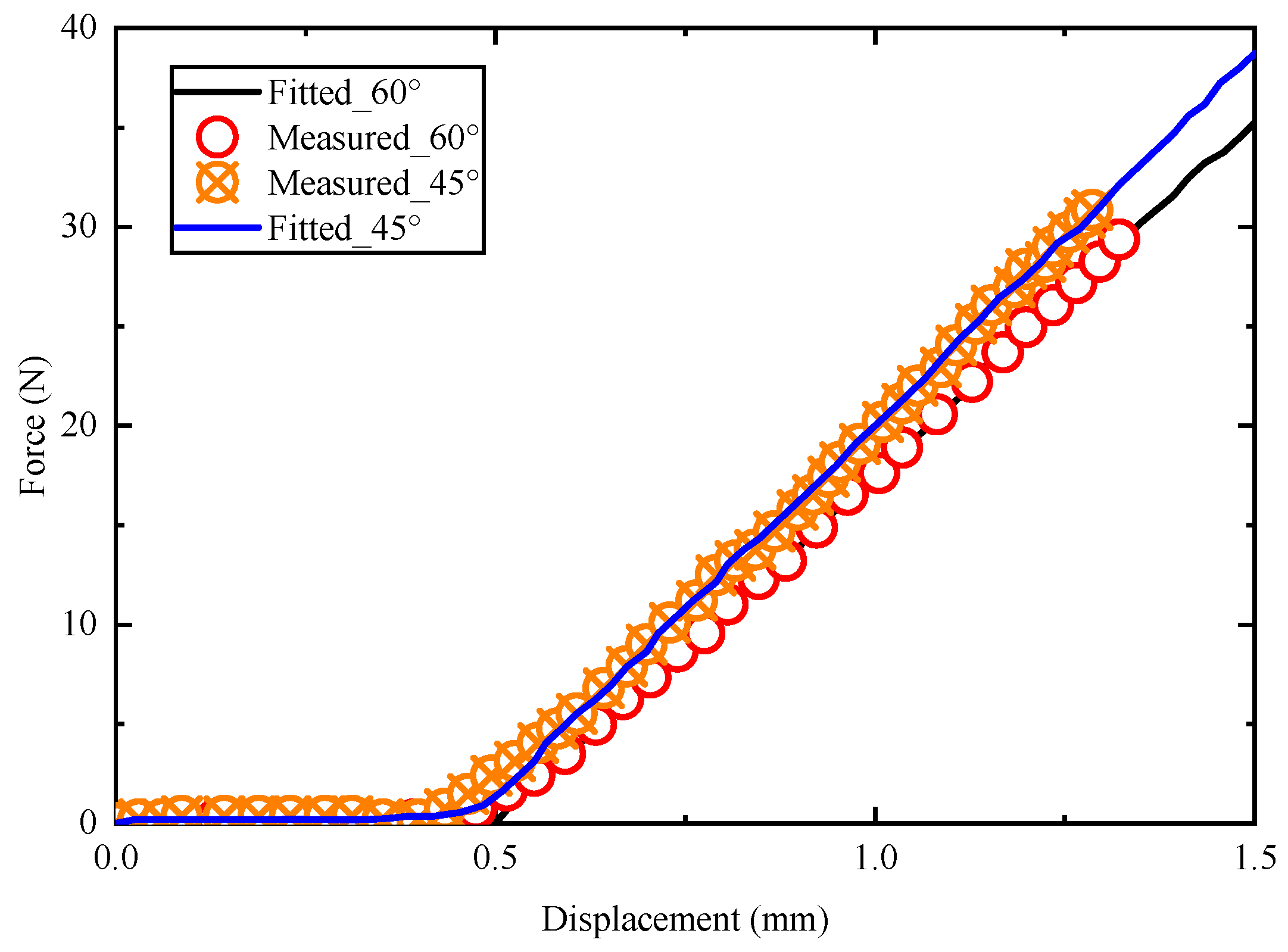
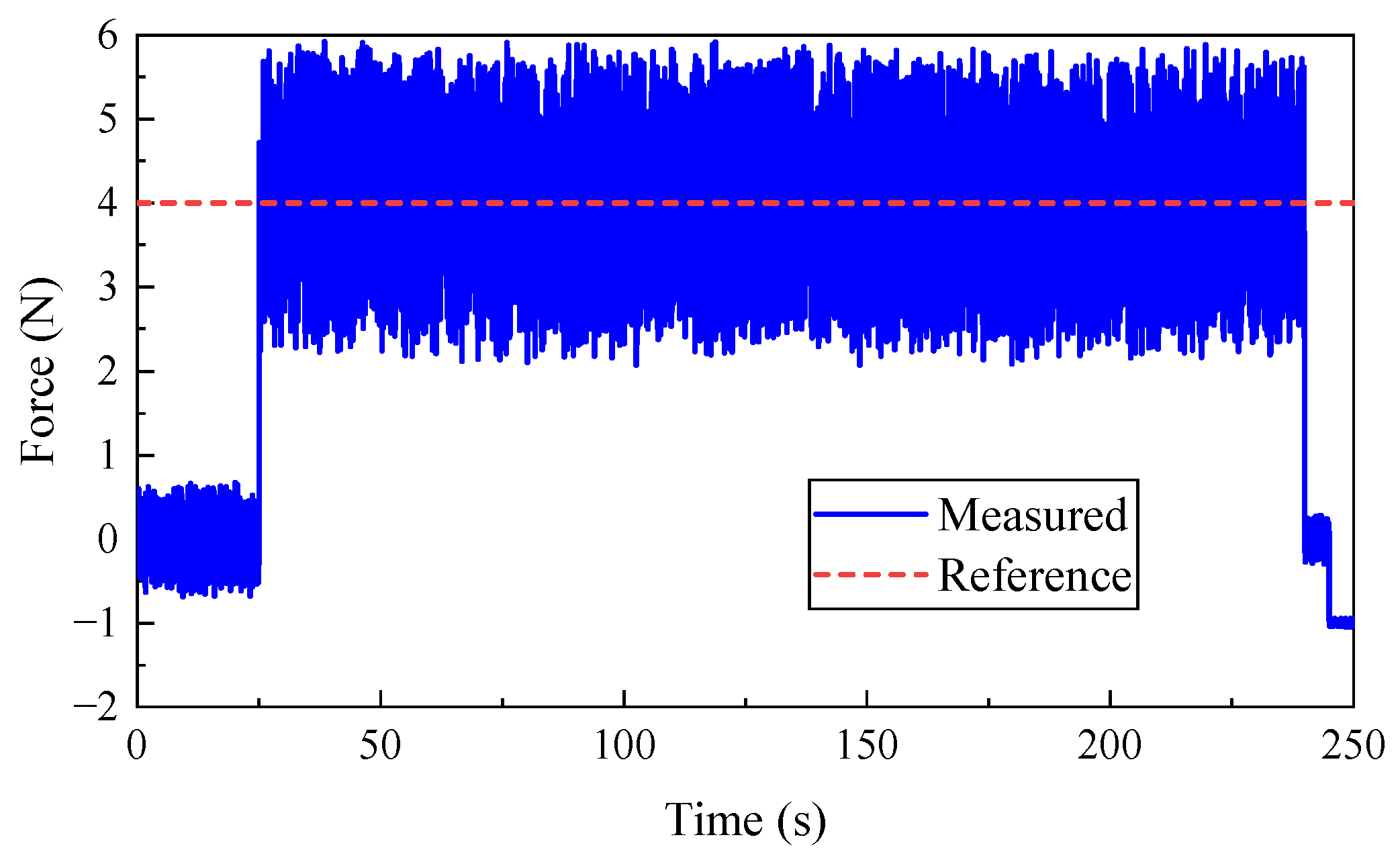
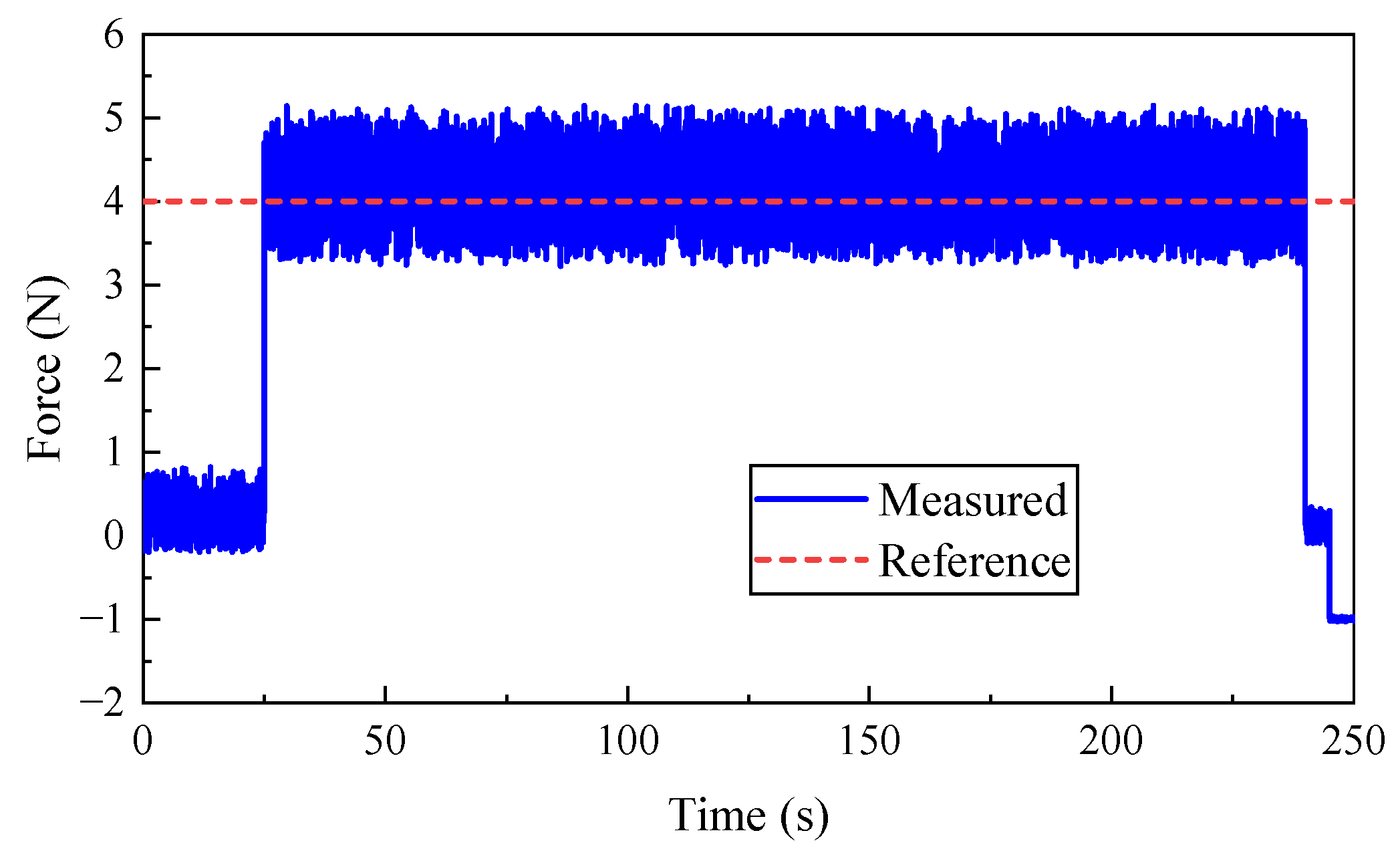
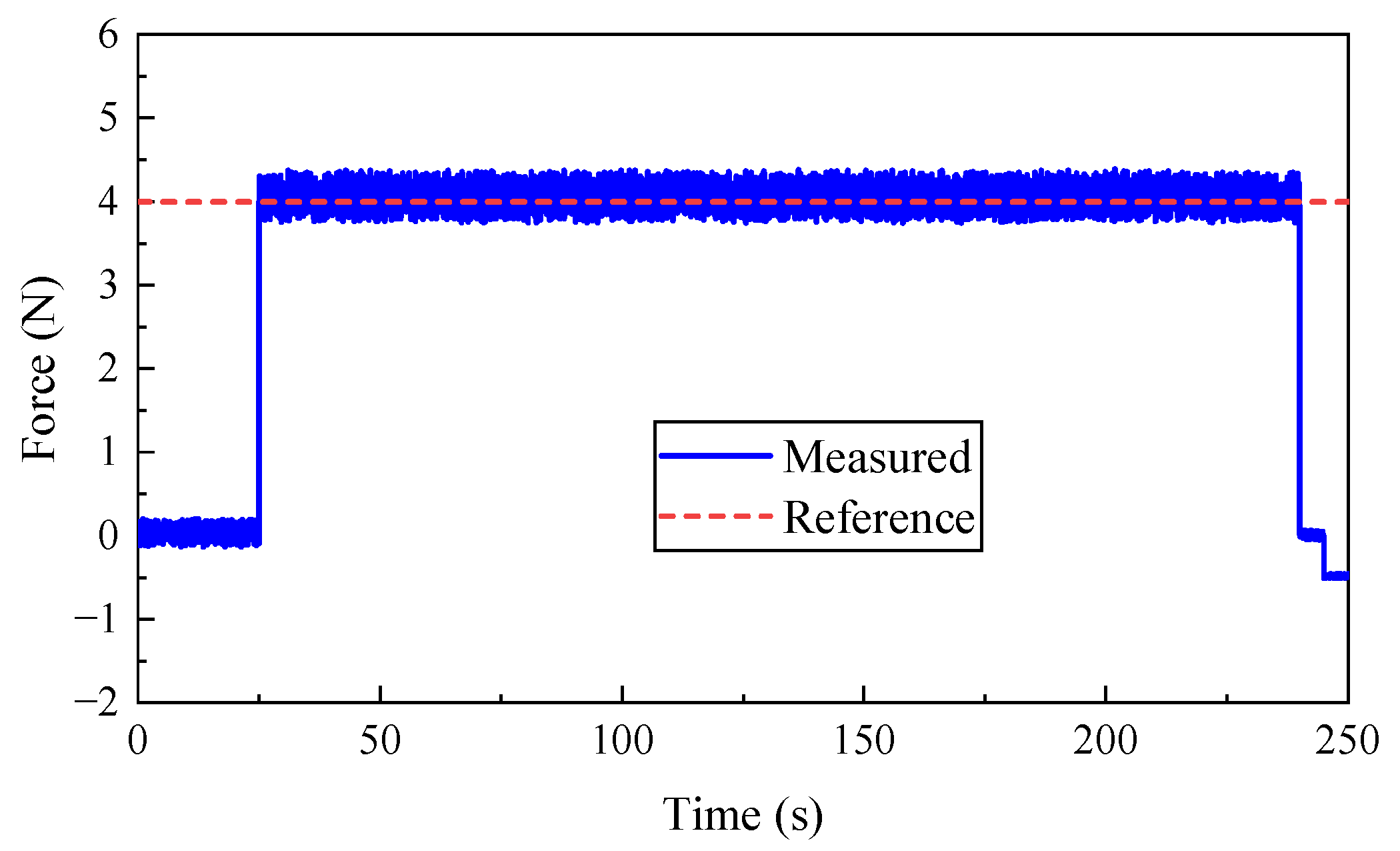
4.2.3. Control Strategy Validation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Perez Dewey, M.; Ulutan, D. Development of Laser Polishing as an Auxiliary Post-Process to Improve Surface Quality in Fused Deposition Modeling Parts. In Proceedings of the International Manufacturing Science and Engineering Conference, American Society of Mechanical Engineers, Los Angeles, CA, USA, 4–8 June 2017; Volume 50732, p. V002T01A006. [Google Scholar]
- Tian, F.; Li, Z.; Lv, C.; Liu, G. Polishing Pressure Investigations of Robot Automatic Polishing on Curved Surfaces. Int. J. Adv. Manuf. Technol. 2016, 87, 639–646. [Google Scholar] [CrossRef]
- Ermergen, T.; Taylan, F. Review on Surface Quality Improvement of Additively Manufactured Metals by Laser Polishing. Arab. J. Sci. Eng. 2021, 46, 7125–7141. [Google Scholar] [CrossRef]
- Ferraguti, F.; Pini, F.; Gale, T.; Messmer, F.; Storchi, C.; Leali, F.; Fantuzzi, C. Augmented Reality Based Approach for On-Line Quality Assessment of Polished Surfaces. Robot. Comput.-Integr. Manuf. 2019, 59, 158–167. [Google Scholar] [CrossRef]
- Khalick Mohammad, A.E.; Hong, J.; Wang, D. Polishing of Uneven Surfaces Using Industrial Robots Based on Neural Network and Genetic Algorithm. Int. J. Adv. Manuf. Technol. 2017, 93, 1463–1471. [Google Scholar] [CrossRef]
- Caggiano, A.; Teti, R.; Alfieri, V.; Caiazzo, F. Automated Laser Polishing for Surface Finish Enhancement of Additive Manufactured Components for the Automotive Industry. Prod. Eng. 2021, 15, 109–117. [Google Scholar] [CrossRef]
- Oba, Y.; Kakinuma, Y. Simultaneous Tool Posture and Polishing Force Control of Unknown Curved Surface Using Serial-Parallel Mechanism Polishing Machine. Precis. Eng. 2017, 49, 24–32. [Google Scholar] [CrossRef]
- Xiao, G.; Huang, Y.; Yin, J. An Integrated Polishing Method for Compressor Blade Surfaces. Int. J. Adv. Manuf. Technol. 2017, 88, 1723–1733. [Google Scholar] [CrossRef]
- Lim, M.S.H. Digitalization of Mass Vibratory Polishing Process for Aerospace Application; Nanyang Technological University: Singapore, 2022. [Google Scholar]
- Krishnan, A.; Fang, F. Review on Mechanism and Process of Surface Polishing Using Lasers. Front. Mech. Eng. 2019, 14, 299–319. [Google Scholar] [CrossRef]
- Zhu, P.; Han, J.; Xie, H.; Li, X. Study of Ultrafast Laser Polishing Technology. In Proceedings of the International Conference on Photonics and Optical Engineering (icPOE 2014), Xi’an, China, 13–15 October 2014; SPIE: Bellingham, WA, USA, 2015; Volume 9449, pp. 821–825. [Google Scholar]
- Tian, F.; Lv, C.; Li, Z.; Liu, G. Modeling and Control of Robotic Automatic Polishing for Curved Surfaces. CIRP J. Manuf. Sci. Technol. 2016, 14, 55–64. [Google Scholar] [CrossRef]
- Walker, D.; Yu, G.Y.; Gray, C.; Rees, P.; Bibby, M.; Wu, H.Y.; Zheng, X. Process Automation in Computer Controlled Polishing. Adv. Mater. Res. 2016, 1136, 684–689. [Google Scholar] [CrossRef]
- Su, Z.; Ying, Z. Polishing Path Planning of Complex Curved Surfaces and the Realization of Automatic Control. Int. J. Smart Home 2016, 10, 233–240. [Google Scholar] [CrossRef]
- Wei, Y.; Xu, Q. Design of a New Passive End-Effector Based on Constant-Force Mechanism for Robotic Polishing. Robot. Comput.-Integr. Manuf. 2022, 74, 102278. [Google Scholar] [CrossRef]
- Zhang, X.; Sun, Y. Development of Pneumatic Force-Controlled Actuator for Automatic Robot Polishing Complex Curved Plexiglass Parts. Machines 2023, 11, 446. [Google Scholar] [CrossRef]
- Li, J.; Guan, Y.; Chen, H.; Wang, B.; Zhang, T.; Liu, X.; Hong, J.; Wang, D.; Zhang, H. A High-Bandwidth End-Effector with Active Force Control for Robotic Polishing. IEEE Access 2020, 8, 169122–169135. [Google Scholar] [CrossRef]
- Lakshminarayanan, S.; Kana, S.; Mohan, D.M.; Manyar, O.M.; Then, D.; Campolo, D. An Adaptive Framework for Robotic Polishing Based on Impedance Control. Int. J. Adv. Manuf. Technol. 2021, 112, 401–417. [Google Scholar] [CrossRef]
- Ochoa, H.; Cortesão, R. Impedance Control Architecture for Robotic-Assisted Mold Polishing Based on Human Demonstration. IEEE Trans. Ind. Electron. 2021, 69, 3822–3830. [Google Scholar] [CrossRef]
- Ding, Y.; Zhao, J.; Min, X. Impedance Control and Parameter Optimization of Surface Polishing Robot Based on Reinforcement Learning. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2023, 237, 216–228. [Google Scholar] [CrossRef]
- Xiao, C.; Wang, Q.; Zhou, X.; Xu, Z.; Lao, X.; Chen, Y. Hybrid Force/Position Control Strategy for Electromagnetic Based Robotic Polishing Systems. In Proceedings of the 2019 Chinese Control Conference (CCC), Guangzhou, China, 27–30 July 2019; pp. 7010–7015. [Google Scholar]
- Gracia, L.; Solanes, J.E.; Muñoz-Benavent, P.; Valls Miro, J.; Perez-Vidal, C.; Tornero, J. Adaptive Sliding Mode Control for Robotic Surface Treatment Using Force Feedback. Mechatronics 2018, 52, 102–118. [Google Scholar] [CrossRef]
- Gal, I.-A.; Ciocîrlan, A.-C.; Mărgăritescu, M. State Machine-Based Hybrid Position/Force Control Architecture for a Waste Management Mobile Robot with 5DOF Manipulator. Appl. Sci. 2021, 11, 4222. [Google Scholar] [CrossRef]
- Luo, Z.; Li, J.; Bai, J.; Wang, Y.; Liu, L. Adaptive Hybrid Impedance Control Algorithm Based on Subsystem Dynamics Model for Robot Polishing. In Proceedings of the Intelligent Robotics and Applications: 12th International Conference, ICIRA 2019, Shenyang, China, 8–11 August 2019; Proceedings, Part VI 12. Springer: Berlin/Heidelberg, Germany, 2019; pp. 163–176. [Google Scholar]
- Zhou, H.; Ma, S.; Wang, G.; Deng, Y.; Liu, Z. A Hybrid Control Strategy for Grinding and Polishing Robot Based on Adaptive Impedance Control. Adv. Mech. Eng. 2021, 13, 16878140211004034. [Google Scholar] [CrossRef]
- Koivumäki, J.; Mattila, J. Stability-Guaranteed Impedance Control of Hydraulic Robotic Manipulators. IEEE/ASME Trans. Mechatron. 2016, 22, 601–612. [Google Scholar] [CrossRef]
- Luo, Z.; Yang, S.; Sun, Y.; Liu, H. Optimized Control for Dynamical Performance of the Polishing Robot in Unstructured Environment. Shock Vib. 2011, 18, 355–364. [Google Scholar] [CrossRef]
- Hamedani, M.H.; Sadeghian, H.; Zekri, M.; Sheikholeslam, F.; Keshmiri, M. Intelligent Impedance Control Using Wavelet Neural Network for Dynamic Contact Force Tracking in Unknown Varying Environments. Control Eng. Pract. 2021, 113, 104840. [Google Scholar] [CrossRef]
- Hamedani, M.H.; Zekri, M.; Sheikholeslam, F.; Selvaggio, M.; Ficuciello, F.; Siciliano, B. Recurrent Fuzzy Wavelet Neural Network Variable Impedance Control of Robotic Manipulators with Fuzzy Gain Dynamic Surface in an Unknown Varied Environment. Fuzzy Sets Syst. 2021, 416, 1–26. [Google Scholar] [CrossRef]
- Cao, H. Design of a Fuzzy Fractional Order Adaptive Impedance Controller with Integer Order Approximation for Stable Robotic Contact Force Tracking in Uncertain Environment. Acta Mech. Autom. 2022, 16, 16–26. [Google Scholar] [CrossRef]
- Li, Z.; Huang, H.; Song, X.; Xu, W.; Li, B. A Fuzzy Adaptive Admittance Controller for Force Tracking in an Uncertain Contact Environment. IET Control Theory Appl. 2021, 15, 2158–2170. [Google Scholar] [CrossRef]
- Mazare, M.; Tolu, S.; Taghizadeh, M. Adaptive Variable Impedance Control for a Modular Soft Robot Manipulator in Configuration Space. Meccanica 2022, 57, 1–15. [Google Scholar] [CrossRef]
- Cao, H.; Zhou, J.; Jiang, P.; Hon, K.K.B.; Yi, H.; Dong, C. An Integrated Processing Energy Modeling and Optimization of Automated Robotic Polishing System. Robot. Comput.-Integr. Manuf. 2020, 65, 101973. [Google Scholar] [CrossRef]
- Ding, Y.; Min, X.; Fu, W.; Liang, Z. Research and Application on Force Control of Industrial Robot Polishing Concave Curved Surfaces. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2019, 233, 1674–1686. [Google Scholar] [CrossRef]
- Nagata, F.; Hase, T.; Haga, Z.; Omoto, M.; Watanabe, K. CAD/CAM-Based Position/Force Controller for a Mold Polishing Robot. Mechatronics 2007, 17, 207–216. [Google Scholar] [CrossRef]
- Yang, L.; Zhang, Y.; Han, Y.; Zhang, B.; Wang, Z. Robot Automatic Polishing Technology of Curved Parts Based on Adaptive Impedance Control. In Proceedings of the International Conference on Mechanism and Machine Science, Yantai, China, 30 July–1 August 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 2073–2086. [Google Scholar]
- Huang, Y.; Chen, H.; Cui, Z.; Zhang, X. An Adaptive Impedance Control Method for Human-Robot Interaction. In Proceedings of the International Conference on Intelligent Robotics and Applications, Hangzhou, China, 5–7 July 2023; Springer: Berlin/Heidelberg, Germany, 2023; pp. 529–539. [Google Scholar]
- Sheng, X.; Zhang, X. Fuzzy Adaptive Hybrid Impedance Control for Mirror Milling System. Mechatronics 2018, 53, 20–27. [Google Scholar] [CrossRef]
- Duan, J.; Gan, Y.; Chen, M.; Dai, X. Adaptive Variable Impedance Control for Dynamic Contact Force Tracking in Uncertain Environment. Robot. Auton. Syst. 2018, 102, 54–65. [Google Scholar] [CrossRef]
- Shen, Y.; Lu, Y.; Zhuang, C. A Fuzzy-Based Impedance Control for Force Tracking in Unknown Environment. J. Mech. Sci. Technol. 2022, 36, 5231–5242. [Google Scholar] [CrossRef]
- Ahmadi, B.; Xie, W.; Zakeri, E. Robust cascade vision/force control of industrial robots utilizing continuous integral sliding-mode control method. IEEE/ASME Trans. Mechatron. 2021, 27, 524–536. [Google Scholar] [CrossRef]
- Zhou, F.; Liu, H.; Zhang, P.; Ouyang, X.; Xu, L.; Ge, Y.; Yao, Y.; Yang, H. High-Precision Control Solution for Asymmetrical Electro-Hydrostatic Actuators Based on the Three-Port Pump and Disturbance Observers. IEEE/ASME Trans. Mechatron. 2023, 28, 396–406. [Google Scholar] [CrossRef]
- Thuilot, B.; Martinet, P.; Cordesses, L.; Gallice, J. Position Based Visual Servoing: Keeping the Object in the Field of Vision. In Proceedings of the 2002 IEEE International Conference on Robotics and Automation (Cat. No. 02CH37292), Washington, DC, USA, 11–15 May 2002; IEEE: New York, NY, USA, 2002; Volume 2, pp. 1624–1629. [Google Scholar]



| ec | ||||||||
| NB | NM | NS | ZE | PS | PM | PB | ||
| e | NB | PB | PM | PS | ZE | ZE | ZE | ZE |
| NM | PB | PM | PS | ZE | ZE | ZE | NS | |
| NS | PB | PS | PS | ZE | ZE | NS | NM | |
| ZE | PB | PS | PS | ZE | NS | NB | NB | |
| PS | PM | PS | ZE | ZE | NS | NM | NB | |
| PM | PS | ZE | ZE | ZE | NS | NM | NB | |
| PB | ZE | ZE | ZE | ZE | NS | NM | NB | |
| Δkd3, Δdd3 | ef3(k) | |||||||
| NB | NM | NS | ZO | PS | PM | PB | ||
| e3(k)Δe3(k) | NB | NB | NB | NB | NB | NM | NS | ZO |
| NM | NB | NB | NB | NM | NS | ZO | PS | |
| NS | NB | NB | NM | NS | ZO | PS | PM | |
| ZO | NB | NM | NS | ZO | PS | PM | PB | |
| PS | NM | NS | ZO | PS | PM | PB | PB | |
| PM | NS | ZO | PS | PM | PB | PB | PB | |
| PB | ZO | PS | PM | PB | PB | PB | PB | |
| Cases | Adjustment Time ts (s) | Maximum Overshoot Mp (%) | Error Integration Es (N·s) | ||
|---|---|---|---|---|---|
| Constant stiffness | Unit step | FAIC | 0.271 | 1.1 | 0.193 |
| AICVG | 0.256 | 0.5 | 0.161 | ||
| TIC | 0.193 | 10.4 | 0.223 | ||
| Sine wave | FAIC | 0.259 | 8.1 | 0.315 | |
| AICVG | 0.263 | 6.3 | 0.351 | ||
| TIC | 0.185 | 12.1 | 0.642 | ||
| Time-varying stiffness | Unit step | FAIC | 0.237 | 9.7 | 0.272 |
| AICVG | 0.244 | 0.8 | 0.177 | ||
| TIC | 0.207 | 11.8 | 0.330 | ||
| Sine wave | FAIC | 0.251 | 18.2 | 0.612 | |
| AICVG | 0.261 | 6.3 | 0.349 | ||
| TIC | 0.258 | 23.2 | 0.671 | ||
| Parameter Category | Parameter Name | Parameter Value | Unit |
|---|---|---|---|
| Robot Body | Model | KUKA KR16 | - |
| Maximum Payload | 16 | kg | |
| Working Radius | 1610 | mm | |
| Repeatability | ±0.05 | mm | |
| Sensors | Model | ATI Gamma SI-130-10 | - |
| Force Measurement Range | ±130 | N | |
| Torque Measurement Range | ±10 | Nm | |
| Sampling Frequency | 1000 | Hz | |
| Polishing Tool | Type | Pneumatic Polishing Tool | - |
| Polishing Head Diameter | 50 | mm | |
| Polishing Material | High-density Polyurethane | - | |
| Maximum Speed | 12,000 | rpm | |
| Workpiece | Type | Concave Curved Surface Product | - |
| Material | 304 Stainless Steel | - | |
| Dimensions | 200 × 150 × 50 | mm | |
| Radius of Curvature | 150 | mm | |
| Vision System | Camera Model | Basler acA2440-35uc | - |
| Resolution | 2448 × 2048 | pixels | |
| Frame Rate | 35 | fps | |
| Control Parameters | Polishing Speed | 30–60 | mm/s |
| Polishing Force | 20–40 | N | |
| Force Control Accuracy | ±1.5 | N | |
| Control Cycle | 1 | ms | |
| Communication Period | 0.012 | s | |
| Visual Sampling Period | 150 | ms | |
| Force Sampling Period | 6 | ms |
| Processes | Tool Material | Speed (r/min) | Expected Force (N) | Feed Rate (mm/s) |
|---|---|---|---|---|
| rough polishing | Spherical grinding wheel | 6000 | 6 | 18 |
| semi-fine polishing | Spherical rubber | 8000 | 4 | 18 |
| fine polishing | Cylindrical Wool Felt | 10,000 | 2 | 9 |
| Method | Ra (μm) | Average Ra (μm) | Reduction Compared to TIC (%) | |||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |||
| TIC | 0.090 | 0.100 | 0.095 | 0.080 | 0.110 | 0.047 | 0.087 | - |
| FAIC | 0.050 | 0.055 | 0.060 | 0.045 | 0.058 | 0.044 | 0.052 | 40.2% |
| AICVG | 0.030 | 0.038 | 0.040 | 0.032 | 0.035 | 0.035 | 0.035 | 59.7% |
| Unpolished | - | 3.75 | - | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Q.; Lian, X. Vision-Guided Fuzzy Adaptive Impedance-Based Control for Polishing Robots Under Time-Varying Stiffness. Machines 2025, 13, 493. https://doi.org/10.3390/machines13060493
Li Q, Lian X. Vision-Guided Fuzzy Adaptive Impedance-Based Control for Polishing Robots Under Time-Varying Stiffness. Machines. 2025; 13(6):493. https://doi.org/10.3390/machines13060493
Chicago/Turabian StyleLi, Qinsheng, and Xiaozhen Lian. 2025. "Vision-Guided Fuzzy Adaptive Impedance-Based Control for Polishing Robots Under Time-Varying Stiffness" Machines 13, no. 6: 493. https://doi.org/10.3390/machines13060493
APA StyleLi, Q., & Lian, X. (2025). Vision-Guided Fuzzy Adaptive Impedance-Based Control for Polishing Robots Under Time-Varying Stiffness. Machines, 13(6), 493. https://doi.org/10.3390/machines13060493





