A Hierarchical Attention-Guided Data–Knowledge Fusion Network for Few-Shot Gearboxes’ Fault Diagnosis

Abstract

To address the limited generalization capability of data-driven fault diagnosis models caused by scarce gearbox fault samples in engineering practice, this paper proposes a hierarchical attention-guided data–knowledge dual-driven fusion network for intelligent fault diagnosis under few-shot conditions. Distinct from traditional single data-driven paradigms, this method breaks through the constraints of limited samples through the synergy of prior knowledge and monitoring data. First, domain knowledge of gearbox fault diagnosis is utilized to construct prior features of monitoring data. Second, a deep convolutional neural network is designed to hierarchically capture abstract features from monitoring data. Subsequently, a hierarchical attention module is proposed to realize adaptive fusion of prior features and abstract features through hierarchical feature weight allocation, generating highly discriminative fused features for accurate gearbox fault identification. Experimental results on gearbox fault data demonstrate that the proposed method achieves 0.9880 recognition accuracy with less than 10% of the training samples, significantly outperforming purely data-driven models such as MGAN and CNET, thus verifying its superior generalization ability to train despite data scarcity. This approach establishes a novel data–knowledge dual-driven fusion paradigm for intelligent fault diagnosis of mechanical equipment under few-shot conditions.

1. Introduction and Literature Review

Gearboxes, as core components in rotating machinery, are widely used in industrial manufacturing, transportation, aerospace, and other fields. Their operational reliability is critical to ensuring the safe and stable operation of rotating machinery [1]. However, gearboxes typically consist of multiple tightly coupled gears with complex internal structures and operate under harsh and variable conditions, making them prone to failures. Once a failure occurs, it may lead to significant economic losses or even casualties [2]. Therefore, analyzing the operational monitoring data of gearboxes to achieve condition monitoring and fault diagnosis is of significant engineering importance.

Since vibration signals are most sensitive to gearbox faults, vibration analysis has become the most widely adopted technical approach for gearbox fault diagnosis [3,4]. Traditionally, researchers have employed frequency-domain analysis, wavelet transforms, and other manual-experience-based methods to analyze gearbox vibration signals and identify faults [5,6]. Such methods suffer from low data processing efficiency and heavy reliance on expert knowledge, making them inadequate for rapidly handling large volumes of monitoring signals in modern industrial systems [7]. With advancements in artificial intelligence and big data technologies, deep learning-based intelligent diagnosis models have emerged as powerful tools for rapid and accurate gearbox fault identification [8,9]. Numerous deep learning models, such as deep convolutional neural networks (DCNNs) and deep generative adversarial networks (GANs), have been extensively applied in constructing intelligent fault diagnosis models for gearboxes [10]. However, due to their massive parameter sizes, existing intelligent diagnosis models rely heavily on extensive fault data for parameter training, and their diagnostic performance is closely tied to the volume of training data [11]. Under insufficient training samples, these models are highly prone to overfitting, resulting in inadequate diagnostic generalization capability. However, in practical engineering applications, the directly obtainable gearbox fault data are often extremely limited. Moreover, conducting fault simulation experiments on gearboxes in laboratory settings to acquire fault data proves to be highly costly. Consequently, the gearbox fault data we can collect fall far short of meeting the training requirements of intelligent models. Thus, this study on intelligent fault diagnosis methods for gearboxes under few-shot conditions is of both academic significance and engineering value.

In recent years, scholars have achieved some progress in few-shot gearbox fault diagnosis. Existing research can be broadly categorized into three approaches: data augmentation-based methods, algorithm optimization-based methods, and transfer learning-based methods [12]. For data augmentation, Su et al. [13] proposed an improved generative adversarial network (GAN)-based vibration data augmentation method for planetary gearbox fault diagnosis. Zhang et al. [14] developed a semi-supervised GAN for gearbox fault data augmentation, where augmented data enhanced diagnostic performance under few-shot conditions. In algorithm optimization, Zhu et al. [15] introduced a contrastive learning and self-attention mechanism-based method for few-shot gear fault recognition. Chen et al. [16] designed a label-assisted semi-supervised adversarial learning network to extract vibration features from limited fault samples. For transfer learning, Li et al. [17] proposed a cross-feature transferable network for gearbox fault diagnosis under data scarcity. However, data augmentation-based methods often demand substantial computational resources, making them less practical for engineering applications. Algorithm optimization-based approaches typically require meticulously designed network architectures or parameter regularization schemes to extract more fault information from limited samples, imposing high demands on model developers’ expertise. Transfer learning-based methods face challenges in selecting appropriate transfer sources and designing meta-transfer tasks, risking negative transfer phenomena that degrade diagnostic performance. In summary, there is an urgent need for innovative research directions and technical solutions for intelligent gearbox fault diagnosis under few-shot conditions.

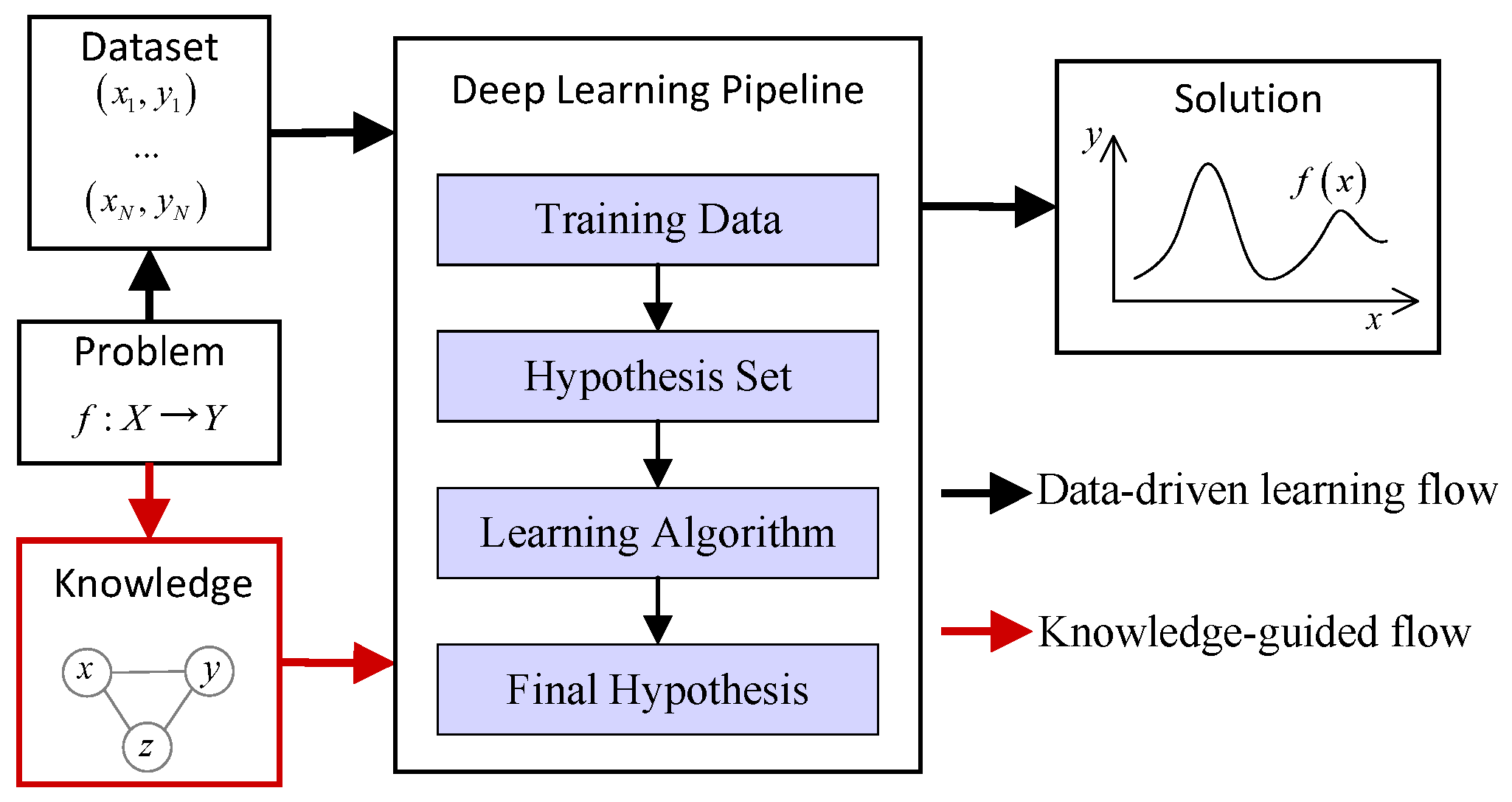
Knowledge-informed deep learning (KDL) is recognized as a powerful tool with which to overcome the data bottleneck of deep learning and has become a new research frontier in artificial intelligence [18], as shown in Figure 1. Unlike traditional deep learning workflows, KDL integrates both data-driven learning and prior knowledge guidance during model construction and training, significantly reducing the demand for training data [19]. In fields such as image recognition, KDL has successfully enabled researchers to achieve strong data generalization capabilities under limited-sample conditions [20]. In recent years, in the field of mechanical fault diagnosis, researchers have begun incorporating diagnostic prior knowledge into models with the aim of achieving fault diagnosis with strong generalization ability despite insufficient fault samples [21]. For instance, Kim et al. [22] proposed a domain adaptation learning method enhanced by bearing prior knowledge for few-shot rolling bearing fault diagnosis. Liu et al. [23] proposed a knowledge-informed cross-category filtering framework for fault diagnosis under small samples. Matania et al. [24] proposed a physical knowledge-informed algorithm to overcome the lack of fault sample for fault severity estimation of gearboxes. Sun et al. [25] presented a physical knowledge based data fusion and reconstruction network for bearing fault diagnosis under incomplete data. Consequently, incorporating gearbox fault diagnosis prior knowledge into the development and training of intelligent models holds great potential for achieving high performance with limited fault samples.

Building on these analyses, this paper proposes a hierarchical attention-guided data–knowledge dual-driven fusion network for intelligent gearbox fault diagnosis under few-shot conditions. Unlike traditional single data-driven paradigms, the proposed method synergizes prior knowledge and monitoring data to overcome limited-sample constraints, establishing a novel data–knowledge dual-driven fusion paradigm for few-shot gearbox fault diagnosis. The main contributions of this paper are as follows:

(1)

A hierarchical attention-guided data–knowledge dual-driven fusion network is proposed, enabling parameter training with limited data and domain knowledge.

(2)

An intelligent fault diagnosis method based on the above network is developed to address the challenge of accurate gearbox fault identification under few-shot conditions.

(3)

Extensive case studies on gearbox fault experiments validate the diagnostic effectiveness and superiority of the proposed method over related methods in few-shot scenarios.

The remainder of this paper is organized as follows: Section 2 introduces the theoretical foundations of CNNs and attention mechanisms. Section 3 details the proposed diagnostic method. Section 4 and Section 5 validate the method’s effectiveness through two gearbox fault diagnosis case studies. Section 6 concludes the paper.

2. Theoretical Foundations

2.1. Convolutional Neural Network

Convolutional neural networks (CNNs) are classical data processing methods in the field of machine learning. Among these, one-dimensional CNNs (1D-CNNs) have become one of the most powerful tools in mechanical fault diagnosis research due to their direct processing capability for one-dimensional time-series data [26].

The data processing in a 1D-CNN is primarily accomplished through convolutional layers and pooling layers. For the ath convolutional layer, its convolution kernel is denoted ${\omega }_a$, and the bias term as $b_a$. The output $c_a$ of this layer is expressed as

$$\begin{array}{c}\hfill c_a^d=relu\left(\sum _{e\in E_a}{g}_{a-1}^d\times {\omega }_a^{d,e}+b_a^d\right)\end{array}$$

(1)

where $E_a$ represents the feature vector from the previous layer. $g_{a-1}$ is the output of the $a-1$th pooling layer. $relu\left(·\right)$ is the Rectified Linear Unit activation function.

$$\begin{array}{c}\hfill relu\left(x\right)=max\left(0,x\right)\end{array}$$

(2)

The output of the $a-1$th pooling layer $g_{a-1}$ is defined as:

$$\begin{array}{c}\hfill g_{a-1}^d=\underset{h\in H}{max}{c}_{a-1}^{h+d·k}\end{array}$$

(3)

where H is the pooling window length and k is the pooling stride.

The primary function of the convolutional layer is to perform convolution operations on input data for feature extraction. The pooling layer reduces network complexity by down-sampling the extracted features. By stacking convolutional and pooling layers, the depth of the CNN increases, enabling the extraction of deep-level features from input data. Typically, the extracted features are fed into a Softmax classifier to complete the final data classification task.

2.2. Attention Mechanism

The attention mechanism is an information selection mechanism that identifies and assigns higher weights to input components exerting greater influence on the output.

For an input sample $x_i$, the attention-weighted sample $x_i^{\prime }$ is computed as

$$\begin{array}{c}\hfill x_i^{\prime }={\alpha }_i{x}_i\end{array}$$

(4)

where ${\alpha }_i$ is the attention weight.

$$\begin{array}{c}\hfill {\alpha }_i={\displaystyle \frac{exp\left(s\left(x_i,q\right)\right)}{{\sum }_{i=1}^{N}exp\left(s\left(x_i,q\right)\right)}}\end{array}$$

(5)

where N is the total number of samples, $s\left(·\right)$ denotes the attention scoring function, and q is a task-dependent query vector that ensures the normalization of weights to sum to 1.

A higher weight ${\alpha }_i$ indicates greater importance of the corresponding sample $x_i$ to the network’s output. By assigning differentiated weights, the attention mechanism enables the network to prioritize critical input samples, thereby enhancing overall performance.

3. Proposed Method

3.1. Overview

This study aims to achieve gear condition monitoring and fault diagnosis through the analysis of gearbox vibration signals, focusing on diagnosing gear cracks and pitting—the most prevalent failure modes during gear operation. Vibration signals are acquired from the gearbox using vibration sensors and data acquisition systems. Through manual signal segmentation and labeling, a dataset $D={\left(x_i,y_i\right)}_{i=1}^N$ is constructed, where $x_i\in {\Re }^{M\times 1}$ represents the ith vibration sample containing M data points, and $y_i=\left\{1,2,\dots ,L\right\}$ denotes the corresponding fault label of $x_i$. The objective is to develop a fault diagnosis model using D that accurately learns the nonlinear mapping $f:x\to y$.

In practical engineering scenarios, the scarcity of gearbox fault signals severely limits the availability of training data for intelligent diagnosis models. The primary challenge lies in training a high-performance diagnostic model with minimal fault samples. To address this, we propose a hierarchical attention-guided data–knowledge dual-driven fusion network. The key innovation of this method is the design of a hierarchical attention module that synergizes prior knowledge with monitoring data, thereby overcoming the constraints imposed by insufficient fault samples on model training.

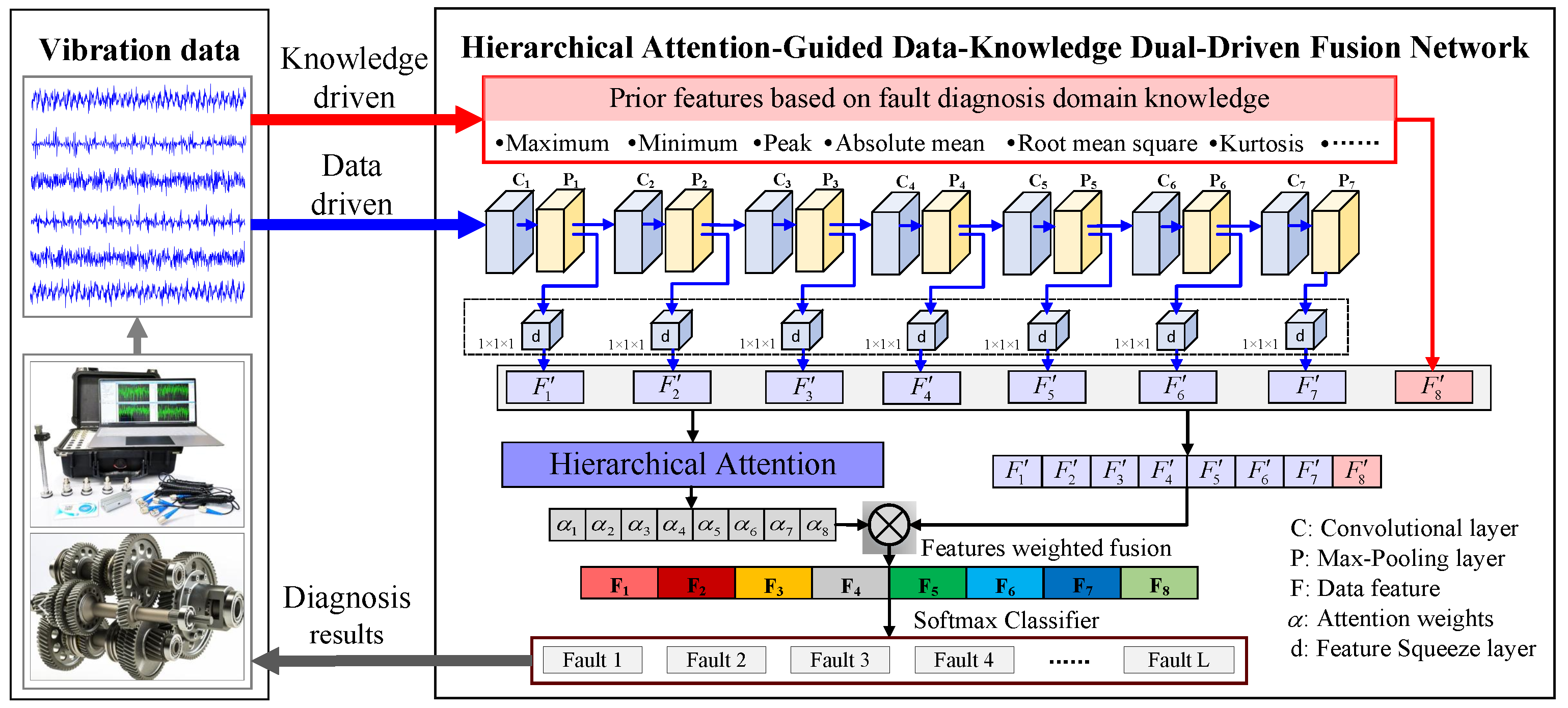
As shown in Figure 2, the proposed method involves three key steps, detailed as follows. (1) Prior Feature Construction: Domain knowledge of fault diagnosis is utilized to extract prior features from monitoring data. (2) Hierarchical Abstract Feature Extraction: A deep convolutional neural network (CNN) is designed to hierarchically capture abstract features from the spectrum of the monitoring data. (3) Hierarchical Attention-Guided Fusion: A hierarchical attention module dynamically allocates feature weights across layers, enabling adaptive fusion of prior features and abstract features. The fused features are then used to achieve accurate fault identification.

3.2. Knowledge-Driven Prior Feature Construction

In the field of fault diagnosis, experts have accumulated substantial domain knowledge, including failure mechanisms, fault characteristics, and signal processing methods, collectively referred to as prior knowledge. Statistical features of vibration signals, such as peak values and kurtosis, can partially characterize gearbox health conditions. Crucially, these features are derived from fault mechanism analyses and require no data-driven parameter training.

Inspired by Reference [27] and supported by preliminary experiments on gearbox fault diagnosis, our method selects 10 signal feature indicators to construct the prior feature vector $P=\left\{p_1,p_2,\dots ,p_{10}\right\}$, where $p_j$ represents the jth feature indicator, as listed in

Table 1. 10 prior features.

Feature	Formula	Feature	Formula
Absolute mean	$p_1={\displaystyle \frac{1}{M}}{\displaystyle \sum _{m=1}^M}\left|x\left(m\right)\right|$	Kurtosis	$p_6={\displaystyle \frac{1}{M}}{\displaystyle \sum _{m=1}^M}{\left(x\right(m\left)\right)}^4$
Peak	$p_2=max\left|x\left(m\right)\right|$	Standard deviation	$p_7=\sqrt{{\displaystyle \frac{1}{M-1}}{\displaystyle \sum _{m=i}^M}{\left[x\left(m\right)-\overline{x}\right]}^2}$
Maximum	$p_3=max\left(x\left(m\right)\right)$	Root amplitude	$p_8={\left({\displaystyle \frac{1}{M}}{\displaystyle \sum _{m=1}^M}\sqrt{\left|x\left(m\right)\right|}\right)}^2$
Minimum	$p_4=min\left(x\left(m\right)\right)$	Variance	$p_9={\displaystyle \frac{1}{M}}{\displaystyle \sum _{m=1}^M}{\left(x\right(m\left)\right)}^2$
Peak-to-Peak	$p_5=max\left(x\left(m\right)\right)-min\left(x\left(m\right)\right)$	Root mean square	$p_{10}=\sqrt{{\displaystyle \frac{1}{M}}{\displaystyle \sum _{m=1}^M}{\left(x\right(m\left)\right)}^2}$

. These 10 prior features are directly computed from input data and subsequently normalized via zero-mean standardization. The constructed prior feature vector demonstrates certain characterization capability for gearbox health conditions. For instance, when gearbox faults occur, peak-to-peak values and root mean square values of vibration signals exhibit significant changes. Moreover, the selected prior feature vector maintains its capability to characterize gearbox health conditions to some extent, even across different mechanical equipment, thus exhibiting certain generalization ability.

3.3. Data-Driven Fault Feature Extraction

When using limited training samples, deep features extracted by neural networks often suffer from insufficient generalization capability in characterizing gearbox health states. To address this, hierarchical feature fusion is adopted to obtain more generalizable data representations.

As shown in Figure 2, the proposed method employs a seven-layer deep convolutional neural network (CNN) for hierarchical automatic feature extraction from the spectrum of the vibration data. The detailed parameters of this CNN are listed in

Table 2. Parameters of the deep convolutional neural network.

Layer	Channels @ Kernel Size * Stride /Pool Size * Stride	Output Shape	Activation Function
Input	/	1 * 1024	/
1D Convolutional	32 @ 32 * 1	32 * 1024	relu
Max pooling	2 * 2	32 * 512	/
1D Convolutional	32 @ 4 * 1	32 * 512	relu
Max pooling	2 * 2	32 * 256	/
1D Convolutional	64 @ 4 * 1	64 * 256	relu
Max pooling	2 * 2	64 * 128	/
1D Convolutional	64 @ 4 * 1	64 * 128	relu
Max pooling	2 * 2	64 * 64	/
1D Convolutional	128 @ 4 * 1	128 * 64	relu
Max pooling	2 * 2	128 * 32	/
1D Convolutional	128 @ 4 * 1	128 * 32	relu
Max pooling	2 * 2	128 * 16	/
1D Convolutional	256 @ 4 * 1	256 * 16	relu
Max pooling	2 * 2	256 * 8	/

. The computational process for each convolutional layer follows Equations (1) and (2). To facilitate hierarchical feature fusion, we first process features from each layer using an identity convolution kernel. Let the kernel size of the identity convolution kernel ${\omega }_u$ be $1\times 1\times 1$. The processed feature ${F_a}^{″}$ at the ath layer is expressed as

$$\begin{array}{c}\hfill {F_a}^{″}=relu\left(g_a\times {\omega }_u+b_u\right)\end{array}$$

(6)

where $g_a$ is the output of the pooling layer at the ath layer. $b_u$ is the bias term of the identity convolution layer.

The compressed feature ${F_a}^{\prime }$ retains essential hierarchical information while balancing the dimensionality across layers, ensuring compatibility for subsequent attention-guided fusion.

$$\begin{array}{c}\hfill F_a^{\prime }=relu\left({F^{\prime }}_a·{\varpi }_a+{b^{\prime }}_a\right)\end{array}$$

(7)

where ${\varpi }_a$ and $b_a^{\prime }$ are the weight matrix and bias term of the ath fully connected layer, respectively.

3.4. Hierarchical Attention-Guided Feature Fusion

Although most intelligent diagnostic models employ deep data features for fault identification, the representational capacity and generalization ability of features at different depths in DCNNs vary significantly due to varying numbers of convolutional operations. In this field, existing studies have demonstrated that assigning different weights to distinct CNN layers can achieve more robust fault feature extraction with enhanced generalization capability [28]. To obtain superior generalization performance, we adopt a weighting strategy to fuse data features from different depths.

Specifically, after obtaining seven abstract features from seven layers of the deep convolutional network, a hierarchical attention module is employed to achieve weighted fusion of the seven abstract features with the prior features, as illustrated in Figure 3.

For the feature $F_a^{\prime }$, its attention score $s_a$ is computed as

$$\begin{array}{c}\hfill s_a=sigmoid\left({F^{\prime }}_a·{\varpi }_{att}+b_{att}\right)\end{array}$$

(8)

where $sigmoid\left(·\right)$ is a nonlinear activation function, ${\varpi }_{att}$ and $b_{att}$ are the weight matrix and bias term of the attention scoring layer. The attention weight ${\alpha }_a$ is then normalized via

$$\begin{array}{c}\hfill {\alpha }_a={\displaystyle \frac{e^{s_a}}{{\sum }_{a=1}^8{e}^{s_a}}}\end{array}$$

(9)

The weighted feature at the ath layer is derived as

$$\begin{array}{c}\hfill F_a={\alpha }_a·{F_a}^{\prime }\end{array}$$

(10)

Finally, a concatenation function $concat\left(·\right)$ fuses all weighted hierarchical features with the prior features:

$$\begin{array}{c}\hfill F=concat{\left(F_1,F_2,\dots ,F_8\right)}_{axis=0}\end{array}$$

(11)

where F denotes the fused feature. $axis=0$ indicates that feature combination is performed along the column direction, ensuring dimensional compatibility of features. The resulting F integrates both multi-layer abstract features (automatically extracted by the deep CNN) and knowledge-informed prior features, forming an optimal fusion that enhances discriminative power for characterizing gearbox health states.

3.5. Method Training Process

After obtaining the weighted fused feature F, it is fed into a Softmax classifier to achieve the final classification of gearbox vibration data. The operation of the Softmax classifier is formulated as

$$\begin{array}{c}\hfill J\left(F_i\right)={\displaystyle \frac{{\left[\begin{array}{cccc}{e}^{{\theta }_1^T{F}_i}& e^{{\theta }_2^T{F}_i}& \dots & e^{{\theta }_L^T{F}_i}\end{array}\right]}^T}{{\sum }_{l=1}^L{e}^{{\theta }_l^T{F}_i}}}\end{array}$$

(12)

where $J\left(·\right)$ is the output of the Softmax classifier, and $\theta$ is the parameter of the Softmax classifier.

The training objective is to minimize the discrepancy between predicted and true labels, for which the cross-entropy loss $C_E$ is adopted:

$$\begin{array}{c}\hfill C_E=-{\displaystyle \frac{1}{N}}\left[\sum _{i=1}^N\sum _{l=1}^{L}1\left\{y_i=l\right\}log\left(J\left(F_i\right)\right)\right]\end{array}$$

(13)

where $1\left\{·\right\}$ is an indicator function that returns 1 if $y_i=l$ and otherwise 0.

The training workflow of the proposed method is summarized in Algorithm 1.

Algorithm 1 Pseudo- code of the training process of the proposed method.
Input:	Gearbox vibration dataset $D={\left(x_i,y_i\right)}_{i=1}^N$
Initialize:	Network parameters (CNN weights, attention weights, classifier parameters)
Configure:	Learning rate, Training Epoch, optimizer (e.g., Adam)
1:	for Epoch do:
2:	Compute prior features Pi for training samples in D using Table 1;
3:	Extract hierarchical abstract features and fuse with prior features via Equations (6)–(11);
4:	Calculate predicted labels using Equation (12);
5:	Compute cross-entropy loss via Equation (13);
6:	Update parameters using the optimizer;
7:	end for

4. Effectiveness Analysis Based on SQ Gearbox Fault Data

4.1. Gearbox Experimental Data and Diagnostic Scenarios

This study utilizes the Spectra Quest (SQ) Machinery Fault Simulator to conduct gearbox fault experiments. As shown in Figure 4, the SQ testbed comprises a drive motor, a gearbox, a load module, a data acquisition unit, and vibration accelerometers. The gearbox includes planetary and sun gears, with vibration sensors of 50 mV/g sensitivity. During experiments, the motor speed is set to 40 Hz, and the sampling frequency of the data acquisition unit is configured to 25.6 kHz.

To simulate diverse gearbox fault conditions, we artificially introduced faults of varying types and severity levels on the planetary and sun gears, as follows. Planetary Gear Faults: (1) Minor pitting (PP-1); (2) Moderate pitting (PP-2); (3) Severe pitting (PP-3); (4) Minor cracking (PC-1); (5) Moderate cracking (PC-2); (6) Severe cracking (PC-3); Sun Gear Faults: (7) Minor pitting (SP-1); (8) Moderate pitting (SP-2); (9) Severe pitting (SP-3); (10) Moderate cracking (SC-2); (11) Severe cracking (SC-3). Figure 5 illustrates the 11 types of artificially induced faulty gears. Additionally, vibration data under normal conditions were collected and labeled Normal Condition (NC-0). The corresponding vibration signal can be seen in Figure 6. After data segmentation, each health condition contained 1500 data samples, with each sample consisting of 1024 data points.

4.2. Parameter Settings and Comparative Methods

In the proposed method, the training epochs are set to 200, with the Adam optimizer employed for parameter optimization at a learning rate of 0.0005. The batchsize is 16. Additionally, we do not employ any dropout strategy or other data augmentation techniques.

To validate the superiority of the proposed method, the following comparative approaches are selected.

(1)

Prior Feature-based Support Vector Machine (PF-SVM): Computes prior features from training data using Table 1 and feeds them into an SVM for classification.

(2)

Deep Convolutional Neural Network (DCNN): A 7-layer CNN directly processes raw vibration data to output classification results.

(3)

Multi-Scale Deep Convolutional Neural Network (MSDCNN): A CNN with the architecture in Table 2; for classification, the data features in different layers are fused.

(4)

Multi-Scale CNN with Prior Features (MCNNPF): A CNN with the architecture in Table 2 used for abstract features’ extraction; the prior features from Table 1 are fused with abstract features using simple averaging.

(5)

Few-Shot Fault Diagnosis via Data Augmentation (MGAN) [29]: This method augments fault data using a generative adversarial network (GAN) and trains a diagnostic model on the augmented dataset.

(6)

Contrastive Learning-based Few-Shot Diagnosis (CNET) [30]: This method extracts discriminative features from limited data using contrastive learning.

(7)

Local and Global Attention-augmented Network (LGAAN) [31]: A network augmented by an attention mechanism based on the fusion of global and local features. It can achieve image classification with few samples in computer vision. We modified the backbone of the network from two-dimensional convolution to one-dimensional convolution to realize the classification of vibration signals.

All experiments are conducted on a 64-bit Windows 10 computer with an Intel Core i3-4170 @3.70GHz CPU. The implementation uses Python 3.6.12 and Keras 2.2.4. Each experiment is repeated 10 times, with averaged results reported. The evaluation metrics include classification accuracy and F1 score.

4.3. Diagnostic Results Under Few-Shot Conditions

To evaluate the proposed method’s performance in few-shot scenarios, we sequentially and randomly selected 4, 8, 16, 32, 64, and 128 samples from each health condition’s data as training data for the diagnostic model, while all remaining data samples were used as test data for the model. Even with 128 training samples (less than 10% of the total 1500 samples per class), the scenario remains few-shot. The diagnostic accuracy and F1-score of the proposed method and comparative approaches are summarized in

Table 3. Fault diagnosis accuracy under small samples using SQ data.

Model	Number of Training Samples
	4	8	16	32	64	128
PF-SVM	0.5343 ± 0.04	0.6346 ± 0.05	0.7467 ± 0.05	0.7676 ± 0.02	0.7979 ± 0.02	0.8035 ± 0.01
DCNN	0.5826 ± 0.03	0.7579 ± 0.05	0.8610 ± 0.02	0.9243 ± 0.02	0.9540 ± 0.03	0.9670 ± 0.02
MSDCNN	0.7113 ± 0.01	0.7679 ± 0.05	0.9146 ± 0.04	0.9436 ± 0.04	0.9623 ± 0.03	0.9682 ± 0.02
MCNNPF	0.7276 ± 0.03	0.7715 ± 0.03	0.9346 ± 0.03	0.9587 ± 0.03	0.9721 ± 0.02	0.9834 ± 0.02
MGAN	0.6125 ± 0.02	0.7530 ± 0.03	0.9329 ± 0.02	0.9617 ± 0.03	0.9776 ± 0.02	0.9809 ± 0.02
CNET	0.6568 ± 0.04	0.7854 ± 0.04	0.9113 ± 0.06	0.9585 ± 0.04	0.9676 ± 0.04	0.9750 ± 0.02
LGAAN	0.6945 ± 0.03	0.7392 ± 0.04	0.9041 ± 0.02	0.9574 ± 0.02	0.9748 ± 0.02	0.9705 ± 0.01
Proposed	0.7382 ± 0.02	0.8041 ± 0.03	0.9540 ± 0.04	0.9835 ± 0.01	0.9857 ± 0.01	0.9880 ± 0.01

and

Table 4. Fault diagnosis F1-scores using a small number of samples and SQ data.

Model	Number of Training Samples
	4	8	16	32	64	128
PF-SVM	0.5221 ± 0.04	0.6378 ± 0.04	0.7452 ± 0.04	0.7664 ± 0.02	0.7967 ± 0.02	0.8018 ± 0.01
DCNN	0.5842 ± 0.03	0.7591 ± 0.04	0.8608 ± 0.02	0.9231 ± 0.02	0.9525 ± 0.03	0.9665 ± 0.01
MSDCNN	0.7105 ± 0.01	0.7684 ± 0.04	0.9139 ± 0.05	0.9422 ± 0.04	0.9615 ± 0.03	0.9675 ± 0.02
MCNNPF	0.7312 ± 0.03	0.7748 ± 0.03	0.9359 ± 0.03	0.9593 ± 0.03	0.9716 ± 0.02	0.9827 ± 0.02
MGAN	0.6137 ± 0.02	0.7528 ± 0.03	0.9331 ± 0.02	0.9612 ± 0.02	0.9768 ± 0.02	0.9811 ± 0.02
CNET	0.6581 ± 0.04	0.7849 ± 0.03	0.9107 ± 0.04	0.9571 ± 0.04	0.9662 ± 0.04	0.9748 ± 0.02
LGAAN	0.6938 ± 0.03	0.7401 ± 0.04	0.9035 ± 0.02	0.9569 ± 0.02	0.9742 ± 0.02	0.9698 ± 0.01
Proposed	0.7365 ± 0.02	0.8032 ± 0.03	0.9536 ± 0.03	0.9827 ± 0.01	0.9854 ± 0.01	0.9878 ± 0.01

.

From Table 3 and Table 4, the proposed method demonstrates significant advantages over comparative approaches in few-shot gearbox fault diagnosis. The key conclusions can be summarized as follows. (1) PF-SVM maintains relatively stable accuracy and F1-score even with minimal training samples, demonstrating the reliability of prior features in fault identification under data scarcity. (2) Compared to DCNN, MSDCNN, which incorporates multi-level abstract feature fusion, demonstrates significant performance advantages. (3) The proposed method outperforms MCNNPF in diagnostic performance, indicating that the hierarchical attention-based feature weighting fusion approach is more effective than simple averaging for feature fusion. (4) Compared to state-of-the-art fault diagnosis methods (MGAN and CNET) and the few-shot learning approach LGAAN from the computer vision domain, the proposed method achieves the highest diagnostic accuracy, validating its superiority in few-shot fault diagnosis scenarios.

Figure 7 displays the confusion matrix of the proposed method and related methods under the 16-sample training condition. Additionally, t-SNE is employed to reduce the dimensionality of fault features learned by different methods to 2D for visualization, as shown in Figure 8. The visualization results provide qualitative evidence of the diagnostic model’s feature extraction capability.

The feature visualization in Figure 8 further reveals the following. (1) Comparative methods exhibit overlapping feature clusters under limited training samples, leading to ambiguous fault separation. (2) Qualitatively, the proposed method demonstrates superior feature extraction capability compared to both baseline methods and state-of-the-art models. The extracted features exhibit enhanced inter-class separability and feature discriminability, substantiating that the fused features can more comprehensively characterize fault states. These results collectively prove that the data–knowledge dual-driven fusion paradigm enables robust feature learning from scarce samples, effectively addressing the generalization challenges of purely data-driven models.

Furthermore, Figure 7 and Figure 8 reveal that the diagnostic models demonstrate superior recognition performance for certain fault types (e.g., planetary gear cracks) compared to others. This enhanced performance may stem from either more distinctive fault characteristics or more pronounced severity variations specific to this fault type. Conversely, the model exhibits relatively lower identification accuracy for sun gear pitting faults. The feature visualization results further confirm that different severity levels of sun gear pitting are more challenging to distinguish compared to other fault types.

In Figure 9, we present the training process of the proposed method, including the changes in loss value and classification accuracy with the training of the model. It can be observed that as the training progresses, the loss value of the proposed method gradually decreases and eventually converges. After the training is completed, the classification accuracy of the proposed method on the training data (16 training samples) reaches 1.0, and the classification accuracy on the test data reaches 0.9580.

4.4. Robustness Analysis Against Noise

In real-world scenarios, vibration data collected from gearboxes are often contaminated by strong background noise, which may obscure fault-related signatures and further complicate fault diagnosis. Thus, noise robustness is a critical metric for evaluating the effectiveness of gearbox fault diagnosis methods.

To simulate realistic noise conditions, Gaussian noise with varying intensities was artificially added to the experimental data. Specifically, noise levels were quantified by signal-to-noise ratio (SNR), with tested SNR values of 0 dB, 5 dB, 10 dB, 15 dB, and 20 dB. Using 128 samples for training, the diagnostic accuracies of the proposed and comparative methods under different noise levels are illustrated in Figure 10. The feature visualization results under different noise levels are shown in Figure 11.

From Figure 10, we can draw the following conclusions. (1) All methods exhibit declining accuracy with increasing noise intensity. (2) The proposed method consistently achieves the highest accuracy across all noise levels. Notably, even under extreme noise (SNR = 0 dB), it attains an accuracy of 0.7870 with minimal training samples. Comparative methods show significant performance degradation, highlighting their sensitivity to noise. These results demonstrate that the proposed method is more suitable for processing noisy vibration data and more adept at identifying fault states in noisy environments compared to existing approaches. The integration of prior knowledge mitigates noise interference by reinforcing physically meaningful features.

5. Effectiveness Analysis Based on THU Gearbox Fault Dataset

5.1. Gearbox Experimental Dataset and Diagnostic Scenarios

The Tsinghua University Gearbox Fault Dataset (THU Dataset) is adopted for further validation of the proposed method. This dataset was collected from a gearbox fault testbed comprising a motor, a two-stage gearbox, a magnetic particle brake, vibration accelerometers, and a data acquisition system. During experiments, the motor speed was set to 1000 rpm, 2000 rpm, and 3000 rpm, with loads of 10 Nm and 20 Nm. The sampling frequency was 12.8 kHz. Since the proposed method focuses on few-shot fault diagnosis rather than variable operating conditions, vibration data under a constant operating condition (3000 rpm, 10 Nm) are selected for analysis. For dataset details, refer to https://github.com/liuzy0708/MCC5-THU-Gearbox-Benchmark-Datasets, accessaed on 20 March 2025).

The THU dataset includes the following gearbox health states: (1) Normal condition (NC-0); (2) Minor gear crack (GC-1); (3) Severe gear crack (GC-2); (4) Minor gear wear (GW-1); (5) Severe gear wear (GW-2); (6) Minor gear tooth breakage (GF-1); (7) Severe gear tooth breakage (GF-2); (8) Minor gear pitting (GP-1); and (9) Severe gear pitting (GP-2). The corresponding vibration signal can be seen in Figure 12. After data integration and segmentation, 500 samples per health state are obtained, with each sample containing 1024 vibration data points. This dataset is used to further validate the proposed method.

Parameter settings and comparative methods remain identical to those in the SQ gear fault experiments (Section 4.2). Each experiment is repeated 10 times, with averaged results reported.

5.2. Fault Diagnosis Results Under Few-Shot Conditions

To further verify the proposed method’s performance, 4, 8, 16, 32, 64, and 128 samples per health state are randomly selected from the THU dataset for training, with the remaining samples used for testing. Diagnostic accuracy and F1-score are summarized in

Table 5. Fault diagnosis accuracy with a small number of samples using THU data.

Model	Number of Training Samples
	4	8	16	32	64	128
PF-SVM	0.4635 ± 0.05	0.5734 ± 0.04	0.6435 ± 0.04	0.7951 ± 0.02	0.8234 ± 0.02	0.8474 ± 0.01
DCNN	0.4367 ± 0.03	0.6893 ± 0.04	0.8326 ± 0.02	0.8942 ± 0.02	0.9632 ± 0.02	0.9744 ± 0.02
MSDCNN	0.5826 ± 0.05	0.7257 ± 0.05	0.9036 ± 0.04	0.9142 ± 0.03	0.9725 ± 0.03	0.9757 ± 0.01
MCNNPF	0.6062 ± 0.04	0.7381 ± 0.03	0.9183 ± 0.03	0.9295 ± 0.02	0.9748 ± 0.02	0.9772 ± 0.01
MGAN	0.6564 ± 0.03	0.7837 ± 0.03	0.9239 ± 0.02	0.9520 ± 0.03	0.9731 ± 0.02	0.9802 ± 0.02
CNET	0.7029 ± 0.04	0.8328 ± 0.03	0.9421 ± 0.04	0.9573 ± 0.04	0.9748 ± 0.03	0.9878 ± 0.02
LGAAN	0.7475 ± 0.04	0.8634 ± 0.02	0.9503 ± 0.02	0.9707 ± 0.02	0.9800 ± 0.01	0.9908 ± 0.01
Proposed	0.7524 ± 0.03	0.8722 ± 0.03	0.9682 ± 0.03	0.9819 ± 0.01	0.9903 ± 0.01	0.9945 ± 0.01

and

Table 6. Fault diagnosis F1-score with a small number of samples using THU data.

Model	Number of Training Samples
	4	8	16	32	64	128
PF-SVM	0.4768 ± 0.04	0.5716 ± 0.04	0.6452 ± 0.03	0.7939 ± 0.02	0.8222 ± 0.02	0.8463 ± 0.01
DCNN	0.4389 ± 0.03	0.6905 ± 0.03	0.8314 ± 0.02	0.8930 ± 0.02	0.9620 ± 0.02	0.9732 ± 0.01
MSDCNN	0.5843 ± 0.04	0.7242 ± 0.05	0.9029 ± 0.04	0.9135 ± 0.03	0.9718 ± 0.03	0.9752 ± 0.01
MCNNPF	0.6154 ± 0.04	0.7452 ± 0.03	0.9257 ± 0.03	0.9351 ± 0.02	0.9683 ± 0.02	0.9836 ± 0.01
MGAN	0.6542 ± 0.03	0.7854 ± 0.03	0.9241 ± 0.02	0.9517 ± 0.03	0.9725 ± 0.02	0.9798 ± 0.02
CNET	0.7015 ± 0.03	0.8331 ± 0.03	0.9417 ± 0.04	0.9569 ± 0.02	0.9742 ± 0.03	0.9865 ± 0.02
LGAAN	0.7532 ± 0.04	0.8589 ± 0.02	0.9457 ± 0.02	0.9763 ± 0.02	0.9835 ± 0.01	0.9884 ± 0.01
Proposed	0.7541 ± 0.03	0.8719 ± 0.03	0.9675 ± 0.02	0.9821 ± 0.02	0.9907 ± 0.01	0.9943 ± 0.01

.

Figure 13 displays the confusion matrix of the proposed method and comparative methods under the 16-sample training condition. Feature visualizations of the proposed and comparative methods are shown in Figure 14. The results demonstrate that the proposed method achieves superior performance across all tasks, with both higher diagnostic accuracy and a higher F1-score. For instance, with only four training samples, the proposed method attains 0.7524 accuracy, outperforming CNET (0.7029), MGAN (0.6564) and LGAAN (0.7475). This confirms the method’s effectiveness in addressing gearbox fault diagnosis in conditions of extreme data scarcity.

The visualized features in Figure 14 reveal that the proposed method generates distinct clusters for different fault types (e.g., a clear separation between GF-1 and GF-2), whereas comparative methods exhibit overlapping distributions. This further validates that the data–knowledge dual-driven fusion enables robust and discriminative feature learning, making the method particularly suitable for real-world scenarios with limited fault samples.

6. Conclusions

This study proposes a hierarchical attention-guided data–knowledge dual-driven fusion network for intelligent gearbox fault diagnosis under few-shot conditions. The method constructs prior features of gearbox vibration data using domain knowledge. A deep convolutional neural network is employed to hierarchically extract abstract features from vibration signals, further refining fault representation. Through a hierarchical attention module, adaptive fusion of prior and abstract features is realized via layer-wise weight allocation, enabling accurate fault identification. Experimental validation on two gearbox fault datasets demonstrates that the proposed method achieves higher diagnostic accuracy with fewer training samples, while exhibiting notable noise robustness. These results confirm the superiority of integrating domain knowledge with data-driven learning to overcome the limitations of purely data-driven models in few-shot scenarios.

Future work will primarily focus on integrating additional forms of domain knowledge into the diagnostic framework to further enhance generalization capability under few-shot conditions. Additionally, investigating the interpretability of intelligent diagnostic models and conducting rigorous analysis of model misdiagnoses will contribute to further improving diagnostic performance. Ultimately, extending the proposed method to cross-domain fault diagnosis and real-time industrial applications will represent a crucial research direction for advancing intelligent maintenance systems.