Data-Driven Digital Twin Framework for Predictive Maintenance of Smart Manufacturing Systems
Abstract
1. Introduction
2. Methods
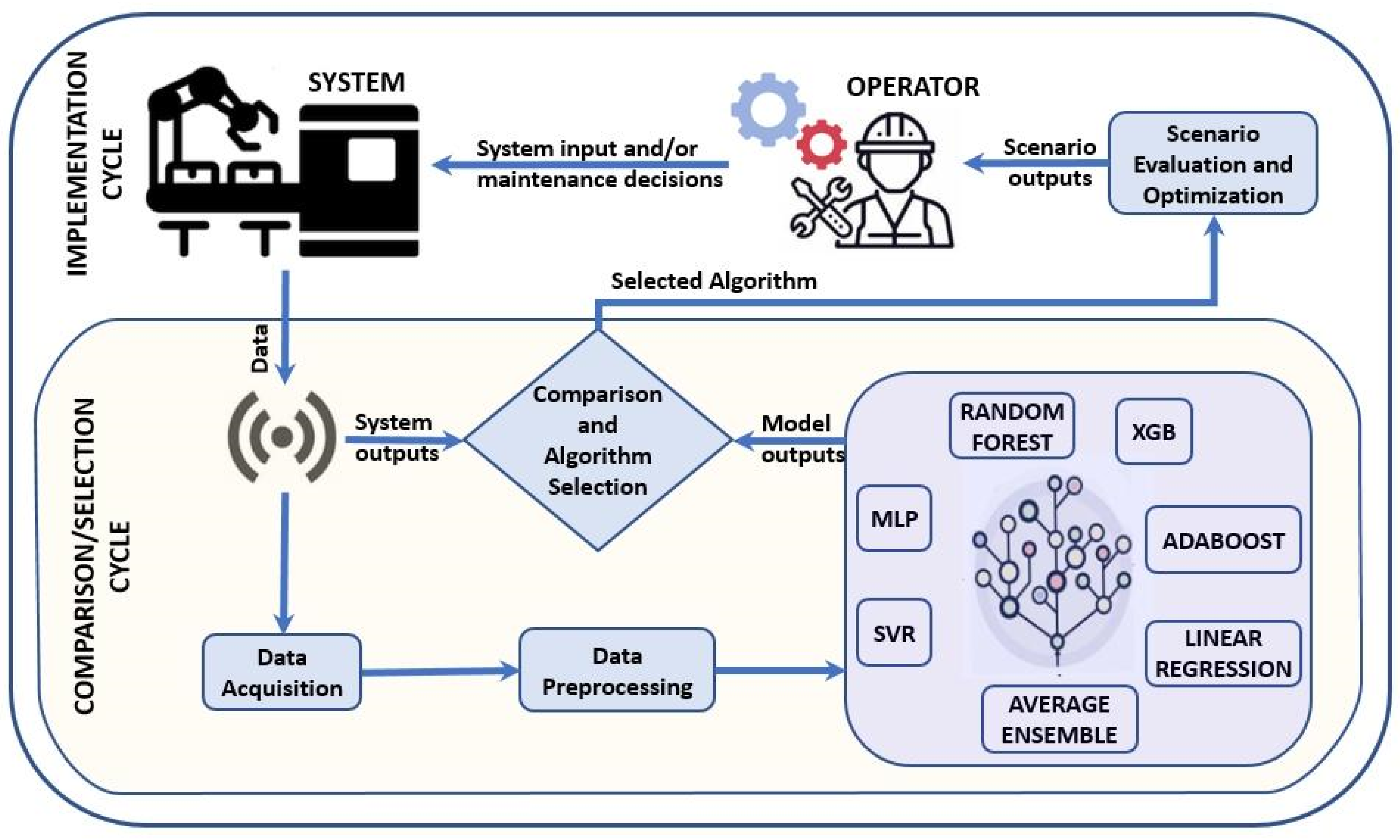
2.1. Framework Development
2.1.1. Maintenance System Architecture
2.1.2. Implementation of the Proposed System Architecture
2.1.3. Training and Testing of ML Models
2.2. Data-Driven Predictive Models
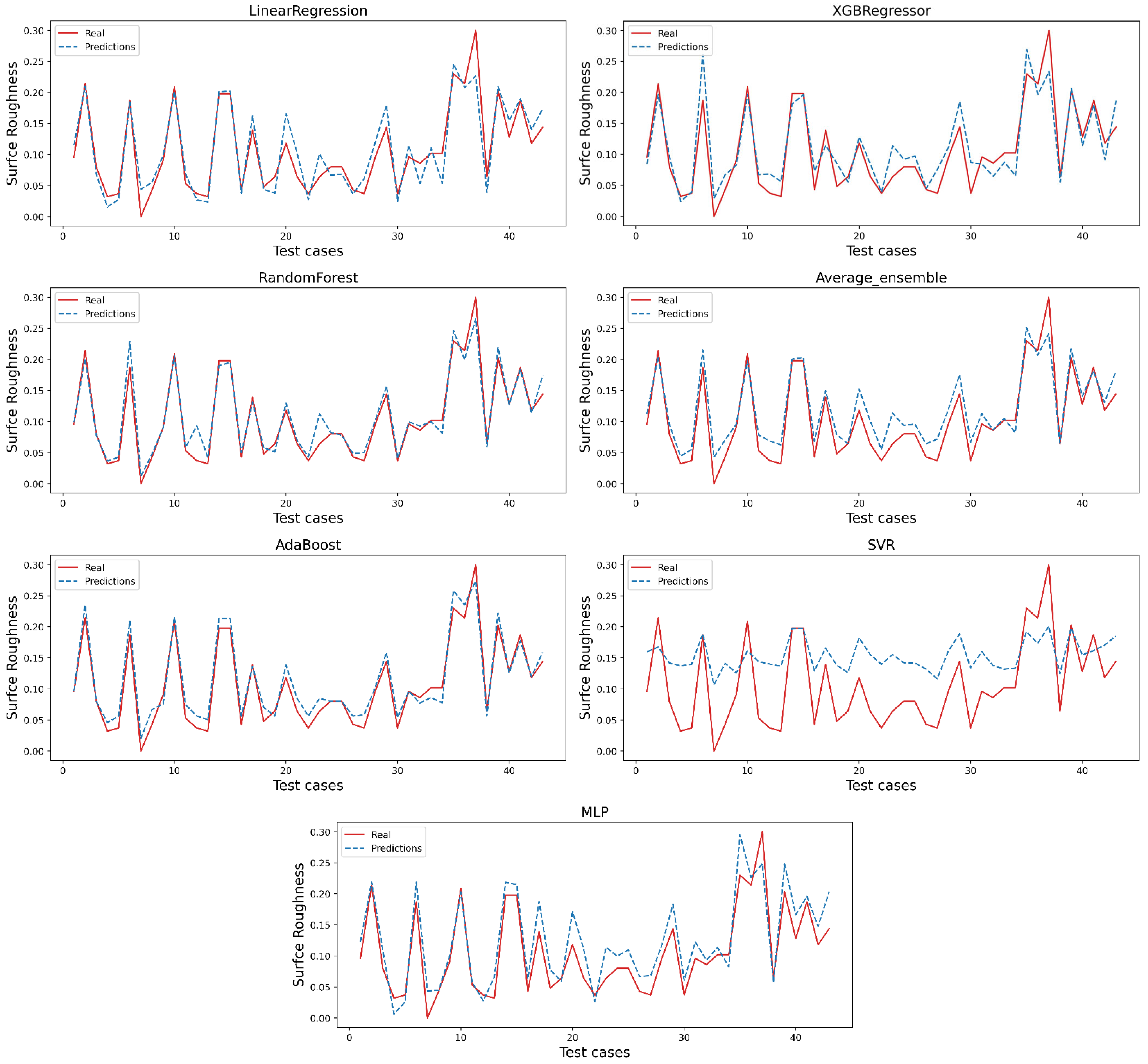
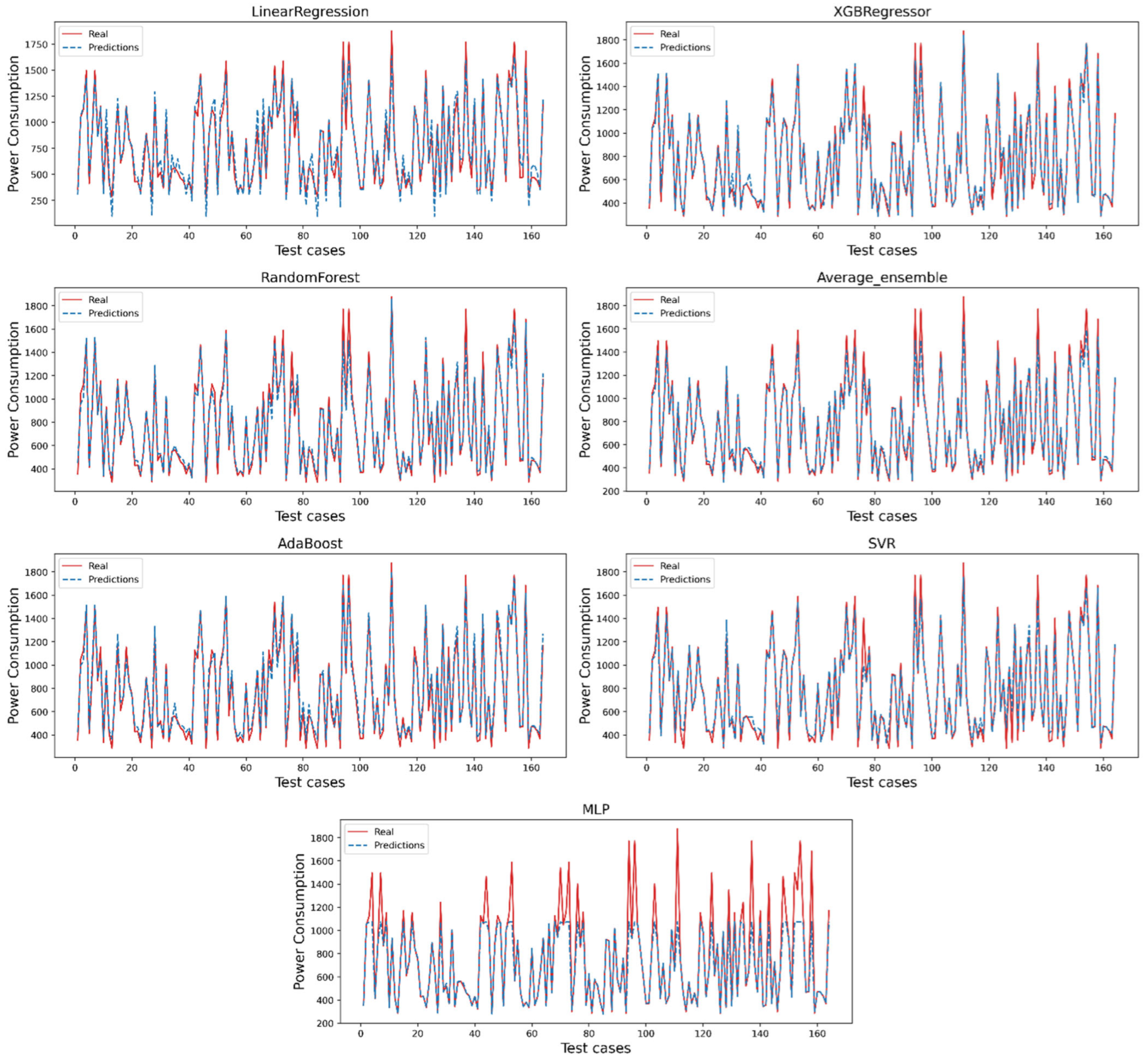
3. Results
4. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Javaid, M.; Haleem, A.; Singh, R.P.; Suman, R.; Gonzalez, E.S. Understanding the adoption of Industry 4.0 technologies in improving environmental sustainability. Sustain. Oper. Comput. 2022, 3, 203–217. [Google Scholar] [CrossRef]
- Hulbert, S.; Mollan, C.; Pandey, V. Fault Diagnosis and Prediction in Automotive Systems with Real-Time Data Using Machine Learning. SAE Tech. Pap. 2022-01-0217 2022. [Google Scholar] [CrossRef]
- Slon, C.; Pandey, V.; Kassoumeh, S. Mixture distributions in autonomous decision-making for industry 4.0. SAE Int. J. Mater. Manuf. 2019, 12, 135–148. [Google Scholar] [CrossRef]
- SCOOP [Internet]. Tessenderlo, Limburg. 2022. Available online: https://www.i-scoop.eu/industry-4-0/ (accessed on 3 July 2024).
- Slon, C.; Pandey, V. Enabling autonomous decision-making in manufacturing systems through preference fusion. SAE Int. J. Mater. Manuf. 2020, 13, 109–124. [Google Scholar] [CrossRef]
- Monostori, L.; Kádár, B.; Bauernhansl, T.; Kondoh, S.; Kumara, S.; Reinhart, G.; Sauer, O.; Schuh, G.; Sihn, W.; Ueda, K. Cyber-physical systems in manufacturing. Cirp Ann. 2016, 65, 621–641. [Google Scholar] [CrossRef]
- Schmitt, R.; Permin, E.; Kerkhoff, J.; Plutz, M.; Böckmann, M.G. Enhancing resiliency in production facilities through cyber physical systems. Ind. Internet Things Cybermanuf. Syst. 2017, 287–313. [Google Scholar] [CrossRef]
- Khan, U.; Haleem, A. Smart organisations: Modelling of enablers using an integrated ISM and fuzzy-MICMAC approach. Int. J. Intell. Enterp. 2012, 1, 248–269. [Google Scholar] [CrossRef]
- Presciuttini, A.; Portioli-Staudacher, A. Applications of IoT and Advanced Analytics for manufacturing operations: A systematic literature review. Procedia Comput. Sci. 2024, 232, 327–336. [Google Scholar] [CrossRef]
- Khan, U.; Haleem, A. Improving to smart organization: An integrated ISM and fuzzy-MICMAC modelling of barriers. J. Manuf. Technol. Manag. 2015, 26, 807–829. [Google Scholar] [CrossRef]
- Canziani, A.; Paszke, A.; Culurciello, E. An analysis of deep neural network models for practical applications. arXiv 2016, arXiv:1605.07678. [Google Scholar] [CrossRef]
- Liu, C.; Jiang, P.; Jiang, W. Web-based digital twin modeling and remote control of cyber-physical production systems. Robot. Comput.-Integr. Manuf. 2020, 64, 101956. [Google Scholar] [CrossRef]
- Qamsane, Y.; Chen, C.Y.; Balta, E.C.; Kao, B.-C.; Mohan, S.; Moyne, J.; Tilbury, D.; Barton, K. A Unified Digital Twin Framework for Real-Time Monitoring and Evaluation of Smart Manufacturing Systems. In Proceedings of the 2019 IEEE 15th International Conference on Automation Science and Engineering (CASE), IEEE, Vancouver, BC, Canada, 22–26 August 2019; pp. 1394–1401. [Google Scholar] [CrossRef]
- Kessels, B.M.; Fey, R.H.; van de Wouw, N. Real-time parameter updating for nonlinear digital twins using inverse mapping models and transient-based features. Nonlinear Dyn. 2023, 111, 10255–10285. [Google Scholar] [CrossRef]
- Rojek, I.; Jasiulewicz-Kaczmarek, M.; Piechowski, M.; Mikołajewski, D. An artificial intelligence approach for improving maintenance to supervise machine failures and support their repair. Appl. Sci. 2023, 13, 4971. [Google Scholar] [CrossRef]
- Blume, C.; Blume, S.; Thiede, S.; Herrmann, C. Data-driven digital twins for technical building services operation in factories: A cooling tower case study. J. Manuf. Mater. Process. 2020, 4, 97. [Google Scholar] [CrossRef]
- Liu, D.; Du, Y.; Chai, W.; Lu, C.; Cong, M. Digital twin and data-driven quality prediction of complex die-casting manufacturing. IEEE Trans. Ind. Inform. 2022, 18, 8119–8128. [Google Scholar] [CrossRef]
- Akinsolu, M.O.; Zribi, K. A generalized framework for adopting regression-based predictive modeling in manufacturing environments. Inventions 2023, 8, 32. [Google Scholar] [CrossRef]
- Xu, Y.; Qamsane, Y.; Puchala, S.; Januszczak, A.; Tilbury, D.M.; Barton, K. A data-driven approach toward a machine-and system-level performance monitoring digital twin for production lines. Comput. Ind. 2024, 157, 104086. [Google Scholar] [CrossRef]
- Rathore, M.M.; Shah, S.A.; Shukla, D.; Bentafat, E.; Bakiras, S. The role of ai, machine learning, and big data in digital twinning: A systematic literature review, challenges, and opportunities. IEEE Access 2021, 9, 32030–32052. [Google Scholar] [CrossRef]
- Wang, P.; Luo, M. A digital twin-based big data virtual and real fusion learning reference framework supported by industrial internet towards smart manufacturing. J. Manuf. Syst. 2021, 58, 16–32. [Google Scholar] [CrossRef]
- Aivaliotis, P.; Georgoulias, K.; Chryssolouris, G. The use of Digital Twin for predictive maintenance in manufacturing. Int. J. Comput. Integr. Manuf. 2019, 32, 1067–1080. [Google Scholar] [CrossRef]
- Ho, S.L.; Xie, M.; Goh, T.N. A comparative study of neural network and Box-Jenkins ARIMA modeling in time series prediction. Comput. Ind. Eng. 2002, 42, 371–375. [Google Scholar] [CrossRef]
- Ran, Y.; Zhou, X.; Lin, P.; Wen, Y.; Deng, R. A Survey of Predictive Maintenance: Systems, Purposes and Approaches. arXiv 2019, arXiv:1912.07383. [Google Scholar] [CrossRef]
- Papacharalampopoulos, A.; Michail, C.K.; Stavropoulos, P. Manufacturing resilience and agility through processes digital twin: Design and testing applied in the LPBF case. Procedia Cirp 2021, 103, 164–169. [Google Scholar] [CrossRef]
- Khazraei, K.; Deuse, J. A strategic standpoint on maintenance taxonomy. J. Facil. Manag. 2011, 9, 96–113. [Google Scholar] [CrossRef]
- Yu, W.; Dillon, T.; Mostafa, F.; Rahayu, W.; Liu, Y. A global manufacturing big data ecosystem for fault detection in predictive maintenance. IEEE Trans. Ind. Inform. 2019, 16, 183–192. [Google Scholar] [CrossRef]
- Sakib, N.; Wuest, T. Challenges and opportunities of condition-based predictive maintenance: A review. Procedia Cirp 2018, 78, 267–272. [Google Scholar] [CrossRef]
- He, Y.; Gu, C.; Chen, Z.; Han, X. Integrated predictive maintenance strategy for manufacturing systems by combining quality control and mission reliability analysis. Int. J. Prod. Res. 2017, 55, 5841–5862. [Google Scholar] [CrossRef]
- Hosseinzadeh, A.; Chen, F.F.; Shahin, M.; Bouzary, H. A predictive maintenance approach in manufacturing systems via AI-based early failure detection. Manuf. Lett. 2023, 35, 1179–1186. [Google Scholar] [CrossRef]
- Garcia, M.C.; Sanz-Bobi, M.A.; Del Pico, J. SIMAP: Intelligent System for Predictive Maintenance: Application to the health condition monitoring of a windturbine gearbox. Comput. Ind. 2006, 57, 552–568. [Google Scholar] [CrossRef]
- Akhavei Bleicher, F. Predictive Modeling to Increase the Reliability of Production Planning in Single-Item Production. In Proceedings of the World Congress on Engineering and Computer Science 2016, San Francisco, CA, USA, 19–21 October 2016; Volume II, pp. 806–811. [Google Scholar]
- Lee, J.; Davari, H.; Singh, J.; Pandhare, V. Industrial Artificial Intelligence for industry 4.0-based manufacturing systems. Manuf. Lett. 2018, 18, 20–23. [Google Scholar] [CrossRef]
- Rahman, M.S.; Ghosh, T.; Aurna, N.F.; Kaiser, M.S.; Anannya, M.; Hosen, A.S. Machine learning and internet of things in industry 4.0: A review. Meas. Sens. 2023, 28, 100822. [Google Scholar] [CrossRef]
- De Simone, V.; Di Pasquale, V.; Miranda, S. An overview on the use of AI/ML in manufacturing MSMEs: Solved issues, limits, and challenges. Procedia Comput. Sci. 2023, 217, 1820–1829. [Google Scholar] [CrossRef]
- Canal, A.D.; Borille, A.V. CNC Turning: Roughness, Forces and Tool Wear [Dataset]. 2021 [Cited 2022]. In Kaggle [Internet]. [CrossRef]
- Plevris, V.; Solorzano, G.; Bakas, N.P.; Ben Seghier, M.E. Investigation of Performance Metrics in Regression Analysis and Machine Learning-Based Prediction Models. In Proceedings of the 8th European Congress on Computational Methods in Applied Sciences and Engineering (ECCOMAS Congress 2022), Oslo, Norway, 5–9 June 2022. [Google Scholar] [CrossRef]
- Mienye, I.D.; Sun, Y. A survey of ensemble learning: Concepts, algorithms, applications, and prospects. IEEE Access 2022, 10, 99129–99149. [Google Scholar] [CrossRef]
- Chicco, D.; Warrens, M.J.; Jurman, G. The coefficient of determination R-squared is more informative than SMAPE, MAE, MAPE, MSE and RMSE in regression analysis evaluation. Peerj Comput. Sci. 2021, 7, e623. [Google Scholar] [CrossRef]
- Willmott, C.J.; Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE)?—Arguments against avoiding RMSE in the literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef]
- Kim, S.; Kim, H. A new metric of absolute percentage error for intermittent demand forecasts. Int. J. Forecast. 2016, 32, 669–679. [Google Scholar] [CrossRef]
- Das, B.R.; Resnick, S.I. QQ plots, random sets and data from a heavy tailed distribution. Stoch. Models 2008, 24, 103–132. [Google Scholar] [CrossRef]


| Model | Tuning Method | Best Parameters |
|---|---|---|
| Linear Regression | Ridge Regression | {‘alpha’: 1, ‘fit_intercept’: True, ‘solver’: ‘auto’} |
| XGB Regressor | Randomized Search | {‘colsample_bytree’: 0.78, ‘gamma’: 0.007, ‘learning_rate’: 0.29, ‘max_depth’: 8, ‘n_estimators’: 341, ‘subsample’: 0.75} |
| Random Forest Regressor | Grid Search | {‘max_depth’: None, ‘max_features’: ‘log2’, ‘min_samples_leaf’: 1, ‘min_samples_split’: 5, ‘n_estimators’: 100} |
| AdaBoost Regressor | Grid Search | {‘estimator__max_depth’: 3, ‘learning_rate’: 1.0, ‘loss’: ‘square’, ’n_estimators’: 50 |
| SVR | Randomized Search | {‘C’: 1.03, ‘epsilon’: 0.105, ‘gamma’: ‘scale’, ‘kernel’: ‘rbf’ |
| MLP | Randomized Search | {‘activation’: ‘tanh’, ‘alpha’: 0.00208, ‘batch_size’: 128, ‘hidden_layer_sizes’: (50, 50), ‘learning_rate_init’: 0.0619} |
| Model | Tuning Method | Best Parameters |
|---|---|---|
| Linear Regression | Ridge Regression | {‘alpha’: 0.01, ‘fit_intercept’: True, ‘solver’: ‘svd’} |
| XGB Regressor | Randomized Search | {learning_rate = 0.29, max_depth = 8, n_estimators = 341, subsample = 0.75, colsample_bytree = 0.78, gamma = 0.007} |
| Random Forest Regressor | Grid Search | {‘estimator__max_depth’: 3, ‘learning_rate’: 1.0, ‘loss’: ‘square’, ‘n_estimators’: 200} |
| AdaBoost Regressor | Grid Search | {‘estimator__max_depth’: 3, ‘learning_rate’: 1.0, ‘loss’: ‘square’, ‘n_estimators’: 50} |
| SVR | Randomized Search | {‘C’: 98.96484985318548, ‘epsilon’: 0.03416347415306914, ‘gamma’: ‘auto’, ‘kernel’: ‘rbf’} |
| MLP | Randomized Search | {‘activation’: ‘logistic’, ‘alpha’: 0.010151348978007608, ‘batch_size’: 32, ‘hidden_layer_sizes’: (50, 50), ‘learning_rate_init’: 0.015226341829186325} |
| ML Algorithm | MAPE | RMSE | ||
|---|---|---|---|---|
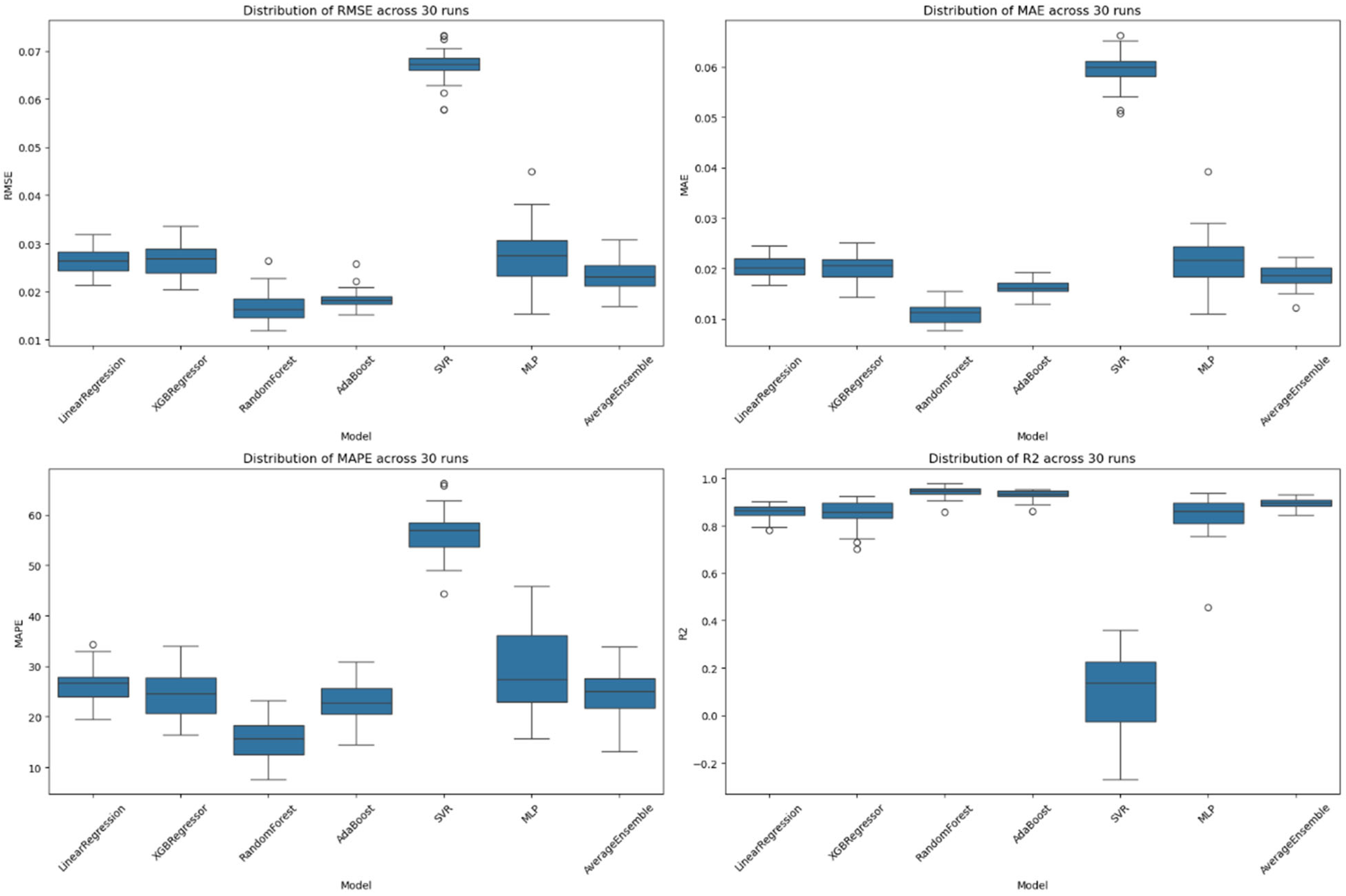
| Linear Regression | 0.020 ± 0.002 | 26.5% ± 3.4% | 0.027 ± 0.003 | 86.0% ± 2.8% |
| XGB Regressor | 0.020 ± 0.003 | 24.6% ± 4.8% | 0.027 ± 0.004 | 85.0% ± 5.3% |
| Random Forest Regressor | 0.011 ± 0.002 | 15.6% ± 4.0% | 0.017 ± 0.003 | 94.2% ± 2.4% |
| Average Ensemble | 0.016 ± 0.001 | 23.0% ± 3.8% | 0.018 ± 0.002 | 93.1% ± 2.1% |
| AdaBoost Regressor | 0.059 ± 0.003 | 56.2% ± 4.6% | 0.067 ± 0.004 | 9.7% ± 18.9% |
| SVR | 0.022 ± 0.005 | 29.4% ± 8.0% | 0.027 ± 0.006 | 84.5% ± 8.5% |
| MLP | 0.018 ± 0.002 | 24.7% ± 4.1% | 0.023 ± 0.003 | 89.4% ± 2.0% |
| Comparison | Z-Score | p-Value | Significant (p < 0.05) |
|---|---|---|---|
| Random Forest vs. Linear Regression | 12.0094 | 2.28606 × 10−17 | True |
| Random Forest vs. XGB Regressor | 8.25095 | 2.32836 × 10−11 | True |
| Random Forest vs. Average Ensemble | 8.20355 | 2.7945 × 10−11 | True |
| Random Forest vs. AdaBoost | 1.95375 | 0.055559 | False |
| Random Forest vs. SVR | 23.9245 | 9.76039 × 10−32 | True |
| Random Forest vs. MLP | 5.9513 | 1.63957 × 10−7 | True |
| ML Algorithm | MAPE | RMSE | |||
|---|---|---|---|---|---|
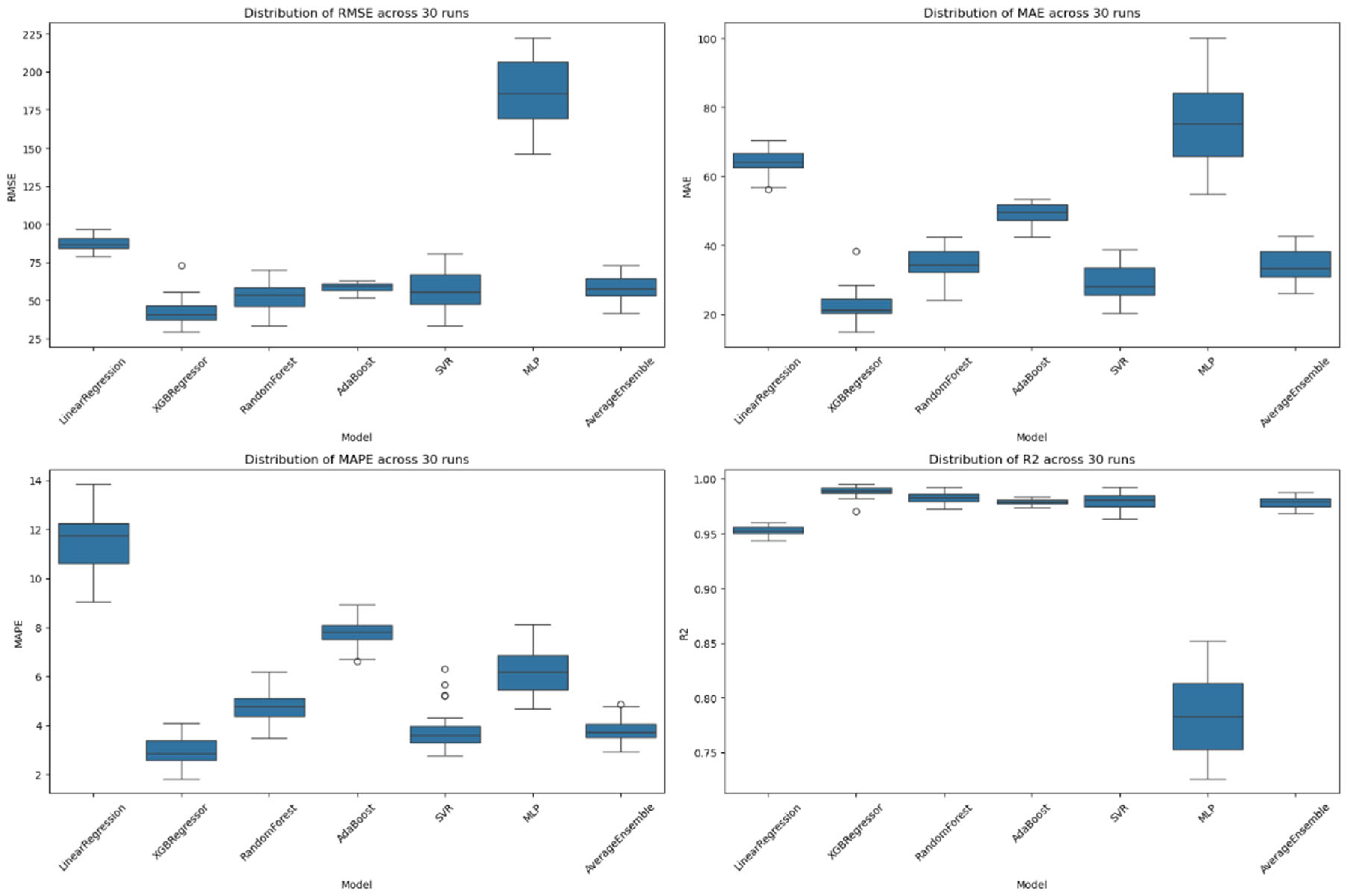
| Linear Regression | 64.076 ± 3.503 | 11.5% ± 1.2% | 87.650 ± 4.477 | 95.2% ± 0.4% | |
| XGB Regressor | 22.513 ± 4.424 | 3.0% ± 0.5% | 42.650 ± 8.933 | 98.9% ± 0.5% | |
| Random Forest Regressor | 34.959 ± 4.336 | 4.7% ± 0.6% | 52.650 ± 7.886 | 98.3% ± 0.5% | |
| Average Ensemble | 49.369 ± 3.001 | 7.8% ± 0.5% | 58.650 ± 3.119 | 97.9% ± 0.3% | |
| AdaBoost Regressor | 29.339 ± 4.861 | 3.8% ± 0.8% | 57.650 ± 11.564 | 97.9% ± 0.7% | |
| SVR | 75.970 ± 12.434 | 6.3% ± 1.0% | 186.650 ± 21.157 | 78.5% ± 3.5% | |
| MLP | 34.231 ± 4.613 | 3.8% ± 0.5% | 58.650 ± 8.667 | 97.8% ± 0.5% | |
| Comparison | Z-Score | p-Value | Significant (p < 0.05) |
|---|---|---|---|
| XGB Regressor vs. Linear Regression | 29.9667 | 5.46433 × 10−37 | True |
| XGB Regressor vs. Random Forest | 4.6573 | 1.914 × 10−5 | True |
| XGB Regressor vs. Average Ensemble | 8.20355 | 2.7945 × 10−11 | True |
| XGB Regressor vs. AdaBoost | 7.78024 | 1.09453 × 10−13 | True |
| XGB Regressor vs. SVR | 5.63292 | 5.44446 × 10−7 | True |
| XGB Regressor vs. MLP | 31.2461 | 5.55743 × 10−38 | True |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, T.; Khan, U.; Khan, A.; Mollan, C.; Morkvenaite-Vilkonciene, I.; Pandey, V. Data-Driven Digital Twin Framework for Predictive Maintenance of Smart Manufacturing Systems. Machines 2025, 13, 481. https://doi.org/10.3390/machines13060481
Khan T, Khan U, Khan A, Mollan C, Morkvenaite-Vilkonciene I, Pandey V. Data-Driven Digital Twin Framework for Predictive Maintenance of Smart Manufacturing Systems. Machines. 2025; 13(6):481. https://doi.org/10.3390/machines13060481
Chicago/Turabian StyleKhan, Tarana, Urfi Khan, Adnan Khan, Calahan Mollan, Inga Morkvenaite-Vilkonciene, and Vijitashwa Pandey. 2025. "Data-Driven Digital Twin Framework for Predictive Maintenance of Smart Manufacturing Systems" Machines 13, no. 6: 481. https://doi.org/10.3390/machines13060481
APA StyleKhan, T., Khan, U., Khan, A., Mollan, C., Morkvenaite-Vilkonciene, I., & Pandey, V. (2025). Data-Driven Digital Twin Framework for Predictive Maintenance of Smart Manufacturing Systems. Machines, 13(6), 481. https://doi.org/10.3390/machines13060481







