Machining Process Optimization Using a Model Based on Criterial Functional Dependence
Abstract
1. Introduction
2. State of the Art
3. Materials and Methods
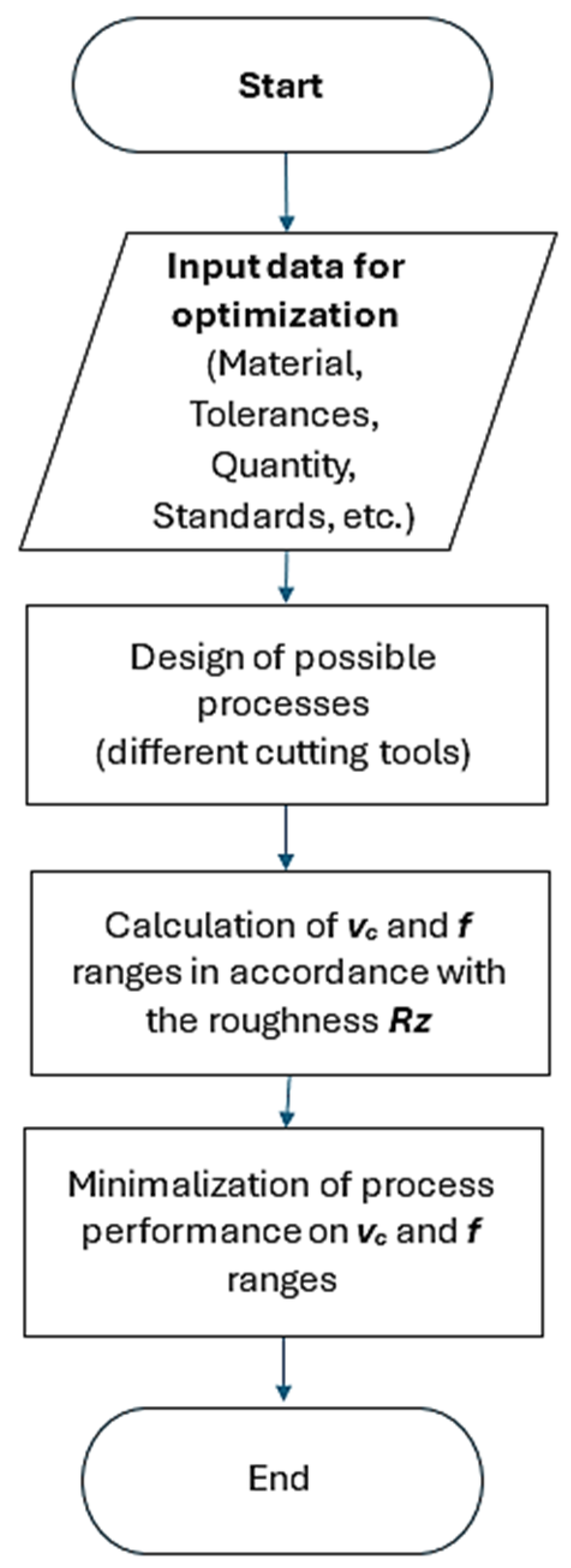
3.1. Methodology
- Qualitative characteristics—conditions determined by the production drawing (type of material, required tolerances and surface roughness), qualitative characteristics of technologies, personnel qualifications, …;
- Quantitative characteristics—required production quantities and productivity, available capacities (personnel, available technologies).
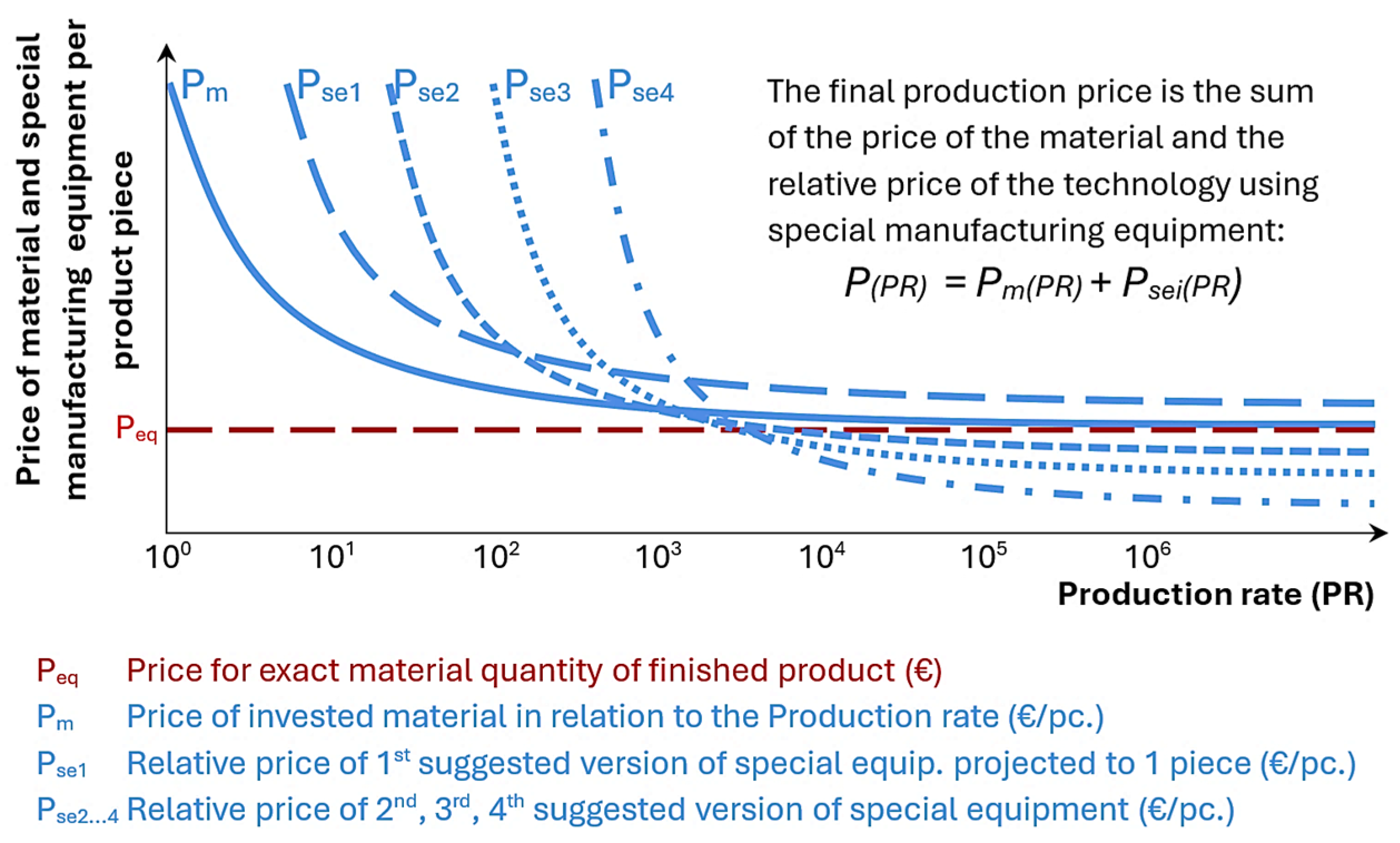
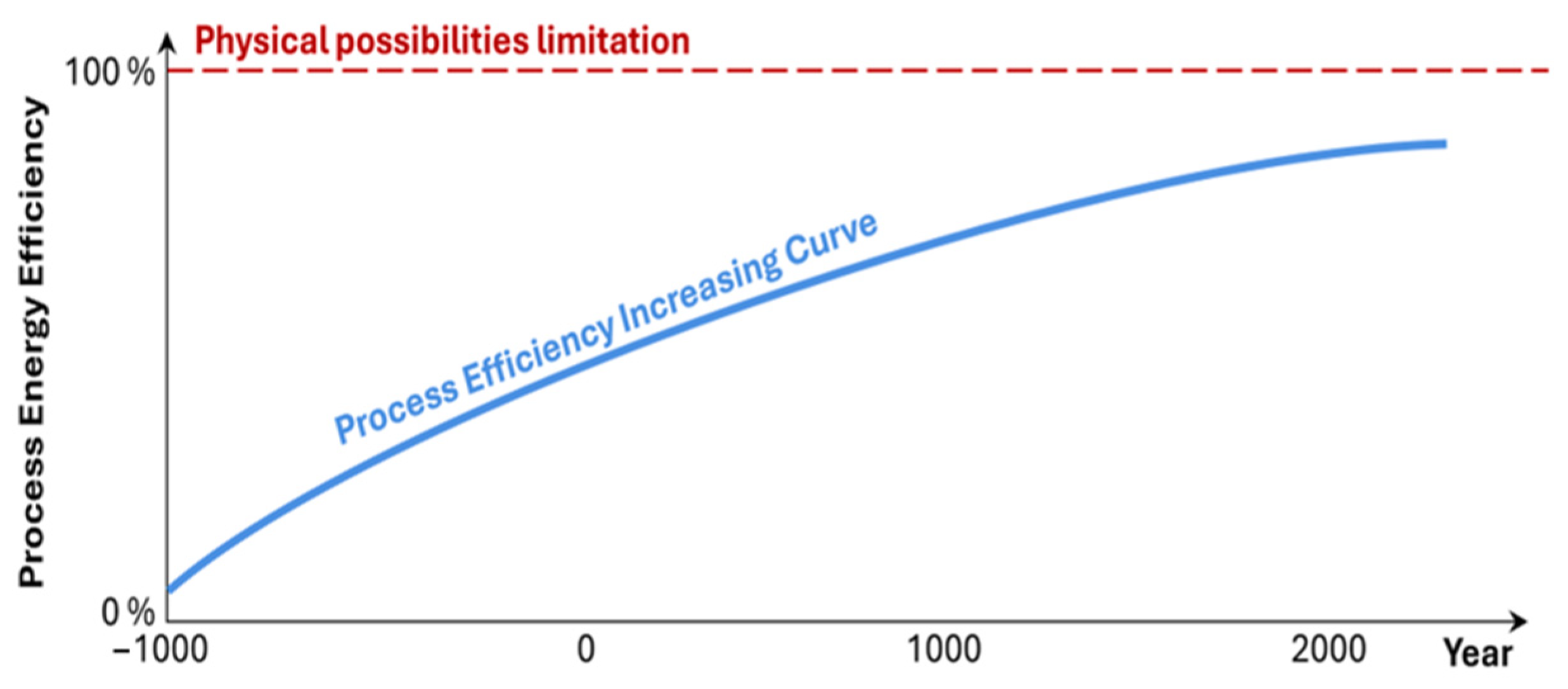
- PPE—Process Power Efficiency—expresses the efficiency of the process (a dimensionless number from 0 to a value approaching 1);
- PT—Theoretically required power to perform the process;
- PR—Real power needed to perform the process.
- Creation—primary shaping, in which a compact object is created from atomized particles, e.g., powder metallurgy processes;
- Preservation—the cohesion of the particles is neither broken nor increased, e.g., forming;
- Reduction—certain volumes of material are separated from the body that will form the final product, e.g., machining;
- Increase—between the partial volumes of the future product there is a joining—e.g., welding.
- The proportion of elastic deformation, which causes certain dimensional and shape changes in the volume of the material to be negated after the end of the production process;
- The proportion of plastic deformation, which causes permanent changes in the volume of the processed material.
- The proportion of brittle failures causing separation between specified volumes of the processed material.
- Chemical composition: One of the most significant factors of the material properties—some chemical elements can significantly change—in a positive or negative sense—the physical and technological properties of the material even in trace amounts.
- Physical properties:
- ○
- State of the material matrix: Theoretically the same material from a chemical point of view has completely different properties if it is in the form of a single crystal or a polycrystalline structure. A polycrystalline structure has different properties if it is fine-grained or coarse-grained.
- ○
- Tensile strength: The resistance of the material to rupture.
- ○
- Yield strength: The stress at which the material begins to deform permanently.
- ○
- Modulus of elasticity: A measure of the stiffness of the material.
- ○
- Density: The mass of the material per unit volume.
- The ratio of the maximum dimensions in space;
- The ratio of the number of atoms on the surface of the object to the number in the volume of the material.
- fx(x0,y0) = fy(x0,y0) = 0;
- either fx(x0,y0) or fy(x0,y0) does not exist.
3.2. Experimental Conditions and Materials
- (i)
- Rz is much more sensitive to extreme fluctuations in the surface profile—it provides better information about the extreme values of the measured surface, which have a significant impact on the functionality of the surface. In the case of scratches or grooves in the surface profile, this characteristic of surface roughness identifies them, which is important for surfaces participating in sealing systems;
- (ii)
- Rz correlates better with the functional properties of surfaces—the measured values are in direct relation with the surface properties affecting tightness, wear and friction properties;
- (iii)
- Rz is more suitable for quality control, because it is more sensitive in detecting surface defects that negatively affect its functionality.
- Surface roughness measurements were performed parallel with the workpiece axis with the measurements repeated three times.
- (A)
- Machined material: 12 050.1 (C45 according to DIN EN, which corresponds to 1045 AISI/SAE steel), ϕ 170 mm—it is an unalloyed structural carbon steel produced to a range of 0.43 ÷ 0.50% Carbon and 0.60 ÷ 0.90% Manganese. It is a high strength steel intended for tempering, popular because of the good balance between machinability and mechanical properties, used primarily in gears, shafts, axles, studs, and other machine parts.
- (B)
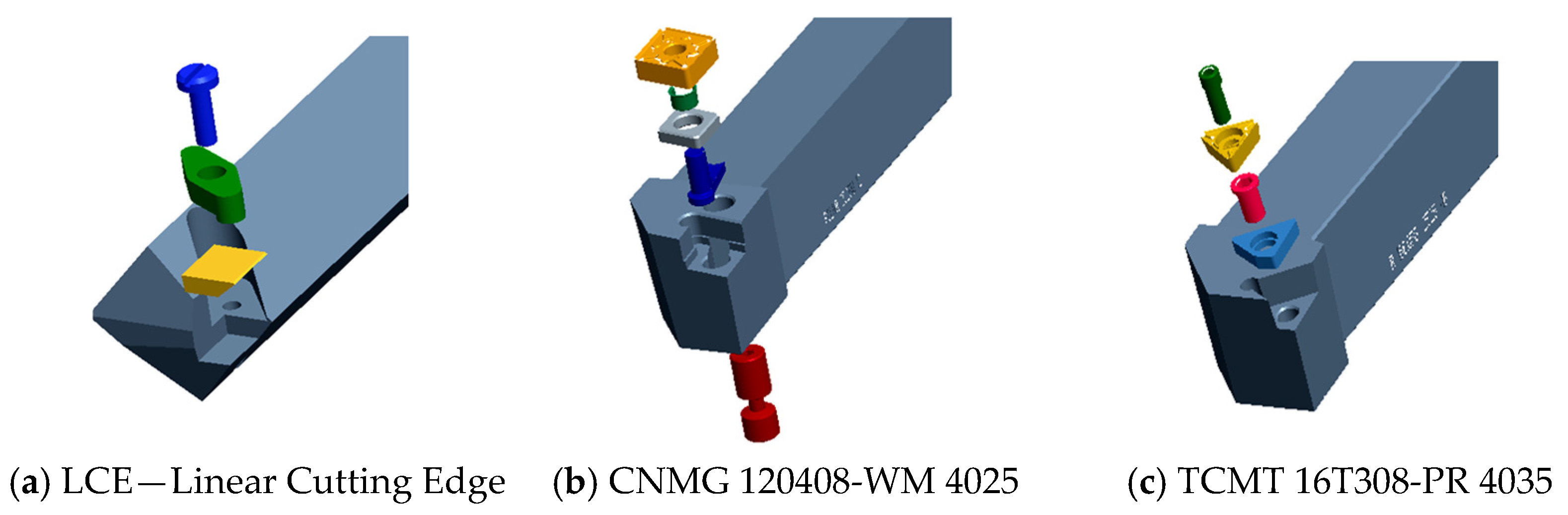
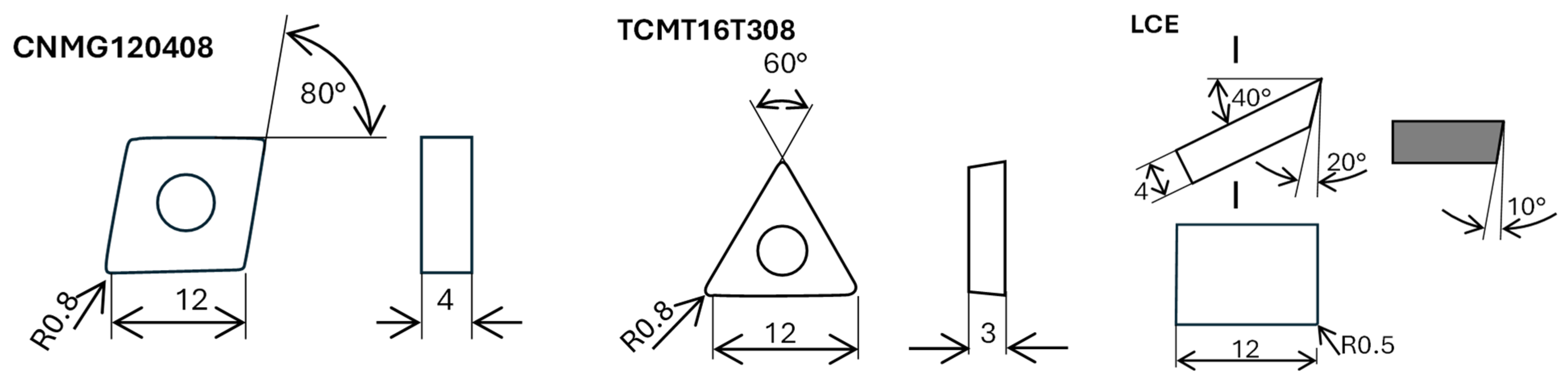
- Cutting tools (Figure 7)—three tools designed for different types of machining were selected for comparison in order to determine the characteristics for their special orientation:
- Tool with a linear cutting edge—self-designed at the Technical University of Košice (Figure 7a).
- Cutting geometry—angles in the tool coordinate system:
The angle of tool orthogonal rake γo1 = 0° The angle of tool orthogonal rake γo2 = 40° Cutting edge inclination angle λs1 = 40° Cutting edge inclination angle λs2 = 0° The angle of tool orthogonal clearance αo1 = 20° The angle of tool orthogonal clearance αo2 = 10° Negative chamfer 0.2 mm Corner radius rε = 0.5 mm
A tool with a linear cutting edge performs machining based on a free cut, with the chip being cut off only by the major cutting edge. This tool is suitable for machining at high feeds, since at low feeds there is a risk of vibrations caused by the small thickness of the chip, and even at high feeds it shows effective values of surface roughness characteristics after machining. Other advantages of a tool designed in this way include that any vibrations of the technological set can be eliminated by the position of the cutting-edge inclination or that the worn part of the cutting edge can be easily regenerated by parallel displacement in the direction of the cutting edge or by changing the position of the tool. The tool material is P30 according to ISO (C6 according to ANSI) with a TiN coating, and the tool is primarily intended for high- power finishing of external cylindrical surfaces.Recommended feed range 0.25–1.0 mm, cutting depth range 0.5–5 mm. - Commercial tool for fine-turning with wiper technology for low values of surface roughness characteristics at high feed rates-CNMG 120408-WM 4025 (Figure 7b)—cutting material GC4025 with CVD coating is intended for machining steels (P10 to P30 according to ISO) with a combination of high wear resistance and good edge stability.Recommended feed range 0.15–0.7 mm, cutting depth range 0.5–5 mm.
- Commercial tool TCMT 16T308-PR 4035 (Figure 7c)—recommended for use in common turning operations and cutting material GC4035 is a universal quality material (P20–P40 according to ISO) with CVD coating. It is intended for medium cutting speeds and feeds usable under adverse working conditions.Recommended feed range 0.12–0.35 mm, cutting depth range 0.2–2 mm.
- (C)
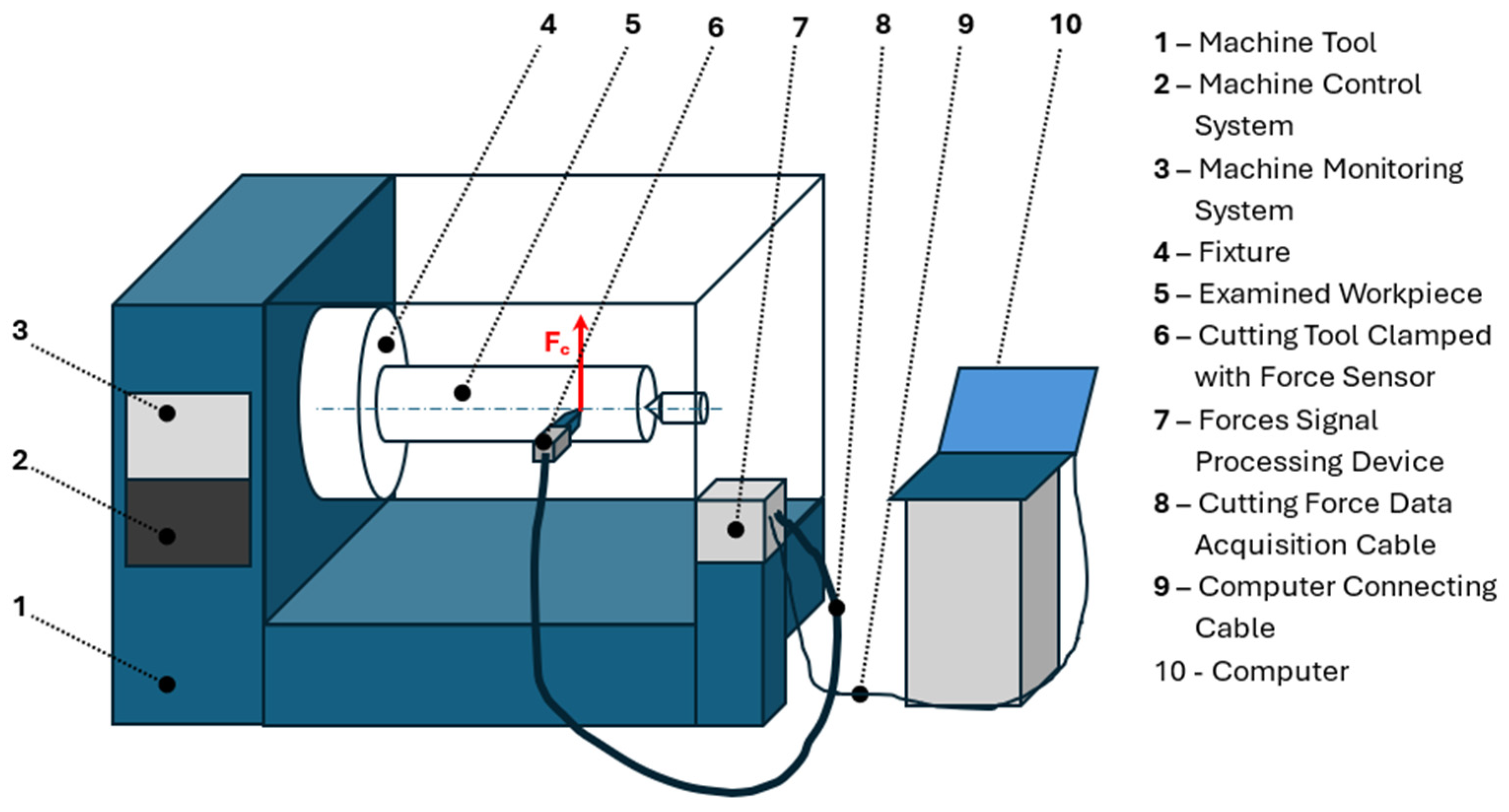
- Machine: Lathe SUI 40;
- (D)
- Devices and instruments for measuring monitored and detected quantities;
- Mitutoyo Surftest 301 (Mitutoyo UK Ltd, Andover, Hampshire)—instrument for measuring the roughness characteristics of the machined surface;
- KISTLER dynamometer (Kistler GmbH, Wien, Austria)—instrument for measuring cutting force components—KISTLER 9411 sensor unit/KISTLER 5006 signal amplifier/KISTLER 5501 analogue indicators;
- Lutron DT 2235A (Lutron EA Ltd., London, UK)—digital contact tachometer for measuring cutting speed.
- (E)
- Machining conditions:
| Cooling | NO |
| Depth of cut | ap = 1 mm |
| Adjustment related to the workpiece axis | |
| Tool with LCE | h = 1 mm above the axis |
| CNMG 120408-WM | h = 0 mm—in the axis |
| TCMT 16T308-PR | h = 0 mm—in the axis |
| Feed per revolution—used values | f = 0.203/0.281/0.405/0.563/0.810 mm |
| Cutting speed—used values | vc = 70/84/100/120/145 m/min |
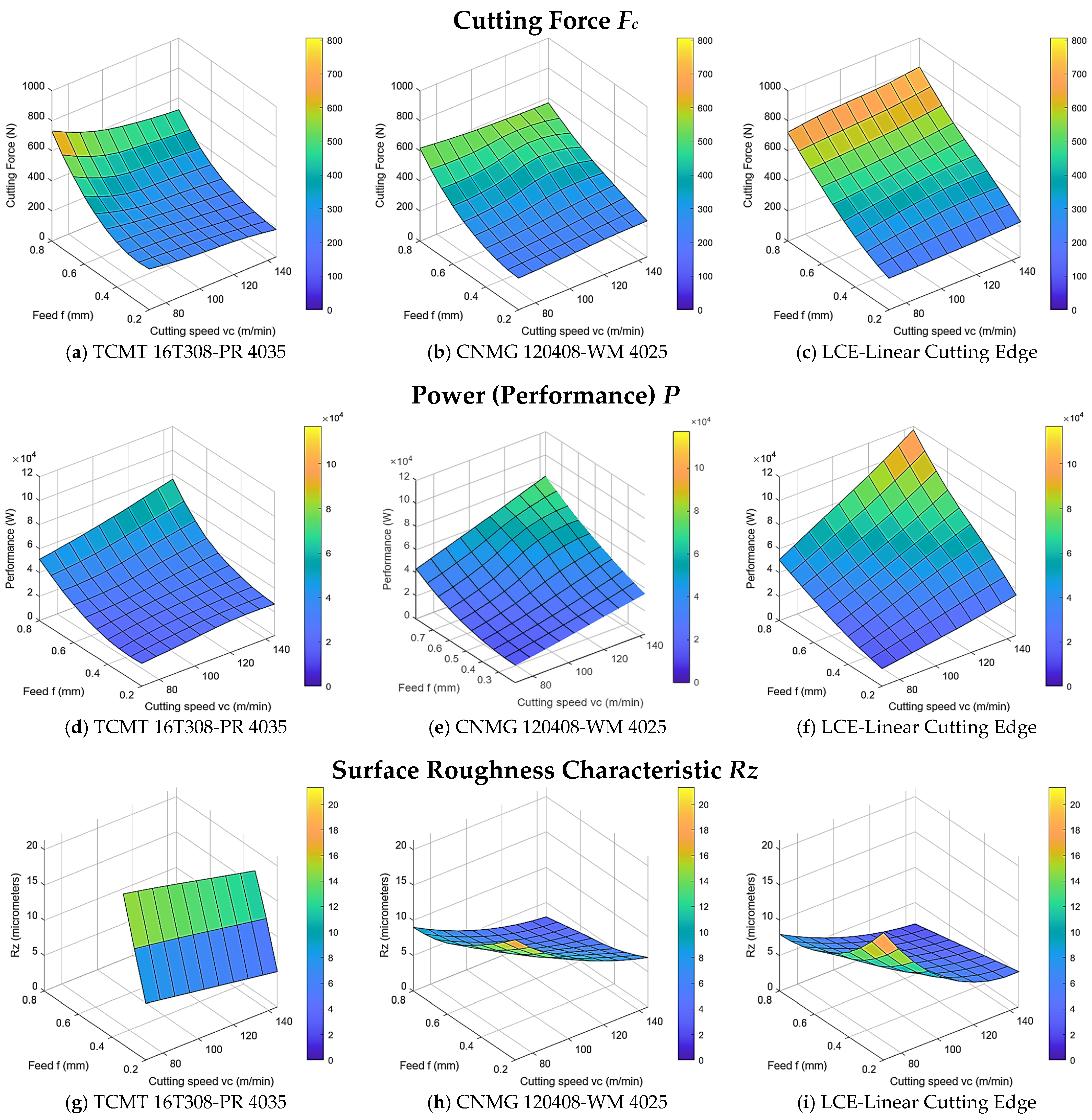
4. Results and Discussion
5. Conclusions
- To verify the model, experimentally obtained data for external longitudinal turning, as the kinematically and technologically simplest manufacturing operation, were processed and evaluated. Three tools with different characteristics were selected for the model verification: a classic commercially available universal tool TCMT16T308-PR 4035 for common machining operations with standard ranges of used technological factors; a commercially available tool CNMG120408-WM 4025 with a wiper geometry designed for very productive universal machining in twice the technological factor ranges compared to the first tool; and an original innovative author’s tool design with a linear cutting edge (LCE) for productive machining with very good values of surface roughness characteristics.
- After obtaining the dependences of experimentally measured and calculated data Fc, Rz and P on the input two independent variables of cutting speed vc and feed f for given conditions, these mathematical formulations were used to optimize the parameters entering the production process. When specifying the extrema of the function in a given range of variables, it was necessary to identify critical points and determine whether these points correspond to local extrema (in our case, minima).
- The evaluation of the behavior of the three tools used under the same conditions showed a diversity of results related to the established criterion. If the criterion of the smallest cutting force Fc had been established (which has a low practical significance for real practice), the most suitable tool would have been the commercially produced TCMT tool (with an achieved value of Fc = 196 N at the input parameters vc = 145 m.min−1 and f = 0.2 mm). However, for the criterion of the smallest roughness, the LCE tool (with the possibility of achieving a roughness of Rz = 2.2 μm at vc = 145 m.min−1 and f = 0.8 mm) was clearly the best, which also dominated from the point of view of the criterion of the lowest process power p = 14,700 W achieved at the same parameters. Therefore, taking into account the importance of individual criteria for real practice and the minimum extreme values achieved, it can be concluded that among the tools studied, the tool with a linear cutting edge (LCE) is the most suitable tool for longitudinal external machining under the given conditions.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
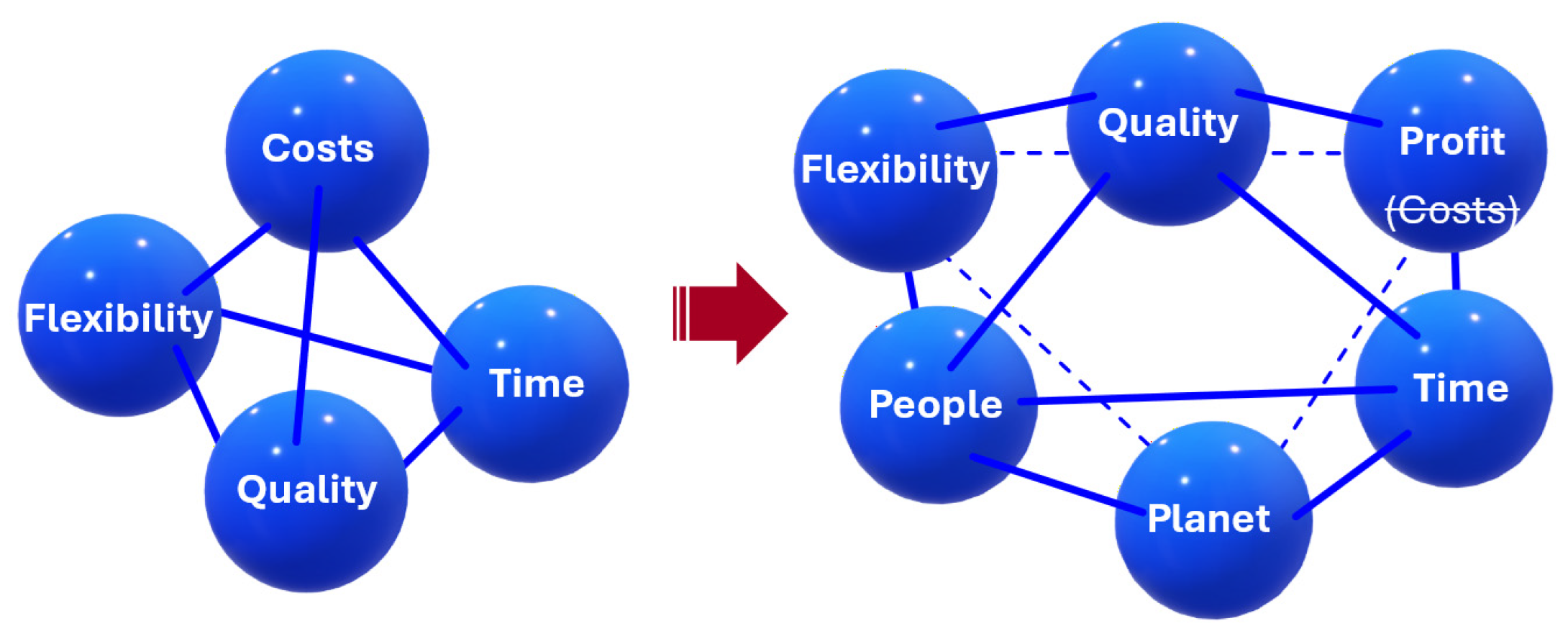
| 3P | People-Planet-Profit/after 2018 in version People-Planet-Prosperity |
| CNMG | Cutting tool with wiper geometry |
| LCE | Tool with linear cutting edge |
| PR | Production rate |
| TCMT | Tool for general purposes |
| LCE | Linear cutting edge |
References
- Bohr, N.; Noll, W. Atomic Physics and Human Knowledge. Am. J. Phys. 1958, 26, 596–597. [Google Scholar] [CrossRef]
- Virilio, P. Speed and Politics; (Originally Published in 1977); Semiotext(e): Los Angeles, CA, USA, 2007; ISBN-10: 1-58435-040-7. [Google Scholar]
- Jeurissen, R. Cannibals With Forks: The Triple Bottom Line of 21st Century Business. J. Bus. Ethics 2000, 23, 229–231. [Google Scholar] [CrossRef]
- Elkington, J. 25 Years Ago I Coined the ‘Triple Bottom Line.’ Here’s Why It’s Time to Rethink It. Harv. Bus. Rev. 2018, 25, 6. [Google Scholar]
- Meadows, D.H. Thinking in Systems; Chelsea Green Publishing: White River Junction, VT, USA, 2015. [Google Scholar]
- Scott, J.C. Seeing Like a State; Yale University: New Haven, CT, USA, 1998; ISBN 0-300-07016-0. [Google Scholar]
- Patole, P.B.; Pol, G.J.; Desai, A.A.; Kamble, S. Analysis of effect of cutting parameters on surface roughness and cutting force during turning of aluminum alloy (AlSi5Cu3). Manuf. Technol. Today 2021, 20, 3–8. [Google Scholar]
- Kumar, R.; Pattnaik, S.K.; Minz, J.K.; Sarangi, S.K. Influence of cutting parameters on cutting forces and surface roughness in dry turning of Al using PCD and different coated tools. Sādhanā 2019, 44, 1–17. [Google Scholar] [CrossRef]
- Rezvan Rostami, R.; Abedini, V. Experimental study on surface roughness and cutting force in turning of Al7032 reinforced with SiC using Taguchi design. Modares Mech. Eng. 2021, 8, 69–76. [Google Scholar]
- Asavarutpokin, A.; Sae-Lee, J.; Kaewdook, D. Power consumption and surface quality optimization of cutting conditions for S50C material in turning process using means utility concept and Taguchi method. J. Eng. Digit. Technol. 2020, 8, 58–62. [Google Scholar]
- Thandra, S.K.; Choudhury, S.K. Effect of cutting parameters on cutting force, surface finish and tool wear in hot machining. Int. J. Mach. Mach. Mater. 2010, 8, 260–273. [Google Scholar] [CrossRef]
- Bhattacharya, A.; Das, S.; Majumder, P.; Yadava, V. Estimating the effect of cutting parameters on surface finish and power consumption during high-speed machining of AISI 1045 steel using Taguchi design and ANOVA. Prod. Eng. 2009, 3, 31–40. [Google Scholar] [CrossRef]
- El-Kady, E.Y.; Gaafer, A.M.; Ghaith MH, G.; Khalil, T.; Mostafa, A.A. The effect of machining parameters on the cutting forces, tool wear, and machined surface roughness of metal matrix nano composite material. Adv. Mater. 2015, 4, 43–50. [Google Scholar] [CrossRef]
- Duman, E.; Özel, T. Prediction and optimization of surface roughness and cutting forces in turning process using ANN, SHAP analysis, and hybrid MCDM method. Appl. Sci. 2024, 14, 11386. [Google Scholar]
- Varga, J.; Szakálos, P. The effects of cutting parameters on cutting force and tribological properties of machined surface under dry turning of AISI304L austenitic stainless steel. J. Manuf. Mater. Process. 2024, 8, 257. [Google Scholar]
- Jeulin, M.; Cahuc, O.; Darnis, P.; Laheurte, R. A 6-components mechanistic model of cutting forces and moments in milling. Forces Mech. 2022, 9, 100130. [Google Scholar] [CrossRef]
- Wen, Y.; Zhou, W.; Tang, J. Composite effects of residual stress and hardness gradient on contact fatigue performance of rough tooth surfaces and optimization design of de-tailed characteristic parameters. Eng. Fail. Anal. 2024, 162, 108424. [Google Scholar] [CrossRef]
- Jaurker, D.; Pradhan, M.K.; Jaurker, S.; Malviya, R. Optimization Techniques Used in Machining Processes: A Review. In Recent Advances in Materials and Manufacturing Technology; ICAMMT 2022. Lecture Notes in Mechanical, Engineering; Nayak, R.K., Pradhan, M.K., Mandal, A., Davim, J.P., Eds.; Springer: Singapore, 2023. [Google Scholar] [CrossRef]
- Xun, C.; Wu, P. A Generic Multi-Objective Optimization of Machining Processes Using an End-to-End Evolutionary Algorithm. Machines 2024, 12, 635. [Google Scholar] [CrossRef]
- Chang, L.; Patel, Y.; Wang, H.; Williams, J.G. The Partitioning of Plastic Energy in Cutting Tests. Procedia Struct. Integr. 2016, 2, 309–315. [Google Scholar] [CrossRef][Green Version]
- Ngoc, T.B.; Duc, T.M.; Tuan, N.M.; Long, T.T. Influence of Al2O3/MoS2 hybrid nanofluid MQL on surface roughness, cutting force, tool wear and tool life in hard turning. Forces Mech. 2024, 16, 100285. [Google Scholar] [CrossRef]
- Mejri, H.; Mehdi, K. Modeling of cutting forces in curvilinear peripheral milling process. Int. J. Adv. Manuf. Technol. 2019, 102, 277–291. [Google Scholar] [CrossRef]
- KBounif, M.; Abbadi, M.; Nouari, R. Selvam, A numerical approach for crack-induced damage in tungsten carbide cutting tools during machining. Eng. Fail. Anal. 2021, 128, 105617. [Google Scholar] [CrossRef]
- ISO 14040:2006; Environmental Management—Life Cycle Assessment—Principles and Framework. International Organization for Standardization: Geneva, Switzerland, 2006; Edition 2, ISO/TC 207/SC 5. p. 20.
- ISO 14044:2006; Environmental Management—Life Cycle Assessment—Requirements and Guidelines. International Organization for Standardization: Geneva, Switzerland, 2006; Edition 1, ISO/TC 207/SC 5. p. 46.
- Karmiris-Obratanski, P.; Thangaraj, M.; Leszczyńska-Madej, B.; Markopoulos, A.P. Advanced Machining Technology for Modern Engineering Materials. Materials 2024, 17, 2064. [Google Scholar] [CrossRef]
- Grzeszik, W. Advanced Machining Processes of Metallic Materials, Theory, Modelling, and Applications; Elsevier: Amsterdam, The Netherlands, 2017; ISBN 978-0-444-63711-6. [Google Scholar]
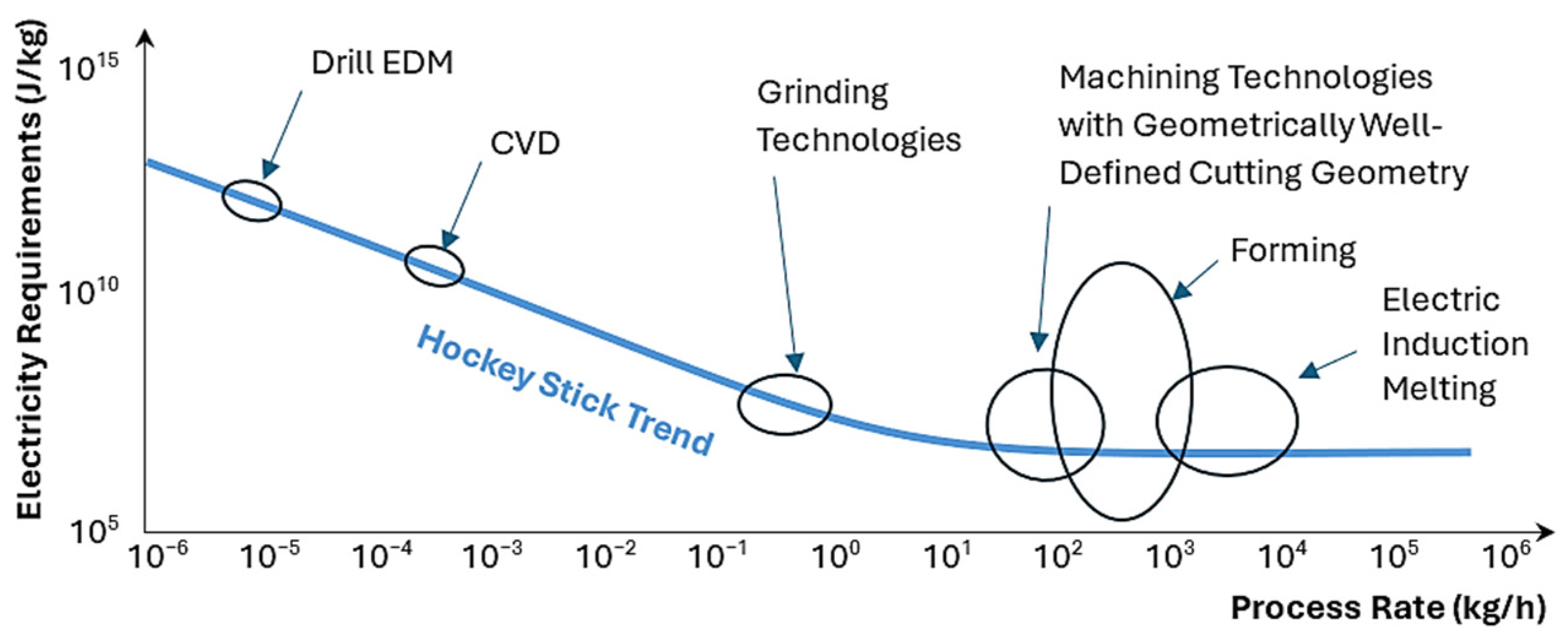
- Gutowski, T.; Jiang, S.; Cooper, D.; Corman, G.; Hausmann, M.; Manson, J.A.; Sekulic, D.P. Note on the Rate and Energy Efficiency Limits for Additive Manufacturing. J. Ind. Ecol. 2017, 21, S69–S79. [Google Scholar] [CrossRef]
- Mehdi, K.; Monka, P.P.; Monkova, K.; Sahraoui, Z.; Glaa, N.; Kascak, J. Investigation of Dynamic Behavior and Process Stability at Turning of Thin-Walled Tubular Workpieces Made of 42CrMo4 Steel Alloy. Machines 2024, 12, 120. [Google Scholar] [CrossRef]
- Monka, P.P.; Monkova, K.; Majstorovic, V.D.; Božić, Ž.; Andrej, A. Optimal cutting parameter specification of newly designed milling tools based on the frequency monitoring. Int. J. Adv. Manuf. Technol. 2021, 115, 777–794. [Google Scholar] [CrossRef]
- DIN 8580:2022-12; Manufacturing Processes—Terms and Definitions, Division. German Institute for Standardisation: Berlin, Germany, 2022; p. 25.
- Lampropoulos, A.D.; Markopoulos, A.P.; Manolakos, D.E. Modeling of Ti6Al4V Alloy Orthogonal Cutting with Smooth Particle Hydrodynamics: A Parametric Analysis on Formulation and Particle Density. Metals 2019, 9, 388. [Google Scholar] [CrossRef]
- Monkova, K.; Monka, P.P.; Sekerakova, A.; Hruzik, L.; Burecek, A.; Urban, M. Comparative Study of Chip Formation in Orthogonal and Oblique Slow-Rate Machining of EN 16MnCr5 Steel. Metals 2019, 9, 698. [Google Scholar] [CrossRef]
- Stal, J.E.; De Vos, P. Metal Cutting: Theories and Models; CRC Press: Boca Raton, FL, USA, 2012; ISBN 9789163713361. [Google Scholar]
- Živković, A.M.; Zeljković, M.V.; Mlađenović, C.D.; Tabaković, S.T.; Milojević, Z.L.; Hadžistević, M.J. A Study of Thermal Behavior of the Machine Tool Spindle. Therm. Sci. 2019, 23, 2117–2130. [Google Scholar] [CrossRef]
- Karmiris-Obratański, P.; Papazoglou, E.L.; Leszczyńska-Madej, B.; Karkalos, N.E.; Markopoulos, A.P. An Optimalization Study on the Surface Texture and Machining Parameters of 60CrMoV18-5 Steel by EDM. Materials 2022, 15, 3559. [Google Scholar] [CrossRef]
- Mladjenovic, C.; Monkova, K.; Zivkovic, A.; Knezev, M.; Marinkovic, D.; Ilic, V. Experimental Identification of Milling Process Damping and Its Application in Stability Lobe Diagrams. Machines 2025, 13, 96. [Google Scholar] [CrossRef]
- Available online: https://www.hoffmann-group.com (accessed on 19 November 2024).
- Available online: https://www.kennametal.com (accessed on 14 October 2024).
- Available online: https://www.sandvik.coromant.com (accessed on 25 November 2024).
- Available online: https://www.walter-tools.com (accessed on 19 November 2024).
- Vargova, M.; Tavodova, M.; Monkova, K.; Dzupon, M. Research of Resistance of Selected Materials to Abrasive Wear to Increase the Ploughshare Lifetime. Metals 2022, 12, 940. [Google Scholar] [CrossRef]
- Michael Quinten: A Practical Guide to Surface Metrology; Springer Nature: Cham, Switzerland, 2019; ISBN 978-3-030-29454-0.
- Rodrigues, A.C.P.; Ribeiro, P.J.N.; Österle, W.; Azevedo, C.R.D.F. Failure analysis as a tool to optimize the design of a ring on disc tribotest investigating the role of surface roughness. Eng. Fail. Anal. 2015, 56, 131–141. [Google Scholar] [CrossRef]
- ISO 3685:1993; Tool-Life Testing with Single-Point Turning Tools. International Organization for Standardization: Geneva, Switzerland, 2017; ISO/TC 29/SC 9. p. 48.


| Findings | Cutting Tool | |||
|---|---|---|---|---|
| TCMT | CNMG | LCE | ||
| Input variables | Cutting speed vc (m/min) | 145 | 70 | 70 |
| Feed per revolution f (mm) | 0.2 | 0.2 | 0.2 | |
| Minimum of the criterial function | Cutting force Fc (N) | 196 | 211 | 210 |
| Input variables | Cutting speed vc (m/min) | 145 | 145 | 145 |
| Feed per revolution f (mm) | 0.2 | 0.8 | 0.8 | |
| Minimum of the criterial function | Surface roughness Rz (μm) | 5.23 | 3.15 | 2.2 |
| Input variable | Cutting speed vc (m/min) | 70 | 70 | 70 |
| Feed per revolution f (mm) | 0.2 | 0.2 | 0.2 | |
| Minimum of the criterial function | Power P (W) | 19,040 | 14,770 | 14,700 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Monka, P.P.; Monkova, K.; Bilek, O.; Reznicek, M. Machining Process Optimization Using a Model Based on Criterial Functional Dependence. Machines 2025, 13, 478. https://doi.org/10.3390/machines13060478
Monka PP, Monkova K, Bilek O, Reznicek M. Machining Process Optimization Using a Model Based on Criterial Functional Dependence. Machines. 2025; 13(6):478. https://doi.org/10.3390/machines13060478
Chicago/Turabian StyleMonka, Peter Pavol, Katarina Monkova, Ondrej Bilek, and Martin Reznicek. 2025. "Machining Process Optimization Using a Model Based on Criterial Functional Dependence" Machines 13, no. 6: 478. https://doi.org/10.3390/machines13060478
APA StyleMonka, P. P., Monkova, K., Bilek, O., & Reznicek, M. (2025). Machining Process Optimization Using a Model Based on Criterial Functional Dependence. Machines, 13(6), 478. https://doi.org/10.3390/machines13060478












