Reference Model-Based Backstepping Control of Semi-Active Suspension for Vehicles Equipped with Non-Pneumatic Wheels
Abstract
1. Introduction
2. System Modeling and Problem Formulation
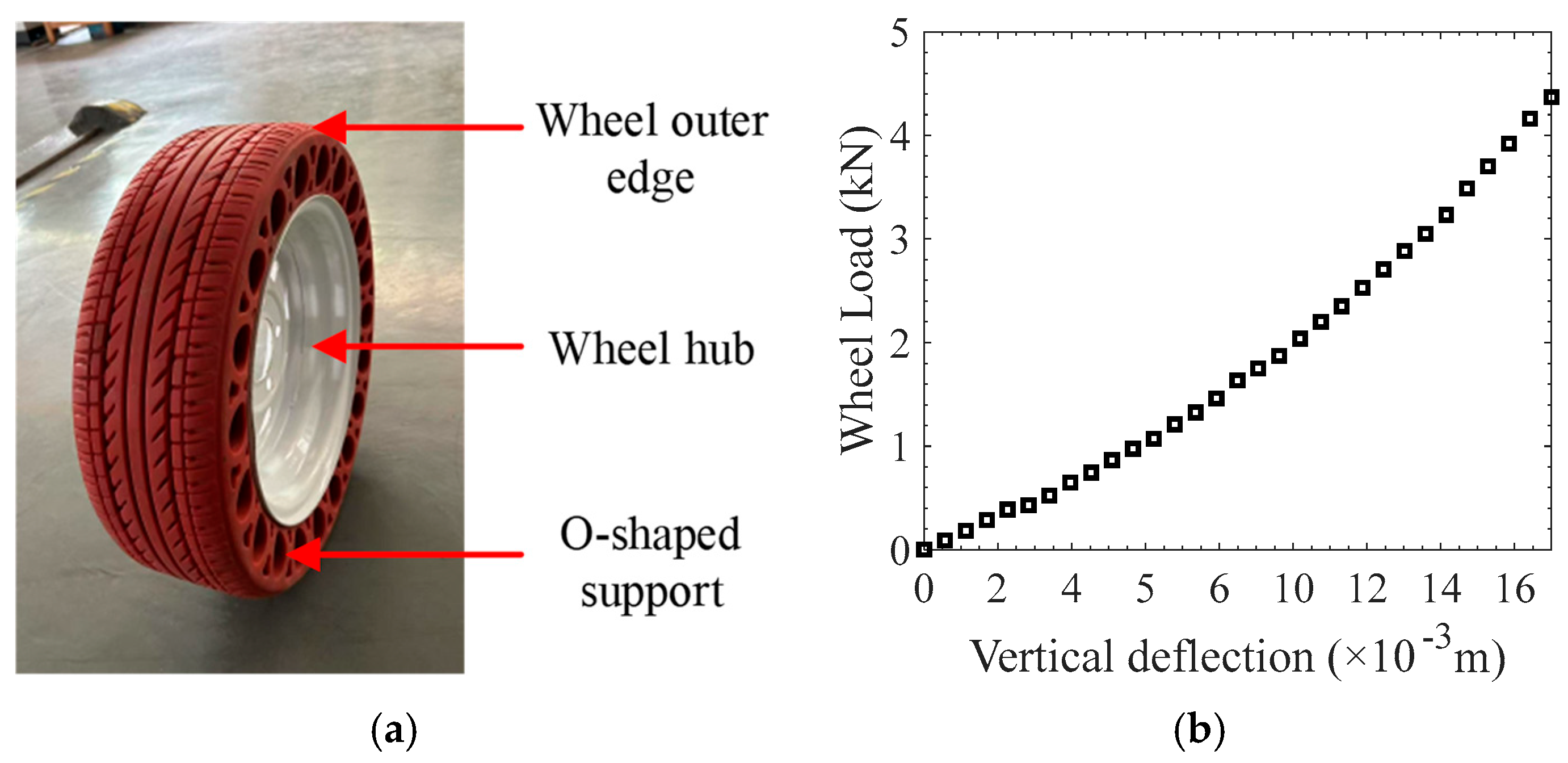
2.1. Stiffness Model of Non-Pneumatic Wheel
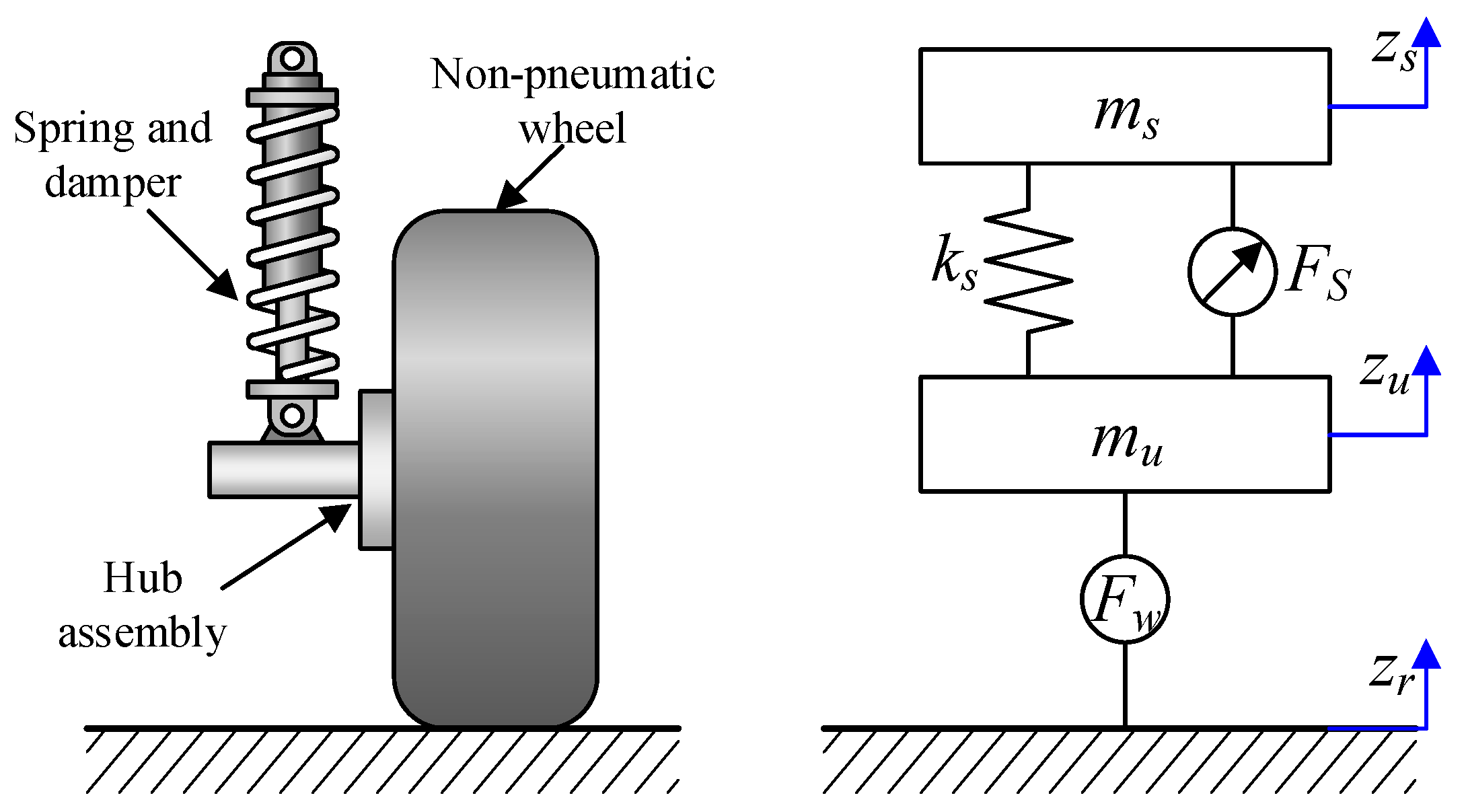
2.2. Integrated Quarter Vehicle Model
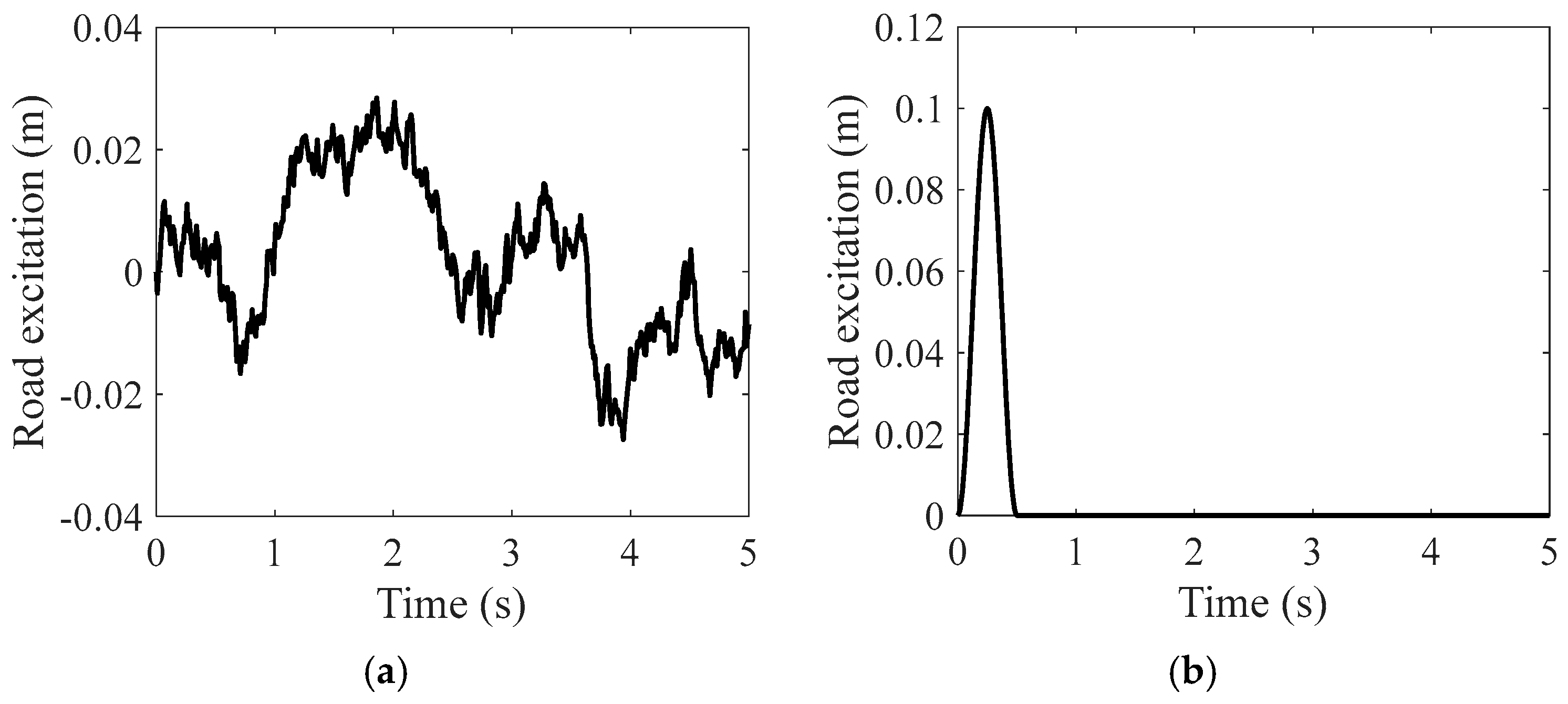
2.3. Road Excitation Model
2.4. Problem Formulation
- To achieve effective coordination between vehicle ride comfort and handling stability, a reference model based on robust control theory is designed to provide ideal reference trajectories for sprung mass displacement and velocity;
- The designed controller is robust and adaptable to time-varying road disturbances;
- In order to ensure the safety of the vehicle during traveling, the system should satisfy three constraints. First, to prevent the suspension from hitting the limit blocks, the suspension working space should be kept within the maximum travel,
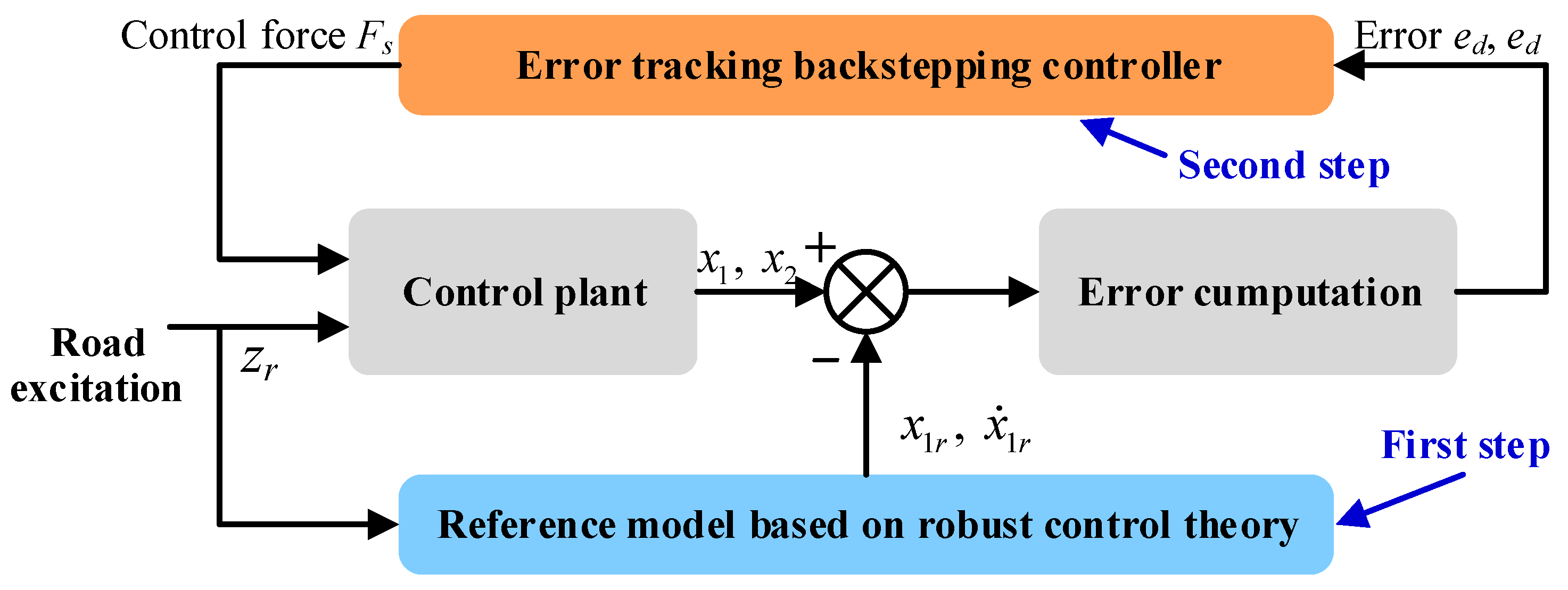
3. Reference Model-Based Backstepping Control
3.1. Reference Model Design
- Closed-loop system (18) asymptotic stabilization;
- The norm of the closed-loop system transfer function from the output z∞ to the perturbation satisfies ;
- The closed-loop system (18) satisfies the time-domain constraints (9)–(11).
3.2. Backstepping Controller Design
4. Simulation Results and Discussion
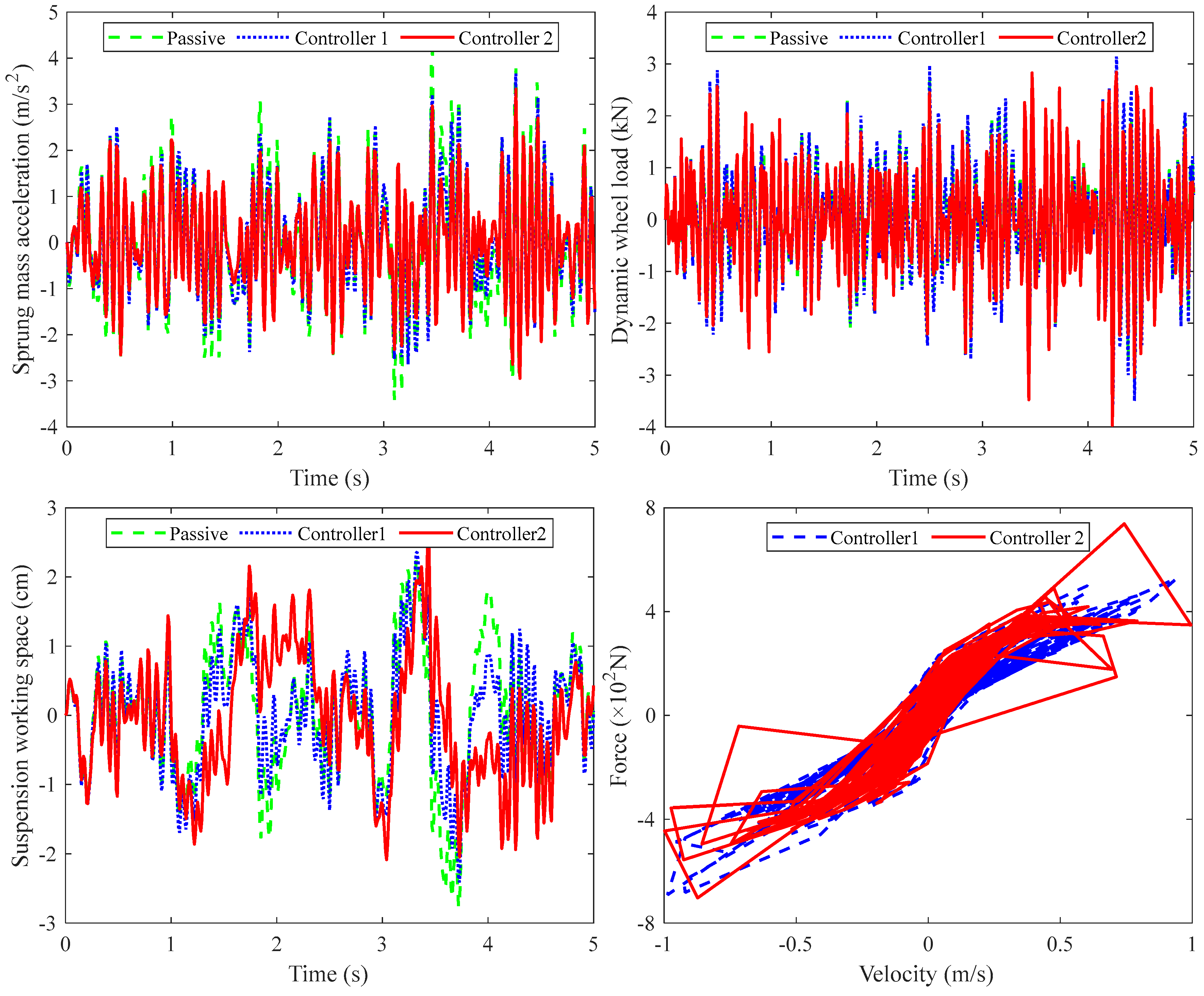
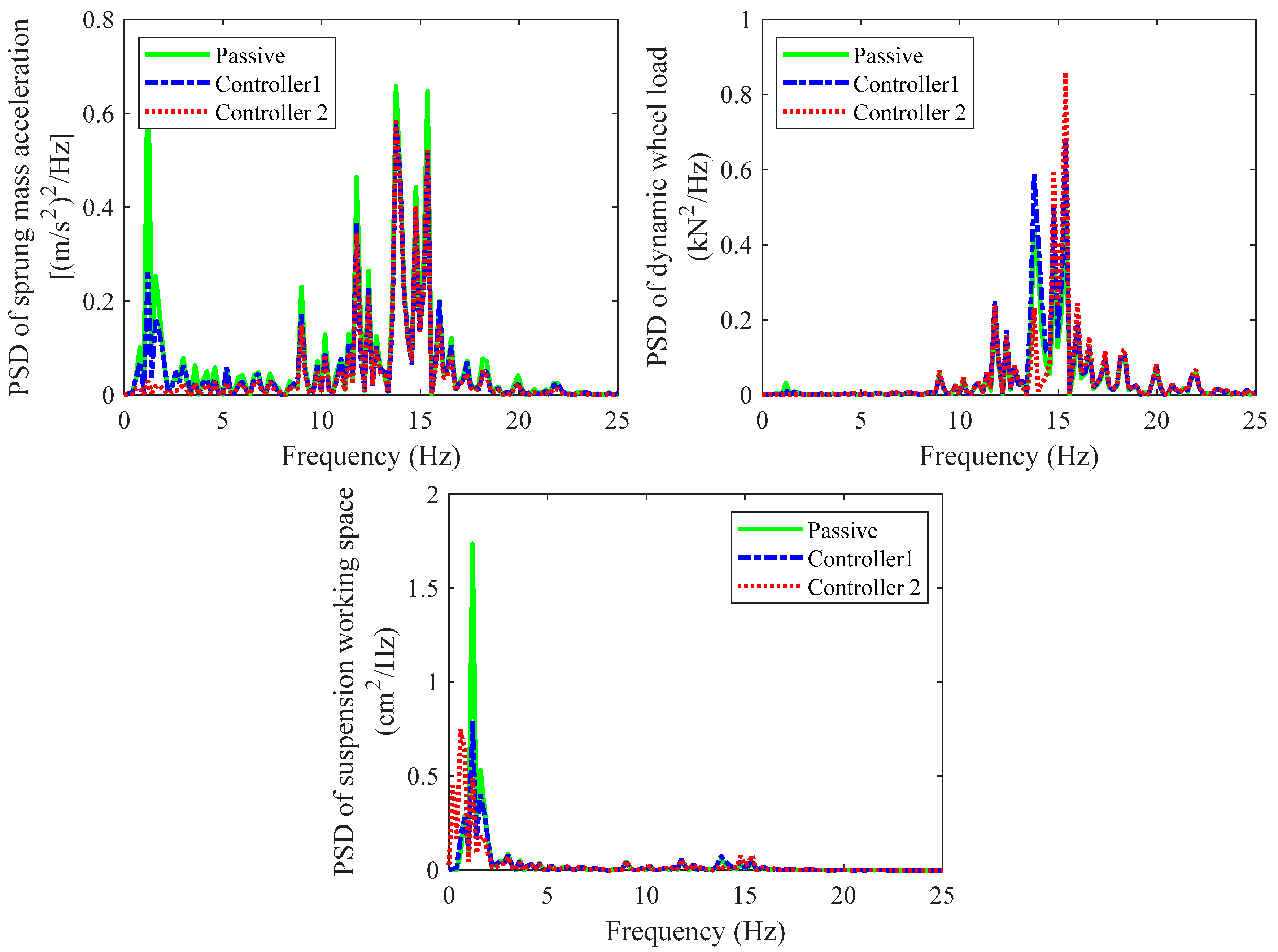
4.1. Simulation Results Under Random Road Excitation
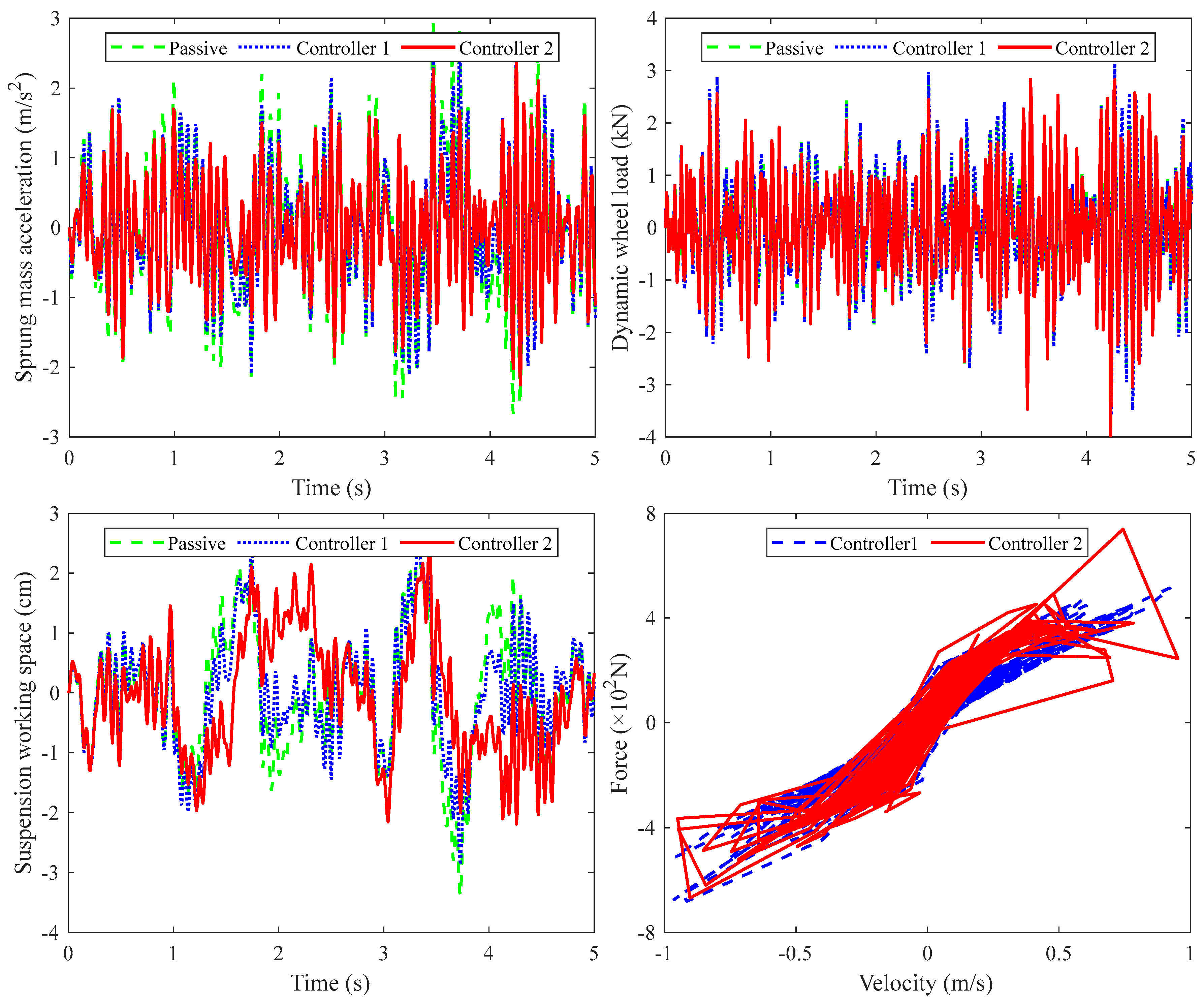
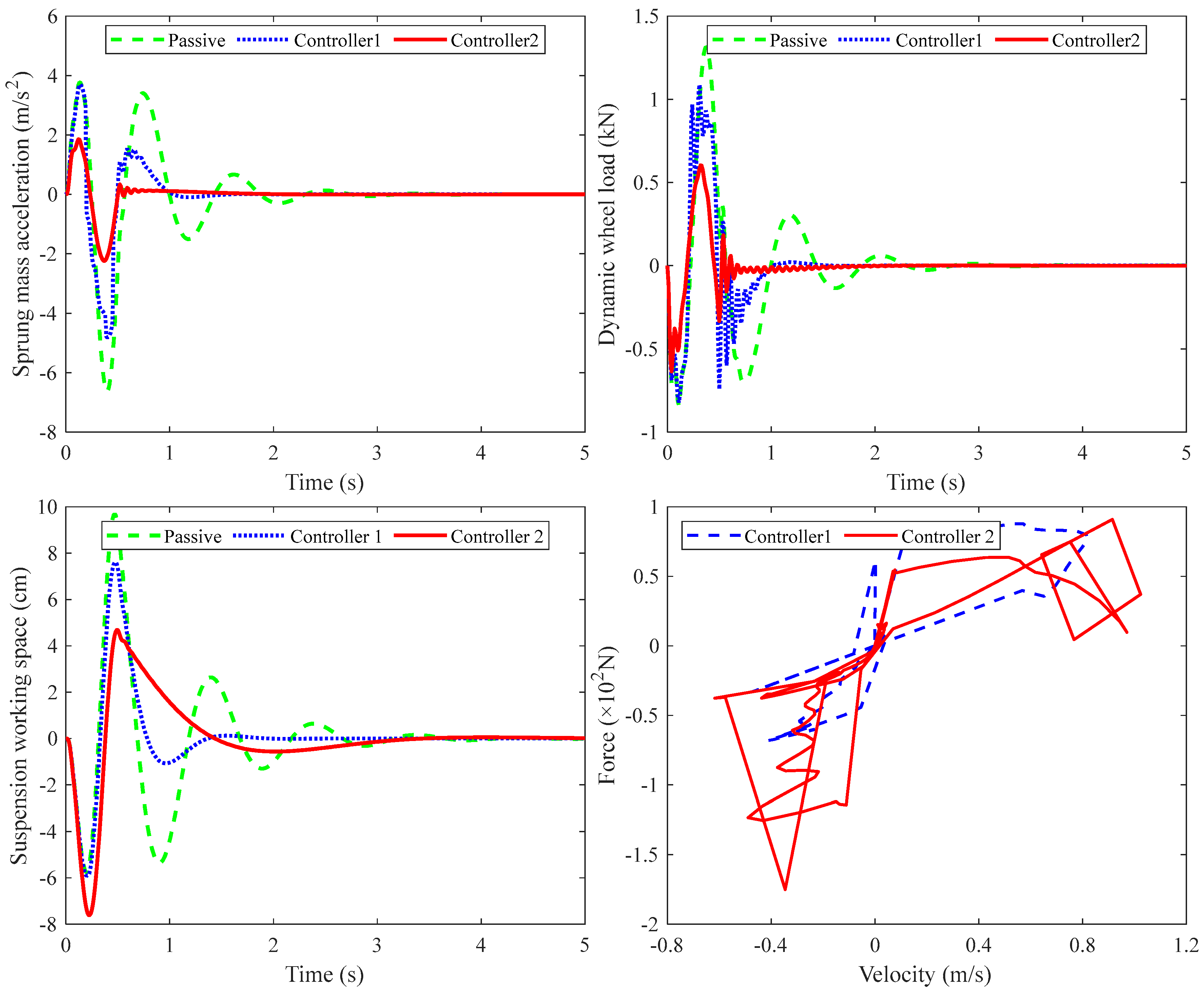
4.2. Simulation Results Under Bumpy Road Excitations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| RMS | Root mean square |
| PSD | Power spectral density |
| P-P | Peak to peak |
References
- Chen, G.; Du, G.; Xia, J.; Xie, X.; Wang, Z. Aperiodic Sampled-Data H∞ Control of Vehicle Active Suspension System: An Uncertain Discrete-Time Model Approach. IEEE Trans. Ind. Inf. 2024, 20, 6739–6750. [Google Scholar] [CrossRef]
- Wong, P.K.; Li, W.; Ma, X.; Yang, Z.; Wang, X.; Zhao, J. Adaptive Event-Triggered Dynamic Output Feedback Control for Nonlinear Active Suspension Systems Based on Interval Type-2 Fuzzy Method. Mech. Syst. Signal Process. 2024, 212, 111280. [Google Scholar] [CrossRef]
- Liu, Z.; Si, Y.; Sun, W. Ride Comfort Oriented Integrated Design of Preview Active Suspension Control and Longitudinal Velocity Planning. Mech. Syst. Signal Process. 2024, 208, 110992. [Google Scholar] [CrossRef]
- Wang, Q.; Zhao, Y.; Xu, H.; Deng, Y. Adaptive Backstepping Control with Grey Signal Predictor for Nonlinear Active Suspension System Matching Mechanical Elastic Wheel. Mech. Syst. Signal Process. 2019, 131, 97–111. [Google Scholar] [CrossRef]
- Zheng, Z.; Rakheja, S.; Sedaghati, R. A Comparative Study of Static and Dynamic Properties of Honeycomb Non-Pneumatic Wheels and a Pneumatic Wheel. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2021, 235, 3631–3646. [Google Scholar] [CrossRef]
- Zheng, Z.; Rakheja, S.; Sedaghati, R. Cornering Stiffness Characteristics of Honeycomb Wheels: A Parametric Analysis Using Response Surface Method. Compos. Struct. 2022, 288, 115418. [Google Scholar] [CrossRef]
- Jin, X.; Hou, C.; Fan, X.; Sun, Y.; Lv, J.; Lu, C. Investigation on the Static and Dynamic Behaviors of Non-Pneumatic Tires with Honeycomb Spokes. Compos. Struct. 2018, 187, 27–35. [Google Scholar] [CrossRef]
- Liu, W.; Liu, S.; Li, X.; Zhang, Q.; Wang, C.; Li, K. Static Stiffness Properties of High Load Capacity Non-Pneumatic Tires with Different Tread Structures. Lubricants 2023, 11, 180. [Google Scholar] [CrossRef]
- Li, H.; Zhao, Y.; Lin, F.; Zhu, M. Nonlinear Dynamics Modeling and Rollover Control of an Off-Road Vehicle with Mechanical Elastic Wheel. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 51. [Google Scholar] [CrossRef]
- Li, H.; Zhou, H.; Yang, J.; Ge, J.; Wang, G.; Xu, T. Study of the Dynamic Performance of Rolling Non-Pneumatic Tires Using Finite Element Method. J. Braz. Soc. Mech. Sci. Eng. 2022, 44, 289. [Google Scholar] [CrossRef]
- Xiao, Z.; Zhao, Y.; Lin, F.; Zhu, M.; Deng, Y.; Zang, L. The Multi-Objective Optimization of a Non-Pneumatic Wheel Based on Its Life Prediction. Eng. Comput. 2019, 36, 997–1020. [Google Scholar] [CrossRef]
- Ali, I.; Rahman, M.Z.U.; Hussain, A.; Ghaffar, A.; Zafar, S. A Finite Element Analysis Based Design of a Non-Pneumatic Wheel Chair Castor. J. Eng. Res. 2025, 13, 351–360. [Google Scholar] [CrossRef]
- Hryciów, Z.; Jackowski, J.; Żmuda, M. The Influence of Non-Pneumatic Tyre Structure on Its Operational Properties. Int. J. Automot. Mech. Eng. 2020, 17, 8168–8178. [Google Scholar] [CrossRef]
- Zang, L.; Wang, X.; Yan, P.; Zhao, Z. Structural Design and Characteristics of a Non-Pneumatic Tire with Honeycomb Structure. Mech. Adv. Mater. Struct. 2022, 29, 4066–4073. [Google Scholar] [CrossRef]
- Zhou, H.; Li, H.; Mei, Y.; Wang, G.; Liu, C.; Zhang, L. Research on Vibration Reduction Method of Nonpneumatic Tire Spoke Based on the Mechanical Properties of Domestic Cat’s Paw Pads. Appl. Bionics Biomech. 2021, 2021, e9976488. [Google Scholar] [CrossRef]
- Xu, H.; Zhao, Y.; Ye, C.; Lin, F. Integrated Optimization for Mechanical Elastic Wheel and Suspension Based on an Improved Artificial Fish Swarm Algorithm. Adv. Eng. Softw. 2019, 137, 102722. [Google Scholar] [CrossRef]
- Zhao, Y.; Xu, H.; Deng, Y.; Wang, Q. Multi-Objective Optimization for Ride Comfort of Hydro-Pneumatic Suspension Vehicles with Mechanical Elastic Wheel. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2019, 233, 2714–2728. [Google Scholar] [CrossRef]
- Ding, R.; Wang, P.; Wang, R.; Sun, D. Design and Optimization of a New Vibration Damping System for the Driving Characteristics of the Selected Case of Replacing Pneumatic Wheels with Nonpneumatic Wheels. Shock Vib. 2023, 2023, e6050633. [Google Scholar] [CrossRef]
- Liu, W.; Wang, R.; Rakheja, S.; Ding, R.; Meng, X.; Sun, D. Vibration Analysis and Adaptive Model Predictive Control of Active Suspension for Vehicles Equipped with Non-Pneumatic Wheels. J. Vib. Control 2023, 30, 3207–3219. [Google Scholar] [CrossRef]
- Jiang, Y.; Wang, R.; Ding, R.; Zhou, Y. Design and Hybrid Control of a New Self-Powered Electromagnetic Suspension Actuator Matched with Non-Pneumatic Tire. Int. J. Automot. Technol. 2023, 24, 159–169. [Google Scholar] [CrossRef]
- Shao, X.; Naghdy, F.; Du, H.; Qin, Y. Coupling Effect between Road Excitation and an In-Wheel Switched Reluctance Motor on Vehicle Ride Comfort and Active Suspension Control. J. Sound Vib. 2019, 443, 683–702. [Google Scholar] [CrossRef]
- ISO 8608; Mechanical Vibration-Road Surface Profiles-Reporting of Measured Data. ISO: Geneva, Switzerland, 1995.
- Guo, L.-X.; Zhang, L.-P. Robust H∞ Control of Active Vehicle Suspension under Non-Stationary Running. J. Sound Vib. 2012, 331, 5824–5837. [Google Scholar] [CrossRef]
- Liu, C.; Chen, L.; Lee, H.P.; Yang, Y.; Zhang, X. Generalized Skyhook-Groundhook Hybrid Strategy and Control on Vehicle Suspension. IEEE Trans. Veh. Technol. 2023, 72, 1689–1700. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, X.; Wong, P.K.; Xie, Z.; Jia, J.; Li, W. Multi-Objective Frequency Domain-Constrained Static Output Feedback Control for Delayed Active Suspension Systems with Wheelbase Preview Information. Nonlinear Dyn. 2021, 103, 1757–1774. [Google Scholar] [CrossRef]
- Hong, K.-S.; Sohn, H.-C.; Hedrick, J.K. Modified Skyhook Control of Semi-Active Suspensions: A New Model, Gain Scheduling, and Hardware-in-the-Loop Tuning. J. Dyn. Syst. Meas. Control 2002, 124, 158–167. [Google Scholar] [CrossRef]
- Wang, R.; Sheng, F.; Ding, R.; Meng, X.; Sun, Z. Vehicle Attitude Compensation Control of Magneto-Rheological Semi-Active Suspension Based on State Observer. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2021, 235, 3299–3313. [Google Scholar] [CrossRef]
- Dugard, L.; Sename, O.; Aubouet, S.; Talon, B. Full Vertical Car Observer Design Methodology for Suspension Control Applications. Control Eng. Pract. 2012, 20, 832–845. [Google Scholar] [CrossRef]

| Description | Unit | Value |
|---|---|---|
| Sprung mass ) | kg | 201 |
| Unsprung mass | kg | 38.8 |
| Spring Stiffness ) | N/m | 11,413 |
| Acceleration due to gravity ) | m/s2 | 9.81 |
| Maximum suspension travel ) | m | 0.06 |
| Maximum output force ) | N | 3000 |
| Wheel Deflection (×10−3 m) | Control Gain |
|---|---|
| Control Scheme | RMS of Sprung Mass Acceleration | RMS of Dynamic Wheel Load | ||
|---|---|---|---|---|
| Value (m/s2) | Improvement | Value (kN) | Improvement | |
| Passive | 1.327 | / | 1.042 | / |
| Controller 1 | 1.188 | 10.5% | 1.136 | −9.0% |
| Controller 2 | 1.061 | 20.0% | 1.087 | −4.3% |
| Control Scheme | RMS of Sprung Mass Acceleration | RMS of Dynamic Wheel Load | ||
|---|---|---|---|---|
| Value (m/s2) | Improvement | Value (kN) | Improvement | |
| Passive | 1.038 | / | 1.041 | / |
| Controller 1 | 0.939 | 9.5% | 1.139 | −9.4% |
| Controller 2 | 0.818 | 21.2% | 1.088 | −4.5% |
| Control Scheme | P-P Value of the Sprung Mass Acceleration (m/s2) | P-P Value of the Dynamic Wheel Load (kN) | ||
|---|---|---|---|---|
| Value | Improvement | Value | Improvement | |
| Passive | 10.392 | / | 2.155 | / |
| Controller 1 | 8.517 | 18.0% | 1.911 | 11.3% |
| Controller 2 | 4.092 | 60.6% | 1.239 | 42.5% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Liu, W.; Ding, R.; Sun, D.; Wang, R. Reference Model-Based Backstepping Control of Semi-Active Suspension for Vehicles Equipped with Non-Pneumatic Wheels. Machines 2025, 13, 476. https://doi.org/10.3390/machines13060476
Chen J, Liu W, Ding R, Sun D, Wang R. Reference Model-Based Backstepping Control of Semi-Active Suspension for Vehicles Equipped with Non-Pneumatic Wheels. Machines. 2025; 13(6):476. https://doi.org/10.3390/machines13060476
Chicago/Turabian StyleChen, Jie, Wei Liu, Renkai Ding, Dong Sun, and Ruochen Wang. 2025. "Reference Model-Based Backstepping Control of Semi-Active Suspension for Vehicles Equipped with Non-Pneumatic Wheels" Machines 13, no. 6: 476. https://doi.org/10.3390/machines13060476
APA StyleChen, J., Liu, W., Ding, R., Sun, D., & Wang, R. (2025). Reference Model-Based Backstepping Control of Semi-Active Suspension for Vehicles Equipped with Non-Pneumatic Wheels. Machines, 13(6), 476. https://doi.org/10.3390/machines13060476







