A Comprehensive Analysis of the Loss Mechanism and Thermal Behavior of a High-Speed Magnetic Field-Modulated Motor for a Flywheel Energy Storage System
Abstract
1. Introduction
2. Theoretical Model of Loss Calculation and Thermal Analysis
2.1. Motor Structure and Key Parameters
2.2. Electromagnetic Principles of Magnetic Field-Modulated Motors
2.3. Comprehensive Loss Classification and Calculation Methods
2.4. Advanced Thermal Modeling Methods
2.5. Innovative Analytical Models for Loss Estimation and Thermal Prediction
3. Finite Element Analysis of Loss Distribution
3.1. Simulation Setup and Parameter Configuration
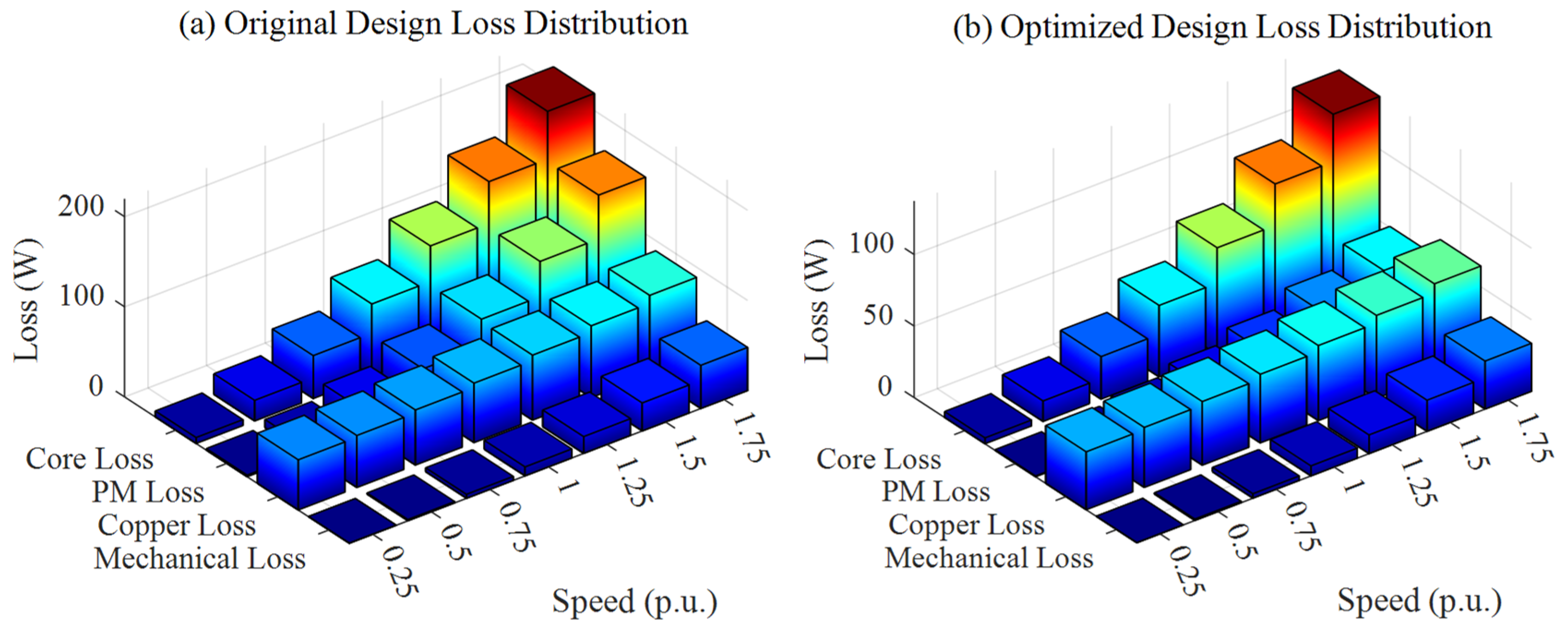
3.2. Comparative Analysis of Loss Distribution in Different Components
3.3. Impact of Operating Speed on Loss Characteristics
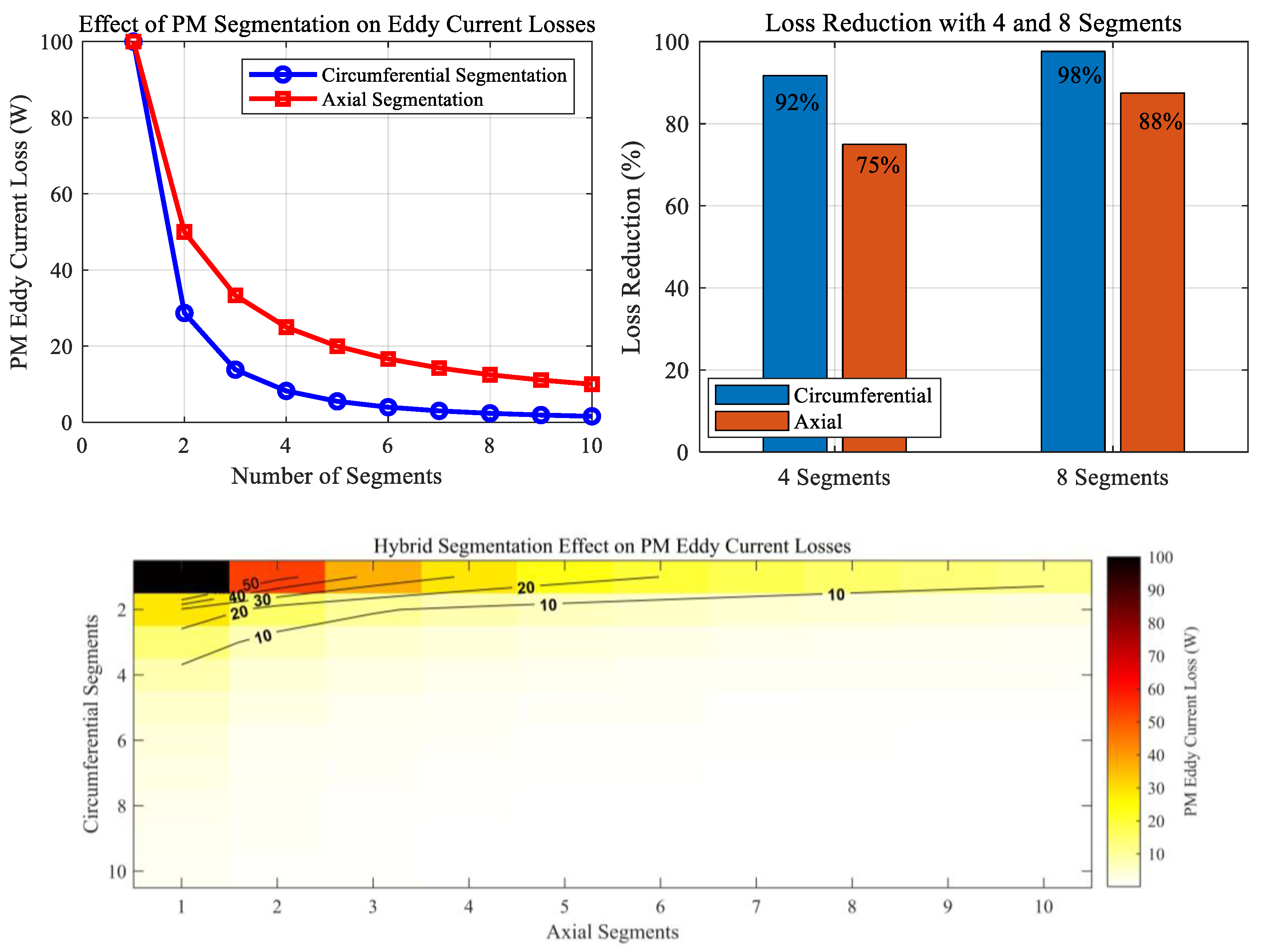
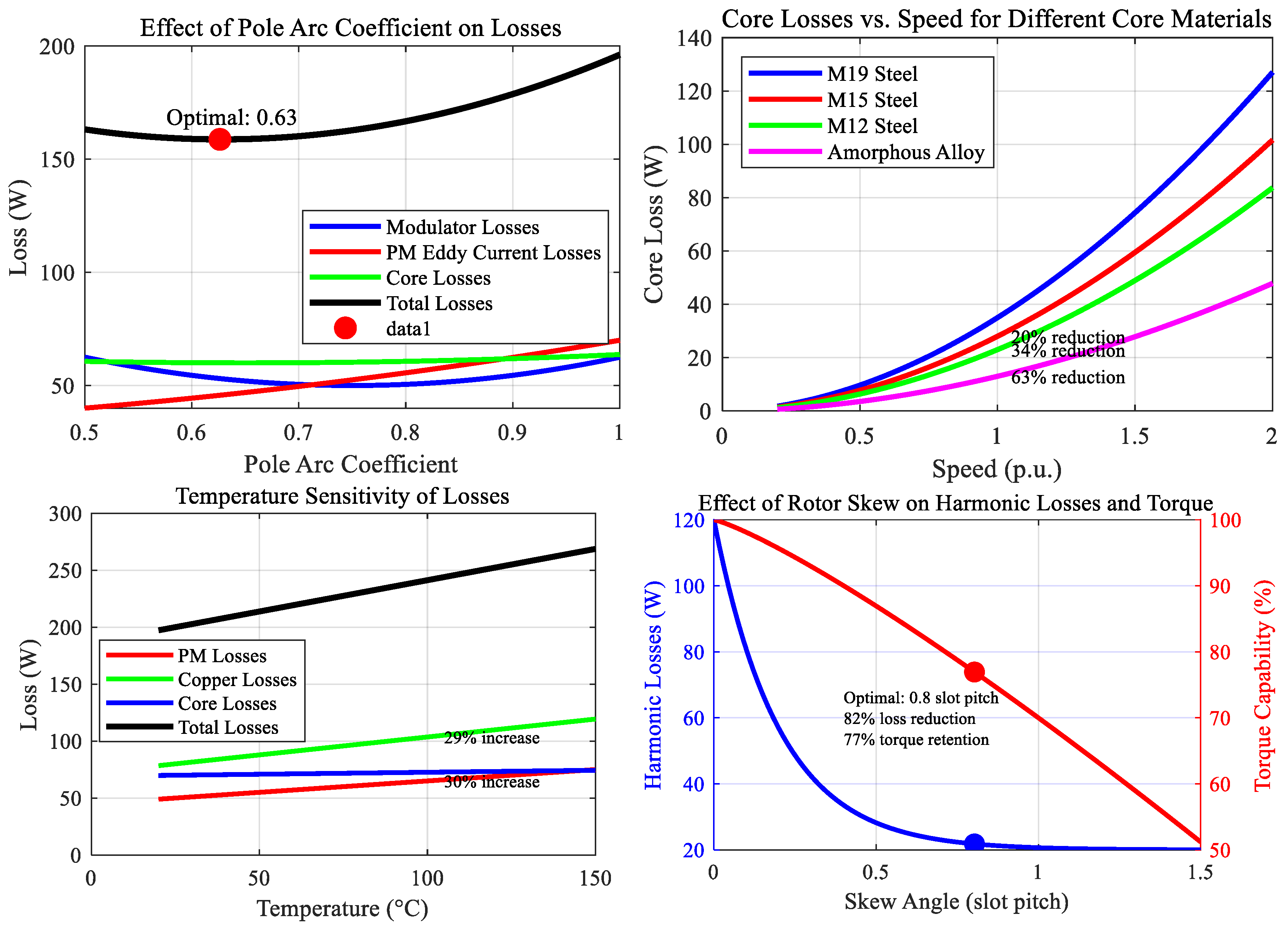
3.4. Sensitivity Analysis of Loss to Design Parameters
4. Loss Reduction Optimization Design
4.1. Proposed Innovative Design Improvements
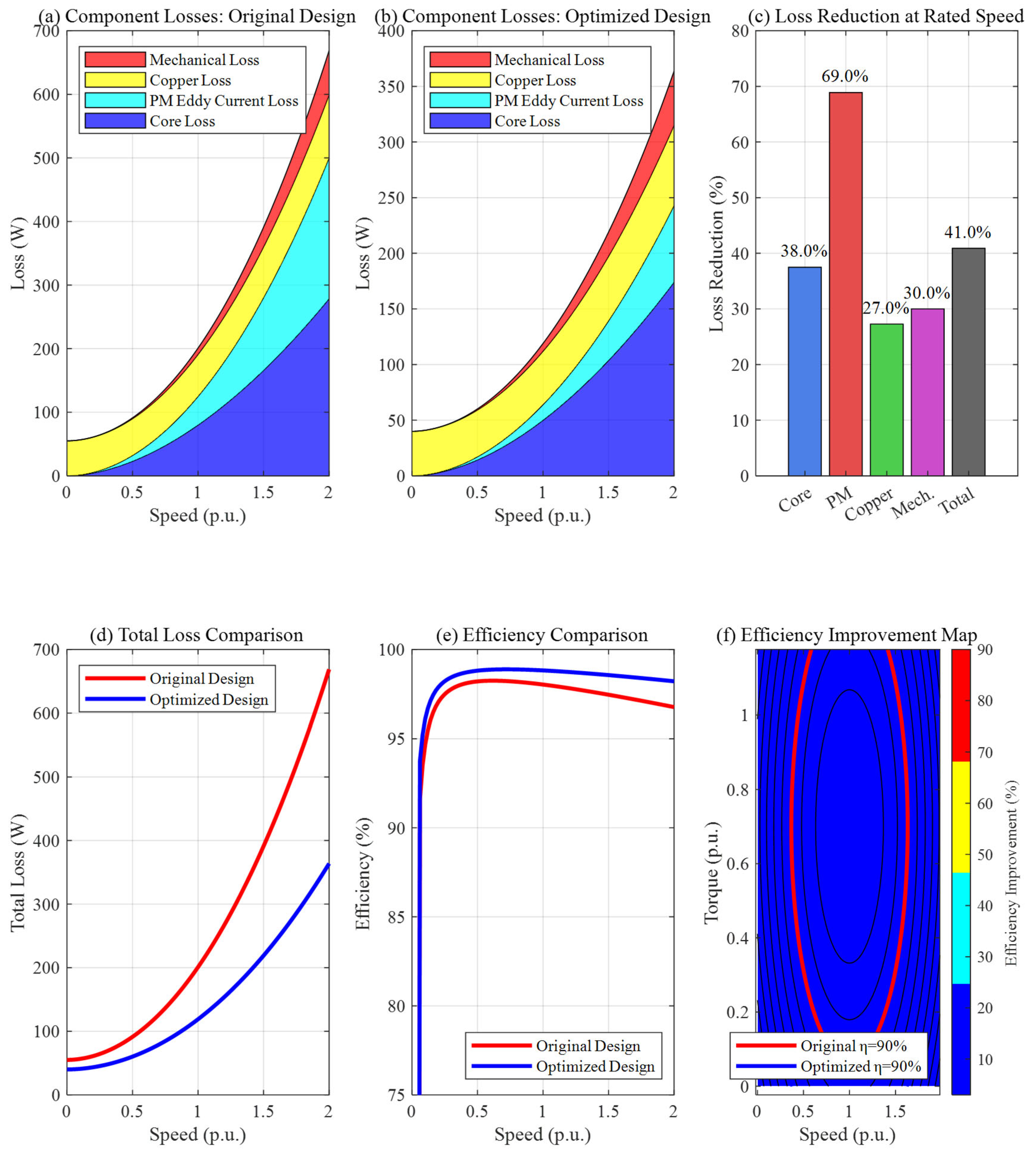
4.2. Comparative Analysis of Losses Before and After Optimization
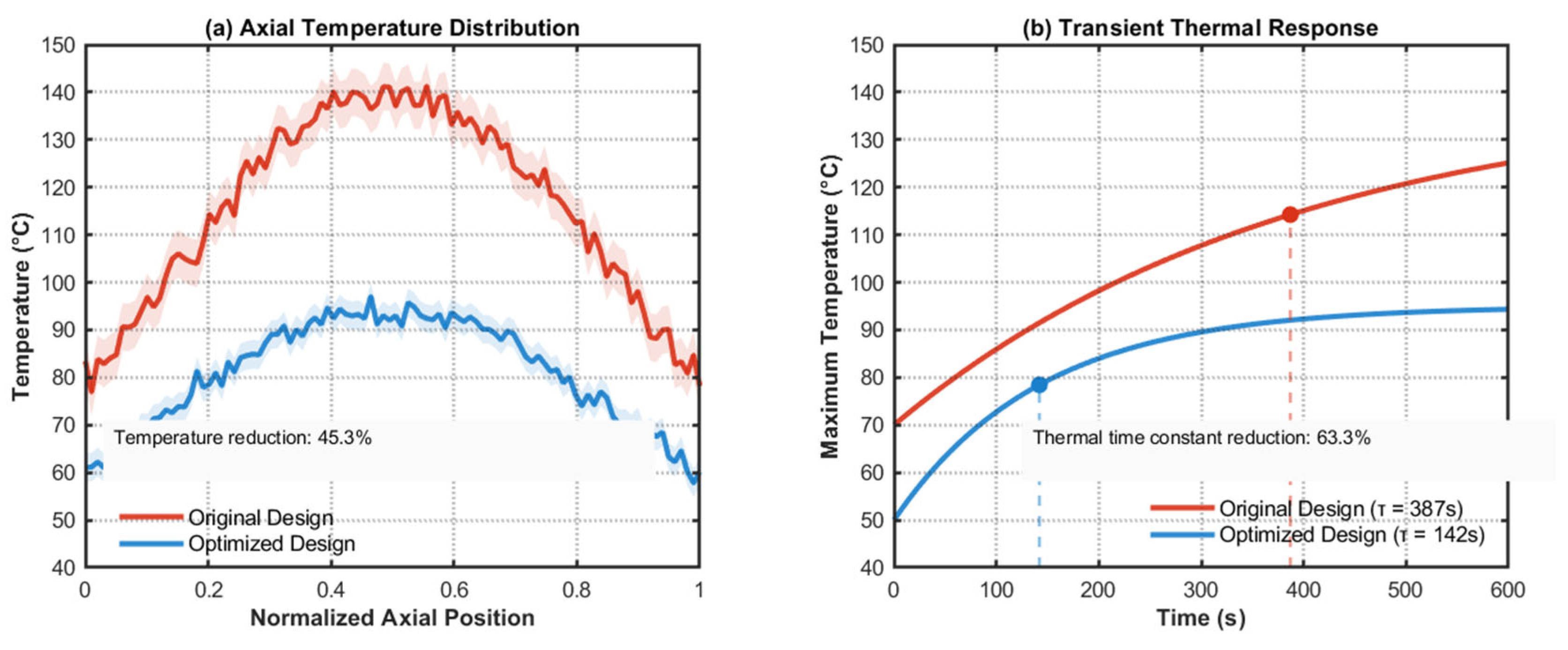
4.3. Thermal Performance Improvement Assessment
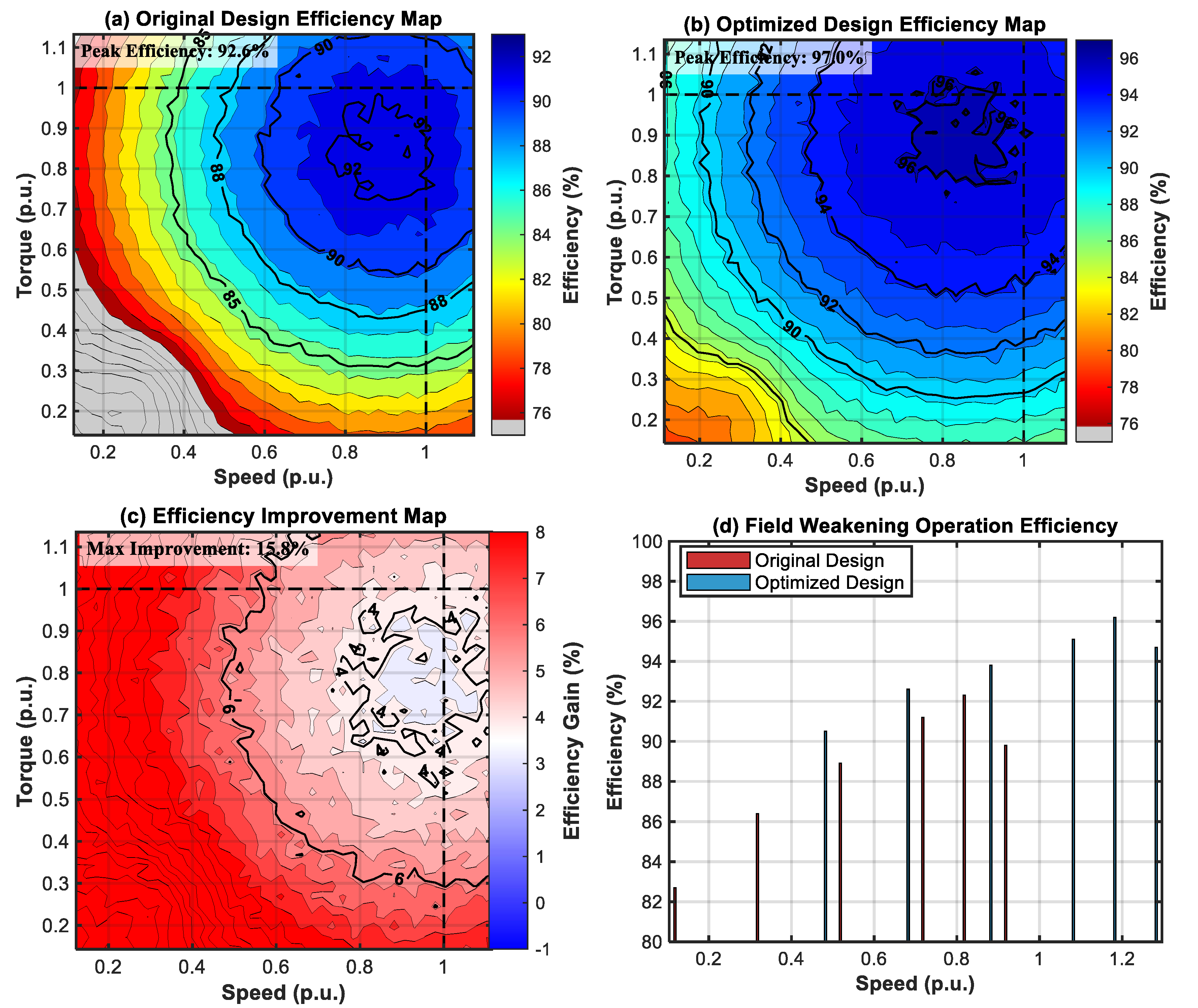
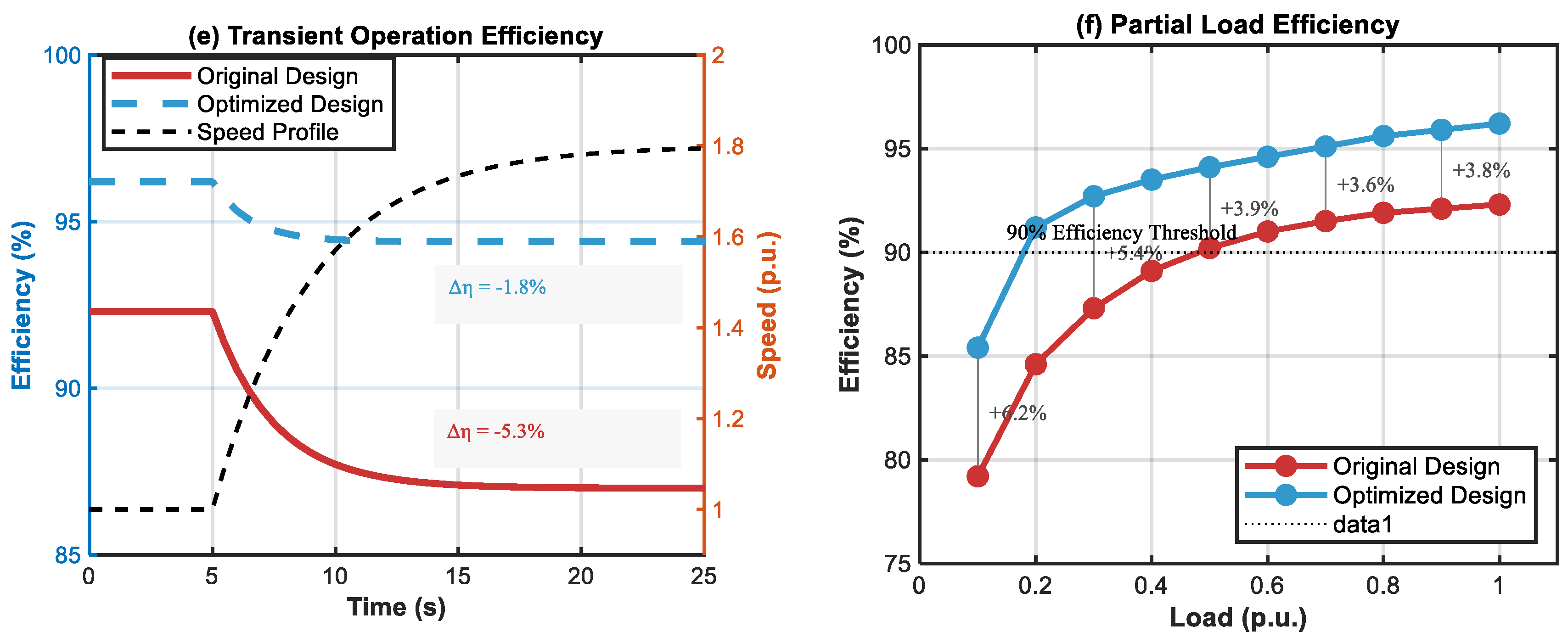
4.4. Efficiency Enhancement Under Various Operating Conditions
5. Experimental Verification
5.1. Prototype Design and Testing Platform
5.2. Measurement Methodology for Different Loss Components
5.3. Experimental Results and Validation of Theoretical and Simulation Models
5.4. Performance Comparison Under Different Operating Conditions
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cao, H.; Kou, B.; Zhang, D.; Li, W.; Zhang, X. Research on loss of high-speed permanent-magnet synchronous motor for flywheel energy storage. In Proceedings of the 2012 16th International Symposium on Electromagnetic Launch Technology, Beijing, China, 15–19 May 2012; pp. 1–5. [Google Scholar]
- Kisling, B.; Ramus, K.; Santora, M.; Berven, C.; Law, J. Active magnetic-bearing control and hardware for an experimental flywheel energy-storage system. In Proceedings of the IECON 2018—44th Annual Conference of the IEEE Industrial Electronics Society, Washington, DC, USA, 21–23 October 2018; pp. 1652–1657. [Google Scholar]
- Bolund, B.; Bernhoff, H.; Leijon, M. Flywheel energy and power storage systems. Renew. Sustain. Energy Rev. 2007, 11, 235–258. [Google Scholar] [CrossRef]
- Zhang, S.; Li, S.; Qu, R. Rotor loss analysis of PMSM in flywheel energy-storage UPS. IEEE Trans. Ind. Appl. 2017, 53, 3425–3435. [Google Scholar]
- Sun, M.; Xu, Y.; Zhang, W. Multiphysics analysis of flywheel energy-storage system based on cup-winding PMSM. IEEE Trans. Energy Convers. 2023, 38, 2684–2694. [Google Scholar] [CrossRef]
- Ionel, D.; Popescu, M.; McGilp, M.; Miller, T.J.E.; Dellinger, S. Assessment of torque components in brushless PM machines. IEEE Trans. Ind. Appl. 2005, 41, 1149–1158. [Google Scholar] [CrossRef]
- Zhang, Z.; McLoone, Y.; Cao, W. Power-loss and thermal analysis of a MW high-speed PMSM. IEEE Trans. Energy Convers. 2017, 32, 1468–1478. [Google Scholar] [CrossRef]
- Huynh, C.; Zheng, L.; McMullen, P. Thermal performance evaluation of a high-speed FESS. In Proceedings of the IECON 2007—33rd Annual Conference of the IEEE Industrial Electronics Society, Taipei, Taiwan, 5–8 November 2007; pp. 163–168. [Google Scholar]
- Pan, W.; Zhang, T.; Su, H. Thermal-management analysis of FESS with water cooling. IEEE Access 2023, 11, 134780–134789. [Google Scholar]
- Choudhury, S.; Bhowmik, M. Flywheel energy-storage systems: A critical review. Int. Trans. Electr. Energy Syst. 2021, 31, e13024. [Google Scholar] [CrossRef]
- Frandsen, T.V.; Mathe, L.; Berg, N.I.; Holm, R.K. Motor-integrated PM gear in a battery EV. IEEE Trans. Ind. Appl. 2015, 51, 1516–1525. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, S.; Song, Y.; Qi, W.; Guo, Q.; Li, X.; Kong, L.; Chen, J. Real-Time Global Optimal Energy Management Strategy for Connected PHEVs Based on Traffic Flow Information. IEEE Trans. Intell. Transp. Syst. 2024, 25, 20032–20042. [Google Scholar] [CrossRef]
- Du, G.; Xu, W.; Zhu, J.; Huang, N. Power-loss and thermal analysis for high-power high-speed PM machines. IEEE Trans. Ind. Electron. 2020, 67, 2722–2733. [Google Scholar] [CrossRef]
- Holm, S.R.; Polinder, H.; Ferreira, J. Analytical modelling of a PM synchronous machine in a flywheel. IEEE Trans. Magn. 2007, 43, 1955–1967. [Google Scholar] [CrossRef]
- Jandura, P.; Richter, A.; Ferková, Ž. Flywheel energy storage system for city railway. In Proceedings of the 2016 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Capri, Italy, 22–24 June 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1155–1159. [Google Scholar]
- Sun, X.; Chen, L.; Yang, Z. Overview of bearingless PMSMs. IEEE Trans. Ind. Electron. 2013, 60, 5528–5538. [Google Scholar] [CrossRef]
- Jara, W.; Tapia, J.; Pyrhonen, J. Bearing-less flywheel drive with homopolar bias. IET Electr. Power Appl. 2014, 8, 189–198. [Google Scholar]
- Xue, B.; Wang, J.; Guo, J. Composite PM rotor design of a 200 kW high-speed PMSM for FESS. IEEE Trans. Transp. Electrif. 2019, 5, 1115–1127. [Google Scholar]
- Zhu, Z.Q.; Ng, K.; Schofield, N.; Howe, D. Improved analytical modelling of rotor eddy-current loss with surface PMs. IEE Proc. Electr. Power Appl. 2004, 151, 641–650. [Google Scholar] [CrossRef]
- Liu, Y.; Ou, M.; Yu, X.; Zhu, Z. Thermal analysis of axial-flux PM flywheel machine. IEEE Access 2021, 9, 37246–37256. [Google Scholar]
- Nguyen, T.D.; Foo, G. Adaptive sliding-mode control for FESS with active magnetic bearings. IEEE Trans. Ind. Electron. 2020, 67, 2249–2258. [Google Scholar]
- IEEE Standard 393-1991; IEEE Standard for Test Procedure for Magnetic Materials—Epstein Frame Method. IEEE: New York, NY, USA, 1991.
- Higginson, I.; Hess, H.L.; Law, J.D. Ironless PMSM stiffness calculation for FESS. In Proceedings of the 2011 IEEE International Electric Machines & Drives Conference (IEMDC 2011), Niagara Falls, ON, Canada, 15–18 May 2011; pp. 1357–1362. [Google Scholar]
- Li, L.; Li, W.; Li, D.; Li, J.; Shen, J.; Fan, Y.; Wang, P. Electromagnetic-field calculation for FESS in discharge mode. In Proceedings of the 2017 20th International Conference on Electrical Machines and Systems (ICEMS), Sydney, Australia, 11–14 August 2017; pp. 1–5. [Google Scholar]
- Isikveren, A.T. Quadrant-based algorithmic nomographs for hybrid/electric-aircraft pre-design. J. Aircr. 2018, 55, 396–405. [Google Scholar] [CrossRef]
- Wang, C.; Shen, J.; Luk, P.; Fei, W.; Jin, M. Design and performance of a high-speed axial-flux PM machine for FESS. IEEE Trans. Magn. 2019, 55, 1–10. [Google Scholar]
- Kim, S.H.; Choi, J.Y.; Hong, J.P.; Jung, S.K. Loss analysis of IPMSM for FESS with temperature variation. In Proceedings of the 2013 International Conference on Electrical Machines and Systems (ICEMS 2013), Busan, Republic of Korea, 26–29 October 2013; pp. 584–587. [Google Scholar]
- Dong, J.; Huang, Y.; Jin, L.; Lin, H. Comparative study of SPM and IPM motors for high-speed applications. IEEE Trans. Appl. Supercond. 2016, 26, 1–4. [Google Scholar]
- Suntharalingam, P.; Pham, T.; Lukic, S.M. Modelling and control of a novel flywheel energy-storage system. In Proceedings of the 2010 IEEE Energy Conversion Congress and Exposition (ECCE 2010), Delft, The Netherlands, 25–27 August 2010; pp. 3159–3166. [Google Scholar]
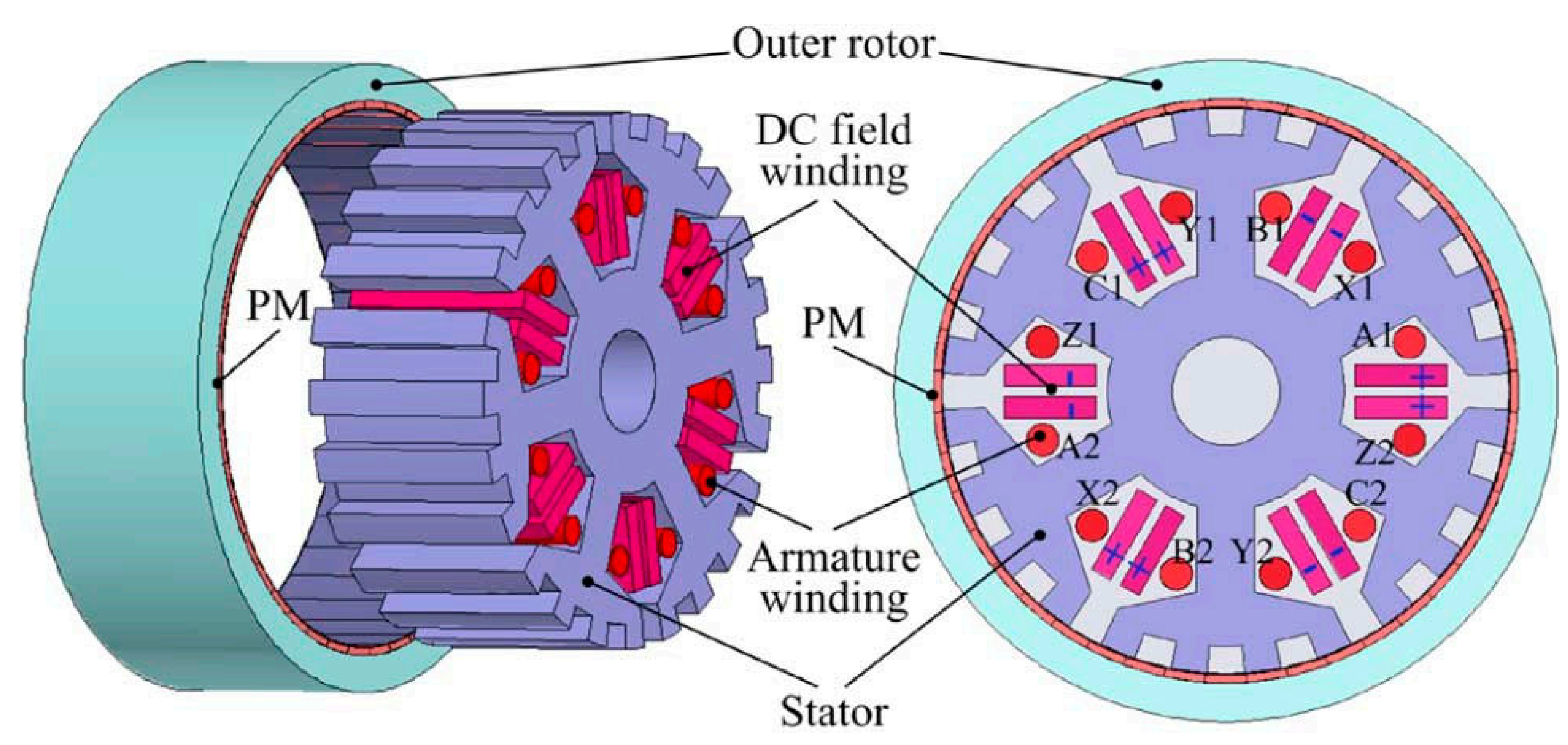
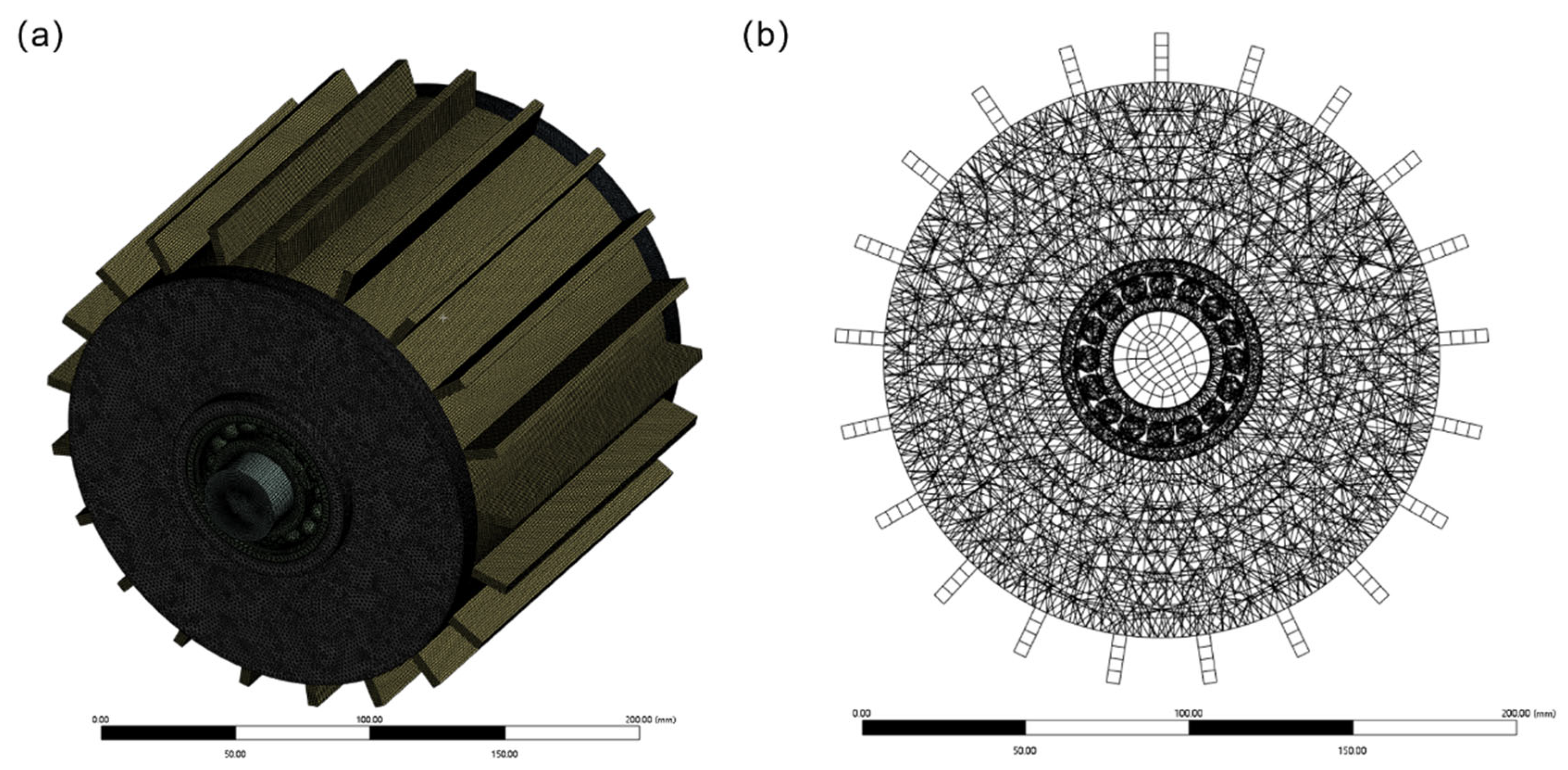
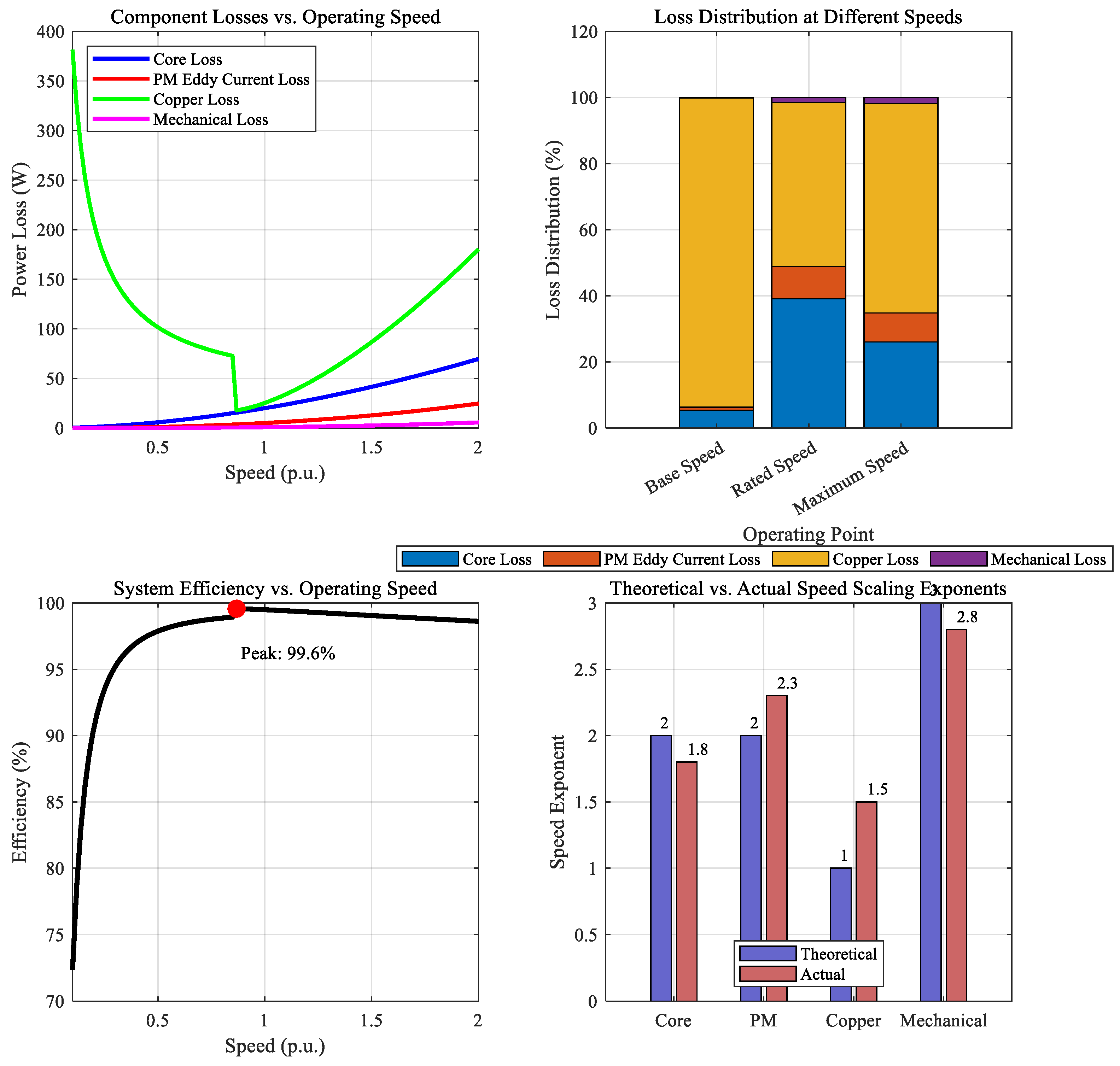





| Parameter | Value |
|---|---|
| Rated power | 5 kW |
| Rated speed | 30,000 rpm |
| Stator outer diameter | 120 mm |
| Rotor outer diameter | 60 mm |
| Active length | 85 mm |
| Air gap length | 0.8 mm |
| Number of stator slots | 12 |
| Number of rotor pole pairs | 4 |
| Number of modulators | 5 |
| Permanent magnet material | N42SH |
| Core material | M250-35A |
| Maximum flux density | 1.6 T |
| Loss Category | Loss Component | Physical Mechanism | Calculation Method | Reference |
|---|---|---|---|---|
| Core Losses | Hysteresis Loss | Magnetic domain wall movement | [14] | |
| Eddy Current Loss | Induced currents in core material | [13] | ||
| Excess Loss | Micro-eddy currents | [13] | ||
| Copper Losses | DC Resistive Loss | Joule heating in conductors | [1] | |
| Skin Effect Loss | Current density redistribution | [15] | ||
| Proximity Effect Loss | Adjacent conductor interaction | [10] | ||
| Mechanical Losses | Bearing Friction Loss | Contact friction in bearings | [4] | |
| Windage Loss | Air friction on rotating surfaces | [9] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mai, Q.; Hu, Q.; Chen, X. A Comprehensive Analysis of the Loss Mechanism and Thermal Behavior of a High-Speed Magnetic Field-Modulated Motor for a Flywheel Energy Storage System. Machines 2025, 13, 465. https://doi.org/10.3390/machines13060465
Mai Q, Hu Q, Chen X. A Comprehensive Analysis of the Loss Mechanism and Thermal Behavior of a High-Speed Magnetic Field-Modulated Motor for a Flywheel Energy Storage System. Machines. 2025; 13(6):465. https://doi.org/10.3390/machines13060465
Chicago/Turabian StyleMai, Qianli, Qingchun Hu, and Xingbin Chen. 2025. "A Comprehensive Analysis of the Loss Mechanism and Thermal Behavior of a High-Speed Magnetic Field-Modulated Motor for a Flywheel Energy Storage System" Machines 13, no. 6: 465. https://doi.org/10.3390/machines13060465
APA StyleMai, Q., Hu, Q., & Chen, X. (2025). A Comprehensive Analysis of the Loss Mechanism and Thermal Behavior of a High-Speed Magnetic Field-Modulated Motor for a Flywheel Energy Storage System. Machines, 13(6), 465. https://doi.org/10.3390/machines13060465






