Abstract
With increasing demand for high-precision motion control systems, high operational speed and load capacity are imposed with piezoelectric stick-slip actuators based on compliant mechanisms, yet their performances are often constrained by the step size and move speed. In this paper, a novel piezoelectric stick-slip actuator featuring flexure beams and a trapezoidal driving foot is proposed for high dynamic performance and load requirements. The trapezoidal structure consists of a trapezoidal driving foot to differentiate the friction in the stick and slip phases, four flexure beams for the high resonant frequency due to distributed compliance and the high load capacity due to structural geometry, and a rigid rod for motion transmission. At first, the mechanism design and the working principle are described in detail. Then, its dominant performances are predicted through finite element analysis, including the step size and the first natural frequency. On this basis, the structural parameters are optimized through the genetic algorithm. As a result, the forward displacement in the stick phase can be obtained as 4.8 m through FEA simulations, where the first natural frequency can be observed as 627 Hz.
1. Introduction
The demand for high-precision motion control systems has grown exponentially in fields such as micro-robotics [1], optical alignment [2], semiconductor manufacturing [3], and biomedical devices [4]. Smart materials, which exhibit responsive behavior to external stimuli such as electrical fields, temperature, stress, or magnetic fields, can respond almost instantaneously to electrical inputs, enabling ideal solutions for high-precision systems [5]. Enabling motion in the sub-nanometer range with no resolution limitations, piezoelectric actuators have gained significant applications and advantages in these systems, leading to the need for mechanisms to transmit output displacement and force [6]. Compared to traditional rigid mechanisms, several advantages have been highlighted by integrating compliant mechanisms, including compact structure, fast response, zero friction, and lightweight [7]. Utilizing the asymmetry between static and dynamic friction, stick-slip piezoelectric actuators can achieve long-range travel while ensuring fine positioning, leading to great prominence and rich development [8]. Despite their advantages, conventional stick-slip actuators are faced with inherent limitations, notably trade-offs with respect to step size, operational speed, and load capacity [9]. Specifically, recent advancements focus on achieving sub-nanometer step sizes, enhancing load capacities through hybrid actuation and compliant mechanisms, and boosting operational speeds via optimized driving waveforms and structural dynamics, enabling broader applications in precision robotics and high-force microsystems [10]. Hence, it underscores the need for a novel structure to achieve objectives of high operational speed and load capacity, accompanied by optimization to minimize the sacrifice of step size.
Compliance segments in compliant mechanisms can be classified by flexibility concentration as lumped compliance and distributed compliance [11]. Flexibility in lumped compliant mechanisms is concentrated in localized areas, primarily in notched hinges, while in distributed compliant mechanisms, it is spread throughout the entire flexure, primarily in flexure beams [12]. Although lumped compliant mechanisms are simpler to design and model, they compromise stress uniformity and motion adaptability [13]. For example, an inchworm-inspired piezoelectric stepper composed of two bridge-type compliant mechanisms with round notched hinges was proposed by Liu et al., in which the stiffness matrix method was applied for kinetostatic modeling, and the finite element analysis was used for structural parameter optimization [14]. Additionally, a piezoelectric injector featuring the parallelogram fixed-guided mechanism with elliptical notched hinges was proposed by Dai et al. for vibration penetration of oocytes, in which the finite element analysis was used for dynamic modeling and parametric optimization [15]. In contrast, distributed compliant mechanisms excel in dynamic, multi-axis applications but require advanced design and complicated modeling [16]. For example, a two-stage constant force mechanism featuring two pairs of bistable fixed-guided flexure beams, parallelly combined with positive stiffness fixed-guided flexure beams, was proposed by Ye et al., in which the elliptical integral method was utilized for nonlinear kinetostatic modeling to map force to displacement analytically [17]. Additionally, a linear piezoelectric actuator composed of symmetrical Z-shaped flexure beams was developed by Xie et al. based on the parasitic motion principle, in which the compliance matrix method was applied for kinetostatic modeling, and the wire electrical discharge machining was adopted for experimental validation [18]. In addition, few piezoelectric stick-slip actuators utilized both lumped compliance and distributed compliance, i.e., hybrid compliant mechanisms, in which the flexure hinges are normally utilized to realize the stick-slip function, and the flexure beams could be used for motion guiding [19] and force measurement [20]. It is useful in certain applications, but leads to more complex modeling and harder manufacturing. Overall, the choice depends on the requirements for precision, durability, and complexity in specific applications.
Numerous piezoelectric stick-slip steppers have been developed over the past decade [21]. As for piezoelectric stick-slip actuators based on lumped compliance, a trapezoidal piezoelectric stick-slip stepper was proposed by Cheng et al. based on four circle notched hinges, in which the friction state changing was determined by the different angles between the driving foot and the slider [22]. The experimental results showed that the maximum output velocity and load are 5.96 mm/s and 3 N at a voltage of 100 Vp−p and a frequency of 500 Hz. A triangular-shaped piezoelectric stick-slip stepper was proposed by Zhang et al. based on two short-arm notched hinges and one arc-notched hinge, in which the clamping-pushing coupling motion would occur with the piezoelectric stack stretching [23]. Its simulation results showed that the maximum stress is concentrated on the thinnest part of the arc-notched hinge as 1.69 GPa. The experimental results showed that the output velocity is raised with increasing driving frequency within the bandwidth of 3500 Hz, while reducing outside the bandwidth. Its maximum output velocity is 46.67 mm/s under the driving voltage of 80 V at 3500 Hz. A L-shaped piezoelectric stick-slip stepper was proposed by Huang et al., in which the slip state was shortened relatively due to the inertial force, leading to the larger step size [24]. The experimental results showed that the maximum motion speed is 16.67 mm/s under the driving frequency of 800 Hz. As for piezoelectric stick-slip actuators based on distributed compliance, a piezoelectric stick-slip actuator was proposed by Yu et al. based on flexure beams, which is composed of a parallelogram structure with two shorter flexure beams combined with a longer flexure beam in parallel [25]. Simulation results showed that the maximum equivalent stress of the stator is 202.46 MPa. Experimental results showed the maximum speed as 70.260 mm/s, the thrust as 1.36 N at an excitation voltage of 8 Vp−p and 33.1 kHz. A piezoelectric rotary motor was proposed by Pan et al. based on flexure beams, which is composed of an asymmetric stator with four driving feet placed in a parallelogram and internally connected to a circular rotor [26]. Experimental results showed that the typical output of the prototype is a no-load speed of 176.5 rpm and a maximum torque of 29.4 N·mm at an excitation voltage of 274 Vp−p and 1.961 kHz. Considering high velocity and load requirements, the bandwidth and the vertical stiffness of the stick-slip stepper need to be focused, while the step size needs to be as large as possible.
To address the identified challenges, a piezoelectric stick-slip actuator is developed in this paper, primarily comprising a piezoelectric stack, a slider, and a connector between them, in which a novel trapezoidal structure is proposed as the connector for high dynamic performance and load requirements. The trapezoidal structure consists of a trapezoidal driving foot to differentiate the friction in the stick and slip phases, four flexure beams to constrain parasitic motion and distribute stresses uniformly, and a rigid rod for motion transmission. The main contributions of this paper are as follows: (i) A piezoelectric stick-slip actuator with a novel trapezoidal structure is proposed to realize stick-slip motion. (ii) The W-shaped structure with four flexure beams is utilized for the high resonant frequency due to distributed compliance and the high load capacity due to structural geometry. (iii) The trapezoidal driving foot is applied to make the friction in the stick-slip process more differentiated to improve the stability and robustness of the system.
The remainder of this paper is organized as follows. The conceptual design of the piezoelectric stick-slip actuator is described in detail in Section 2, where the mechanism design is presented as to the topological arrangement and the motion transmission, as well as the working principle. Then, the dominant performances are predicted by finite element analysis (FEA) in Section 3, while the structural parameters are optimized for the designed objectives. FEA simulations are conducted to validate the design and optimization in Section 4. Finally, the main works are concluded and discussed in Section 5.
2. Conceptual Design
2.1. Mechanism Design
As shown in Figure 1, a piezoelectric stick-slip actuator is developed, in which a novel trapezoidal structure is proposed for high dynamic performance and load requirements. It can be seen that the proposed piezoelectric stick-slip actuator is composed of a slider, a piezoelectric stack (model: Coremorrow PSt150/5 × 5/20 L, maximum driving voltage: 150 V, stroke: 20 m, resonant frequency: 50 kHz), four fixed screws, a preloading screw, and the trapezoidal structure. The function of each component in the mechanism can be detailed as follows. The inverse piezoelectric effect is utilized to achieve nanometer-scale displacements for the piezoelectric stack, serving as the primary driving element. When an electrical voltage is applied, the stack expands or contracts, generating precise movements essential for high-resolution positioning. The slider is regarded as the moving component, translating the deformation of the piezoelectric stack into linear displacement, which ensures efficient transfer of motion, allowing for smooth and accurate movement along the desired path. The rigid alignment and structural integrity are provided to the assembly, in which the fixed screws are arranged symmetrically to constrain the degrees of freedom, ensuring linear motion while minimizing parasitic tilting or bending. This arrangement enhances the overall stability and reliability of the system. The preloading screw is used to adjust the normal force between the piezoelectric stack and the slider. Enabling precise and adjustable preload, the stick-slip transition is enabled, thereby enhancing the repeatability of movements and reducing wear on the mechanical parts, which promotes durability and performance in high-frequency applications. The driving foot, four flexure beams, and the rigid rod are included in the trapezoidal structure, in which the driving foot is regarded as the output interface by converting the input motion from the piezoelectric stack into external displacement; four flexure beams are strategically configured in a ‘W’ shape to connect the driving foot to the rigid rod, which significantly determines the system’s first natural frequency and load capacity; the rigid rod is anchored to assemble the piezoelectric stack and take over its displacements.
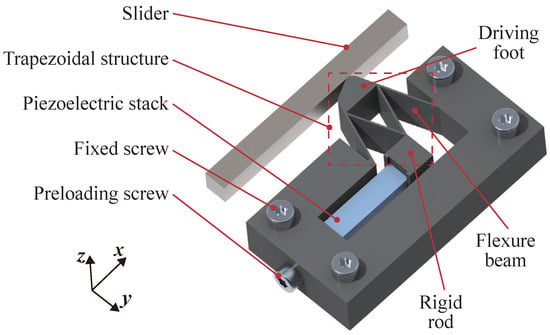
Figure 1.
Scheme of the proposed piezoelectric stick-slip actuator based on novel trapezoidal structure.
Regarding the topological arrangement, the assembly features a well-defined structural layout that ensures stability and optimal performance. Serving as the structural backbone, the rigid frame is securely anchored by four fixed screws arranged symmetrically, which provides exceptional rigidity and alignment, preventing unwanted movement during operation. Centrally positioned within the frame, the piezoelectric stack is mechanically anchored at one end to the frame and connected at the other end to the rigid rod of the trapezoidal structure, enabling effective transfer of output displacements. Four flexure beams are arranged between the rigid rod and the driving foot. The driving foot is in direct contact with the slider, providing the interface for displacement output, whose trapezoidal geometry enhances friction control and stress distribution.
As for the motion transmission, the actuator converts electrical energy into controlled linear motion. A ramped voltage is applied to the piezoelectric stack, causing it to expand linearly along the x-axis. The rigid rod takes over the linear displacement from the piezoelectric stack, causing it to move linearly along the x-axis. Fixed to the rigid frame through two sides of the W-shaped structure, an arc movement of the driving foot centered on the rigid rod is triggered on the plane due to the geometric arrangement. When static friction occurs, the slider moves in the x direction along with the driving foot.
2.2. Working Principle
As shown in Figure 2, the proposed piezoelectric stick-slip actuator converts electrical energy into controlled linear motion, governed by the following sequence in one cycle:
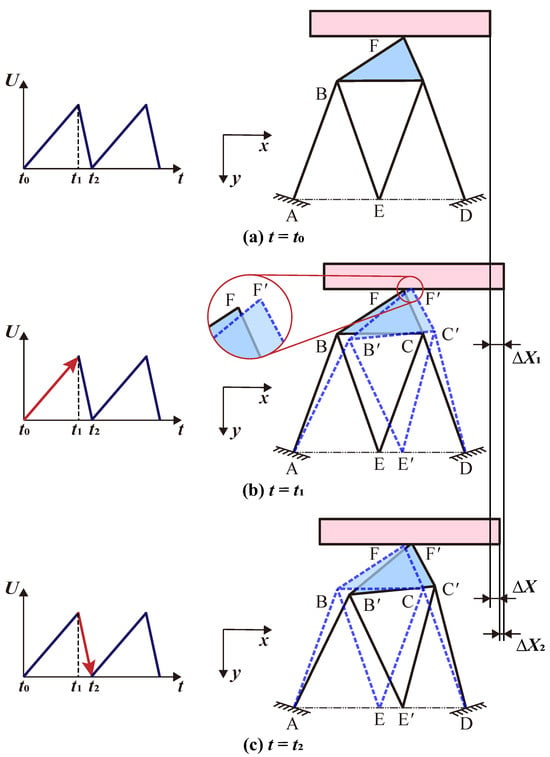
Figure 2.
Illustrator of the working principle of the proposed piezoelectric stick-slip actuator.
- (i)
- Initial phase (): When no voltage is applied to the piezoelectric stack, the system remains in its initial position, as shown in Figure 2a. In this configuration, point E receives the input displacement from the piezoelectric stack, while the flexure beams are fixed at points A and D. The driving foot is in direct contact with the slider at point F. Before commencing operation, it is crucial to determine the necessary preloading force to ensure optimal performance.
- (ii)
- Stick phase (): A slowly ramped voltage is applied to the piezoelectric stack, causing slow extension along the x direction, as shown in Figure 2b. Through the W-shaped flexure beams, the driving foot moves from point F to point F’ at through the arc path. Zooming in, the tiny displacement in the y-direction is very obvious, which can effectively increase positive pressure to ensure that the friction is becoming stronger during this phase, thereby making the stick motion stable. Additionally, the trapezoidal driving foot presses against the slider with its wider base to maximize the contact area, which increases static friction, ensuring a robust grip for controlled forward motion. Then, the slider moves forward incrementally, adhering to the driving foot’s motion .
- (iii)
- Slip phase (): When the voltage is abruptly reduced, the piezoelectric stack rapidly retracts. The driving foot moves from point F’ back to point F at , as shown in Figure 2c. This fast retraction causes the driving foot to pull away faster than the slider can respond, momentarily overcoming static friction. As a result, dynamic friction decreases, allowing the foot to slip backward in relation to the slider. Due to inertia and the reduction in friction, the slider remains in its forward position, resulting in a net forward displacement. During this rapid retraction, the tapered geometry of the foot minimizes the contact area with the slider, further reducing dynamic friction. This asymmetry in frictional forces allows for minimal backward slippage of the slider, ultimately facilitating substantial net forward displacement.
Repeated voltage cycles generate stepwise motion, enabling long-range travel with nanometer-scale resolution. The trapezoidal shape of the driving foot features sloped sides that impart directional stiffness, keeping the foot rigid during the stick phase while allowing for slight elastic deflection during the slip phase, facilitating a smooth decoupling. In addition, the absence of sharp corners in the trapezoidal design helps to evenly distribute mechanical stress across the contact interface. This even distribution minimizes localized wear and fatigue, significantly extending the lifespan.
3. Analysis and Optimization
In this Section, FEA is utilized to predict the dominant performances of the proposed piezoelectric stick-slip actuator precisely, including the step length, the coupling ratio, and the first natural frequency, as shown in Figure 3. Those structural parameters of the proposed trapezoidal structure, consisting of the trapezoidal driving foot, the W-shaped flexure beams, and the rigid rod, can be listed as follows:
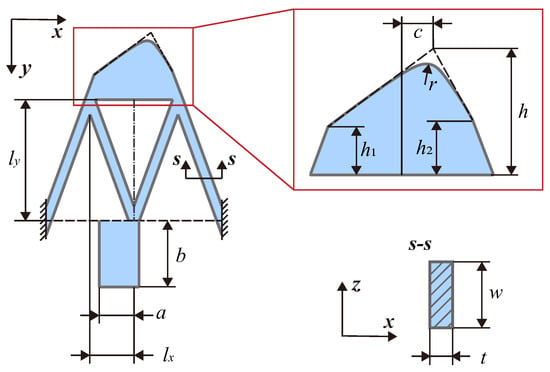
Figure 3.
Structural parameters of the proposed trapezoidal structure consisting of the trapezoidal driving foot, the W-shaped flexure beams, and the rigid rod.
- (i)
- Rigid rod: Width a of the rigid rod in the x direction; width b of the rigid rod in the y direction; width w of the rigid rod in the z direction.
- (ii)
- Flexure beam: Width of each flexure beam in the x direction; width of each flexure beam in the y direction; width w of each flexure beam in the z direction.
- (iii)
- Trapezoidal driving foot: Position of the top anchor point with respect to the middle point at bottom as c and h in x and y directions; radius r of the top fillet; height of left and right corners as and ; width w of the driving foot in the z direction.
Initially, structural parameters are assigned based on prior experience to generate a parametric 3D model of the proposed actuator, as outlined in Table 1. Structural steel is selected as the material, featuring a density of 7850 kg/m3, a Young’s modulus of 200 GPa, and a Poisson’s ratio of 0.3. Next, tetrahedral meshing is performed for the mechanism. In detail, the flexure beam elements are refined to 0.4 mm, while coarser meshing is used for the rigid rod and trapezoidal driving foot, given their minimal sectional deformation. Fixed constraints are symmetrically applied to both ends of the flexure beams. To achieve frictionless displacement of the driving foot, displacement loads are applied at the contact plane between the rigid rod and the piezoelectric stack, with a maximum stroke of 20 m under an input voltage of 150 V. For reliability and lifespan considerations, the peak displacement of 16 m is selected as the input signal for the actuator. Finally, to determine the first natural frequency, the modal analysis needs to be conducted.

Table 1.
Available ranges, and optimized values of structural parameters.
To achieve an optimal balance between amplification ratio and movement velocity, an optimization framework based on the genetic algorithm is utilized to refine the actuator’s structural parameters. The governing variables are defined within the allowable ranges specified in Table 1. The optimization objectives can be defined as:
where the optimization targets two conflicting objectives: maximizing the frictionless displacement of the driving foot, which is critical for enhancing step size and motion resolution, and maximizing the first natural frequency f, which is essential for avoiding resonance and ensuring dynamic stability within the effective bandwidth proportional to the first natural frequency.
Constraints are applied based on geometric and functional requirements. For example, the thickness t of each flexure beam is constrained between 0.4 mm and 1 mm. If the beam is too thin, it risks buckling and processing difficulties; if it is too thick, it may exhibit poor flexibility and excessive stress. Hence, the lower value and upper value of each parameter are listed in Table 1. The formulation of the constraints that characterize the relationship between the structural parameters can be given as follows:
As shown in Figure 4, the iterative optimization process consists of the following steps:
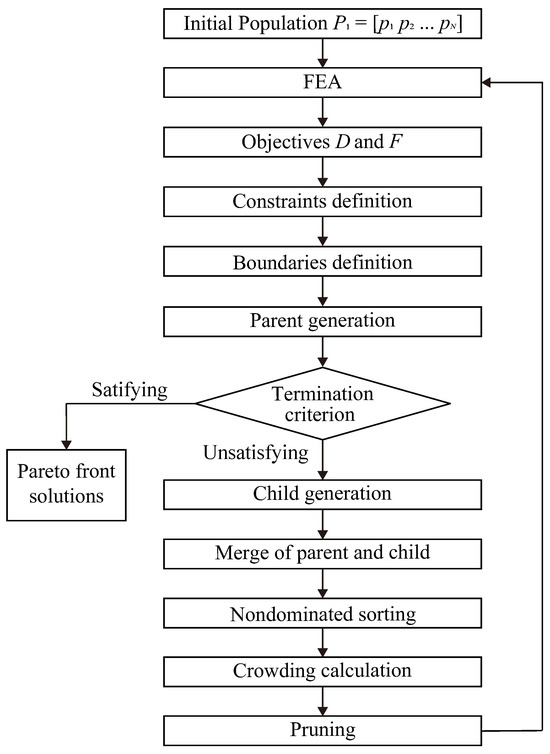
Figure 4.
Iterative optimization process.
- (i)
- For each set of parameters , the frictionless displacement and the first natural frequency are assessed via FEA with 44,894 elements.
- (ii)
- Improved NSGA-II algorithm is utilized to conduct optimization through genetic algorithm in MATLAB R2018b, i.e., the gamultiobj function, in which population size is set to be 200; the crossover fraction is set to be 0.8; the proportion of points on the Pareto front to the population is set to be 0.35.
- (iii)
- The convergence relative value is set to be 0.001, which is regarded as the iteration termination criterion. If the termination criteria are satisfied, the Pareto front solutions are populated; otherwise, the population will evolve.
- (iv)
- The child population is generated from the parent population through crossover and mutation. Divide their merged population into multiple ranks, which represent the superiority of the objectives, and calculate the crowding distance among individuals of the same rank, which represents the distribution range. The individuals with low rank and high crowding distance are prioritized for pruning.
As shown in Figure 5, this approach yields 70 sets of Pareto front solutions, from which the solution with the largest normal stiffness against the slider, as 117.5 N/m, is prioritized and marked with the red triangle, addressing compactness requirements for applications in micro-robotics or portable medical devices. The optimized parameters are presented in Table 1.
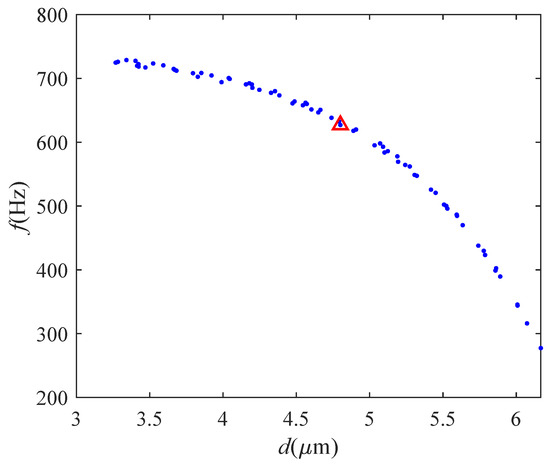
Figure 5.
Pareto front solutions are expressed with blue dots, in which the solution with the red triangle is selected.
4. Results
4.1. Static Performances
To thoroughly evaluate and assess the performance of the proposed piezoelectric stick-slip actuator, comprehensive finite element analysis (FEA) simulations are meticulously conducted utilizing the powerful capabilities of the software ANSYS 19.0. In this analytical process, the rigid frame of the actuator is securely anchored with fixed supports at the base, which are implemented through fixed holes, as illustrated in Figure 6a. A refined meshing approach is adopted, ensuring that the element size for each flexure beam is set at 0.4 mm to achieve high accuracy in the simulation results.
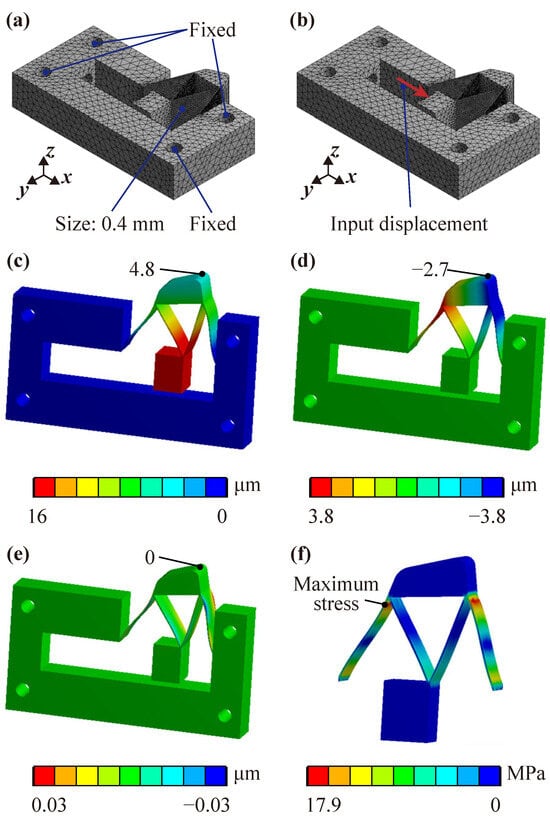
Figure 6.
Static performances: (a) fixed supports and element refinement, (b) input displacement, (c) x-direction deformation, (d) y-direction deformation, (e) z-direction deformation, and (f) stress distribution.
The input displacement required for the actuator’s operation is generated by the piezoelectric stack, which interfaces with the rigid rod at their contact plane. This input displacement reaches an impressive peak value of 16 m, with an extraordinary resolution of 0.1 nm, as demonstrated in Figure 6b. The outcomes derived from the FEA simulations provide critical and insightful information regarding the actuator’s directional deformation behavior, as well as its overall structural performance. The essential findings from these simulations are outlined below for clarity and emphasis:
- (i)
- The driving foot of the actuator exhibits a notable displacement of 4.8 µm, as depicted in Figure 6c. This measurement confirms the actuator’s exceptional capability to generate motion effectively along the intended axis. The displacement observed along the x-axis signifies the actuator’s effective step size during the stick phase, which directly influences both motion resolution and the load capacity that can be handled.
- (ii)
- In terms of directional deformation along the y-axis, the measurement stands at 2.7 µm, as portrayed in Figure 6d. This particular displacement indicates a vertical movement toward the slider component, suggesting that the normal pressure exerted on the slider increases throughout the stick phase, thereby leading to a rise in static friction that must be overcome for movement.
- (iii)
- It is noteworthy that the z-axis deformation is minimal, as illustrated in Figure 6e, which serves to emphasize the design’s robustness and inherent stability against out-of-plane forces that could potentially compromise operational integrity.
With the maximum input displacement set at a peak value of 16 m, it can be revealed that the maximum equivalent stress experienced within the system occurs specifically at the edges of each individual flexure beam, registering the value of 17.9 MPa, as shown in Figure 6f. This stress level is significantly lower than the established yield strength of structural steel, which stands at 784 MPa. This substantial difference in values indicates that the actuator operates well within safe limits, thereby ensuring reliable and effective functioning during both the stick and slip phases of its operational cycle. Such findings affirm the structural integrity and durability of the design, providing confidence in its performance capabilities under various loading conditions. Compliance with safety standards is a crucial aspect, allowing for consistent operation without the risk of material failure and ultimately resulting in enhanced performance and longevity of the actuator.
Additionally, the reaction force-input displacement curve and the maximum stress-input displacement curve are provided in Figure 7, in which the large deflection is considered. It can be seen that no nonlinear problems are reflected in the two curves, that is, no buckling phenomenon occurs in the entire working process.
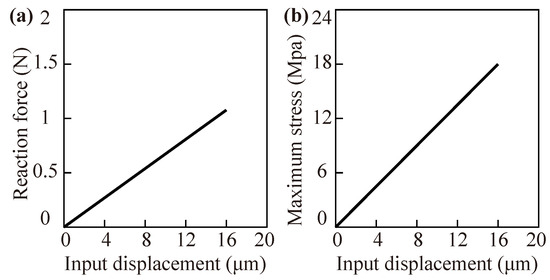
Figure 7.
Buckling analysis: (a) reaction force-input displacement curve, and (b) maximum stress-input displacement curve.
In conclusion, the comprehensive static simulations yield useful insights into the operational characteristics of the actuator, effectively validating its design effectiveness and suitability for practical applications. These results underscore the actuator’s potential for reliable performance in demanding environments.
4.2. Dynamic Performances
With the fixed support securely positioned on the designated fixing holes, a comprehensive modal analysis is performed to accurately compute the resonant frequencies of the system. The results reveal that the first six resonant frequencies are 627 Hz, 1543 Hz, 3351 Hz, 6747 Hz, 11,643 Hz, and 11,989 Hz, respectively. Despite encountering challenges related to densely packed modes resulting from the symmetric nature of the structure, the achieved bandwidth of the proposed piezoelectric stick-slip actuator encompasses a notably high-frequency range. The vibration modes corresponding to the first six frequencies are illustrated in Figure 8. Upon examination of these modes, it becomes apparent that the first mode primarily manifests in the x direction, indicating that this axis is the predominant motion direction for the mechanism. This insight effectively rules out the likelihood of resonance in other degrees of freedom, thereby preserving the operational bandwidth and enhancing the overall efficiency of the actuator. The careful analysis of these resonant frequencies and their associated vibration patterns underscores the actuator’s design optimization and performance reliability.
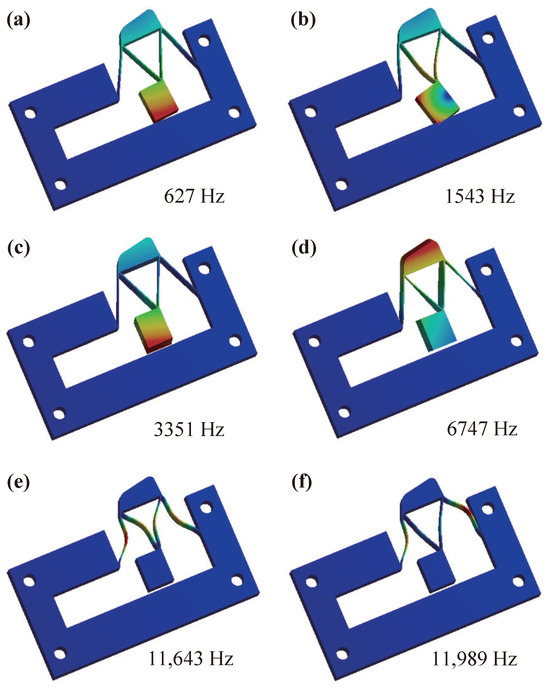
Figure 8.
Modal analyses of proposed piezoelectric stick-slip actuator: (a) Total deformation in the first mode (627 Hz). (b) Total deformation in the second mode (1543 Hz). (c) Total deformation in the third mode (3351 Hz). (d) Total deformation in the fourth mode (6747 Hz). (e) Total deformation in the fifth mode (11,643 Hz). (f) Total deformation in the sixth mode (11,989 Hz).
As shown in Figure 9, transient simulations are conducted to indirectly observe the output displacement under the friction force corresponding to different preloading forces with peak input displacement of 16 m and of 0.9. It can be seen that the effect of 200 N preload on the motion of the driving foot is at the submicron level, but the relationship between the two is not linear.
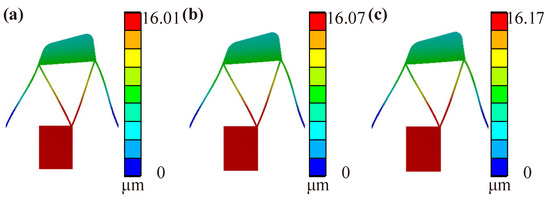
Figure 9.
Transient analyses of proposed piezoelectric stick-slip actuator: (a) Total deformation under 0 N, (b) Total deformation under 100 N, and (c) Total deformation under 200 N.
5. Conclusions
This paper presents the design and optimization of a novel piezoelectric stick-slip actuator featuring distributed compliance and a trapezoidal driving foot, which primarily integrates a piezoelectric stack, a slider, and a novel trapezoidal structure, optimized via genetic algorithm to balance motion amplification, dynamic stability, and compactness. The main work can be summarized as follows. At first, the mechanism design and the working principle are described in detail, featuring the improved role of the trapezoidal driving foot to differentiate the friction in the stick and slip phases. Then, its dominant performances are predicted through finite element analysis, including the step size and the first natural frequency. On this basis, a multi-objective optimization framework maximizes frictionless displacement and first natural frequency while constraining the normal stiffness against the slider, yielding Pareto-optimal solutions. Simulation results showed that the forward displacement in the stick phase can be obtained as 4.8 m, and the first natural frequency can be observed as 627 Hz. This work advances precision actuation technology, offering enhanced durability and scalability for micro-robotics, biomedical devices, and semiconductor manufacturing, while the physical validation, waveform design, and preloading analysis are still necessary, and will be conducted in future works.
Author Contributions
Conceptualization, T.Y.; data curation, T.Y.; investigation, T.Y.; methodology, T.Y.; validation, T.Y.; writing—original draft preparation, T.Y.; writing—review and editing, T.Y., Z.F. and Y.L.; supervision, Y.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Research Impact Fund of Hong Kong (Grant No. R5047-22), the Knowledge Innovation Program of Wuhan-Shuguang Project (Grant No. 2023010201020252), and the Aeronautical Science Foundation of China (Grant No. ASFC202400020S5001).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Dou, W.; Zhong, G.; Yang, J.; Shen, J. Design and modeling of a hybrid soft robotic manipulator with compliant mechanism. IEEE Robot. Autom. Lett. 2023, 8, 2301–2308. [Google Scholar] [CrossRef]
- Liang, C.; Wang, F.; Huo, Z.; Shi, B.; Tian, Y.; Zhao, X.; Zhang, D. A 2-DOF monolithic compliant rotation platform driven by piezoelectric actuators. IEEE Trans. Ind. Electron. 2019, 67, 6963–6974. [Google Scholar] [CrossRef]
- Li, Y.; Ye, T.; Ling, J.; Xiao, X.; Feng, Z. A novel F-shaped linear guiding mechanism based compliant positioning stage with restricted parasitic motion. Precis. Eng. 2024, 88, 674–685. [Google Scholar] [CrossRef]
- Ye, T.; Feng, Z.; Ling, J.; Li, Y. A novel w-shaped flexure-guided mechanism for high-frequency piezo-actuated micromanipulations. IEEE/ASME Trans. Mechatron. 2024. [Google Scholar] [CrossRef]
- Yu, X.; Cheng, H.; Zhang, M.; Zhao, Y.; Qu, L.; Shi, G. Graphene-based smart materials. Nat. Rev. Mater. 2017, 2, 17046. [Google Scholar] [CrossRef]
- Zhou, X.; Wu, S.; Wang, X.; Wang, Z.; Zhu, Q.; Sun, J.; Huang, P.; Wang, X.; Huang, W.; Lu, Q. Review on piezoelectric actuators: Materials, classifications, applications, and recent trends. Front. Mech. Eng. 2024, 19, 6. [Google Scholar] [CrossRef]
- Ling, J.; Ye, T.; Feng, Z.; Zhu, Y.; Li, Y.; Xiao, X. A survey on synthesis of compliant constant force/torque mechanisms. Mech. Mach. Theory 2022, 176, 104970. [Google Scholar] [CrossRef]
- Qiao, G.; Li, H.; Lu, X.; Wen, J.; Cheng, T. Piezoelectric stick-slip actuators with flexure hinge mechanisms: A review. J. Intell. Mater. Syst. Struct. 2022, 33, 1879–1901. [Google Scholar] [CrossRef]
- Xu, Z.; Sun, W.; Li, X.; Huang, H.; Dong, J. A stick-slip piezoelectric actuator with high assembly interchangeability. Int. J. Mech. Sci. 2022, 233, 107662. [Google Scholar] [CrossRef]
- Lin, Y.; An, D.; Lin, Z.; Chen, X.; Huang, W. Progress in high-performance stick-slip piezoelectric actuators: A review. Int. J. Smart Nano Mater. 2024, 15, 652–696. [Google Scholar] [CrossRef]
- Howell, L.L. Compliant mechanisms. In 21st Century Kinematics: The 2012 NSF Workshop; Springer: London, UK, 2013; pp. 189–216. [Google Scholar]
- Chi, Y.; Li, Y.; Zhao, Y.; Hong, Y.; Tang, Y.; Yin, J. Bistable and multistable actuators for soft robots: Structures, materials, and functionalities. Adv. Mater. 2022, 34, 2110384. [Google Scholar] [CrossRef] [PubMed]
- Ling, M.; Howell, L.L.; Cao, J.; Chen, G. Kinetostatic and dynamic modeling of flexure-based compliant mechanisms: A survey. Appl. Mech. Rev. 2020, 72, 030802. [Google Scholar] [CrossRef]
- Ma, X.; Liu, Y.; Deng, J.; Gao, X.; Cheng, J. A compact inchworm piezoelectric actuator with high speed: Design, modeling, and experimental evaluation. Mech. Syst. Signal Process. 2023, 184, 109704. [Google Scholar] [CrossRef]
- Dai, C.; Xin, L.; Zhang, Z.; Shan, G.; Wang, T.; Zhang, K.; Wang, X.; Chu, L.T.; Ru, C.; Sun, Y. Design and control of a piezo drill for robotic piezo-driven cell penetration. IEEE Robot. Autom. Lett. 2019, 5, 339–345. [Google Scholar] [CrossRef]
- Zhu, B.; Zhang, X.; Zhang, H.; Liang, J.; Zang, H.; Li, H.; Wang, R. Design of compliant mechanisms using continuum topology optimization: A review. Mech. Mach. Theory 2020, 143, 103622. [Google Scholar] [CrossRef]
- Ye, T.; Ling, J.; Kang, X.; Feng, Z.; Xiao, X. A novel two-stage constant force compliant microgripper. J. Mech. Des. 2021, 143, 053302. [Google Scholar] [CrossRef]
- Xie, Y.; Li, Y.; Cheung, B.C. A new symmetrical Z-shaped compliant linear actuator based on parasitic motion principle. Smart Mater. Struct. 2022, 31, 125017. [Google Scholar] [CrossRef]
- Qiu, C.; Ling, J.; Zhang, Y.; Ming, M.; Feng, Z.; Xiao, X. A novel cooperative compensation method to compensate for return stroke of stick-slip piezoelectric actuators. Mech. Mach. Theory 2021, 159, 104254. [Google Scholar] [CrossRef]
- Xu, Z.; Huang, H.; Dong, J. A stick-slip piezoelectric actuator with measurable contact force. Mech. Syst. Signal Process. 2020, 144, 106881. [Google Scholar] [CrossRef]
- Zhong, B.; Liao, Z.; Hu, H.; Liu, S.; He, C.; Sun, L. A review of recent studies on piezoelectric stick-slip actuators. Precis. Eng. 2025, 94, 175–190. [Google Scholar] [CrossRef]
- Cheng, T.; He, M.; Li, H.; Lu, X.; Zhao, H.; Gao, H. A novel trapezoid-type stick–slip piezoelectric linear actuator using right circular flexure hinge mechanism. IEEE Trans. Ind. Electron. 2017, 64, 5545–5552. [Google Scholar] [CrossRef]
- Zhang, Y.; Peng, Y.; Sun, Z.; Yu, H. A novel stick–slip piezoelectric actuator based on a triangular compliant driving mechanism. IEEE Trans. Ind. Electron. 2018, 66, 5374–5382. [Google Scholar] [CrossRef]
- Huang, H.; Xu, Z.; Wang, J.; Dong, J. A low frequency operation high speed stick-slip piezoelectric actuator achieved by using a L-shape flexure hinge. Smart Mater. Struct. 2020, 29, 065007. [Google Scholar] [CrossRef]
- Yu, Y.; Gao, Q.; Qiao, G.; Zhang, X.; Lu, X.; Cheng, T. A direction-guidance hybrid excitation method for inertial flexible hinge piezoelectric actuator with high speed performance. Sens. Actuators A Phys. 2020, 314, 112229. [Google Scholar] [CrossRef]
- Pan, Q.; Hu, J.; Miao, E.; Chen, S.; Shu, S.; Hu, P.; Huang, B. Novel piezoelectric rotary motor driven by a single-phase sine wave with an asymmetric stator. Sens. Actuators A Phys. 2019, 90, 075006. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).