Improved QT-Opt Algorithm for Robotic Arm Grasping Based on Offline Reinforcement Learning
Abstract
1. Introduction
2. Related Work
3. Definition of the Robotic Arm Grasping Problem
4. Markov Modeling
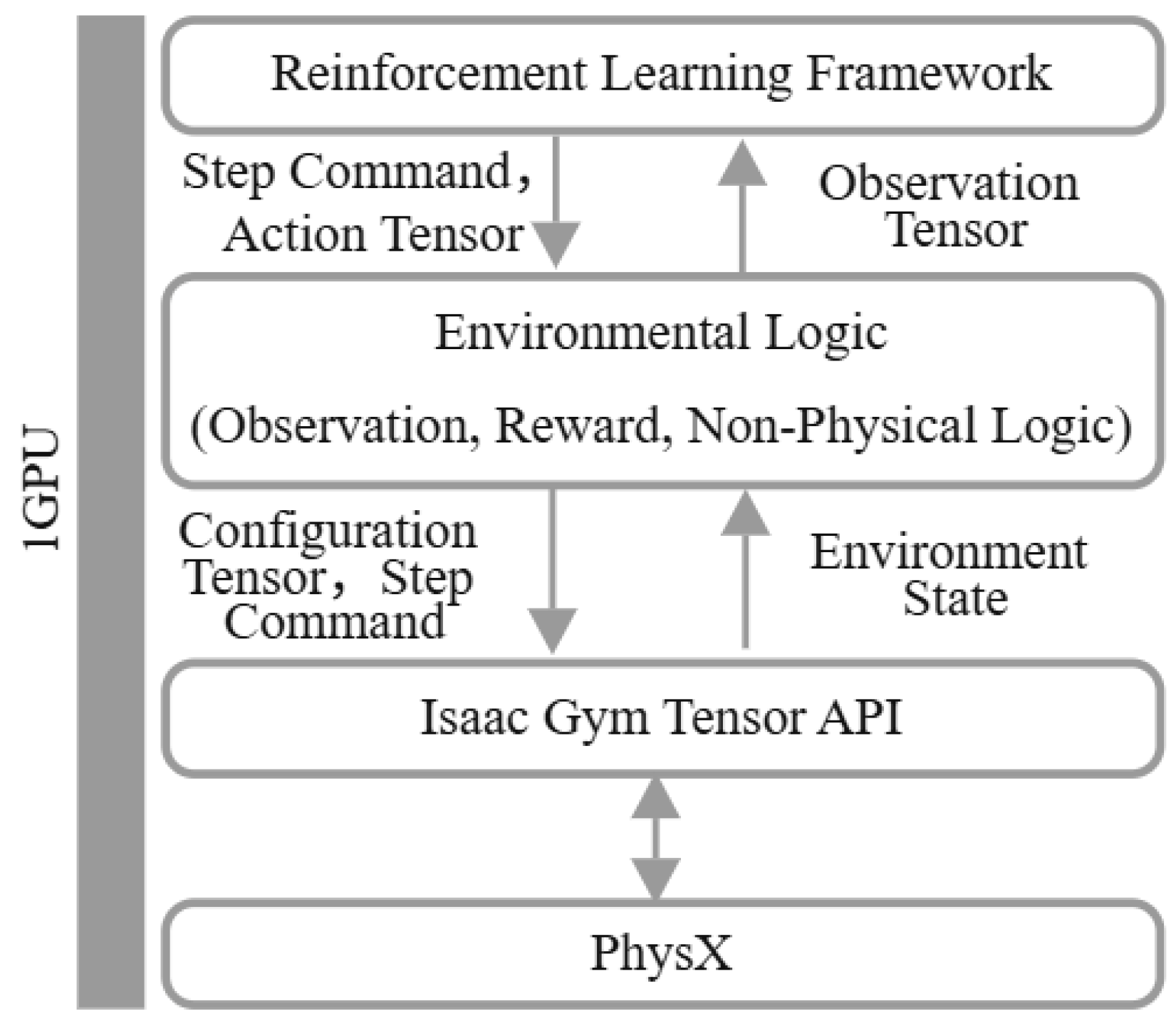
5. Improved QT-Opt Algorithm with Offline Reinforcement Learning
5.1. Offline Grasping Datasets
- (a)
- Random Policy: For the robotic arm grasping task, the purely random sampling strategy results in excessively low grasping success rates and the collected data has limited value. Therefore, a heuristic random strategy is adopted for data collection. This strategy directs the gripper to move approximately towards the vicinity of the object while maintaining an open position. Upon descending below a predetermined height threshold, the gripper automatically closes and returns to the starting position.
- (b)
- Expert Policy: During the online reinforcement learning training process, the policy is continuously updated, and the data collected throughout this process are consistently added to the experience replay buffer. Consequently, the replay buffer can be regarded as a dataset compiled from a mixture of multiple behavior policies. An online reinforcement learning algorithm can be utilized to train the robotic arm grasping policy, resulting in a grasping dataset generated by a hybrid policy. Given that the robotic arm grasping task relies on high-dimensional visual information as input, the DrQ-v2 algorithm [28], which performs effectively in visual tasks, is employed for the online training of the grasping policy. Upon completion of the training, the experience replay buffer is preserved as an offline grasping dataset generated by the hybrid policy.
- (c)
- Mixed Policy: For online reinforcement learning algorithms, pretraining on expert datasets can significantly enhance the efficiency of the learning process for the agent. Therefore, we adopt a high-success-rate grasping policy trained using the DrQ-v2 algorithm as the expert policy for collecting grasping data. The rewards in the collected grasping trajectories consist only of a sparse reward given at the final step.
5.2. Q-Network
5.3. PSO Algorithm
- (a)
- Before initiating the iteration process, it is essential to determine the number of particles and to initialize their respective positions and velocities. Typically, the positions of the particles are randomly distributed within the search space, while their initial velocities are set to zero. Each particle serves as a potential solution. The position and velocity of each particle are denoted as and , respectively.
- (b)
- The objective function can be defined as a mathematical expression that quantifies the performance of a solution. In each iteration, the fitness value of all particles is evaluated according to this objective function. Subsequently, the personal best position of each particle is updated based on its current fitness value. Finally, the global best position is determined by selecting the position with the highest fitness value from all particles’ personal best positions. The personal best position is denoted as , and the global best position of all particles is denoted as .
- (c)
- The last step is to update the velocity of each particle according to Equation (7), where represents the inertia weight, is the individual learning factor, is the social learning factor, and and are random numbers within the range [0, 1]. After determining the velocity of each particle, update its position according to Equation (8).
5.4. Conservative Estimation of Target Q-Value
6. Experiments
6.1. Experimental Metrics
6.2. Experimental Results
6.2.1. Ablation Experiment
6.2.2. Comparative Experiment
6.2.3. Q-Function Visualization Analysis
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tian, H.; Song, K.; Li, S.; Ma, S.; Xu, J.; Yan, Y. Data-driven robotic visual grasping detection for unknown objects: A problem-oriented review. Expert Syst. Appl. 2023, 211, 118624. [Google Scholar] [CrossRef]
- Newbury, R.; Gu, M.; Chumbley, L.; Mousavian, A.; Eppe, C.; Leitner, J. Deep learning approaches to grasp synthesis: A review. IEEE Trans. Robot. 2023, 39, 1–22. [Google Scholar] [CrossRef]
- Kalashnikov, D.; Ipran, A.; Pastor, P.; Ibarz, J.; Herzog, A.; Jang, E.; Quillen, D.; Holly, E.; Kalakrishnam, M.; Vanhoucke, V.; et al. QT-Opt: Scalable deep reinforcement learning for vision-based robotic manipulation. In Proceedings of the 2nd Conference on Robot Learning, Zürich, Switzerland, 29–31 October 2018; pp. 651–673. [Google Scholar]
- Zeng, A.; Song, S.; Welker, S.; Lee, J.; Rodriguez, A.; Funkhouser, T. Learning synergies between pushing and grasping with self-supervised deep reinforcement learning. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 4238–4245. [Google Scholar]
- Qi, L.; Jang, E.; Nachum, O.; Finn, C.; Ibarz, J. Deep reinforcement learning for vision-based robotic grasping: A simulated comparative evaluation of off-policy methods. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 6284–6291. [Google Scholar]
- Shi, S.; Kumra, S.; Sahin, F. Robotic grasping using deep reinforcement learning. In Proceedings of the 2020 IEEE 16th International Conference on Automation Science and Engineering (CASE), Hong Kong, China, 20–21 August 2020; pp. 1461–1466. [Google Scholar]
- Zhang, J.; Zhang, W.; Song, R.; Ma, L.; Li, Y. Grasp for stacking via deep reinforcement learning. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 2543–2549. [Google Scholar]
- Shukla, P.; Kumar, H.; Nandi, G.C. Robotic grasp manipulation using evolutionary computing and deep reinforcement learning. Int. Serv. Robot. 2021, 14, 61–77. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, F.; Wang, J.; Cui, B. Robot grasping method optimization using improved deep deterministic policy gradient algorithm of deep reinforcement learning. Rev. Sci. Instrum. 2021, 92, 2. [Google Scholar] [CrossRef] [PubMed]
- Chen, P.; Lu, W. Deep reinforcement learning based moving object grasping. Inf. Sci. 2021, 565, 62–76. [Google Scholar] [CrossRef]
- Chen, Y.L.; Cai, Y.R.; Cheng, M.Y. Vision-based robotic object grasping—A deep reinforcement learning approach. Machines 2023, 11, 275. [Google Scholar] [CrossRef]
- Tang, Z.; Shi, Y.; Xu, X. CSGP: Closed-loop safe grasp planning via attention-based deep reinforcement learning from demonstrations. IEEE Rob. Autom. 2023, 8, 3158–3165. [Google Scholar] [CrossRef]
- Zuo, G.; Tong, J.; Wang, Z.; Gong, D. A graph-based deep reinforcement learning approach to grasping fully occluded objects. Cogn. Comput. 2023, 15, 36–49. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, S.; Yao, Y.; Yang, X.; Zhong, M. Research Status of Robotic Grasping Detection Technology. Control Decis. 2020, 35, 2817–2828. [Google Scholar]
- Fujimoto, S.; Meger, D.; Precup, D. Off-policy deep reinforcement learning without Exploration. In Proceedings of the 36th International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; pp. 2052–2062. [Google Scholar]
- Kumar, A.; Fu, J.; Tucker, G.; Levine, S. Stabilizing off-policy q-learning via bootstrapping error reduction. In Proceedings of the Advances in Neural Information Processing Systems 32 (NeurIPS 2019), Vancouver, BC, Canada, 8–14 December 2019; Volume 32. [Google Scholar]
- Fujimoto, S.; Hoof, H.; Meger, D. Addressing function approximation error in actor-critic Methods. In Proceedings of the 35th International Conference on Machine Learning, Stockholmsmässan, Stockholm, Sweden, 10–15 July 2018; pp. 1587–1596. [Google Scholar]
- Fujimoto, S.; Gu, S.S. A minimalist approach to offline reinforcement learning. Adv. Neural Inf. Process. Syst. 2021, 34, 20132–20145. [Google Scholar]
- Kumar, A.; Zhou, A.; Tucker, G.; Levine, S. Conservative q-learning for offline reinforcement learning. Adv. Neural Inf. Process. Syst. 2020, 33, 1179–1191. [Google Scholar]
- Lyu, J.; Ma, X.; Li, X.; Lu, Z. Mildly conservative q-learning for offline reinforcement learning. Adv. Neural Inf. Process. Syst. 2022, 35, 1711–1724. [Google Scholar]
- Qiu, L.; Li, X.; Liang, L.; Sun, M.; Yan, J. Adaptive Conservative Q-Learning for Offline Reinforcement Learning. In Proceedings of the Chinese Conference on Pattern Recognition and Computer Vision (PRCV), Xiamen, China, 13–15 October 2023; pp. 200–212. [Google Scholar]
- Bousmalis, K.; Vezzani, G.; Rao, D.; Devin, C.; Lee, A.X.; Bauza, M.; Davchev, T.; Zhou, Y.; Gupta, A.; Raju, A.; et al. RoboCat: A Self-Improving Generalist Agent for Robotic Manipulation. arXiv 2023, arXiv:2306.11706. [Google Scholar]
- Black, K.; Nakamoto, M.; Atreya, P.; Walke, H.; Finn, C.; Kumar, A.; Levine, S. Zero-shot robotic manipulation with pretrained image-editing diffusion models. arXiv 2023, arXiv:2310.10639. [Google Scholar]
- Chi, C.; Feng, S.; Du, Y.; Xu, Z.; Cousineau, E.; Burchfiel, B.; Song, S. Diffusion Policy: Visuomotor Policy Learning via Action Diffusion. In Proceedings of the Robotics: Science and Systems (RSS), Daegu, Republic of Korea, 10–14 July 2023; pp. 1–10. [Google Scholar]
- Du, G.; Wang, K.; Lian, S.; Zhao, K. Vision-based robotic grasping from object localization, object pose estimation to grasp estimation for parallel grippers: A review. Artif. Intell. Rev. 2021, 54, 1677–1734. [Google Scholar] [CrossRef]
- Bellman, R. A Markov decision process. Indiana Univ. Math. J. 1957, 6, 679–684. [Google Scholar] [CrossRef]
- Rubinstein, R.Y.; Kroese, D.P. A Tutorial Introduction to the Cross-Entropy Method. In The Cross-Entropy Method: A Unified Approach to Combinatorial Optimization, Monte-Carlo Simulation, and Machine Learning; Rubinstein, R.Y., Kroese, D.P., Eds.; Springer: New York, NY, USA, 2004; pp. 147–148. [Google Scholar]
- Yarats, D.; Fergus, R.; Lazaric, A.; Pinto, L. Mastering visual continuous control: Improved data augmented reinforcement learning. arXiv 2021, arXiv:2107.09645. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 1–27 August 1995; pp. 1942–1948. [Google Scholar]
- Chen, L.; Lu, K.; Rajeswaran, A.; Lee, K.; Grover, A.; Laskin, M.; Abbeel, P.; Srinivas, A.; Mordatch, I. Decision transformer: Reinforcement learning via sequence modeling. Adv. Neural Inf. Process. Syst. 2021, 34, 15084–15097. [Google Scholar]

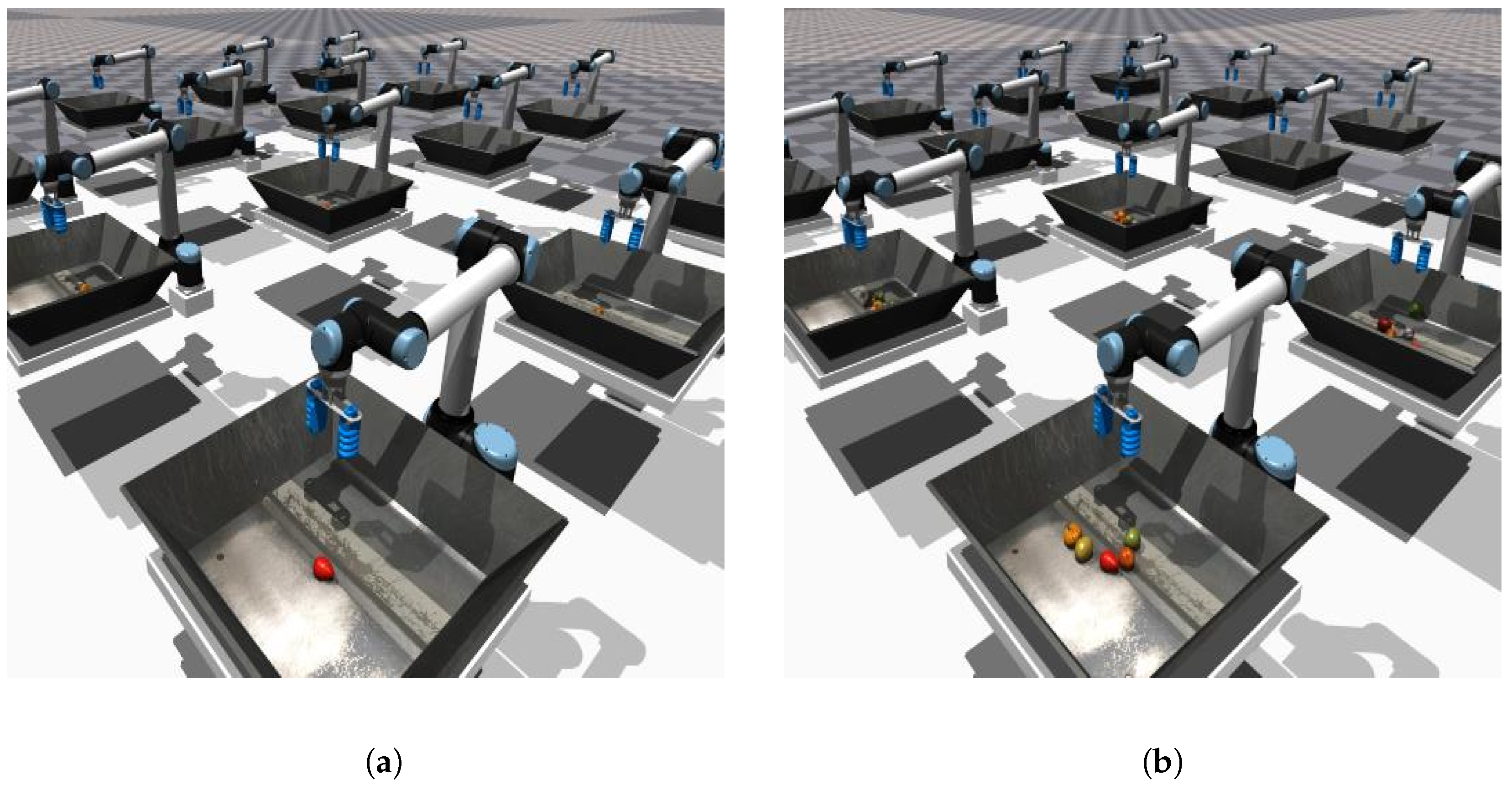








| Grasp Datasets Name | Trajectory Count | Average Trajectory Steps |
|---|---|---|
| Single-Object Random | 2w | 6.44 |
| Single-Object Replay | 2w | 5.02 |
| Single-Object Expert | 2w | 5.29 |
| Multi-Object Random | 2w | 6.61 |
| Multi-Object Replay | 2w | 6.10 |
| Multi-Object Expert | 2w | 6.18 |
| Training Datasets | Grasping Algorithm | AUGSRC | CV |
|---|---|---|---|
| Single-object Random | QT-Opt(CEM) | 62.67 | 36.19 |
| QT-Opt(PSO) | 72.30 | 39.01 | |
| QT-Opt(PSO)+Regular | 82.85 | 25.26 | |
| Single-object Experience Replay | QT-Opt(CEM) | 63.98 | 40.69 |
| QT-Opt(PSO) | 74.25 | 34.07 | |
| QT-Opt(PSO)+Regular | 84.3 | 20.6 | |
| Single-object Expert | QT-Opt(CEM) | 10.89 | 54.09 |
| QT-Opt(PSO) | 11.48 | 777.1 | |
| QT-Opt(PSO)+Regular | 677.7 | 28.2 | |
| Multi-object Random | QT-Opt(CEM) | 80.99 | 20.76 |
| QT-Opt(PSO) | 87.41 | 19.8 | |
| QT-Opt(PSO)+Regular | 89.2 | 12.3 | |
| Multi-object Experience Replay | QT-Opt(CEM) | 48.5 | 49.9 |
| QT-Opt(PSO) | 51.7 | 42.4 | |
| QT-Opt(PSO)+Regular | 68.9 | 22.5 | |
| Multi-object Expert | QT-Opt(CEM) | 13.05 | 98.2 |
| QT-Opt(PSO) | 19.12 | 76.3 | |
| QT-Opt(PSO)+Regular | 71.1 | 16.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Zeng, S.; Hou, Y.; Huang, H.; Xu, Z. Improved QT-Opt Algorithm for Robotic Arm Grasping Based on Offline Reinforcement Learning. Machines 2025, 13, 451. https://doi.org/10.3390/machines13060451
Zhang H, Zeng S, Hou Y, Huang H, Xu Z. Improved QT-Opt Algorithm for Robotic Arm Grasping Based on Offline Reinforcement Learning. Machines. 2025; 13(6):451. https://doi.org/10.3390/machines13060451
Chicago/Turabian StyleZhang, Haojun, Sheng Zeng, Yaokun Hou, Haojie Huang, and Zhezhuang Xu. 2025. "Improved QT-Opt Algorithm for Robotic Arm Grasping Based on Offline Reinforcement Learning" Machines 13, no. 6: 451. https://doi.org/10.3390/machines13060451
APA StyleZhang, H., Zeng, S., Hou, Y., Huang, H., & Xu, Z. (2025). Improved QT-Opt Algorithm for Robotic Arm Grasping Based on Offline Reinforcement Learning. Machines, 13(6), 451. https://doi.org/10.3390/machines13060451







