Methodology for Human–Robot Collaborative Assembly Based on Human Skill Imitation and Learning

Abstract

With the growing demand for personalized and flexible production, human–robot collaboration technology receives increasing attention. However, enabling robots to accurately perceive and align with human motion intentions remains a significant challenge. To address this, a novel human–robot collaborative control framework is proposed, which utilizes electromyography (EMG) signals as an interaction interface and integrates human skill imitation with reinforcement learning. Specifically, to manage the dynamic variation in muscle coordination patterns induced by joint angle changes, a temporal graph neural network enhanced with an Angle-Guided Attention mechanism is developed. This method adaptively models the topological relationships among muscle groups, enabling high-precision three-dimensional dynamic arm force estimation. Furthermore, an expert reward function and a fuzzy experience replay mechanism are introduced in the reinforcement learning model to guide the human skill learning process, thereby enhancing collaborative comfort and smoothness. The proposed approach is validated through a collaborative assembly task. Experimental results show that the proposed arm force estimation model reduces estimation errors by 10.38%, 8.33%, and 11.20% across three spatial directions compared to a conventional Deep Long Short-Term Memory (Deep-LSTM). Moreover, it significantly outperforms state-of-the-art methods, including traditional imitation learning and adaptive admittance control, in terms of collaborative comfort, smoothness, and assembly accuracy.

1. Introduction

In recent years, robotic technologies have been increasingly applied in industrial production, particularly in domains such as welding and assembly [1,2]. However, the level of automation remains constrained when facing a wide range of unstructured environments and flexible manufacturing tasks [3]. To address this issue, the concept of human–robot collaboration (HRC) has been proposed, aiming to integrate human decision-making capabilities with the high payload capacity of robots, thereby demonstrating substantial application potential [4].

A key challenge in the development of HRC technologies lies in the lack of efficient human–robot interaction interfaces, which hampers accurate transmission of human motion intent. Currently, physical interaction, primarily based on force sensors, remains the dominant mode of HRC [5]. However, since force sensors acquire signals based on contact-induced strain, it is often difficult to distinguish between forces originating from the human operator and those resulting from interactions with the external environment [6,7]. This significantly limits the accuracy of capturing actual human-applied forces.

With the continuous integration of interdisciplinary research, scholars have increasingly recognized the strong correlation between EMG signals, commonly used in the medical field to assess human motion, and muscle force output [8]. Early arm force estimation methods primarily relied on muscle dynamics models, such as the Hill-type model and its variants [9]. However, constructing these models requires precise acquisition of individual-specific anatomical parameters, including muscle and skeletal structures. As the dimensionality of force estimation increases, the complexity and computational burden of these models rise sharply, presenting significant challenges for practical deployment [10].

With the advancement of computational technologies, researchers have increasingly turned to machine learning algorithms to directly model EMG signals, enabling force estimation without depending on musculoskeletal structural parameters. Several EMG-to-force mapping approaches have been proposed, including Artificial Neural Networks (ANNs) [11], Long Short-Term Memory networks (LSTMs) [12], Principal Component Interaction (PCI) modeling [13], and Convolutional Neural Networks (CNNs) [14].

However, current machine learning models often emphasize unidirectional force estimation, which limits their effectiveness in complex industrial applications [15,16]. To enhance model generalizability, Su et al. proposed decomposing arm force output into three orthogonal directions in Cartesian space and modeling each direction independently using a Deep Convolutional Neural Network (DCNN) [17]. Building on this idea, Zhang et al. introduced a Bayesian approach that first identifies the dominant force direction and then applies parallel LSTM networks for direction-specific force estimation [18]. While these methods improve multidimensional force prediction, they overlook a key physiological reality: in real-world tasks, muscle groups typically operate in a coordinated, multi-directional fashion, resulting in complex interdependencies and mutual interference. As a result, modeling each direction separately may oversimplify the intricate dynamics of muscle coordination and limit the model’s ability to capture the underlying biomechanical interactions.

As demand grows for multidimensional dynamic arm force estimation, researchers have increasingly recognized the importance of arm posture in modeling. During human movement, joint angles reflect physiological factors such as muscle length variations and contraction types. These not only affect the amplitude dynamics of EMG signals but also modulate inter-muscle coordination, thereby significantly influencing the generalization ability of force estimation models [19,20]. To address this, Mobasser et al. proposed a Fast Orthogonal Search (FOS)-based elbow joint force estimation model that incorporates both EMG and joint angle information. The method demonstrated its effectiveness under isometric, isobaric, and low-load conditions [21].

Although incorporating joint angles improves model accuracy, increasing movement dimensionality and complexity introduces greater challenges for training and fitting. To address this, Xie et al. proposed a method that takes both joint angles and EMG signals as inputs and constructs a Deep Long Short-Term Memory (Deep-LSTM) network for dynamic arm force estimation [22]. This approach is considered one of the most effective techniques for improving dynamic force estimation accuracy. However, current methods lack explicit modeling of how posture affects muscle synergy. Instead, these approaches rely on the model to implicitly learn the complex nonlinear coupling between EMG features and joint configurations from data, which undoubtedly increases the learning burden and may limit generalization under multi-task conditions. Therefore, achieving accurate multidimensional dynamic arm force estimation remains a substantial challenge.

Beyond perception of human intent, another core issue in HRC lies in the design of effective collaboration control strategies [23]. To enhance the responsiveness and compliance of robotic systems during collaboration, mainstream approaches commonly utilize impedance or admittance control frameworks, which dynamically adjust control parameters to adapt to interaction forces [24]. For instance, Bednarczyk et al. proposed a variable impedance control method that integrates human-applied forces into the control model to optimize robot interaction performance [25]. Yao introduced an adaptive admittance control method using an admittance filter, which adjusts parameters based on estimated joint torques, thereby improving the applicability of rehabilitation robots in assisted motion [26].

Meanwhile, data-driven strategies have gradually been integrated into variable impedance frameworks due to advancements in machine learning, significantly enhancing the adaptability of control models. For example, impedance parameter optimization via iterative learning has been successfully applied in industrial tasks such as polishing and assembly [27,28]. Yang and Anand introduced reinforcement learning (RL) into controller design, enabling adaptive adjustment of impedance parameters through policy optimization, thus substantially improving compliant control performance [29,30]. However, despite notable success in improving flexibility and precision, these methods still struggle to meet real-world demands in highly dynamic and uncertain HRC environments, due to limitations of static models and single-strategy optimization [31].

In recent years, imitation learning has emerged as a promising approach for real-time HRC. By learning from human demonstrations, robots can participate in collaborative tasks more naturally [32,33]. Liao et al. restructured the Dynamic Movement Primitives (DMP) formulation using Riemannian metrics, incorporating position, orientation, and stiffness information to enable the transfer and reproduction of humanoid multi-space skills [34]. Additionally, traditional machine learning techniques such as Gaussian Mixture Models, Random Forests, and Hidden Markov Models have laid solid foundations for imitation learning [35,36]. However, since traditional imitation learning typically relies on predefined trajectories and is more suited for offline behavior cloning, it faces limitations in processing high-dimensional data and handling dynamic real-time interactions, which restricts its effectiveness in collaborative scenarios [37].

Notably, reinforcement learning has demonstrated outstanding performance even in the absence of precise dynamic models, making it well-suited for complex and frequently changing collaborative environments [38]. For example, Zhang proposed using RL to directly extract force-related information from EMG signals, enabling robot motion control without relying on traditional control models, and successfully validated this approach in a human–robot collaborative sawing task [39]. The organic integration of imitation learning and reinforcement learning is expected to become a promising direction for novel skill acquisition and the exploitation of advanced collaborative control models. Currently, imitation reinforcement learning has been predominantly applied in domains such as autonomous driving and robotic manipulation [32,40]. However, research specifically targeting human skill acquisition and the enhancement of human–robot collaborative control through this paradigm remains relatively limited.

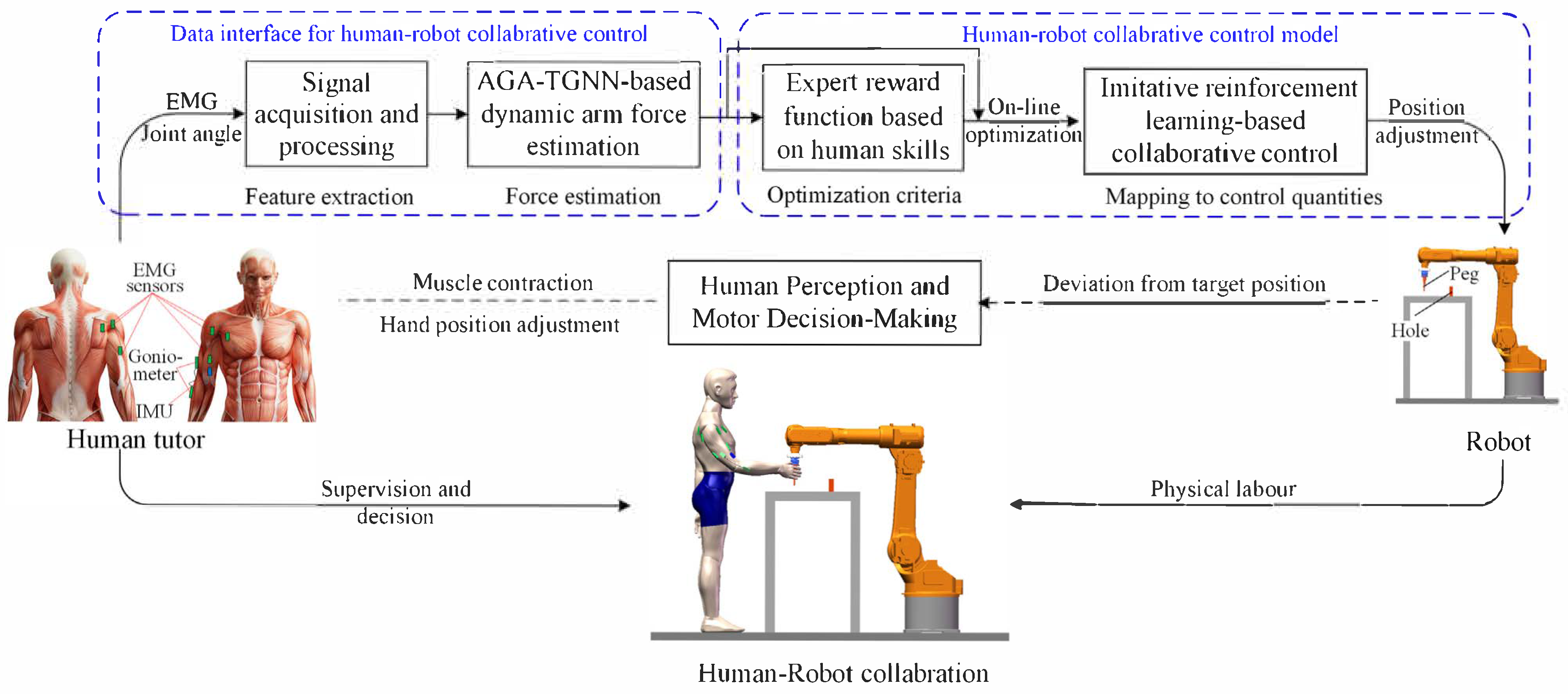
To address the aforementioned challenges, an EMG-driven dynamic arm force estimation model and an imitation reinforcement learning-based collaborative control framework are proposed to enhance performance in human–robot collaborative assembly. The overall research framework is illustrated in Figure 1.

First, joint angle information and EMG signals collected from the human body are processed to extract features for arm force estimation. To account for the influence of joint angle variations on force estimation, a Temporal Graph Neural Network incorporating an Angle-Guided Attention mechanism (AGA-LSTM) is introduced to capture changes in inter-muscle synergies and estimate three-dimensional (3D) arm force. The estimated human arm force is then used to extract key indicators of human skill from demonstration data. Specifically, this skill refers to the ability to adjust speed in response to changes in external collaborative forces. Additionally, the estimated arm force also serves as an interface for human–robot interaction.

Based on the skill indicators extracted from human demonstrations, an expert reward function is constructed. A performance-optimized control model is then trained using an imitation reinforcement learning algorithm, enhanced with a fuzzy rule-based experience replay partitioning strategy. The proposed control framework adopts a human-in-the-loop design, converting human interaction forces directly into robot motion commands. By leveraging human perceptual and decision-making abilities, the robot is guided to collaborate effectively with the operator. In cases of trajectory deviations, the operator can intuitively correct the robot’s motion by adjusting the applied force. This approach avoids rigid trajectory replication, enabling more flexible and autonomous human–robot interaction.

2. Construction of an EMG Signals-Based Dynamic Arm Force Estimation Model

To meet the requirements for interaction force smoothness and accuracy in human–robot collaborative control, this section focuses on the acquisition and processing of arm motion signals and the construction of arm force estimation model.

2.1. Acquisition and Processing of Arm Motion Signals

2.1.1. Methods for Acquiring Arm Motion Signals

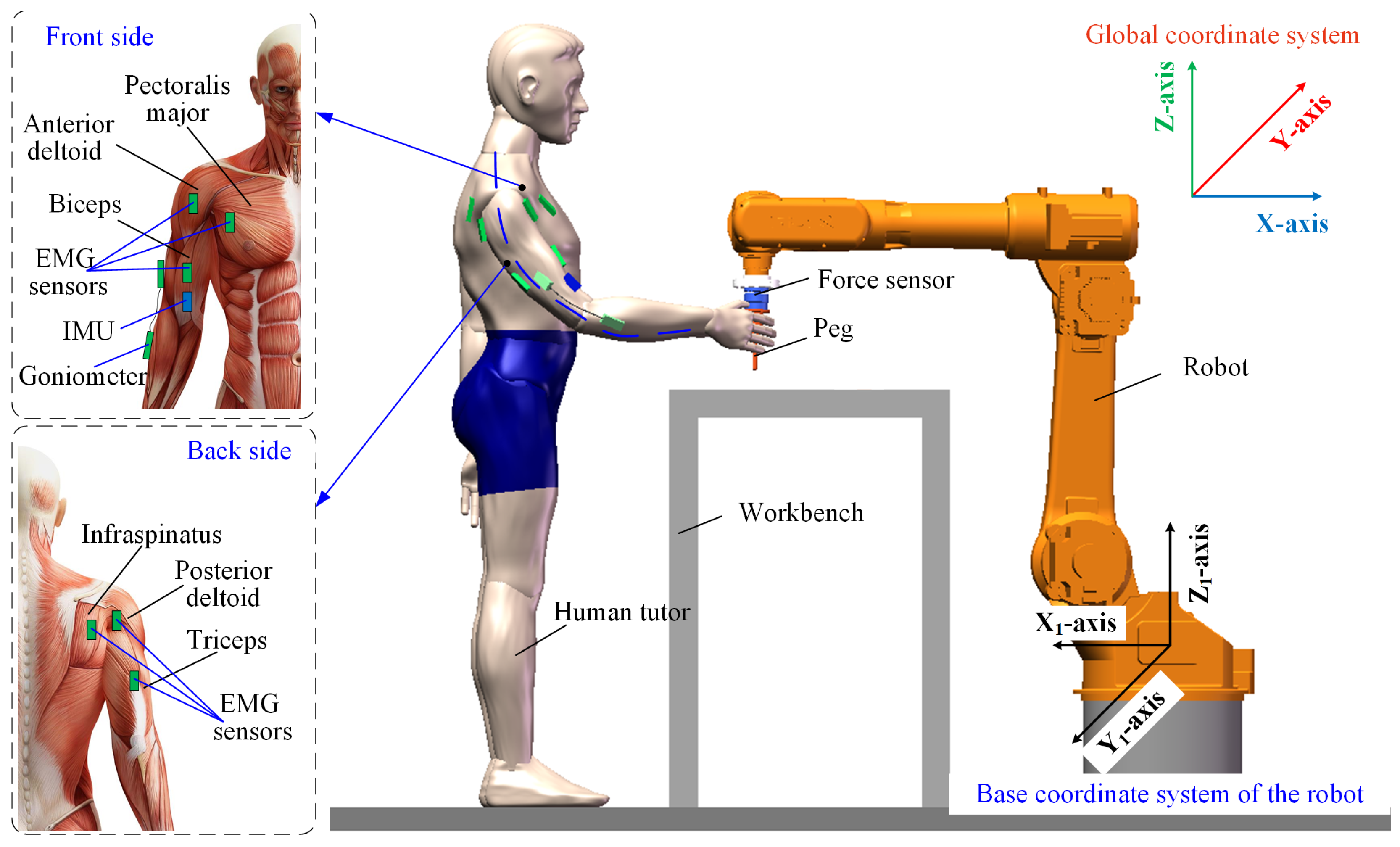
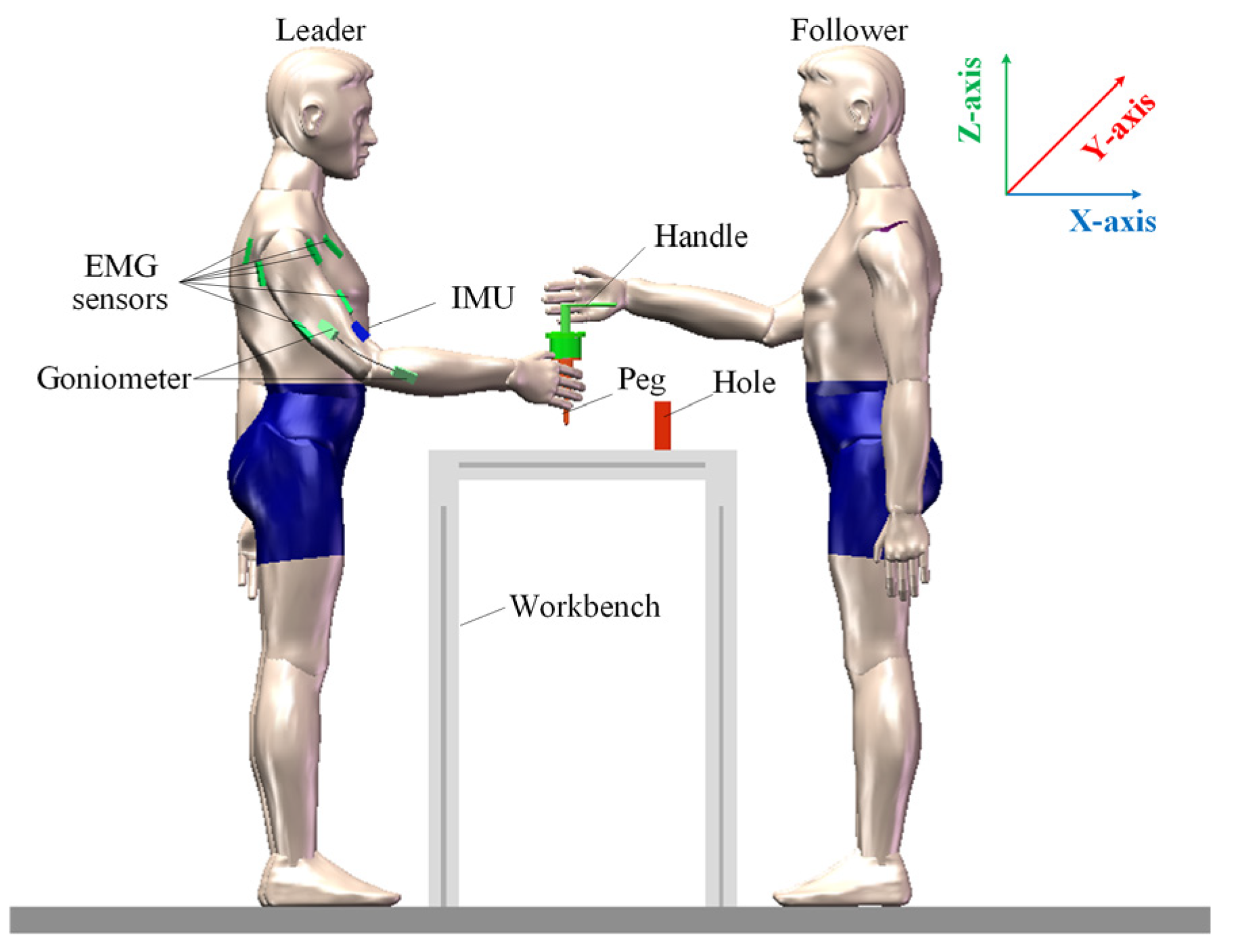
Figure 2 presents the human arm motion signal acquisition platform, which supplies training data for the EMG-based dynamic force estimation model. A goniometer is positioned on the outer side of the elbow to record one-dimensional elbow joint angle data. An IMU, attached to the inner side of the upper arm, captures the shoulder’s three-dimensional Euler angles. Six EMG electrodes are placed on key muscle groups, including the biceps/triceps brachii, anterior/posterior deltoids, pectoralis major, and infraspinatus. Arm-generated forces are simultaneously recorded using a six-axis force sensor.

During data collection, a human operator manually guides the robot by applying forces with varying intensities and directions, enabling free movement. At the same time, EMG intensity, joint angles, and force measurements are recorded. The operator is oriented toward the YZ-plane of the robot’s base frame, and the applied forces are decomposed into three orthogonal components (X, Y, and Z) relative to the robot’s coordinate system.

2.1.2. Feature Extraction from EMG Signals

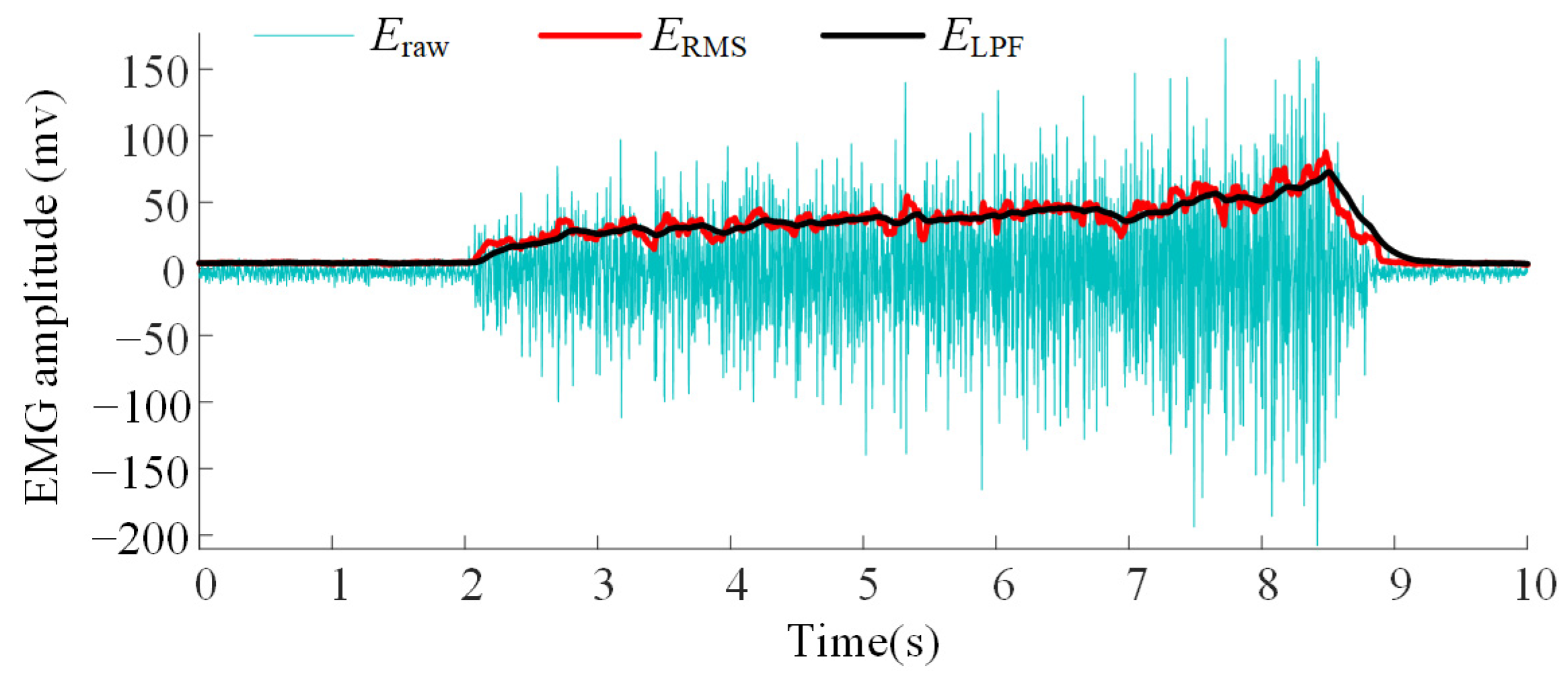
It is necessary to extract features that correlate with the arm force from these time-varying signals. Given that the amplitude of the EMG signal is strongly correlated with arm force, a moving root mean square (RMS) filter is applied to the raw EMG signal to extract amplitude features. The processing is described by the following equation:

$$E_{\mathrm{RMS}}\left[i\right]=\sqrt{{\displaystyle \frac{1}{N}}{{\displaystyle \sum _{\mathrm{m}=i-N+1}^i{E}_{\mathrm{raw}}\left[m\right]}}^2}$$

(1)

where, E_raw[m] denotes the m-th denoised EMG signal and E_RMS[i] represents the i-th signal after processing by the RMS filter with a sliding window of size N.

As shown in Figure 3, even after RMS filtering, the feature signal still exhibits considerable fluctuations. Therefore, a simple discrete low-pass filter is applied to smooth the extracted features. The smoothing process can be described as follows:

$$E_{\mathrm{LPF}}\left[n\right]=\xi E_{\mathrm{RMS}}\left[n\right]+(1-\xi )E_{\mathrm{LPF}}\left[n-1\right]$$

(2)

where E_LPF[n] denotes the n-th output of the low-pass filter and ξ is the filter’s difference weight.

According to Ref. [41], the sliding window size N and the filter’s difference weight ξ are set to 64 and 0.00628, respectively, demonstrating a good balance between signal smoothness and responsiveness.

2.2. A 3D Arm Force Estimation Model Based on an Angle-Guided Attention Temporal Graph Neural Network (AGA-TGNN)

In EMG-based arm force estimation model, muscle activation patterns are significantly influenced by joint angles. The contribution of individual muscles varies with different joint angles; for instance, the biceps brachii exerts more force at smaller flexion angles, whereas its contribution diminishes during extension, with the triceps brachii taking a dominant role during extension. Moreover, muscle coordination patterns change with joint angle variations—alterations in shoulder angles, for example, can modify the synergistic behavior between the pectoralis major and the anterior deltoid. These angle-dependent dynamics make it challenging to accurately estimate arm force using traditional methods.

Existing approaches such as CNNs are effective at extracting local spatial features from EMG signals but fall short in capturing the global inter-muscle cooperative relationships. Although LSTM networks are well-suited for temporal modeling, they lack the capability to capture the spatial dependencies among muscles, making them less adaptable to the variations in muscle coordination under different joint angles. Therefore, a model that can simultaneously capture the topological structure of muscle groups and their temporal variations is needed to more accurately model muscle coordination patterns under varying joint angles.

Graph Neural Networks (GNNs) provide an effective approach to modeling the topological structure of EMG signals by employing an adjacency matrix to represent inter-muscle relationships. However, conventional GNNs typically rely on a fixed adjacency matrix, which fails to capture the dynamic changes in muscle coordination induced by variations in joint angles. To overcome this limitation, an Angle-Guided Attention mechanism is introduced, enabling the adaptive adjustment of the adjacency matrix based on joint angle information. This enhancement significantly improves the model’s generalization capability across diverse motion conditions.

To further strengthen the temporal dependency modeling of EMG signals, an LSTM is integrated following the GNN, forming a Temporal Graph Neural Network (TGNN). In this architecture, the GNN extracts spatial features related to muscle topology, while the LSTM models the time dependencies of the EMG signals. The combination of GNN and LSTM enables the model to capture both the spatial cooperation among muscles and the temporal patterns, thereby improving the accuracy of arm force estimation. Based on these considerations, the AGA-TGNN is proposed.

(a) Motivation of EMG Signals Modulated by Joint Angles

Human arm output force arises from the coordinated activation of multiple muscle groups, governed by both muscular dynamics and skeletal biomechanics. According to physiological coordination dynamics, muscle-generated tension is first transformed into joint torques through a moment matrix R(θ) and then mapped to the arm output force via the Jacobian matrix J(θ). The dynamic formulation of the estimated arm force F_estm is given by the following:

$$F_{estm}=J^{-\mathrm{T}}\left(\theta \right)R^{\mathrm{T}}\left(\theta \right)F_{\mathrm{msc}}$$

(3)

where, F_msc is the muscle force, and both R(θ) and J(θ) are functions of joint angles θ.

This formulation illustrates that the resulting arm output force is influenced not only by muscle activity (as measured by EMG) but also by the arm’s current posture. In this paper, the muscle force F_msc is modeled using a neural network, leading to an updated force estimation expression:

$$F_{estm}=J^{-\mathrm{T}}\left(\theta \right)R^{\mathrm{T}}\left(\theta \right)f_{\mathrm{NN}}\left(E_{\mathrm{LPF}}\right)$$

(4)

Given the complexity of directly measuring muscle forces and modeling the analytical forms of R(θ) and J(θ), joint angle information is incorporated as a prior into the neural network to guide the learning process. This allows the model to learn the topological coordination pattern among muscle groups. Accordingly, the dynamic force estimation model consists of two submodules as follows:

$$F_{estm}=f_{\mathrm{NN}1}\left(E_{adj}\right)=f_{\mathrm{NN}1}\left(E_{\mathrm{LPF}}{f}_{\mathrm{NN}2}\left(\theta \right)\right)$$

(5)

where, E_adj denotes the EMG amplitudes modulated by joint angles; f_NN1 represents a Temporal Graph Neural Network (TGNN) that estimates 3D arm force based on EMG signals; f_NN2 is the Angle-Guided Attention (AGA) module that learns a posture-dependent adjacency matrix to guide the TGNN. By integrating joint angle information as a prior, this mechanism enables the network to dynamically capture inter-muscle coordination patterns under varying postures.

(b) Angle-Guided Attention Module

Traditional attention mechanisms, such as the self-attention mechanism in Transformers, adjust weights by computing the “importance” or “relevance” between elements. Inspired by this principle, the Angle-Guided Attention mechanism is developed to dynamically capture changing muscle coordination patterns. Specifically, a three-layer multilayer perceptron (MLP) is used to transform the joint angle information θ[t] into an adjacency matrix A′[t]:

$$A\prime \left[t\right]=\mathrm{ReLU}\left(W_3\left(\mathrm{ReLU}\left(W_2\left(\mathrm{ReLU}\left(W_1\theta \left[t\right]+b_1\right)\right)+b_2\right)\right)+b_3\right)$$

(6)

where, θ[t] is a four-dimensional vector comprising the joint angles of the elbow and the Euler angles of the shoulder; W₁, W₂, and W₃ are the weight matrices of the MLP; b₁, b₂, and b₃ are the bias vectors of the MLP.

Since the adjacency matrix must satisfy a row-normalization constraint (i.e., the sum of the connection probabilities for each node equals 1), A′[t] is normalized using the softmax function to obtain the final adjacency matrix A[t]:

$$A_{i,j}\left[t\right]={\displaystyle \frac{\exp \left(A_{i,j}^{\text{'}}\left[t\right]\right)}{{\displaystyle {\sum }_{k=1}^{N_{\mathrm{A}}}\exp \left(A_{i,k}^{\text{'}}\left[t\right]\right)}}}$$

(7)

where, A_i,j[t] represents the connection weight between EMG channel i and j at time t. In this study, six muscles were utilized for arm force estimation. Accordingly, to represent the interactions between all pairs of muscle groups, the adjacency matrix was designed with a dimension of 6 × 6.

(c) Temporal Graph Neural Network Model

The GNN employs a graph convolution operation based on the Angle-Guided Attention-derived adjacency matrix to extract spatial dependencies among EMG signals. The resulting temporal features are then fed into an LSTM network for sequential modeling. The LSTM’s hidden state is passed through a fully connected (FC) layer to obtain the final force estimation. This process is illustrated in the following network structure:

$$\left\{\begin{array}{l}G\left[t\right]=\sigma \left(A\left[t\right]H\left[t\right]W_g\right)\\ h\left[t\right]=\mathrm{LSTM}\left(G\left[t\right],h\left[t-1\right]\right)\\ F_{\mathrm{pred}}\left[t\right]=W_{f}h\left[t\right]+b_f\end{array}\right.$$

(8)

where, H[t] represents the GNN input consisting of d₁ time-series E_LPF from six muscle groups (with d₁ = 6 in this parper); W_g is the weight matrix of the GNN; G[t] is the GNN’s feature matrix at time t; h(t) denotes the LSTM’s hidden state at time t; F_pred[t] represents the estimated arm force at time t.

(d) Loss Function and Regularization

To minimize the estimation error, the mean squared error (MSE) between the true arm force F_true[t] and the estimated arm force F_pred[t] is used as the loss function:

$$L_1={\displaystyle \frac{1}{N_L}}{\displaystyle \sum _{t=1}^{N_L}{\left(F_{\mathrm{true}}\left[t\right]-F_{\mathrm{pred}}\left[t\right]\right)}^2}$$

(9)

where, N_L is the number of samples.

Additionally, to prevent overfitting and to ensure that the adjacency matrix A(t) does not undergo extreme variations, a regularization term based on the Frobenius norm is added:

$$L={\displaystyle \frac{1}{N_L}}{\displaystyle \sum _{t=1}^{N_L}{\left(F_{\mathrm{true}}\left[t\right]-F_{\mathrm{pred}}\left[t\right]\right)}^2}+\lambda {‖A\left[t\right]-A\left[t-1\right]‖}_{\mathrm{F}}^2$$

(10)

where, λ is the regularization coefficient. The regularization parameter λ is selected from a commonly used range between 1 × 10⁻⁵ and 1 × 10⁻³. In this paper, preliminary experimental results show that λ = 1 × 10⁻⁴ achieve the best balance between training accuracy and generalization performance, yielding the lowest validation error and minimal overfitting.

The overall loss function thus combines the MSE and the regularization term, guiding the model to learn a more accurate and stable arm force estimation.

3. Mathematical Modeling of Human Skill Imitation and Learning Algorithm

3.1. Skill Criteria from Human Demonstrations

Most current imitation learning control models rely on fitting speed and force curves from human demonstrations to replicate movements. However, the application of this skill imitation approach is heavily limited by the demonstration tasks. In human–robot collaboration tasks, the uncertainty of movement increases the demand for skill generalization. To address this, this paper aims to extract key skill criteria from human demonstrations to guide the online learning and optimization of the control model, enabling it to more closely mimic human behavior.

(1)

Collaborative comfort

During collaboration, the human’s output force primarily guides the robot’s movement, while the robot handles most of the physical labor. For a given task, a smaller control force from the operator indicates stronger robot assistance, and greater comfort. Therefore, the concept of the equivalent output force is introduced as a measure of collaborative comfort.

In human demonstrations, the equivalent output force F_imt is defined as the ratio of the energy exerted by the leader to the total displacement. It is calculated as follows:

$$F_{\mathrm{imt}}={\displaystyle \frac{1}{3}}{\displaystyle \sum _{d=1}^3\left(\frac{{\displaystyle \sum _{t=1}^N\left|F_d[t]\ast \Delta x_d[t]\right|}}{{\displaystyle \sum _{t=1}^N\left|\Delta x_d[t]\right|}}\right)}$$

(11)

where, $F_d[t]$ and $\Delta x_d[t]$ are the leader output force and the follower movement displacement at time t, respectively; the subscript d represents the direction of the follower movement.

In the human–robot collaboration scenario, the equivalent output force F_cnt is defined as the ratio of the energy exerted by the operator to the robot’s effective motion distance. Since the robot may occasionally move against the operator’s intended direction during the training of collaborative control models, such reverse motion should be excluded from the calculation of effective motion distance. Accordingly, F_cnt is expressed as follows:

$$F_{\mathrm{cnt}}={\displaystyle \frac{1}{3}}{\displaystyle \sum _{d=1}^3\left(\frac{{\displaystyle \sum _{t=1}^T\left|F_d[t]\ast \Delta x_d[t]\right|}}{{\displaystyle \sum _{t=1}^T\mathrm{sign}(F_d[t]\ast \Delta x_d[t])\ast \left|\Delta x_d[t]\right|}}\right)}$$

(12)

where, T is the number of samples.

To evaluate actual behavior using the skill criteria from human demonstrations, according to the Ref. [42], the collaborative comfort R_F in the expert reward function is defined as follows:

$$R_{\mathrm{F}}=1-\left({\displaystyle \frac{F_{\mathrm{cnt}}-F_{\mathrm{imt}}}{F_{\mathrm{cnt}}+F_{\mathrm{imt}}}}\right)$$

(13)

(2)

Collaborative smoothness

Collaborative smoothness refers to the continuity of a robot’s movements during task execution. It plays a critical role in human–robot interaction, particularly in scenarios that demand precision and coordinated actions. Smooth robotic motion ensures stable and sustained force assistance, enhances predictability, and improves both safety and controllability. For the robot, smoothness is typically characterized by speed, while for the human operator, it is reflected in the consistency of the applied control force.

In human demonstrations, the smoothness of both motion speed V_imt and control force P_imt can be quantified as follows:

$$\left\{\begin{array}{l}{V}_{\mathrm{imt}}={\displaystyle \frac{{\displaystyle \sum _{d=1}^3{\displaystyle \sum _{t=1}^N\left|V_d[t]-V_d[t-1]\right|}}}{3N}}\\ P_{\mathrm{imt}}={\displaystyle \frac{{\displaystyle \sum _{d=1}^3{\displaystyle \sum _{t=1}^N\left|F_d[t]-F_d[t-1]\right|}}}{3N}}\end{array}\right.$$

(14)

where, V_d[_t] is the robot speed at time t.

In the human–robot collaboration scenario, the smoothness of both motion speed V_cnt and control force P_cnt can be quantified as follows:

$$\left\{\begin{array}{l}{V}_{\mathrm{cnt}}={\displaystyle \frac{{\displaystyle \sum _{d=1}^3{\displaystyle \sum _{t=1}^T\left|V_d[t]-V_d[t-1]\right|}}}{3T}}\\ P_{\mathrm{cnt}}={\displaystyle \frac{{\displaystyle \sum _{d=1}^3{\displaystyle \sum _{t=1}^T\left|F_d[t]-F_d[t-1]\right|}}}{3T}}\end{array}\right.$$

(15)

Thus, the collaborative smoothness R_V in the expert reward function is defined as follows:

$$R_{\mathrm{V}}=1-{\displaystyle \frac{1}{2}}\left({\displaystyle \frac{V_{\mathrm{cnt}}-V_{\mathrm{imt}}}{V_{\mathrm{cnt}}+V_{\mathrm{imt}}}}\right)-{\displaystyle \frac{1}{2}}\left({\displaystyle \frac{P_{\mathrm{cnt}}-P_{\mathrm{imt}}}{P_{\mathrm{imt}}+P_{\mathrm{cnt}}}}\right)$$

(16)

3.2. Expert Reward Function Construction

Based on the skill criteria defined in the previous section, the optimization problem for the human–robot collaborative control model is formulated as learning a decision-making policy that maps human arm forces to robot motion velocities, with the objective of maximizing both comfort and smoothness during collaboration.

$$\begin{array}{c}\mathrm{P}1:\underset{v,F_{\mathrm{cnt}}}{\max }\left\{R_{\mathrm{F}},R_{\mathrm{V}}\right\}\hfill \\ s.t.\mathrm{C}1: -0.02\le V_d\left[t\right]\le 0.02\\ \mathrm{C}2:V_d\left[t\right]\ast F_d[t]>0\end{array}$$

(17)

Here, C1 represents the constraint on the robot’s speed; C2 denotes the constraint on the control signal, ensuring that the robot’s motion aligns with the direction of the force applied by the human, thereby enhancing the naturalness of the control.

In the collaboration performance evaluation, collaborative comfort and smoothness are considered equally important, requiring the combined rewards to be maximized. An auxiliary penalty strategy is introduced to help the control system adapt more effectively to the operator’s movement habits. An auxiliary penalty value R_a is introduced when the direction of the guiding force is misaligned with the robot’s motion, which has been shown to facilitate the robot’s rapid adaptation to human motion tendencies. When the learned behavior aligns closely with human demonstrations, the combined reward for collaborative comfort and motion smoothness approaches a total value of two. Experimental evaluations demonstrated that values greater than two are effective in accelerating training; however, excessively large penalties are found to negatively impact long-term reward optimization. In this study, a value of R_a = two is selected to ensure that the reward function retains a clear distinction between positive and negative values after applying the penalty mechanism. The expert reward function of human skill imitation learning algorithm r is as follows:

$$\left\{\begin{array}{cc}r=R_{\mathrm{F}}+R_{\mathrm{V}}& V_d\left[t\right]\ast F_d[t]>0\\ r=R_{\mathrm{F}}+R_{\mathrm{V}}-R_{\mathrm{a}}& V_d\left[t\right]\ast F_d[t]\le 0\end{array}\right.$$

(18)

3.3. Human–Robot Collaborative Control Model Based on Imitation Reinforcement Learning Algorithm

3.3.1. Construction of Imitation Reinforcement Learning Model Based on Actor–Critic Algorithm

In imitation learning, particularly in scenarios with limited data or insufficient human demonstrations, traditional behavior cloning methods are prone to overfitting. This overfitting leads to learned strategies that become excessively reliant on the expert’s examples, resulting in poor generalization to new situations. The integration of reinforcement learning algorithms addresses this issue by allowing the model to not only learn from expert demonstrations but also improve the strategy through continuous interaction with the environment, thereby enhancing the generalization capability of the control strategy.

As shown in Figure 4, the Actor–Critic (AC) reinforcement learning algorithm is applied to human–robot collaborative control. The AC algorithm combines both policy optimization and value evaluation methods by assessing the current value function to optimize the policy function. The control model consists of AC networks and an experience replay pool.

During the human–robot collaboration, the human output force serves as a crucial interaction medium and plays an important role in determining the robot’s interaction speed. Therefore, the state space of the agent S[t] includes two key features: the current force F_d[t] and the force change ΔF_d[t], i.e., S[t] = [F_d[t], ΔF_d[t]]. The action space of the agent corresponds to the robot’s speed v[t]. Using the policy function π(v[t]|S[t]) learned through the Actor network, the agent determines V_d[t] based on the current force state S[t] and sends v[t] to the robot. The operators adjust their arm force according to the intended movement, enabling human-in-the-loop control.

The reward value r[t] is used to evaluate how well the operator’s motion intention is achieved, and the generated samples {S[t], v[t], r[t], and S[t − 1]} are stored in the experience replay pool for model training and updating. The specific structural framework of the imitation learning model based on the AC algorithm is as follows:

(1)

Actor network architecture

In the control model, both the Actor and Critic networks use artificial neural network structures. To ensure the exploration ability of the Actor network, the output of the Actor network consists of the mean $\mu$ and variance $\sigma$ of the robot speed. The network structure is as follows:

$$\left\{\begin{array}{l}{h}_{1a}=f_{\mathrm{ReLU}}\left(W_{1\mathrm{a}}\left[F_d\left[t\right],\Delta F_d\left[t\right]\right]+b_{1\mathrm{a}}\right)\\ h_{2a}=f_{\mathrm{ReLU}}\left(W_{2a}\cdot h_{1a}+b_{2\mathrm{a}}\right)\\ \mu \left(F_d\left[t\right],\Delta F_d\left[t\right]\right)=W_{\mu }\cdot h_{2a}+b_{\mu }\\ \sigma \left(F_d\left[t\right],\Delta F_d\left[t\right]\right)=f_{\mathrm{softplus}}\left(W_{\sigma }\cdot h_{2a}+b_{\sigma }\right)\end{array}\right.$$

(19)

where, h_1a and h_2a represent the outputs of the first and second hidden layers, respectively; $b_{1\mathrm{a}}$, $b_{2\mathrm{a}}$, $b_{\mu }$, and $b_{\sigma }$ are the bias vectors for each layer of the network; $W_{1\mathrm{a}}$, $W_{2a}$, $W_{\mu }$, and $W_{\sigma }$ are the weight matrices for each layer of the network; $f_{\mathrm{ReLU}}\left(•\right)$ represents ReLU activation function; $f_{\mathrm{softplus}}\left(•\right)$ represents Softplus activation function.

The actual robot speed v[t] is determined by sampling from this distribution:

$$v\left[t\right]~\mathcal{N}\left(\mu \left(F_d\left[t\right],\Delta F_d\left[t\right]\right),\sigma \left(F_d\left[t\right],\Delta F_d\left[t\right]\right)\right)$$

(20)

(2)

Critic network architecture

The Critic network’s output is the value function $V\left(F_d\left[t\right],\Delta F_d\left[t\right]\right)$, which evaluates the value of the robot speed v[t] under the current human output force state $\left[F_d\left[t\right],\Delta F_d\left[t\right]\right]$. The Critic network structure is as follows:

$$\left\{\begin{array}{l}{h}_{1\mathrm{c}}=f_{\mathrm{ReLU}}\left(W_{1\mathrm{a}}\left[F_d\left[t\right],\Delta F_d\left[t\right],v\left[t\right]\right]+b_{1\mathrm{c}}\right)\\ h_{2c}=f_{\mathrm{ReLU}}\left(W_{2c}\cdot h_{1c}+b_{2c}\right)\\ V\left(F_d\left[t\right],\Delta F_d\left[t\right]\right)=W_{3c}\cdot h_{2c}+b_{3c}\end{array}\right.$$

(21)

where, h_1c and h_2c represent the outputs of the first and second hidden layers, respectively; b_1c, b_2c, and b_3c are the bias vectors for each layer of the network; W_1c, W_2c, and W_3c are the weight matrices or each layer of the network.

3.3.2. Fuzzy Rule-Based Experience Replay Partitioning Mechanism

Figure 5 illustrates a leader–follower collaborative assembly demonstration. During the human demonstration data collection, the follower completes peg-in-hole by responding to the guiding forces applied by the leader. To eliminate the influence of visual feedback and ensure the purity of physical interaction, the follower is blindfolded throughout the entire procedure. Moreover, the demonstration speed is limited to match the robot’s motion constraints, which in this study is set to no more than 0.02 m/s.

As shown in Figure 6, the curves of the arm force and speed in the Y-direction during human demonstrations are presented. It can be observed that the estimated arm-applied force and motion velocity exhibit a strong correlation during the collaborative assembly process. Additionally, the assembly task naturally decomposes into four distinct sub-motions: Acceleration (Accel), Rapid Transfer (RT), Deceleration (Decel), and Fine Adjustment (FA). In fact, the vast majority of collaborative tasks are composed of these four sub-motions.

Considering that key indicators, such as arm force stability and equivalent output force, differ significantly across these sub-motion phases, directly mixing all demonstration data into a single training stream would introduce substantial variance in reward estimation, thereby impairing convergence and overall learning stability. To mitigate this, a fuzzy rule-based experience replay partitioning strategy is proposed. This strategy classifies each sample into a corresponding sub-motion phase based on the magnitude of the arm force and its rate of change. Each motion phase maintains its own dedicated experience buffer and stores its phase-specific reward function values accordingly.

Although sub-motion types can be roughly identified by analyzing the magnitude and temporal trends of interaction forces, the inherent physiological uncertainty and the fuzzy nature of human force output make rigid classification unreliable. To address this challenge, the proposed fuzzy rule-based experience replay partitioning strategy incorporates a fuzzy-rule-based sub-motion inference mechanism to enhance adaptability and robustness under dynamic conditions.

Table 1. The fuzzy rules in the experience replay partitioning mechanism.

		Arm Force Level
		PH	PM	PS	NS	NM	NH
Arm Force Change Level	PH	Accel	Accel	Accel	Decel	Decel	Decel
	PM	RT	Accel	Accel	Decel	Decel	RT
	PS	RT	RT	FA	FA	RT	RT
	NS	RT	RT	FA	FA	RT	RT
	NM	RT	Decel	Decel	Accel	Accel	RT
	NH	Decel	Decel	Decel	Accel	Accel	Accel

presents the fuzzy rules adopted in the experience replay partitioning method. Arm force and its rate of change are categorized into six levels based on direction (positive or negative) and magnitude (high, medium, or small), denoted as Positive High (PH), Positive Medium (PM), Positive Small (PS), Negative Small (NS), Negative Medium (NM), and Negative High (NH), respectively.

Both the arm force and its rate of change are fuzzified using triangular membership functions, as illustrated in Figure 7. Taking the positive-direction arm force (or the rate of change of arm force) as an example, its membership function is defined as follows:

$${\lambda }_A\left(F_d\left[t\right]\right)=\left\{\begin{array}{l}\max \left(\min \left(1,{\displaystyle \frac{a-\left(F_d\left[t\right]\right)}{a}}\right),0\right)\begin{array}{cc}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}0\le F_d\left[t\right]\le a& \Rightarrow F_d\left[t\right]\in \mathrm{PS}\end{array} \\ \max \left(\min \left({\displaystyle \frac{\left(F_d\left[t\right]\right)}{a}},{\displaystyle \frac{b-\left(F_d\left[t\right]\right)}{b-a}}\right),0\right)\begin{array}{cc}\hspace{1em}0\le F_d\left[t\right]\le b& \Rightarrow F_d\left[t\right]\in \mathrm{PM}\end{array} \\ \max \left(\min \left(1,{\displaystyle \frac{\left(F_d\left[t\right]\right)-a}{b-a}}\right),0\right)\begin{array}{cc}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}b\le F_d\left[t\right]& \Rightarrow F_d\left[t\right]\in \mathrm{PH}\end{array}\end{array}\right.$$

(22)

where, ${\lambda }_A\left(•\right)$ denotes the membership function for force, with parameters a and b defining the boundaries of the membership levels. In the triangular membership function for positive arm force, a represents half of the preset maximum interaction force (or maximum rate of change), while b corresponds to the preset maximum interaction force (or maximum rate of change).

This configuration provides practical benefits: In real-world human–robot interaction scenarios, a considerable portion of movements falls within medium-force levels. A narrow classification margin may lead to misclassification of such transitional actions. By setting a to half of the maximum expected value, the model not only aligns better with realistic force distributions but also broadens the central membership region. This enhances the system’s robustness to boundary fuzziness and improves its ability to discriminate intermediate-force motions under dynamic conditions.

The arm force and its changes are fuzzified according to the fuzzy rule table using the maximum membership method to determine the current sub-motion type. The process is expressed as follows:

$$\left\{\begin{array}{l}{z}_{p_i}={\displaystyle \sum _{A\&B\in p_i}{\lambda }_A\left(F_d\left[\mathrm{t}\right]\right){\lambda }_B\left(\Delta F_d\left[\mathrm{t}\right]\right)}\\ p_i^{*}=\underset{p_i}{\arg \max }\left(z_{p_1},z_{p_2},z_{p_3},z_{p_4}\right)\end{array}\right.$$

(23)

where, $z_{p_i}$ represents the membership value of each sub-motion type; ${\lambda }_B\left(•\right)$ represents the membership function of the force change; $p_i^{*}$ represents the current sub-motion type corresponds to the state space.

This fuzzy-rule-based sub-motion inference mechanism enables a soft partitioning of motion types. Based on the identified sub-motion types, actions, behaviors, and reward values in imitation reinforcement learning are stored in separate partitions. By incorporating partitioned experience replay, the method ensures balanced sampling and training across the four sub-motion types, thereby significantly improving learning stability and adaptability to complex motion dynamics.

3.3.3. Imitation Reinforcement Learning Model Update

The value function V(S[t]) represents the expected return at state S[t], but it alone cannot fully assess policy quality. To address this, the advantage function is introduced as a metric to quantify the relative the excellence of an action in a given state. For computational simplicity, the Temporal Difference (TD) error from the Critic is used as an approximation of the advantage function. The advantage function A(S[t], v[t]) is defined as follows [43]:

$$A\left(S\left[t\right],v\left[t\right]\right)=Q\left(S\left[t\right],v\left[t\right]\right)-V\left(S\left[t\right]\right)$$

(24)

where, Q(S[t], v[t]) is the state-action value function, representing the expected return after taking action v[t] at state S[t], which includes both the current action and all future rewards.

According to the Bellman equation, the state-action value function Q(S[t], v[t]) and the action reward value V(S[t]) are related as follows:

$$Q\left(S\left[t\right],v\left[t\right]\right)=r\left[t\right]+\gamma V\left(S\left[t+1\right]\right)$$

(25)

where, γ is the discount factor, used to balance the relative importance of current rewards and future rewards. Experimental results show that lower discount factors (e.g., γ = 0.96) lead to faster convergence but result in suboptimal task performance, suggesting an overemphasis on immediate rewards. In contrast, higher discount factors (e.g., γ > 0.98) slow down the learning process without yielding substantial improvements in final performance. A value of γ = 0.97 is found to offer the best trade-off, enabling efficient learning while preserving strong generalization to dynamic task variations.

Thus, combining the Equations (24) and (25), A(S[t], v[t]) can be expressed as follows:

$$A\left(S\left[t\right],v\left[t\right]\right)=r\left[t\right]+\gamma V\left(S\left[t+1\right]\right)-V\left(S\left[t\right]\right)$$

(26)

To balance the optimization of various sub-motion types and prevent dominance by any single sub-motion mode, the experience replay pools from different regions are sampled evenly. The sample size for each pool is T. In this case, the gradient update for the Actor-Critic network can be expressed as follows:

$$\left\{\begin{array}{l}{\nabla }_{{\theta }_c}L\left({\theta }_c\right)={\displaystyle \frac{1}{4T}}{\displaystyle \sum _d{\left(\frac{1}{2}A\left(S\left[t\right],v\left[t\right]\right){\nabla }_{{\theta }_c}V\left(S\left[t\right]\right)\right)}_d}\\ {\nabla }_{{\theta }_a}J\left({\theta }_a\right)={\displaystyle \frac{1}{4T}}{\displaystyle \sum _d{\left({\nabla }_{{\theta }_a}\log \pi \left(S\left[t\right]|v\left[t\right]\right)A\left(S\left[t\right],v\left[t\right]\right)\right)}_d}\end{array}\right.$$

(27)

where, ${\nabla }_{{\theta }_c}L\left({\theta }_c\right)$ represents the gradient of the loss function of the Critic network with respect to the parameters ${\theta }_c$; ${\nabla }_{{\theta }_a}J\left({\theta }_a\right)$ represents the gradient of the objective function of the Actor network with respect to the parameters ${\theta }_a$.

4. Experimental Analysis and Discussion

4.1. Experimental Setup

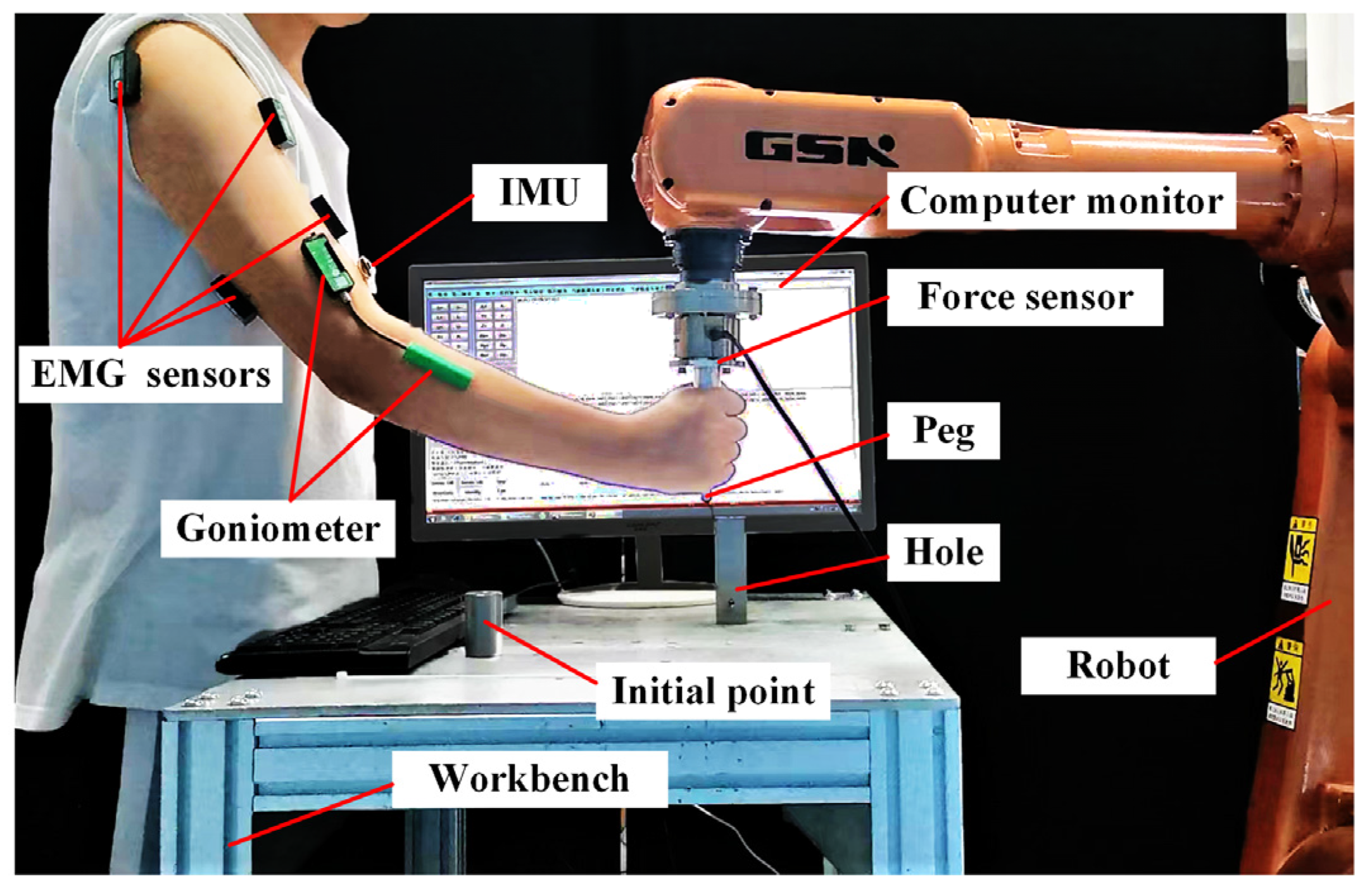
Figure 8 illustrates the schematic of the human–robot collaborative assembly experimental platform. The platform is built using a GSK 8 kg industrial robot Guangzhou GSK Technology Co., Ltd. Guangzhou, China). EMG signals and elbow joint angles are collected using sensors and goniometers from Biometrics Ltd. (Cwmfelinfach, UK), while the shoulder joint Euler angles are acquired through an inertial measurement unit (IMU) from Hipnuc Electronics Technology Co., Ltd. (Beijing, China). A six-axis force/torque sensor from Me-Systeme GmbH (Stuttgart, Germany) is mounted at the robot’s end-effector; however, it is not involved in the control loop. Instead, it is used to collect ground-truth force data for evaluating the performance of the force estimation model.

During the experiment, the robot adjusts its position by following the human arm force, enabling collaborative assembly between the human and the robot. The initial offset between the peg and the hole is set to Lx = 300, Ly = 200 mm, and Lz = 40 mm along the X, Y, and Z axes, respectively. The assembly peg has a diameter of 9.98 mm, while the hole diameter is 11.03 mm.

4.2. Ablation Study of the Proposed Arm Force Estimation Model

To validate the effectiveness of the AGA module, two ablation models are constructed for comparison:

Fixed-Adjacency Matrix TGNN: This model constructs inter-muscle connections using a static adjacency matrix. The model uses the same EMG and joint angle inputs as the full AGA-TGNN, enabling a fair comparison and highlighting the limitations of Fixed-Adjacency Matrix structures under dynamic tasks.

LSTM-only (TGNN without GNN): In this version, the GNN is removed entirely, and only a LSTM is used to process EMG sequences. Joint angle inputs and spatial topology information are excluded, allowing assessment of the importance of spatial topology and joint angle information in modeling muscle coordination.

The results are summarized in Figure 9 and

Table 2. Performance summary of the ablation study for the proposed arm force estimation model.

Method	Direction	Median Error	Mean Error	Maximum Error
AGA-TGNN	Froce_x	1.832	2.693	11.228
	Froce_y	1.889	2.579	10.482
	Froce_z	1.586	1.806	9.896
Fixed-Adjacency Matrix TGNN	Froce_x	3.248	3.784	17.469
	Froce_y	2.776	3.437	17.545
	Froce_z	2.361	2.948	16.166
LSTM-only	Froce_x	4.664	5.136	17.583
	Froce_y	3.702	4.327	16.898
	Froce_z	2.908	3.471	15.392

. The AGA-TGNN model achieves superior performance across all key metrics, including median, mean, and maximum estimation errors. The performance gains are primarily attributed to the following factors:

The Fixed-Adjacency Matrix TGNN lacks adaptability to joint angles (arm posture) variations, as its connectivity structure remains constant regardless of joint configuration. This limits its ability to capture joint angles-dependent muscle coordination patterns.

The LSTM-only model fails to incorporate spatial topology and joint angles information, resulting in poor representation of the nonlinear coupling between muscle activations and arm output force.

In conclusion, the Angle-Guided Attention module effectively integrates joint angle information to dynamically adjust muscle interaction modeling, significantly improving the accuracy of force estimation in dynamic scenarios.

4.3. Validation of Arm Force Estimation Model

This study selects several representative models that have demonstrated strong performance in force estimation tasks. The specific configurations are as follows:

Comparison Model 1 (FOS Model): The FOS model constructs an arm force fitting model based on joint angles and the amplitude of EMG signals using an orthogonal search strategy. It represents a traditional analytical approach to force estimation.

Comparison Model 2 (LSTM Model): This model employs LSTM networks to model the temporal sequences of EMG signals. As a widely adopted method for force estimation, it exhibits strong capabilities in learning temporal dependencies.

Comparison Model 3 (Deep-LSTM Model): Based on Deep-LSTM, this model performs feature extraction and modeling of EMG signals. With its powerful spatial pattern recognition and nonlinear modeling capabilities, it is one of the most competitive end-to-end force estimation approaches to date.

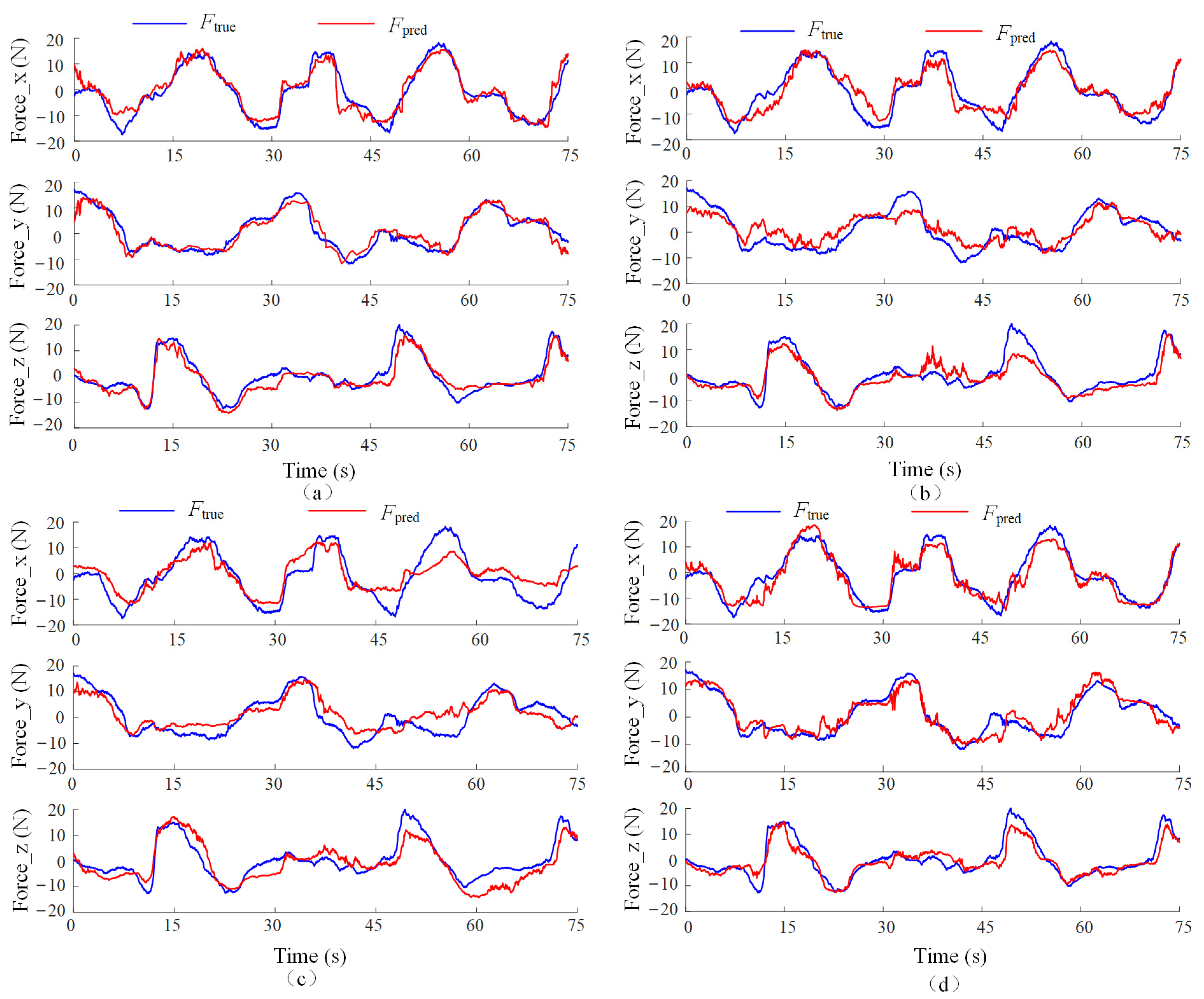
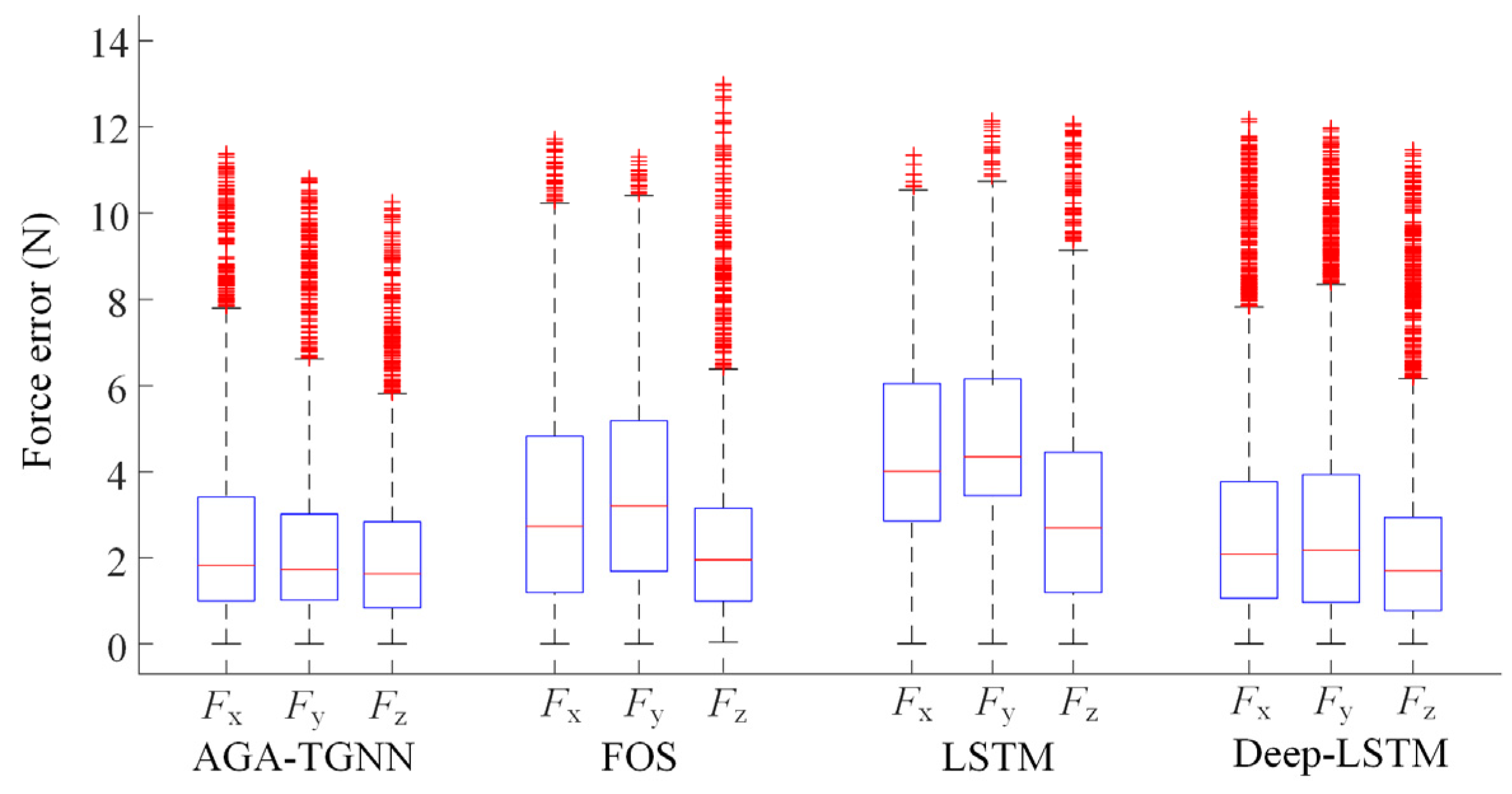
The experimental results of the three comparison models are shown in Figure 10, with the corresponding error distribution box plots presented in Figure 11. The statistical performance metrics are listed in

Table 3. Performance statistics of different arm force estimation models.

Method	Direction	Median Error	Mean Error	Maximum Error
AGA-TGNN	Froce_x	1.825	2.616	11.388
	Froce_y	1.725	2.561	10.805
	Froce_z	1.626	2.090	10.237
FOS	Froce_x	2.730	3.264	11.726
	Froce_y	3.201	3.631	11.302
	Froce_z	2.003	2.308	13.034
LSTM	Froce_x	4.012	5.443	11.346
	Froce_y	4.346	5.028	12.143
	Froce_z	2.692	2.997	12.068
Deep-LSTM	Froce_x	2.082	2.854	12.191
	Froce_y	2.181	2.884	11.974
	Froce_z	1.699	2.332	11.473

.

As observed from Table 3, Figure 10 and Figure 11, the proposed AGA-TGNN model outperforms existing methods in terms of median error, maximum error, and mean error across all three force components. Compared with the Deep-LSTM model, the proposed model achieves reductions in mean estimation error of 10.38%, 8.33%, and 11.20% in the X, Y, and Z directions, respectively, demonstrating a significant performance advantage.

The performance differences can be attributed to the following factors:

First, FOS is a traditional model based on analytical expressions. While it can rapidly construct predictive functions in low-dimensional spaces, it lacks sufficient expressive power to capture the highly nonlinear relationship between EMG signals and arm forces. Furthermore, its fitting process is sensitive to signal fluctuations and lacks the ability to model dynamic features, resulting in unstable estimation performance. As the number of input muscles increases, the computational complexity of FOS grows exponentially without a corresponding improvement in fitting accuracy, limiting its performance in multi-dimensional dynamic scenarios.

Second, while LSTM and Deep-LSTM are both deep learning approaches with strong temporal modeling and feature extraction capabilities, respectively, neither considers the dynamic variation in inter-muscle coordination arising from changing joint states. Specifically, both models directly couple EMG and angle signals without explicitly accounting for the underlying physiological and physical interaction mechanisms. By completely relying on neural networks to decouple the relationship between EMG signals and joint angles, they fail to capture the complex, dynamic interactions, leading to insufficient generalization ability.

In contrast, the proposed method introduces an Angle-Guided Attention mechanism, which dynamically adjusts the adjacency matrix of the GNN based on joint angles. This approach effectively decouples the dynamic relationships between muscle groups and joint angles, enhancing the physiological plausibility of the input signal structure. By improving the model’s sensitivity to key muscle coordination patterns, this mechanism significantly enhances the robustness and generalization ability of the network, enabling stable and accurate force estimation across varying motion conditions.

4.4. Training of the Imitation Reinforcement Learning Model

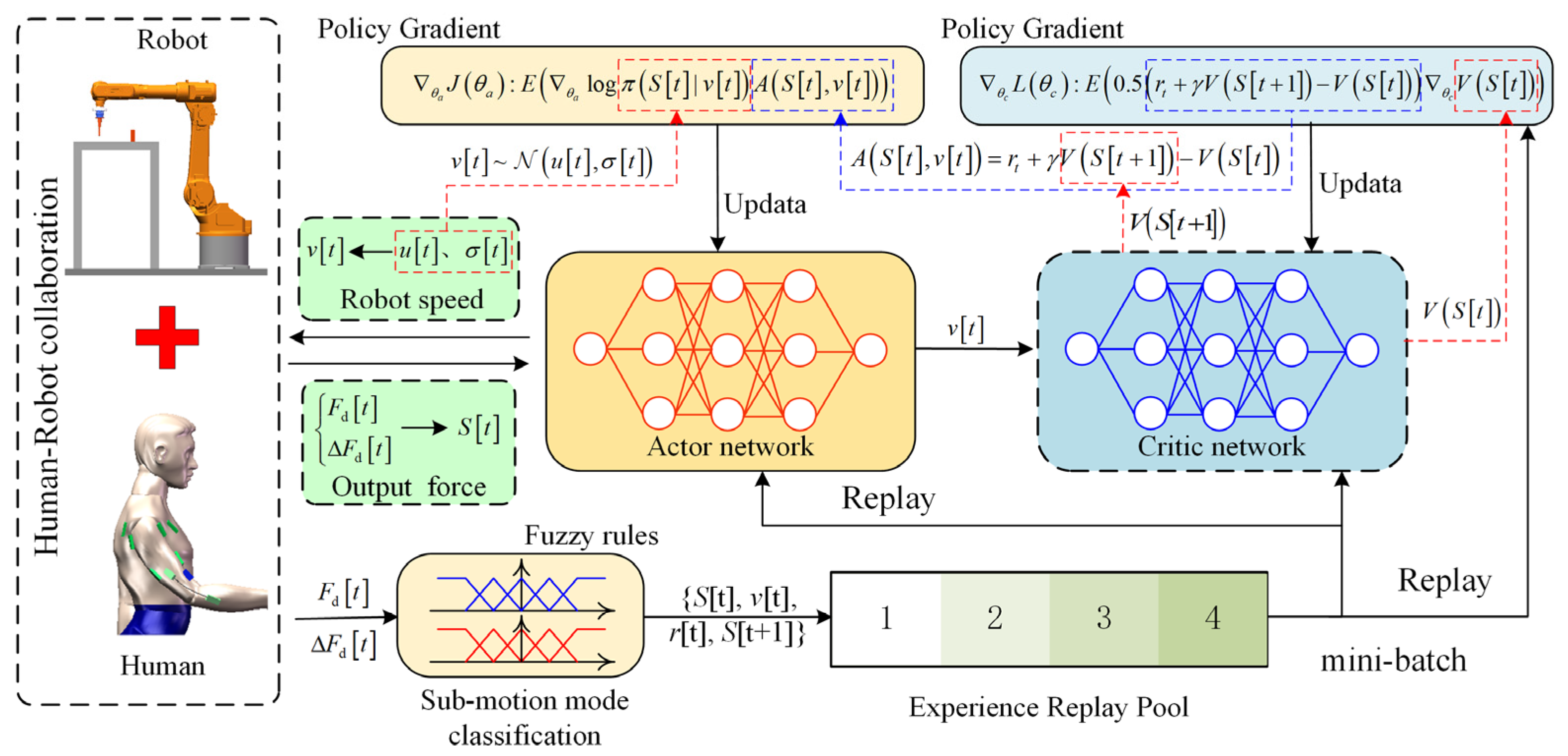
As illustrated in Figure 4, the imitation reinforcement learning framework employed in this work comprises an Actor–Critic (AC) network and an experience replay pool. Based on the reward mechanism defined in Equation (17), the model is trained online with the goal of directly translating human arm forces into robot control commands. This approach aims to overcome the parameter tuning challenges inherent in conventional impedance control strategies.

However, as the initial imitation reinforcement learning model is untrained, it cannot immediately perform collaborative assembly tasks. To ensure the safety of both the experimental equipment and human participants, the training process is divided into two phases: pre-training and task training.

In the pre-training phase, a kinesthetic teaching setup is adopted, where the human operator physically guides the robot without engaging in actual assembly. It is assumed that human motor adaptation skills in response to external collaborative forces are generally similar across different directions. Therefore, to reduce training complexity, motion coordination is learned along a single axis, the X-direction, as a representative case. The human operator repetitively moves the robot along this axis to help the model acquire basic motion alignment and compliance characteristics.

Following pre-training, the imitation reinforcement learning model gains an initial ability to coordinate with human motion—namely, aligning the robot’s movement direction with the direction of human-applied forces while maintaining a degree of compliance. The model then enters the task training phase, which takes place in the collaborative assembly scenario shown in Figure 8. To prevent excessive contact forces during training, a safety mechanism is implemented: if the force between the peg and assembly hole exceeds 50 N, the current cycle is terminated, and the robot returns to its initial position before restarting. This task training stage aims to further improve motion smoothness and collaborative comfort by optimizing the policy with respect to the expert-defined reward.

During training, the robot operates on a 50 ms control cycle. In each cycle, the system performs arm force estimation, sub-motion classification, policy update via imitation reinforcement learning, and robot control command generation.

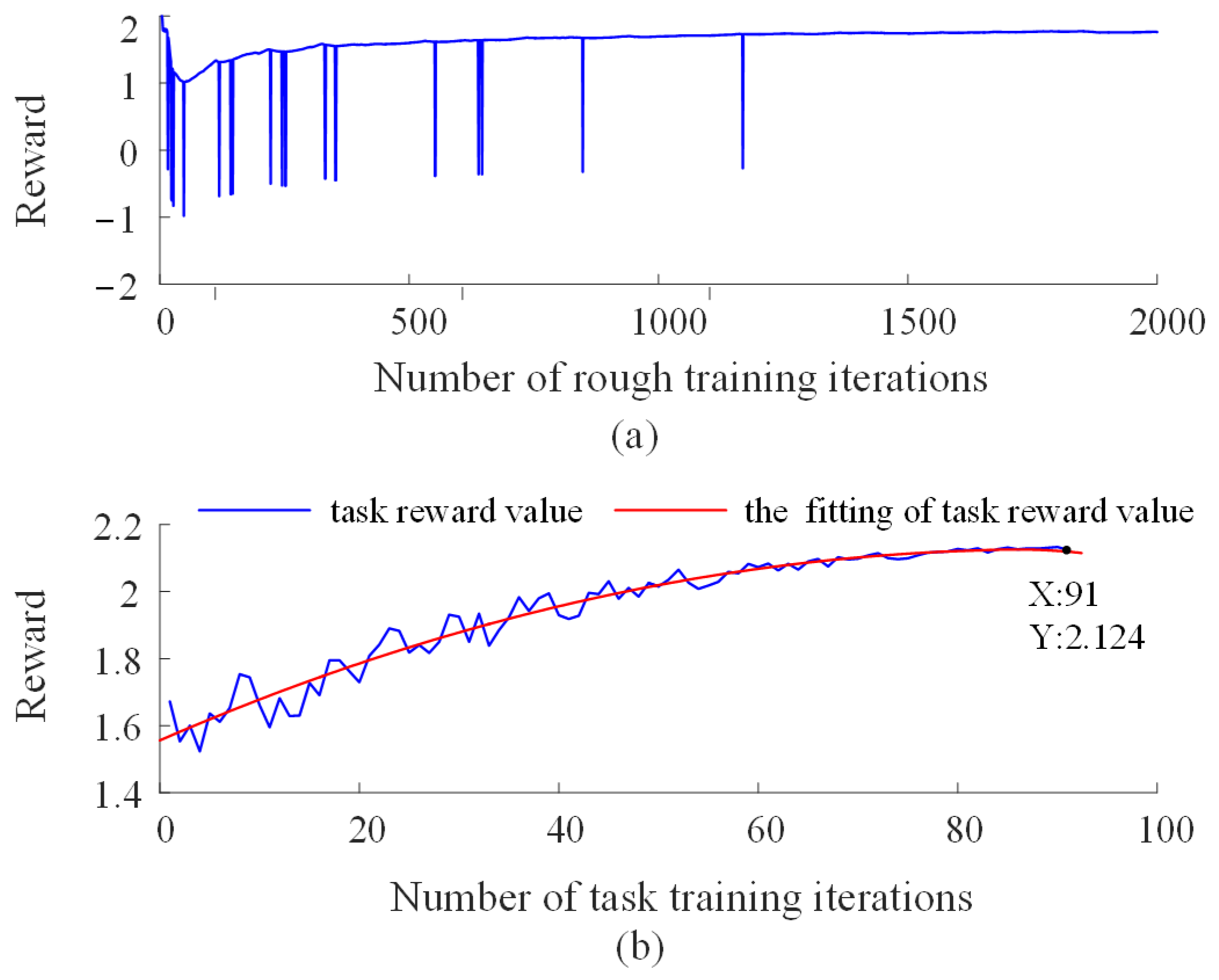
Figure 12a shows the reward curve during the pre-training stage. It can be observed that, under the guidance of the penalty mechanism, the robot achieves alignment between its movement direction and the human’s applied force direction after approximately 2000 training iterations, demonstrating good following behavior. However, due to the limited diversity of movement in long-term reciprocating training, this phase tends to result in high robot velocities even in response to small human forces. Therefore, once the robot has acquired basic following ability, further optimization through task training becomes necessary.

In Figure 12b, the blue curve represents the total reward for each task cycle. Significant fluctuations in the early training stages suggest that the control model at that time did not fully conform to the expert demonstration trajectories. The red curve shows a fitted trend for the task rewards, indicating an overall upward trend with fluctuations, eventually converging to a stable value. After multiple rounds of training, the model’s performance surpasses that of the demonstration (the reward value of the expert demonstration is 2). This outcome may be attributed to the challenges of collecting human data, which is often limited by the degree of coordination and synergy between the leader and follower.

4.5. Comparative Analysis of Control Models

To evaluate the collaboration performance of the proposed imitation reinforcement learning-based control strategy, a comparative study is conducted against two state-of-the-art control approaches: the Adaptive Admittance Control (ADC) model [18] and the Gaussian Process Regression-based Imitation Learning (GPRIL) model [26].

To ensure a fair comparison within the experimental context of this study, necessary adaptations are made to each of the comparison models.

For the ADC model, the algorithm proposed in Ref. [21] is considered, which employs joint stiffness estimation to adaptively tune PD parameters. This approach is particularly effective in addressing the trade-off between precise trajectory tracking and compliant assistance. However, since this study does not involve joint stiffness estimation, it is substituted with the estimated arm output force. Under this modification, the PD parameters are adjusted as follows:

$$\left\{\begin{array}{l}{k}_{\mathrm{d}}=0.2{\sqrt{k}}_{\mathrm{p}}\\ k_p=\left(k_p^{\max }-k_p^{\min }\right){\displaystyle \frac{F_d-F_{\min }}{F_{\max }-F_{\min }}}+k_p^{\min }\end{array}\right.$$

(28)

where, k_d is the derivative term parameter, k_p is the proportional term parameter, $k_p^{\max }$ and $k_p^{\min }$ indicates the maximum and minimum value of the parameter k_p, and $F_{\max }$ and $F_{\min }$ are the maximum and minimum arm output forces from the operator during the experiment.

Regarding the GPRIL model, the multi-model Gaussian Process Regression technique, as proposed in the Ref. [26], is employed to model the relationship between the leader’s force and the follower’s speed during demonstrations.

To further evaluate the effectiveness of the proposed fuzzy experience replay mechanism, an ablation model, used as an additional comparison model, is constructed by removing this component from the original imitation reinforcement learning framework.

In this study, each control model is evaluated through 30 repeated experiments to assess the collaborative comfort, smoothness, task completion speed, and accuracy under different control methods. The performance statistics are summarized in

Table 4. Performance statistics of different control models.

Method	GPRIL Model	ADC Model	The Proposed Model	The Ablation Model
Collaborative Comfort	0.95	1.09	1.12	1.02
Collaborative Smoothness	0.94	0.95	1.03	0.93
Assembly Time (s)	19.2	18.4	18.1	19.7
Assembly Error (mm)	0.62	0.51	0.42	0.61
Assembly Success Rate	90%	93.3%	100%	86.7%

, while Figure 13 illustrates the operator’s output force and the robot’s movement speed across the three control models. The methods used to calculate collaborative comfort and smoothness are detailed in Equations (13) and (16). The evaluation criteria for accuracy and task completion speed are outlined as follows:

(a) Assembly Accuracy

Assembly error is a commonly used metric to evaluate collaboration precision. After the robot reaches the target position, the deviation between the robot’s final position and the desired position in the XY plane is used to assess the accuracy of the collaborative assembly. The assembly deviation can be expressed as follows:

$$e=\sqrt{e_x^2+e_y^2}$$

(29)

where, $e_x$ and $e_y$ denote the assembly errors in the X and Y directions, respectively.

(b) Success Rate

The success rate of assembly serves as a direct indicator of collaboration effectiveness. To avoid collisions during the process, a safety threshold is set: if the contact force between the peg and hole surpasses 50 N, the robot stops instantly, and the attempt is deemed unsuccessful. Likewise, if the assembly duration exceeds 30 s, the task is also classified as a failure.

(c) Efficiency

The time from task initiation to the moment the assembly peg is inserted more than 10 mm into the assembly hole is defined as the assembly time. In collaborative scenarios, human operators typically prefer shorter assembly times to improve task efficiency.

As shown in Table 4, the GPRIL model achieves collaborative comfort and smoothness values close to one. However, due to its limited learning capacity, it struggles to surpass expert-level performance.

In the ADC model, PD parameters are adjusted proportionally to the output force: higher forces lead to increased PD gains, while lower forces reduce them. This adjustment enables the robot to perform precise control when the operator exerts low force and executes rapid movements under high force. However, auxiliary motions during collaborative tasks often require coordination across three dimensions, and not all directions are suitable for high-speed execution. As a result, frequent acceleration and deceleration occur, as illustrated by the orange and blue curves in Figure 13f.

As shown in Figure 13, the robot’s motion under the proposed imitation reinforcement learning-based control model is noticeably smoother than that of the comparison models. As shown in Table 4, the proposed method achieves comprehensive improvements over the ADC model across all evaluation metrics. Specifically, collaborative comfort increases by 2.75%, and collaborative smoothness improves by 8.42%, reflecting enhanced physical interaction quality. In terms of task efficiency, the assembly time is reduced by 1.63%, and the assembly error decreases by 17.65%, indicating higher precision. Moreover, the assembly success rate improves by 7.2%.

Moreover, as shown in Table 4, the removal of the fuzzy experience replay mechanism resulted in significant performance degradation. Without sub-motion-based categorization, experiences from different motion phases interfered with each other during training, leading to decreased learning efficiency, reduced task execution accuracy, and visibly diminished coordination between human and robot during collaboration. These findings underscore the critical role of fuzzy experience replay in mitigating motion interference, promoting balanced learning across diverse sub-motion patterns, and ultimately enhancing the stability and responsiveness of human–robot collaboration under dynamic conditions.

To further validate the robustness of the proposed method across different individuals, two healthy adult participants are recruited to perform both the calibration of the arm force estimation model and the human–robot collaborative assembly tasks. The corresponding performance metrics are summarized in

Table 5. Performance statistics of different participants.

Participant	Collaborative Comfort	Collaborative Smoothness	Assembly Time (s)	Assembly Error (mm)	Assembly Success Rate
Participant 1	1.13	1.01	17.6	0.47	100%
Participant 2	1.09	1.01	18.3	0.39	100%

. The experimental results indicate that both participants successfully complete the assembly tasks with high accuracy, which further confirms the effectiveness of the proposed method.

Notably, inter-subject variability in EMG signals remains a significant challenge. The proposed dynamic force estimation model is designed as a learning framework rather than a universal solution. Different individuals require personalized calibration following the outlined training procedure. Applying a model trained on one subject directly to another leads to a marked decline in estimation accuracy and overall collaborative performance. Future work will explore transfer learning techniques with the aim of reducing the training time required to adapt force estimation models across different users.

5. Conclusions

Inspired by the remarkable human ability to coordinate force and speed in collaborative tasks, this study proposes an innovative framework addressing two key challenges: three-dimensional arm force estimation and human-robot collaborative control.

For force estimation, an AGA-TGNN algorithm is designed, which significantly enhances the model’s capacity to capture dynamic interactions between muscle coordination patterns and joint states. Experimental results demonstrate that the proposed model outperforms representative comparison methods (FOS, LSTM, and Deep-LSTM) across multiple metrics, including median error, mean error, and maximum error. Specifically, compared to the Deep-LSTM model, estimation errors in the three directions are reduced by 10.38%, 8.33%, and 11.20%, respectively.

In the domain of collaborative control, to overcome the limitations of traditional methods in compliance and generalization, an expert reward mechanism is introduced alongside a fuzzy rule-based experience replay partitioning strategy. A novel imitation reinforcement learning algorithm is developed, which requires no explicit control model and exhibits strong adaptability. This approach enables the robot to respond flexibly to operator motion intentions by perceiving arm forces in real time, thereby enhancing the comfort and smoothness of human–robot collaboration.

The proposed method is validated in a human–robot collaborative assembly scenario. Experimental results demonstrate that, compared with the representative GPRIL and ADC models, the proposed approach achieves substantial improvements across key performance metrics, including collaborative comfort, motion stability, task efficiency, and assembly accuracy. Specifically, compared to the ADC model, collaborative comfort increases by 2.75%, collaborative smoothness improves by 8.42%, assembly time is reduced by 1.63%, assembly error decreases by 17.65%, and the assembly success rate improves by 7.2%. These findings support the feasibility of the proposed approach in practical human–robot collaboration.

The current arm force estimation model only predicts three-dimensional Cartesian forces and does not account for torque components. As a result, the human–robot collaborative assembly system lacks the capability to perform posture adjustments, which limits its effectiveness in tasks requiring precise rotational control. To address this, future work will explore the correlation between EMG signals and arm torques, with the goal of enabling posture-aware collaboration.