Tactile Force Sensing for Admittance Control on a Quadruped Robot
Abstract
1. Introduction
- 1.
- Development of a fast 3D force reconstruction method for spherical pressure sensor-based tactile sensors.
- 2.
- Design of a tactile admittance controller that augments the control of each leg of the quadruped robot using the interaction force measured at the feet by the spherical tactile sensor.
- 3.
- Experiments that demonstrate the improved redistribution of ground reaction forces and impact attenuation during both static and dynamic balance disturbances using the presented tactile admittance controller.
2. Materials and Methods
2.1. Tweelie: A Tactile Wheel-Shaped Foot Sensor
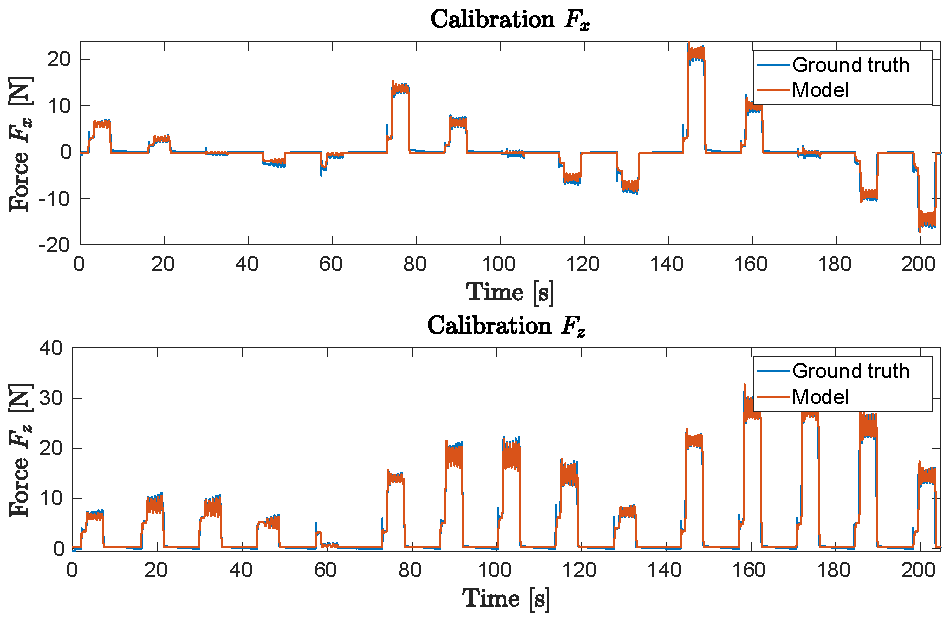
2.2. Data Collection from a Single Tactile Foot
2.3. Integration of Tactile Feet with the Unitree A1 Legged Robot
3. Fast GRF Reconstruction Using Tactile Sensor Data
4. Tactile Admittance Control
- : The estimated force vector provided by the tactile foot sensor and model.
- ,: The desired force and Cartesian position of the foot, provided by the trajectory planner.
- : The joint position of the leg, provided by the robot state. From the joint position, the Cartesian position, , of the leg is calculated using the forward kinematics function, denoted as in the diagram.
5. Results
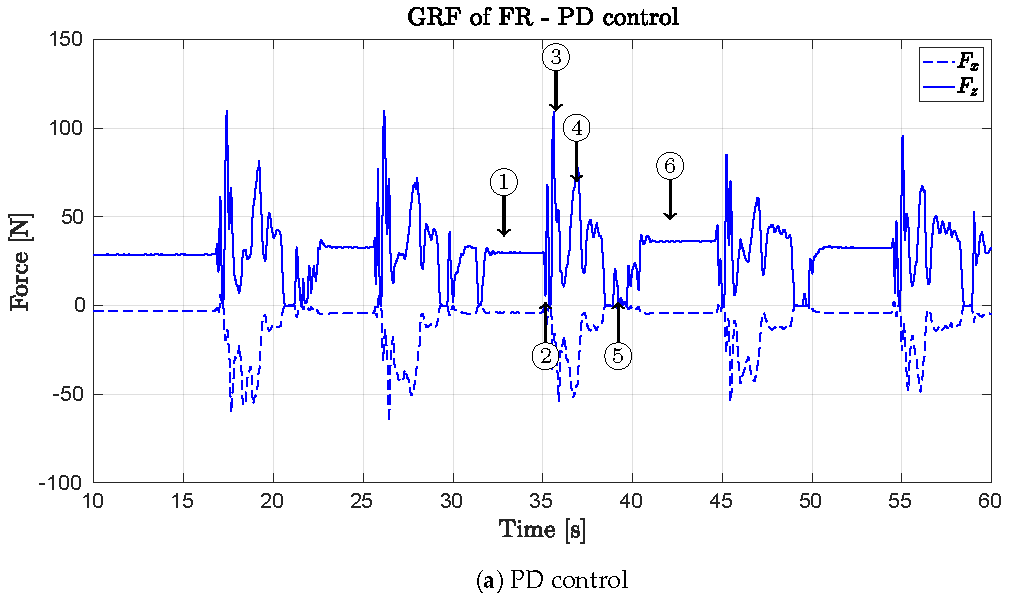
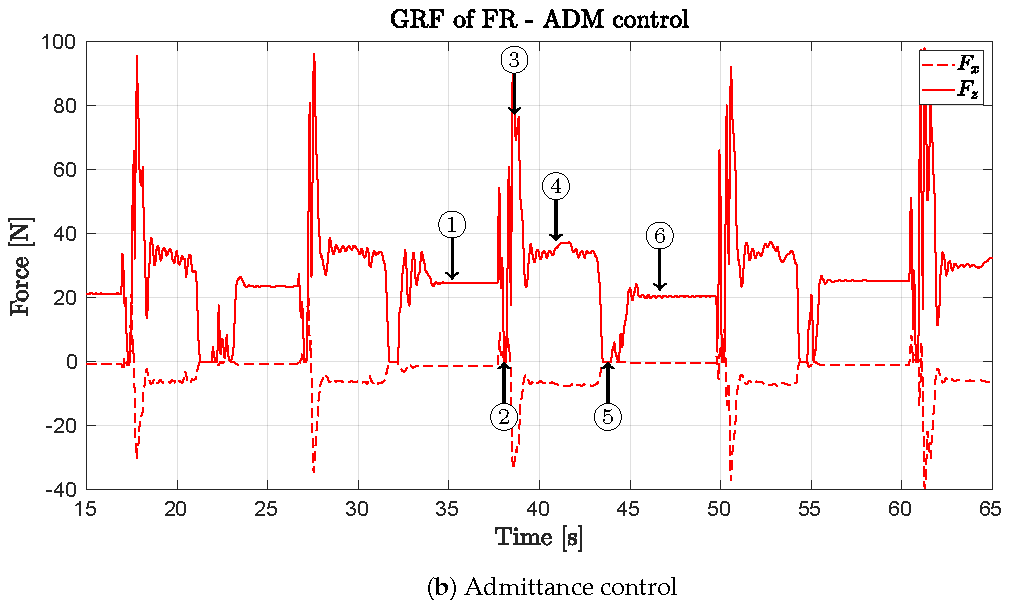
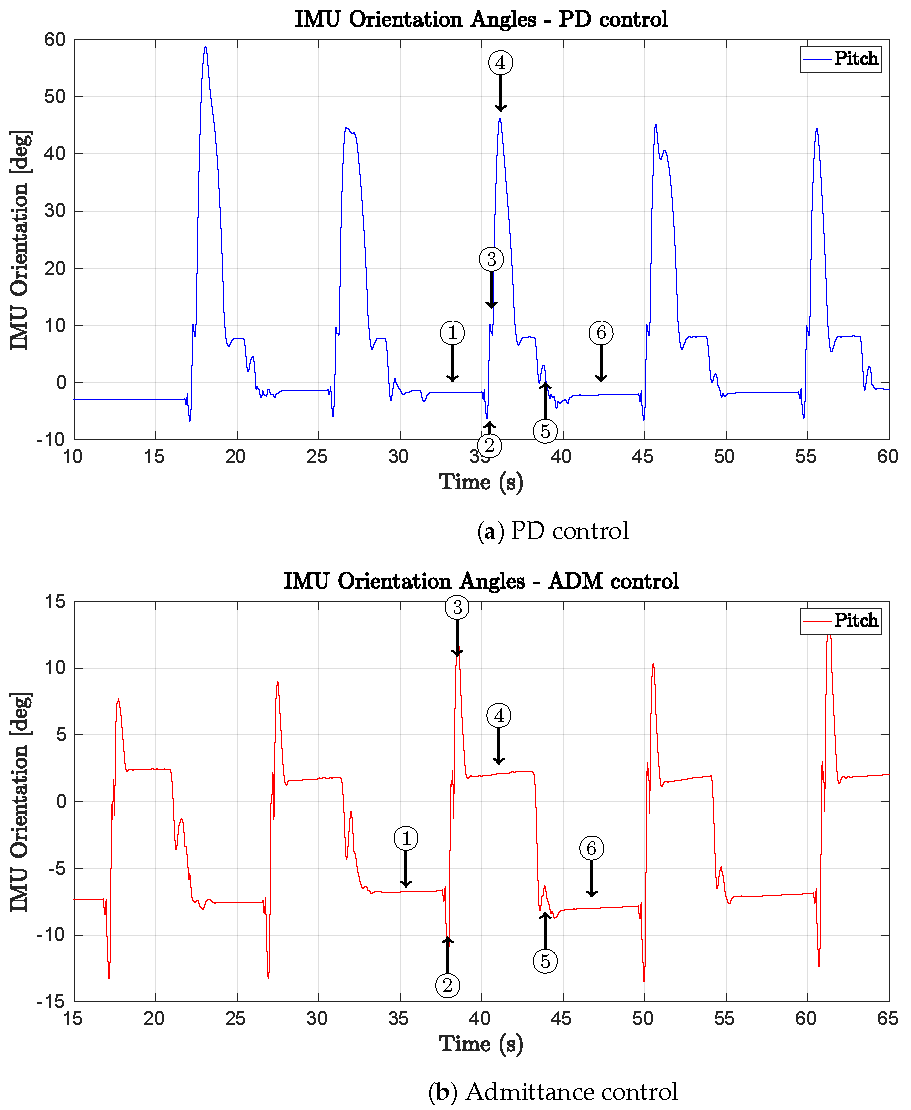
5.1. Static Balance Experiment on a Beam Using Admittance Control
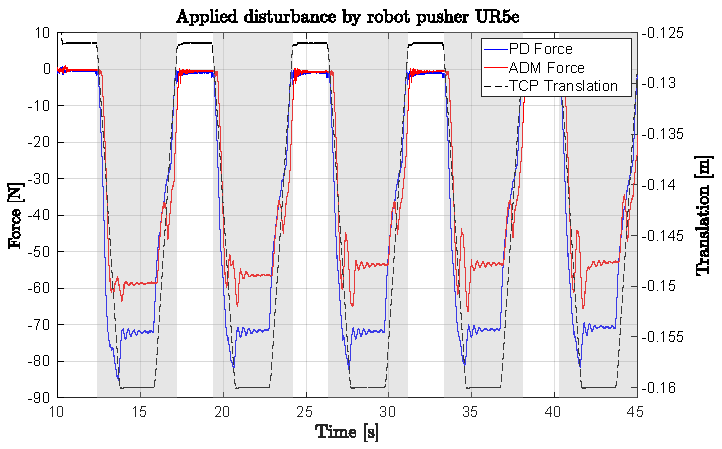
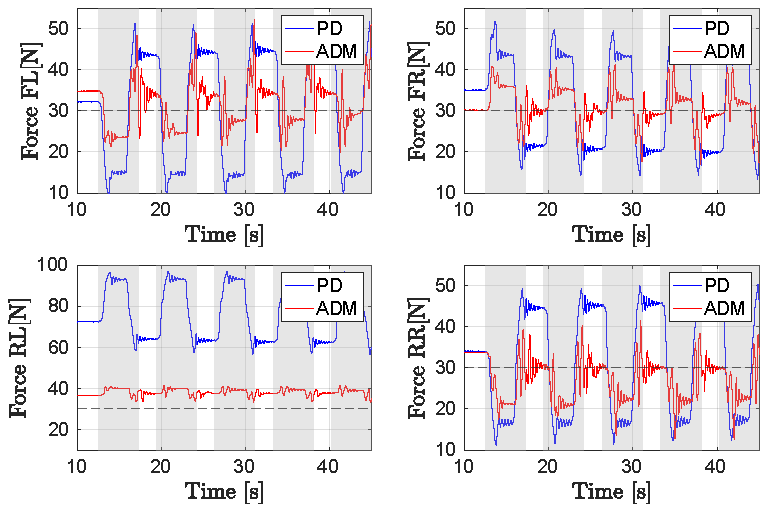
5.2. Dynamic Balance Experiment Using Admittance Control
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| MEMS | Micro-Electromechanical System |
| IMU | Inertial Measurement Unit |
| PCB | Printed Circuit Board |
| PD Control | Proportional–Derivative Control |
| I2C | Inter-integrated Circuit |
| MUX | Multiplexer |
| IP | Internet Protocol |
| UDP | User Datagram Protocol |
| API | Application Program Interface |
| MPC | Model Predicitve Control |
| CoM | Center of Mass |
| FR | Front Right (leg) |
| FL | Front Left (leg) |
| RR | Rear Right (leg) |
| RL | Rear Left (leg) |
| GRF | Ground Reaction Forces |
| HAA | Hip Abduction Adduction |
| HFE | Hip Flexion Extension |
| KFE | Knee Flexion Extension |
| ADM | Admittance Control Mode |
Appendix A. Kinematic Description of a Single Leg of the Unitree A1 Quadruped Robot
- , the transform from the base to the HAA joint.
- , the transform from the base to the HFE joint.
- , the transform from the base to the KFE joint.
- (HAA rotation, x-axis rotation) is , the first column of .
- (HFE rotation, y-axis rotation) is of .
- (KFE rotation, y-axis rotation) is of .
- (HAA position) is of .
- (HFE position) is of .
- (KFE position) is of .
References
- Cheng, X.; Kumar, A.; Pathak, D. Legs as Manipulator: Pushing Quadrupedal Agility Beyond Locomotion. In Proceedings of the 2023 IEEE International Conference on Robotics and Automation (ICRA), London, UK, 29 May–2 June 2023; pp. 5106–5112. [Google Scholar] [CrossRef]
- Hoeller, D.; Rudin, N.; Sako, D.; Hutter, M. ANYmal parkour: Learning agile navigation for quadrupedal robots. Sci. Robot. 2024, 9, eadi7566. [Google Scholar] [CrossRef] [PubMed]
- Arm, P.; Mittal, M.; Kolvenbach, H.; Hutter, M. Pedipulate: Enabling Manipulation Skills using a Quadruped Robot’s Leg. In Proceedings of the 2024 IEEE International Conference on Robotics and Automation (ICRA), Yokohama, Japan, 13–17 May 2024; pp. 5717–5723. [Google Scholar] [CrossRef]
- Majithia, A.; Shah, D.; Dave, J.; Kumar, A.; Rathee, S.; Dogra, N.; Vishwanathah, H.M.; Chiniwar, D.S.; Hiremath, S. Design, motions, capabilities, and applications of quadruped robots: A comprehensive review. Front. Mech. Eng. 2024, 10, 1448681. [Google Scholar] [CrossRef]
- Jang, Y.; Seol, W.; Lee, K.; Kim, K.S.; Kim, S. Development of quadruped robot for inspection of underground pipelines in nuclear power plants. Electron. Lett. 2022, 58, 234–236. [Google Scholar] [CrossRef]
- Gehring, C.; Fankhauser, P.; Isler, L.; Diethelm, R.; Bachmann, S.; Potz, M.; Gerstenberg, L.; Hutter, M. ANYmal in the Field: Solving Industrial Inspection of an Offshore HVDC Platform with a Quadrupedal Robot. In Field and Service Robotics; Ishigami, G., Yoshida, K., Eds.; Springer: Singapore, 2021; pp. 247–260. [Google Scholar]
- Pencelli, M.; Bonacchi, L.B.; Fiorucci, M.; Schillaci, G.; Youssef, A.; Politano, A.; Bettini, A.; Porciani, D.; Salusti, L.; Cioncolini, S.; et al. Testing the Robustness of Quadruped Robots for Unmanned Inspection Activities in the Energy Industry. In Proceedings of the IPTC International Petroleum Technology Conference, Dhahran, Saudi Arabia, 13 February 2024. [Google Scholar] [CrossRef]
- Cheng, Y.; Liu, H.; Pan, G.; Liu, H.; Ye, L. Quadruped robot traversing 3D complex environments with limited perception. In Proceedings of the 2024 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Abu Dhabi, United Arab Emirates, 14–18 October 2024; pp. 9074–9081. [Google Scholar] [CrossRef]
- Barasuol, V.; Buchli, J.; Semini, C.; Frigerio, M.; De Pieri, E.R.; Caldwell, D.G. A reactive controller framework for quadrupedal locomotion on challenging terrain. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; pp. 2554–2561. [Google Scholar] [CrossRef]
- Bledt, G.; Powell, M.J.; Katz, B.; Di Carlo, J.; Wensing, P.M.; Kim, S. MIT Cheetah 3: Design and Control of a Robust, Dynamic Quadruped Robot. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 2245–2252. [Google Scholar] [CrossRef]
- Aractingi, M.; Léziart, P.A.; Flayols, T.; Perez, J.; Silander, T.; Souères, P. Controlling the Solo12 quadruped robot with deep reinforcement learning. Sci. Rep. 2023, 13, 11945. [Google Scholar] [CrossRef]
- Miki, T.; Lee, J.; Hwangbo, J.; Wellhausen, L.; Koltun, V.; Hutter, M. Learning robust perceptive locomotion for quadrupedal robots in the wild. Sci. Robot. 2022, 7, eabk2822. [Google Scholar] [CrossRef] [PubMed]
- Gu, S.; Meng, F.; Liu, B.; Zhang, Z.; Sun, N.; Wang, M. Stability Control of Quadruped Robot Based on Active State Adjustment. Biomimetics 2023, 8, 112. [Google Scholar] [CrossRef] [PubMed]
- Shi, G.; Yao, C.; Liu, X.; Zhao, Y.; Zhu, Z.; Jia, Z. Foot Vision: A Vision-Based Multi-Functional Sensorized Foot for Quadruped Robots. IEEE Robot. Autom. Lett. 2024, 9, 6720–6727. [Google Scholar] [CrossRef]
- Stone, E.A.; Lepora, N.F.; Barton, D.A.W. Walking on TacTip toes: A tactile sensing foot for walking robots. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24 October 2020–24 January 2021; pp. 9869–9875. [Google Scholar]
- Zhang, G.; Du, Y.; Zhang, Y.; Wang, M.Y. A Tactile Sensing Foot for Single Robot Leg Stabilization. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 14076–14082. [Google Scholar] [CrossRef]
- Van Hauwermeiren, T.; Sianov, A.; Coene, A.; Crevecoeur, G. Integrated Barometric Pressure Sensors on Legged Robots for Enhanced Tactile Exploration of Edges. IEEE Robot. Autom. Lett. 2024, 9, 6368–6375. [Google Scholar] [CrossRef]
- Sun, C.; Chen, Z.; Ye, S.; Lin, J.; Shi, W.; Li, B.; Teng, F.; Li, X.; Zhang, A. Highly-time-resolved FMCW LiDAR with synchronously-nonlinearity-corrected acquisition for dynamic locomotion. Opt. Express 2023, 31, 7774–7788. [Google Scholar] [CrossRef] [PubMed]
- Bledt, G.; Wensing, P.M.; Ingersoll, S.; Kim, S. Contact Model Fusion for Event-Based Locomotion in Unstructured Terrains. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018; pp. 4399–4406. [Google Scholar] [CrossRef]
- Van Hauwermeiren, T.; Sianov, A.; Coene, A.; Crevecoeur, G. Tweelie: Tactile Wheel-Shaped Sensor for Force Reconstruction and Localization Over Curved Spherical Surface. IEEE Sens. Lett. 2025, 9, 6003004. [Google Scholar] [CrossRef]
- Ott, C.; Mukherjee, R.; Nakamura, Y. Unified Impedance and Admittance Control. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 3–7 May 2010; pp. 554–561. [Google Scholar] [CrossRef]
- Schimmels, J.; Peshkin, M. Admittance matrix design for force-guided assembly. IEEE Trans. Robot. Autom. 1992, 8, 213–227. [Google Scholar] [CrossRef]
- Cong, Z.; Honglei, A.; Wu, C.; Lang, L.; Wei, Q.; Hongxu, M. Contact Force Estimation Method of Legged-Robot and Its Application in Impedance Control. IEEE Access 2020, 8, 161175–161187. [Google Scholar] [CrossRef]
- Jin, B.; Sun, C.; Zhang, A.; Ding, N.; Lin, J.; Deng, G.; Zhu, Z.; Sun, Z. Joint Torque Estimation toward Dynamic and Compliant Control for Gear-Driven Torque Sensorless Quadruped Robot. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 3–8 November 2019; pp. 4630–4637. [Google Scholar] [CrossRef]
- NXP Semiconductors. UM10204 I2C-Bus Specification and User Manual. 2014. Rev. 6. Available online: https://www.nxp.com/docs/en/user-guide/UM10204.pdf (accessed on 15 March 2025).
- Katayama, S.; Ohtsuka, T. Lifted contact dynamics for efficient optimal control of rigid body systems with contacts. In Proceedings of the 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2022), Kyoto, Japan, 23–27 October 2022. [Google Scholar]
- Karan, F.S.N.; Chakraborty, S. The Advantages of Velocity Control for Reactive Robot Motion. In Proceedings of the Dynamic Systems and Control Conference, Columbus, OH, USA, 28–30 October 2015; Volume 3. [Google Scholar] [CrossRef]
- Palejiya, D.; Tanner, H.G. Hybrid velocity/force control for robot navigation in compliant unknown environments. Robotica 2006, 24, 745–758. [Google Scholar] [CrossRef]
- Spong, M.W.; Hutchinson, S.; Vidyasagar, M. Robot Modeling and Control; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]

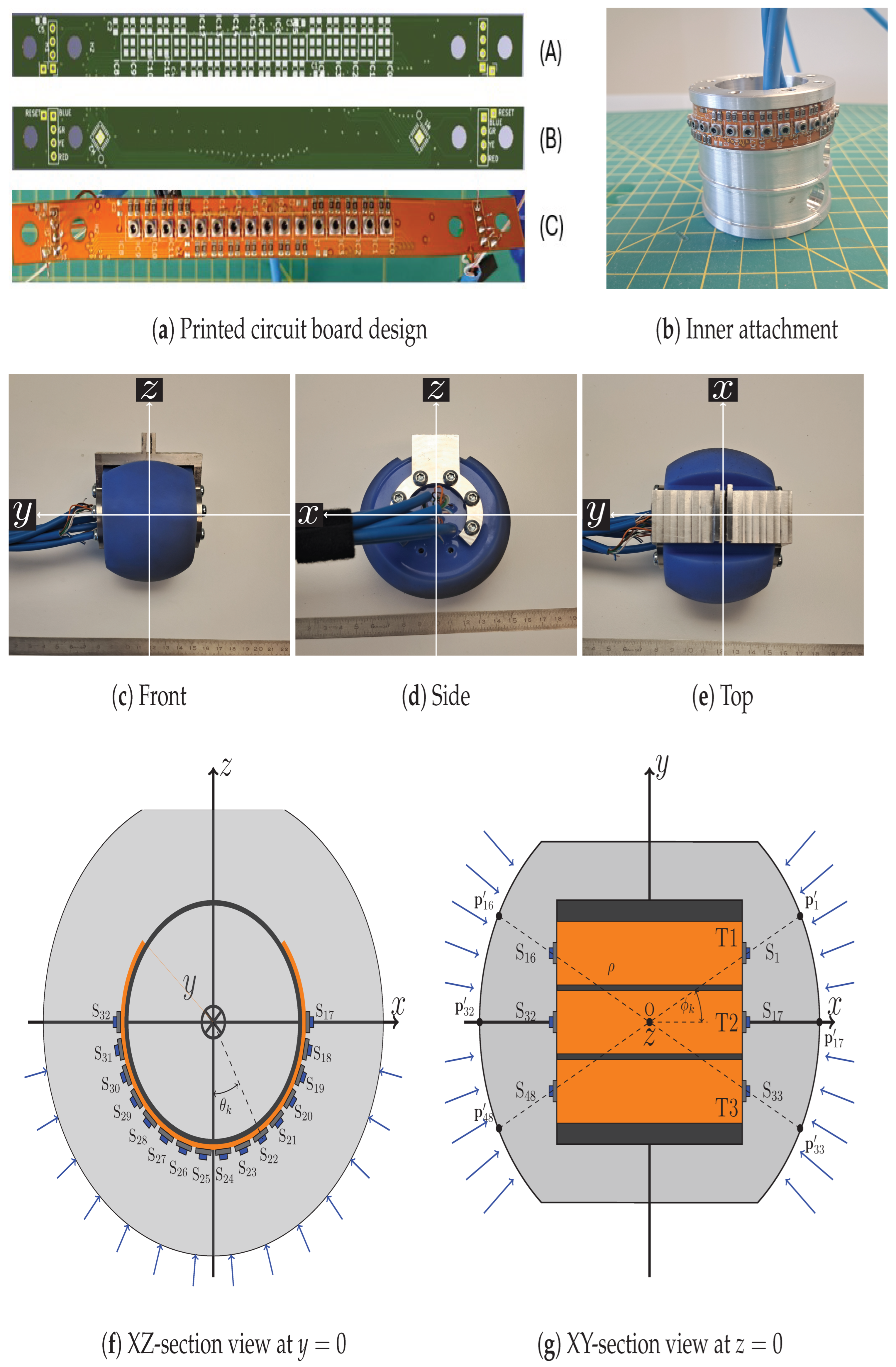






| Track 1 (T1) | [°] | [°] | Track 2 (T2) | [°] | [°] | Track 3 (T3) | [°] | [°] |
|---|---|---|---|---|---|---|---|---|
| S1 | 90 | 28.4 | S17 | 90 | 0 | S33 | 90 | −28.4 |
| S2 | 78 | 28.4 | S18 | 78 | 0 | S34 | 78 | −28.4 |
| S3 | 66 | 28.4 | S19 | 66 | 0 | S35 | 66 | −28.4 |
| S4 | 54 | 28.4 | S20 | 54 | 0 | S36 | 54 | −28.4 |
| S5 | 42 | 28.4 | S21 | 42 | 0 | S37 | 42 | −28.4 |
| S6 | 30 | 28.4 | S22 | 30 | 0 | S38 | 30 | −28.4 |
| S7 | 18 | 28.4 | S23 | 18 | 0 | S39 | 18 | −28.4 |
| S8 | 6 | 28.4 | S24 | 6 | 0 | S40 | 6 | −28.4 |
| S9 | −6 | 28.4 | S25 | −6 | 0 | S41 | −6 | −28.4 |
| S10 | −18 | 28.4 | S26 | −18 | 0 | S42 | −18 | −28.4 |
| S11 | −30 | 28.4 | S27 | −30 | 0 | S43 | −30 | −28.4 |
| S12 | −42 | 28.4 | S28 | −42 | 0 | S44 | −42 | −28.4 |
| S13 | −54 | 28.4 | S29 | −54 | 0 | S45 | −54 | −28.4 |
| S14 | −66 | 28.4 | S30 | −66 | 0 | S46 | −66 | −28.4 |
| S15 | −78 | 28.4 | S31 | −78 | 0 | S47 | −78 | −28.4 |
| S16 | −90 | 28.4 | S32 | −90 | 0 | S48 | −90 | −28.4 |
| Sensor | Axis | A [-] | b [-] | RMSE [-] | [-] |
|---|---|---|---|---|---|
| TW1 | Fx | 11.97 ± 0.03 | 0.00 ± 0.004 | 0.13 ± 0.01 | 0.98 ± 0.004 |
| Fy | 11.91 ± 0.03 | 0.15 ± 0.002 | 0.16 ± 0.008 | 0.97 ± 0.002 | |
| Fz | 11.99 ± 0.02 | −0.18 ± 0.009 | 0.14 ± 0.008 | 0.98 ± 0.002 | |
| TW2 | Fx | 11.51 ± 0.04 | −0.60 ± 0.006 | 0.20 ± 0.02 | 0.96 ± 0.007 |
| Fy | 11.24 ± 0.02 | 1.26 ± 0.006 | 0.22 ± 0.007 | 0.95 ± 0.003 | |
| Fz | 11.01 ± 0.01 | 1.25 ± 0.008 | 0.21 ± 0.02 | 0.96 ± 0.007 | |
| TW3 | Fx | 11.57 ± 0.03 | 0.92 ± 0.01 | 0.22 ± 0.02 | 0.95 ± 0.009 |
| Fy | 11.75 ± 0.04 | 0.17 ± 0.006 | 0.25 ± 0.03 | 0.93 ± 0.02 | |
| Fz | 11.66 ± 0.05 | 2.42 ± 0.01 | 0.23 ± 0.01 | 0.95 ± 0.006 | |
| TW4 | Fx | 11.67 ± 0.02 | −0.93 ± 0.007 | 0.16 ± 0.01 | 0.97 ± 0.003 |
| Fy | 12.09 ± 0.04 | 0.24 ± 0.004 | 0.19 ± 0.01 | 0.96 ± 0.004 | |
| Fz | 11.28 ± 0.01 | 3.41 ± 0.007 | 0.12 ± 0.003 | 0.99 ± 0.0008 |
| Parameter | FR | FL | RR | RL |
|---|---|---|---|---|
| [m] | (0.18, −0.13, −0.25) | (0.18, 0.13, −0.25) | (−0.18, −0.13, −0.25) | (−0.18, 0.13, −0.25) |
| [N] | (0, 0, 30) | (0, 0, 30) | (0, 0, 30) | (0, 0, 30) |
| [kg] | diag (10, 10, 10) | diag (10, 10, 10) | diag (10, 10, 10) | diag (10, 10, 10) |
| [Ns/m] | diag (1, 1, 1) | diag (1, 1, 1) | diag (1, 1, 1) | diag (1, 1, 1) |
| [N/m] | diag (10, 10, 10) | diag (10, 10, 10) | diag (10, 10, 10) | diag (10, 10, 10) |
| [m/s] | (0, 0, 0.1) | (0, 0, 0.1) | (0, 0, 0.1) | (0, 0, 0.1) |
| Parameter | FR | FL | RR | RL |
|---|---|---|---|---|
| [m] | (0.18, −0.13, −0.25) | (0.18, 0.13, −0.25) | (−0.18, −0.13, −0.25) | (−0.18, 0.13, −0.25) |
| [N] | (0, 0, 60) | (0, 0, 60) | (0, 0, 20) | (0, 0, 20) |
| [kg] | diag (10, 10, 10) | diag (10, 10, 10) | diag (10, 10, 10) | diag (10, 10, 10) |
| [Ns/m] | diag (1, 1, 1) | diag (1, 1, 1) | diag (1, 1, 1) | diag (1, 1, 1) |
| [N/m] | diag (10, 10, 10) | diag (10, 10, 10) | diag (10, 10, 10) | diag (10, 10, 10) |
| [m/s] | (0, 0, 0.25) | (0, 0, 0.25) | (0, 0, 0.25) | (0, 0, 0.25) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Van Hauwermeiren, T.; Coene, A.; Crevecoeur, G. Tactile Force Sensing for Admittance Control on a Quadruped Robot. Machines 2025, 13, 426. https://doi.org/10.3390/machines13050426
Van Hauwermeiren T, Coene A, Crevecoeur G. Tactile Force Sensing for Admittance Control on a Quadruped Robot. Machines. 2025; 13(5):426. https://doi.org/10.3390/machines13050426
Chicago/Turabian StyleVan Hauwermeiren, Thijs, Annelies Coene, and Guillaume Crevecoeur. 2025. "Tactile Force Sensing for Admittance Control on a Quadruped Robot" Machines 13, no. 5: 426. https://doi.org/10.3390/machines13050426
APA StyleVan Hauwermeiren, T., Coene, A., & Crevecoeur, G. (2025). Tactile Force Sensing for Admittance Control on a Quadruped Robot. Machines, 13(5), 426. https://doi.org/10.3390/machines13050426






