Kinematics and Dynamics Analysis of a New 5-Degrees of Freedom Parallel Mechanism with Two Double-Driven Chains

Abstract

This paper focuses on the design analysis of a novel 5-degrees of freedom (DOF) double-driven parallel mechanism (PM). By arranging two independent actuators on one branch chain, the mechanism can realize the five degrees of freedom of the moving platform only by relying on three branch chains, which have the characteristics of a compact structure and large workspace. Subsequently, the kinematic model of the mechanism is established, and the workspace, dexterity, and singularity characteristics are analyzed based on the derived model. Additionally, an explicit dynamic model of the mechanism is established based on the principle of virtual work. Finally, based on the dynamic model, the manipulability ellipsoid index and the inertial coupling strength index are proposed, and the distribution of these two kinds of dynamic performance indexes in the workspace is studied.

1. Introduction

Manufacturing is the cornerstone of modern industrial systems, with its development level directly impacting national industrial competitiveness. The pressing demand for precision and efficient machining of key components in high-end equipment manufacturing has become a critical bottleneck in industrial technological advancement. These components typically feature complex geometric characteristics such as large dimensions, intricate curved surfaces, and thick walls while constrained by stringent processing conditions and technical requirements that traditional manual and CNC can no longer adequately fulfill. Therefore, designing five-axis machining equipment with high performance, flexibility, and adaptability has inevitably become a trend in developing an advanced manufacturing industry [1,2,3,4].

Current machining robots are primarily categorized into three configurations: serial [5,6], hybrid [7,8], and parallel [9,10]. Serial robots excel in large curved surface component processing due to their extensive workspace and high flexibility [11]. Hybrid robots compensate for the low rigidity of serial architectures, offering new alternatives for aluminum alloy component machining [12]. Parallel 5-DOF robots (e.g., Metrom [13] and DiaRom [14,15]) demonstrate unique advantages in aerospace precision machining owing to their high stiffness, accuracy, and coupled motion characteristics. Although existing parallel robots have exhibited distinct advantages in large-scale component machining and achieved success in respective applications, the more significant number of branch chains and joints leads to more structural constraints, and these factors lead to small workspace and rotation capacity [16]. Therefore, the research and development of novel five-DOF parallel mechanisms represent a crucial technological pathway and potential breakthrough for advancing high-performance machining equipment [17].

In conventional parallel mechanisms, each actuated branch chain connecting the moving platform to the fixed base is typically equipped with a single active joint. This design paradigm establishes a direct correlation between the number of DOF and the number of actuated branch chains, such that the mechanism’s mobility is precisely determined by its number of independently driven chains [18]. Consequently, five actuated branch chains must achieve independent motion with five DOF. However, as the number of branch chains increases, the mechanism’s topology becomes more complex, significantly elevating design and manufacturing costs and exacerbating issues related to interference and dynamic coupling among the branches [19]. To solve the above problems, some scholars have combined the parallel mechanism with the series mechanism to form a hybrid mechanism with complementary advantages, which not only effectively expands the operating space of the mechanism but also overcomes the shortcomings of the traditional series mechanism, such as insufficient stiffness and error accumulation to a certain extent [20,21]. However, stiffness and positioning accuracy of the end effector of the hybrid mechanism are still affected by the serial structure, so it is difficult to achieve the high precision characteristic of the pure parallel mechanism [22].

In order to address both the requirements for DOF and overall mechanism performance, the double-driven PM, as a novel PM, has gradually attracted increasing attention in the academic community [23,24,25]. Integrating multiple actuators within a single branch chain can significantly reduce the number of branch chains while still satisfying the desired DOF, simplifying the overall structure and minimizing the potential for interference. As a member of the parallel topology family, the dual-drive PM retains the advantages of compact design, high stiffness, and excellent positioning accuracy, demonstrating strong potential for future development. Lu et al. [26] proposed a compound rotational/linear UPS and used it to design a three branch chain, 2UPS-SPR dual-drive PM with 5-DOF and analyzed its kinematics and statics. Zhao et al. [27] proposed and studied a 6-(PRRR)US dual-drive PM based on a planar five-bar mechanism, demonstrating its strong capabilities in attitude adjustment and vibration isolation through kinematic and dynamic analysis. Wang et al. [22] designed a 5-DOF double-driven PM (PUU-2PRRS) and analyzed its workspace, dexterity, volume, and dimensional optimization. Niu et al. [28] proposed a dual-driven PM (2PRPS/PSR) and optimized motion performance based on transmissibility, workspace/volume ratio, and mass. Rong et al. [29] proposed a dual-driven 5-DOF parallel mechanism 2PRPU/PRPS with only three limbs and 17 joints based on Lie group theory, the simplest structural form of 5-DOF PMs. Nevertheless, research in this area is still in its early stages, with limited studies on structural design and practical engineering applications. Further support through systematic theoretical modeling and prototype validation is urgently needed to advance this promising field.

As can be seen from the above, research on 5-DOF PM with two double-driven branch chains is still in its early stages, and such mechanisms exhibit promising application prospects. This paper proposes a novel P(2PRPU)/PRPS PM with two double-driven branch chains based on the dual-drive concept. Innovatively, the mechanism consists of only three double-driven branches, which significantly reduces branch interference. Moreover, some of the actuators are fixed on the base, thereby reducing the mass of the moving parts, improving dynamic response speed, and minimizing the impact of inertial loads on the structure. Compared with the current 5-DOF PMs, the mechanism proposed in this paper not only has only 3 branch chain, 17 single-DOF motion pairs as a whole, with a simpler structure, but also reduces the motion mass by fixing some drive pairs, enabling it to have a good dynamic response.

The structure of this paper is as follows. In Section 2, the structure of the proposed PM is introduced, and its kinematic performance is analyzed through the derivation of a 5 × 5 Jacobian matrix. In Section 3, the dynamic model of the proposed mechanism is established, along with an analysis of its dynamic manipulability ellipsoid and the inertia coupling strength of the branch chains. Conclusions are drawn in Section 4.

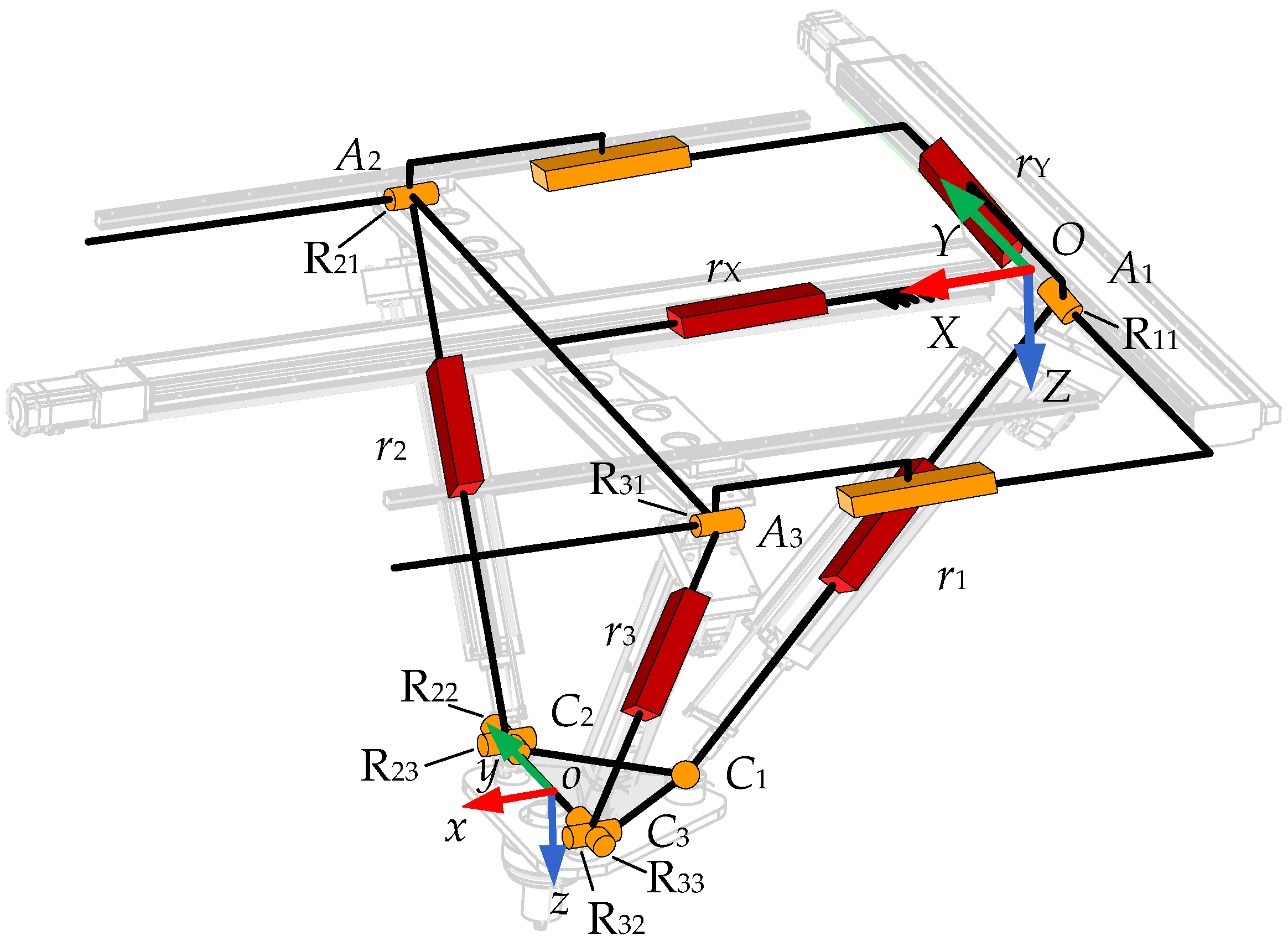
2. Structural and Kinematic Analysis

2.1. Configuration Description and Mobility Analysis

Figure 1 shows the new 5-DOF PM with two double-driven chains. It consists of a base and a moving platform, which are connected by branch chain r₁, branch chain r₂, branch chain r₃, linear modules, and guide rails. Branch chain 1 comprises three key components: a revolute joint, an electric push rod (i.e., prismatic joint), and a sphere joint, which, together with the linear module r_Y constitute a PRPS-type branch chain. Branch chains 2 and 3 comprise three key components: a revolute joint, an electric push rod, and a universal joint, which, together with the passive guide rails, constitute a PRPU-type branch chain.

The linear modules r_X and r_Y are rigidly mounted on the base among the five driving components. Linear modules r_X propels the branch chains 2 and 3 for anteroposterior motion, while linear modules r_Y drive branch chain 1 for lateral movement, constituting a parallel mechanism with two double-driven chains. This innovative configuration achieves two significant advancements compared to traditional 5-DoF PMs: it reduces the number of required branch chains to only three, significantly minimizing inter-branch interference, and it incorporates more actuators arranged on the base, which helps reduce vibration and improve precision. The PM proposed in references [30,31] also adopts the design of fixing the drive motor on the frame or the static platform. As a result, this parallel mechanism has potential applications in machine tools, walking robots, industrial robotic arms, naval cargo handling systems, and satellite monitoring platforms.

For convenience of description, let point A₁ denote the rotation center of the revolute joint in the RPS branch chain, and let point C₁ represent the rotation center of the spherical joint. For branch chains 2 and 3, the rotation centers of their revolute joints are defined as A₂ and A₃, respectively, whereas the rotation centers of their universal joints are designated as C₂ and C₃. The fixed coordinate frame O-XYZ (denoted as {B}) is established with the midpoint O of branch chain Y as the origin; here, the X-axis aligns with branch chain X, the Y-axis with branch chain Y, and the Z-axis is determined by the right-hand rule. The moving coordinate frame o-xyz (denoted as {m}) is defined with the midpoint o of C₁C₂ as the origin: the y-axis coincides with C₁C₂, the z-axis is perpendicular to the plane formed by points C₁, C₂, and C₃, and the x-axis is oriented according to the right-hand rule. Moreover, points A₂, A₃, C₂, C₃, and o are coplanar, with the normal vector of this plane parallel to the X-axis.

Let ǁ be a parallel constraint, | be a collinear constraint, and ⊥ be a perpendicular constraint, respectively. Let R_ij (i = 1, 2, 3; j = 1, 2) be the j-th R joint in the i-th branch chain r_i. Some geometrical constraints are satisfied for the P(2PRPU)/PRPS PM as follows (see Figure 1):

$$\left\{\begin{array}{l}{r}_Y\left|Y,{\mathrm{R}}_{11}\right|Y,r_1\perp Y,r_X|X,A_2{A}_3\parallel Y\\ r_i\perp {\mathrm{R}}_{i1},{\mathrm{R}}_{i1}\parallel {\mathrm{R}}_{i2},{\mathrm{R}}_{i2}\perp {\mathrm{R}}_{i3},{\mathrm{R}}_{i3}|y\left(i=2,3\right)\end{array}\right.$$

(1)

Since the P(2PRPU) branch chain is equivalent to a 2PRPU branch chain, the P(2PRPU)/PRPS PM can be regarded as a 2PRPU/PRPS PM, the twist system of the two PRPU branch chains can be expressed as:

$$\left\{\begin{array}{l}{\mathsf{\$}}_{i1}=\left(0\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}0\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}0;\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}1\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}0\hspace{0.33em}\hspace{0.33em}0\right)\\ {\mathsf{\$}}_{i2}=\left(1\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}0\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}0;\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}0\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}0\hspace{0.33em}\hspace{0.33em}0\right)\\ {\mathsf{\$}}_{i3}=\left(0\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}0\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}0;\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}0\hspace{0.33em}\hspace{0.33em}{m}_{i3}\hspace{0.33em}{n}_{i3}\right)\\ {\mathsf{\$}}_{i4}=\left(1\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}0\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}0;\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}0\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}{q}_{i4}\hspace{0.33em}\hspace{0.33em}{r}_{i4}\right)\\ {\mathsf{\$}}_{i5}=\left(0\hspace{0.33em}\hspace{0.33em}{m}_{i5}\hspace{0.33em}\hspace{0.33em}{n}_{i5};\hspace{0.33em}{p}_{i5}\hspace{0.33em}\hspace{0.33em}{q}_{i5}\hspace{0.33em}\hspace{0.33em}{r}_{i5}\right)\end{array}\right.$$

(2)

Adopting the reciprocal screw theory, the branch chain wrench system can be expressed as:

$${\mathsf{\$}}_i^r=\left(0\hspace{0.33em}0\hspace{0.33em}0;\hspace{0.33em}0\hspace{0.33em}-n_{i5}\hspace{0.33em}{m}_{i5}\right)$$

(3)

where ${\mathrm{S}}_i^r$ represents the constrained torque perpendicular to R_i2 and R_i3, based on the constraint relationship in Equation (3), it is deduced that R_i2 is parallel to the X-axis, while R₂₃ and R₃₃ are collinear with the y-axis. Consequently, the U-joint planes in the two PRPU branch chains are mutually parallel, and the constrained torque of the two branch chains is likewise parallel, forming a common constraint. As a result, the 2PRPU/PRPS is constrained solely by a constrained torque along the z-axis. Moreover, since the constraint relationships remain invariant during motion, the expression of the wrench system is constant, and the 2PRPU/PRPS or P(2PRPU)/PRPS PM always remain 2-rotational and 3-translational (2R3T) five DOF.

2.2. Jacobian Matrix Analysis

Let the rotational transformation matrix ^BR_m from the reference frame {B} to {m}, A_i and C_i represent the vector of A_i and C_i in {B}, A_i and C_i can be written as:

$$\begin{array}{l}{\mathit{A}}_1=\left[\begin{array}{l}0\\ \left(-e_1{s}_{\alpha }{s}_{\beta }+y\right)\\ 0\end{array}\right],{\mathit{A}}_2=\left[\begin{array}{l}x\\ 0.5L\\ 0\end{array}\right],{\mathit{A}}_3=\left[\begin{array}{l}x\\ -0.5L\\ 0\end{array}\right],\mathit{o}=\left[\begin{array}{l}x\\ y\\ z\end{array}\right]\\ {\mathit{C}}_1={}^B\mathit{R}_m\left[\begin{array}{l}-h\\ 0\\ 0\end{array}\right]+\mathit{o},{\mathit{C}}_2={}^B\mathit{R}_m\left[\begin{array}{l}0\\ 0.5e\\ 0\end{array}\right]+\mathit{o},{\mathit{C}}_3={}^B\mathit{R}_m\left[\begin{array}{l}0\\ -0.5e\\ 0\end{array}\right]+\mathit{o}\\ {}^B\mathit{R}_m=\left[\begin{array}{ccc}{c}_{\beta }& 0& s_{\beta }\\ s_{\alpha }{s}_{\beta }& c_{\alpha }& -s_{\alpha }{c}_{\beta }\\ -c_{\alpha }{s}_{\beta }& s_{\alpha }& c_{\alpha }{c}_{\beta }\end{array}\right]\end{array}$$

(4)

where L is the distance from A₂ to A₃, e denotes the distance from C₂ to C₃, h denotes the distance from o to C₁, α and β are Euler angles, c_i and s_i denote cos(θ_i) and sin(θ_i), o is the position vector of point o.

From Equation (4), l_i can be derived by the following:

$$\begin{array}{l}{l}_i=‖{\mathit{C}}_i-{\mathit{A}}_i‖\\ l_1=\sqrt{{\left(-e_1{c}_{\beta }+x\right)}^2+{\left(e_1{c}_{\alpha }{s}_{\beta }+z\right)}^2},l_2=\sqrt{{\left(e_2{c}_{\alpha }+y-L\right)}^2+{\left(e_2{s}_{\alpha }+z\right)}^2}\\ l_3=\sqrt{{\left(-e_3{c}_{\alpha }+y+L\right)}^2+{\left(-e_3{s}_{\alpha }+z\right)}^2},l_x=x,l_y=\left(-e_1{s}_{\alpha }{s}_{\beta }+y\right)\end{array}$$

(5)

Let δ_i, δ_X = [1 0 0]^T, and δ_Y = [0 1 0]^T be the unit vector of branch chains r_i (i = 1, 2, 3, X, Y). Based on Equation (5), the closed-loop constraint equation associated with each branch chain can be written as:

$$\begin{array}{l}{l}_Y{\mathit{\delta }}_Y+l_1{\mathit{\delta }}_1-{\mathit{e}}_1=\mathit{o}\\ l_X{\mathit{\delta }}_X+l_i{\mathit{\delta }}_i-{\mathit{e}}_i=\mathit{o},i=2,3\end{array}$$

(6)

here e_i is the vector of oC_i. Let v, a be the velocity and acceleration vectors of o in {B}, ω and Ɛ be angular velocity and angular acceleration of {m} relative to {B}. By differentiating Equation (6) concerning time, it leads to:

$$\begin{array}{l}{v}_{rY}{\mathit{\delta }}_Y+v_{r1}{\mathit{\delta }}_1+{\mathit{\omega }}_1\times l_1{\mathit{\delta }}_1-\mathit{\omega }\times {\mathit{e}}_1=\mathit{v}\\ v_{rX}{\mathit{\delta }}_X+v_{ri}{\mathit{\delta }}_i+{\mathit{\omega }}_i\times l_i{\mathit{\delta }}_i-\mathit{\omega }\times {\mathit{e}}_i=\mathit{v},\left(i=2,3\right)\end{array}$$

(7)

where v_ri and ω_i are actuated joint rate and angular velocity of branch r_i. Dot multiply both sides of Equation (7) by δ_i, δ_X, and δ_Y, respectively. It leads to:

$$\left[\begin{array}{l}{v}_{rX}\\ v_{rY}\\ v_{ri}\end{array}\right]={\mathit{J}}_m\left[\begin{array}{l}\mathit{v}\\ \mathit{\omega }\end{array}\right],{\mathit{J}}_m=\left[\begin{array}{l}{\mathit{J}}_X\\ {\mathit{J}}_Y\\ {\mathit{J}}_i\end{array}\right]=\left[\begin{array}{l}{\mathit{\delta }}_X^{\mathrm{T}}\hspace{0.33em}{\left({\mathit{e}}_2\times {\mathit{\delta }}_X\right)}^{\mathrm{T}}\\ {\mathit{\delta }}_Y^{\mathrm{T}}\hspace{0.33em}{\left({\mathit{e}}_1\times {\mathit{\delta }}_Y\right)}^{\mathrm{T}}\\ {\mathit{\delta }}_i^{\mathrm{T}}\hspace{0.33em}{\left({\mathit{e}}_i\times {\mathit{\delta }}_i\right)}^{\mathrm{T}}\end{array}\right]$$

(8)

For the P(2PRPU)/PRPS PM in this paper, the relationship between V = [v ω]^T and the independent kinematic parameter q = [x, y, z, α, β]^T can be expressed as:

$$\left[\begin{array}{l}\mathit{v}\\ \mathit{\omega }\end{array}\right]={\mathit{J}}_B\left[\begin{array}{l}\dot{x}\\ \dot{y}\\ \dot{z}\\ \dot{\alpha }\\ \dot{\beta }\end{array}\right],{\mathit{J}}_B=\left[\begin{array}{l}{\mathit{E}}_3 \hspace{0.33em}\hspace{0.33em}{\mathsf{0}}_{3\times 2}\\ {\mathsf{0}}_{3\times 3}\hspace{0.33em}{\mathit{J}}_{\omega }\end{array}\right],{\mathit{J}}_{\omega }=\left[\begin{array}{cc}1& 0\\ 0& c_{\alpha }\\ 0& s_{\alpha }\end{array}\right]$$

(9)

Substitute Equation (9) into Equation (8) and the relationship between the input and output parameters can be expressed as follows:

$$\begin{array}{l}{\mathit{V}}_q={\mathit{J}}_D^{-1}{\mathit{V}}_r,\hspace{0.33em}{\mathit{J}}_D={\mathit{J}}_m{\mathit{J}}_B\\ {\mathit{V}}_q={\left[\dot{x}\hspace{0.33em}\dot{y}\hspace{0.33em}\dot{z}\hspace{0.33em}\dot{\alpha }\hspace{0.33em}\dot{\beta }\right]}^{\mathrm{T}}\\ {\mathit{V}}_r={\left[v_{rX}\hspace{0.33em}{v}_{rY}\hspace{0.33em}{v}_{r1}\hspace{0.33em}{v}_{r2}\hspace{0.33em}{v}_{r3}\right]}^{\mathrm{T}}\end{array}$$

(10)

where ${\mathit{J}}_D^{-1}$ is the Jacobian matrix of P(2PRPU)/PRPS PM.

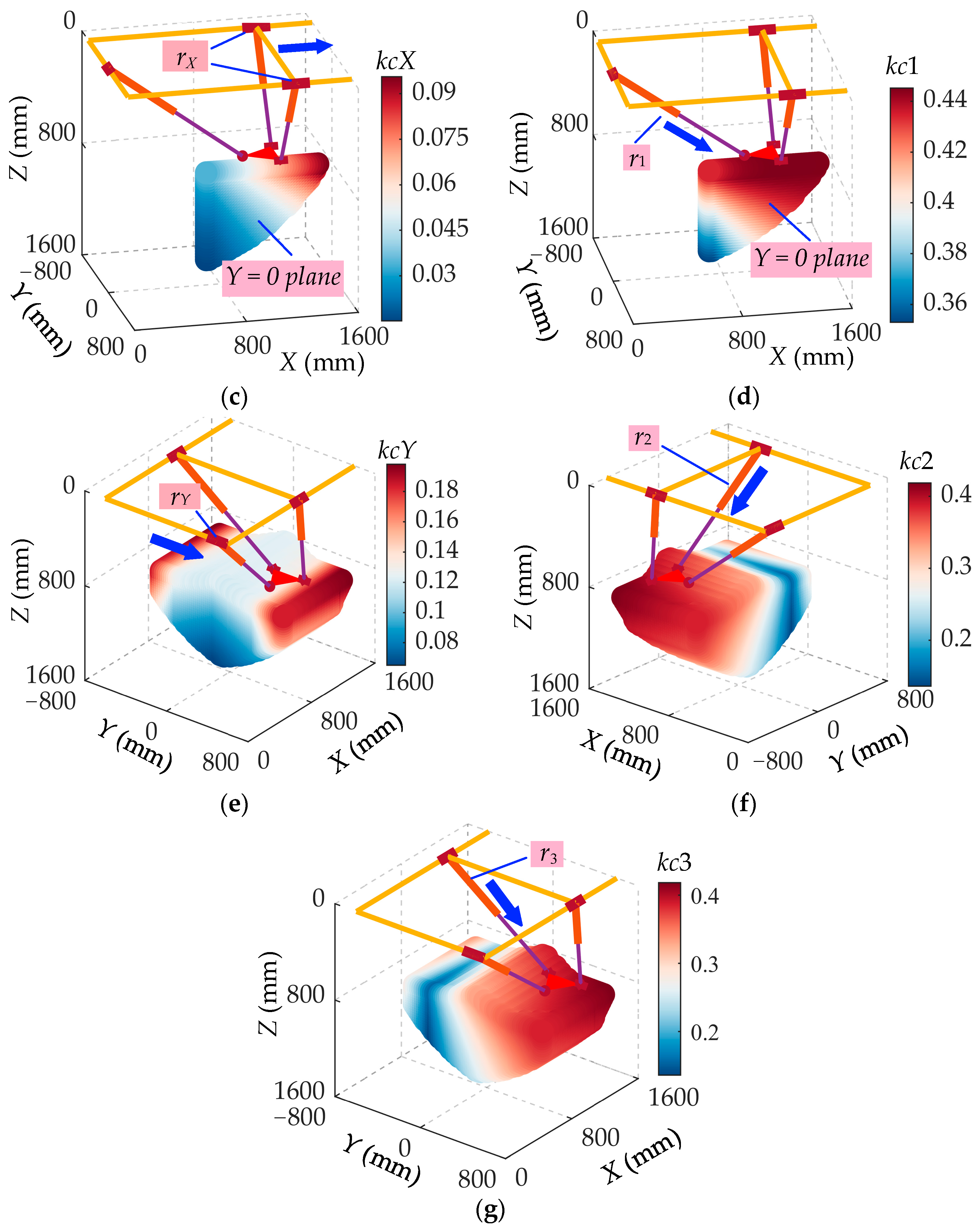
2.3. Kinematic Performance Analysis and Optimization

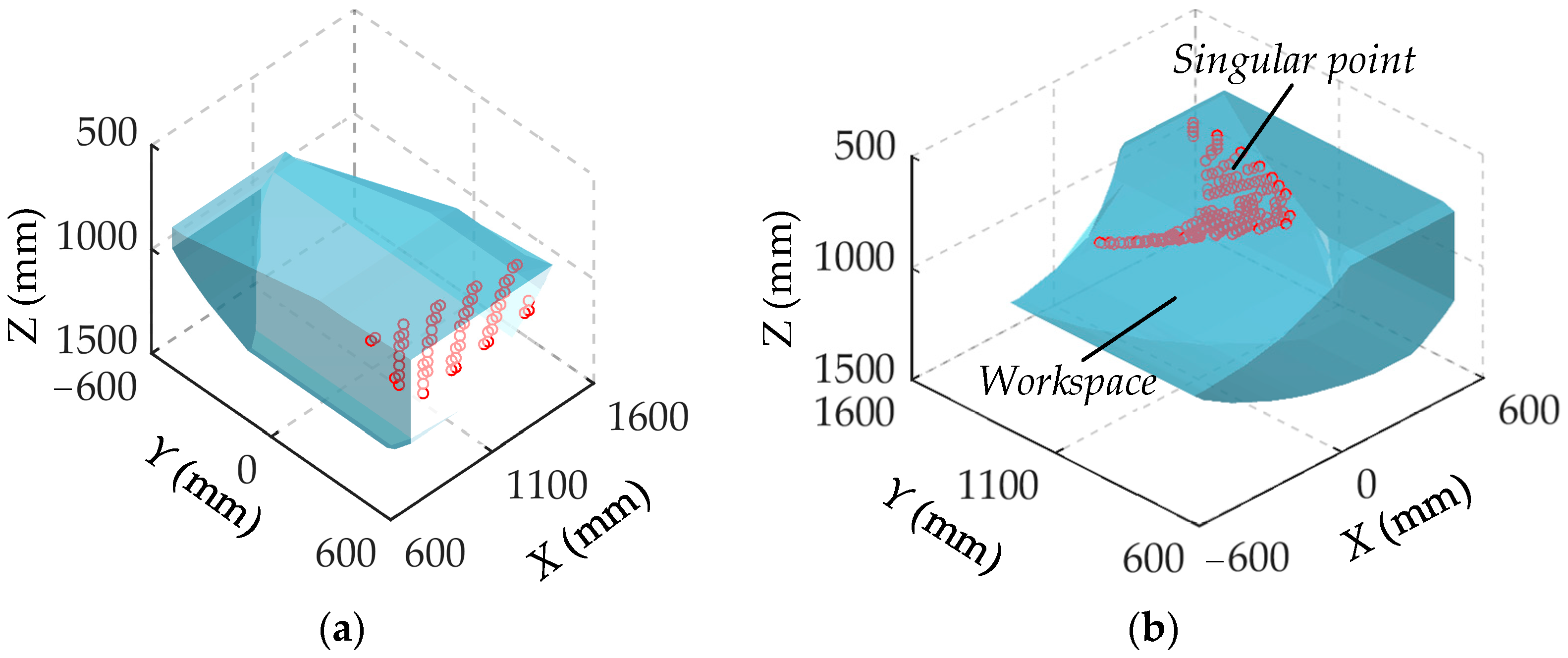
2.3.1. Singularity Analysis

Singularity analysis is a fundamental issue of kinematic analysis and performance evaluation. The kinematic performance of the PM deteriorates in singular configurations. In this study, singularities are investigated through the analysis of the velocity performance of the mechanism. With an input velocity fixed at 10 mm/s, the output velocity at the center of the moving platform is expected to remain relatively moderate under normal operating conditions. However, if the output velocity at a given position exceeds 1000 mm/s, this paper considers that the transmission characteristics have changed, which means that the mechanism has encountered a singularity and can no longer work properly.

Figure 2 shows the distribution of singular points within the workspace of the P(2PRPU)/PRPS PM at different orientation angles, where L = 1200 mm, e = 300 mm, h = 240 mm, 990 mm ≤ l_i ≤ 1490, 600 mm ≤ l_X ≤ 1600 mm, −700 mm ≤ l_Y ≤ 700. As shown in Figure 2, these singular points can not only form a continuous surface but also demonstrate that the workspace of the mechanism and the distribution of its singular points are highly dependent on changes in the orientation angle. This phenomenon indicates that when the P(2PRPU)/PRPS PM performs operational tasks, it is essential to thoroughly consider the characteristics of singularity surfaces under varying orientations and adjust the control strategy accordingly to ensure stable operation across all poses.

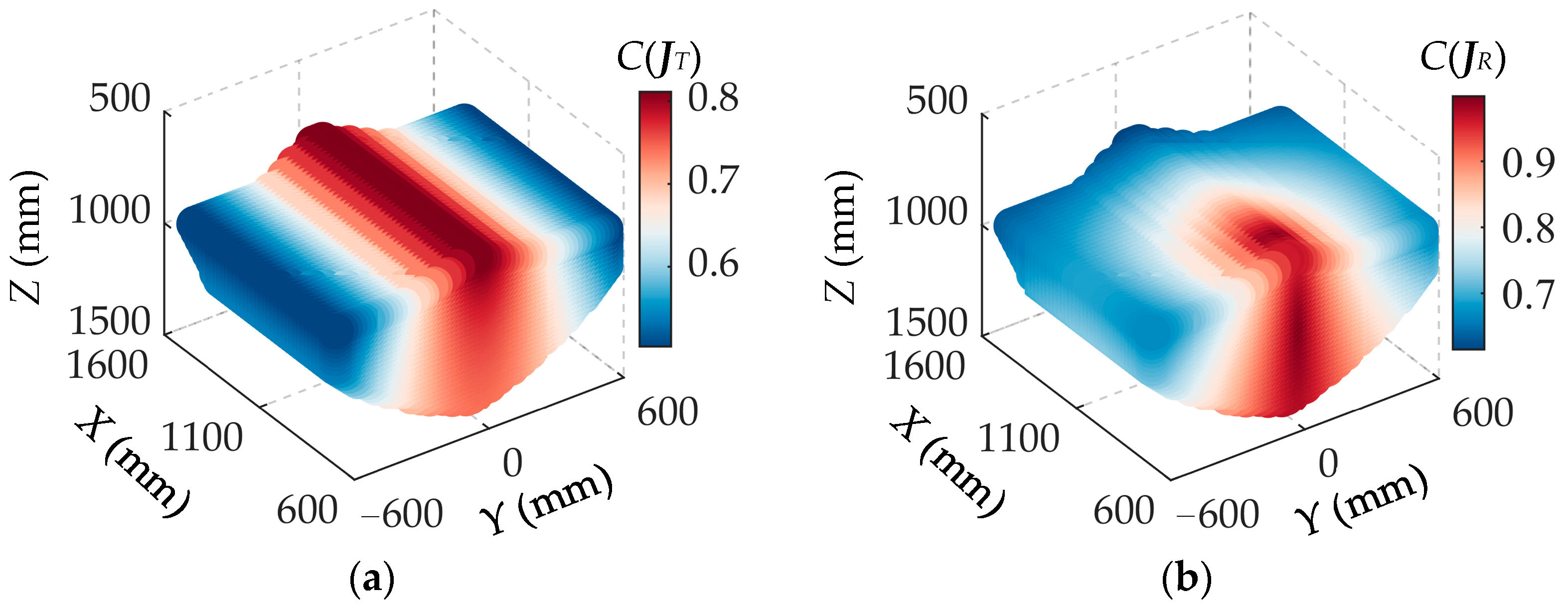
2.3.2. Dexterity Analysis

Dexterity is an important performance index that directly reflects the kinematic performance of the PM. Local condition indicators should be used to analyze a mechanism with both translational and rotational DOF. Equation (10) can be rewritten as:

$$\left[\begin{array}{l}\dot{x}\\ \dot{y}\\ \dot{z}\end{array}\right]={\mathit{J}}_{\mathrm{T}}{\mathit{V}}_r,\left[\begin{array}{l}\dot{\alpha }\\ \dot{\beta }\end{array}\right]={\mathit{J}}_R{\mathit{V}}_r$$

(11)

where J_T is a 3 × 5 form matrix formed by taking the first three rows of ${\mathit{J}}_D^{-1}$, J_R is a 2 × 5 form matrix formed by taking the last two rows of ${\mathit{J}}_D^{-1}$. J_T and J_R are the local matrices related to the Jacobian matrix. Based on this, the local dexterity index (LDI) of the position and orientation parts of the Jacobian matrix can be obtained, denoted as C(J_T) and C(J_R), as follows:

$$C\left({\mathit{J}}_T\right)={\displaystyle \frac{1}{k\left({\mathit{J}}_T\right)}},\hspace{0.33em}C\left({\mathit{J}}_R\right)={\displaystyle \frac{1}{k\left({\mathit{J}}_R\right)}}$$

(12)

where k(J_T) and k(J_R) are the condition numbers of the Jacobian matrixes J_T and J_R, respectively. k(J_T) and k(J_R) are calculated as follows:

$$k\left({\mathit{J}}_T\right)=‖{\mathit{J}}_T‖‖{\mathit{J}}_T^{+1}‖,k\left({\mathit{J}}_R\right)=‖{\mathit{J}}_R‖‖{\mathit{J}}_R^{+1}‖$$

(13)

The local dexterity index ranges from 0 to 1. The local dexterity index is 1, and the mechanism has the highest sensitivity and is isotropic. Conversely, the mechanism enters a singular configuration as the local dexterity index tends to 0. When the posture is fixed to take α = β = 0, the local dexterity index for the mechanism is shown in Figure 3.

As shown in Figure 3, the translational velocity dexterity index C(J_T) exhibits symmetry about the Y = 0 plane, peaking near the Y = 0 plane and progressively decreasing with increasing Y coordinates, ultimately reaching its minimum at the extremities of the workspace along the Y-axis. Similarly, the angular velocity dexterity index C(J_R) demonstrates symmetry about the Y = 0 plane, with its high-performance zones predominantly concentrated in the central workspace region near the origin.

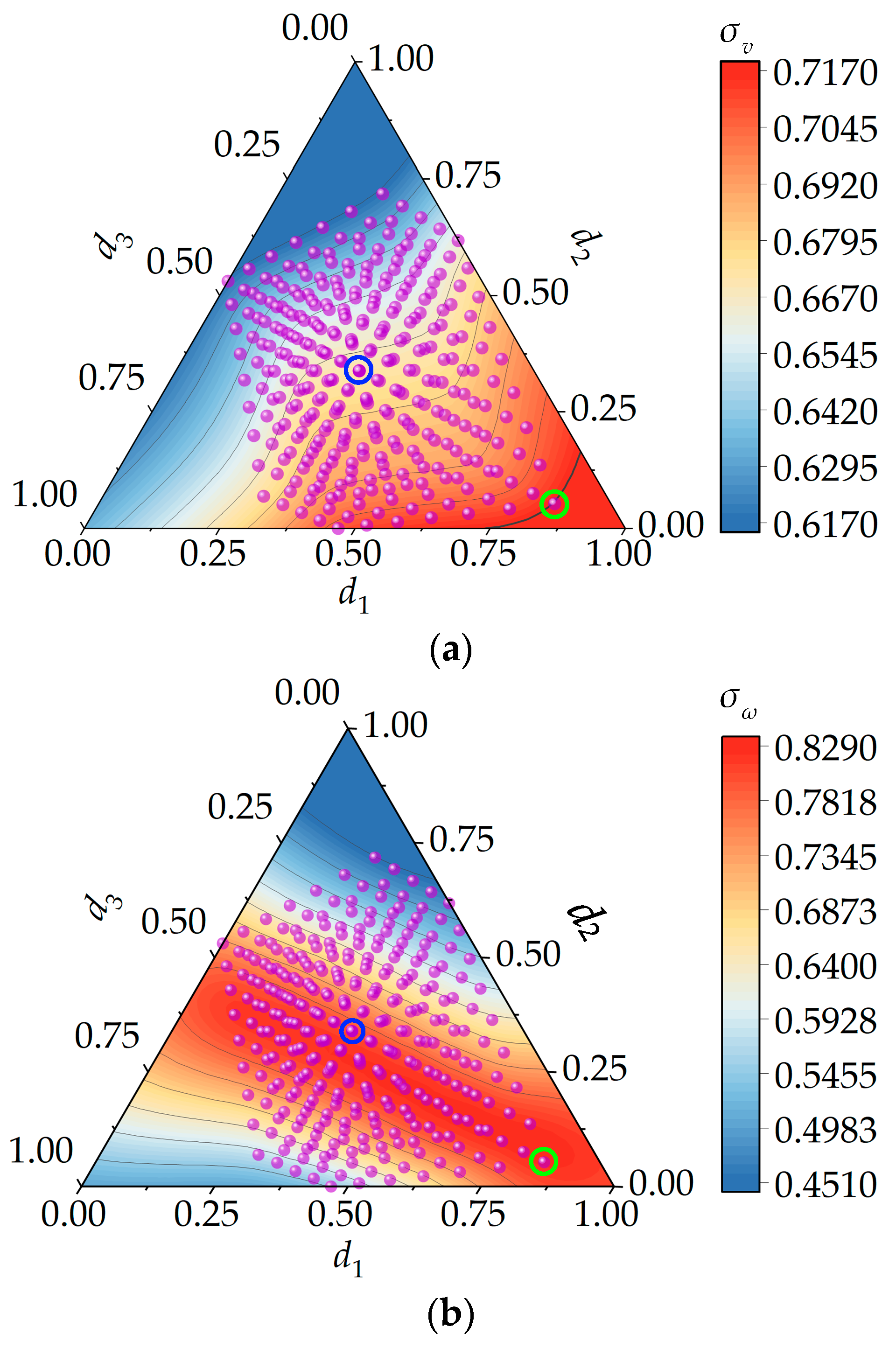
2.3.3. Optimization of Design Parameters

The kinematic performance of PMs exhibits significant dependence on their dimensional parameters. This study employs the global kinematic performance indexes σ_v and σ_ω for parametric optimization, formulated as:

$${\sigma }_v={\displaystyle \frac{{\displaystyle \sum _{i=1}^{N_{r\omega }}C({\mathit{J}}_T)\left(i\right)}}{N_{r\omega }}},{\sigma }_{\omega }={\displaystyle \frac{{\displaystyle \sum _{i=1}^{N_{r\omega }}C({\mathit{J}}_R)\left(i\right)}}{N_{r\omega }}}$$

(14)

where N_rw denotes the number of pose parameter points discretizing the workspace, with its physical interpretation corresponding to the workspace volume under the current dimensional parameters. Consequently, the geometrical meaning of indices σ_v and σ_ω can be interpreted as the mean value of global kinematic performance indexes over the workspace.

The architectural parameters are as follows: L = 1100 mm: 50 mm: 1300 mm, e = 200 mm: 25 mm: 400 mm: 150 mm, h = 180 mm: 20 mm: 300 mm. Using the parameter design space (PDS), the design parameters are normalized as follows:

$$\left\{\begin{array}{l}T=L+h+e\\ d_1={\displaystyle \frac{L}{T}},\hspace{0.33em}{d}_2={\displaystyle \frac{h}{T}},\hspace{0.33em}{d}_3={\displaystyle \frac{e}{T}}\\ 0<d_1,\hspace{0.33em}{d}_2,\hspace{0.33em}{d}_3<1\\ d_1+d_2+d_3=1\end{array}\right.$$

(15)

where T is a normalized factor, and d_i is a normalized nondimensional parameter. d₁, d₂, and d₃ are assigned as the coordinate axes of a ternary plot. Each point within this plot corresponds to the values of the global kinematic indices under the current d design parameters of the mechanism.

The distributions of σ_v and σ_ω can be obtained as shown in Figure 4, the σ_v is directly proportional to d₁ and inversely proportional to d₂, with the optimal region located in the lower right corner of the figure. The optimal region for σ_ω exhibits a distinct band-like distribution.

Based on these observations, we can select the parameter combination that achieves the relatively optimal dexterity performance, corresponding to the coordinates marked by the green circle in Figure 4—the 253st scale combination: d₁ = 0.7738, d₂ = 0.1190, d₃ = 0.1071, L = 1300 mm, e = 300 mm, h = 180 mm. This combination results in dexterity indices of σ_v = 0.7157 and σ_ω = 0.8267. For comparison, the original configuration (blue circle) yields σ_v = 0.6707, σ_ω = 0.8007.

3. Dynamic Analysis of the P(2PRPU)/PRPS PM

3.1. Velocity and Acceleration of Branch Chains

Taking the cross product with δ_i on both sides of Equation (7), we have:

$$\begin{array}{l}{\mathit{\delta }}_1\times \left(v_{rY}{\mathit{\delta }}_Y\right)+{\mathit{\omega }}_1{l}_1-{\mathit{\delta }}_1\times \left(\mathit{\omega }\times {\mathit{e}}_1\right)={\delta }_1\times \mathit{v}\\ {\mathit{\delta }}_i\times \left(v_{rX}{\mathit{\delta }}_X\right)+{\mathit{\omega }}_i{l}_i-{\mathit{\delta }}_i\left({\mathit{\omega }}_i\cdot l_i{\mathit{\delta }}_i\right)-{\mathit{\delta }}_i\times \left(\mathit{\omega }\times {\mathit{e}}_i\right)={\mathit{\delta }}_i\times \mathit{v},\left(i=2,3\right)\end{array}$$

(16)

According to the principle of motion synthesis, the velocity vector of point C_i on the moving platform can be expressed as:

$${\mathit{v}}_i=\mathit{v}+\mathit{\omega }\times {\mathit{e}}_i$$

(17)

Substituting Equation (16) into Equation (17), the angular velocity of r_i(i = 1, 2, 3) can be derived as:

$$\begin{array}{l}{\mathit{\omega }}_i={\mathit{J}}_{\omega i}\mathit{V}\\ {\mathit{J}}_{\omega 1}={\displaystyle \frac{1}{l_1}}\left(\left[{\hat{\mathit{\delta }}}_1\hspace{0.33em}-{\hat{\mathit{\delta }}}_1{\hat{\mathit{e}}}_1\right]-{\mathit{\delta }}_Y{\mathit{J}}_Y\right)\\ {\mathit{J}}_{\omega i}={\displaystyle \frac{1}{l_i}}\left(\left[{\hat{\mathit{\delta }}}_i\hspace{0.33em}-{\hat{\mathit{\delta }}}_i{\hat{\mathit{e}}}_i\right]-{\mathit{\delta }}_X{\mathit{J}}_X\right),\hspace{0.33em}i=2,3\end{array}$$

(18)

Here ê_i represents the skew-symmetric matrix of the e_i. Taking the time derivative of Equation (9), we can obtain angular acceleration and acceleration of the moving platform, respectively:

$$\begin{array}{l}\mathit{a}={\mathit{J}}_v{\mathit{A}}_q+{\mathit{V}}_q^{\mathrm{T}}{\mathit{H}}_v{\mathit{V}}_q,{\mathit{H}}_v={\left[{\mathit{h}}_{v1}\hspace{0.33em}{\mathit{h}}_{v2}\hspace{0.33em}{\mathit{h}}_{v3}\right]}^{\mathrm{T}},{\mathit{A}}_q={\left[\ddot{x}\hspace{0.33em}\hspace{0.33em}\ddot{y}\hspace{0.33em}\hspace{0.33em}\ddot{z}\hspace{0.33em}\hspace{0.33em}\ddot{\alpha }\hspace{0.33em}\hspace{0.33em}\ddot{\beta }\right]}^{\mathrm{T}}\\ \mathit{\epsilon }={\mathit{J}}_{\omega }{\mathit{A}}_q+{\mathit{V}}_q^{\mathrm{T}}{\mathit{H}}_{\omega }\mathit{V},{\mathit{H}}_{\omega }={\left[{\mathit{h}}_{\omega 1}\hspace{0.33em}{\mathit{h}}_{\omega 2}\hspace{0.33em}{\mathit{h}}_{\omega 3}\right]}^{\mathrm{T}}\\ {\mathit{h}}_{\omega 2}=\left[\begin{array}{cccc}0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& -s_{\alpha }& 0\end{array}\right],{\mathit{h}}_{\omega 3}=\left[\begin{array}{cccc}0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& c_{\alpha }& 0\end{array}\right]\end{array}$$

(19)

where h_v1 = h_v2 = h_v3 = h_ω1 = 0_5×5, 0_u×w denotes a u × w from zero matrix with u and w being two arbitrary positive integers. Taking the time derivative of Equation (19), we can obtain the angular acceleration of r_i (i = 1, 2, 3):

$$\begin{array}{l}{\mathit{\epsilon }}_i={\dot{\mathit{J}}}_{\omega i}\mathit{V}+{\mathit{J}}_{\omega i}\mathit{A},\mathit{A}={[\mathit{a}\hspace{0.33em}\mathit{\epsilon }]}^{\mathrm{T}}\\ {\dot{\mathit{J}}}_{\omega 1}={\displaystyle \frac{\left(\left[{\dot{\hat{\mathit{\delta }}}}_1\hspace{0.33em}-{\dot{\hat{\mathit{\delta }}}}_1{\hat{\mathit{e}}}_1-{\hat{\mathit{\delta }}}_1\widehat{\left(\mathit{\omega }\times {\mathit{e}}_1\right)}\right]-{\dot{\hat{\mathit{\delta }}}}_1{\mathit{\delta }}_Y{\mathit{J}}_Y-{\hat{\mathit{\delta }}}_1{\dot{\mathit{\delta }}}_Y{\mathit{J}}_Y-{\hat{\mathit{\delta }}}_1{\mathit{\delta }}_Y{\dot{\mathit{J}}}_Y\right)l_1}{l_1^2}}-{\displaystyle \frac{\left(\left[{\hat{\mathit{\delta }}}_1\hspace{0.33em}-{\hat{\mathit{\delta }}}_1{\hat{\mathit{e}}}_1\right]-{\hat{\mathit{\delta }}}_1{\mathit{\delta }}_Y{\mathit{J}}_Y\right)v_{r1}}{l_1^2}}\\ {\dot{J}}_{\omega i}={\displaystyle \frac{\left(\left[{\dot{\hat{\mathit{\delta }}}}_i\hspace{0.33em}-{\dot{\hat{\mathit{\delta }}}}_i{\hat{\mathit{e}}}_i-{\hat{\mathit{\delta }}}_i\widehat{\left(\mathit{\omega }\times {\mathit{e}}_i\right)}\right]-{\dot{\hat{\mathit{\delta }}}}_i{\mathit{\delta }}_X{\mathit{J}}_X-{\hat{\mathit{\delta }}}_i{\dot{\mathit{\delta }}}_X{\mathit{J}}_X-{\hat{\mathit{\delta }}}_i{\mathit{\delta }}_X{\dot{\mathit{J}}}_X\right)l_i}{l_i^2}}-{\displaystyle \frac{\left(\left[{\hat{\mathit{\delta }}}_i\hspace{0.33em}-{\hat{\mathit{\delta }}}_i{\hat{\mathit{e}}}_i\right]-{\hat{\mathit{\delta }}}_i{\mathit{\delta }}_X{\mathit{J}}_X\right)v_{ri}}{l_i^2}}\\ {\dot{\mathit{\delta }}}_X={\dot{\mathit{\delta }}}_Y={\mathsf{0}}_{3\times 1},{\dot{\hat{\mathit{\delta }}}}_i=\widehat{\left({\mathit{\omega }}_i\times {\mathit{\delta }}_i\right)},{\dot{\mathit{J}}}_Y=\left[{\mathsf{0}}_{3\times 1}^{\mathrm{T}}\hspace{0.33em}{\left(\left(\mathit{\omega }\times {\mathit{e}}_1\right)\times {\mathit{\delta }}_Y\right)}^{\mathrm{T}}\right],{\dot{\mathit{J}}}_X=\left[{\mathsf{0}}_{3\times 1}^{\mathrm{T}}\hspace{0.33em}{\left(\left(\mathit{\omega }\times {\mathit{e}}_2\right)\times {\mathit{\delta }}_X\right)}^{\mathrm{T}}\right]\end{array}$$

(20)

Before deducing the velocity of the mass center of r_i (i = 1, 2, 3), it is necessary to establish some key definitions and assumptions. The branch chain r_i consists of the cylinder (connected to the base) and the piston (connected to the moving platform). Let p_bi (i = 1, 2, 3) be the mass center of the cylinder, l_bi be the distance from A_i to p_bi, p_bi be the vector of p_bi in {B}, p_bi can be expressed as below:

$$\begin{array}{l}{\mathit{p}}_{b1}=l_Y{\mathit{\delta }}_Y+l_{b1}{\mathit{\delta }}_1\\ {\mathit{p}}_{bi}=l_X{\mathit{\delta }}_X+l_{bi}{\mathit{\delta }}_i,i=1,2,3\end{array}$$

(21)

Taking the time derivative of Equation (21), it leads to:

$$\begin{array}{l}{\mathit{v}}_{b1}=v_{rY}{\mathit{\delta }}_Y+{\mathit{\omega }}_1\times l_{b1}{\mathit{\delta }}_1\\ {\mathit{v}}_{\mathrm{bi}}=v_{rX}{\mathit{\delta }}_X+{\mathit{\omega }}_i\times l_{bi}{\mathit{\delta }}_i,i=1,2,3\end{array}$$

(22)

where v_bi is the velocity of the mass center of the cylinder, combined Equation (18) with Equation (22), it leads to:

$$\begin{array}{l}{\mathit{v}}_{b1}=\left[{\mathit{\delta }}_Y\hspace{0.33em}-l_{b1}{\hat{\mathit{\delta }}}_1\right]\left[\begin{array}{l}{v}_{rY}\\ {\mathit{\omega }}_1\end{array}\right]=\left[{\mathit{\delta }}_Y\hspace{0.33em}-l_{b1}{\hat{\mathit{\delta }}}_1\right]\left[\begin{array}{l}{\mathit{\delta }}_Y^{\mathrm{T}}\hspace{0.33em}{\left({\mathit{e}}_1\times {\mathit{\delta }}_Y\right)}^{\mathrm{T}}\\ {\mathit{J}}_{\omega 1}\end{array}\right]\left[\begin{array}{l}\mathit{v}\\ \mathit{\omega }\end{array}\right]={\mathit{J}}_{b1}\left[\begin{array}{l}\mathit{v}\\ \mathit{\omega }\end{array}\right]\\ {\mathit{v}}_{\mathit{bi}}=\left[{\mathit{\delta }}_X\hspace{0.33em}-l_{\mathit{bi}}{\hat{\mathit{\delta }}}_i\right]\left[\begin{array}{l}{v}_{rX}\\ {\mathit{\omega }}_i\end{array}\right]=\left[{\mathit{\delta }}_X\hspace{0.33em}-l_{\mathit{bi}}{\hat{\mathit{\delta }}}_1\right]\left[\begin{array}{l}{\mathit{\delta }}_X^{\mathrm{T}}\hspace{0.33em}{\left({\mathit{e}}_i\times {\mathit{\delta }}_X\right)}^{\mathrm{T}}\\ {\mathit{J}}_{\mathit{\omega }i}\end{array}\right]\left[\begin{array}{l}\mathit{v}\\ \mathit{\omega }\end{array}\right]={\mathit{J}}_{\mathit{bi}}\left[\begin{array}{l}\mathit{v}\\ \mathit{\omega }\end{array}\right]\end{array}$$

(23)

By taking the derivative of Equation (23) concerning time, the acceleration a_bi of the mass center of the cylinder is derived as follows:

$$\begin{array}{l}{\mathit{a}}_{\mathit{bi}}={\mathit{J}}_{\mathit{bi}}\mathit{A}+{\dot{\mathit{J}}}_{\mathit{bi}}\mathit{V}\\ {\dot{J}}_{bi}=\left[\left({\mathsf{0}}_{3\times 1}\times {\mathit{\delta }}_Y\right)\hspace{0.33em}-l_{b1}\widehat{\left({\mathit{\omega }}_1\times {\mathit{\delta }}_1\right)}\right]\left[\begin{array}{l}{\mathit{\delta }}_j^{\mathrm{T}}\hspace{0.33em}{\left({\mathit{e}}_i\times {\mathit{\delta }}_j\right)}^{\mathrm{T}}\\ {\mathit{J}}_{\omega i}\end{array}\right]+\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\left[{\mathit{\delta }}_j\hspace{0.33em}-l_{b1}{\hat{\mathit{\delta }}}_1\right]\left[\begin{array}{l}{\left({\mathit{\omega }}_y\times {\mathit{\delta }}_y\right)}^{\mathrm{T}}\hspace{0.33em}{\left(\left(\mathit{\omega }\times {\mathit{e}}_i\right)\times {\mathit{\delta }}_y+\left({\mathit{e}}_i\times \left({\mathit{\omega }}_j\times {\mathit{\delta }}_j\right)\right)\right)}^{\mathrm{T}}\\ J_{\mathit{\omega }i}\end{array}\right],i=1,2,3,\hspace{0.33em}j=X,Y\end{array}$$

(24)

Let p_si (i = 1, 2, 3) be the mass center of the piston, l_si be the distance from C_i to p_si, p_si be the vector of p_si in {B}, then p_si can be expressed as below:

$$\begin{array}{l}{\mathit{p}}_{s1}=l_Y{\mathit{\delta }}_Y+\left(l_1-l_{s1}\right){\mathit{\delta }}_1\\ {\mathit{p}}_{si}=l_X{\mathit{\delta }}_X+\left(l_i-l_{si}\right){\mathit{\delta }}_i,i=1,2,3\end{array}$$

(25)

Taking the time derivative of Equation (25), it leads to:

$$\begin{array}{l}{\mathit{v}}_{s1}=v_{rY}{\mathit{\delta }}_Y+v_{r1}{\mathit{\delta }}_1-\left(l_1-l_{s1}\right){\hat{\mathit{\delta }}}_1{\mathit{\omega }}_1\\ {\mathit{v}}_{\mathit{si}}=v_{rX}{\mathit{\delta }}_X+v_{ri}{\mathit{\delta }}_i-\left(l_i-l_{si}\right){\hat{\mathit{\delta }}}_i{\mathit{\omega }}_i,i=1,2,3\end{array}$$

(26)

where v_si is the velocity of the mass center of the piston, combined Equation (18) with Equation (26), it leads to:

$$\begin{array}{l}{\mathit{v}}_{s1}=\left[{\mathit{\delta }}_Y\hspace{0.33em}{\mathit{\delta }}_1\hspace{0.33em}-\left(l_1-l_{s1}\right){\hat{\mathit{\delta }}}_1\right]\left[\begin{array}{l}{\mathit{\delta }}_Y^{\mathrm{T}}\hspace{0.33em}{\left({\mathit{e}}_1\times {\mathit{\delta }}_Y\right)}^{\mathrm{T}}\\ {\mathit{\delta }}_1^{\mathrm{T}}\hspace{0.33em}{\left({\mathit{e}}_1\times {\mathit{\delta }}_1\right)}^{\mathrm{T}}\\ {\mathit{J}}_{\omega 1}\end{array}\right]\left[\begin{array}{l}\mathit{v}\\ \mathit{\omega }\end{array}\right]={\mathit{J}}_{s1}\left[\begin{array}{l}\mathit{v}\\ \mathit{\omega }\end{array}\right]\\ \\ {\mathit{v}}_{\mathit{si}}=\left[{\mathit{\delta }}_X\hspace{0.33em}{\mathit{\delta }}_i\hspace{0.33em}-\left(l_i-l_{si}\right){\hat{\mathit{\delta }}}_i\right]\left[\begin{array}{l}{\mathit{\delta }}_X^{\mathrm{T}}\hspace{0.33em}{\left({\mathit{e}}_i\times {\mathit{\delta }}_X\right)}^{\mathrm{T}}\\ {\mathit{\delta }}_i^{\mathrm{T}}\hspace{0.33em}{\left({\mathit{e}}_i\times {\mathit{\delta }}_i\right)}^{\mathrm{T}}\\ {\mathit{J}}_{\omega i}\end{array}\right]\left[\begin{array}{l}\mathit{v}\\ \omega \end{array}\right]={\mathit{J}}_{\mathit{si}}\left[\begin{array}{l}\mathit{v}\\ \mathit{\omega }\end{array}\right],\hspace{0.33em}i=2,3\end{array}$$

(27)

By taking the derivative of Equation (27) concerning time, the acceleration a_si of the mass center of the piston is derived as follows:

$$\begin{array}{l}{\mathit{a}}_{\mathit{si}}={\mathit{J}}_{\mathit{si}}\mathit{A}+{\dot{\mathit{J}}}_{\mathit{si}}\mathit{V}\\ {\dot{\mathit{J}}}_{s1}=\left[\left({\mathsf{0}}_{3\times 1}\times {\mathit{\delta }}_j\right)\hspace{0.33em}\left({\mathit{\omega }}_i\times {\mathit{\delta }}_i\right)\hspace{0.33em}-{\mathit{v}}_{ri}{\hat{\mathit{\delta }}}_i-\left(l_i-l_{si}\right)\widehat{\left({\mathit{\omega }}_i\times {\mathit{\delta }}_i\right)}\right]\left[\begin{array}{l}{\mathit{\delta }}_j^T\hspace{0.33em}{\left({\mathit{e}}_1\times {\mathit{\delta }}_j\right)}^T\\ {\mathit{\delta }}_i^T\hspace{0.33em}{\left({\mathit{e}}_i\times {\mathit{\delta }}_i\right)}^T\\ {\mathit{J}}_{\mathit{\omega }i}\end{array}\right]+\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\left[{\mathit{\delta }}_j\hspace{0.33em}\hspace{0.33em}{\mathit{\delta }}_i\hspace{0.33em}\hspace{0.33em}-\left(l_i-l_{si}\right){\underset{^}{\mathit{\delta }}}_i\right]\left[\begin{array}{l}{\left({\mathit{\omega }}_j\times {\mathit{\delta }}_j\right)}^T\hspace{0.33em}{\left(\left(\mathit{\omega }\times {\mathit{e}}_i\right)\times {\mathit{\delta }}_j+\left({\mathit{e}}_i\times \left({\mathit{\omega }}_j\times {\mathit{\delta }}_j\right)\right)\right)}^T\\ {\left({\mathit{\omega }}_i\times {\mathit{\delta }}_i\right)}^T\hspace{0.33em}{\left(\left(\mathit{\omega }\times {\mathit{e}}_i\right)\times {\mathit{\delta }}_i+\left({\mathit{e}}_i\times \left({\mathit{\omega }}_i\times {\mathit{\delta }}_i\right)\right)\right)}^T\\ {\dot{\mathit{J}}}_{\omega 1}\end{array}\right],i=1,2,3,\hspace{0.33em}j=X,Y\end{array}$$

(28)

3.2. Dynamic Model of the Proposed Mechanism

Let m_o, I_o, f_o, n_o, and G_o, be the mass, inertia matrix, inertia force, inertia torque, and the gravity of the moving platform. Let F and T be the workloads applied to the moving platform at o. Let m_bi, I_bi, f_bi, n_bi, and G_bi (i = 1, 2, 3) be the mass, inertia matrix, inertia force, inertia torque, and gravity of the cylinder, respectively. Let m_si, I_si, f_si, n_si, and G_si (i = 1, 2, 3) be the mass, inertia matrix, inertia force, inertia torque, and gravity of the piston, respectively. Let m_j, f_j, and G_j (j = X, Y) be the mass, inertia force, and gravity of the moving parts in the linear module r_j, respectively. The inertia force, torque, and the gravity can be derived as follows:

$$\left\{\begin{array}{l}{\mathit{G}}_o=m_o\mathit{g},\hspace{0.33em}{\mathit{f}}_o=-m_o\mathit{a},\hspace{0.33em}{\mathit{n}}_o=-{\tilde{I}}_o\mathsf{\epsilon }-\mathit{\omega }\times \left[{\tilde{I}}_o\mathit{\omega }\right]\\ {\mathit{G}}_{bi}=m_{bi}\mathit{g},\hspace{0.33em}{\mathit{f}}_{bi}=-m_{bi}{\mathit{a}}_{bi},\hspace{0.33em}{\mathit{n}}_{bi}=-{\tilde{\mathit{I}}}_{bi}{\mathsf{\epsilon }}_{bi}-{\mathit{\omega }}_{bi}\times \left[{\tilde{\mathit{I}}}_{bi}{\mathit{\omega }}_{bi}\right]\\ {\mathit{G}}_{si}=m_{si}\mathit{g},\hspace{0.33em}{\mathit{f}}_{si}=-m_{si}{\mathit{a}}_{si},\hspace{0.33em}{\mathit{n}}_{si}=-{\tilde{\mathit{I}}}_{si}{\mathsf{\epsilon }}_{si}-{\mathit{\omega }}_{si}\times \left[{\tilde{\mathit{I}}}_{si}{\mathit{\omega }}_{bi}\right]\\ {\mathit{G}}_X=m_X\mathit{g},{\mathit{f}}_X=-m_X{\mathit{a}}_X,\hspace{0.33em}{\mathit{G}}_Y=m_Y\mathit{g},{\mathit{f}}_Y=-m_Y{\mathit{a}}_Y\\ {\tilde{\mathit{I}}}_o=\left({}^B\mathit{R}_m\right){\mathit{I}}_o{\left({}^B\mathit{R}_m\right)}^{\mathrm{T}},\hspace{0.33em}\hspace{0.33em}{\tilde{\mathit{I}}}_{bi}=\left({\mathit{R}}_i\right){\mathit{I}}_{ci}{\left({\mathit{R}}_i\right)}^{\mathrm{T}},{\tilde{\mathit{I}}}_{si}=\left({\mathit{R}}_i\right){\mathit{I}}_{si}{\left({\mathit{R}}_i\right)}^{\mathrm{T}}\\ {\mathit{R}}_1=[{\mathit{\delta }}_Y\hspace{0.33em}{\mathit{\delta }}_Y\times {\mathit{\delta }}_1\hspace{0.33em}{\mathit{\delta }}_1]\hspace{0.33em}{R}_i=[{\mathit{\delta }}_X\hspace{0.33em}{\mathit{\delta }}_X\times {\mathit{\delta }}_i\hspace{0.33em}{\mathit{\delta }}_i],i=2,3\end{array}\right.$$

(29)

where ω_si = ω_bi = ω_i, ε_si = ε_bi = ε_i.

Let F_q be the active force applied on branch chains. Based on the principle of virtue work, we obtain:

$$\begin{array}{l}{\mathit{F}}_q^{\mathrm{T}}{\mathit{J}}_m\left[\begin{array}{l}\mathit{v}\\ \mathit{\omega }\end{array}\right]+\left[{\mathit{F}}^{\mathrm{T}}+{\mathit{f}}_o^{\mathrm{T}}+{\mathit{G}}_o^{\mathrm{T}}\hspace{0.33em}\hspace{0.33em}{\mathit{T}}^{\mathrm{T}}+{\mathit{n}}_o^{\mathrm{T}}\right]\left[\begin{array}{l}\mathit{v}\\ \mathit{\omega }\end{array}\right]+\left(\begin{array}{l}\left[{\mathit{f}}_X^{\mathrm{T}}+{\mathit{G}}_X^{\mathrm{T}}\hspace{0.33em}\hspace{0.33em}{\mathsf{0}}_{3\times 1}^{\mathrm{T}}\right]{\mathit{J}}_X+\\ \left[{\mathit{f}}_Y^{\mathrm{T}}+{\mathit{G}}_Y^{\mathrm{T}}\hspace{0.33em}\hspace{0.33em}{\mathsf{0}}_{3\times 1}^{\mathrm{T}}\right]{\mathit{J}}_Y\end{array}\right)\left[\begin{array}{l}\mathit{v}\\ \mathit{\omega }\end{array}\right]\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}+{\displaystyle \sum _{i=1}^3\left(\left[{\mathit{f}}_{bi}^{\mathrm{T}}+{\mathit{G}}_{bi}^{\mathrm{T}}\hspace{0.33em}\hspace{0.33em}{\mathit{n}}_{bi}^{\mathrm{T}}\right]{\mathit{J}}_{Bi}\left[\begin{array}{l}\mathit{v}\\ \mathit{\omega }\end{array}\right]+\left[{\mathit{f}}_{si}^{\mathrm{T}}+{\mathit{G}}_{si}^{\mathrm{T}}\hspace{0.33em}\hspace{0.33em}{\mathit{n}}_{si}^{\mathrm{T}}\right]{\mathit{J}}_{Si}\left[\begin{array}{l}\mathit{v}\\ \mathit{\omega }\end{array}\right]\right)}=0\end{array}$$

(30)

where Fq = [f_rX f_rY f_r1 f_r2 f_r3]^T, J_Bi = [J_bi J_ωi]^T, J_Si = [J_si J_ωi]^T. From Equation (30), the actuation force matrix of the branch chains can be expressed as:

$${\mathit{F}}_q=\mathit{DA}+\mathit{HV}+\mathit{G}+\mathit{E}$$

(31)

where $\mathit{D}={\left({\mathit{J}}_D\right)}^{\mathrm{T}}{\mathit{J}}_B^{\mathrm{T}}{\displaystyle \sum _{i=1}^3\left(\begin{array}{l}{\mathit{J}}_{bi}^{\mathrm{T}}{\mathit{J}}_{bi}{m}_{bi}+{\mathit{J}}_{si}^{\mathrm{T}}{\mathit{J}}_{si}{m}_{si}+{\mathit{J}}_{\omega i}^{\mathrm{T}}\left({\tilde{\mathit{I}}}_{bi}+{\tilde{\mathit{I}}}_{si}\right){\mathit{J}}_{\omega i}+\\ {\left[{\mathit{J}}_X\hspace{0.33em}{\mathsf{0}}_{2\times 6}\right]}^T\left[{\mathit{J}}_X\hspace{0.33em}{\mathsf{0}}_{2\times 6}\right]m_X+\\ {\left[{\mathsf{0}}_{1\times 6}\hspace{0.33em}{\mathit{J}}_Y\hspace{0.33em}{\mathsf{0}}_{1\times 6}\right]}^T\left[{\mathsf{0}}_{1\times 6}\hspace{0.33em}{\mathit{J}}_Y\hspace{0.33em}{\mathsf{0}}_{1\times 6}\right]m_Y+{\mathit{J}}_Q\end{array}\right)}$

$\mathit{H}={\left({\mathit{J}}_D\right)}^{\mathrm{T}}{\mathit{J}}_B^{\mathrm{T}}{\displaystyle \sum _{i=1}^3\left(\begin{array}{l}{\mathit{J}}_{bi}^{\mathrm{T}}{\dot{\mathit{J}}}_{bi}{m}_{bi}+{\mathit{J}}_{si}^{\mathrm{T}}{\dot{\mathit{J}}}_{si}{m}_{si}+{\mathit{J}}_{\omega i}^{\mathrm{T}}\left({\tilde{\mathit{I}}}_{bi}+{\tilde{\mathit{I}}}_{si}\right){\dot{\mathit{J}}}_{\omega i}+\\ {\left[{\mathit{J}}_{mx}\hspace{0.33em}{\mathsf{0}}_{2\times 6}\right]}^T\left[{\dot{\mathit{J}}}_{mx}\hspace{0.33em}{\mathsf{0}}_{2\times 6}\right]m_{sx}+\\ {\left[{\mathsf{0}}_{1\times 6}\hspace{0.33em}{\mathit{J}}_{my}\hspace{0.33em}{\mathsf{0}}_{1\times 6}\right]}^T\left[{\mathsf{0}}_{1\times 6}\hspace{0.33em}{\dot{\mathit{J}}}_{my}\hspace{0.33em}{\mathsf{0}}_{1\times 6}\right]-\\ {\mathit{J}}_{\omega i}^{\mathrm{T}}\widehat{\left(\left({\tilde{\mathit{I}}}_{bi}+{\tilde{\mathit{I}}}_{si}\right){\mathit{\omega }}_i\right)}{\mathit{J}}_{\omega i}+{\mathit{J}}_R\end{array}\right)}$

$\begin{array}{l}\mathit{G}=-{\left({\mathit{J}}_D\right)}^{\mathrm{T}}{\mathit{J}}_B^{\mathrm{T}}{\displaystyle \sum _{i=1}^3\left(\begin{array}{l}{\mathit{J}}_{bi}^{\mathrm{T}}{m}_{bi}\mathit{g}+{\mathit{J}}_{si}^{\mathrm{T}}{m}_{si}\mathit{g}+{\left[{\mathit{J}}_{mx}\hspace{0.33em}{\mathsf{0}}_{2\times 6}\right]}^T{m}_X\mathit{g}+\\ {\left[{\mathsf{0}}_{1\times 6}\hspace{0.33em}{\mathit{J}}_Y\hspace{0.33em}{\mathsf{0}}_{1\times 6}\right]}^T{m}_Y\mathit{g}+{\mathit{J}}_S\end{array}\right)}\\ \mathit{E}=-{\left({\mathit{J}}_D^{-1}\right)}^{\mathrm{T}}{\mathit{J}}_B^{\mathrm{T}}\left(\begin{array}{l}\mathit{F}\\ \mathit{T}\end{array}\right),{\mathit{J}}_Q=\left[\begin{array}{l}{m}_o{\mathit{E}}_{3\times 3}\hspace{0.33em}{\mathsf{0}}_{3\times 3}\\ \hspace{0.33em}\hspace{0.33em}{\mathsf{0}}_{3\times 3}\hspace{0.33em}\hspace{0.33em}{\tilde{\mathit{I}}}_o\end{array}\right],{\mathit{J}}_R=\left[\begin{array}{l}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}{\mathsf{0}}_{6\times 6}\\ -\widehat{\left({\tilde{\mathit{I}}}_o\mathit{\omega }\right)}{\mathit{J}}_{0E}\end{array}\right]\\ {\mathit{J}}_S={\left[m_o\mathit{g}\hspace{0.33em}0\hspace{0.33em}0\hspace{0.33em}0\right]}^{\mathrm{T}},\hspace{0.33em}{\mathit{J}}_{E0}=\left[{\mathit{E}}_{3\times 3}\hspace{0.33em}\hspace{0.33em}{\mathsf{0}}_{3\times 3}\right],{\mathit{J}}_{0E}=\left[{\mathsf{0}}_{3\times 3}\hspace{0.33em}{\mathit{E}}_{3\times 3}\right]\end{array}$

From Equation (31), the actuation forces of five branch chains can be solved. Validation of the analytical dynamic model of P(2PRPU)/PRPS PM is necessary before evaluating the dynamic performance. Here, an Adams simulation is carried out to verify the dynamic model, as shown in Figure 5. In the simulation model of Figure 5, the structural parameters of P(2PRPU)/PRPS PM are L = 1300 mm, e = 300 mm, and h = 180 mm. The mechanism mass and inertia parameters are extracted from Adams, and the specific values are shown in

Table 1. Mass properties and moment of inertia of the P(2PRPU)/PRPS PM.

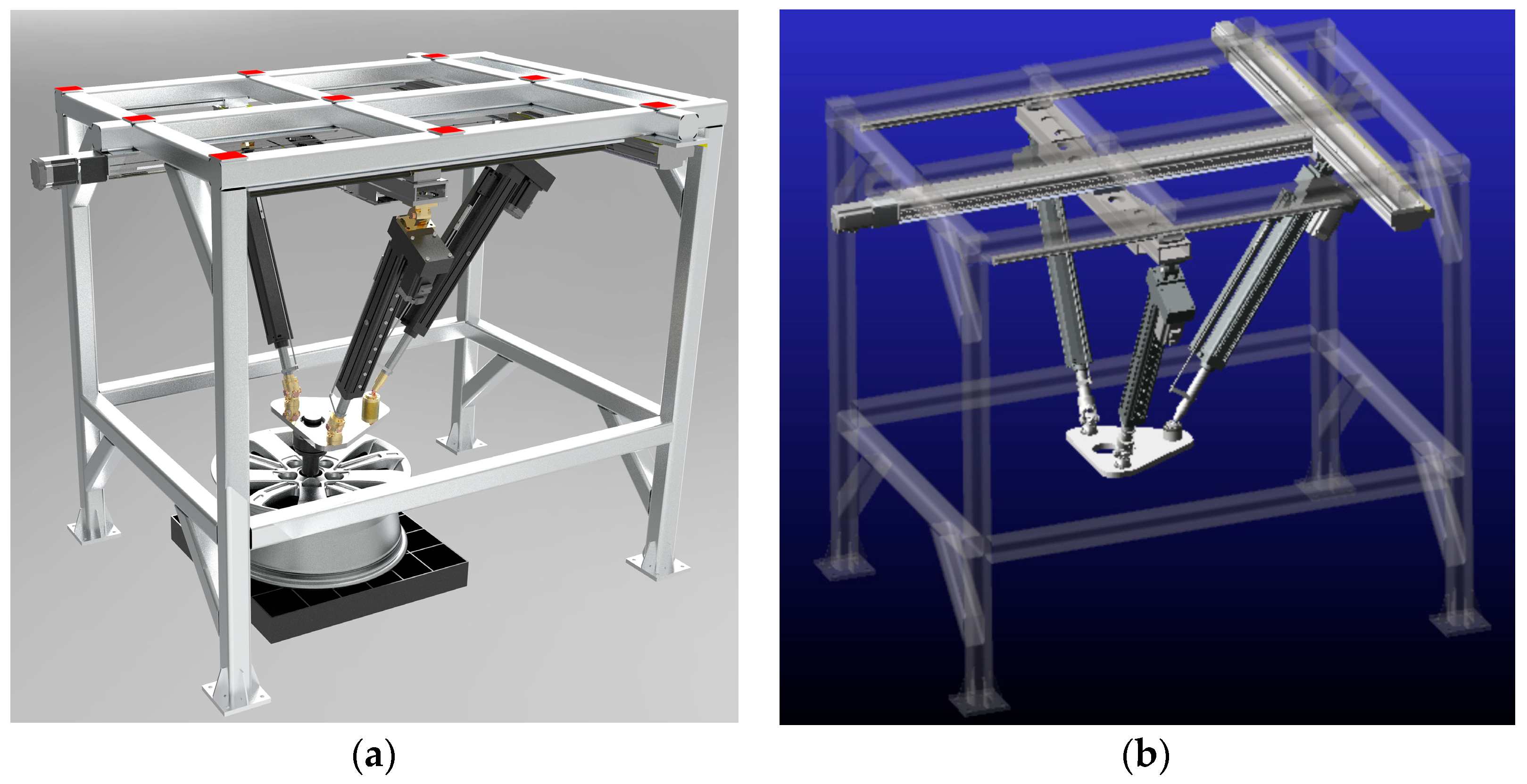
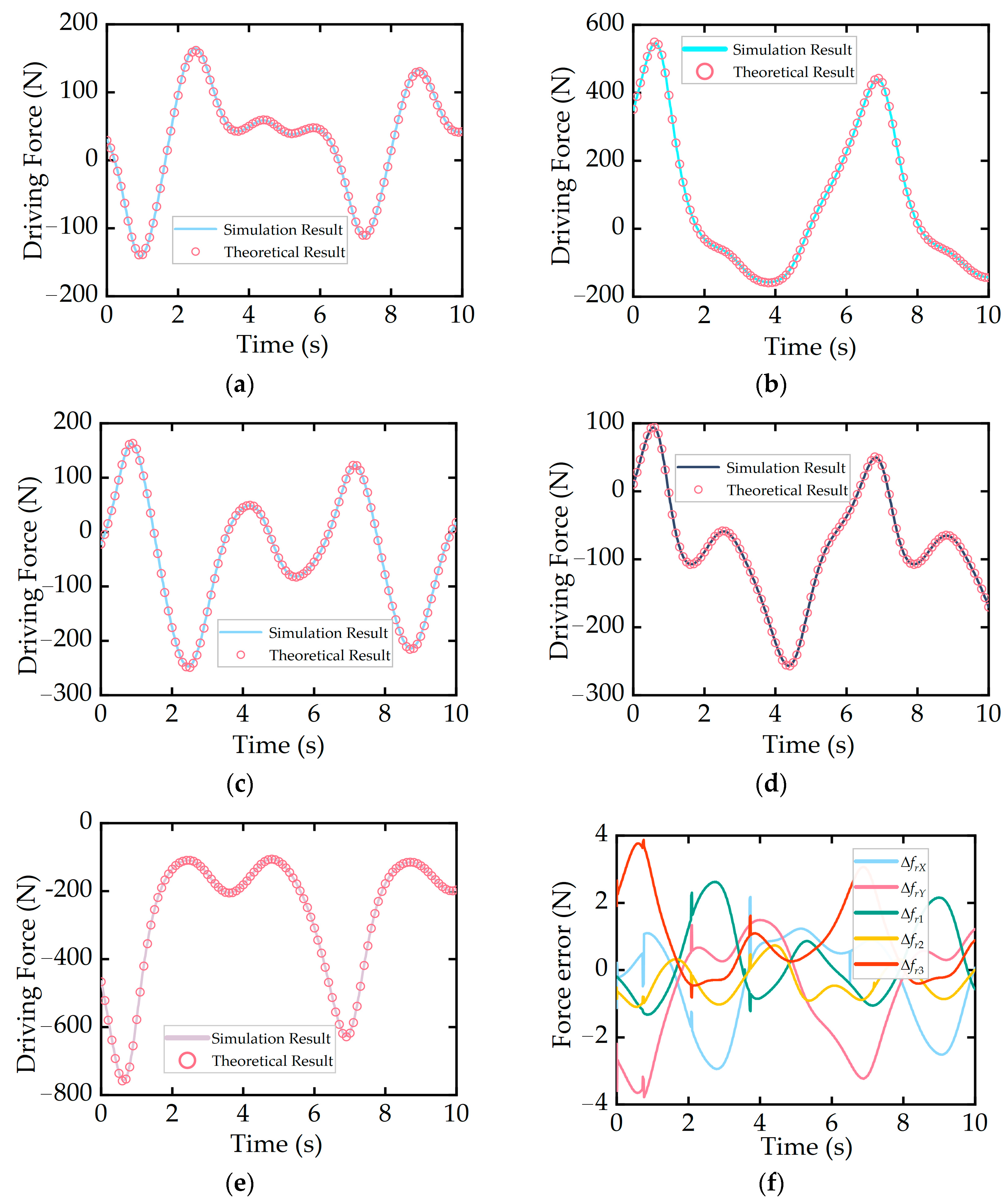
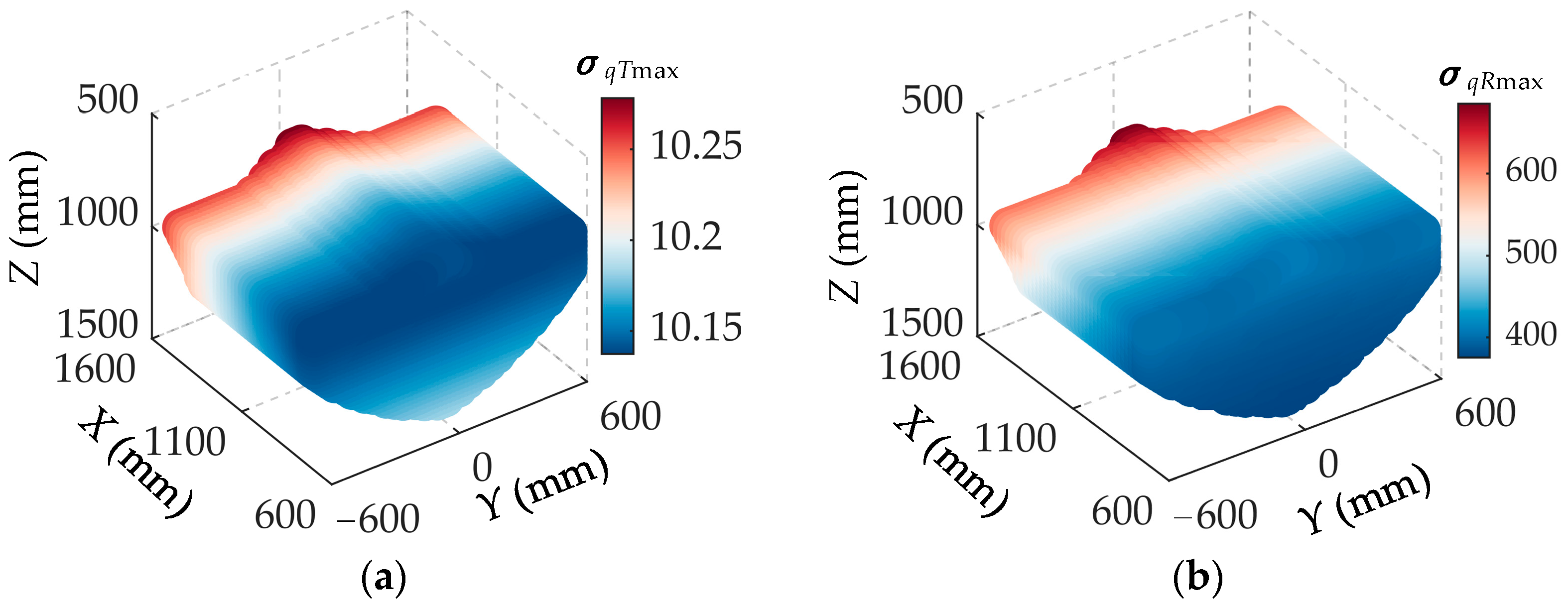
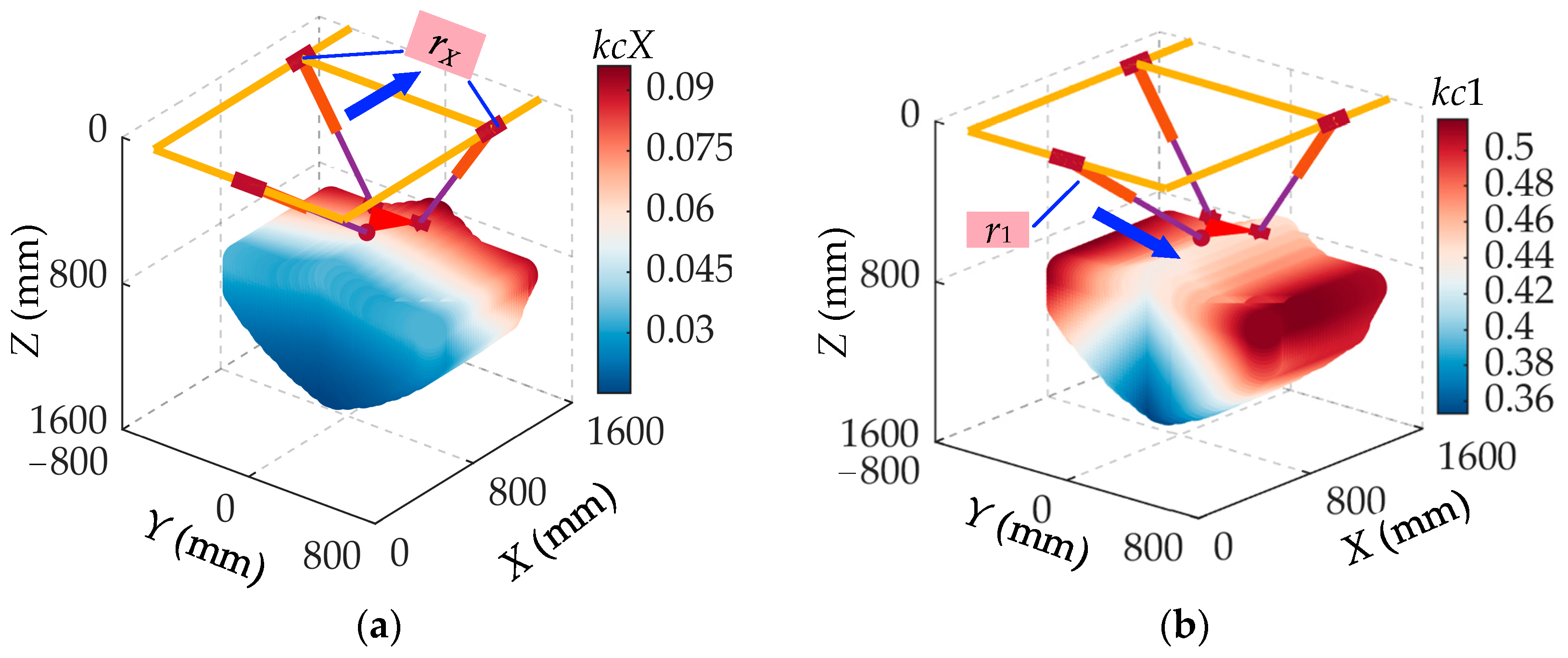
Symbol	Mass (kg)	Local Inertial Matrix (kg∙mm2)
mo	17.83	diag(367,124 191,975 181,594)
mb1, mb2, mb3	25.42	diag(1,437,939 1,375,778 97,592)
ms1	2.85	diag(118,804, 117,521 1,849)
ms2, ms3	3.79	diag(173,612, 172,451 2,340)
mX	33.57	diag(5,541,785 5,528,349 88,156)
mY	4.55	diag(8,732 7,620 7,522)

. The motion of the end-effector is given as x = 800 + 200sint mm, y = 200cost mm, z = 1000 + 10t mm, α = πsint/9 rad, β = πcost/9 rad.

The numerical results of the forces exerted by the five actuators under the specified motion trajectory are obtained and presented in Figure 6 through theoretical analysis and simulation. The computational results demonstrate a strong agreement between the analytical dynamic and Adams models regarding magnitude and variation trends. Therefore, it is verified that all derived theoretical formulae of kinematics and dynamics are correct.

3.3. Dynamic Performance Analysis

3.3.1. Dynamic Manipulability of the P(2PRPU)/PRPS PM

This section investigates the dynamic performance of the P(2PRPU)/PRPS PM using the dynamic model in Equation (31). The Dynamic Manipulability Ellipsoid (DME) is adopted to evaluate the uniformity of the PM’s ability to change the MP’s position/orientation under the stated driving forces. Subsequently, the distribution and characteristics of the DME index within the workspace of the P(2PRPU)/PRPS PM are investigated.

Substituting Equation (9) into Equation (31), the dynamic equation can be derived as:

$${\mathit{F}}_q=\mathit{D}{\mathit{J}}_B{\mathit{A}}_q+\left(\mathit{D}{\dot{\mathit{J}}}_B+\mathit{H}{\mathit{J}}_B\right){\mathit{V}}_q+\mathit{G}+\mathit{E}$$

(32)

In investigating the acceleration/deceleration characteristics of parallel manipulators, where acceleration-dependent terms dominate the dynamic model, Equation (32) can be appropriately simplified by neglecting the centrifugal, Coriolis, and gravitational items for the time being:

$$\begin{array}{l}{\mathit{F}}_q={\mathit{M}}_q{\mathit{A}}_q\\ {\mathit{M}}_q=\mathit{D}{\mathit{J}}_B,{\mathit{A}}_q={\left[{\mathit{a}}_T\hspace{0.33em}{\mathit{a}}_R\right]}^{\mathrm{T}}\end{array}$$

(33)

Here a_T represents the translational acceleration, a_R is the rotational acceleration. The DME of P(2PRPU)/PRPS PM is separated into the rotation and translation parts by dividing the matrix Mq to evaluate the dynamic performance. Based on Equation (33), the driving forces Fq can be reformulated as [32]:

$${\mathit{F}}_q={\mathit{F}}_{qT}+{\mathit{F}}_{qR}={\mathit{M}}_{qT}{\mathit{a}}_T+{\mathit{M}}_{qR}{\mathit{a}}_R$$

(34)

where F_qT represents the driving forces caused by the translational acceleration, and F_qR represents the driving forces caused by the rotational acceleration. M_qT represents the matrix composed of the first three columns of matrix M_q, and M_qR is the matrix composed of the last two columns of the matrix M_q.

This section evaluates the dynamic performance of the P(2PRPU)/PRPS parallel manipulator (PM) using the maximum singular values (σ_qTmax and σ_qRmax) of matrices M_qT and M_qR at specified poses, where smaller values indicate better dynamic performance. Figure 7 presents the spatial distribution of both rotational and translational dynamic performance indices across the P(2PRPU)/PRPS PM’s workspace. The results demonstrate that all performance metrics exhibit perfect symmetry about the X = 0 plane, reflecting the inherent structural symmetry of the P(2PRPU)/PRPS PM. Moreover, the dynamic performance is optimal near the initial region of the workspace, while both the rotational and translational manipulability indices gradually increase as the X-coordinate grows, indicating progressively worse dynamic performance.

3.3.2. Coupling Property of the P(2PRPU)/PRPS PM

In the motion of PMs, each actuated branched chain is influenced by its inertia and coupled inertial effects from other branched chains, affecting the system’s overall dynamic performance. In order to study the coupling properties among active branched chains of the P(2PRPU)/PRPS PM, it is necessary to transform the dynamic model into the joint space. From Equation (31), the dynamic model of the P(2PRPU)/PRPS PM in the joint space can be expressed as:

$$\left\{\begin{array}{l}{\mathit{F}}_q={\mathit{M}}_J{\dot{\mathit{V}}}_r+{\mathit{H}}_J{\mathit{V}}_r+\mathit{G}+\mathit{E}\\ {\mathit{M}}_J=\mathit{D}{\mathit{J}}_B{\mathit{J}}_D^{-1}\\ {\mathit{H}}_J=\left(\mathit{D}{\mathit{J}}_B{\dot{\mathit{J}}}_D^{-1}+\left(\mathit{D}{\dot{\mathit{J}}}_B+\mathit{H}{\mathit{J}}_B\right){\mathit{J}}_D^{-1}\right)\end{array}\right.$$

(35)

A monotonically increasing logarithmic function evaluates the inertial coupling intensity between actuated branched chains. The coupling intensity index kci, (i = X, Y, 1, 2, 3) for each branch can be expressed as:

$$kci=1-{\displaystyle \frac{1}{e^{{\lambda }_i}}},\hspace{0.33em}{\lambda }_i={\displaystyle \frac{{\displaystyle \sum _{j=1,j\ne i}^5‖{\mathit{M}}_{Jij}‖}}{‖{\mathit{M}}_{Jii}‖}}$$

(36)

The inertia matrix of the PMs has the property that the diagonal elements dominate so that λ_i is always in the range of [0, 1], so the value of the inertia coupling strength evaluation index kci is defined in the interval [0, 1]. When the index approaches 1, the inertia coupling strength of the branched chain becomes more significant, whereas when the index approaches zero, the inertia coupling strength of the branched chain decreases. The larger the coupling strength index, the greater the influence of other branched chains’ inertia on a given branched chain.

Figure 8 shows that the inertia coupling strength of each branched chain of the P(2PRPU)/PRPS PM changes with the motion attitude of the moving platform, the blue arrows indicate the movement directions of the corresponding side chains. The coupling intensity indices of branched chains kcX, kcY, and kc₁ are symmetrical about the Y = 0 plane, consistent with the mechanism’s structural characteristics, while limbs kc₂ and kc₃ exhibit identical variation trends in opposite directions.

As can be seen from Figure 8, the coupling intensity of each branch is proportional to the length of the branch. When the moving platform t moves in the direction away from one of the branched chains, the inertia coupling strength index of this branched chain will gradually increase. By comparing Figure 8a,f, as well as Figure 8b,e, it can be observed that for the P(2PRPU)/PRPS PM, the first-stage driving branches of the dual-driven limbs PRPS and PRPU exhibit significantly lower coupling intensity than the second-stage driving branches.

According to the distribution law of branched chains’ inertia coupling strength in the workspace, the coupling between the branch chains is inevitable, but the motion trajectory of PMs can be rationally planned to reduce the influence of inertia coupling.

Through the analysis of the kinematics and dynamics of the mechanism, it can be noted that this mechanism has significant advantages in structural design and performance optimization, and has strong potential for engineering applications. In the future, this type of mechanism can be widely applied in high-end equipment fields such as five-axis machining of large aerospace components, precision polishing systems for high-accuracy optical elements, fine pointing adjustment platforms for space telescopes, and mold machining platforms for large wind turbine blades.

4. Conclusions

This paper proposes a novel 5-DOF PM with two double-driven chains. This mechanism features only three kinematic branches, which help reduce interference between branches. The PM exhibits approximate axial symmetry and adopts a rational constraint strategy along with a double-driven joint design, significantly enhancing the flexibility of the moving platform. The main conclusions of this work are summarized as follows:

Firstly, a novel P(2PRPU)/PRPS PM is proposed based on double-driven limbs. While maintaining the required DOF, the mechanism reduces the number of branches, simplifies the overall structure, and minimizes mutual interference between branches. The mobility of the mechanism is analyzed using screw theory, and the results confirm that it possesses five independent degrees of freedom.

Secondly, based on the geometric characteristics of the mechanism, its kinematic model is derived, and its kinematic performance is analyzed. The atlas method is employed to carry out the kinematic optimization design of the proposed parallel mechanism.

Furthermore, based on screw theory, an inverse dynamic model of the P(2PRPU)/PRPS PM is established with concise expressions and clear physical interpretations. The rotational dynamic motion evaluation index (σ_qRmax) and translational dynamic motion evaluation index (σ_qTmax) are adopted to assess the dynamic performance of the PM. The evaluation results indicate that the mechanism performs optimally in most workspace regions.

Finally, based on the dynamic model, an evaluation model is developed to quantify the inertial coupling strength of the active branches. The results reveal that the inertial coupling strength of each active branch is inversely proportional to its length and increases as the moving platform deviates from the corresponding branch chain’s layout direction.

Future research will focus on stiffness modeling and analysis to further facilitate the practical application of the proposed 5-DOF PM in engineering.