Active Torsional Vibration Suppression Strategy for Power-Split-HEV Driveline System Based on Dual-Loop Control
Abstract
1. Introduction
2. Modeling and Vibration Mechanism Analysis of Power-Split-HEV Driveline System
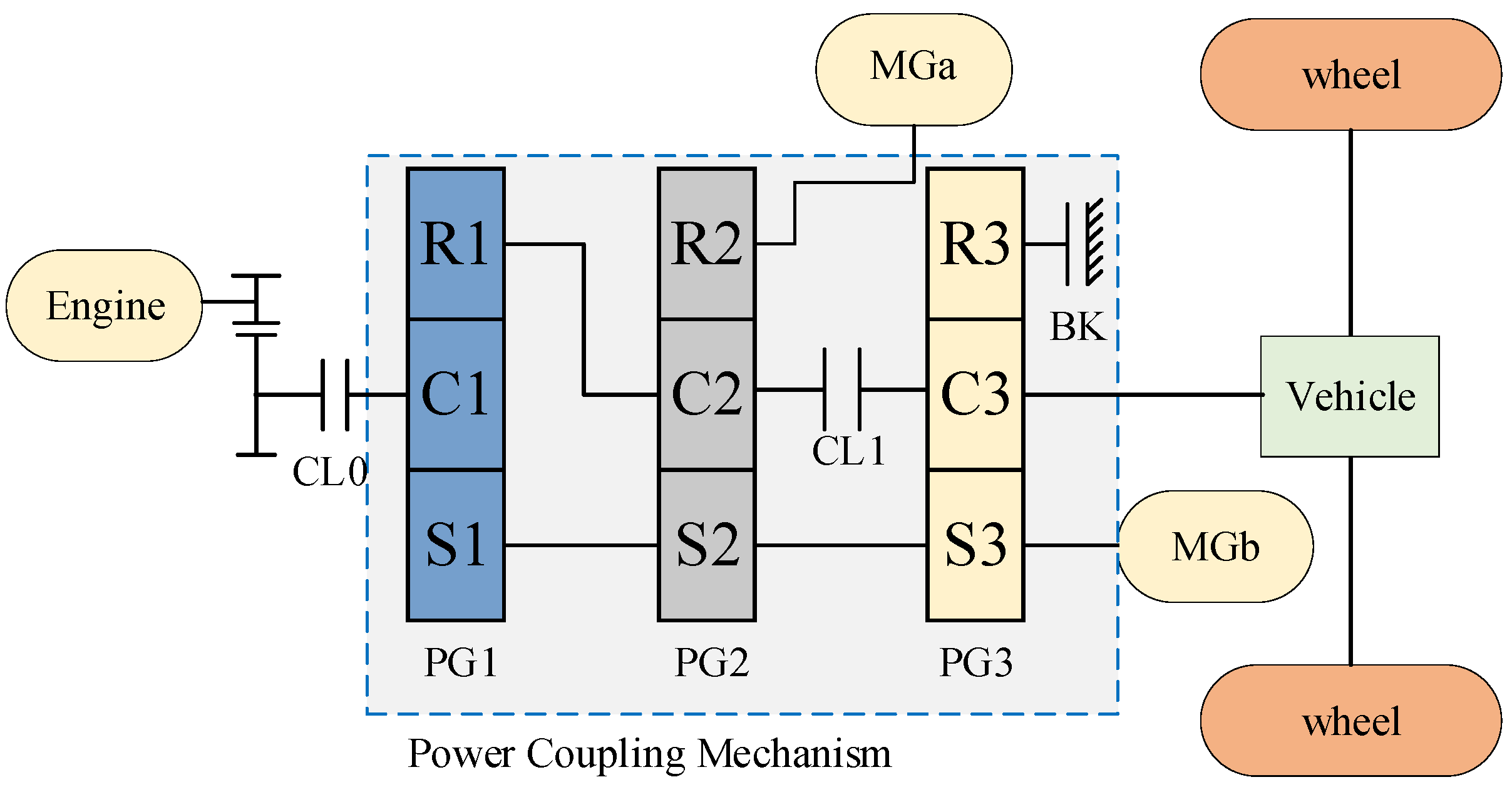
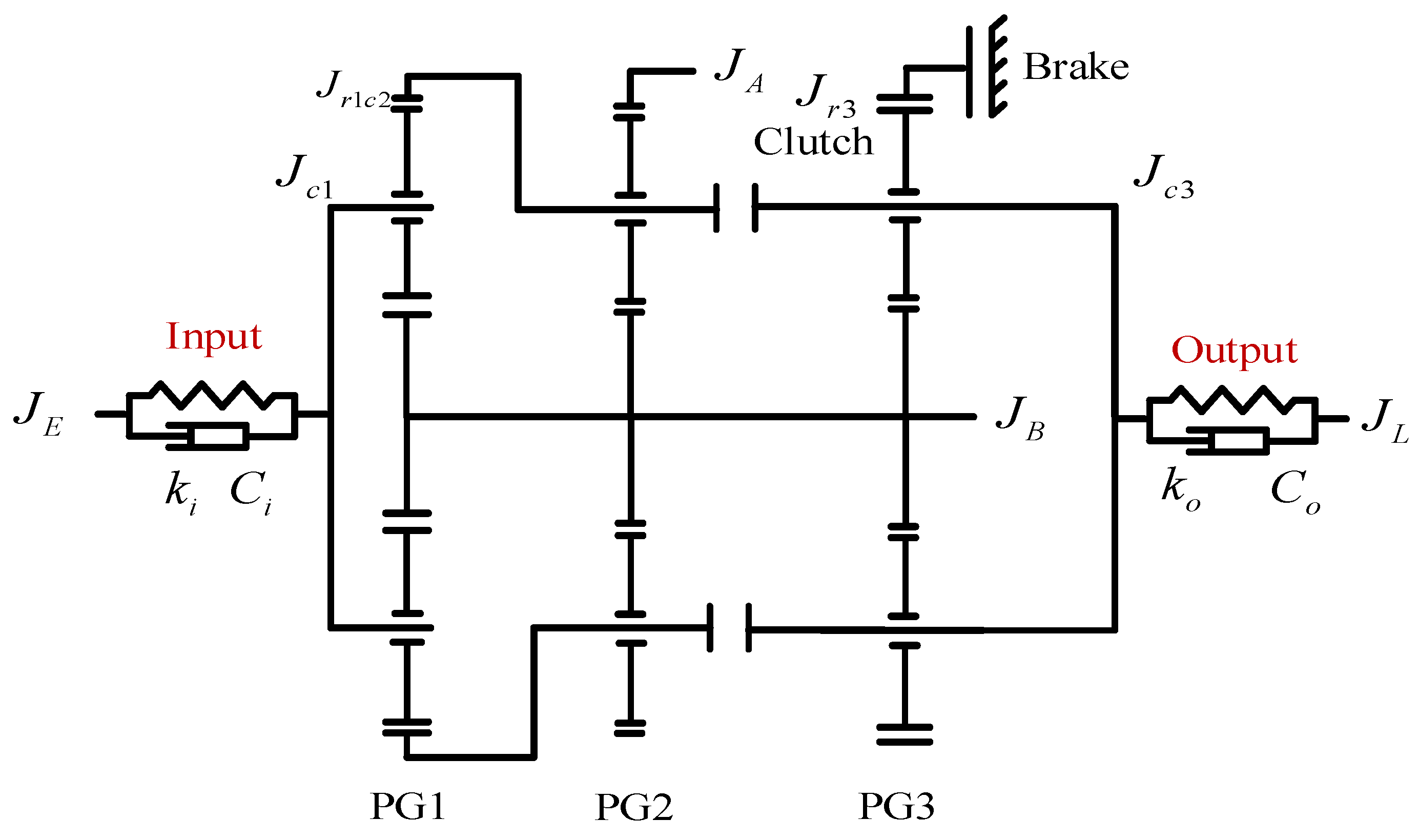
2.1. Driveline System Modeling
2.1.1. Input and Output Speed and Torque Analysis of Driveline System
2.1.2. Engine Torque Modeling and Motor Torque Modeling
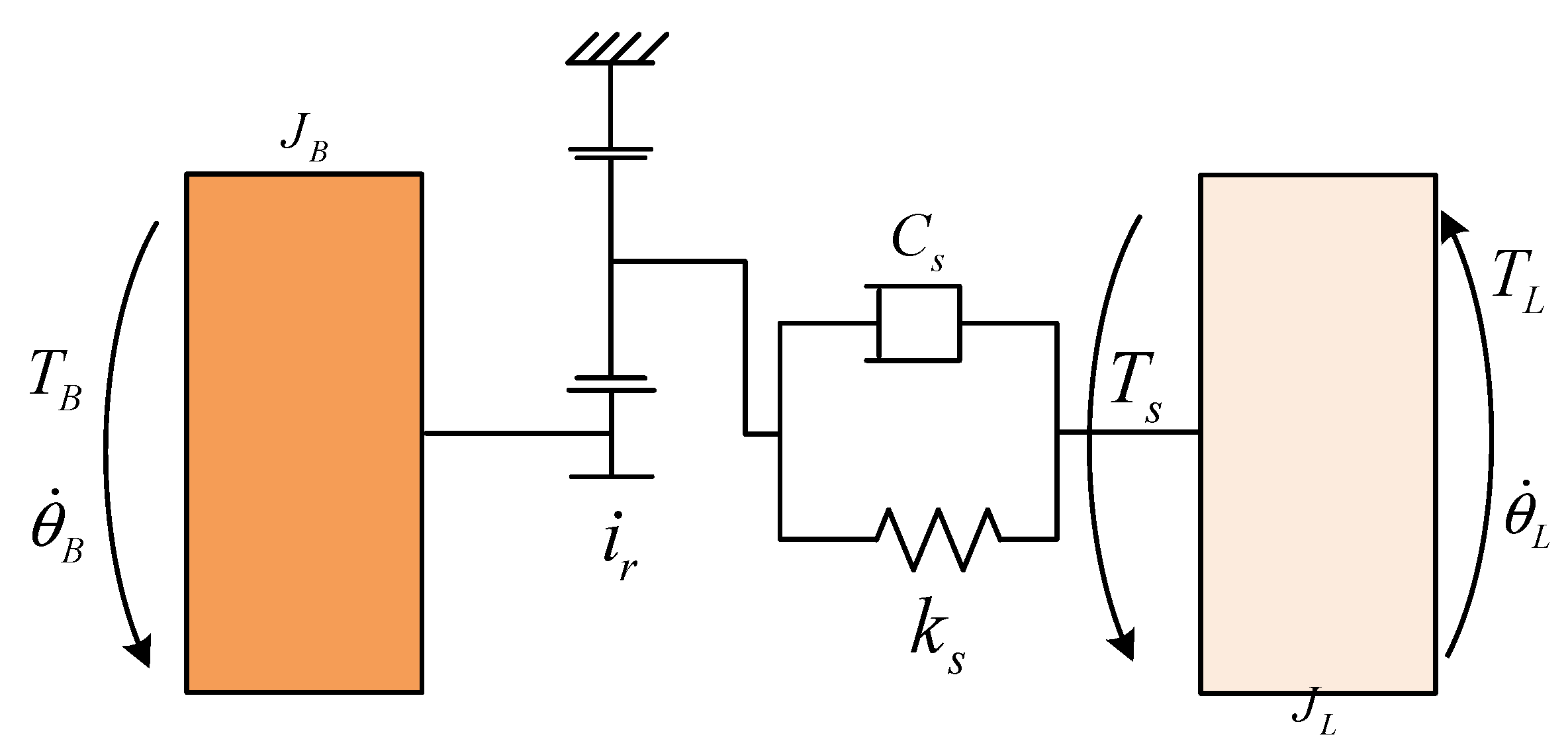
2.1.3. Transmission Mechanism Model
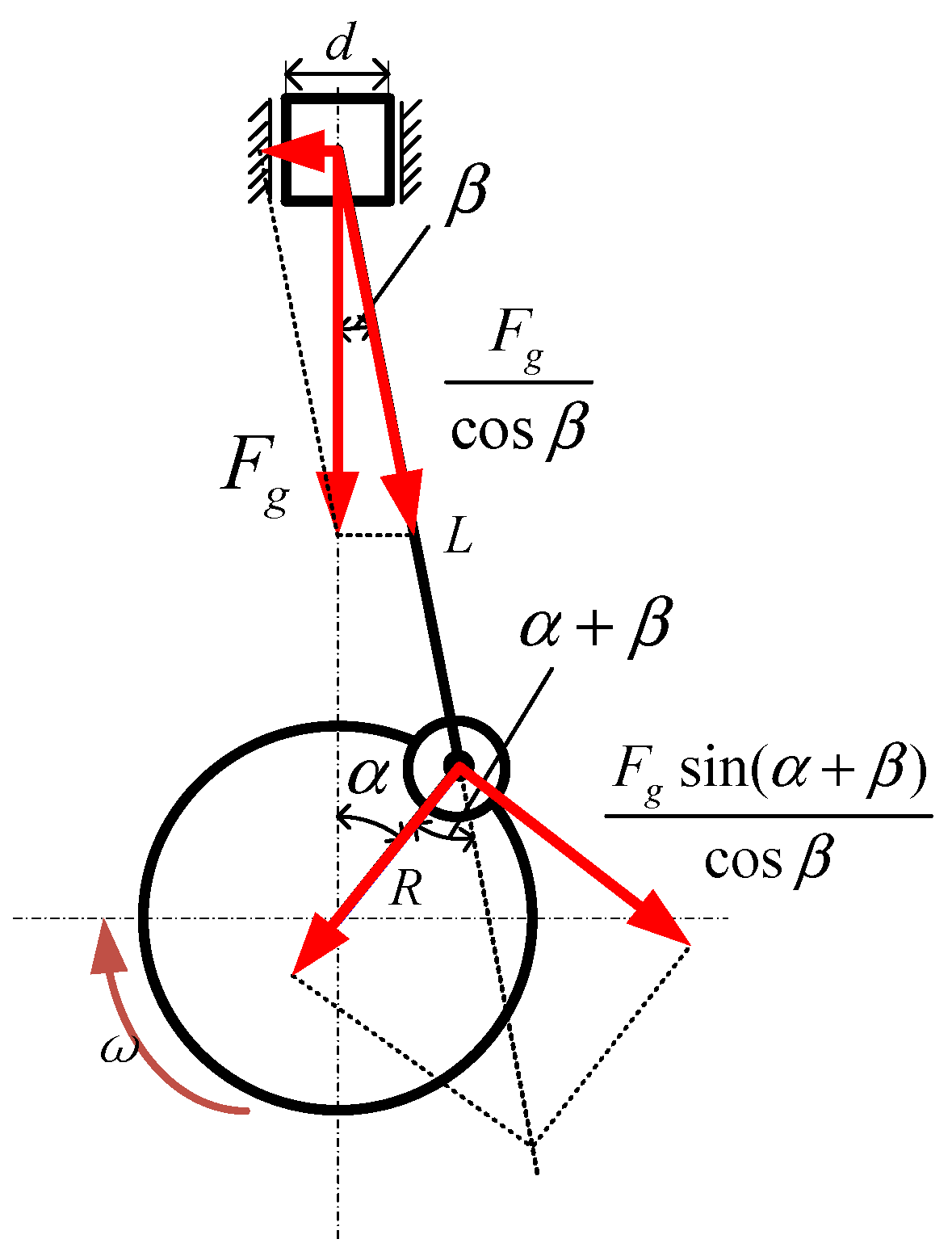
2.2. Torsional Vibration Mechanism Analysis
2.2.1. Analysis of Torsional Vibration Mechanism in Hybrid Mode
2.2.2. Analysis of Torsional Vibration Mechanism in Pure Electric Mode
3. Torsional Vibration Control Strategy for HEV Based on Dual-Loop Decoupling Control
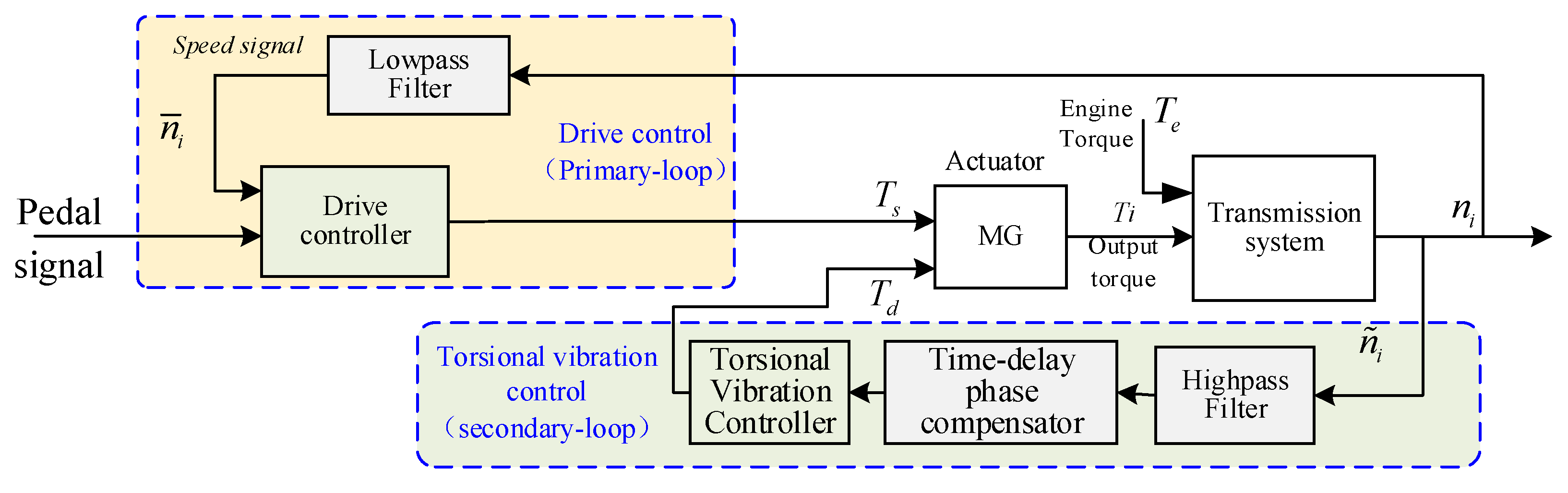
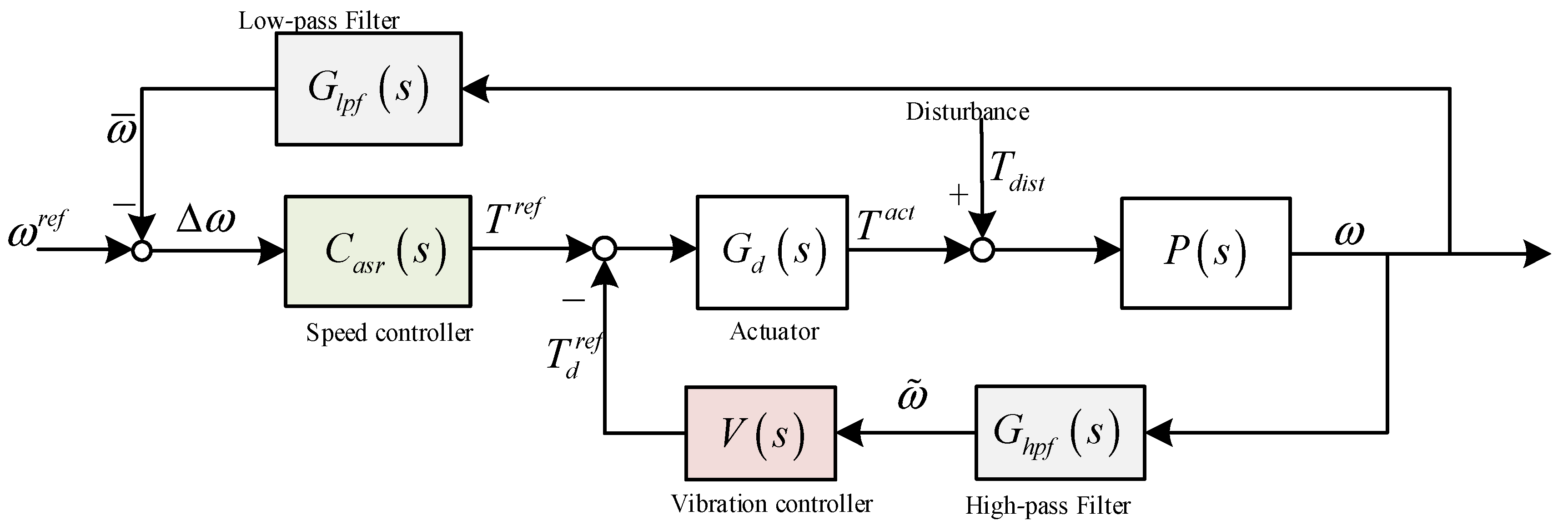
3.1. Dual-Loop Control Framework for Drivetrain Systems
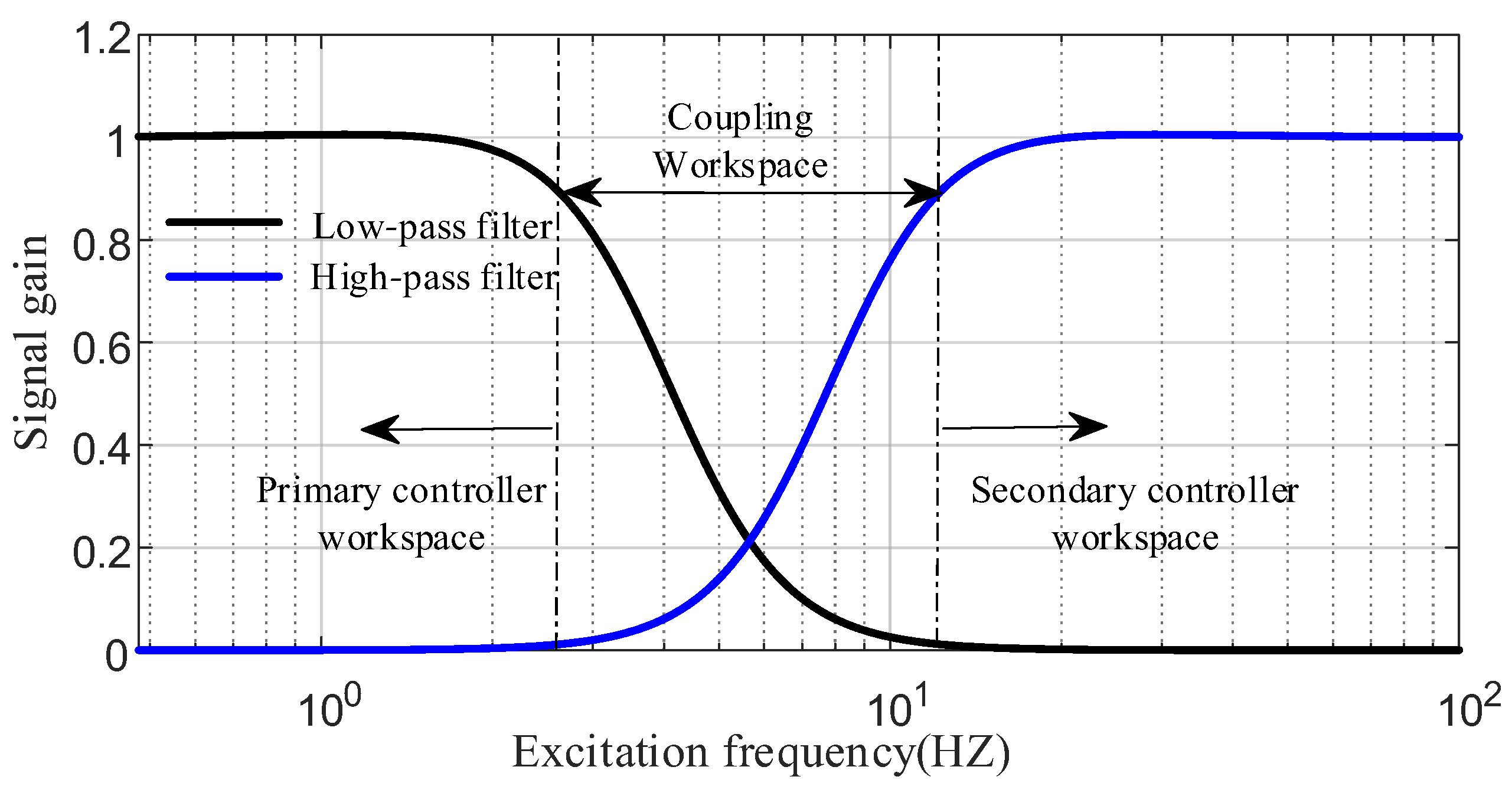
3.2. Frequency-Domain Decoupling Method for Dual-Loop Control of Motor
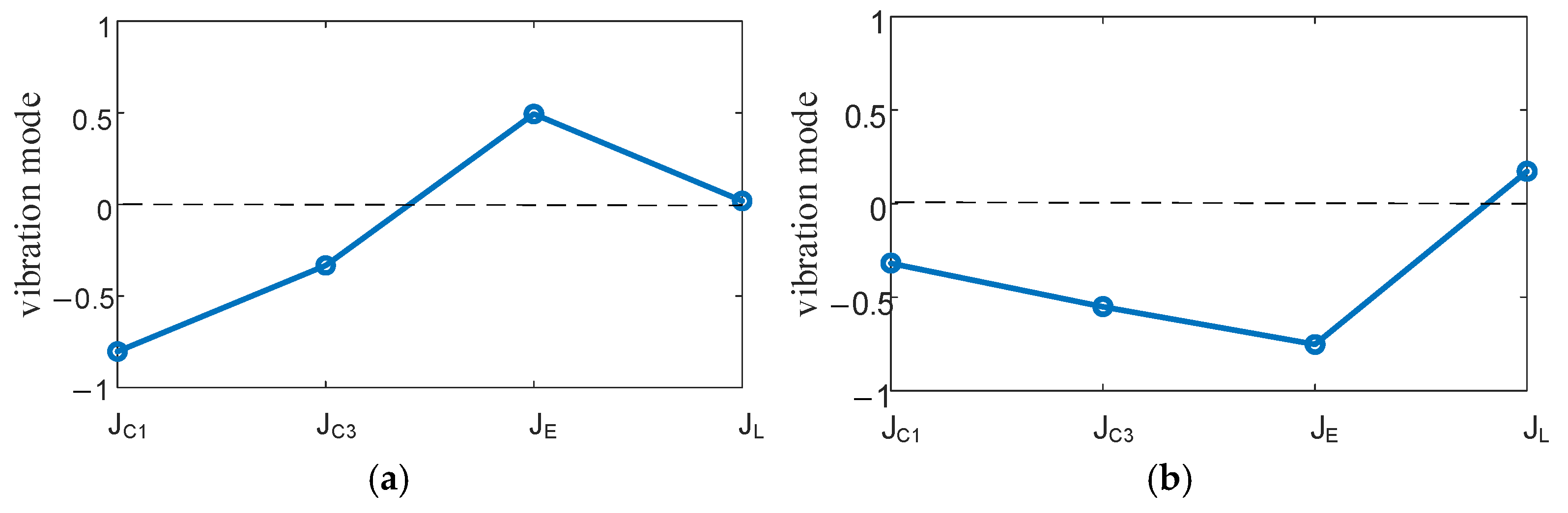
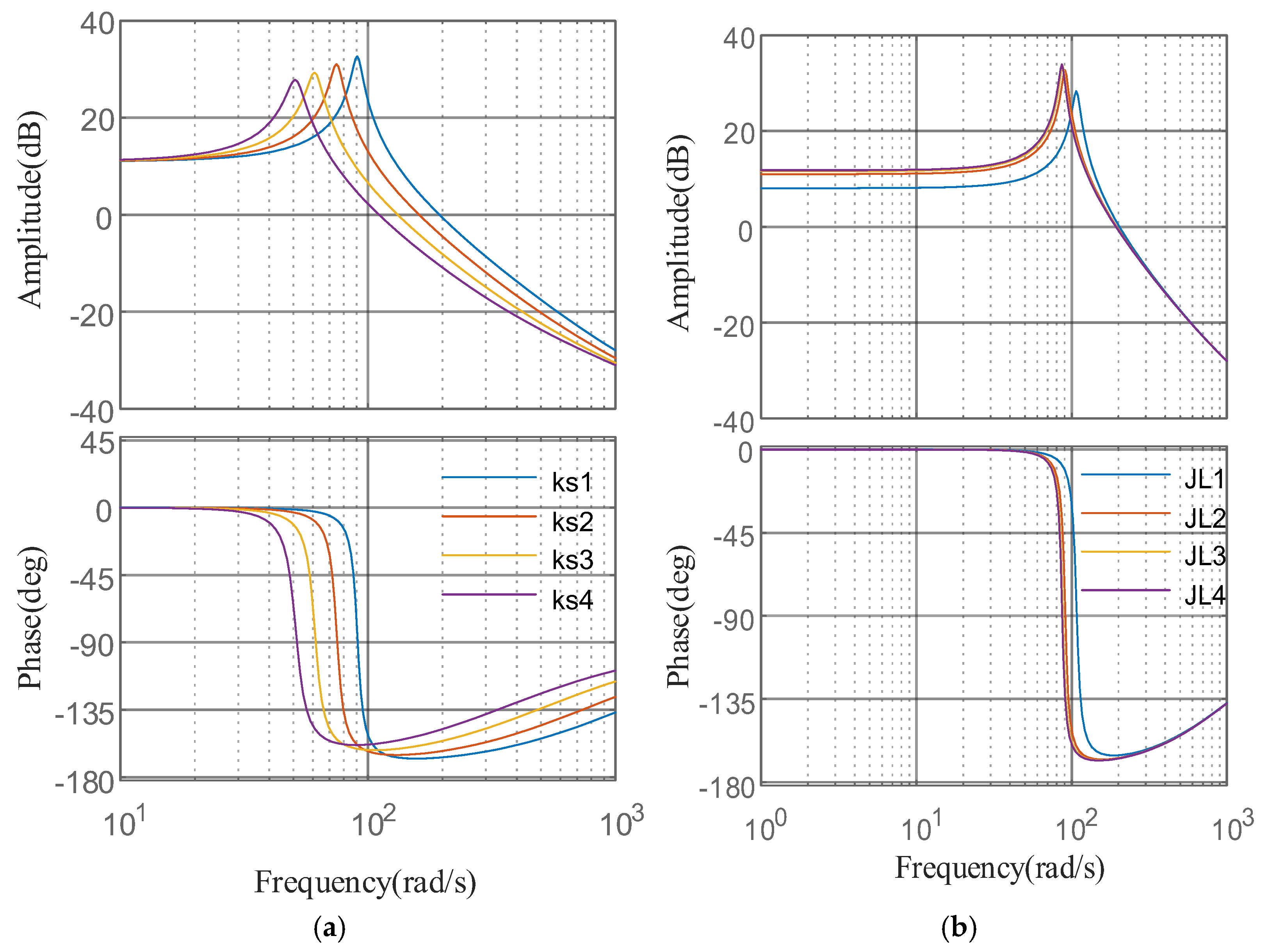
Sensitivity Analysis of Controllers
3.3. Active Torsional Vibration Suppression Method Based on Filtered RLS Algorithm
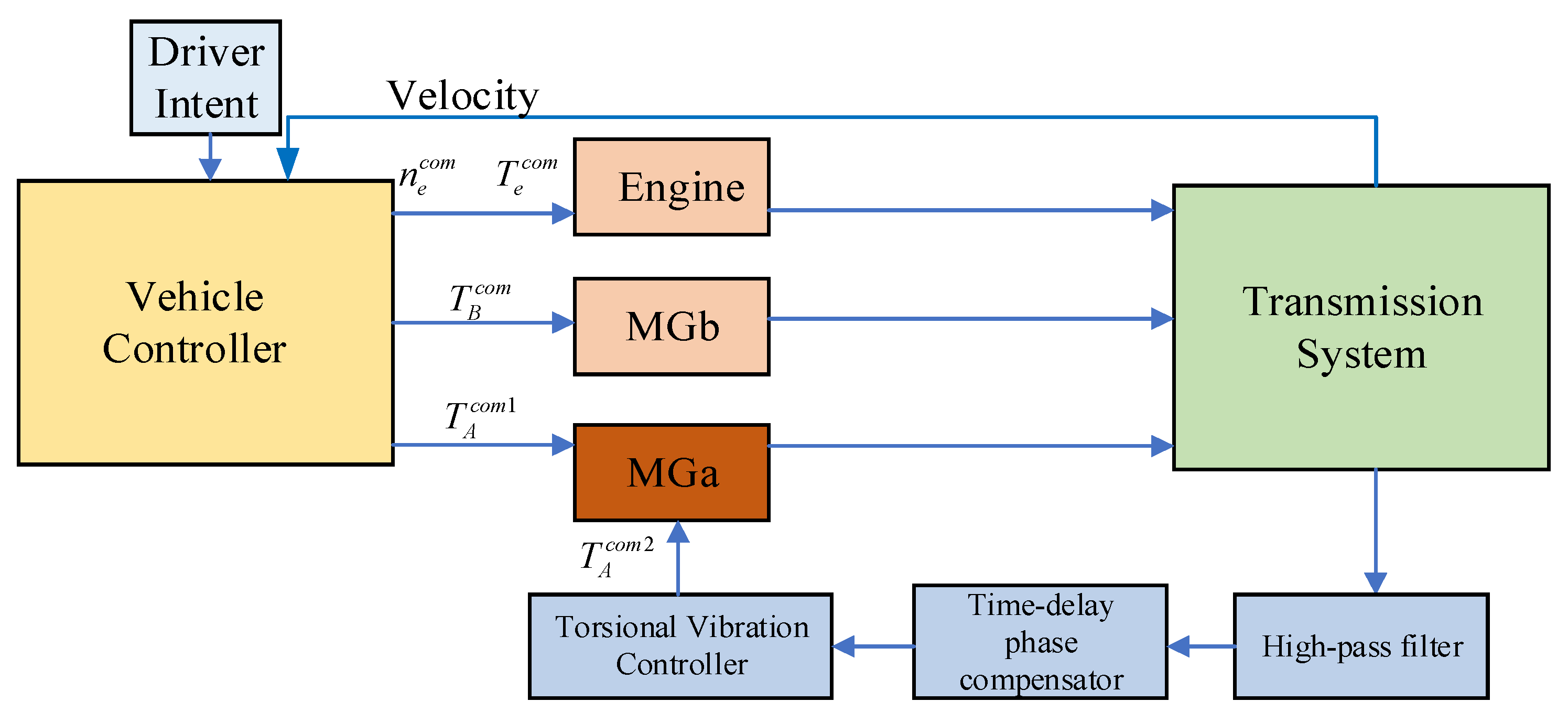
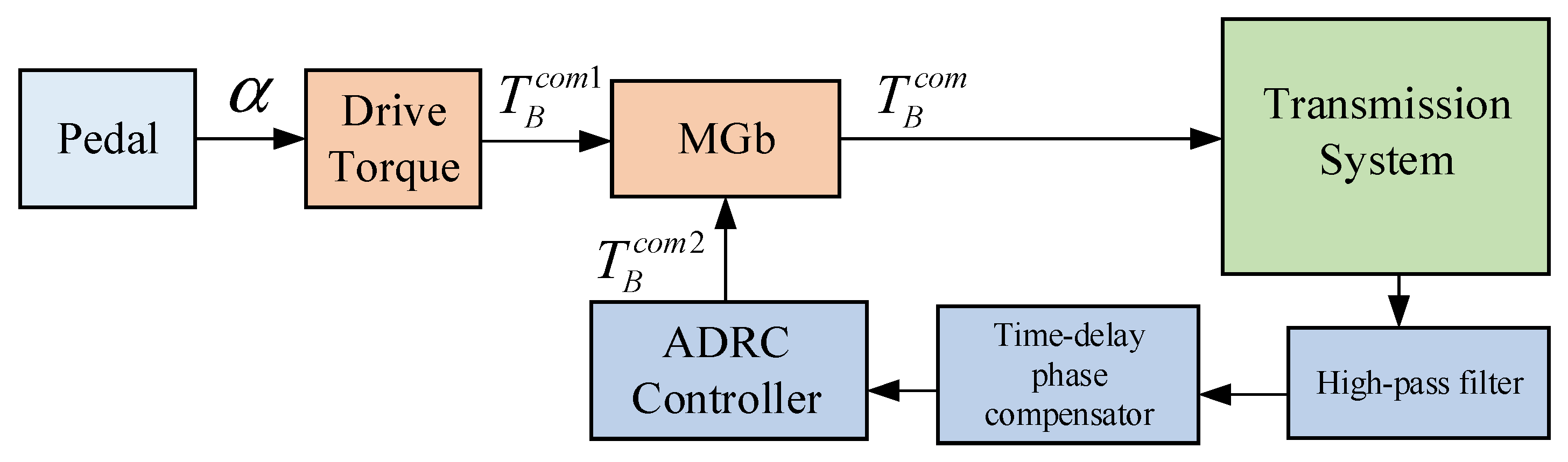
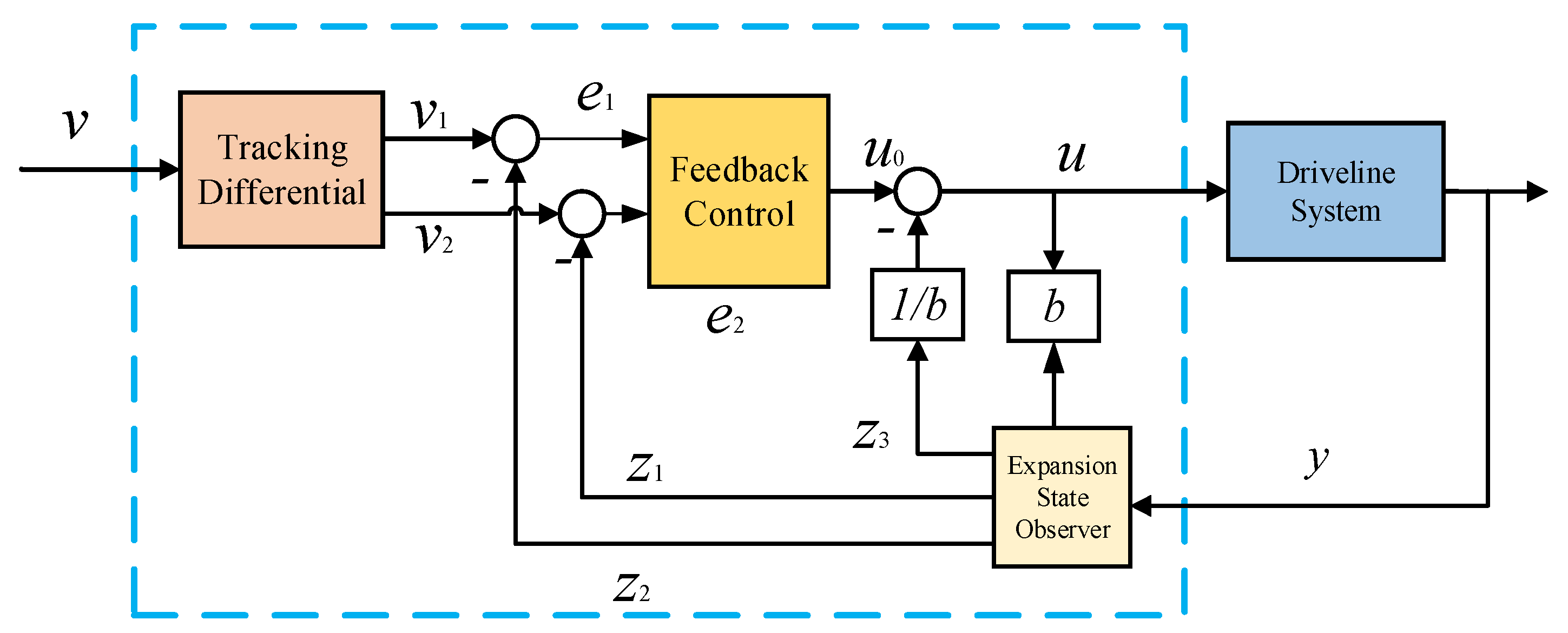
3.4. Active Torsional Vibration Suppression Method Based on ADRC Algorithm
4. Simulation and Result Analysis
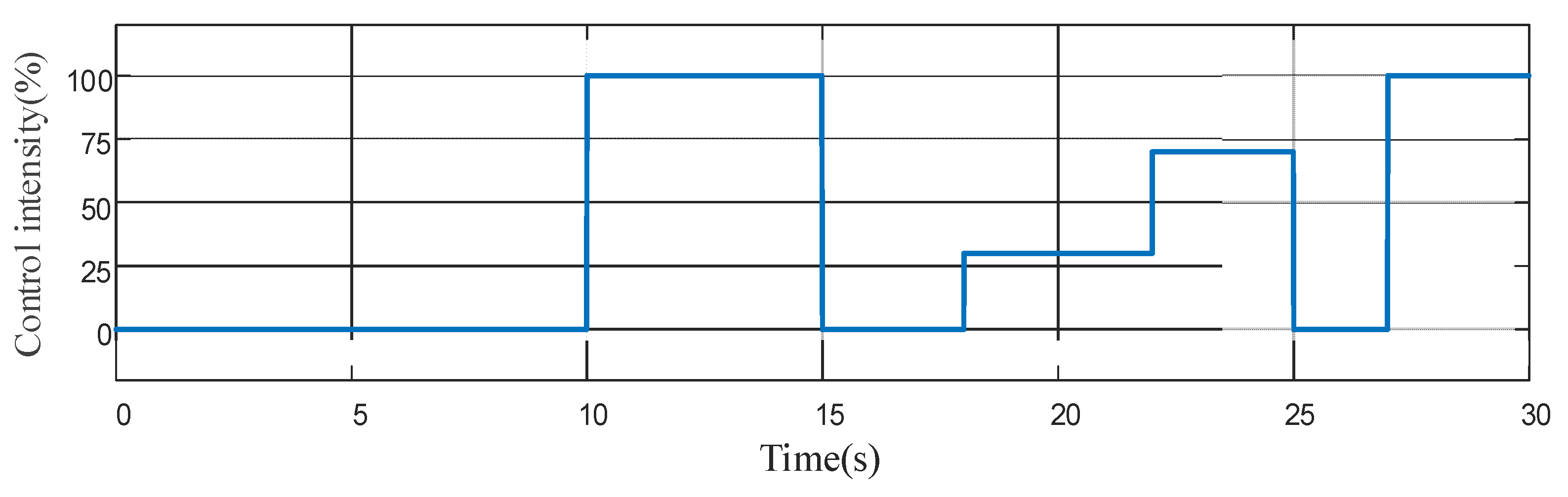
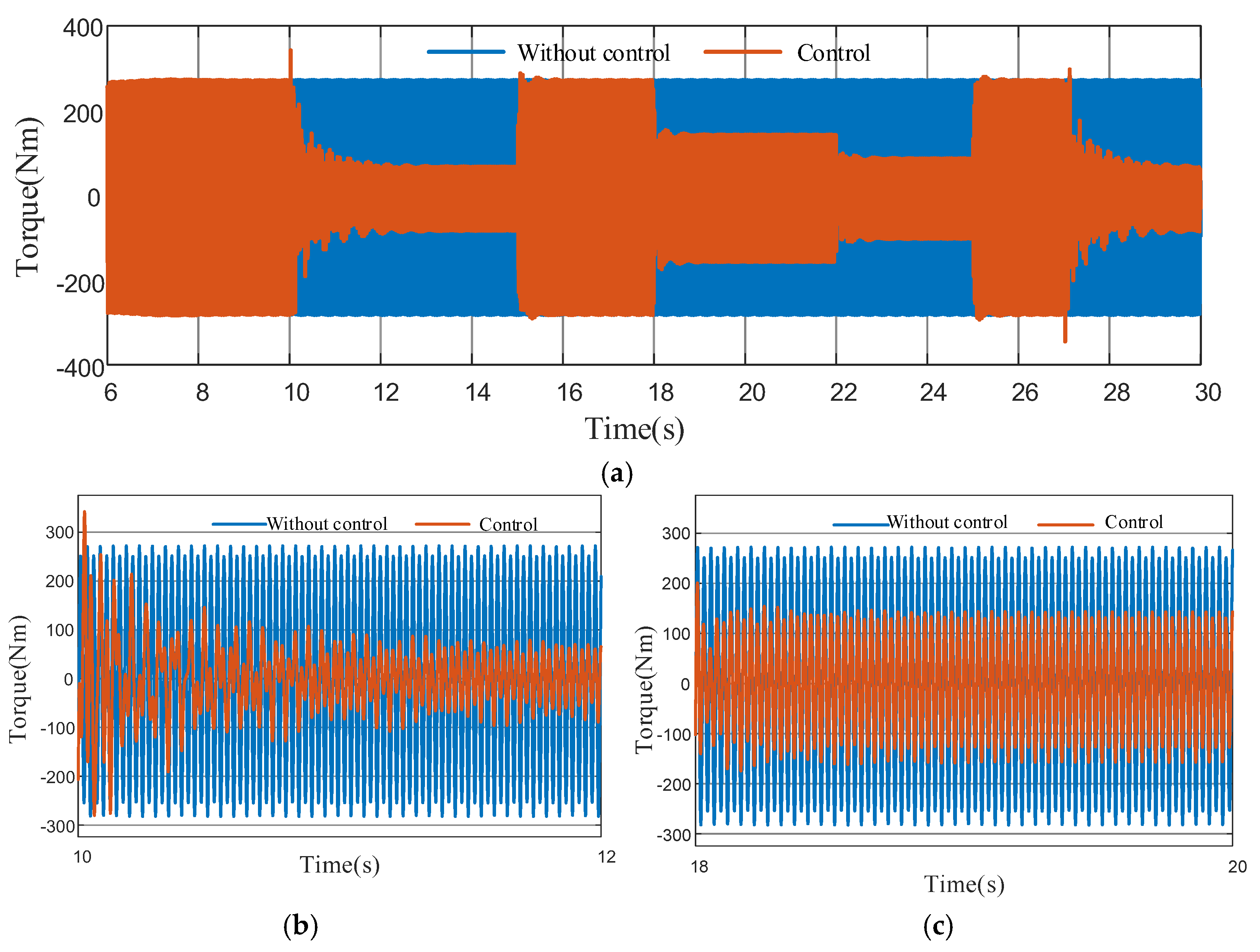
4.1. Analysis of the Effect of Active Torsional Vibration Suppression Under Hybrid Drive Conditions
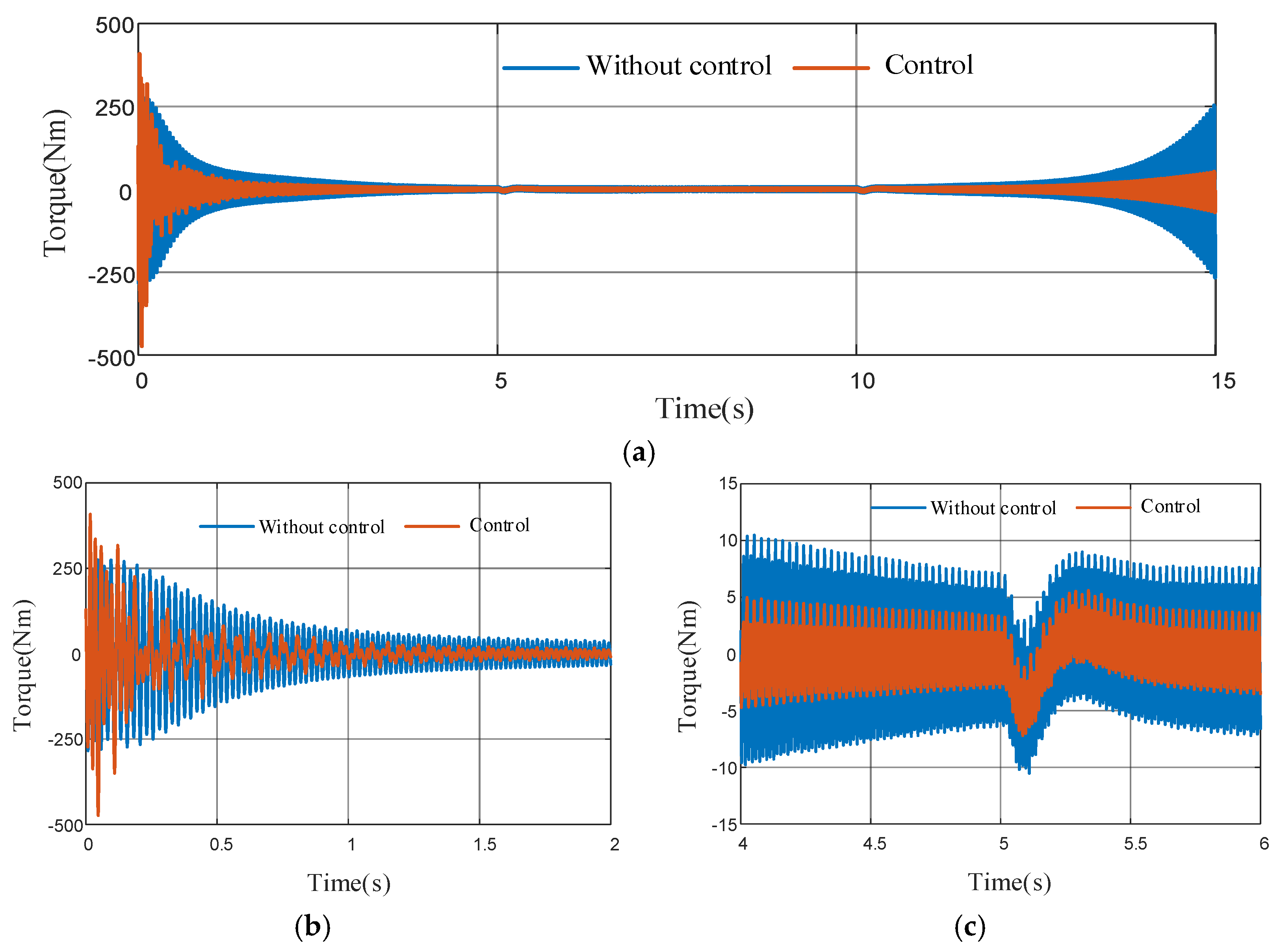
4.1.1. Constant-Speed Working Condition Analysis
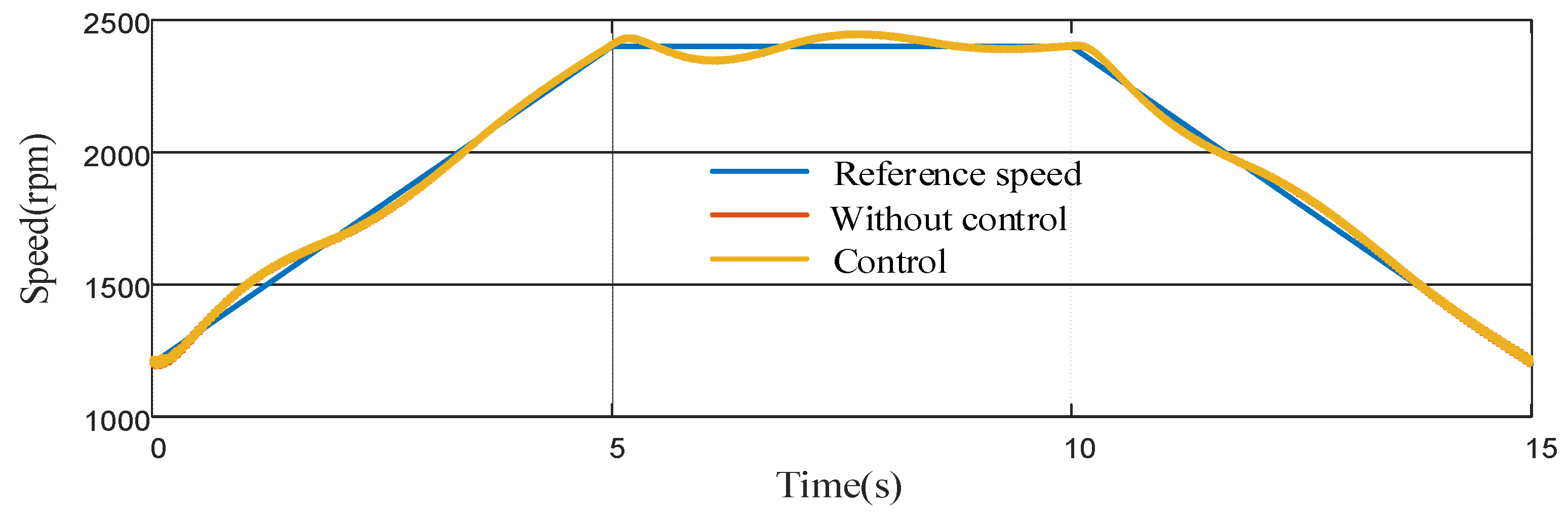
4.1.2. Variable-Speed Working Condition Analysis
4.2. Analysis of the Effect of Active Torsional Vibration Suppression Under Pure Electric Drive Conditions
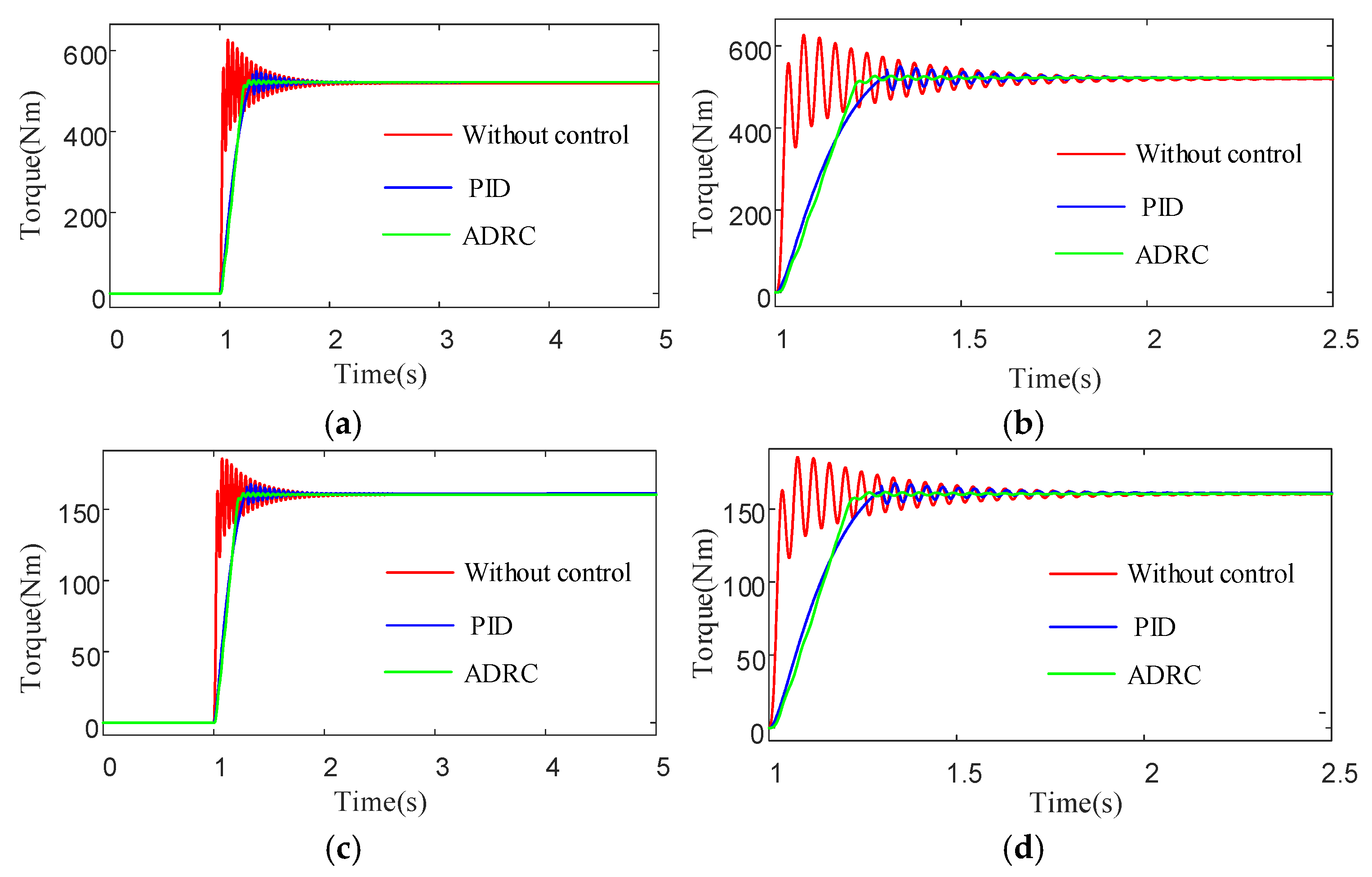
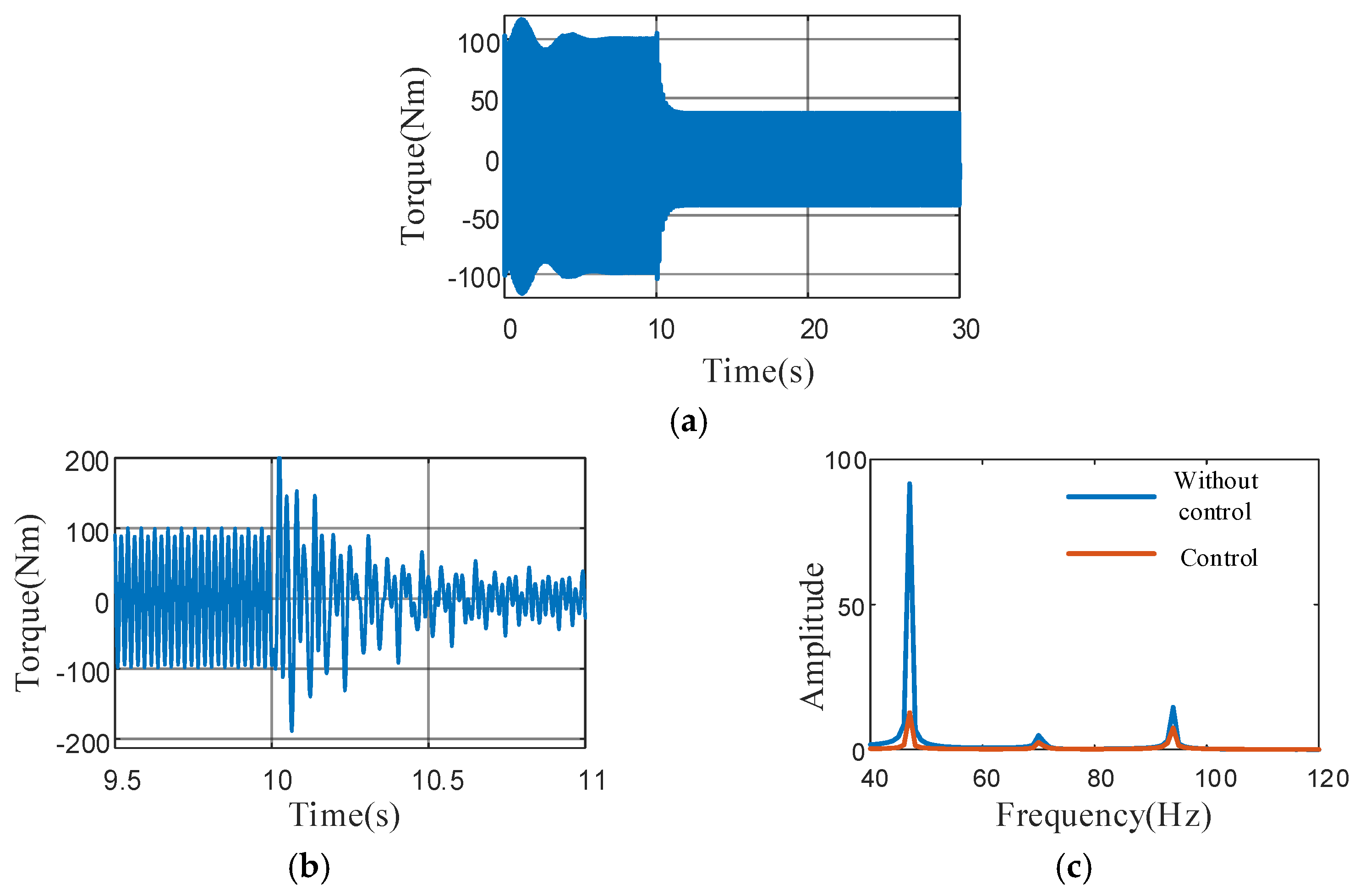
4.2.1. Analysis of Start-Up Acceleration Condition
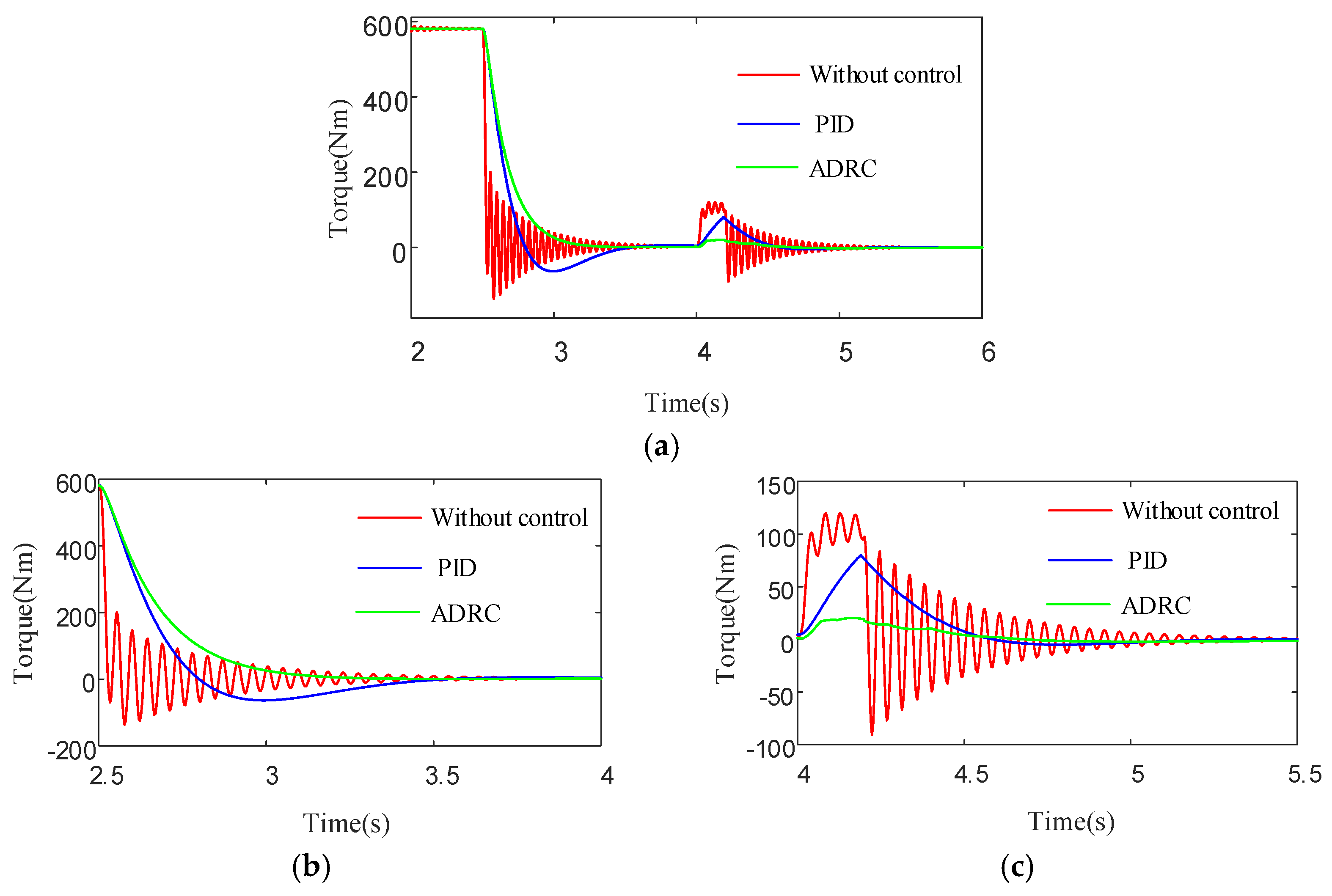
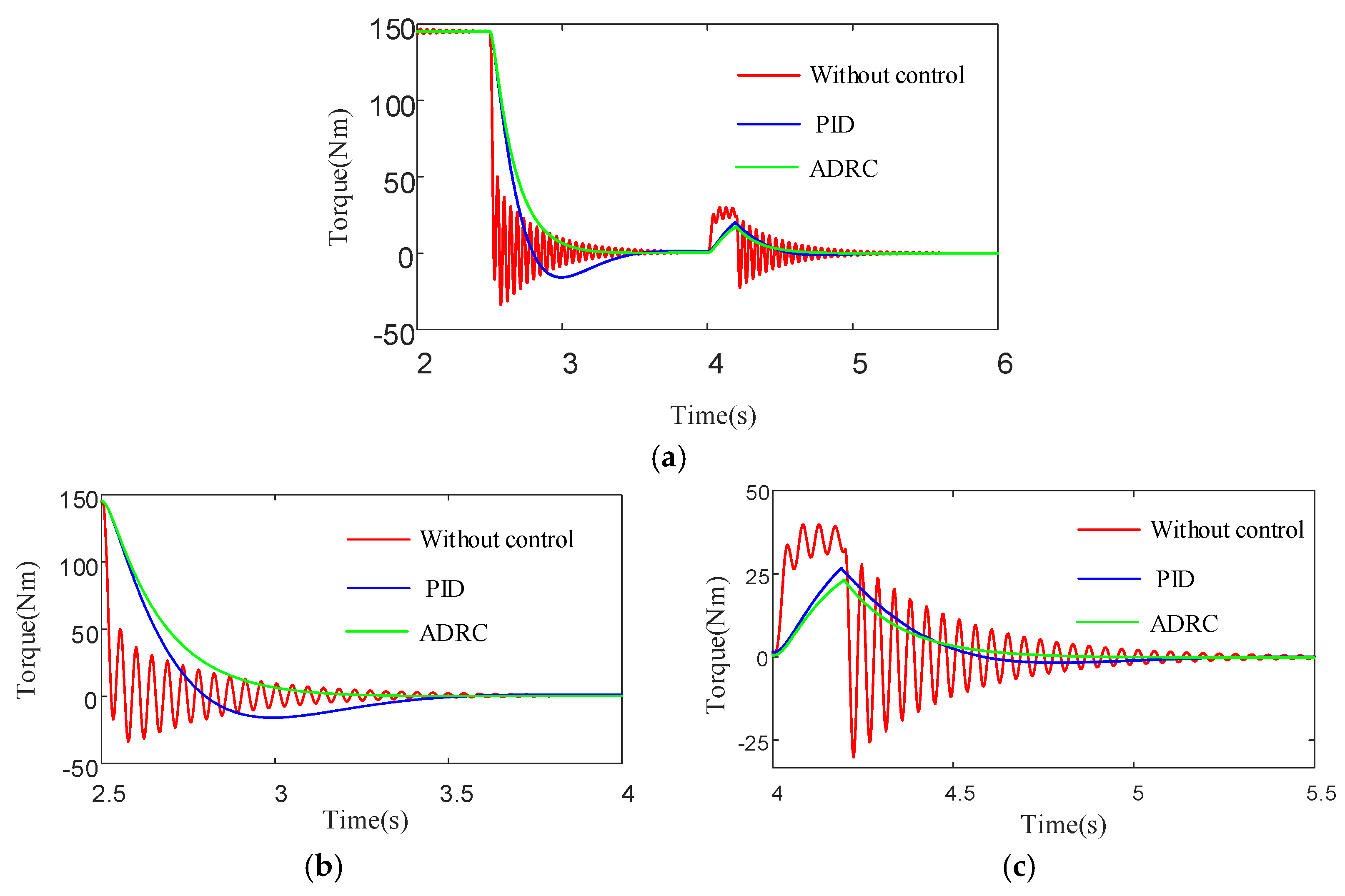
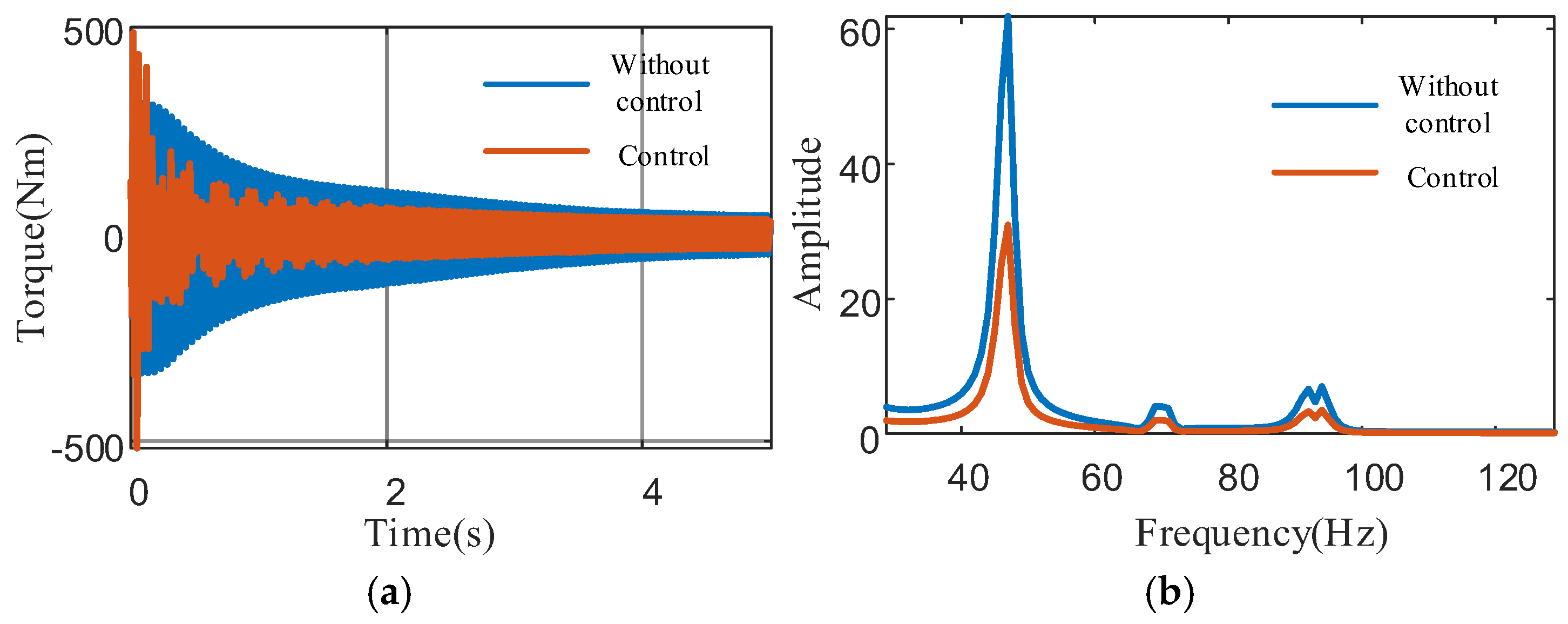
4.2.2. Analysis of Rapid Deceleration Conditions
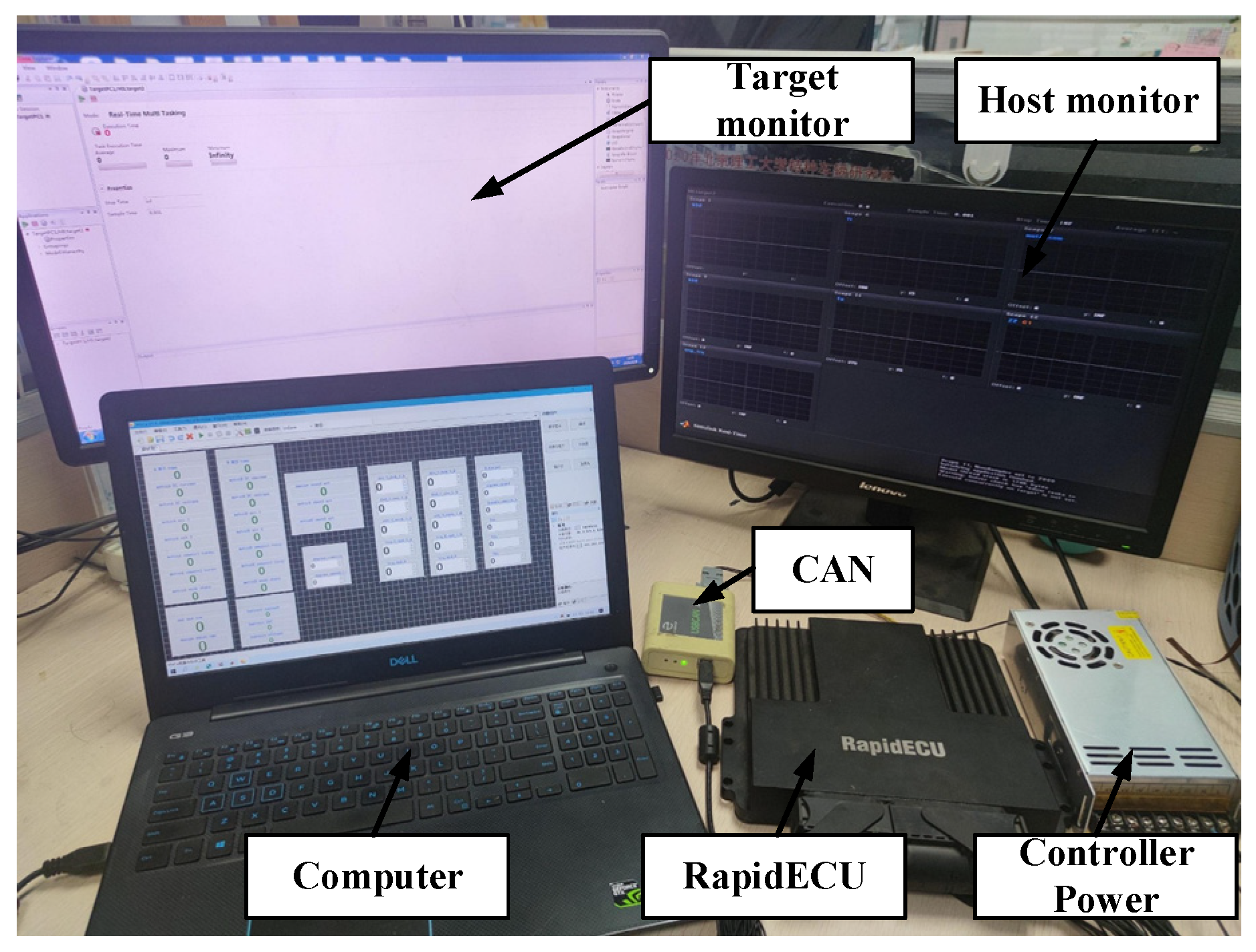
5. HIL Validation of Active Torsional Vibration Suppression Algorithm
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gauto, M.A.; Carazzolle, M.F.; Rodrigues, M.E.P.; de Abreu, R.S.; Pereira, T.C.; Pereira, G.A.G. Hybrid vigor: Why hybrids with sustainable biofuels are better than pure electric vehicles. Energy Sustain. Dev. 2023, 76, 101261. [Google Scholar] [CrossRef]
- Qin, Y.; Tang, X.; Jia, T.; Duan, Z.; Zhang, J.; Li, Y.; Zheng, L. Noise and vibration suppression in hybrid electric vehicles: State of the art and challenges. Renew. Sustain. Energy Rev. 2020, 124, 109782. [Google Scholar] [CrossRef]
- Cauet, S.; Coirault, P.; Njeh, M. Diesel engine torque ripple reduction through LPV control in hybrid electric vehicle powertrain: Experimental results. Control. Eng. Pract. 2013, 21, 1830–1840. [Google Scholar] [CrossRef]
- Tang, X.; Jin, Y.; Zhang, J.; Zou, L.; Yu, H. Torsional vibration and acoustic noise analysis of a compound planetary power-split hybrid electric vehicle. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2014, 228, 94–103. [Google Scholar] [CrossRef]
- Zhu, X.; Liu, Z.; Shen, R.; Wang, Q.; Tang, A.; You, X.; Yu, W.; Wang, W.; Mao, L. Research on an Improved Carbon Emission Flow Model Considering Electric Vehicle Charging Fluctuation and Hybrid Power Transaction. Energies 2023, 16, 6835. [Google Scholar] [CrossRef]
- Aletras, N.; Broekaert, S.; Bitsanis, E.; Fontaras, G.; Samaras, Z.; Ntziachristos, L. Energy management algorithm based on average power demand prediction for plug-in hybrid electric trucks. Energy Convers. Manag. 2024, 299, 117785. [Google Scholar] [CrossRef]
- Song, D.; Wu, J.; Yang, D.; Chen, H.; Zeng, X. An active multiobjective real-time vibration control algorithm for parallel hybrid electric vehicle. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2023, 237, 21–33. [Google Scholar] [CrossRef]
- Hall, C.M. The impact of hybridization, engine combustion method, and energy management system connectivity on heavy-duty vehicle operation. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2021, 235, 2265–2280. [Google Scholar] [CrossRef]
- Wang, F.; Xia, J.; Zhu, X.; Xu, X.; Ni, Y.Q. An Online Predictive Energy Management Strategy for Multi-Mode Plug-in Hybrid Electric Vehicle With Mode Transition Schedule Optimization. IEEE/ASME Trans. Mechatron. 2024, 29, 1972–1984. [Google Scholar] [CrossRef]
- Liu, H.; Li, X.; Han, L.; Wang, W.; Xiang, C. Research on real-time control strategy of multi-power flow of dual-mode power-split hybrid electric vehicle. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2022, 236, 2519–2543. [Google Scholar] [CrossRef]
- Zhang, X.M.; Yang, D.P.; Zeng, X.H.; Wu, Q.T.; Qian, Q.F.; Song, D.F. Data-Driven FMPC Based Dynamic Coordination Control Strategy for Power-Split Hybrid Electric Bus. IEEE Trans. Veh. Technol. 2023, 72, 9999–10012. [Google Scholar] [CrossRef]
- Liu, T.; Zeng, X.; Song, D. MPC-Based Coordinated Control of Gear Shifting Process for a Power-split Hybrid Electric Bus with a Clutchless AMT. Chin. J. Mech. Eng. 2022, 35, 144. [Google Scholar] [CrossRef]
- Han, L.; Zhou, X.; Yang, N. The Coordinated Control Strategy of Engine Starting Process in Power Split Hybrid Electric Vehicle Based on Load Observation. Electronics 2024, 13, 3373. [Google Scholar] [CrossRef]
- Xue, H.; Ballo, F.; Previati, G.; Gobbi, M. Eco-Driving of Electric Vehicles: Objective and Subjective Evaluation of Passenger Comfort by a Dynamic Driving Simulator. IEEE Trans. Veh. Technol. 2025, 74, 402–412. [Google Scholar] [CrossRef]
- Yan, D.; Lu, L.; Li, Z.; Feng, X.; Ouyang, M.; Jiang, F. Durability comparison of four different types of high-power batteries in HEV and their degradation mechanism analysis. Appl. Energy 2016, 179, 1123–1130. [Google Scholar] [CrossRef]
- Gao, P.; Xiang, C.; Liu, H.; Walker, P.; Zhang, N. Design of the frequency tuning scheme for a semi-active vibration absorber. Mech. Mach. Theory. 2019, 140, 641–653. [Google Scholar] [CrossRef]
- Chen, K.; Hu, J.; Peng, Z. Analysis of torsional stability and the dynamical characteristics of electromechanical systems. Adv. Mech. Eng. 2017, 9, 1–12. [Google Scholar] [CrossRef]
- Ning, D.; Sun, S.; Du, H.; Li, W.; Li, W. Control of a multiple-DOF vehicle seat suspension with roll and vertical vibration. J. Sound Vib. 2018, 435, 170–191. [Google Scholar] [CrossRef]
- Magliacano, D.; Viscardi, M.; Ciminello, M.; Dimino, I. Feasibility study for a tonal vibration control system of a mounting bracket for automotive gearboxes. Int. J. Mech. 2016, 10, 403–410. [Google Scholar]
- Elsisi, M.; Soliman, M.; Aboelela, M.A.S.; Mansour, W. ABC based design of PID controller for two area load frequency control with nonlinearities. TELKOMNIKA Indones. J. Electr. Eng. 2015, 16, 58–64. [Google Scholar] [CrossRef]
- Chen, S.; Hu, M. Active torsional vibration suppression of hybrid electric vehicle drive system based on optimal harmonic current instruction calculation method. Mech. Syst. Signal Process. 2023, 205, 110837. [Google Scholar] [CrossRef]
- Bouchard, M. New recursive-least-squares algorithms for nonlinear active control of sound and vibration using neural networks. IEEE Trans. Neural Netw. 2001, 12, 135–147. [Google Scholar] [CrossRef] [PubMed]
- Aslam, M.S.; Shi, P.; Lim, C.C. Robust Active Noise Control Design by Optimal Weighted Least Squares Approach. IEEE Trans. Circuits Syst. I Regul. Pap. 2019, 66, 3955–3967. [Google Scholar] [CrossRef]
- Jimenez-Gonzalez, J.; Gonzalez-Montañez, F.; Jimenez-Mondragon, V.M.; Liceaga-Castro, J.U.; Escarela-Perez, R.; Olivares-Galvan, J.C. Parameter Identification of BLDC Motor Using Electromechanical Tests and Recursive Least-Squares Algorithm: Experimental Validation. Actuators 2021, 10, 143. [Google Scholar] [CrossRef]
- Lamraoui, H.C.; Qidan, Z. Path following control of fully-actuated autonomous underwater vehicle in presence of fast-varying disturbances. Appl. Ocean Res. 2019, 86, 40–46. [Google Scholar] [CrossRef]
- Ahmed, N.; Humaidi, A.; Sabah, A. Clinical trajectory control for lower knee rehabilitation using ADRC method. J. Appl. Res. Technol. 2022, 20, 576–583. [Google Scholar] [CrossRef]
- Wu, Z.; Li, D.; Liu, Y.; Chen, Y. Performance Analysis of Improved ADRCs for a Class of High-Order Processes With Verification on Main Steam Pressure Control. IEEE Trans. Ind. Electron. 2023, 70, 6180–6190. [Google Scholar] [CrossRef]
- Zhou, Z.; Guo, R. A Disturbance-Observer-Based Feedforward-Feedback Control Strategy for Driveline Launch Oscillation of Hybrid Electric Vehicles Considering Nonlinear Backlash. IEEE Trans. Veh. Technol. 2022, 71, 3727–3736. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, J.; Xu, X.; Cai, Y.; Ni, S.; Que, H. Torsional oscillation-considered mode transition coordinated control for a power-split PHEV based on action dependent heuristic dynamic programming. ISA Trans. 2021, 126, 597–616. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, H.; Zhan, Z.; Wu, Y.; Zhang, W.; Taha, M.; Yan, P. Modelling and active damping of engine torque ripple in a power-split hybrid electric vehicle. Control. Eng. Pract. 2020, 104, 104634. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, X.; Chen, Y.; Taha, M.; Xu, H. Active damping of driveline vibration in power-split hybrid vehicles based on model reference control. Control. Eng. Pract. 2019, 91, 104085. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, H.; Zhang, X.; Wu, Y.; Gao, P.; Wang, Z.; Zhang, W. Torque ripple compensation control for hybrid UGVs in mode transition based on current harmonic control of a PMSM. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2021, 235, 920–932. [Google Scholar] [CrossRef]
- Jinyu, Z.; Song, H.; Longyu, J.; Fuyuan, Y. Active Vibration Control Strategy for Online Application in a Range Extender. IEEE Access 2023, 11, 26686–26702. [Google Scholar] [CrossRef]
- Xie, Y.; Lim, K.; Liu, H.; Zhan, Z.; Ren, X.; Li, X.; Zhou, R.; Gao, P.; Xiang, C. Modelling of electromechanical coupling dynamics for high-speed EHT system used in HEV and characteristics analysis. Appl. Math. Model. 2024, 136, 115614. [Google Scholar] [CrossRef]
- Hu, J.; Wang, Z.; Liu, Y.; Liu, X.; Yang, X. Vibration characteristics of industrial robot joint servo transmission system based on electromechanical coupling. Meas. Sci. Technol. 2023, 34, 125147. [Google Scholar] [CrossRef]
- Ge, S.; Qiu, L.; Zhang, Z.; Wang, H.; Hu, M. Electromechanical coupling dynamic characteristics of electric drive system for electric vehicle. Nonlinear Dyn. 2024, 112, 6101–6136. [Google Scholar] [CrossRef]
- Urbaś, A.; Stadnicki, J. Applications of dynamics metamodels of an eccentric crank-slider mechanism in the initial phase of their design. Mech. Mach. Theory 2025, 205, 105886. [Google Scholar] [CrossRef]
- Yang, D.; Liu, H.; Gao, P.; Zhang, W.; Yan, Q.; Chen, K.; Yang, H. Research on Drive Torque Command Optimization and System Disturbance Rejection Mechanism for Torsional Vibration Control of Electro-Mechanical Transmission System. IEEE Trans. Transp. Electrif. 2025; early access. [Google Scholar]
- Zhang, W.; Liu, H.; Liu, J.G.; Yan, P.; Fu, B. Adaptive phase compensation method for primary harmonic disturbance in electromechanical composite transmission. J. Mech. Eng. 2024, 60, 354–365. [Google Scholar]


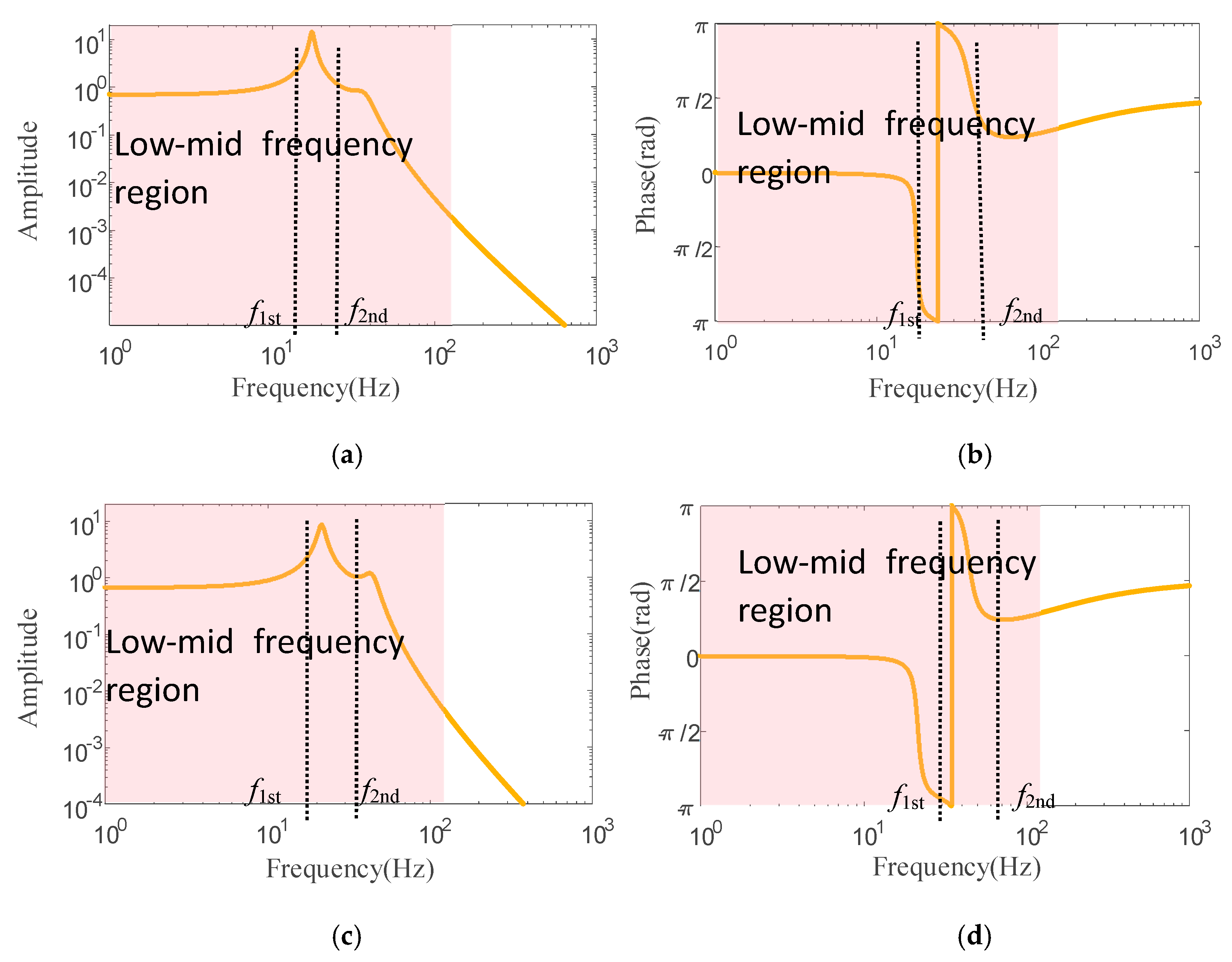



| Order | First-Order Frequency f1 (Hz) | Second-Order Frequency f2 (Hz) |
|---|---|---|
| EVT1 | 17.55 | 37.43 |
| EVT2 | 21.40 | 44.19 |
| Parameters Setting | |||
|---|---|---|---|
| ks1 | ks2 | ks3 | ks4 |
| 4.4 × 104 Nm/rad | 3 × 104 Nm/rad | 2 × 104 Nm/rad | 1.4 × 104 Nm/rad |
| JL1 | JL2 | JL3 | JL4 |
| 10 kg·m2 | 40 kg·m2 | 80 kg·m2 | 120 kg·m2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, W.; Liang, X.; Han, Z.; Bu, L.; Liu, J.; Fu, B.; Jiang, M. Active Torsional Vibration Suppression Strategy for Power-Split-HEV Driveline System Based on Dual-Loop Control. Machines 2025, 13, 418. https://doi.org/10.3390/machines13050418
Zhang W, Liang X, Han Z, Bu L, Liu J, Fu B, Jiang M. Active Torsional Vibration Suppression Strategy for Power-Split-HEV Driveline System Based on Dual-Loop Control. Machines. 2025; 13(5):418. https://doi.org/10.3390/machines13050418
Chicago/Turabian StyleZhang, Wei, Xiaocong Liang, Zhengda Han, Lei Bu, Jingang Liu, Bing Fu, and Mozhang Jiang. 2025. "Active Torsional Vibration Suppression Strategy for Power-Split-HEV Driveline System Based on Dual-Loop Control" Machines 13, no. 5: 418. https://doi.org/10.3390/machines13050418
APA StyleZhang, W., Liang, X., Han, Z., Bu, L., Liu, J., Fu, B., & Jiang, M. (2025). Active Torsional Vibration Suppression Strategy for Power-Split-HEV Driveline System Based on Dual-Loop Control. Machines, 13(5), 418. https://doi.org/10.3390/machines13050418





