Research on the Dynamic Response of a Cracked-Spur Gear System with Parameter Uncertainty
Abstract
1. Introduction
2. Modeling and Verification of Time-Varying Mesh Stiffness
2.1. Time-Varying Mesh Stiffness of Healthy Spur Gear Pair
2.2. Time-Varying Mesh Stiffness of Cracked Spur Gear Pair
- Case 1
- Case 2
- Case 3
2.3. Verification of Time-Varying Mesh Stiffness
3. Dynamic Characteristics of Deterministic Gear System
4. Description of Interval Uncertainty
5. Dynamic Characteristics of Uncertain Gear System
6. Experiments and Verification
7. Conclusions
- For the deterministic system, as the crack depth and angle increase, the time-varying mesh stiffness decreases, and the presence of cracks leads to periodic pulse signals in the dynamic transmission error.
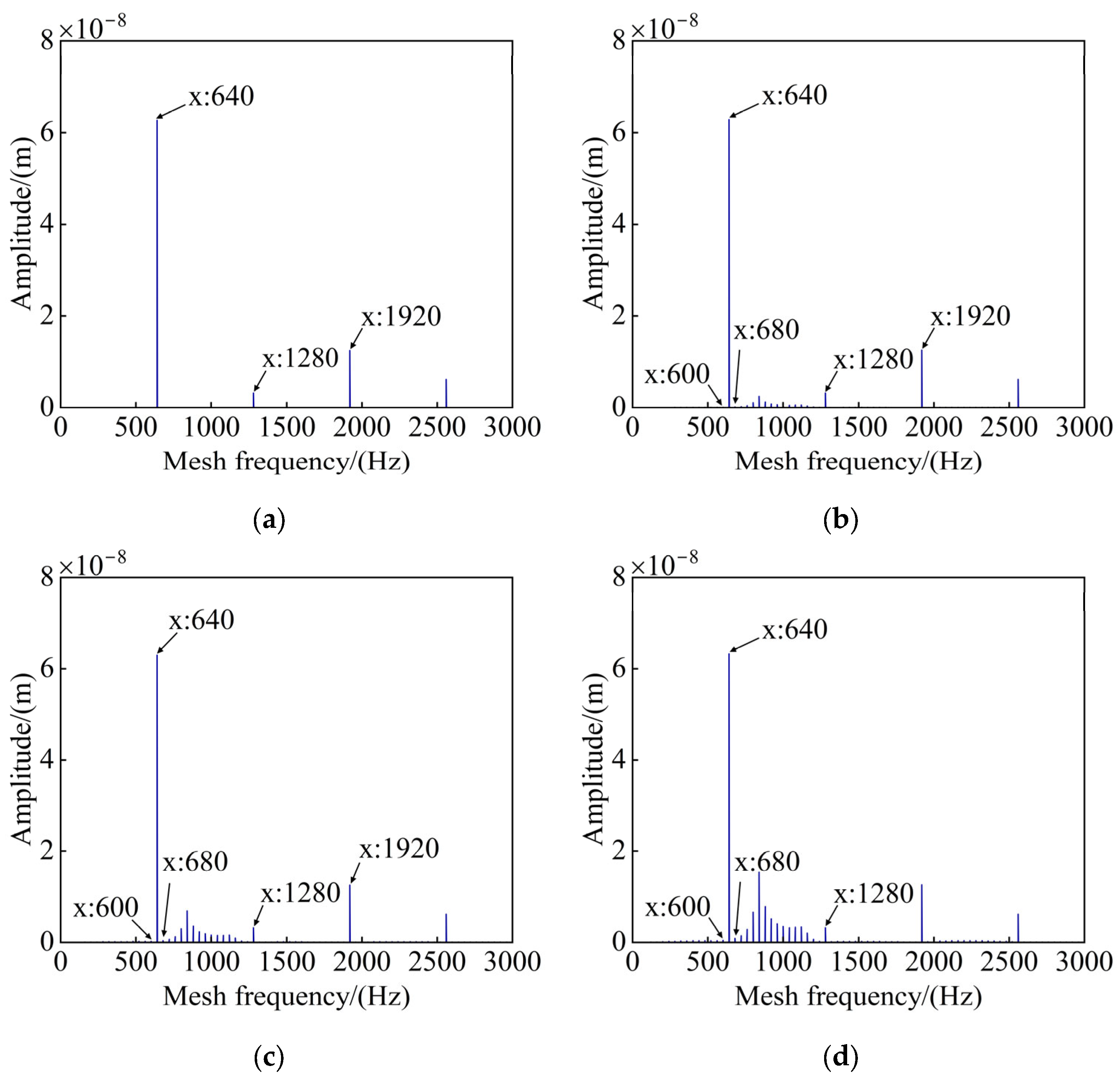
- In the frequency-domain response of a deterministic system, it is experimentally verified that the meshing frequency and its harmonic components are usually included.
- Under the influence of parameter uncertainties, the amplitude–frequency response of the gear system exhibits an envelope shape, and in this situation, multi-source uncertainties result in a more pronounced deviation in the system response compared to single-source uncertainty.
- In the uncertain gear system, the interval vibration response of the dynamic transmission error is far more sensitive to the uncertainty of Young’s modulus than to the uncertainties of support stiffness and gear mass.
- Under parameter uncertainty, the influence of a tooth crack on the vibration behaviors of the spur gear system is further amplified, which significantly weakens the stability and reliability of the system.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, F.H.; Zhang, L.; Jiang, H.J.; Zhang, J.L. Nonlinear dynamic analysis of two external excitations for the gear system using an original computational algorithm. Mech. Syst. Signal Process. 2020, 144, 106823. [Google Scholar] [CrossRef]
- Kashani, S.A.A. Design and optimization of coaxial reluctance magnetic gear with different rotor topologies. IEEE. Trans. Ind. Electron. 2021, 69, 101–109. [Google Scholar] [CrossRef]
- Mohammed, O.D.; Rantatalo, M. Dynamic response and time-frequency analysis for gear tooth crack detection. Mech. Syst. Signal Process. 2016, 66, 612–624. [Google Scholar] [CrossRef]
- Chen, Z.G.; Shao, Y.M. Mesh stiffness calculation of a spur gear pair with tooth profile modification and tooth root crack. Mech. Mach. Theory 2013, 62, 63–74. [Google Scholar] [CrossRef]
- Jiang, H.J.; Liu, F.H. Dynamic features of three-dimensional helical gears under sliding friction with tooth breakage. Eng. Fail. Anal. 2016, 70, 305–322. [Google Scholar] [CrossRef]
- Sun, Y.N.; Ma, H.; Huang, Y.F.; Chen, K.K.; Che, L.Y.; Wen, B.C. A revised time-varying mesh stiffness model of spur gear pairs with tooth modifications. Mech. Mach. Theory 2018, 129, 261–278. [Google Scholar] [CrossRef]
- Yang, D.C.H.; Lin, J.Y. Hertzian damping, tooth friction and bending elasticity in gear impact dynamics. J. Mech. Des. 1987, 109, 189–196. [Google Scholar] [CrossRef]
- Tian, X.H. Dynamic Simulation for System Response of Gearbox Including Localized Gear Faults. Master’s Thesis, University of Alberta Edmonton, Edmonton, AB, Canada, 2004. [Google Scholar]
- Wu, S.Y.; Zuo, M.J.; Parey, A. Simulation of spur gear dynamics and estimation of fault growth. J. Sound Vib. 2008, 317, 608–624. [Google Scholar] [CrossRef]
- Mohammed, O.D.; Rantatalo, M.; Aidanpää, J.-O. Improving mesh stiffness calculation of cracked gears for the purpose of vibration-based fault analysis. Eng. Fail. Anal. 2013, 34, 235–251. [Google Scholar] [CrossRef]
- Ma, H.; Song, R.Z.; Pang, X.; Wen, B.C. Time-varying mesh stiffness calculation of cracked spur gears. Eng. Fail. Anal. 2014, 44, 179–194. [Google Scholar] [CrossRef]
- Liang, X.H.; Zuo, M.J.; Pandey, M. Analytically evaluating the influence of crack on the mesh stiffness of a planetary gear set. Mech. Mach. Theory 2014, 76, 20–38. [Google Scholar] [CrossRef]
- Saxena, A.; Parey, A.; Chouksey, M. Effect of shaft misalignment and friction force on time varying mesh stiffness of spur gear pair. Eng. Fail. Anal. 2015, 45, 79–91. [Google Scholar] [CrossRef]
- Yu, W.N.; Shao, Y.M.; Mechefske, C.K. The effects of spur gear tooth spatial crack propagation on gear mesh stiffness. Eng. Fail. Anal. 2015, 54, 103–119. [Google Scholar] [CrossRef]
- Luo, Y.; Baddour, N.; Liang, M. Effects of gear center distance variation on time varying mesh stiffness of a spur gear pair. Eng. Fail. Anal. 2017, 75, 37–53. [Google Scholar] [CrossRef]
- HuangFu, Y.F.; Chen, K.K.; Ma, H.; Che, L.Y.; Li, Z.W.; Wen, B.C. Deformation and meshing stiffness analysis of cracked helical gear pairs. Eng. Fail. Anal. 2019, 95, 30–46. [Google Scholar] [CrossRef]
- Jiang, H.J.; Liu, F.H. Analytical models of mesh stiffness for cracked spur gears considering gear body deflection and dynamic simulation. Meccanica 2019, 54, 1889–1909. [Google Scholar] [CrossRef]
- Meng, Z.; Shi, G.X.; Wang, F.L. Vibration response and fault characteristics analysis of gear based on time-varying mesh stiffness. Mech. Mach. Theory 2020, 148, 103786. [Google Scholar] [CrossRef]
- Yang, Y.; Tang, J.Y.; Hu, N.Q.; Shen, G.J.; Li, Y.H.; Zhang, L. Research on the time-varying mesh stiffness method and dynamic analysis of cracked spur gear system considering the crack position. J. Sound Vib. 2023, 548, 117505. [Google Scholar] [CrossRef]
- Zhou, W.G.; Zhu, R.P.; Li, Z.W.; Wang, J.J. An improved dynamic model of spur gears considering delayed meshing out of the contact point due to root crack. Mech. Syst. Signal Process. 2024, 212, 111325. [Google Scholar] [CrossRef]
- Soize, C. Uncertainty Quantification: An Accelerated Course with Advanced Applications in Computational Engineering; Springer International Publishing: Berlin, Germany, 2017. [Google Scholar] [CrossRef]
- Fu, C.; Sinou, J.J.; Zhu, W.D.; Lu, K.; Yang, Y.F. A state-of-the-art review on uncertainty analysis of rotor systems. Mech. Syst. Signal Process. 2023, 183, 109619. [Google Scholar] [CrossRef]
- Tobe, T.; Sato, K. Statistical analysis of dynamic loads on spur gear teeth. Bull. JSME 1977, 20, 882–889. [Google Scholar] [CrossRef]
- Tobe, T.; Sato, K.; Takatsu, N. Statistical analysis of dynamic loads on spur gear teeth: Experimental study. Bull. JSME 1977, 20, 1315–1320. [Google Scholar] [CrossRef]
- Kumar, A.S.; Osman, M.O.M.; Sankar, T.S. On statistical analysis of gear dynamic loads. J. Vib. Acoust. 1986, 108, 362–368. [Google Scholar] [CrossRef]
- Gelman, L.; Giurgiutiu, V.; Bayoumi, A. Statistical analysis of the dynamic mean excitation for a spur gear. J. Vib. Acoust. 2005, 127, 204–207. [Google Scholar] [CrossRef]
- Deng, C.S.; Yang, B.; Liu, Z.M. Dynamic analysis of gear system based on the random gear errors. J. Mech. Transm. 2011, 35, 31–34. [Google Scholar] [CrossRef]
- Chen, H.T.; Qin, D.T.; Wu, X.L.; Zhou, Z.G.; Yang, J. Dynamic characteristics of planetary gear transmission system of wind turbine with random manufacturing error. Chin. J. Mech. Eng. 2012, 48, 77–83. [Google Scholar] [CrossRef]
- Yang, J.M. Vibration analysis on multi-mesh gear-trains under combined deterministic and random excitations. Mech. Mach. Theory 2013, 59, 20–33. [Google Scholar] [CrossRef]
- Wen, Y.B.; Yang, J.M.; Wang, S.Y. Random dynamics of a nonlinear spur gear pair in probabilistic domain. J. Sound Vib. 2014, 333, 5030–5041. [Google Scholar] [CrossRef]
- Wei, S.; Zhao, J.S.; Han, Q.K.; Chu, F.L. Dynamic response analysis on torsional vibrations of wind turbine geared transmission system with uncertainty. Renew. Energy 2015, 78, 60–67. [Google Scholar] [CrossRef]
- Beyaoui, M.; Tounsi, M.; Abboudi, K.; Feki, N.; Walha, L.; Haddar, M. Dynamic behaviour of a wind turbine gear system with uncertainties. C. R. Mec. 2016, 344, 375–387. [Google Scholar] [CrossRef]
- Guerine, A.; Hami, A.E.; Walha, L.; Fakhfakh, T.; Haddar, M. A polynomial chaos method for the analysis of the dynamic behavior of uncertain gear friction system. Eur. J. Mech. A/Solid 2016, 59, 76–84. [Google Scholar] [CrossRef]
- Mabrouk, I.B.; Hami, A.E.; Walha, L.; Zghal, B.; Haddar, M. Dynamic response analysis of Vertical Axis Wind Turbine geared transmission system with uncertainty. Eng. Struct. 2017, 139, 170–179. [Google Scholar] [CrossRef]
- Fang, Y.N.; Liang, X.H.; Zuo, M.J. Effects of friction and stochastic load on transient characteristics of a spur gear pair. Nonlinear Dyn. 2018, 93, 599–609. [Google Scholar] [CrossRef]
- Ma, Y.H.; Wang, Y.F.; Wang, C.; Hong, J. Interval analysis of rotor dynamic response based on Chebyshev polynomials. Chin. J. Aeronaut. 2020, 33, 2342–2356. [Google Scholar] [CrossRef]
- Wei, S.; Chu, F.L.; Ding, H.; Chen, L.Q. Dynamic analysis of uncertain spur gear systems. Mech. Syst. Signal Process. 2021, 150, 107280. [Google Scholar] [CrossRef]
- Chen, Z.; Jiang, Y.B.; Li, S.; Tong, Z.M.; Tong, S.G.; Tang, N. Uncertainty propagation of correlated lubricant properties in gear tribodynamic system. Tribol. Int. 2023, 179, 107812. [Google Scholar] [CrossRef]
- Hu, Y.H.; Du, Q.G.; Xie, S.H. Nonlinear dynamic modeling and analysis of spur gears considering uncertain interval shaft misalignment with multiple degrees of freedom. Mech. Syst. Signal Process. 2023, 193, 110261. [Google Scholar] [CrossRef]
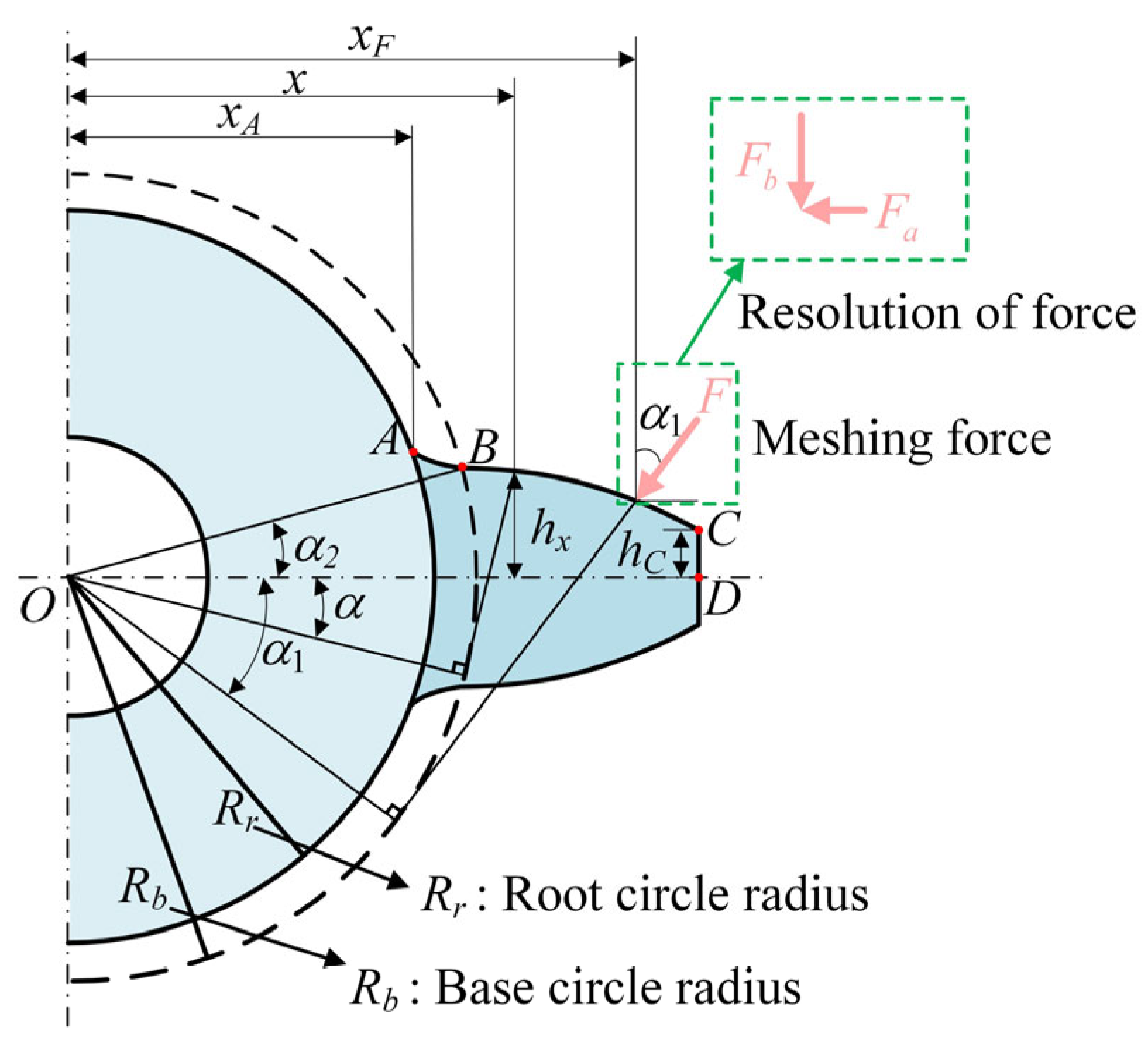
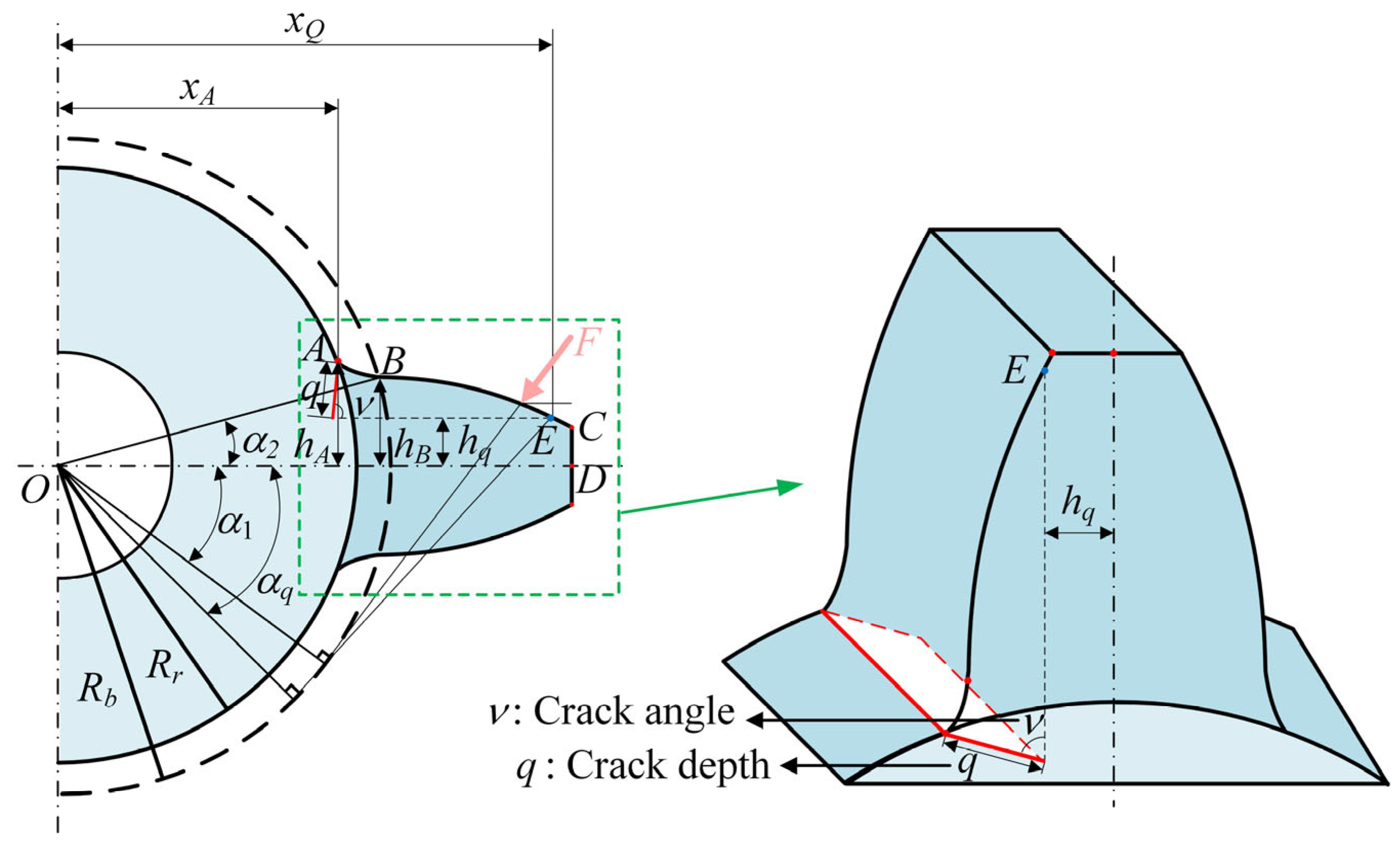













| Parameters | Driving Gear | Driven Gear |
|---|---|---|
| Young’s modulus E (GPa) | 200 | 200 |
| Poisson’s ratio | 0.3 | 0.3 |
| Density ρ (kg/m3) | 7850 | 7850 |
| Tooth number | 16 | 24 |
| Module (mm) | 3 | 3 |
| Pressure angle (deg) | 20 | 20 |
| Teeth width (mm) | 15 | 15 |
| Support stiffness in x direction (N/m) | ||
| Support stiffness in y direction (N/m) | ||
| Mass (kg) | 0.75 | 1.25 |
| Condition | FEM (108 N/m) | Proposed Methed (108 N/m) | Difference (%) |
|---|---|---|---|
| Health | 2.832 | 2.695 | 4.8 |
| q = 2 mm, = 45° | 2.761 | 2.644 | 4.2 |
| q = 3 mm, = 45° | 2.662 | 2.548 | 4.2 |
| q = 4 mm, = 45° | 2.554 | 2.407 | 5.7 |
| q = 3 mm, = 30° | 2.745 | 2.632 | 4.1 |
| q = 3 mm, = 60° | 2.576 | 2.426 | 5.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, P.; Yang, Y.; Zeng, J. Research on the Dynamic Response of a Cracked-Spur Gear System with Parameter Uncertainty. Machines 2025, 13, 395. https://doi.org/10.3390/machines13050395
Fang P, Yang Y, Zeng J. Research on the Dynamic Response of a Cracked-Spur Gear System with Parameter Uncertainty. Machines. 2025; 13(5):395. https://doi.org/10.3390/machines13050395
Chicago/Turabian StyleFang, Ping, Yang Yang, and Jin Zeng. 2025. "Research on the Dynamic Response of a Cracked-Spur Gear System with Parameter Uncertainty" Machines 13, no. 5: 395. https://doi.org/10.3390/machines13050395
APA StyleFang, P., Yang, Y., & Zeng, J. (2025). Research on the Dynamic Response of a Cracked-Spur Gear System with Parameter Uncertainty. Machines, 13(5), 395. https://doi.org/10.3390/machines13050395







