Numerical Simulation of Aerodynamic Characteristics of Trailing Edge Flaps for FFA-W3-241 Wind Turbine Airfoil
Abstract
1. Introduction
2. Calculation Model
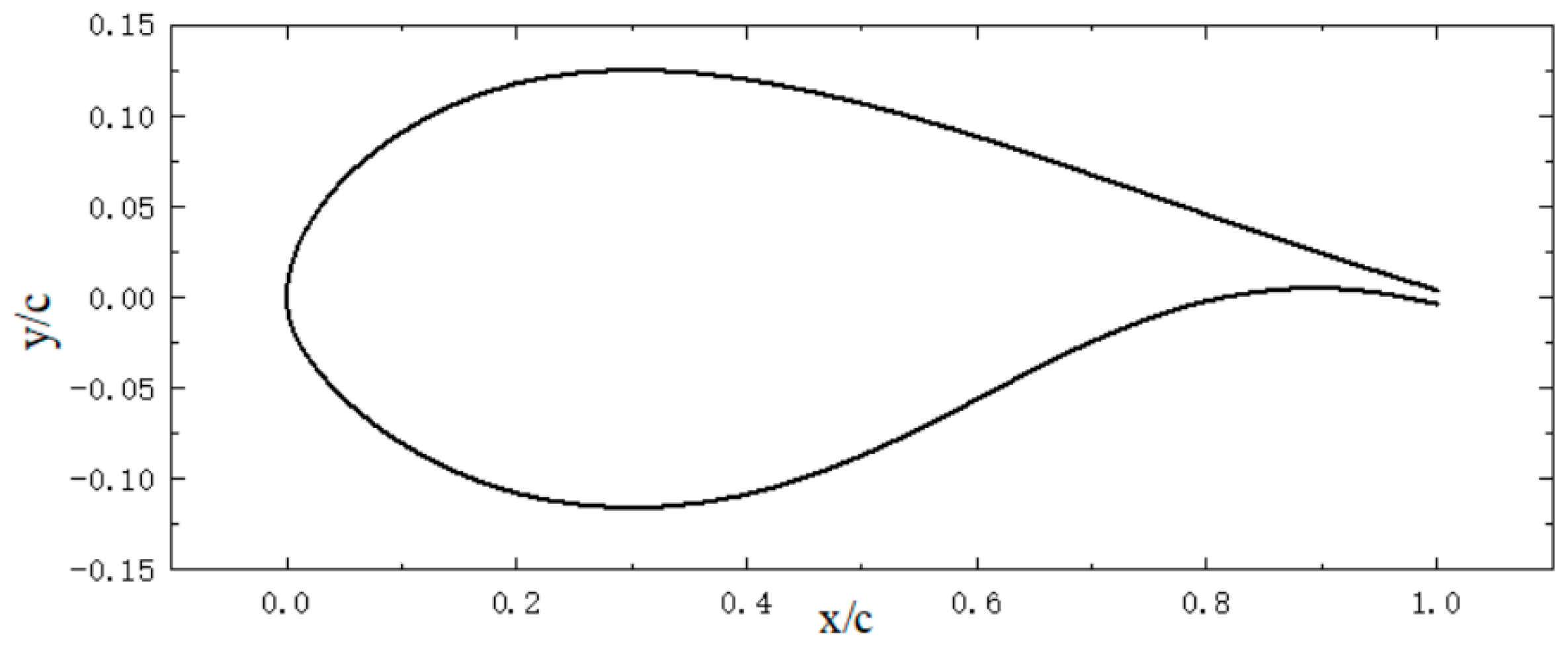
2.1. Basic Airfoil Geometry
2.2. Trailing Edge Flaps Model
2.3. Numerical Method
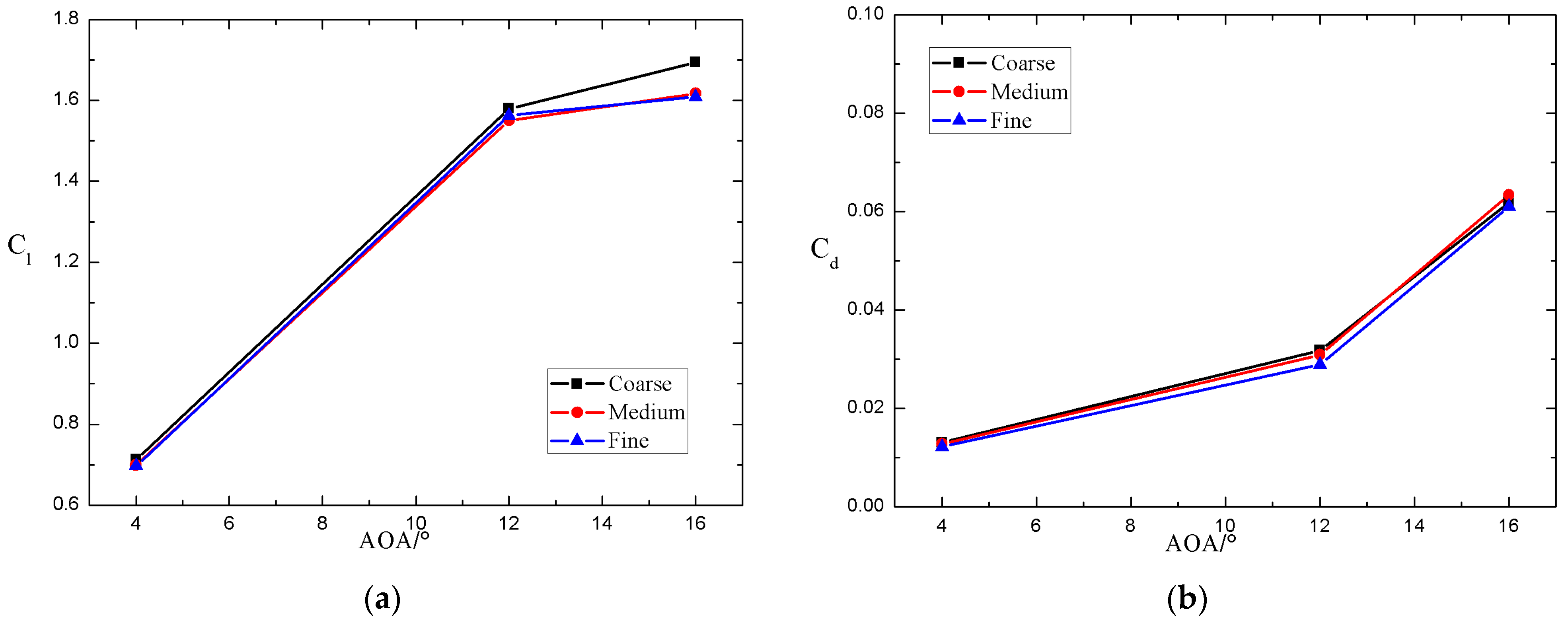
3. Grid Independence Verification
4. Experimental Verification
5. Calculation Results and Analysis
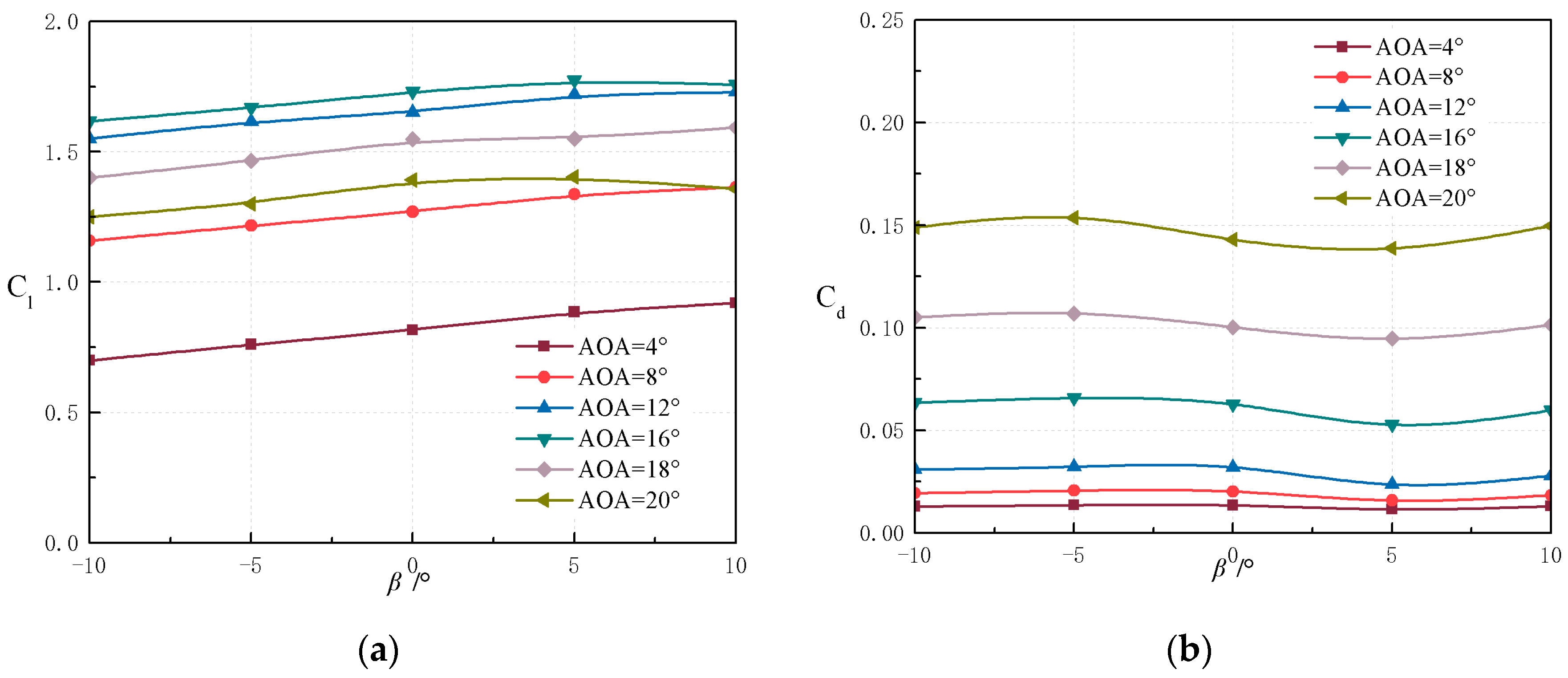
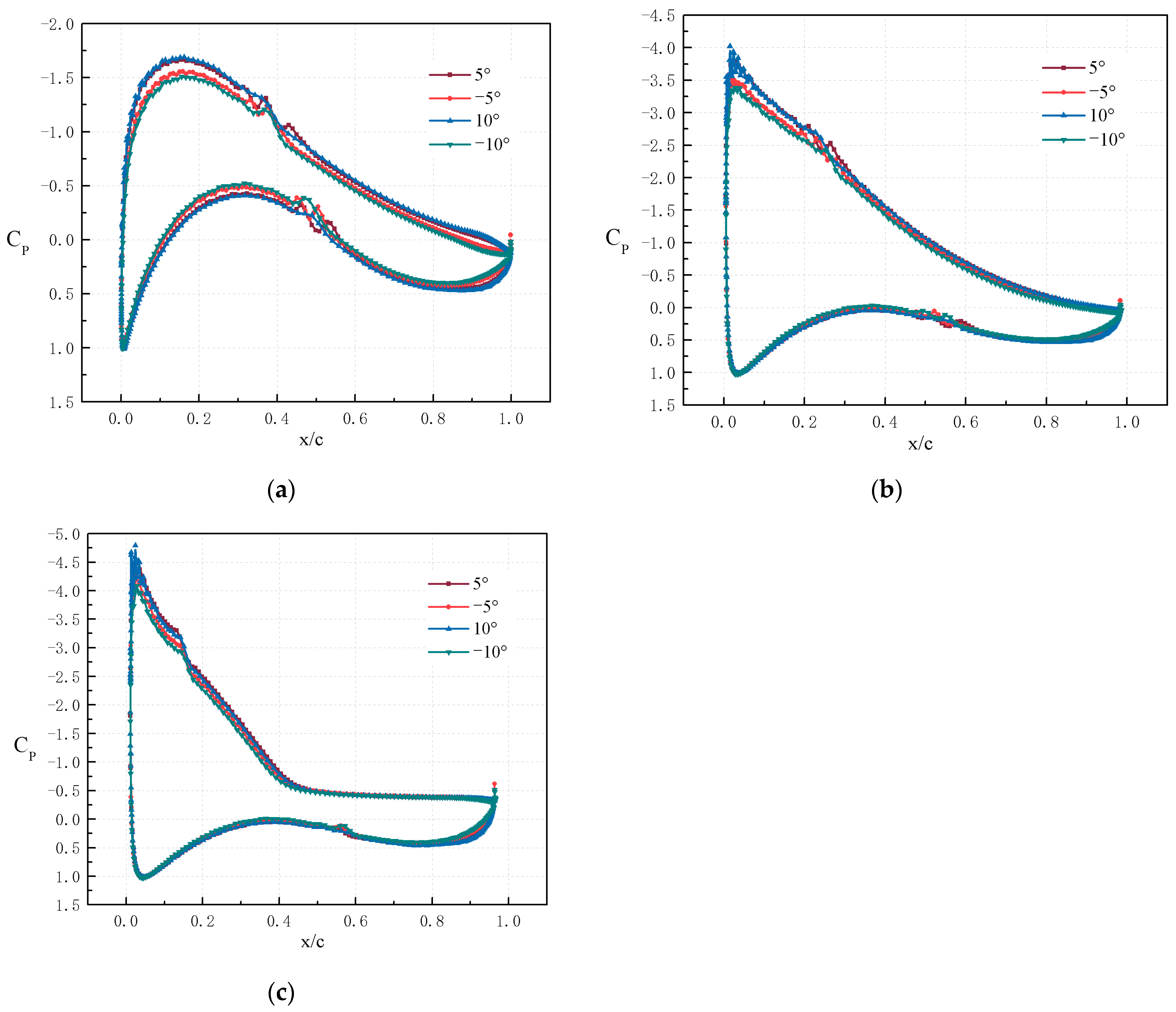
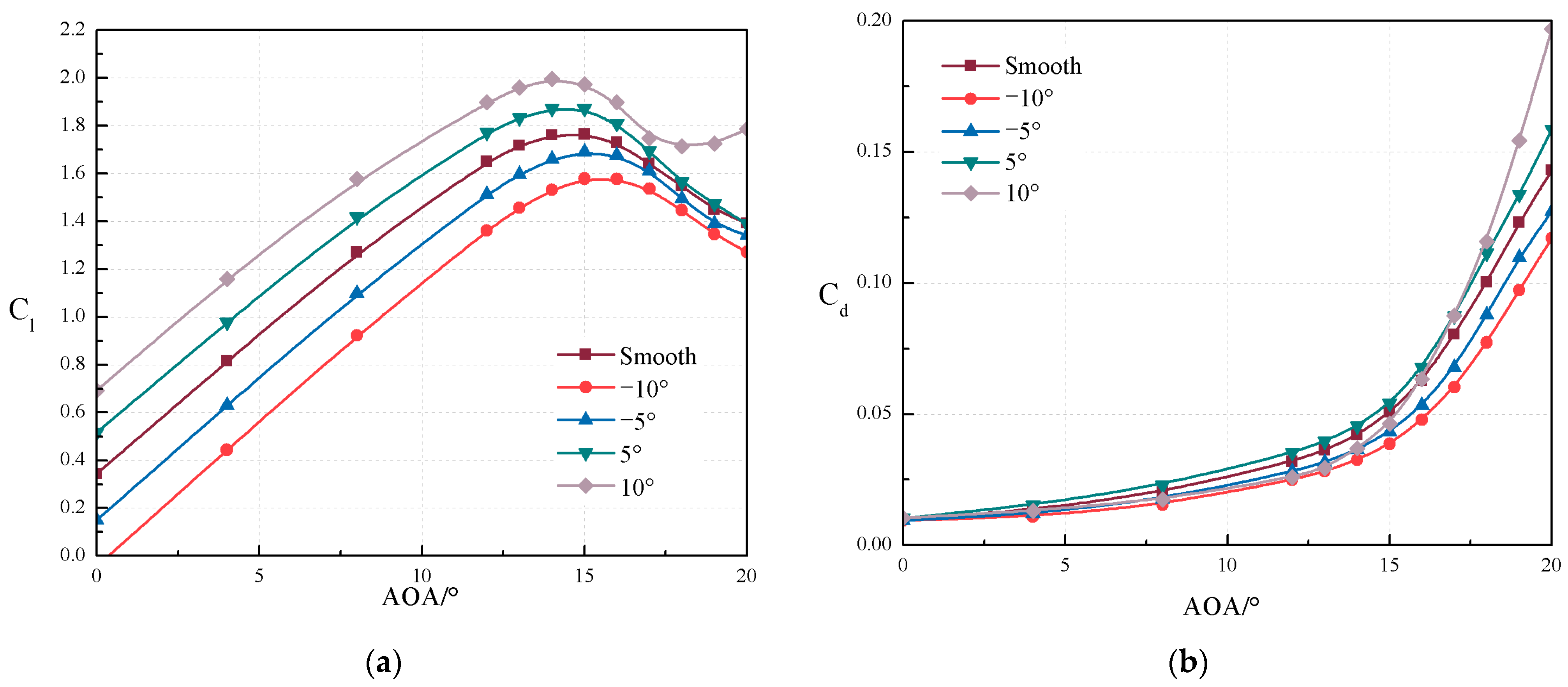
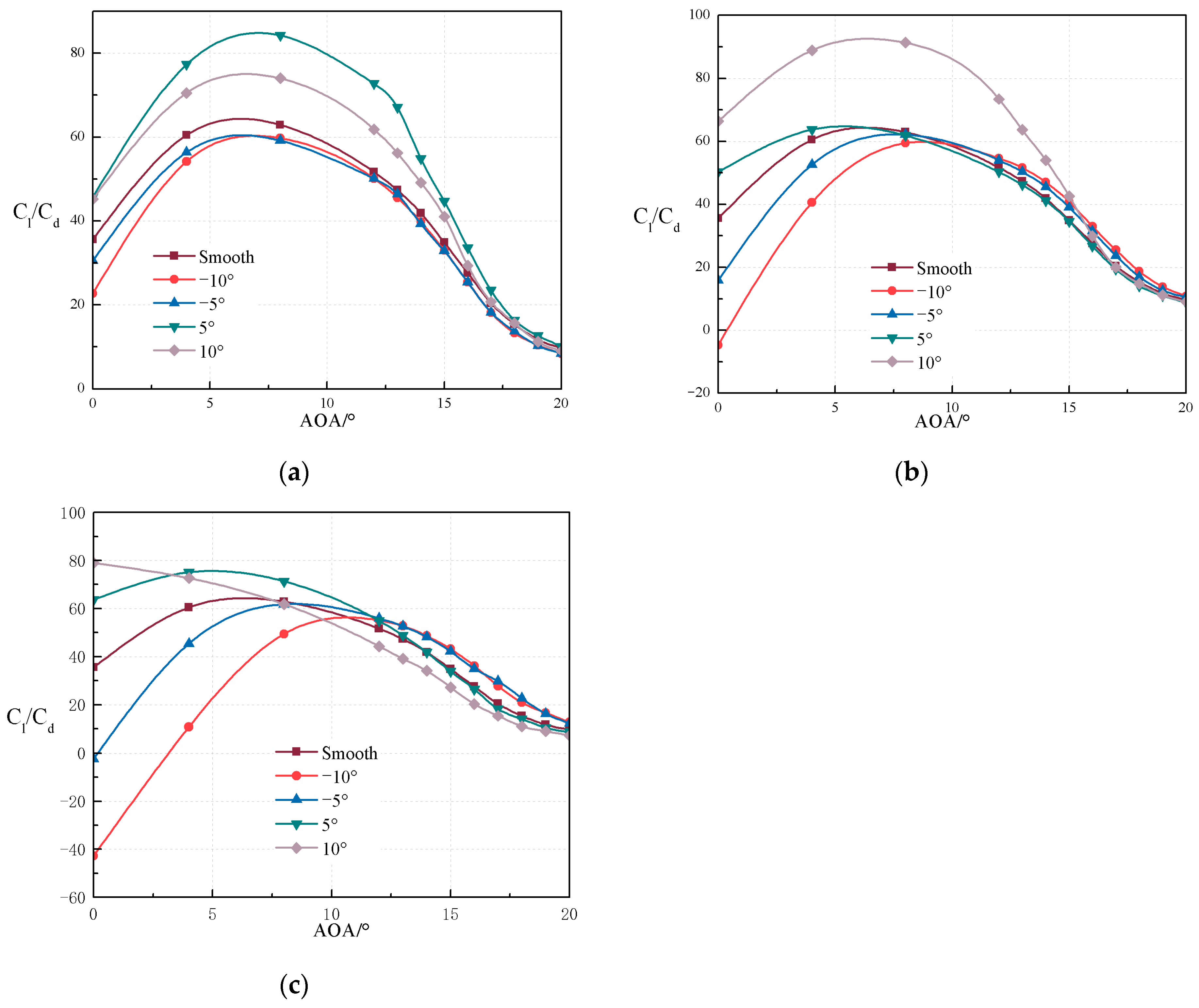
5.1. Influence of Flap Deflection Angle
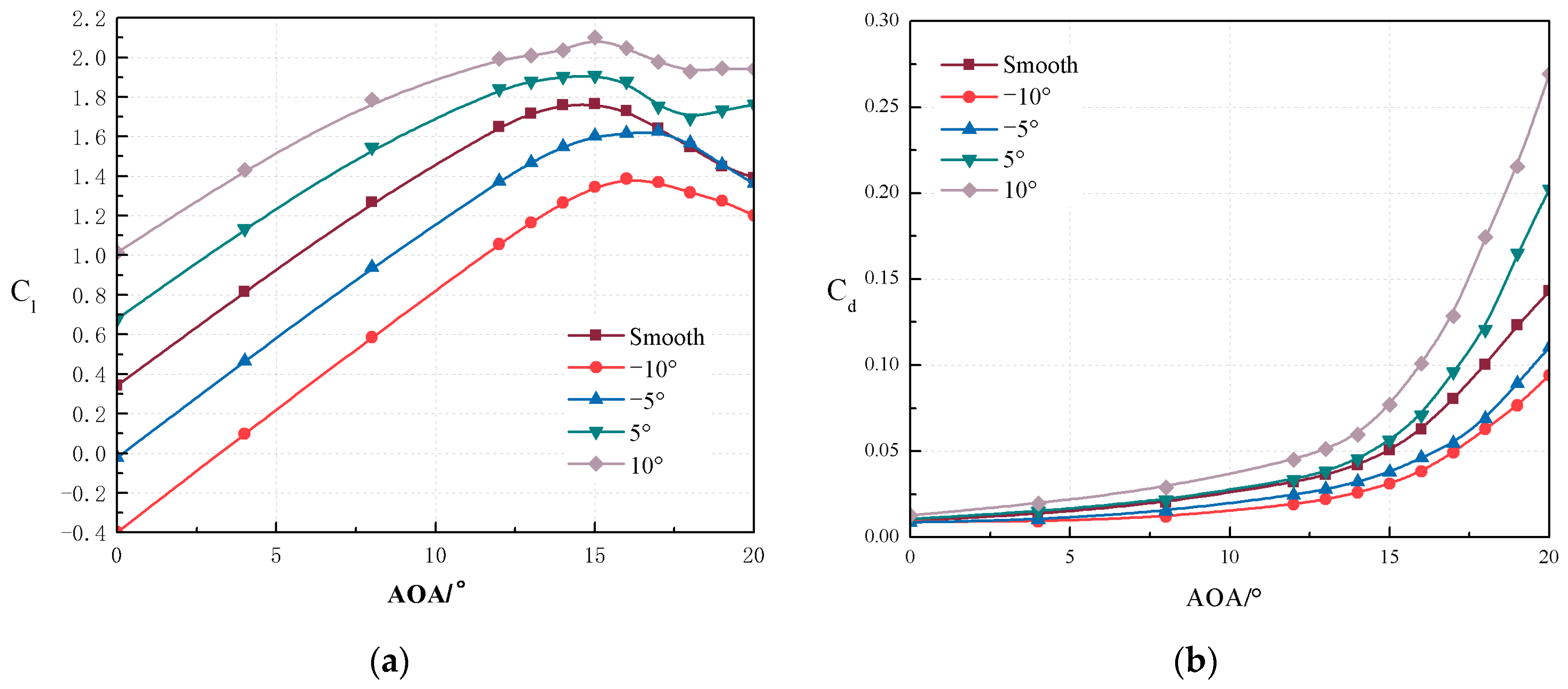
5.2. Influence of Flap Length
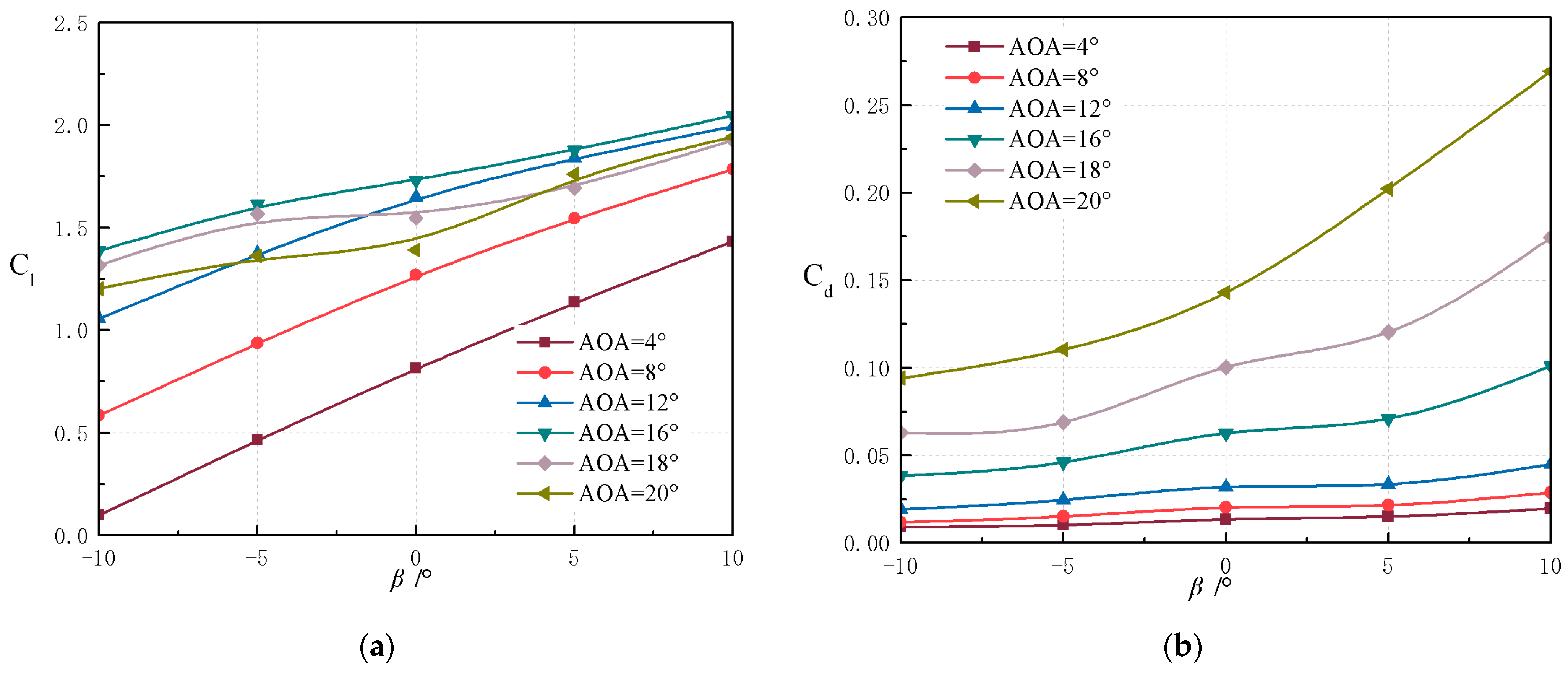
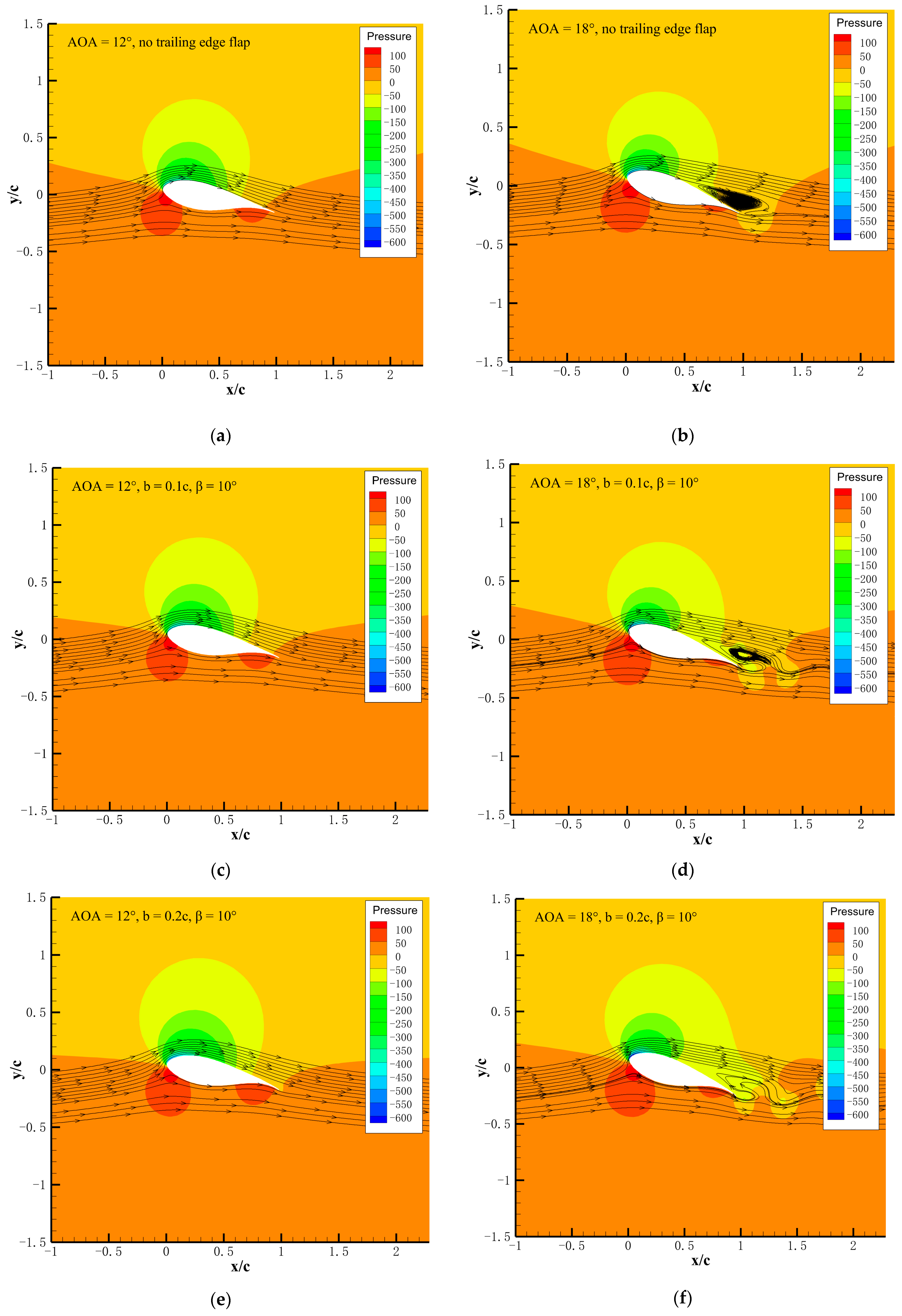
5.3. Comprehensive Optimal Parameters
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bošnjaković, M.; Katinić, M.; Santa, R.; Marić, D. Wind turbine technology trends. Appl. Sci. 2022, 12, 8653. [Google Scholar] [CrossRef]
- Mansi, A.; Aydin, D. The impact of trailing edge flap on the aerodynamic performance of small-scale horizontal axis wind turbine. Energy Convers. Manag. 2022, 256, 115396. [Google Scholar] [CrossRef]
- Sun, Y.; Qian, Y.; Gao, Y.; Wang, T.; Wang, L. Stall control on the wind turbine airfoil via the single and dual-channel of combining bowing and suction technique. Energy 2024, 290, 130224. [Google Scholar] [CrossRef]
- Qian, Y.; Zhang, Y.; Sun, Y.; Wang, T. Numerical investigations of the flow control effect on a thick wind turbine airfoil using deformable trailing edge flaps. Energy 2023, 265, 126327. [Google Scholar] [CrossRef]
- Zhu, H.; Hao, W.; Li, C.; Luo, S.; Liu, Q.; Gao, C. Effect of geometric parameters of Gurney flap on performance enhancement of straight-bladed vertical axis wind turbine. Renew. Energy 2021, 165, 464–480. [Google Scholar] [CrossRef]
- Wilson, D.; Barlas, T.; Berg, D.; van Kuik, G.; Resor, B. Active aerodynamic blade distributed flap control design procedure for load reduction on the UPWIND 5MW wind turbine. In Proceedings of the 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2010; p. AIAA-2010-254. [Google Scholar]
- Timmer, W.A.; Van Rooij, R.P.J.O.M. Summary of the Delft University wind turbine dedicated airfoils. J. Sol. Energy Eng. 2003, 125, 488–496. [Google Scholar] [CrossRef]
- McWilliam, M.K.; Barlas, T.K.; Madsen, H.A.; Zahle, F. Aero-elastic wind turbine design with active flaps for AEP maximization. Wind. Energy Sci. 2018, 3, 231–241. [Google Scholar] [CrossRef]
- Hao, W.; Mao, H.; Lyu, S.; Li, C. Study on aerodynamic load reduction and efficiency improvement of VAWT based on DTEF. Ocean. Eng. 2022, 260, 111966. [Google Scholar] [CrossRef]
- Daynes, S.; Weaver, P.M. Design and testing of a deformable wind turbine blade control surface. Smart Mater. Struct. 2012, 21, 105019. [Google Scholar] [CrossRef]
- Bak, C.; Gaunaa, M.; Andersen, P.B.; Buhl, T.; Hansen, P.; Clemmensen, K. Wind tunnel test on airfoil Risø-B1-18 with an Active Trailing Edge Flap. Wind. Energy 2010, 13, 207–219. [Google Scholar] [CrossRef]
- Troldborg, N. Computational study of the risø-b1-18 airfoil with a hinged flap providing variable trailing edge geometry. Wind. Eng. 2005, 29, 89–113. [Google Scholar] [CrossRef]
- Wolff, T.; Ernst, B.; Seume, J.R. Aerodynamic behavior of an airfoil with morphing trailing edge for wind turbine applications. J. Phys. Conf. Ser. 2014, 524, 012018. [Google Scholar] [CrossRef]
- Gerontakos, P.; Lee, T. Piv study of flow around unsteady airfoil with dynamic trailing-edge flap deflection. Exp. Fluids 2008, 45, 955. [Google Scholar] [CrossRef]
- Troolin, D.R.; Longmire, E.K.; Lai, W.T. Time resolved PIV analysis of flow over a NACA 0015 airfoil with Gurney flap. Exp. Fluids 2006, 41, 241–254. [Google Scholar] [CrossRef]
- Hao, L.S.; Gao, Y.W. Effect of gurney flap geometry on a S809 airfoil. Int. J. Aerosp. Eng. 2019, 2019, 9875968. [Google Scholar] [CrossRef]
- Özden, M.; Genç, M.S.; Koca, K. Investigation of the effect of hidden vortex generator-flap integrated mechanism revealed in low velocities on wind turbine blade flow. Energy Convers. Manag. 2023, 287, 117107. [Google Scholar] [CrossRef]
- LI, C.; XU, Y.; XU, J. Influence of slot on wind turbine airfoil with trailing-edge flaps. J. Eng. Thermophys. 2011, 32, 1851–1854. [Google Scholar]
- Hao, W.; Bashir, M.; Li, C.; Sun, C. Flow control for high-solidity vertical axis wind turbine based on adaptive flap. Energy Convers. Manag. 2021, 249, 114845. [Google Scholar] [CrossRef]
- Hao, W.; Li, C.; Ye, Z.; Zhu, H.; Ding, Q. Numerical investigation of the load reduction potential of trailing edge flap based on closed-loop control. J. Renew. Sustain. Energy 2018, 10, 053301. [Google Scholar] [CrossRef]
- Seyednia, M.; Vakilipour, S.; Masdari, M. Numerical investigation of dynamic stall over a wind turbine pitching airfoil by using openfoam. Int. J. Mech. Aerosp. Ind. Mechatron. Manuf. Eng. 2017, 11, 1466–1477. [Google Scholar]
- Seyednia, M.; Masdari, M.; Vakilipour, S. The influence of oscillating trailing-edge flap on the dynamic stall control of a pitching wind turbine airfoil. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 192. [Google Scholar] [CrossRef]
- Zhu, W.; Behrens, T.; Shen, W. Hybrid immersed boundary method for airfoils with a trailing-edge flap. AIAA J. 2013, 51, 30–41. [Google Scholar] [CrossRef]
- Liu, Q.; Miao, W.; Li, C.; Hao, W.; Zhu, H.; Deng, Y. Effects of trailing-edge movable flap on aerodynamic performance and noise characteristics of VAWT. Energy 2019, 189, 116271. [Google Scholar] [CrossRef]
- Arredondo-Galeana, A.; Young, A.M.; Smyth, A.S.; Viola, I.M. Unsteady load mitigation through a passive trailing-edge flap. J. Fluids Struct. 2021, 106, 103352. [Google Scholar] [CrossRef]
- Mancini, P.; Medina, A.; Jones, A.R. Experimental and analytical investigation into lift prediction on large trailing edge flaps. Phys. Fluids 2019, 31, 013106. [Google Scholar] [CrossRef]
- Zhuang, C.; Yang, G.; Zhu, Y.; Hu, D. Effect of morphed trailing-edge flap on aerodynamic load control for a wind turbine blade section. Renew. Energy 2020, 148, 964–974. [Google Scholar] [CrossRef]
- He, G.; Deparday, J.; Siegel, L.; Henning, A.; Mulleners, K. Stall delay and leading-edge suction for a pitching airfoil with trailing-edge flap. AIAA J. 2020, 58, 5146–5155. [Google Scholar] [CrossRef]
- Tian, H.; Shan, X.; Wang, H.; Li, X.; Su, Y.; Wang, J. Enhanced piezoelectric energy harvesting performance using trailing-edge flap. Ocean. Eng. 2023, 285, 115443. [Google Scholar] [CrossRef]
- Rivero, A.E.; Fournier, S.; Manolesos, M.; Cooper, J.E.; Woods, B.K. Experimental aerodynamic comparison of active camber morphing and trailing-edge flaps. AIAA J. 2021, 59, 2627–2640. [Google Scholar] [CrossRef]
- Watkins, J.; Bouferrouk, A. The effects of a morphed trailing-edge flap on the aeroacoustic and aerodynamic performance of a 30P30N aerofoil. Acoustics 2022, 4, 248–267. [Google Scholar] [CrossRef]
- Haldar, A.; Jansen, E.; Hofmeister, B.; Bruns, M.; Rolfes, R. Analysis of novel morphing trailing edge flap actuated by multistable laminates. AIAA J. 2020, 58, 3149–3158. [Google Scholar] [CrossRef]
- Ameduri, S.; Galasso, B.; Noviello, M.C.; Dimino, I.; Concilio, A.; Catalano, P.; Shreedharan, S. Design and optimization of a compliant morphing trailing edge for high-lift generation. Appl. Sci. 2025, 15, 2529. [Google Scholar] [CrossRef]
- Chen, Z.J.; Stol, K.A.; Mace, B.R. Wind turbine blade optimisation with individual pitch and trailing edge flap control. Renew. Energy 2017, 103, 750–765. [Google Scholar] [CrossRef]
- Li, X.; Yang, K.; Wang, X. Experimental and numerical analysis of the effect of vortex generator height on vortex characteristics and airfoil aerodynamic performance. Energies 2019, 12, 959. [Google Scholar] [CrossRef]
- Yue, H.; Zhang, H.; Zhu, Q.; Ai, Y.; Tang, H.; Zhou, L. Wake dynamics of a wind turbine under real-time varying inflow turbulence: A coherence mode perspective. Energy Convers. Manag. 2025, 332, 119729. [Google Scholar] [CrossRef]






| Parameter | Value |
|---|---|
| Average inflow velocity | 14.8 m/s |
| Reynolds number | 106 |
| Turbulence intensity | 1% |
| Attack of angle | 0–20° |
| Flap length | 0.1, 0.2, 0.3 |
| Flap deflection angle | ±5°, ±10° |
| Scheme | Grid Number | AOA = 4° | AOA = 12° | AOA = 16° | |||
|---|---|---|---|---|---|---|---|
| coarse grid | 31992 | 0.7125 | 0.0131 | 1.5793 | 0.0318 | 1.6937 | 0.0619 |
| medium grid | 52416 | 0.6986 | 0.0128 | 1.5502 | 0.0309 | 1.6170 | 0.0634 |
| fine grid | 131838 | 0.6967 | 0.0122 | 1.5628 | 0.0289 | 1.6084 | 0.0610 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, J.; Ji, Z.; Zhang, Y.; Yao, G.; Qian, Y.; Wang, Z. Numerical Simulation of Aerodynamic Characteristics of Trailing Edge Flaps for FFA-W3-241 Wind Turbine Airfoil. Machines 2025, 13, 366. https://doi.org/10.3390/machines13050366
Xu J, Ji Z, Zhang Y, Yao G, Qian Y, Wang Z. Numerical Simulation of Aerodynamic Characteristics of Trailing Edge Flaps for FFA-W3-241 Wind Turbine Airfoil. Machines. 2025; 13(5):366. https://doi.org/10.3390/machines13050366
Chicago/Turabian StyleXu, Jiaxin, Zhongyao Ji, Yihuang Zhang, Geye Yao, Yaoru Qian, and Zhengzhi Wang. 2025. "Numerical Simulation of Aerodynamic Characteristics of Trailing Edge Flaps for FFA-W3-241 Wind Turbine Airfoil" Machines 13, no. 5: 366. https://doi.org/10.3390/machines13050366
APA StyleXu, J., Ji, Z., Zhang, Y., Yao, G., Qian, Y., & Wang, Z. (2025). Numerical Simulation of Aerodynamic Characteristics of Trailing Edge Flaps for FFA-W3-241 Wind Turbine Airfoil. Machines, 13(5), 366. https://doi.org/10.3390/machines13050366







