Design Methodology and Economic Impact of Small-Scale HAWT Systems for Urban Distributed Energy Generation

Abstract

Integrating wind turbines within urban environments, either as building-mounted units or standalone installations, represents a valuable step toward sustainable city development. Vertical axis wind turbines (VAWTs) are commonly favored in these settings due to their ability to handle turbulent winds; however, they generally exhibit lower energy conversion efficiency compared to horizontal axis wind turbines (HAWTs). Selecting optimal urban or suburban locations with favorable wind conditions opens the possibility of deploying HAWTs, leveraging their higher efficiency even at comparable wind speeds. This paper presents a methodology for designing highly efficient HAWTs for urban use, supported by computational fluid dynamics (CFD) analyses to produce power curves and evaluate the energy conversion efficiency of both bare and augmented turbine designs. Differing from prior studies, this work also incorporates a detailed economic analysis, examining how reductions in the Levelized Cost of Energy (LCOE) enhance the cost-effectiveness of small-scale distributed wind systems. The findings offer insights into the technical and economic viability of small-scale HAWT configurations for distributed energy generation across diverse urban locations with varying wind profiles.

1. Introduction

Wind energy, a rapidly growing renewable energy source, is traditionally harnessed through large wind farms. However, energy production within urban areas requires smaller, localized wind turbines due to limited space. Installing small wind turbines on buildings or nearby locations allows for electricity generation directly at the point of consumption, promoting the concept of distributed micro-generation—a distinct advantage in urban settings. The challenges and potential of wind resource assessment in the urban habitat are presented in [1], but the emphasis has been placed on the need for further research, especially in the field of urban aerodynamics. Due to unpredictable wind behavior in the urban environment and incorrect location selection, large discrepancies in the estimated and produced energy are often reported in the literature [2]. Therefore, the selection of the proper locations for the installation of urban wind turbines is crucial to ensure efficient operation and supply residential loads. Recent studies have emerged focusing on the development of precise methods for accurately forecasting energy production from urban wind turbines. The study presented in [3] focuses on the development of precise forecasting methods using advanced deep learning techniques. It is centered on the energy production of horizontal and vertical axis wind turbines, along with an analysis of their construction costs.

While the contribution of urban wind energy is expected to grow, particularly in cities with abundant wind resources or where it is integrated into urban planning, its potential is limited by factors such as low wind speeds and high turbulence, meaning it is more likely to serve as a complementary resource within a diversified urban energy strategy rather than a primary energy source [4].

The method for estimating wind speeds in urban areas based on background wind speeds and morphological parameters such as volume fraction of buildings, the plane area fraction of buildings, and an average height of buildings is presented in [5]. The potential of urban wind sector development and micro-turbine performance analysis in Djibouti-city, Djibouti, is presented in [6]. The methodology for vertical axis urban wind turbine power estimation is presented in [7], assuming the mean wind speed and turbulence intensities can be estimated at the considered location.

While HAWTs dominate large-scale applications due to their superior efficiency, VAWTs are frequently considered for smaller, urban applications. This preference is largely attributed to VAWTs’ ability to operate at lower cut-in speeds and their lack of need for yawing mechanisms [8]. Several studies have explored VAWT designs enhanced with shrouds to boost efficiency in urban environments, though the power coefficient for these configurations typically hovers around 30% [9]. By implementing diffuser-shaped walls in combination with dual-pitched roof structures, some designs have achieved power coefficient improvements of up to 50% [10]. The study presented in [11] emphasizes the importance of architectural design due to its significant impact on the wind energy potential in cities. The results show that building corner modifications have a notable effect on turbulence intensity and wind speed.

The methodology for determining the annual energy production of potential urban wind projects, organized into four stages and illustrated with a case study from Spain, is presented in [12]. The results of the techno–economic feasibility assessment, presented in [13], demonstrate the high competitiveness of the low-speed wind turbine based on a Ferris wheel is for low wind speed applications in Africa. The use of diffuser for horizontal axis small wind turbines is suggested in [14], at low wind speed conditions. The improved duct design for augmentation of horizontal axis micro-wind turbine is presented in [15]. In addition to the increased power coefficient, reduced noise level generation is reported. Experimental measurements of the performance of horizontal axis micro-wind turbine in an urban area and its economic feasibility, based on the LCOE is reported in [16]. LCOE approach was also used in [17], to conclude of the potential cost of wind energy. The reasons for the slow acceptance of ducted wind turbines on the market, despite their higher power coefficient, are addressed in [18]. The comparison of vertical and horizontal axis wind turbines from the load point of view (under normal power production) indicates that the equivalent 1 Hz fatigue base bottom bending moments of VAWT are much higher than that of the HAWT equivalent [19]. The method developed for predicting the performance of HAWTs in urban flow conditions is presented in [20]. This method provides insights into fluid flow and rotor performance at reduced computational costs, enabling the analysis of spanwise variations in the angle of attack. This approach can help optimize blade design for rooftop HAWT.

The review of the current state of urban wind energy, presented in [21], highlights the necessity for ongoing research to address numerous questions regarding the performance and economic viability of wind turbines. This paper aims to design highly efficient small-scale horizontal axis wind turbines, both with and without diffusers, and to assess their applicability in urban areas characterized by diverse wind conditions, thereby contributing to sustainable urban development. The LCOE metric is employed to evaluate the economic viability of the bare rotor turbine concept in comparison to the diffuser-augmented turbine across the selected locations. Additionally, a sensitivity analysis is conducted to examine the impact of potential uncertainties such as inflation, rising maintenance costs, or overestimated energy production on the LCOE. This analysis offers further insight into the economic viability of such projects in urban environments, particularly in the context of inaccurate energy production estimates, which are commonly observed with urban wind turbines, as well as other real-world uncertainties, such as rising investment and maintenance costs.

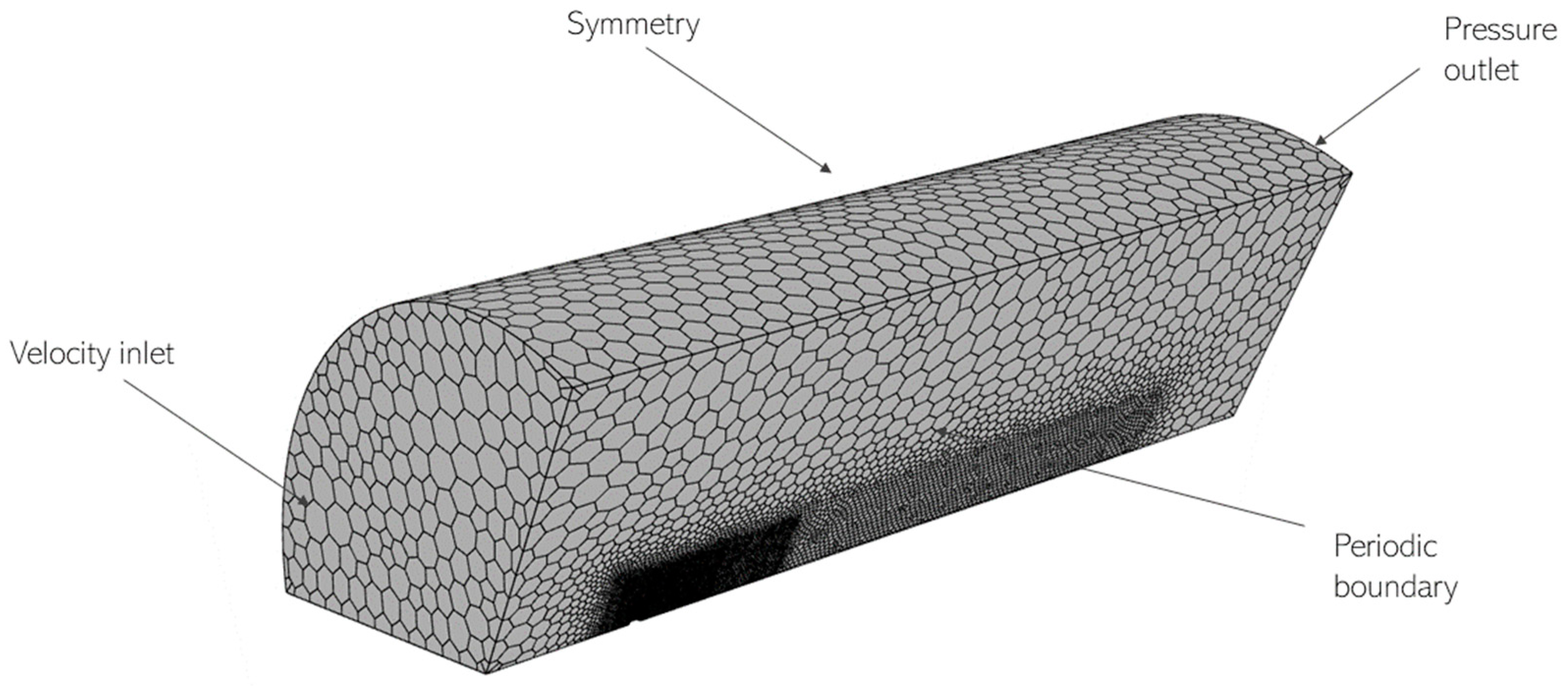
2. Methodology

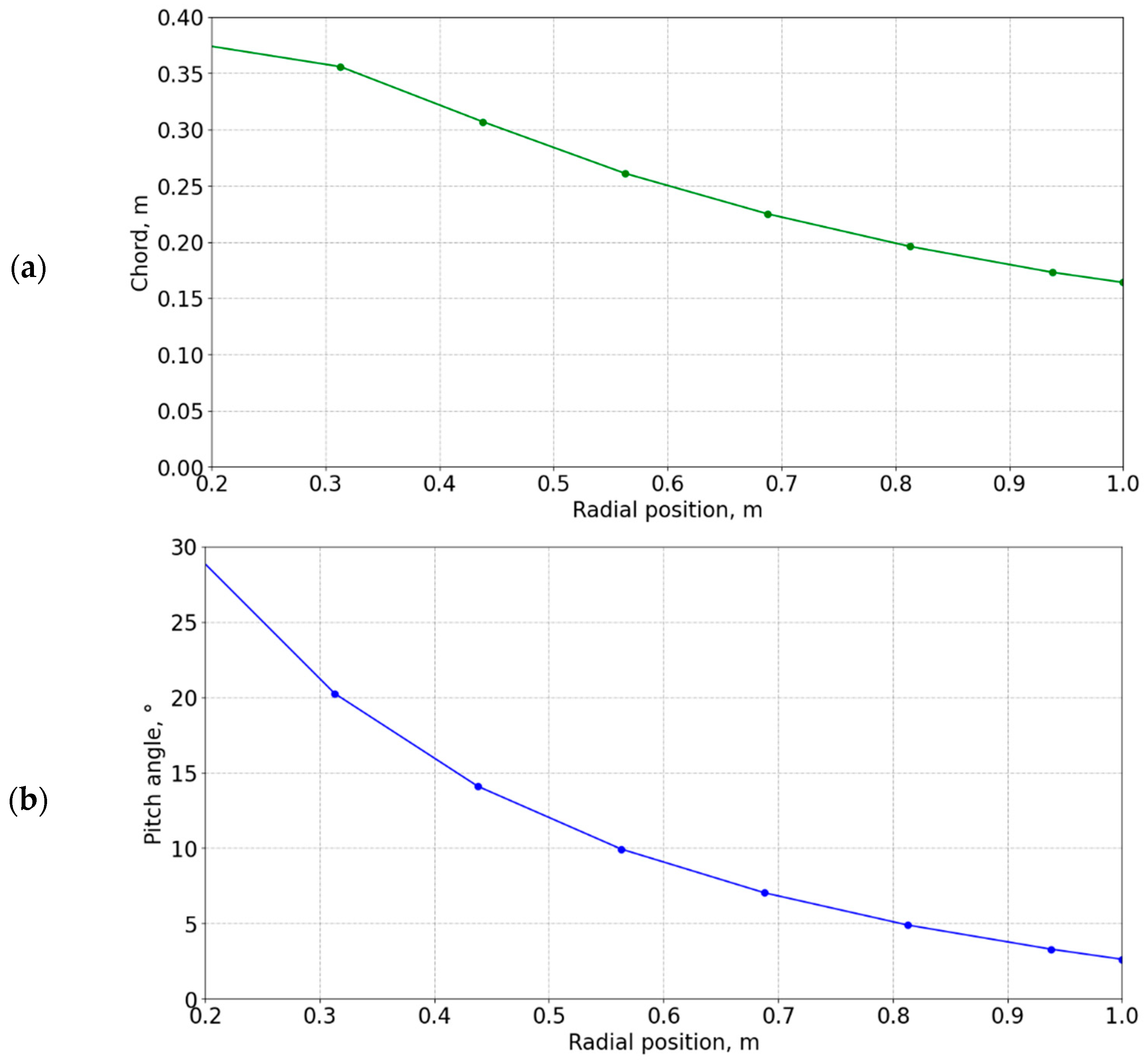
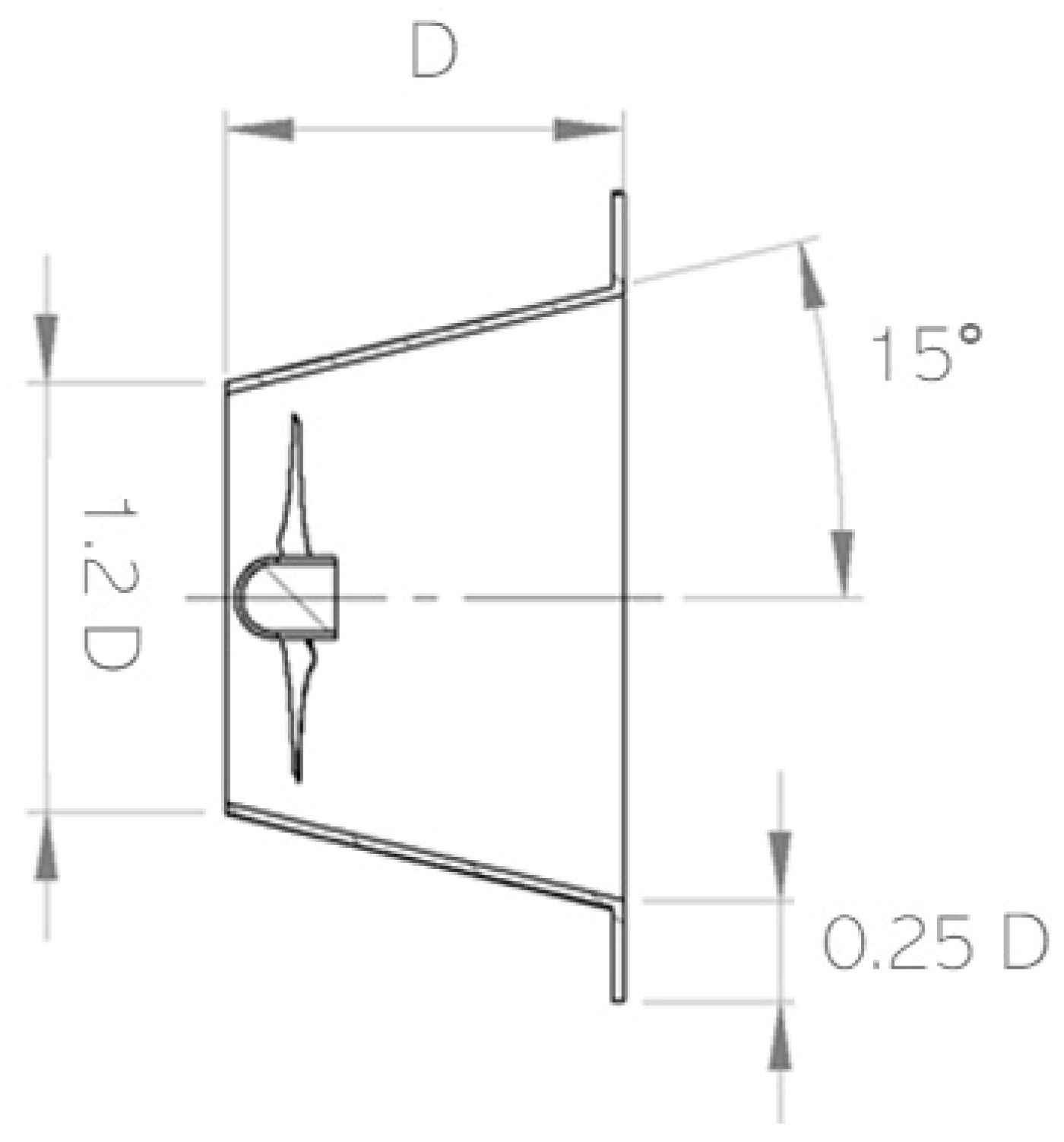
2.1. Turbine Design

The turbine was designed using in-house code primarily developed for the micro hydrokinetic turbine design, which was adapted for the small wind turbine application. The optimization-based method used in this work is presented in the Appendix A. It couples Blade Element Momentum Theory (BEM) and genetic algorithm. The original method is presented in [22] in more detail.

Prior to designing the airfoil and blade geometry, it is essential to select key parameters, such as turbine rotor diameter and the blade tip to speed ratio (TSR). The turbine diameter is influenced not only by the required power output but also by the specific conditions at the installation site. Utilizing the methodology outlined in the Appendix A, the optimal values for chord lengths and the distribution of twist angles along the blade span are calculated for the initial airfoil profile. Following this, the design and optimization of a new airfoil are conducted. Upon determining the optimal airfoil (blade profile), the final design parameters—namely, chord lengths and the distribution of twist angles along the blade span—are calculated. This objective function, given by Equation (A1) in the Appendix A, was designed to maximize the value of the power coefficient ($C_P)$, guiding the design towards configurations that maximize the turbine’s ability to extract energy from the wind. The power coefficient is a fundamental parameter for assessing the performance and efficiency of wind turbines. It is mathematically defined as the ratio of the actual power extracted by the turbine to the theoretical maximum power available in the wind, providing a quantifiable measure of a turbine’s ability to convert wind energy into mechanical energy:

$$C_P={\displaystyle \frac{P}{\frac{1}{2}\rho A_1{v_0}^3}}.$$

(1)

In Equation (1), $P$ is turbine’s power output, $\rho$ is the air density $A_1$ is the rotor’s swept area and $v_0$ is wind speed. Importantly, $C_P$ is a dimensionless quantity with a theoretical upper limit known as the Betz limit, which states that no bare rotor turbine can harness more than 59.3% of the kinetic energy from the wind. This parameter plays a pivotal role in several aspects of wind energy systems. First, it serves as a direct indicator of aerodynamic efficiency, enabling meaningful comparisons between different turbine designs and configurations. Second, it informs the optimization process for turbine components, such as blade design, as a higher $C_P$corresponds to more effective energy capture. Finally, an optimized $C_P$ contributes to reducing the LCOE, making wind projects more economically viable by maximizing energy output for given wind resources.

The original objective function for the blade profile optimization, proposed in [22], has been corrected by eliminating the last term that takes the cavitation occurrence into account. The corrected objective function that was used for airfoil optimization is given by Equation (2).

$$\min f={\sum }_{i=7}^{12}{w}_{1,\alpha =i}·{\displaystyle \frac{1}{C_{L,\alpha =i}}}+{\sum }_{i=7}^{12}{w}_{2,\alpha =i}·C_{D,\alpha =i}.$$

(2)

In Equation (2), $w_{1,\alpha =i}$ and $w_{2,\alpha =i}$ are weighting factors that multiply the reciprocal of the lift coefficient $\left(C_L\right)$ and drag coefficient $\left(C_D\right),$ respectively. The weighting factors values can be selected based on the estimated importance of each design requirement. In this work, the following weighting factors were chosen $w_{1,\alpha =i}=20$, $w_{2,\alpha =i}=5$. For wind turbines, the aerodynamic performance of the blades, determined by the lift coefficient $\left(C_L\right)$ and drag coefficient $\left(C_D\right)$, directly influences $C_p$, a measure of how efficiently the turbine converts wind energy into mechanical energy. These coefficients are used to quantify the forces acting on an airfoil due to its interaction with the surrounding air. Achieving a high $C_L$ and a low $C_D$ is essential for maximizing the aerodynamic efficiency of turbine blades, enhancing energy production, and improving the overall economic viability of wind energy systems.

Typically, airfoils are represented by using a quite large number of coordinate points. In the optimization process, these coordinate points also represent decision variables, which leads to computational complexity. To increase computational efficiency, parametrization is used to mathematically describe airfoil. Thus, the airfoil was described using two different (Non-Uniform Rational Basis Spline) NURBS curves. One curve was used for the suction side of the profile, and the other for the pressure side. In this way, the number of decision variables is reduced to 12, with a very good ability to describe different airfoil shapes. Once the final airfoil shape is achieved through the optimization process, the distribution of chord lengths and twist angles along the blade span are calculated using the equations provided in the Appendix A. These values have been calculated using new data on lift and drag coefficients of the optimized airfoil, obtained by calculation in XFoil code [23]. The chosen design angle of attack of the optimized airfoil is 8º, as it gives the lowest $C_D/C_L$ ratio. As the selection of tip to speed ratio TSR influence the wind speed at which the turbine starts to operate [24], TSR is selected to be 3.5 to enable lower cut-in speeds. The calculated geometric parameters for a 1 m radius small wind turbine are shown in Figure 1.

The optimized rotor is a bare rotor with a horizontal axis of rotation, as shown in Figure 2a. In addition to the optimized bare rotor design, the diffuser-augmented turbine is also investigated, as shown in Figure 2b. The concept of adding a diffuser to the turbine rotor is aimed at increasing the wind speed at the rotor plane, thereby surpassing the theoretical efficiency limit of 59.3% applicable to bare rotors in open wind flow. The main geometric parameters of the diffuser under consideration are shown in Figure 3.

Numerical calculations were conducted using ANSYS Fluent 2020 R2 Academic software package to evaluate the aerodynamic performance of turbine design concepts under varying wind speed conditions. The computational domain, containing the turbine, is shaped as a one-third cylinder with a radius of three turbine diameters (3D). The final dimensions of the computational domain were selected after assessing the impact of domain size on simulation accuracy. The inlet is positioned 3 diameters (3D) upstream of the turbine, and the outlet is located 10 diameters (10D) downstream. Stationary calculations were performed using the Moving Reference Frame (MRF) method, with the computational domain divided into two zones: one rotating and one stationary. An unstructured polyhedral mesh was used to discretize the domain, with refinement zones near the turbine to minimize control volume count while preserving accuracy. The mesh and applied boundary conditions are illustrated in Figure 4.

Uncertainty was evaluated through the Grid Convergence Index (GCI) calculation. The procedure used for the GCI calculation is elaborated in [25], and results are given in

Table 1. GCI calculation.

Mesh	$\mathit{N}$	$\mathit{\varphi }$	${\mathit{r}}_{\mathit{i}\mathit{j}}$	${\mathit{\epsilon }}_{21}/{\mathit{\epsilon }}_{32}$	$\mathit{p}$	${\mathbf{G}\mathbf{C}\mathbf{I}}_{21}$
1	2.0 M	0.7902	1.66	0.938 Monotonic convergence	1.6	1.14%
2	1.2 M	0.7994	2.4
3	0.5 M	0.8092	-

. shows the area or “band” of the error i.e., how far the solution is from the asymptotic value.

To validate the reliability of the numerical simulation results obtained through the described model and calculation procedure, a comparison was made with experimental data available in the literature. Only a few studies provide detailed turbine geometry used in the experiments. Therefore, a study was selected that presents experimental results for a wind turbine with a diameter of 720 mm, featuring three twisted blades and NACA 4418 airfoils [26]. The detailed blade geometry provided in [26] was used to create the CAD model. This blade geometry was then employed in the creation of the computational domain. The domain was discretized using the previously described method, and boundary conditions were applied according to Figure 4. The power coefficients obtained from the numerical simulations were compared with those derived from experimental studies, and the comparison is presented in Figure 5. As shown in Figure 5, despite some discrepancies, the results obtained from the numerical simulations align well with the experimental data. The maximum relative error is less than 5%.

Although the positive effect of diffusers on the efficiency increase has already been confirmed, its effectiveness strongly depends on the chosen geometric parameters (such as diffuser length and diffuser expansion angle). In addition, the high cost related to the diffuser is often attributed to this design concept in the literature. Therefore, this work is focused not only on the highly efficient design from a technical point of view, but also on the economic aspect of the proposed technologies.

2.2. Economic Analysis

The economic analysis of small wind turbine design concepts is based on LCOE, which is defined as follows [17]:

$$LCOE={\displaystyle \frac{\sum _{t=1}^N\frac{I_t+{OM}_t+F_t}{{(1+r)}^t}}{\sum _{t=1}^N\frac{E_t}{{(1+r)}^t}}},$$

(3)

where $N$ is lifetime of the technology (project) in years, $E_t$ is energy produced in year $t$, ${OM}_t$ is operation and maintenance cost in year $t$, $F_t$ is fuel expenditures in year $t$, $I_t$ is capital cost, and $r$ is the weighted average cost of capital (WACC). LCOE is frequently used to compare different renewable energy technologies and projects [27,28]. The cost of capital differs widely across the countries and technologies [29]. According to [30], wind onshore WACC values in Croatia are in the range from 6.5% to 9%. Thus, in this study WACC is selected to be 8%. Croatian cities in Dalmatia region (Zadar, Šibenik, Knin and Split) are selected for the proposed small wind turbines installation. To estimate the cost of wind power generation with proposed turbine designs, wind speed distribution data are required to estimate expected energy produced in year. The wind data measured at 10 m height in the years 2015–2021 were obtained from the Croatian Meteorological and Hydrological Service [31]. The wind speed data were further corrected to consider town environment using Hellman exponential law [32]:

$${\displaystyle \frac{v}{v_0}}={\left({\displaystyle \frac{H}{H_0}}\right)}^{\alpha },$$

(4)

where $v$is the speed to the height $H{v}_0$ is the speed to the height $H_0=10\mathrm{m}$, and $\alpha$ is the friction coefficient or Hellman exponent. The friction coefficient depends on topography and landscapes and values can be found in [32].

According to recommendations given in [32], the friction exponent of 0.30 is taken for Šibenik, Zadar and Knin, while the exponent of 0.40 is selected for Split. The corrected wind speeds have been translated into histograms, given in Figure 6, that will be used for the calculation of the energy yield of wind turbines.

3. Results

Numerical simulations were performed for both bare and diffuser-augmented small wind turbines under varying wind speed conditions to analyze their aerodynamic behavior and energy conversion efficiency. In these simulations, as the turbine blades interact with the incoming wind, a portion of the kinetic energy is extracted, leading to a reduction in velocity within the wake region downstream of the turbine. This velocity reduction is accompanied by the formation of a recirculation zone, where flow characteristics are dominated by turbulence. Turbulence intensity is notably elevated within this wake region, particularly in proximity to the diffuser flange, where significant eddy currents develop. These eddy currents and the recirculation zone behind the diffuser flange contribute to a localized pressure drop, a phenomenon that effectively increases the velocity at the rotor plane by enhancing the wind inflow. This effect, driven by the diffuser’s geometry and positioning, is central to its role in potentially surpassing the efficiency limits typical of bare rotor designs.

3.1. Power Coefficient and Power Curves

Based on an extensive series of numerical simulations conducted across a wide range of operating conditions, power coefficients were calculated for both the bare small wind turbine (BSWT) and the diffuser-augmented small wind turbine (DSWT). The relationship between the power coefficient and TSR for each turbine configuration is illustrated in Figure 7, highlighting the comparative performance of BSWT and DSWT under varying TSR values.

The results reveal a notable increase in the power coefficient for the diffuser-augmented small wind turbine (DSWT) compared to the bare rotor configuration (BSWT). The maximum power coefficient for BSWT is achieved at a TSR of 3.5, whereas DSWT reaches its peak power coefficient at a higher TSR of 4.5. The $C_P$-TSR curves characterize the aerodynamic performance of each turbine design and form the basis for deriving their respective power curves.

Predicting the power output of these wind turbines as a function of wind speed requires additional consideration of the generator and control system. The power generated at a given wind speed depends on the selected operational strategy. Under a fixed rotational speed control strategy, the turbine achieves its maximum power coefficient only at a single wind speed. For the BSWT configuration, this optimal wind speed-to-rotational speed ratio is attained at a wind speed of 10 m/s and a rotor speed of 333 rpm. In contrast, DSWT reaches maximum efficiency at a wind speed of 7.7 m/s and the same rotor speed.

Alternatively, a variable rotational speed strategy enables the turbine to sustain peak performance by adjusting rotor speed in response to wind speed changes. While variable speed turbines offer greater operational flexibility and enhanced efficiency, they are generally more costly than their fixed-speed counterparts. In this study, both control strategies are examined, with the resulting power curves for BSWT and DSWT, derived from the corresponding $C_P$-TSR curves, presented in Figure 8.

3.2. LCOE Comparison

Annual energy production (AEP) for each turbine design was calculated by applying city-specific wind speed histograms, with detailed results presented in

Table 2. Annual energy production (APP) and LCOE.

		City
	Turbine	Zadar	Šibenik	Knin	Split
APP (kWh)	BSWT-FS	558.6	863.1	818.7	1463.5
	BSWT-VS	840.4	1070.4	1021.6	1693.8
	DSWT-FS	1193.8	1703.4	1650.7	2744.3
	DSWT-VS	1544.4	1970.9	1861.4	3124.8
LCOE (€/kWh)	BSWT-FS	0.363	0.235	0.248	0.139
	BSWT-VS	0.314	0.246	0.258	0.156
	DSWT-FS	0.229	0.161	0.166	0.100
	DSWT-VS	0.222	0.174	0.184	0.110

. This table also includes the calculated LCOE over a 25-year technology lifetime, encompassing all examined turbine designs, control strategies, and locations. Estimating LCOE across turbine concepts necessitates an in-depth cost analysis. For the bare rotor wind turbine (BSWT) with a rated output of 2 kW, capital costs are projected at €1784 for the fixed-speed generator and €2319 for the variable-speed generator. The diffuser, fabricated from aluminum sheeting, represents an additional cost of approximately 10% over the bare rotor turbine. Consequently, the capital expenditure for the diffuser-augmented wind turbine (DSWT) with a rated power of 4 kW is €2409 for the fixed-speed generator and €3010 for the variable-speed generator. Projected annual operation and maintenance costs are estimated at 2% of capital cost.

4. Discussion

The findings of this study clearly demonstrate that diffuser-augmented small wind turbines (DSWT) exhibit lower (LCOE values across all evaluated locations, irrespective of the control strategy employed. Notably, Split emerged as the location with the most favorable wind conditions for small wind turbines, achieving an impressive minimum LCOE of 0.10 €/kWh for the DSWT design utilizing a fixed rotational speed configuration.

Interestingly, the results reveal that implementing a more advanced variable speed control strategy sometimes resulted in higher LCOE values compared to the fixed speed generator. This trend is particularly pronounced for DSWT designs, which benefit from high efficiency across a broad range of operating conditions. This observation reinforces the strategic advantage of incorporating diffuser augmentation, as it enables the utilization of more robust and cost-effective generators.

Furthermore, the analysis of the impact of diffuser augmentation costs on LCOE reveals compelling insights. Even when the cost of the diffuser is projected to be 35% higher than the estimates used in this analysis, the DSWT design still yields lower LCOE values compared to the bare rotor small wind turbine (BSWT) at some locations. This indicates that the economic benefits of employing diffuser technology remain significant, even under less favorable cost scenarios. The utilization of diffusers represents a promising strategy for enhancing the economic competitiveness of urban wind technologies. This innovation has the potential to significantly contribute to the development of sustainable urban environments by facilitating the efficient harnessing of wind energy in diverse urban settings.

To evaluate the potential impact of inflation, rising material costs, and overestimated energy production on the LCOE, a comprehensive sensitivity analysis was conducted to examine how variations in capital and maintenance costs, as well as discrepancies between estimated and actual energy production, influence the LCOE for each turbine configuration. In Figure 9, it is evident that an increase in capital costs results in an expected rise in the LCOE, representing the cost per kilowatt-hour (kWh) of energy generated by the examined technology. A particularly noteworthy observation across all evaluated locations is that turbine configurations equipped with diffusers (especially the DSWT-FS model) maintain a lower LCOE compared to conventional bare turbines (BSWT) even when capital costs increase by 30% to 40%. This highlights the economic efficiency of diffuser-augmented turbines under scenarios of rising investment costs, making them a competitive alternative despite significant financial constraints.

The analysis also considered the impact of increased maintenance costs, expressed as a percentage of the initial capital cost. This approach reflects the methodology used in the baseline assessment, where maintenance expenses were estimated as a proportion of the capital cost. Figure 10. reveals that, as maintenance costs rise, the LCOE also increases. However, the analysis further confirms that selecting a turbine with a diffuser remains advantageous. Even under scenarios of significantly higher maintenance costs (approaching 6% of the capital cost) diffuser augmented turbines still achieve lower LCOE values compared to the BSWT technology. This demonstrates the superior economic resilience and efficiency of diffuser-augmented turbines, particularly in scenarios where operational expenses escalate. It is reasonable to assume that any increase in the investment or maintenance costs for DSWT technology would similarly affect the costs of BSWT technology. Consequently, the relative advantage of DSWT technology is likely to become even more pronounced under such conditions.

Additionally, an analysis was performed to assess the impact of inaccurate energy production estimates, focusing on the implications of overestimating energy production at a given location on the LCOE and results are presented in Figure 11. The sensitivity analysis of overestimated energy production provides valuable insights, as large discrepancies between estimated and actual energy output are frequently reported in the literature. These discrepancies are often attributed to unpredictable wind behavior in urban environments and incorrect location selection. The results of the analysis reveal that, even in scenarios with significant overestimations, DSWT technology continues to demonstrate advantages over standard BSWT technology, reinforcing its robustness and efficiency under varying conditions. It can be observed that even with a 20% reduction in energy production from the DSWT technology compared to the estimated production, the LCOE remains either lower or equal to that of the BSWT technology (depending on the location), where the estimated and actual energy production align. This comparison highlights that the LCOE of DSWT technology remains competitive, either lower or equal, even when actual energy production is significantly lower than estimated.

The enhanced efficiency of diffuser-augmented turbines positions them as an ideal solution for urban environments, where maximizing energy generation within limited space is crucial. These turbines achieve high power coefficients, underscoring their potential for effective distributed energy generation in densely populated areas.

Nonetheless, scaling and integrating such technologies into urban settings present challenges that merit further investigation. Key considerations include mitigating urban-specific issues like noise, safety, and aesthetic impacts, as well as ensuring compatibility with supportive policy frameworks. Advancing this technology will require innovative approaches to structural adaptation, strategic economic incentives, and tailored designs to enhance its feasibility and sustainability within the urban energy landscape.

5. Conclusions

The wind turbine design method based on the optimization approach was used to design highly efficient small wind turbines for distributed energy generation in urban and sub-urban areas, which can contribute to the development of sustainable cities. In addition to bare rotor design, diffuser augmented small wind turbine design was investigated. The proposed design concepts were compared from the technical and economical point of view, to conclude on the economic viability of improved small wind turbines in urban areas. To take into consideration the influence of wind conditions at the considered location on the economics of a particular wind turbine design, several cities in Croatia with different wind conditions were compared. The numerical calculations were performed to determine aerodynamic performance of the turbine design concepts at different wind speed conditions. The power curves were derived from the numerical simulations results. The reliability of the simulation results was confirmed by performing the numerical uncertainty assessment using GCI method. Based on the above analysis following conclusions are derived:

• The numerical simulation results indicate that significant increase in the power coefficient is obtained with diffuser augmentation DSWT compared to bare rotor design BSWT. Moreover, DSWT power coefficients are relatively high in a wide range of operating conditions (at different wind speeds). The maximum power coefficient of 0.43 is achieved at TSR of 3.5 for BSWT while for DSWT the maximum power coefficient of 0.78 is achieved at TSR of 4.5.
• The calculated LCOE is the lowest for the diffuser augmented turbines (DSWT) at all the considered locations, but the best wind conditions for small wind turbine installation are in Split. It worth noting that the use of a more sophisticated variable speed control strategy resulted in a higher LCOE than in the case of the fixed speed generator in Split, Knin and Šibenik, while in Zadar it is lower. This can be explained by comparing histograms. Most of the time, the wind speeds are far from the design conditions and there is more of an advantage of a variable rotational speed generator that enables operation at maximum efficiency even in the case of these off-design wind conditions. This leads to the conclusion that the use of a more expensive and more sophisticated variable rotational speed generator is justified mainly at locations where there is a significant frequency of wind speeds (above 40–50%) that are far from the design wind speed value.
• The sensitivity analysis demonstrates that diffuser-augmented turbines, particularly the DSWT-FS model, remain economically competitive, even with significant increases in investment and maintenance costs, offering a promising alternative to traditional bare turbine technologies. Moreover, the analysis of overestimated energy production reveals that, even when DSWT technology experiences a 20% reduction in actual energy production compared to the estimated value, its LCOE remains comparable to or lower than that of BSWT technology, where actual production matches the initial estimate.
• To ensure the reliable operation of small wind turbines with the diffuser in the urban areas, it is necessary to further consider the protection of diffuser augmented turbines in extreme wind conditions.