Research on Rolling Bearing Fault Diagnosis Method Based on MPE and Multi-Strategy Improved Sparrow Search Algorithm Under Local Mean Decomposition
Abstract
1. Introduction
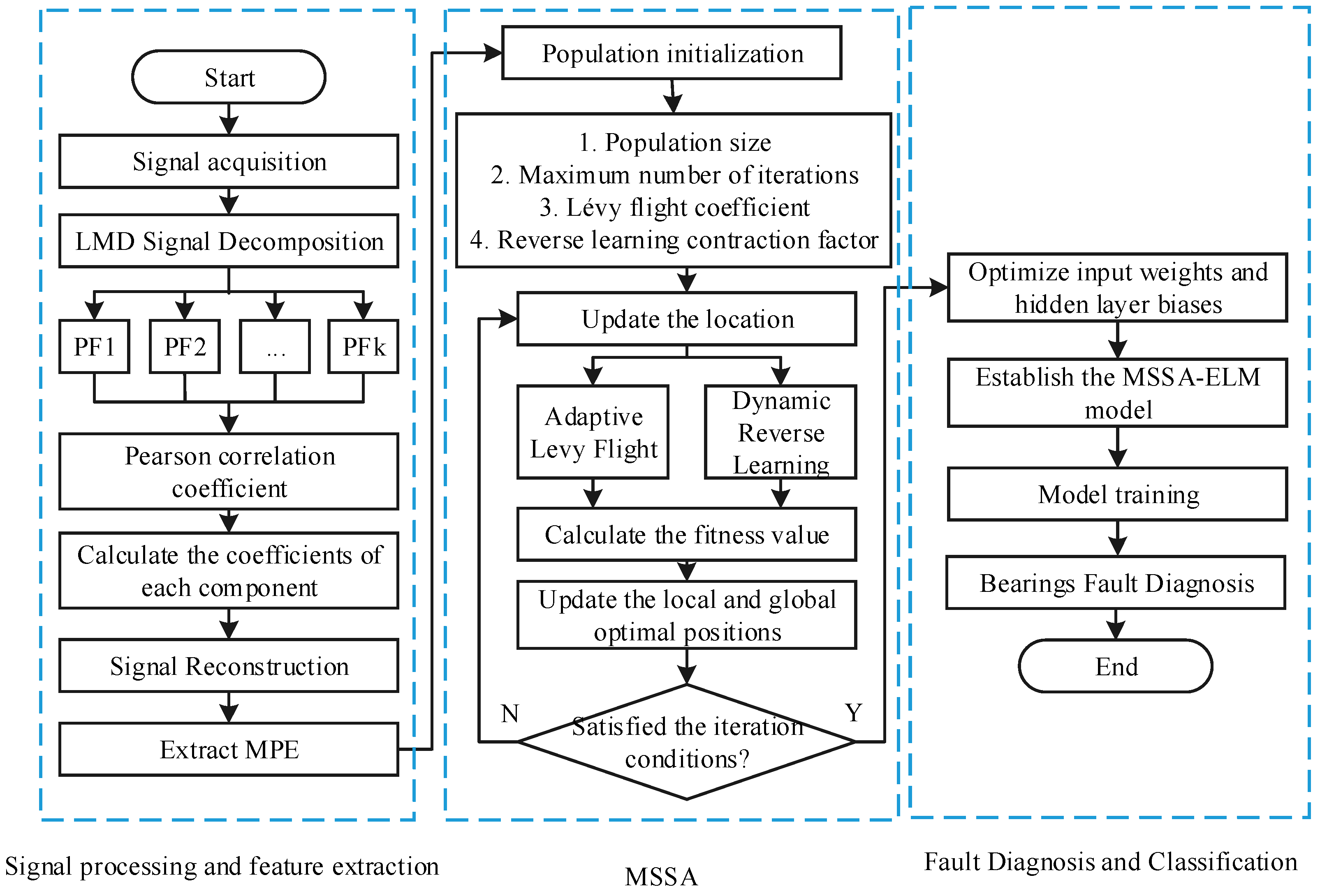
2. Signal Decomposition, Reconstruction, and Feature Extraction
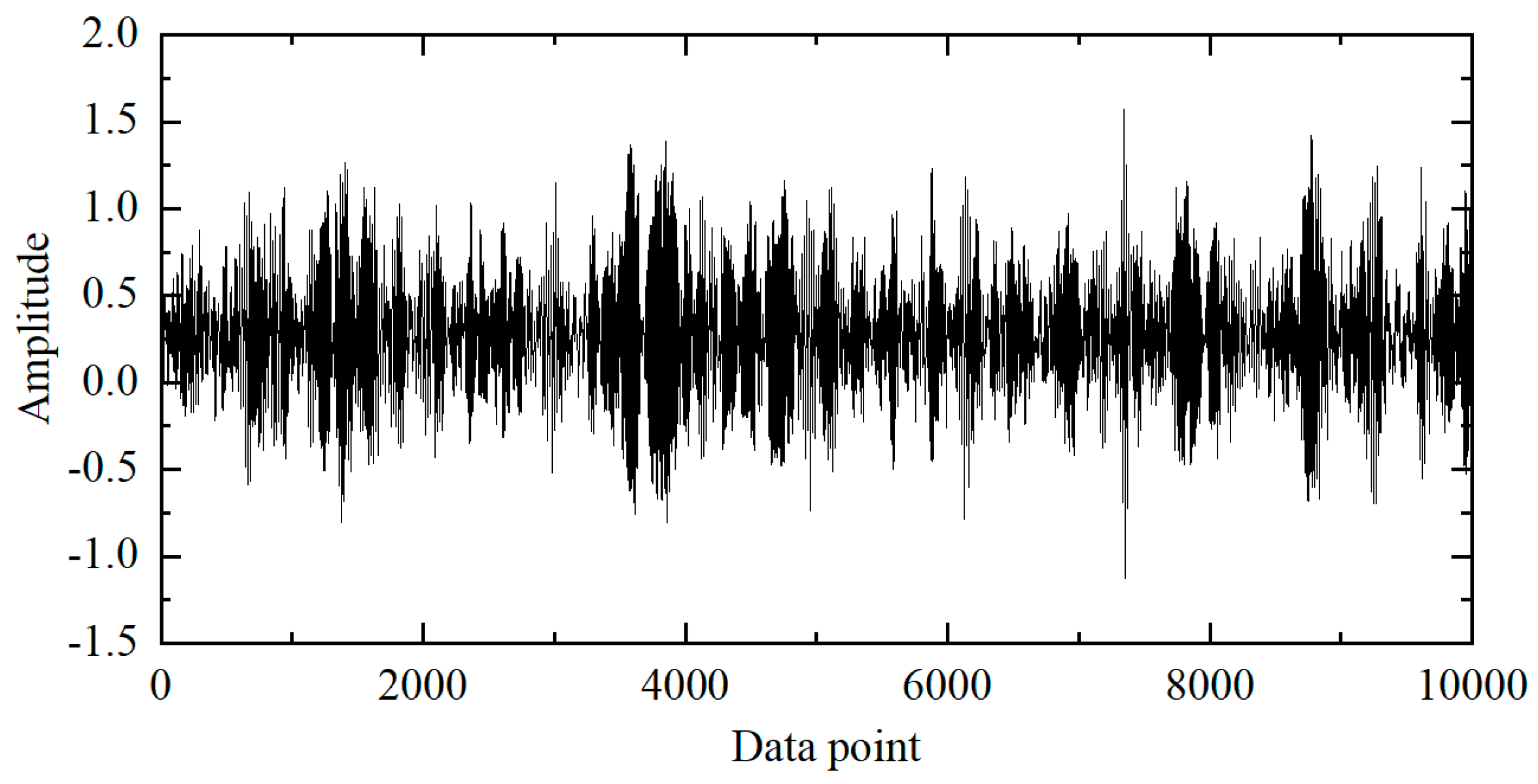
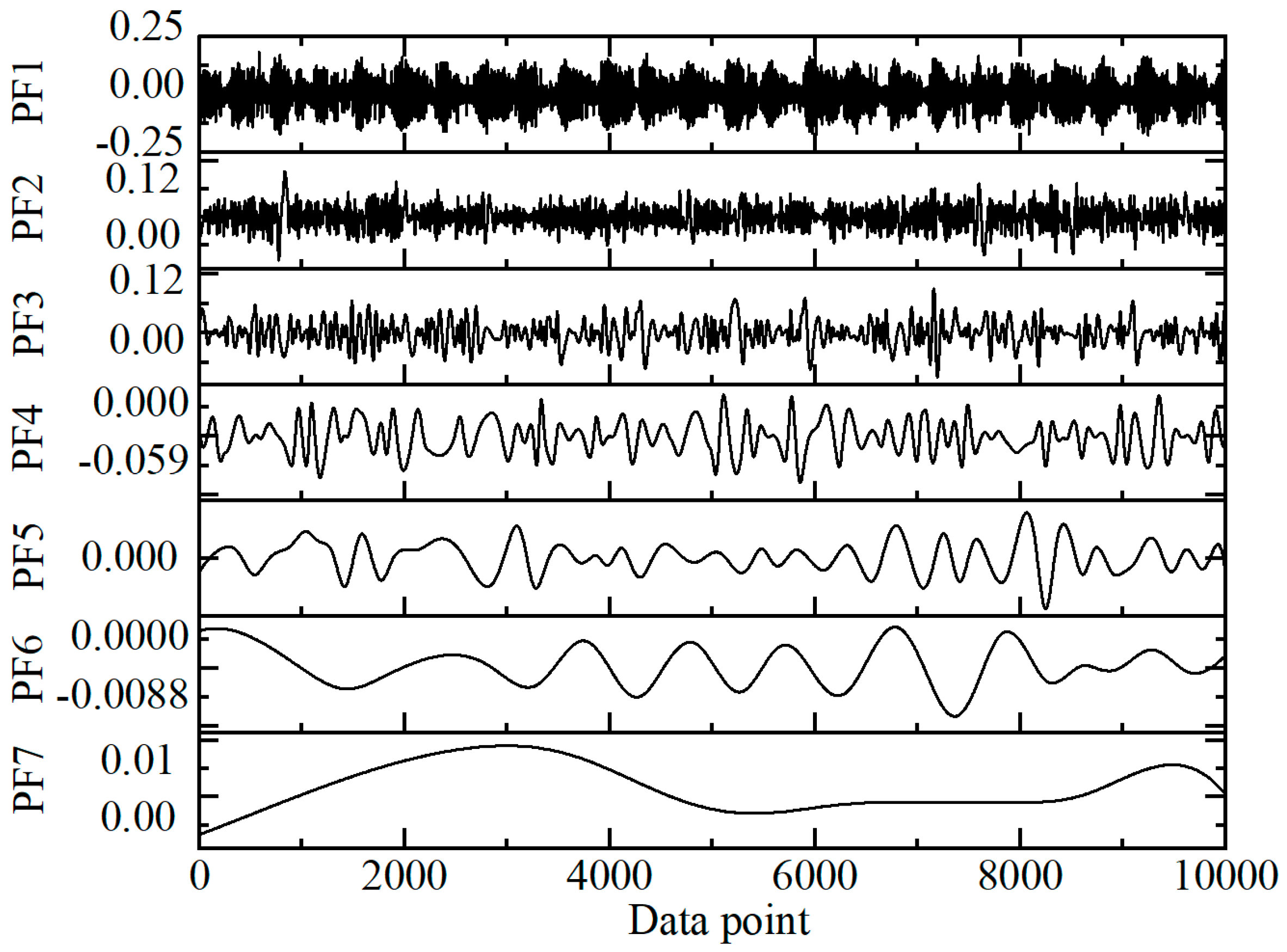
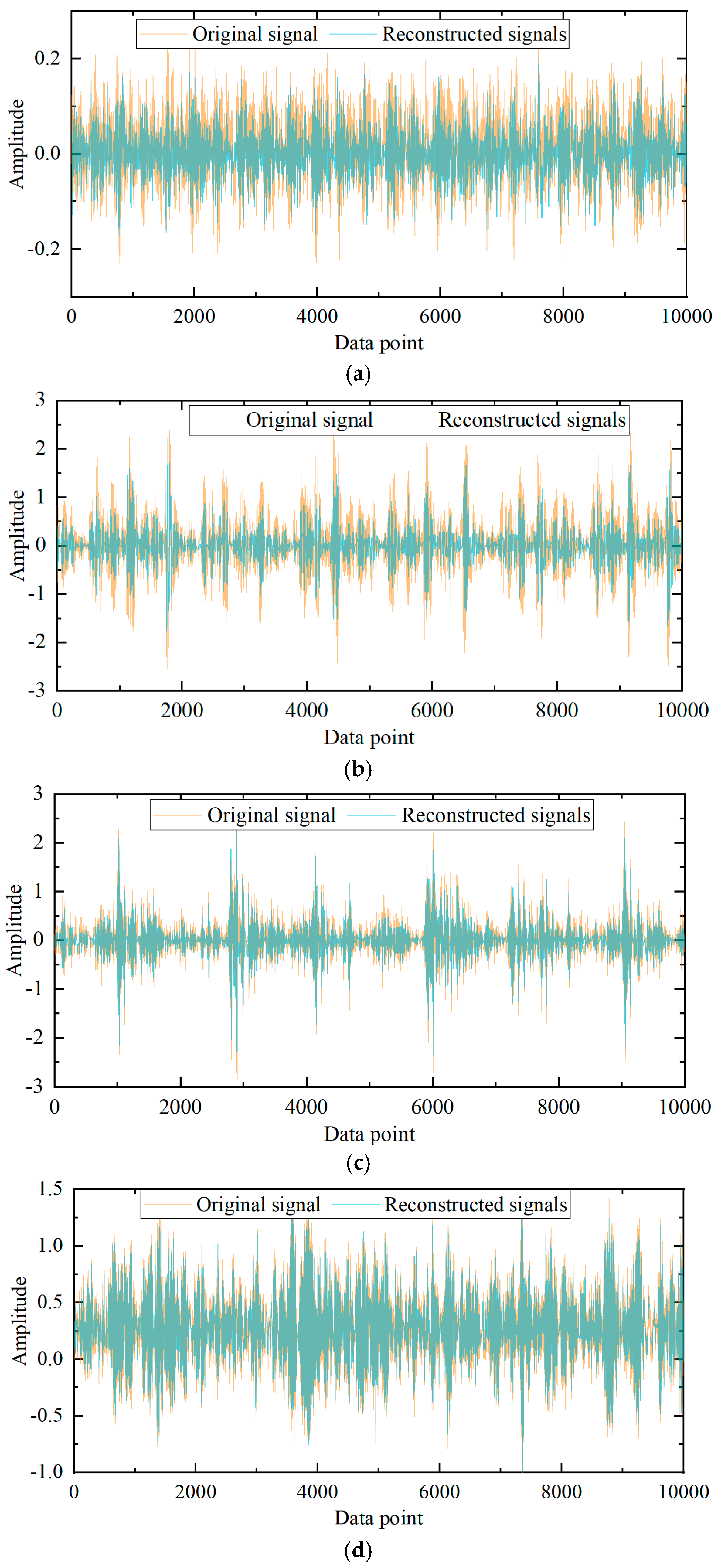
2.1. Bearing Signal Decomposition and Reconstruction
- (1)
- Extraction of Extremum Points and Interpolation: Given a bearing vibration signal , the local extremum points are first identified, including the sequence of local maxima and the sequence of local minima . Using cubic spline interpolation, the local mean function and the envelope estimation function are constructed.where the represents the Local mean function derived during the first iteration of the first decomposition stage, and is the envelope estimation function computed in the first iteration of the first decomposition stage.
- (2)
- Iterative Demodulation to Generate Frequency-Modulated Components: The local mean function is removed to obtain the mean-corrected signal .where the is the mean-corrected residual signal after removing in the first iteration of PF1.
- (3)
- PF Component Generation and Residual Signal Update: After iterations, the first PF component is obtained by multiplying the final frequency-modulated component with the cumulative envelope function.
2.2. Multi-Scale Permutation Entropy Feature Extraction
3. Rolling Bearing Fault Diagnosis Method Based on Multi-Strategy Improved Sparrow Search Algorithm Optimize ELM
3.1. Extreme Learning Machine
3.2. Multi-Strategy Improved Sparrow Search Algorithm
3.3. MSSA-ELM-Based Bearing Fault Diagnosis Model
4. Experimental Analysis
5. Conclusions
- (1)
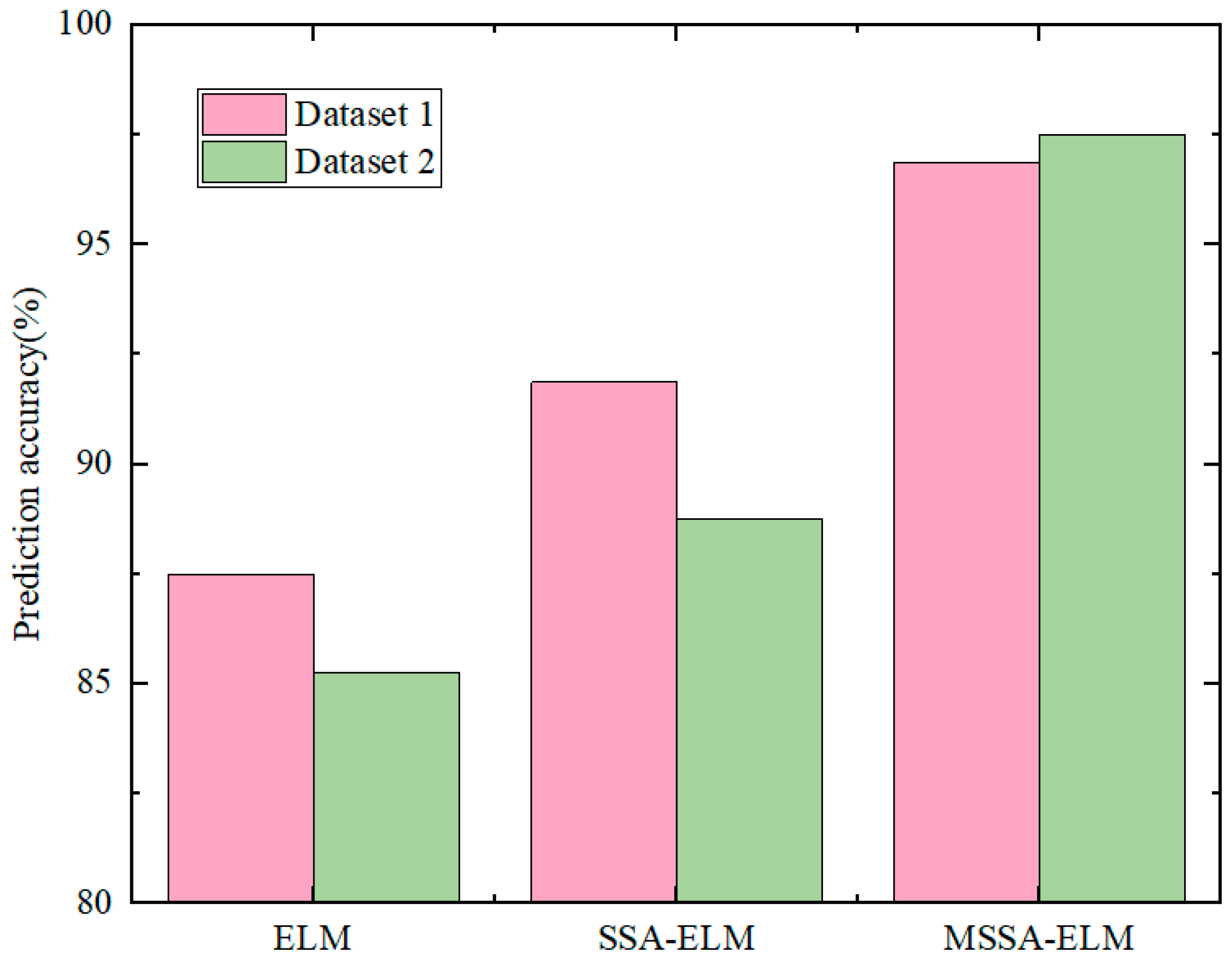
- Effectiveness of signal preprocessing: To address the challenge of fault signal interference and feature ambiguity under low-speed conditions, LMD combined with Pearson correlation coefficient-based reconstruction was applied. This method effectively removed irrelevant noise while preserving high-frequency features indicative of local faults and abnormal wear. The experimental results show that this preprocessing step improves model accuracy from 93.75% to 96.875%, providing a clearer and more reliable data foundation for subsequent feature extraction.
- (2)
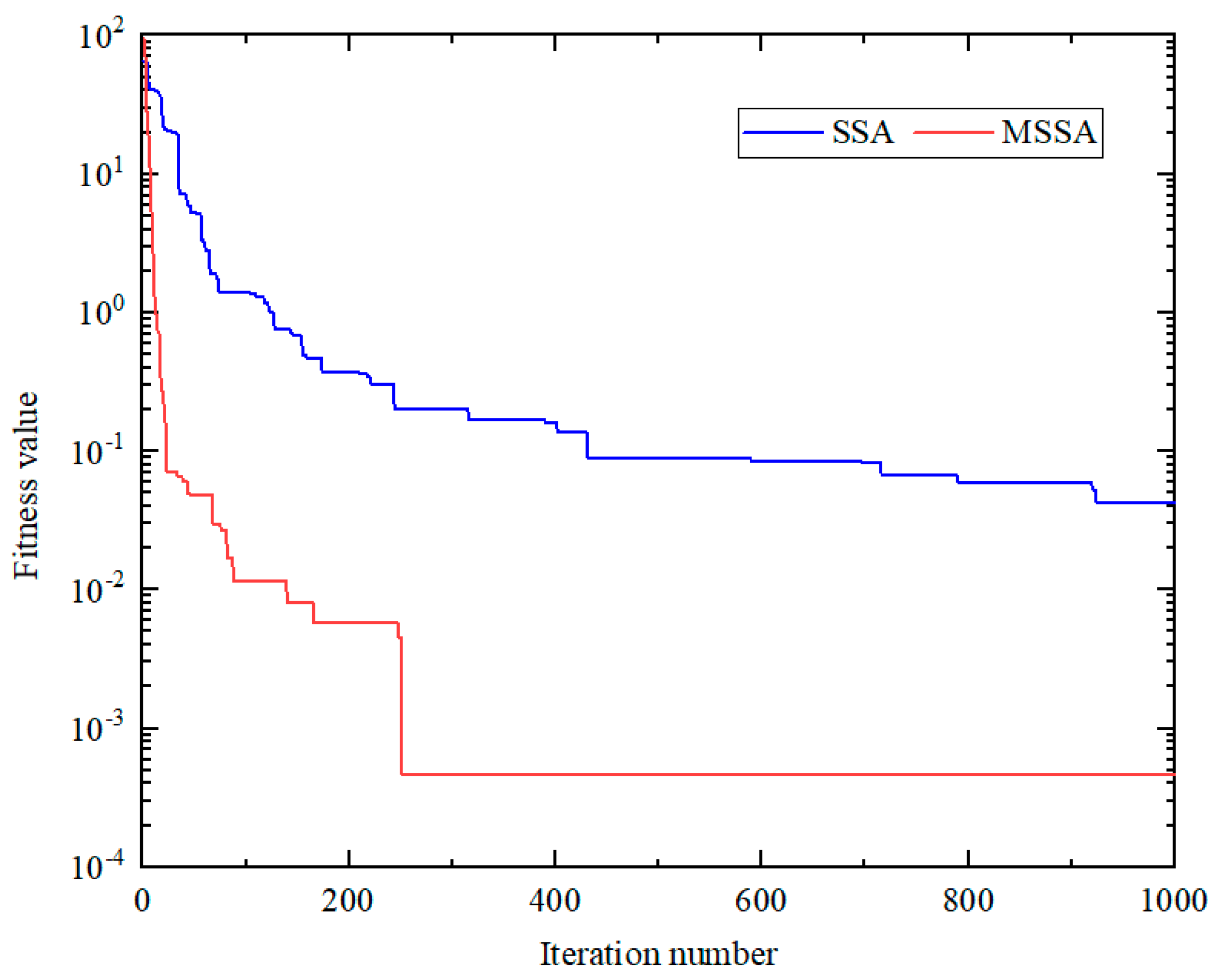
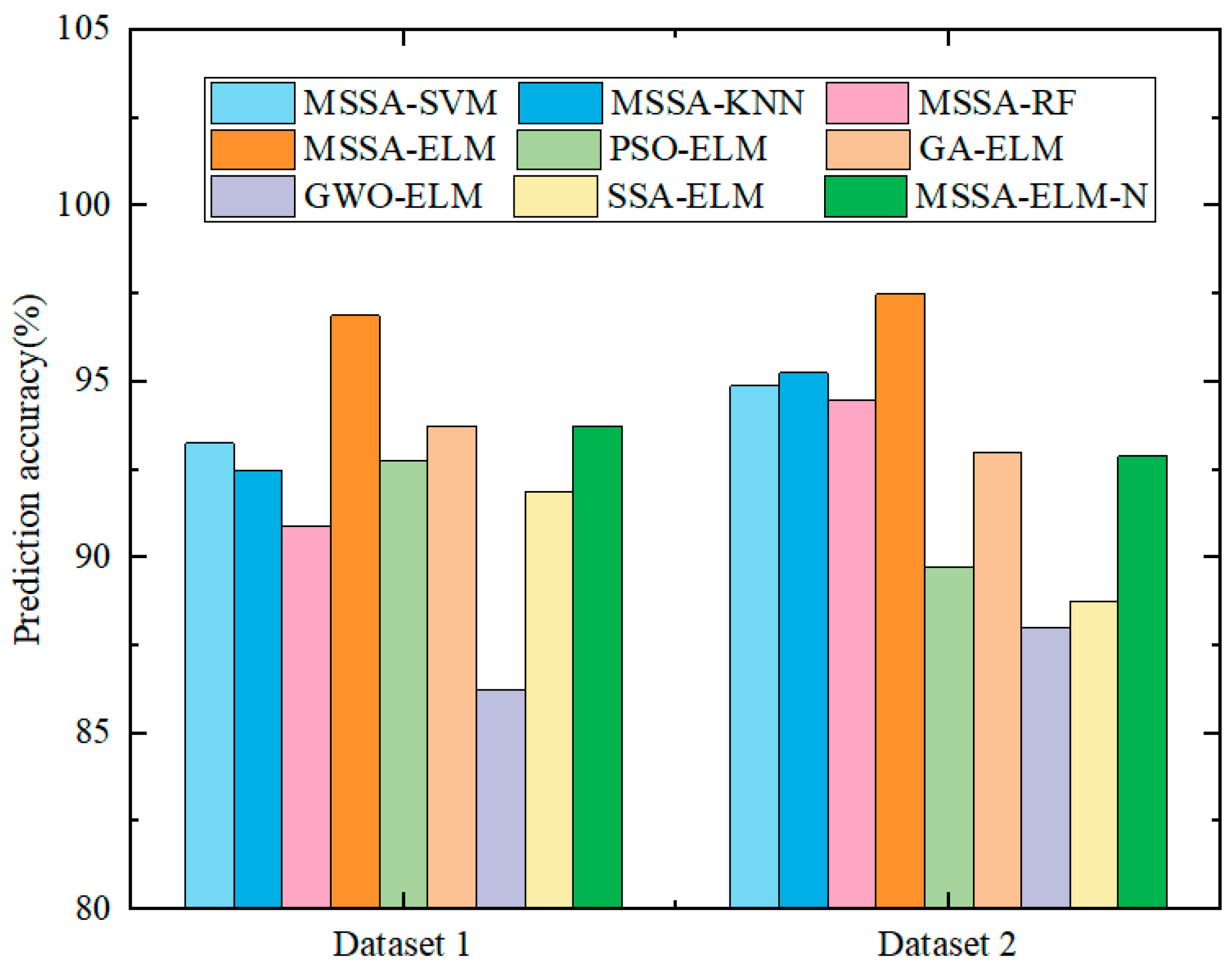
- An enhanced optimization strategy: To overcome the local optima problem and slow convergence of traditional SSA, this study integrates adaptive Levy flight and dynamic opposition-based learning into the optimization framework. Levy flight expands the search space via long-tail jumps, while dynamic opposition-based learning enhances population diversity, achieving a well-balanced global and local search process. The experimental results confirm that models optimized using MSSA consistently exceed 96% accuracy across multiple datasets, demonstrating its superior parameter optimization capability.
- (3)
- Comprehensive performance validation: The proposed method, integrating signal preprocessing and multi-strategy optimization, achieves over 95% accuracy on both the Xi’an Jiaotong University bearing dataset and the laboratory-collected dataset, proving its robustness and adaptability across different working conditions and noisy environments.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cerrada, M.; Sánchez, R.V.; Li, C.; Pacheco, F.; Cabrera, D.; Oliveira, J.; Vásquez, R. A review on data-driven fault severity assessment in rolling bearings. Mech. Syst. Signal Process. 2018, 99, 169–196. [Google Scholar] [CrossRef]
- Jain, P.H.; Bhosle, S.P. Analysis of vibration signals caused by ball bearing defects using time-domain statistical indicators. Int. J. Adv. Technol. Eng. Explor. 2022, 9, 700. [Google Scholar]
- Jawad, S.M.; Jaber, A.A. Bearings health monitoring based on frequency-domain vibration signals analysis. Eng. Technol. J. 2022, 41, 86–95. [Google Scholar] [CrossRef]
- Li, Y.; Zhou, J.; Li, H.; Meng, G.; Bian, J. A fast and adaptive empirical mode decomposition method and its application in rolling bearing fault diagnosis. IEEE Sens. J. 2022, 23, 567–576. [Google Scholar] [CrossRef]
- Nishat Toma, R.; Kim, C.H.; Kim, J.M. Bearing fault classification using ensemble empirical mode decomposition and convolutional neural network. Electronics 2021, 10, 1248. [Google Scholar] [CrossRef]
- Hu, C.; Xing, F.; Pan, S.; Yuan, R.; Lv, Y. Fault diagnosis of rolling bearings based on variational mode decomposition and genetic algorithm-optimized wavelet threshold denoising. Machines 2022, 10, 649. [Google Scholar] [CrossRef]
- Liang, T.; Lu, H. A novel method based on multi-island genetic algorithm improved variational mode decomposition and multi-features for fault diagnosis of rolling bearing. Entropy 2020, 22, 995. [Google Scholar] [CrossRef]
- Wang, L.; Liu, Z.; Miao, Q.; Zhang, X. Complete ensemble local mean decomposition with adaptive noise and its application to fault diagnosis for rolling bearings. Mech. Syst. Signal Process. 2018, 106, 24–39. [Google Scholar] [CrossRef]
- Han, M.; Wu, Y.; Wang, Y.; Liu, W. Roller bearing fault diagnosis based on LMD and multi-scale symbolic dynamic information entropy. J. Mech. Sci. Technol. 2021, 35, 1993–2005. [Google Scholar] [CrossRef]
- Zhao, D.; Liu, S.; Cheng, S.; Sun, X.; Wang, L.; Wei, Y.; Zhang, H. Parallel multi-scale entropy and it’s application in rolling bearing fault diagnosis. Measurement 2021, 168, 108333. [Google Scholar] [CrossRef]
- Ying, W.; Tong, J.; Dong, Z.; Pan, H.; Liu, Q.; Zheng, J. Composite multivariate multi-Scale permutation entropy and laplacian score based fault diagnosis of rolling bearing. Entropy 2022, 24, 160. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Wang, H.; Ren, M.; He, M.; Jin, L. Rolling bearing fault diagnosis based on multiscale permutation entropy and SOA-SVM. Machines 2022, 10, 485. [Google Scholar] [CrossRef]
- He, C.; Wu, T.; Gu, R.; Jin, Z.; Ma, R.; Qu, H. Rolling bearing fault diagnosis based on composite multiscale permutation entropy and reverse cognitive fruit fly optimization algorithm–extreme learning machine. Measurement 2021, 173, 108636. [Google Scholar] [CrossRef]
- Chen, Y.; Yuan, Z.; Chen, J.; Sun, K. A novel fault diagnosis method for rolling bearing based on hierarchical refined composite multiscale fluctuation-based dispersion entropy and PSO-elm. Entropy 2022, 24, 1517. [Google Scholar] [CrossRef]
- Meng, L.; Liu, M.; Wei, P.; Qin, H. Rolling Bearing Fault Diagnosis Based on Improved VMD And GA-ELM. In Proceedings of the 2021 40th Chinese Control Conference (CCC), Shanghai, China, 26–28 July 2021; pp. 4414–4419. [Google Scholar]
- Gao, S.; Xu, L.; Zhang, Y.; Pei, Z. Rolling bearing fault diagnosis based on SSA optimized self-adaptive DBN. ISA Trans. 2022, 128, 485–502. [Google Scholar] [CrossRef]
- Chen, D.; Zhao, J.D.; Huang, P.; Deng, X.; Lu, T. An improved sparrow search algorithm based on levy flight and opposition-based learning. Assem. Autom. 2021, 41, 697–713. [Google Scholar] [CrossRef]
- Yu, X.; Peng, W.; Liu, Y. WSN node localization algorithm of sparrow search based on elite opposition-based learning and Levy flight. Telecommun. Syst. 2023, 84, 521–531. [Google Scholar] [CrossRef]
- Xu, L.; Li, W.; Zhang, B.; Zhu, Y.; Lang, C. Fault diagnosis of mine truck hub drive system based on LMD multi-component sample entropy fusion and LS-SVM. Actuators 2023, 12, 468. [Google Scholar] [CrossRef]
- Qin, L.; Yang, G.; Sun, Q. Maximum correlation Pearson correlation coefficient deconvolution and its application in fault diagnosis of rolling bearings. Measurement 2022, 205, 112162. [Google Scholar] [CrossRef]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef]
- Costa, M.; Goldberger, A.L.; Peng, C.K. Multiscale entropy analysis of complex physiologic time series. Phys. Rev. Lett. 2002, 89, 068102. [Google Scholar] [CrossRef] [PubMed]
- Suthar, V.; Vakharia, V.; Patel, V.K.; Shah, M. Detection of compound faults in ball bearings using multiscale-SinGAN, heat transfer search optimization, and extreme learning machine. Machines 2022, 11, 29. [Google Scholar] [CrossRef]
- Lv, J.; Sun, W.; Wang, H.; Zhang, F. Coordinated approach fusing RCMDE and sparrow search algorithm-based SVM for fault diagnosis of rolling bearings. Sensors 2021, 21, 5297. [Google Scholar] [CrossRef] [PubMed]
- Lv, J.; Xiao, Q.; Zhai, X.; Shi, W. A high-performance rolling bearing fault diagnosis method based on adaptive feature mode decomposition and Transformer. Appl. Acoust. 2024, 224, 110156. [Google Scholar] [CrossRef]
- Houssein, E.H.; Helmy, B.E.; Rezk, H.; Nassef, A.M. An efficient orthogonal opposition-based learning slime mould algorithm for maximum power point tracking. Neural Comput. Appl. 2022, 34, 3671–3695. [Google Scholar] [CrossRef]



| Parameter Name | Value | Parameter Name | Value |
|---|---|---|---|
| Inner ring raceway diameter (mm) | 29.30 | Ball diameter (mm) | 7.92 |
| Outer ring raceway diameter (mm) | 39.80 | Number of balls | 8 |
| Bearing pitch diameter (mm) | 34.55 | Contact angle (°) | 0 |
| Basic dynamic load rating (N) | 12,820 | Basic static load rating (kN) | 6.65 |
| Condition Number | 1 | 2 | 3 |
|---|---|---|---|
| Rotational speed (r/min) | 2100 | 2250 | 2400 |
| Radial force (kN) | 12 | 11 | 10 |
| Component | Normal | Inner Race Fault | Outer Race Fault | Roller Fault |
|---|---|---|---|---|
| PF1 | 0.6251 | 0.8562 | 0.6653 | 0.5694 |
| PF2 | 0.4395 | 0.5328 | 0.6257 | 0.5328 |
| PF3 | 0.3640 | 0.3365 | 0.4962 | 0.4013 |
| PF4 | 0.3326 | 0.2143 | 0.3851 | 0.3610 |
| PF5 | 0.1203 | 0.1896 | 0.1694 | 0.2681 |
| PF6 | 0.0033 | 0.0963 | 0.1125 | 0.1549 |
| PF7 | 0 | 0.0574 | 0.0743 | 0.0395 |
| Model | Fault Type | Overall | |||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||
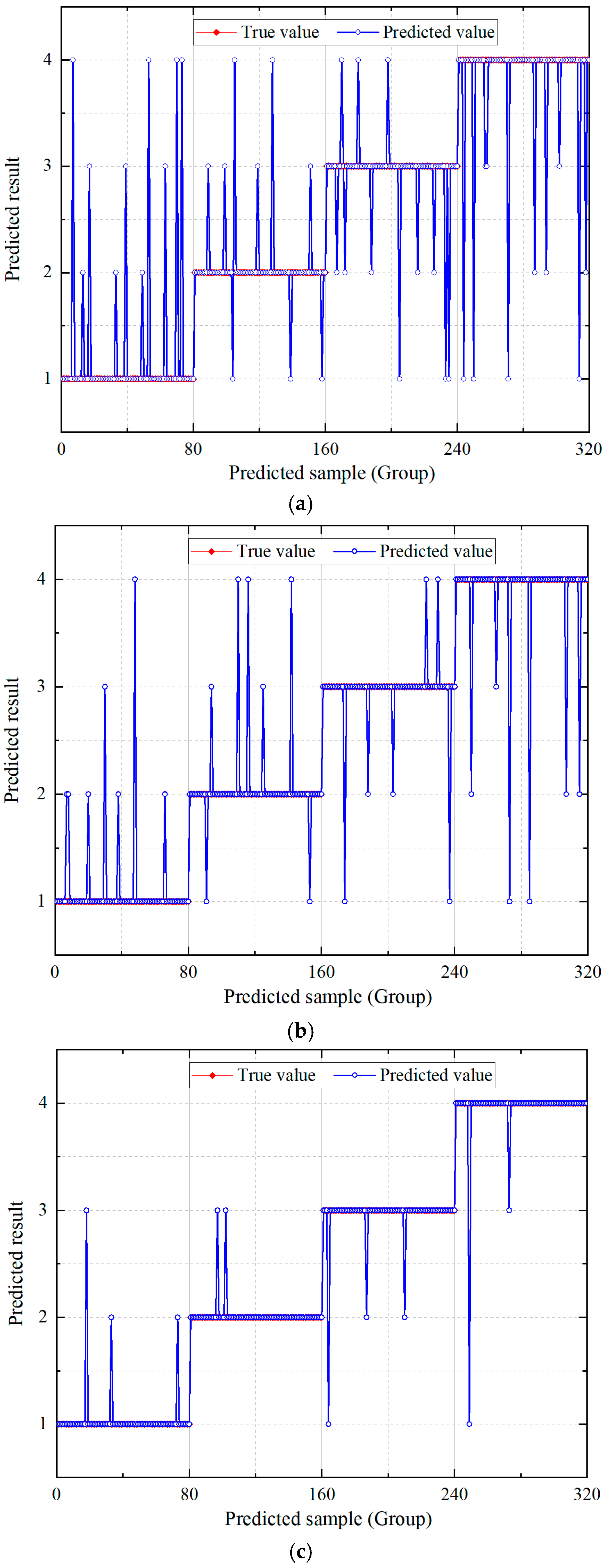
| ELM | 87.5 | 88.75 | 86.25 | 87.5 | 87.5 |
| SSA-ELM | 91.25 | 91.25 | 92.5 | 92.5 | 91.875 |
| MSSA-ELM | 96.25 | 97.5 | 96.25 | 97.5 | 96.875 |
| Method | Average Runtime (s) | Accuracy (%) |
|---|---|---|
| LMD-MPE-MSSA-ELM | 3.9 | 96.875 |
| VMD-MPE-MSSA-ELM | 3.6 | 92.19 |
| EEMD-MPE-MSSA-ELM | 5.8 | 89.06 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chi, H.; Chen, H. Research on Rolling Bearing Fault Diagnosis Method Based on MPE and Multi-Strategy Improved Sparrow Search Algorithm Under Local Mean Decomposition. Machines 2025, 13, 336. https://doi.org/10.3390/machines13040336
Chi H, Chen H. Research on Rolling Bearing Fault Diagnosis Method Based on MPE and Multi-Strategy Improved Sparrow Search Algorithm Under Local Mean Decomposition. Machines. 2025; 13(4):336. https://doi.org/10.3390/machines13040336
Chicago/Turabian StyleChi, Haodong, and Huiyuan Chen. 2025. "Research on Rolling Bearing Fault Diagnosis Method Based on MPE and Multi-Strategy Improved Sparrow Search Algorithm Under Local Mean Decomposition" Machines 13, no. 4: 336. https://doi.org/10.3390/machines13040336
APA StyleChi, H., & Chen, H. (2025). Research on Rolling Bearing Fault Diagnosis Method Based on MPE and Multi-Strategy Improved Sparrow Search Algorithm Under Local Mean Decomposition. Machines, 13(4), 336. https://doi.org/10.3390/machines13040336





