Fatigue Crack Growth Simulation of R260 Grade Pearlitic Rail Steel Using the Discrete Element Method

Abstract

Fatigue-induced crack initiation and propagation are a major concern in pearlitic railway rails and wheels. Rails and wheels undergo significant plastic deformation on their near-surface layers during service, leading to the initiation and propagation of cracks within the deformed region. Existing models typically use finite element models (FEMs) to describe these kinds of fatigue phenomena. However, they fail to establish a strong connection between the microstructure of the undeformed and the deformed materials and their corresponding fatigue properties. Therefore, a model based on the soft-contact discrete element method (DEM) was developed that considers microstructural details such as prior austenite grains (PAGs), pearlite blocks, pearlite colonies, and lamellar orientation of the ferrite–cementite structure of the pearlite. The Voronoi Tessellation method was used to generate a hierarchical mesh to represent these microstructural details, considering the distribution of microstructural details. Crack propagation is simulated by applying damage laws on the microstructural interface level that degrade the stiffness of the fibers connecting the mesh elements. The model’s crack growth predictions are compared with experimental results from the literature to validate its accuracy for different deformation degrees. The developed model can be used in the designing and material selection phase in the railway industry to help select the material with optimum microstructural features. Also, it can be used for the selection of the optimum heat treatment process considering materials resistance to the fatigue crack growth.

1. Introduction

The contact forces at the wheel–rail interface are the result of the vehicle’s weight, acceleration, braking, and steering forces [1]. If stresses in the contact areas are greater than the plastic yield limit, the material experiences plastic deformation. Pearlitic steel is the common material used in manufacturing rails and wheels in Europe [1]. The mechanical characteristics of pearlitic steel are highly dependent on its microstructural features. For pearlitic steel, the interlamellar spacing is a critical microstructural feature. There is a correlation between the interlamellar spacing and the steel’s strength, as demonstrated by Dollar et al. [2]. Bouaziz et al. [3] also developed a relationship to predict the effect of the interlamellar spacing on the flow stress. Grain size is one of the parameters that can influence the mechanical properties of pearlitic steel. The Hall–Petch relation is one of the most well-known relationships describing grain size’s effect on yield strength [4]. Pearlitic steel shows mechanical properties resulting from the mixture of ferrite and cementite, making it strong and resistant to wear without being too brittle; therefore, it can withstand the heavy cyclic loads experienced by railway infrastructure [1].

The contact zone between train wheels and rails is tiny, resulting in high contact pressures that can cause localized severe plastic deformations (SPDs) near the surface. Cracks originate mainly from the highly deformed regions below the surface [5]. Improving the crack growth model’s reliability and accuracy in SPD regions can increase maintenance planning reliability and traffic safety [6]. Scientists have developed techniques to produce severely deformed microstructures, such as high-pressure torsion (HPT) [7]. The scheme for creating a severely plastically deformed microstructure through the HPT process involves applying substantial torque and hydrostatic pressure to a disk-shaped sample. The usual experimental approach to investigate the effect of severe plastic deformation on the mechanical properties of railway material is to find a relationship between the microstructure, mechanical properties, and the local strain for lab-produced severely deformed microstructure or worn rails [8,9,10,11,12]. The effect of SPD microstructure on fatigue behavior has also been widely researched experimentally [13,14,15,16,17,18,19].

Additionally, the effect of plastic deformation on fatigue life was investigated numerically using a parameter that accounts for microstructural characteristics [20,21]. The T-γ model [22] was developed to predict crack initiation using damage function. The finite element method, FEM, combined with cohesive zone modeling, is often used for modeling fatigue crack growth in the literature [23]. Vijay et al. [24] developed a 3D FEM model to analyze the anisotropy in rolling contact fatigue as a result of anisotropic material properties (randomness) in crystals. Integrating cohesive zone modeling and extended finite element methods enabled Dekker et al. to model crack growth in arbitrary paths [25]. Arata et al. [26] used the cohesive zone modeling method to investigate the crack path within the lamellar structure of titanium aluminide grains. Another alternative approach to model fatigue crack growth is to use the crack growth resistance function in the domain of interest. With the help of such functions, Larijani et al. [27] developed a model to calculate the fatigue crack growth rate anisotropy in near-surface layers of deformed wheel materials without explicitly considering microstructural features. Nezhad et al. [28] developed a 3D finite element model to predict the rolling contact fatigue (RCF) crack growth direction and rate in railheads under combined stress and thermal loading.

Other than FEM, some methods are capable of modeling crack growth, such as the discrete element method (DEM) and Peridynamic model. The DEM is typically used for granular materials. However, it can be employed to model solid-state materials. The discrete element method was first introduced by Cundall and Strack in 1979 to analyze granular material [29]. The DEM is a strong computational method for discontinuous material [30,31,32,33,34]. Raje et al. [35,36,37] used the soft contact discrete element model (which is in the family of the DEM) to investigate RCF in roller bearings. Januschewsky et al. [38] developed a DEM model capable of predicting the rolling contact model (RCF) with a novel bond law considering crack closure behavior.

This research presents a method to predict the fatigue crack growth (FCG) rate via DEM in deformed and undeformed microstructures of pearlitic steels. The model is designed to account for the impact of plastic deformation during service life on the microstructure and behavior of cracks. The model employs a hierarchical mesh introduced by Davoodi Jooneghani et al. [39]. In the hierarchical mesh, each layer represents a distinct microstructural feature. The model combines the DEM and damage criteria. This combination allows for the prediction of the crack growth rate. The influence of plastic deformation on the FCG rate is determined to be substantial, and this outcome is further analyzed by comparing it with crack growth rate data for a particular variant of pearlitic steel, identified as R260, as documented in existing research. The developed model can connect microstructural features and plastic deformation with the material’s fatigue behavior during cyclic loading.

2. Experimental Methods and Materials

The experimental data used for this research were obtained from the i. high-pressure torsion (HPT) and ii. fatigue crack growth (FCG) studies conducted on undeformed, moderately deformed, and severely deformed R260 that were published in [18,19,40]. Their experiment started with cutting disks from an R260 rod with a 30 mm diameter cut longitudinally from the rail. These 8 mm thick disks were then sheared via HPT under a pressure of 5.6 GPa, producing two degrees of deformation: 0.25 and 3 rotations. The degree of deformations reached were moderately deformed ($\gamma =2$) and severely deformed ($\gamma =30$), where $\gamma$ is the shear strain. Compact tension (CT) specimens were then machined from these deformed disks according to ASTM E647 standard [41] with orientations as A-T, T-A, R-T, and T-R; the first letter refers to the crack plane normal vector direction and the second letter shows the expected propagation directions relative to the axial (A), tangential (T), and radial (R) directions of the HPT disk [18,19,40]. The shear plane normal vector as the result of deformation is in the axial direction. In this study, the focus is on A-T and T-A orientations. For FCG testing, the CT specimens undergo further preparation. A fatigue pre-crack is introduced to the specimen using a resonance testing machine. Specimens are subjected to a sinusoidal load with different load ratios (R = 0.1 and 0.7). The crack length was measured using the potential drop technique [18,19,40]. In this research, the load ratio of 0.1 was selected.

This experimental setup was designed to investigate the effects of severe plastic deformation induced by HPT on the fatigue crack growth behavior of the material. The FCG results for different deformation states are shown in Figure 1 [18,19,40].

3. Meshing Methodology

The meshing methodology used in this paper is based on a hierarchical mesh methodology for R260 pearlitic steel developed in previous research [39]. In this methodology, the 2D representation of the pearlitic steel microstructure was generated by subdividing a domain into cells based on some randomly generated seed points, from which Voronoi polygons were created. These polygons represent the pearlitic steel’s microstructural elements like prior austenite grains (PAGs), pearlite colonies, and pearlite blocks. The colony, block, and PAG sizes for the undeformed microstructure of R260 were measured. Colony size measurements were derived from several scanning electron microscope (SEM) images, with an average colony size of 15 µm. Since blocks are not visible in SEM, electron backscatter diffraction (EBSD) was used for block size analysis, measuring ~30 µm. Low-magnification optical microscopy (OM) images provided PAG size measurements similarly, which were calculated to be ~60 µm.

The undeformed state, moderately deformed states in the A-T and T-A orientations and severely deformed states in the A-T and T-A orientations were all represented by meshes created using the mesh methodology outlined in [39]. Three repetitions were made for each of the five deformation states to guarantee model robustness, yielding 20 meshes. These repetitions were similar in PAG size, pearlite block size, and pearlite colony size, as in the original mesh. The only variation among the repetitions was due to the randomness within the hierarchical mesh methodology [39]. These generated meshes were then analyzed for FCG behavior.

A shear strain of 2 was applied for the moderately deformed state. In contrast, a shear strain of 30 was used for the severely deformed (SPD) condition, as these values correspond to data available from Leitner’s studies [18,19,40], including data for the undeformed state. The meshes representing different deformation degree microstructures are shown in Figure 2.

Figure 3 shows the angular distribution of lamellae orientations for undeformed, moderately deformed, and severely deformed meshes. The severely deformed microstructure mostly aligned parallel to the shear plane, indicating the highest degree of alignment among the three deformations. However, the moderately deformed microstructure exhibited greater alignment than the undeformed state, but less than that of the severely deformed one.

4. FCG Modeling Using DEM

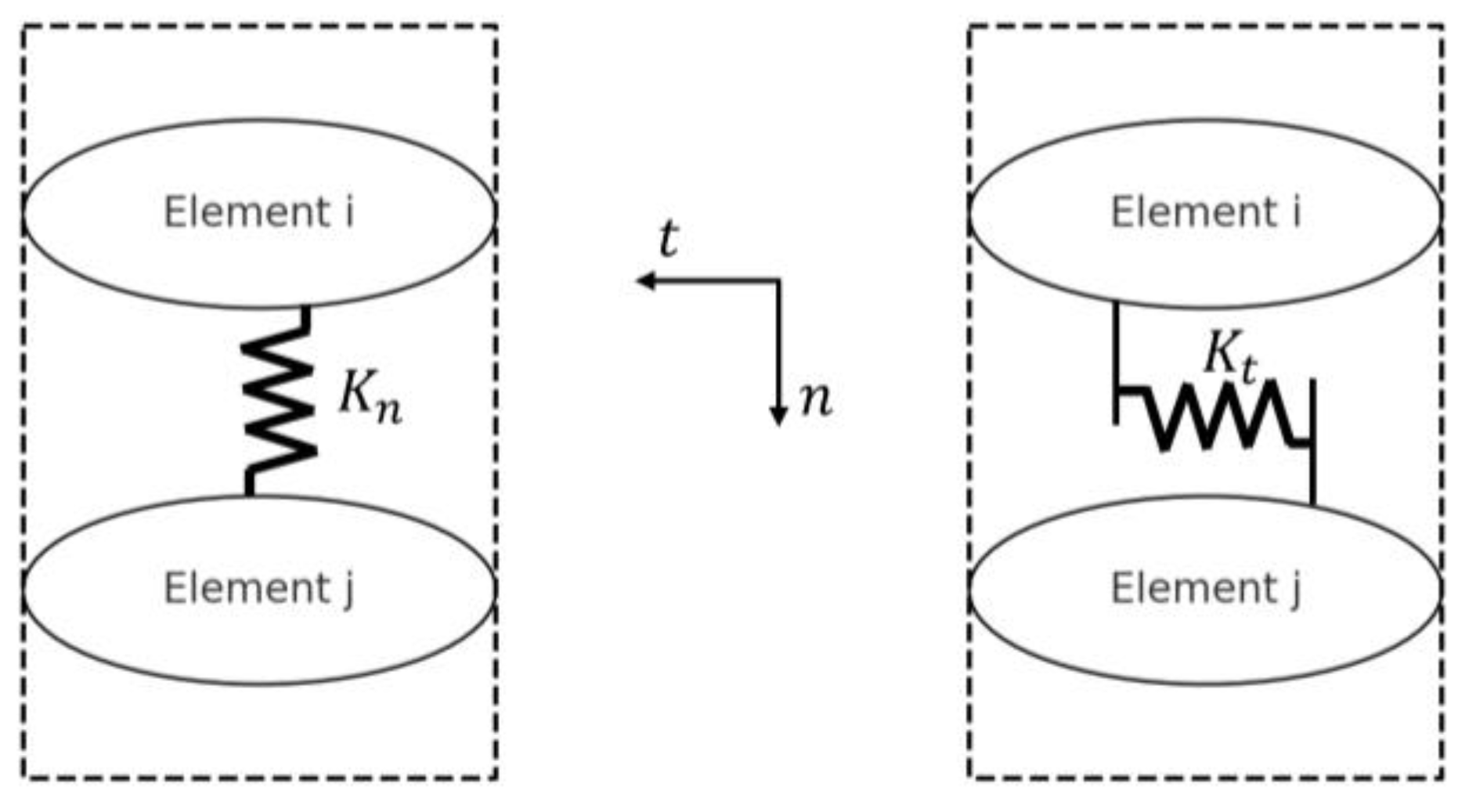
DEM is an appropriate approach to model fatigue crack growth in undeformed and shear-deformed microstructures because the microstructure can be explicitly considered. A DEM simulation is needed to calculate the stress field around the initial crack in the domain, which ultimately results in fatigue crack growth. The material is modeled in DEM as discrete, rigid entities interacting at their interfaces. Such interactions are modeled with springs, which link the elements together. The springs that join the elements are the only parts that deform; the elements do not deform. A two-element DEM setup is shown in Figure 4. Two discrete elements, $i$ and $j$, are in contact in this setup. The contact between these elements is modeled using springs in normal and tangential directions. The springs in the normal direction control the compressive and tensile interactions, while the tangential springs are responsible for the shear interactions between the elements. Here, $K_n$ and $K_t$ are the stiffness properties in these springs’ normal and tangential directions, respectively. The springs’ stiffnesses will degrade as a response to load cycles, following the applied damage law, and eventually, a crack will form.

The springs in a general DEM model can also exhibit damping properties. This damping usually takes the form of damping coefficients that scale with the springs’ stiffnesses. In the current work, damping is not included in the interface formulation. This simplification was used to isolate the measurement of the material’s static behavior because only the quasi-static results are of interest for the current study.

The stiffness values in the normal ($K_n$) and tangential ($K_t$) directions in the DEM are derived by integrating the distributed local stiffness along the contact surface length in $k_n$ and $k_t$. By integrating these local stiffness values over the length of contact ($l$), the global stiffness parameters, $K_n$ and $K_t$, for the interface are obtained. To derive the governing equilibrium equation in the DEM, two contacting elements, $i$ and $j$, were considered. When an external load is applied, deformation occurs in the contacting springs between these two elements (see Figure 5). In this figure, ${fc}_{ij}$ represents the center of the contact interface between elements $i$ and $j$. $c_{ij}$ is the point located on element $i$ at the distance of $x$ from ${fc}_{ij}$. $c_{ji}$ is the point located on element $j$, which was in contact with $c_{ij}$ prior to any deformation. Other parameters will be clarified in the following paragraphs.

The normal force $F_{n_{ij}}$ and the tangential force $F_{t_{ij}}$ can be described as follows in Equations (1)–(4), based on Figure 5:

$$F_{n_{ij}}=\underset{-{\displaystyle \frac{l}{2}}}{\overset{{\displaystyle \frac{l}{2}}}{\int }}{k}_{n_{ij}} {ds}_{n_{ij}} dx,$$

(1)

where $k_{n_{ij}}$ represents the distributed stiffness of the spring connecting elements $i$ and $j$. Furthermore, ${ds}_{n_{ij}}$ is the normal component of ${\overrightarrow{ds}}_{\mathrm{i}\mathrm{j}}$, which describes the fiber stretch connecting two points $c_{ij}$ and $c_{ji}$ in Figure 5. This normal displacement component is used to calculate the normal force generated in the spring, accounting for the stiffness and relative displacement between the elements.

$${ds}_{n_{ij}}\stackrel{\mathit{Relativity} for small \theta \left(sin\theta =\theta \right), @ position x}{\to }={ds}_{{{fc}_{ij}}_n}+x {\theta }_{{\displaystyle \frac{c_{ij}}{fc}}}={ds}_{{{fc}_{ij}}_n}+x \left({\theta }_j-{\theta }_i\right),$$

(2)

$$F_{n_{ij}}={\int }_{-{\displaystyle \frac{l}{2}}}^{{\displaystyle \frac{l}{2}}}{k}_{n_{ij}} {ds}_{n_{ij}} dx={\int }_{-{\displaystyle \frac{l}{2}}}^{{\displaystyle \frac{l}{2}}}{k}_{n_{ij}} \left( {ds}_{{{fc}_{ij}}_n}+x \left({\theta }_j-{\theta }_i\right)\right)dx=k_{n_{ij}} {ds}_{{{fc}_{ij}}_n} l,$$

(3)

Tangential force resists the sliding motion between the elements like the normal force resists compression or separation. The tangential force can be calculated by Equation (4).

$$F_{t_{ij}}=\underset{-{\displaystyle \frac{l}{2}}}{\overset{{\displaystyle \frac{l}{2}}}{\int }}{k}_{t_{ij}} {ds}_{t_{ij}} dx=\underset{-{\displaystyle \frac{l}{2}}}{\overset{{\displaystyle \frac{l}{2}}}{\int }}{k}_{t_{ij}} {ds}_{t_{ij}} dx=k_{t_{ij}} {ds}_{{{fc}_{ij}}_t} l,$$

(4)

where ${ds}_{{{fc}_{ij}}_n}$ and ${ds}_{{{fc}_{ij}}_t}$ represent the displacements of the springs at the midpoint of the contact face in the normal and tangential directions for element $i$, which is in contact with element $j$. ${\theta }_{{\displaystyle \frac{c_{ij}}{fc}}}$ is the rotational stretch of spring at the distance of $x$. ${\theta }_i$ and ${\theta }_j$ are the rotational displacement at elements $i$ and $j$. To proceed, it is necessary to relate ${ds}_{{{fc}_{ij}}_n}$ and ${ds}_{{{fc}_{ij}}_t}$ to the displacement of the center point of elements. The displacements of the center point of elements $i$ and $j$ are shown in Equation (5).

$$displacement at element i=\left\{\begin{array}{c}{X}_i\\ Y_i\\ {\theta }_i\end{array} and j=\left\{\begin{array}{c}{X}_j\\ Y_j\\ {\theta }_j\end{array}\right.\right.,$$

(5)

where $X$, $Y$, and $\theta$ are displacements in global coordinates in the $x$ and $y$ directions and rotational displacement of the element.

The displacements of the springs at the midpoint of the contact face are described in Equations (6) and (7).

$${\overrightarrow{ds}}_{{fc}_{ij}}=\left(X_j-X_i\right) \widehat{i}+( Y_j-Y_i) \widehat{j}+{L_{en}}_{{ji}_1} {\theta }_j \widehat{i}+{L_{en}}_{{ji}_2} {\theta }_j \widehat{j}-{L_{en}}_{{ij}_1} {\theta }_i \widehat{i}-{L_{en}}_{{ij}_2} {\theta }_i \widehat{j},$$

(6)

$${\overrightarrow{ds}}_{{\mathrm{f}\mathrm{c}}_{ij}}=\left[X_j-X_i+{L_{en}}_{{ji}_1} {\theta }_j-{L_{en}}_{{ij}_1} {\theta }_i\right] \widehat{i}+\left[Y_j-Y_i+{L_{en}}_{{ji}_2} {\theta }_j-{L_{en}}_{{ij}_2} {\theta }_i\right] \widehat{j},$$

(7)

where ${\overrightarrow{L}}_{en}$ is defined as a unit vector perpendicular to the vector connecting the center point of element $i$ to the midpoint of the contact face between elements $i$ and $j$ (see Figure 6). ${L_{en}}_{{ij}_1}$ is the component of ${\overrightarrow{L_{en}}}_{ij}$ in the $\widehat{i}$ direction and ${L_{en}}_{{ij}_2}$ is the component of ${\overrightarrow{L_{en}}}_{ij}$ in the $\widehat{j}$ direction.

To project the displacement vector ${\overrightarrow{ds}}_{{fc}_{ij}}$ in normal and tangential directions, the step shown in Equation (8) was taken.

$${ds}_{{fc}_{i{j}_n}}={\overrightarrow{n}}_{ij}·{\overrightarrow{ds}}_{{\mathrm{f}\mathrm{c}}_{ij}}=n_{{ij}_1} \left[X_j-X_i+{L_{en}}_{{ji}_1}{\theta }_j-{L_{en}}_{{ij}_1}{\theta }_i\right]+n_{{ij}_2} \left[Y_j-Y_i+{L_{en}}_{{ji}_2} {\theta }_j-{L_{en}}_{{ij}_2} {\theta }_i\right],$$

(8)

where $·$ is the dot product, $n_{{ij}_1}$ is the component of a normal vector (${\overrightarrow{n}}_{ij}$) in the $\widehat{i}$ direction, and $n_{{ij}_2}$ is the component of a normal vector in the $\widehat{j}$ direction. Similarly, the projection of the displacement vector ${\overrightarrow{ds}}_{{fc}_{ij}}$ in tangential directions is achieved with Equation (9).

$${ds}_{{fc}_{i{j}_t}}={{\overrightarrow{t}}_{ij}·{\overrightarrow{ds}}_{{fc}_{ij}}=t}_{{ij}_1}\left[X_j-X_i+{L_{en}}_{{ji}_1}{\theta }_j-{L_{en}}_{{ij}_1}{\theta }_i\right]+t_{{ij}_2} \left[Y_j-Y_i+{L_{en}}_{{ji}_2} {\theta }_j-{L_{en}}_{{ij}_2} {\theta }_i\right],$$

(9)

Therefore, the following expressions in Equations (10) and (11) for the normal and tangential components of the force were obtained.

$$F_{n_{ij}}=k_{n_{ij}} {ds}_{{fc}_{i{j}_n}} l=k_{n_{ij}} \left(n_{{ij}_1} \left[X_j-X_i+{L_{en}}_{{ji}_1}{\theta }_j-{L_{en}}_{{ij}_1}{\theta }_i\right]+n_{{ij}_2} \left[Y_j-Y_i+{L_{en}}_{{ji}_2} {\theta }_j-{L_{en}}_{{ij}_2} {\theta }_i\right]\right) l,$$

(10)

$$F_{t_{ij}}=k_{t_{ij}} {ds}_{{fc}_{i{j}_t}} l=k_{t_{ij}} \left(t_{{ij}_1} \left[X_j-X_i+{L_{en}}_{{ji}_1}{\theta }_j-{L_{en}}_{{ij}_1}{\theta }_i\right]+t_{{ij}_2} \left[Y_j-Y_i+{L_{en}}_{{ji}_2} {\theta }_j-{L_{en}}_{{ij}_2} {\theta }_i\right]\right) l,$$

(11)

Given the displacements of the two contacting elements $i$ and $j$, the force acting on the surface between these two elements can be calculated. Additionally, momentum (or torque) acting on the surface must be considered. The momentum should be calculated around the center point of the element. The momentum around the element center point is calculated as in Equation (12).

$${\overrightarrow{M}}_{ij}={\overrightarrow{M}}_{F_{ij}}+{\overrightarrow{M}}_{M_{ij}},$$

(12)

where ${\overrightarrow{M}}_{F_{\{i,j\}}}$ in Equation (13) is the momentum resulting from concentrated forces acting on the contacting surface between elements $i$ and $j$; ${\overrightarrow{M}}_{M_{\{i,j\}}}$ is the momentum resulting from distributed forces acting on the contacting surface between elements $i$ and $j$; and ${\overrightarrow{M}}_{\{i,j\}}$ is the momentum around the center point of the element.

$${\overrightarrow{M}}_{F_{ij}}={\overrightarrow{L}}_{ev}⨯\left(k_{n_{ij}} {ds}_{{fc}_{i{j}_n}} l {\overrightarrow{n}}_{ij}+k_{t_{ij}} {ds}_{{fc}_{i{j}_t}} l {\overrightarrow{t}}_{ij}\right),$$

(13)

where $⨯$ is the cross-product and ${\overrightarrow{L}}_{ev}$ is the lever vector shown in Figure 6. This equation translates the local momentum from the contact face to the element’s center by adding the moment caused by the distance between the two points. Therefore, $M_{M_{\{i,j\}}}$ can be expressed as Equation (14).

$${\overrightarrow{M}}_{M_{ij}}=\underset{-{\displaystyle \frac{l}{2}}}{\overset{{\displaystyle \frac{l}{2}}}{\int }}\overrightarrow{x} ⨯k_{n_{ij}} {\overrightarrow{ds}}_{ij} dx=\underset{-{\displaystyle \frac{l}{2}}}{\overset{{\displaystyle \frac{l}{2}}}{\int }}\overrightarrow{x} ⨯k_{n_{ij}} \left({\overrightarrow{ds}}_n+{\overrightarrow{ds}}_t+{\overrightarrow{ds}}_{\theta }\right) dx,$$

(14)

In Equation (14), ${\overrightarrow{ds}}_n$, ${\overrightarrow{ds}}_t$, and ${\overrightarrow{ds}}_{\theta }$ are the stretch of the spring due to displacement in the normal, tangential, and rotational directions. By expanding Equation (14), Equation (15) was obtained.

$$\begin{gathered} M_{M_{\left\{i,j\right\}}}=\left|k_{n_{ij}} \underset{-{\displaystyle \frac{l}{2}}}{\overset{{\displaystyle \frac{l}{2}}}{\int }}\overrightarrow{x} ⨯ {\overrightarrow{ds}}_n dx+k_{n_{ij}} \underset{-{\displaystyle \frac{l}{2}}}{\overset{{\displaystyle \frac{l}{2}}}{\int }}\overrightarrow{x} ⨯ {\overrightarrow{ds}}_t dx+k_{n_{ij}} \underset{-{\displaystyle \frac{l}{2}}}{\overset{{\displaystyle \frac{l}{2}}}{\int }}\overrightarrow{x} ⨯ {\overrightarrow{ds}}_{\theta } dx\right|=0+0+k_{n_{ij}} \underset{-{\displaystyle \frac{l}{2}}}{\overset{{\displaystyle \frac{l}{2}}}{\int }}x \left(x \left({\theta }_j-{\theta }_i\right)\right)dx \\ =k_{n_{ij}} \left({\theta }_j-{\theta }_i\right) {\displaystyle \frac{l^3}{12}}, \end{gathered}$$

(15)

Until now, the forces and the momentum acting on element $i$ due to contacting element $j$ were calculated. However, in the meshes, element $i$ has contact with several other elements. The other contacting elements are as $j_1$, $j_2$, ……, and $j_K$, assuming that element $i$ has contact with $K$ other elements. To achieve equilibrium for element $i$, the sum of all forces and moments due to contacts with each neighboring element must be balanced. Therefore, for the equilibrium of the element in the global $x$, $y$, and rotational directions, Equations (16)–(18) can be used.

$${\sum }_{k=1}^K{F}_{x, i{j}_k}=0, in global x-direction$$

(16)

$${\sum }_{k=1}^K{F}_{y, i{j}_k}=0, in global y-direction$$

(17)

$${\sum }_{k=1}^K{M}_{i{j}_k}=0, in rotational direction$$

(18)

In Equations (16)–(18), the contacting elements ($j_1$, $j_2$, ……, and $j_K$) should be known. To improve efficiency, a faster method [36] for finding the contacting elements is employed by restricting the search region to the immediate vicinity of the element. The details of this method can be seen in Figure 7.

To solve Equations (16)–(18) for a mesh containing $N$ elements, they can be rewritten in a more generalized matrix form, which will help to facilitate the solution process. As mentioned earlier, it has already been identified that the contacting elements ($j_1$, $j_2$, ……, and $j_K$) are for element $i$. For a system with $N$ elements, Equations (19)–(21) can be expressed.

In $x$-direction:

$$AA1·X_i+{\sum }_{k=1}^K\left(AA2\left\{j_k\right\}\right) ·X_{j_k})+AA3·Y_i+{\sum }_{k=1}^K\left(AA4\left\{j_k\right\}\right)·Y_{j_k})+AA5·{\theta }_i+{\sum }_{k=1}^K\left(AA6\left\{j_k\right\}\right)·{\theta }_{j_k})=0,$$

(19)

In $y$-direction:

$$BB1·X_i+{\sum }_{k=1}^K\left(BB2\left\{j_k\right\}\right)·X_{j_k})+BB3·Y_i+{\sum }_{k=1}^K\left(BB4\left\{j_k\right\}\right)·Y_{j_k})+BB5·{\theta }_i+{\sum }_{k=1}^K\left(BB6\left\{j_k\right\}\right)·{\theta }_{j_k})=0,$$

(20)

In $\theta$ -direction:

$$CC1·X_i+{\sum }_{k=1}^K\left(CC2\left\{j_k\right\}\right)·X_{j_k})+CC3· Y_i+{\sum }_{k=1}^K\left(CC4\left\{j_k\right\}\right)·Y_{j_k})+CC5·{\theta }_i+{\sum }_{k=1}^K\left(CC6\left\{j_k\right\}\right)·{\theta }_{j_k})=0,$$

(21)

$AAi$, $BBi$, and $CCi$ ($i=1, \dots , 6$) are calculated from the expansion of equations considering all the contacting elements. To solve Equations (19)–(21), they were organized like a stiffness matrix in equilibrium analysis. Just like in a traditional stiffness matrix formulation, where the relationship between forces and displacements is represented through a global matrix equation, it can be described as the equilibrium of forces and moments acting on elements as Equation (22).

$$\left[K\right]\left\{u\right\}=\left\{F\right\},$$

(22)

where $\left[K\right]$ is the stiffness matrix that incorporates the interaction between all contacting elements. This matrix would include contributions from the neighboring elements ($j_1$, $j_2$, ……, and $j_K$) in contact with element $i$. Vector $\left\{u\right\}$ represents the unknown displacements, and $\left\{F\right\}$ represents the forces acting on the elements due to the forces at the boundaries of the mesh domain. If $\left[K\right]$ matrix is expanded and no boundary forces are assumed, Equation (22) can be expressed in its expanded form as Equation (23).

$$\left|\begin{array}{ccc}\begin{array}{cc}\begin{array}{ccc}AA1\left(1\right)& & \dots \\ & AA1\left(2\right)& \cdots \\ ⋮& & AA1\left(3\right)\end{array}& \begin{array}{ccc} & & \\ & AA2\left\{j_k\right\}& \\ & & \end{array}\\ \begin{array}{ccc} & & \\ & AA2\left\{j_k\right\}& \\ & & \end{array}& \begin{array}{ccc}\ddots & & \\ & \ddots & \\ \dots & & AA1\left(N\right)\end{array}\end{array}& \begin{array}{cc}\begin{array}{ccc}AA3\left(1\right)& & \dots \\ & AA3\left(2\right)& \cdots \\ ⋮& & AA3\left(3\right)\end{array}& \begin{array}{ccc} & & \\ & AA4\left\{j_k\right\}& \\ & & \end{array}\\ \begin{array}{ccc} & & \\ & AA4\left\{j_k\right\}& \\ & & \end{array}& \begin{array}{ccc}\ddots & & \\ & \ddots & \\ \dots & & AA3\left(N\right)\end{array}\end{array}& \begin{array}{cc}\begin{array}{ccc}AA5\left(1\right)& & \dots \\ & AA5\left(2\right)& \cdots \\ ⋮& & AA5\left(3\right)\end{array}& \begin{array}{ccc} & & \\ & AA6\left\{j_k\right\}& \\ & & \end{array}\\ \begin{array}{ccc} & & \\ & AA2\left\{j_k\right\}& \\ & & \end{array}& \begin{array}{ccc}\ddots & & \\ & \ddots & \\ \dots & & AA5\left(N\right)\end{array}\end{array}\\ \begin{array}{cc}\begin{array}{ccc}BB1\left(1\right)& & \dots \\ & BB1\left(2\right)& \cdots \\ ⋮& & BB1\left(3\right)\end{array}& \begin{array}{ccc} & & \\ & BB2\left\{j_k\right\}& \\ & & \end{array}\\ \begin{array}{ccc} & & \\ & BB2\left\{j_k\right\}& \\ & & \end{array}& \begin{array}{ccc}\ddots & & \\ & \ddots & \\ \dots & & BB1\left(N\right)\end{array}\end{array}& \begin{array}{cc}\begin{array}{ccc}BB3\left(1\right)& & \dots \\ & BB3\left(2\right)& \cdots \\ ⋮& & BB3\left(3\right)\end{array}& \begin{array}{ccc} & & \\ & BB4\left\{j_k\right\}& \\ & & \end{array}\\ \begin{array}{ccc} & & \\ & BB4\left\{j_k\right\}& \\ & & \end{array}& \begin{array}{ccc}\ddots & & \\ & \ddots & \\ \dots & & BB3\left(N\right)\end{array}\end{array}& \begin{array}{cc}\begin{array}{ccc}BB5\left(1\right)& & \dots \\ & BB5\left(2\right)& \cdots \\ ⋮& & BB5\left(3\right)\end{array}& \begin{array}{ccc} & & \\ & BB6\left\{j_k\right\}& \\ & & \end{array}\\ \begin{array}{ccc} & & \\ & BB6\left\{j_k\right\}& \\ & & \end{array}& \begin{array}{ccc}\ddots & & \\ & \ddots & \\ \dots & & BB5\left(N\right)\end{array}\end{array}\\ \begin{array}{cc}\begin{array}{ccc}CC1\left(1\right)& & \dots \\ & CC1\left(2\right)& \cdots \\ ⋮& & CC1\left(3\right)\end{array}& \begin{array}{ccc} & & \\ & CC2\left\{j_k\right\}& \\ & & \end{array}\\ \begin{array}{ccc} & & \\ & CC2\left\{j_k\right\}& \\ & & \end{array}& \begin{array}{ccc}\ddots & & \\ & \ddots & \\ \dots & & CC1\left(N\right)\end{array}\end{array}& \begin{array}{cc}\begin{array}{ccc}CC3\left(1\right)& & \dots \\ & CC3\left(2\right)& \cdots \\ ⋮& & CC3\left(3\right)\end{array}& \begin{array}{ccc} & & \\ & CC4\left\{j_k\right\}& \\ & & \end{array}\\ \begin{array}{ccc} & & \\ & CC4\left\{j_k\right\}& \\ & & \end{array}& \begin{array}{ccc}\ddots & & \\ & \ddots & \\ \dots & & CC3\left(N\right)\end{array}\end{array}& \begin{array}{cc}\begin{array}{ccc}CC5\left(1\right)& & \dots \\ & CC5\left(2\right)& \cdots \\ ⋮& & CC5\left(3\right)\end{array}& \begin{array}{ccc} & & \\ & CC6\left\{j_k\right\}& \\ & & \end{array}\\ \begin{array}{ccc} & & \\ & CC6\left\{j_k\right\}& \\ & & \end{array}& \begin{array}{ccc}\ddots & & \\ & \ddots & \\ \dots & & CC5\left(N\right)\end{array}\end{array}\end{array}\right| \left(\begin{array}{c}X1\\ \begin{array}{c}X2\\ \begin{array}{c}⋮\\ \begin{array}{c}⋮\\ \begin{array}{c}⋮\\ \begin{array}{c}XN\\ \begin{array}{c}Y1\\ \begin{array}{c}Y2\\ \begin{array}{c}⋮\\ \begin{array}{c}⋮\\ \begin{array}{c}⋮\\ \begin{array}{c}YN\\ \begin{array}{c}\theta 1\\ \begin{array}{c}\theta 2\\ \begin{array}{c}⋮\\ \begin{array}{c}⋮\\ ⋮\\ \theta N\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\right)=\left(\begin{array}{c}0\\ \begin{array}{c}0\\ \begin{array}{c}⋮\\ \begin{array}{c}⋮\\ \begin{array}{c}⋮\\ \begin{array}{c}⋮\\ \begin{array}{c}⋮\\ \begin{array}{c}⋮\\ \begin{array}{c}⋮\\ \begin{array}{c}⋮\\ \begin{array}{c}⋮\\ \begin{array}{c}⋮\\ \begin{array}{c}⋮\\ \begin{array}{c}⋮\\ \begin{array}{c}⋮\\ \begin{array}{c}⋮\\ \begin{array}{c}⋮\\ 0\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\right),$$

(23)

Normal and tangential stiffness calibration directly impacts stress and strain calculation. As a result, many studies have focused on calibrating these stiffnesses to enhance the prediction of stress and strain for different materials in DEM. Following the findings of Raje et al. [36], the stiffness values as detailed below in Equations (24) and (25) were selected. In this context, $L_{eq}$ represents the distance between the centers of elements i and j, projected along the normal direction, and $t$ is the thickness of the elements, $E$ is the elastic modulus, and $\nu$ is the Poisson’s ratio.

$${k_n}_{ij}={\displaystyle \frac{E t}{\left(1-v\right) L_{eq}}},[{\displaystyle \frac{\mathrm{N}}{{\mathrm{\mu }\mathrm{m}}^2}}]$$

(24)

$${k_t}_{ij}={\displaystyle \frac{E \left(1-3 v\right) t}{\left(1-v^2\right) L_{eq}}},[{\displaystyle \frac{\mathrm{N}}{{\mathrm{\mu }\mathrm{m}}^2}}]$$

(25)

The stress near the initial crack is calculated in the model by applying a force to the domain’s boundary. The magnitude of the applied force is determined based on available data from the literature, which are in the form of stress intensity factors. Linear elastic fracture mechanics principles convert stress intensity factors into boundary forces. The corresponding boundary forces were calculated to match the stress intensity factor values reported in the literature. Then, based on the damage law proposed by Raje et al. [36], the springs’ stiffnesses will degrade as a response to load cycles, leading to crack propagation from the initial crack (see Equations (26) and (27)). A damage parameter D is defined and assigned to each interface. Initially, D is set to zero, and it gradually increases to a maximum value of 1 as load cycles progress.

$$k_n=\left(1-D\right) {k_n}^0$$

(26)

$$k_t=\left(1-D\right) {k_t}^0$$

(27)

where ${k_n}^0$ and ${k_t}^0$ are the initial stiffnesses in the normal and tangential directions.

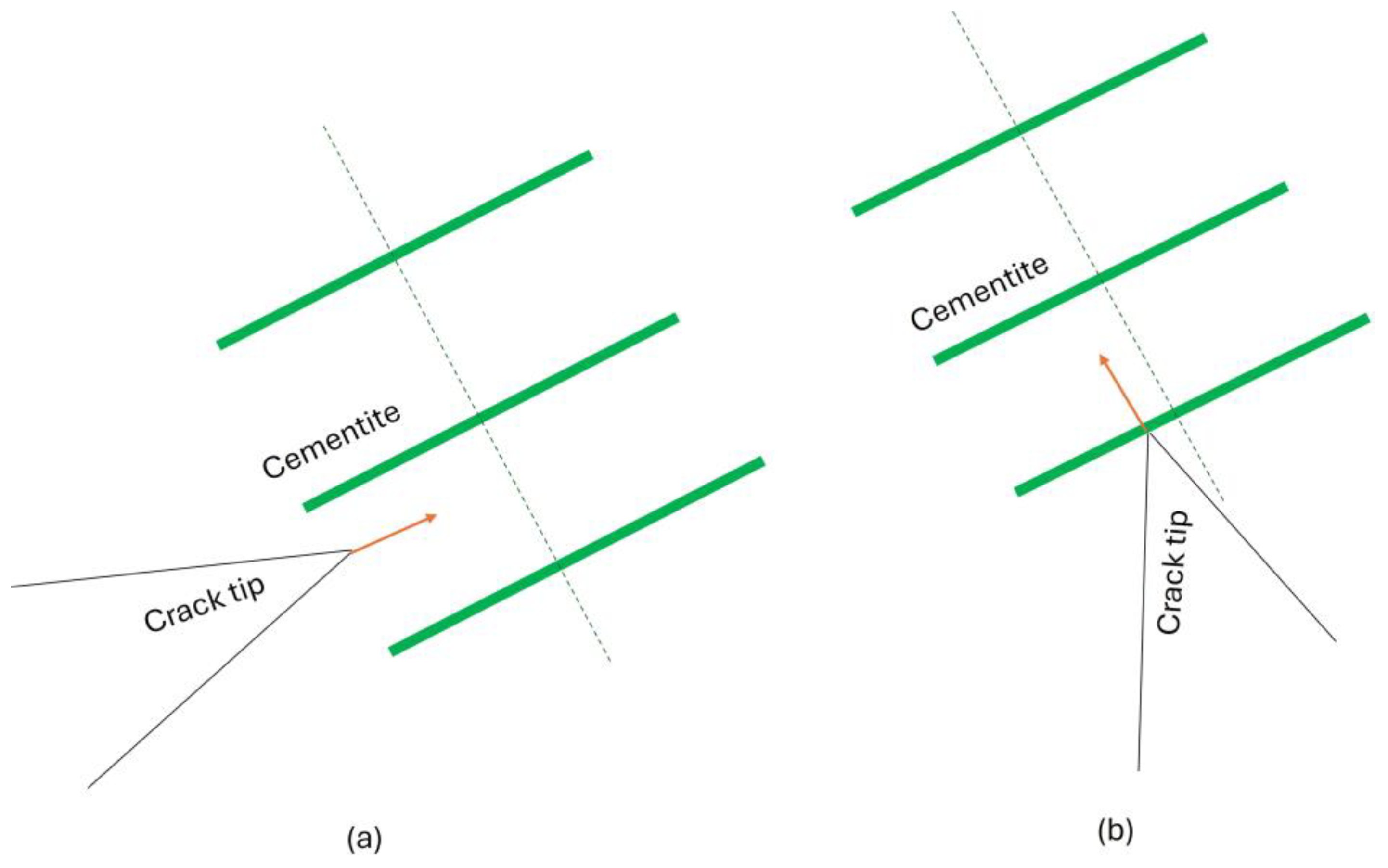
The damage parameter must increase with load cycles and the amplitude of applied stresses at the interface. For a damage law suitable for the proposed meshing methodology, it is essential to account for the multi-layered mesh structure. Since crack growth behavior differs based on whether it grows along or breaks through cementite lamellae, two distinct conditions are proposed: one for when the crack propagates along the cementite layers and another for when it penetrates through them (see Figure 8).

When a crack grows alongside the cementite and ferrite interface, as shown in Figure 8a, the following power–law relation is proposed for the rate of damage evolution in an interface. This relation combines the ideas and approaches of the Peridynamic fatigue cracking model of Silling and Askari [43] and the fatigue threshold model of Lucas and Gerberich [44].

$${\displaystyle \frac{dD}{dN}}\left(n\right)={\displaystyle \frac{C}{{{\sigma }_{yield} L}_{int}}}{ \left(\mathsf{\Delta }{\sigma }_n-\mathsf{\Delta }{\sigma }_{th}\right)}^3,$$

(28)

In this context, ${\displaystyle \frac{dD}{dN}}(n)$ represents the damage evolution at the interface due to the normal stress $\mathit{\Delta }{\sigma }_n$ acting on it. Here, ${\sigma }_{yield}$ is the material’s yield stress, $C$ is a constant, $L_{int}$ is the length of the contacting interface, while $\mathit{\Delta }{\sigma }_{th}$ is the threshold stress below which the crack does not propagate. The stress of the threshold may also depend on other material properties. Similarly, the damage evolution when the stress is tangential to the interface of ferrite and cementite (damage because of tangential stress ($\mathit{\Delta }{\sigma }_t$)) can be defined.

$${\displaystyle \frac{dD}{dN}}\left(t\right)={\displaystyle \frac{C}{{{\sigma }_{yield} L}_{int}}}{\left(\mathsf{\Delta }{\sigma }_t-\mathsf{\Delta }{\sigma }_{th}\right)}^3,$$

(29)

Equations (28) and (29) apply when the crack propagates along the interface between cementite and ferrite. However, when the crack breaks through the cementite lamellae, it must overcome stress greater than ${\sigma }_{yield}$ due to the higher strength of the cementite. In this scenario, the crack must surpass critical stress (characteristic strength of cementite (${\sigma }_c$)), representing the strength required to fracture the cementite, typically exceeding the yield stress. For this case, Equations (30) and (31) govern the damage evolution under normal and tangential loading conditions.

$${\displaystyle \frac{dD}{dN}}\left(n\right)={\displaystyle \frac{C}{{{\sigma }_c L}_{int}}} {\left(\mathsf{\Delta }{\sigma }_n-\mathsf{\Delta }{\sigma }_{th}\right)}^3,$$

(30)

$${\displaystyle \frac{dD}{dN}}\left(t\right)={\displaystyle \frac{C}{{{\sigma }_c L}_{int}}} {\left(\mathsf{\Delta }{\sigma }_t-\mathsf{\Delta }{\sigma }_{th}\right)}^3$$

(31)

Thus, after calculating the separate damage evolutions for normal and tangential loads, the overall damage evolution can be determined as in Equation (32).

$${\displaystyle \frac{dD}{dN}}(eff)=\sqrt{{{\displaystyle \frac{dD}{dN}}(n)}^2+\beta {{\displaystyle \frac{dD}{dN}}(t)}^2},where \beta is constant$$

(32)

It is worth noting that, for other interfaces within the mesh, such as block, colony, and PAG boundaries, Equations (28) and (29) are used because a crack propagating through these interfaces does not require cementite breakage.

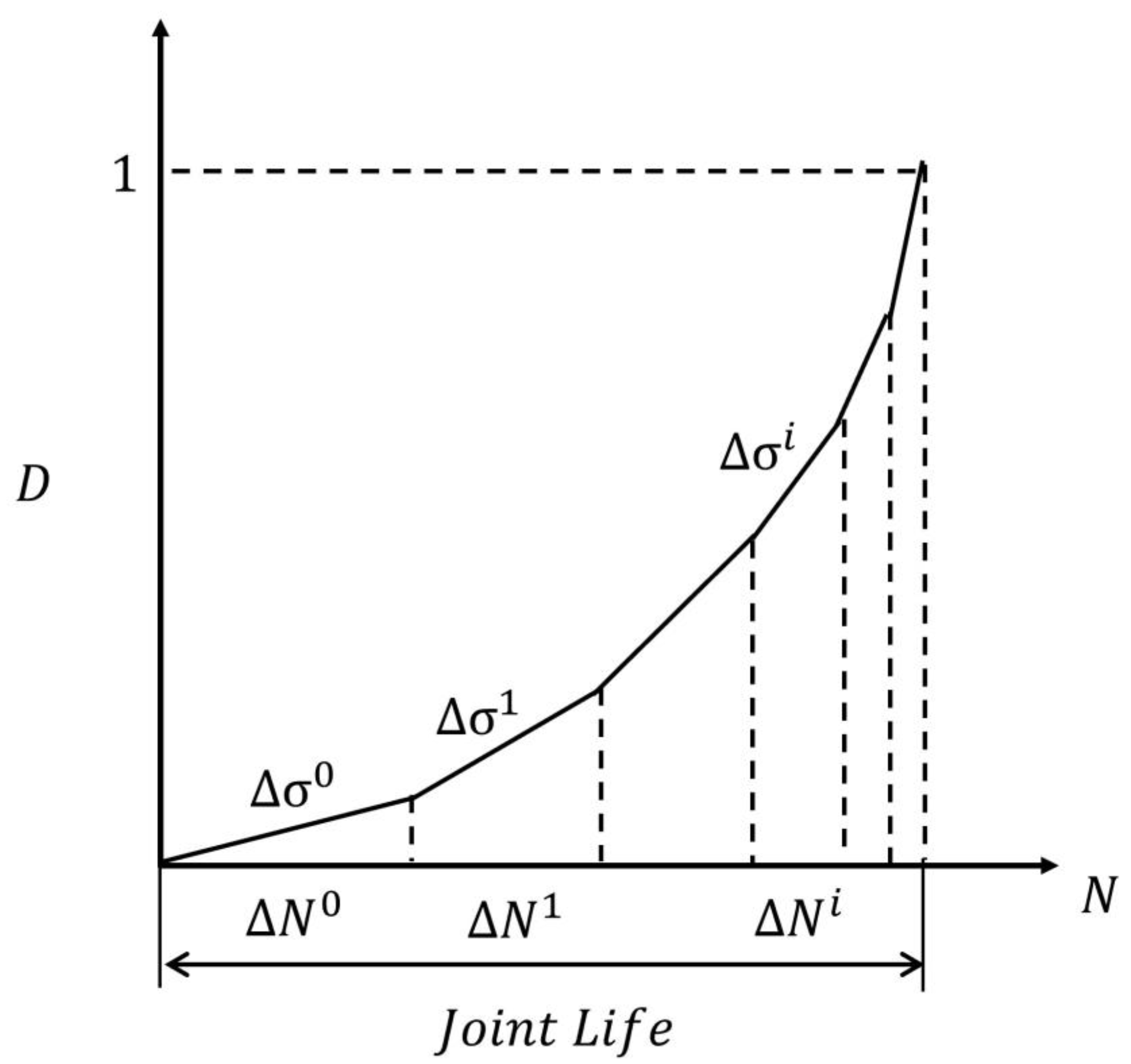
Once damage parameter $D$ reaches a value of 1, a crack propagates along the interface, requiring multiple load cycles. Simulating each load cycle, however, is computationally time-consuming. Therefore, the jump-in-cycles method, described by [36], is used to model fatigue damage. This method applies a small increment, $\mathit{\Delta }D$, to the damage variable for each cycle block, $\mathit{\Delta }N$, while keeping the stress level constant (Figure 9).

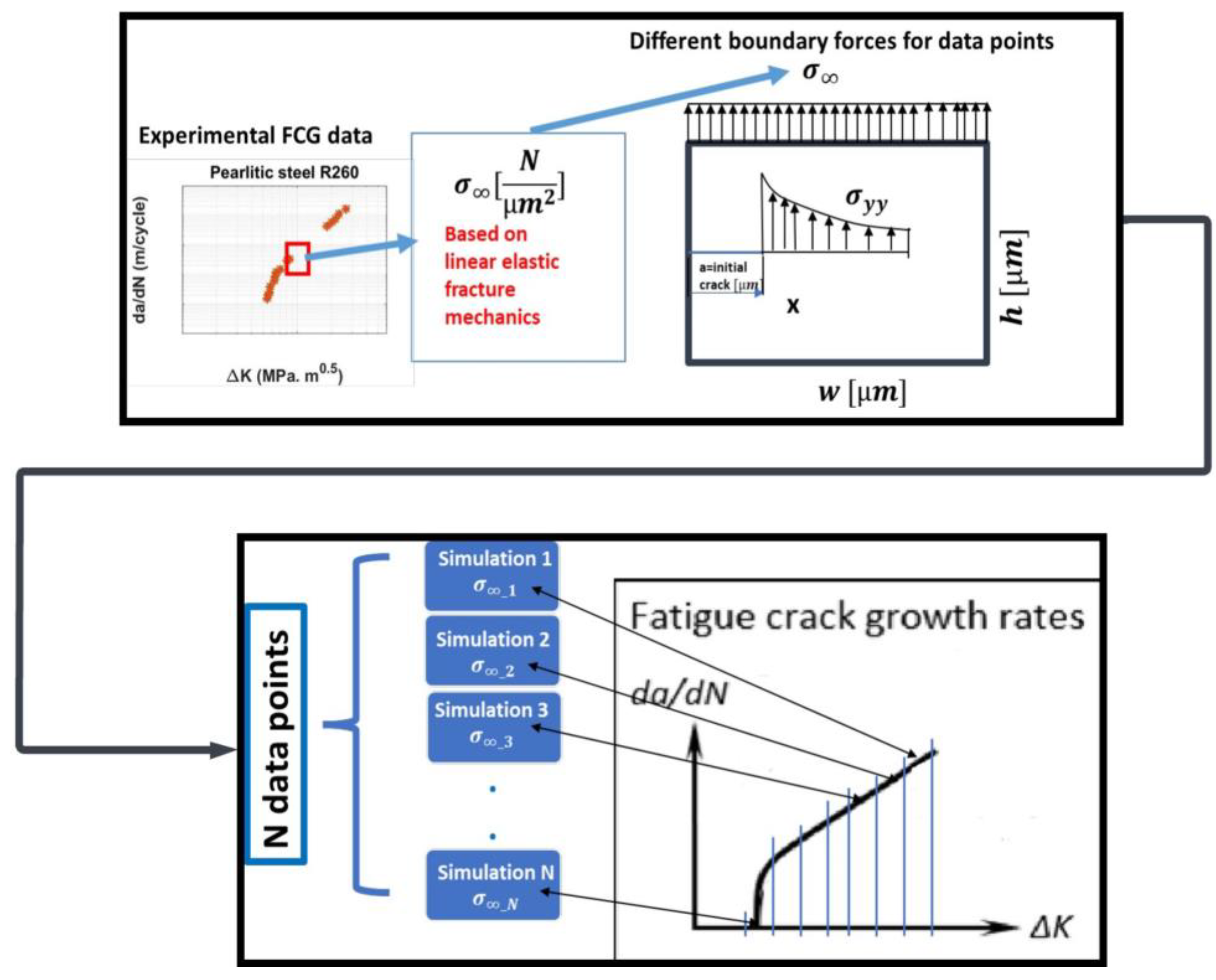
When the desired crack length is reached by degrading several interfaces, the average slope of crack length versus the load cycles graph is calculated. This slope represents the crack growth rate under the specific load value related to the applied stress or stress intensity factor. This procedure is repeated for multiple data points (different load values), and each crack growth rate is used in the fatigue crack growth (FCG) graph. The structure of the calculation is shown in detail in Figure 10. As previously described and shown in this figure, the boundary stresses in the simulation (${\sigma }_{\infty }$) are chosen based on the target stress intensity factors using linear elastic fracture mechanics (LEFMs). A crack growth simulation is performed for each selected boundary stress (data point) until the desired crack length is reached. The crack growth rate for each data point is then recorded. By repeating the procedure for $N$ data points, the final fatigue crack growth rate diagram can be plotted.

5. Results and Discussion

The meshes described in Figure 2 and their repetitions were used in the DEM model. For the simulation process, damage model parameters must be chosen for each level of deformation. The damage model explained in Equations (28)–(32) was calibrated to match the undeformed state and tested and validated for both moderately deformed and severely deformed states. For determining the yield stress, ${\sigma }_{yield}$, in the damage model, the research by Tomlison et al. [45] was used. In their study, they modeled the yield stress as a function of the shear strain ($\gamma$) using Equation (33) for R260.

$${\sigma }_{yield}=m{(1-e^{-n \gamma })}^p, m=1626 \mathrm{M}\mathrm{P}\mathrm{a}, n=0.003105 \mathrm{a}\mathrm{n}\mathrm{d} p=0.191$$

(33)

By using Equation (33), the yield stress for the undeformed state was calculated to be $470 \mathrm{M}\mathrm{P}\mathrm{a}$, for moderately deformed ($\gamma =2$), $616 \mathrm{M}\mathrm{P}\mathrm{a}$, and for severely deformed ($\gamma =30$), $1024 \mathrm{M}\mathrm{P}\mathrm{a}$. The threshold stress ($\mathit{\Delta }{\sigma }_{th}$) can be derived proportional to the stress intensity factor threshold ($\mathsf{\Delta }{K}_{th}$) with the help of previously mentioned linear elastic fracture mechanics (LEFMs). The values for $\mathsf{\Delta }{K}_{th}$ for different deformation states are $5 {\mathrm{M}\mathrm{P}\mathrm{a}.\mathrm{m}}^{{\displaystyle \frac{1}{2}}}$ for undeformed, $4 {\mathrm{M}\mathrm{P}\mathrm{a}.\mathrm{m}}^{{\displaystyle \frac{1}{2}}}$ for moderately deformed ($\gamma =2$), and $2.3 {\mathrm{M}\mathrm{P}\mathrm{a}.\mathrm{m}}^{{\displaystyle \frac{1}{2}}}$ for severely deformed ($\gamma =30$) based on the experiments conducted by Leitner et al. [18,19,40]. The characteristic strength of cementite (${\sigma }_c$) is approximately $20 \mathrm{G}\mathrm{P}\mathrm{a}$ based on the research conducted by Garvik et al. [46]. 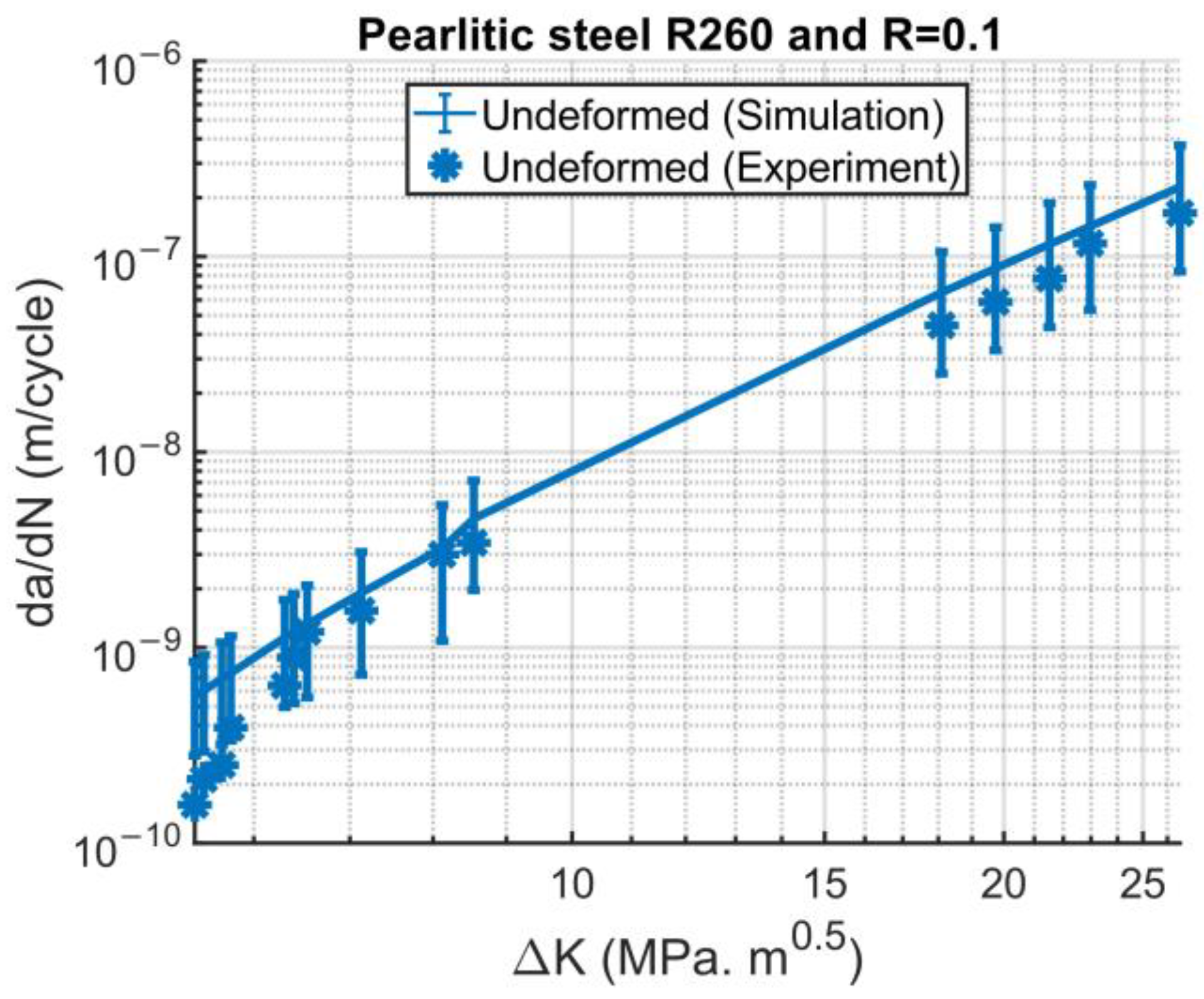$C$ and $\beta$ in Equations (28)–(32) were fitted for the undeformed state (see Figure 11) to be $4410[{\displaystyle \frac{{\mathrm{\mu }\mathrm{m}}^5}{{\mathrm{N}}^2}}]$ and $0.3$, and were used to validate other deformation degrees. 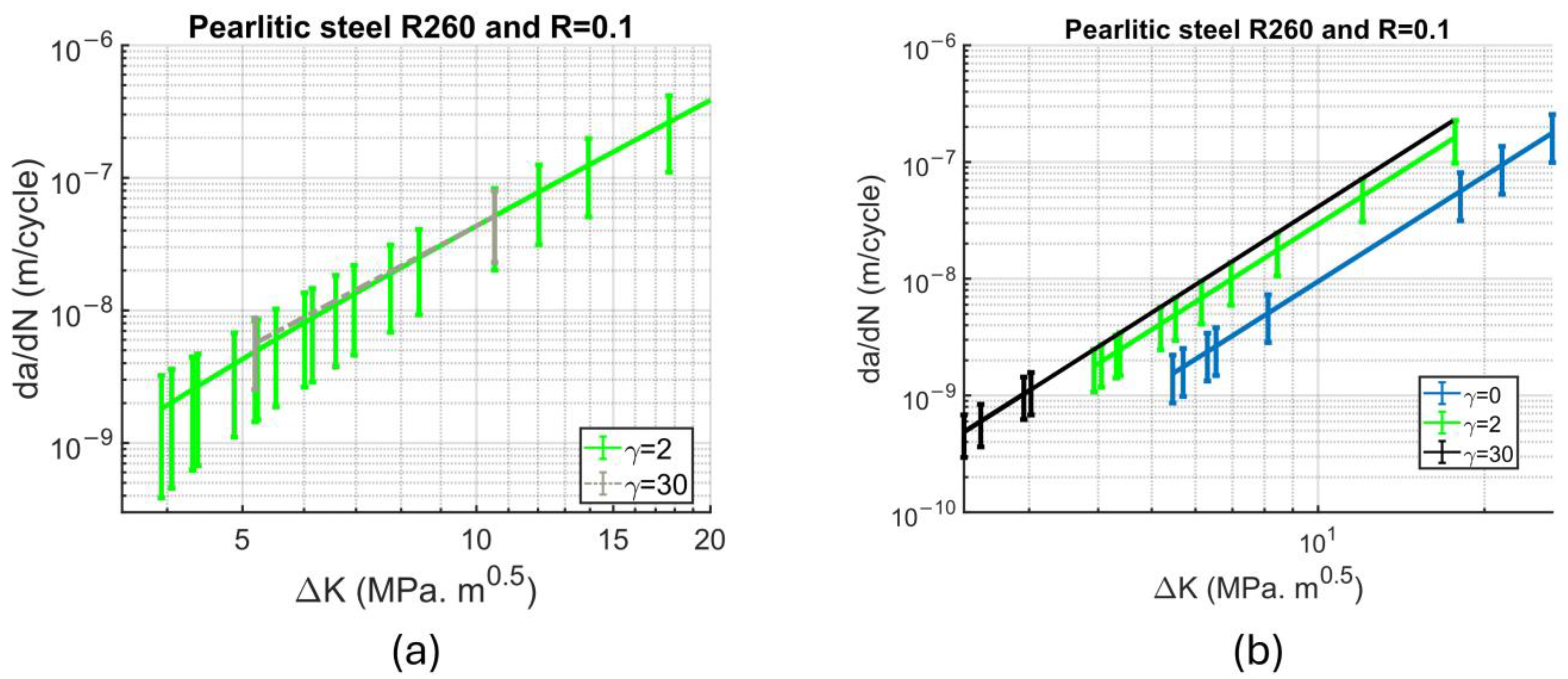The results exhibit scattering, according to the range shown by the error bars in Figure 11. This scattering is likely due to inherent randomness in the model.

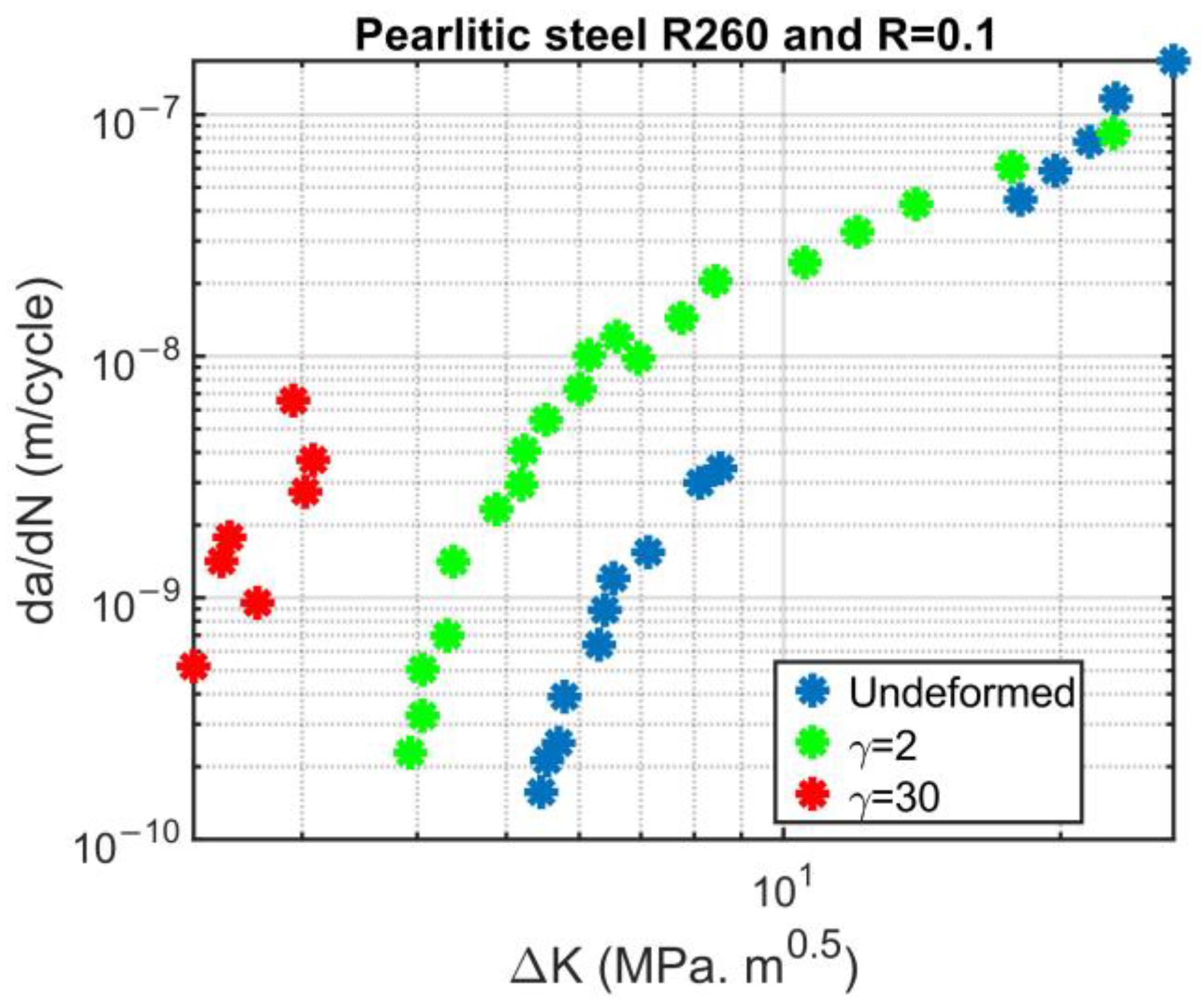
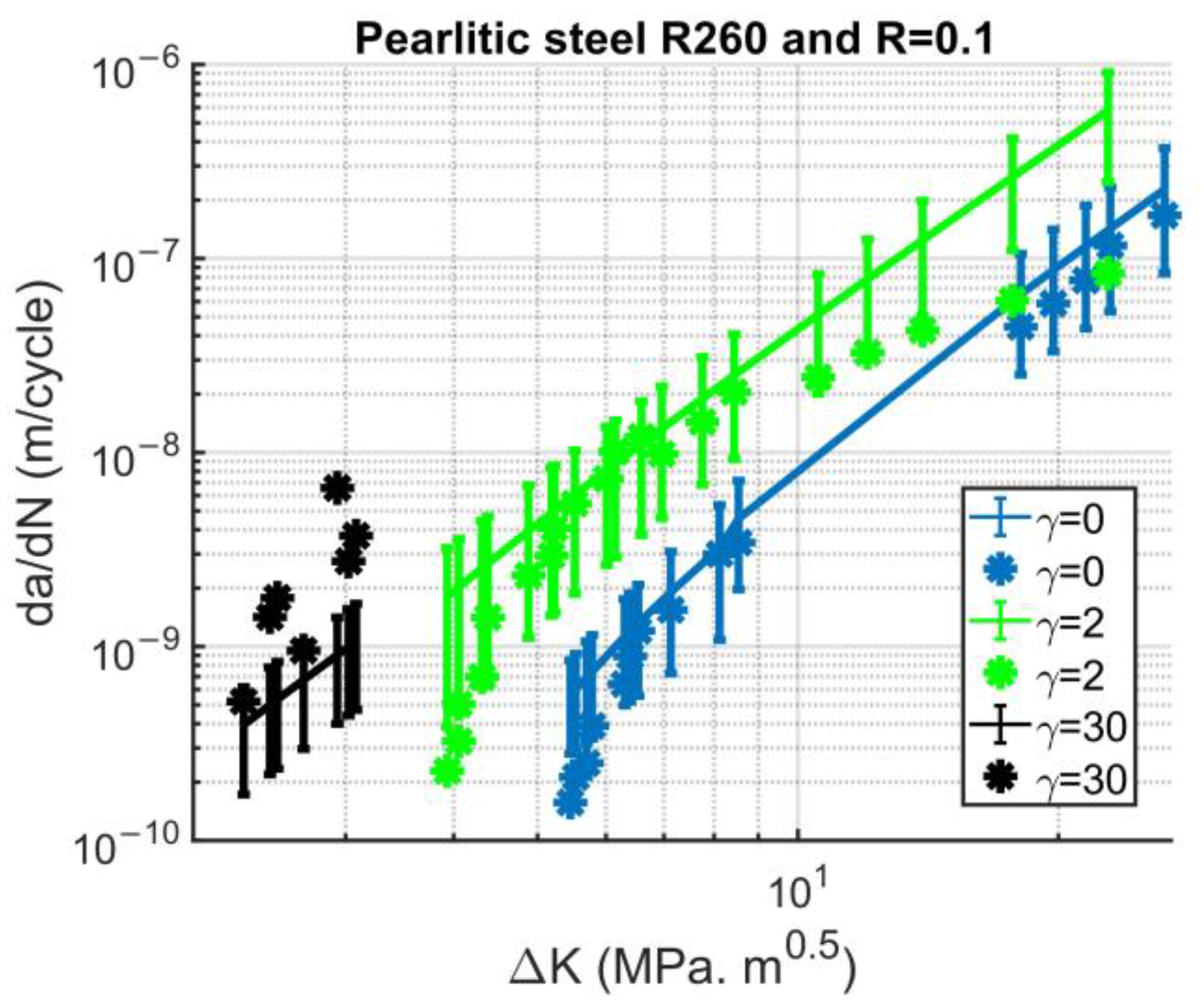
The result of fatigue crack simulation and the experimental results for different deformation states are shown in Figure 12. To generate Figure 12, all four repetitions of three deformation state meshes needed to be run, and the combined result with the error bar was calculated and is shown in this figure. It is worth emphasizing again that these results are parameterized for the undeformed state and validated for both deformed and severely deformed states. Measurement errors or unaccounted parameters may cause a difference in the FCG rate for the severely deformed state between simulation and experiments. However, the results are sufficiently acceptable because the same damage law and constant parameters were used throughout the analysis. The model parameters used in the simulations can be seen in Appendix A.

Another interesting set of results that can be concluded from the DEM simulation is the crack paths for each deformation state. The crack path for the meshes is shown in Figure 13. The results show that, when the deformation goes higher, the crack path tends to be smoother, which is in agreement with the observation reported by Leitner et al. [18,19,40].

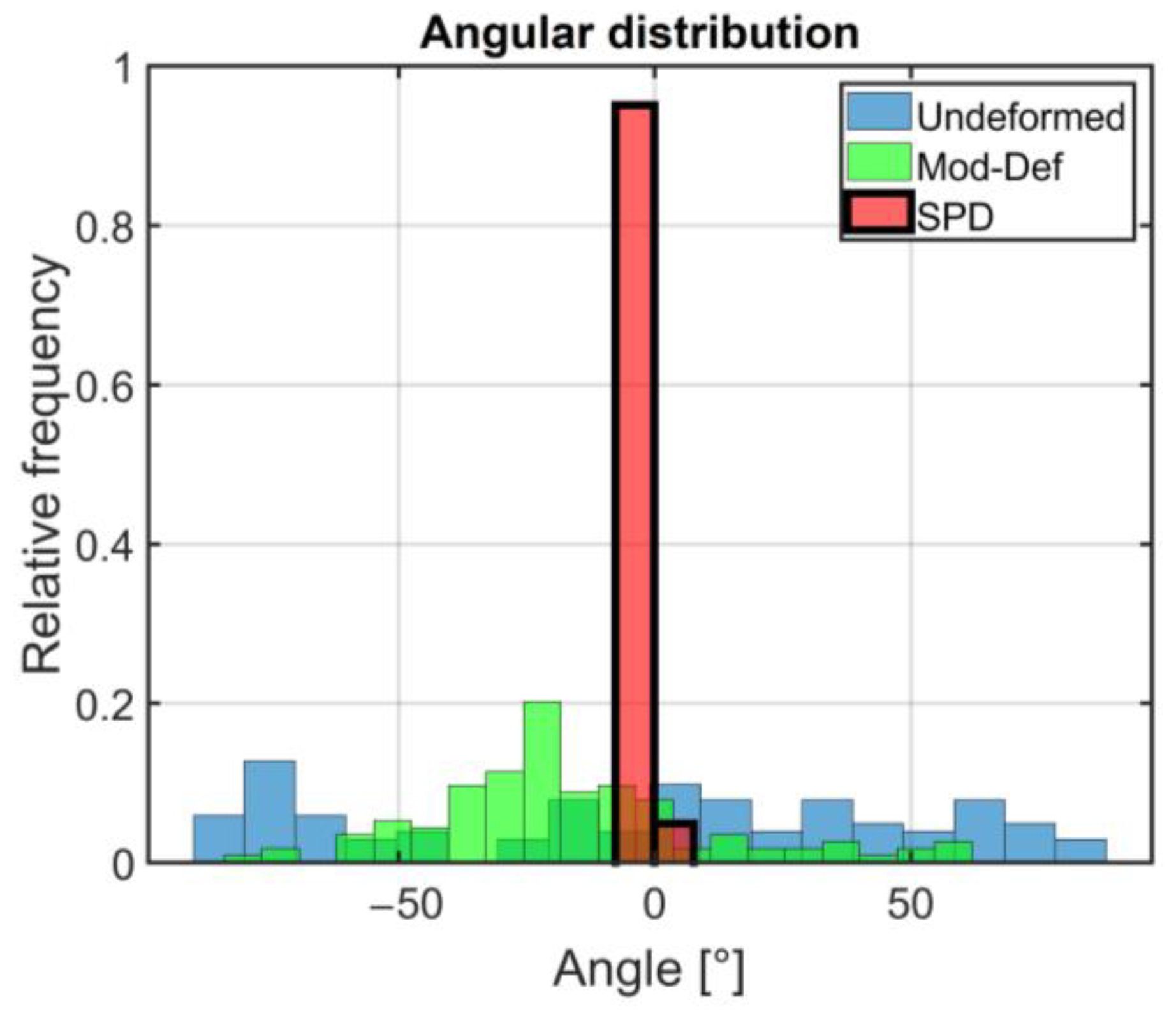
As shown in Figure 13, the degree of deformation and its orientation significantly influence the crack trajectory. The model predicts that cracks primarily grow along the interface between cementite and ferrite lamellae when there are no geometrical constraints. This prediction is consistent with the findings of Leitner et al. [40], which state that, in pearlitic steels, cracks predominantly propagate along the interface between the ferritic and carbon-rich (previously cementite) phase. Crack tortuosity is a parameter that can describe how twisted or curved a crack path is compared with a straight-line crack path. The crack tortuosity parameter measures the deviation of a crack path from a perfectly straight path. It is defined as the ratio of the actual path to the straight-line distance between the crack’s beginning and end (in this case, the distance along the x-coordinate). Figure 14 shows the crack tortuosity for different deformation states simulated by DEM. It is important to note that tortuosity was not calculated for the severely deformed state in the T–A orientation because of the extremely short crack length along the x-coordinate; this value would be much higher than others. The higher values of crack tortuosity may explain the crack growth rate anisotropy in pearlitic rail steel material. For a slower orientation, e.g., T–A orientation, the crack should encounter more deviation in its path when it needs to reach a specific length.

To investigate the influence of the different deformation states on fatigue resistance, the crack evolution of SPD and moderately deformed meshes under similar stress intensity factor ranges were simulated. The results shown in Figure 15a were obtained with the previously adjusted values of $\mathsf{\Delta }{K}_{th}$ and ${\sigma }_{yield}$. Figure 15a shows that the differences in the FCG rate between the SPD and moderately deformed conditions were minimal. This means that the increment in the FCG rate predicted by the model started already at a moderate deformation level of $\gamma =2$ (see comparison with undeformed state in Figure 12). Furthermore, simulations were performed using the same values of ${\sigma }_{yield}$ and $\mathsf{\Delta }{K}_{th}=0$ to isolate the effect of mesh deformation on FCG (see Figure 15b). The results show that the FCG rate increased mainly due to the re-orientation of microstructural components occurring already at moderate deformation of $\gamma =2$. Finally, it can be concluded that the strain hardening that modified the yield strength did not considerably affect the FCG rate.

6. Summary and Conclusions

This paper presents a methodology to predict the relation of microstructural parameters to the fatigue crack growth behavior in plastically deformed pearlitic steel using DEM and hierarchical meshing methods presented in earlier work [39]. This meshing methodology enabled us to model complex meshes representing various microstructural features of pearlitic steel. Plastic deformation was also considered in the mesh via simple geometrical shearing. Several meshes were generated and analyzed using the DEM model to investigate the crack growth and the effect of plastic deformation. The model can capture the fatigue crack growth rate anisotropy induced in the material due to the deformation.

From this work, it can be concluded that:

-

The crack grows faster in deformed pearlite than in undeformed microstructure due to the orientation of the microstructural features;

-

The crack growth rate slightly decreases with the strain hardening from the plastic deformation (yield strength);

-

The reorientation of the pearlite lamellae results in lower tortuosity in SPD conditions compared with the undeformed condition. The lower tortuosity leads to a higher FCG rate.

The model can correlate the plastic deformation with the microstructural features and the fatigue properties to estimate the RCF lifetime of wheel–rail material. Finally, the reasons for slight deviations between measurements and modeled results can be that the models do not account for the plasticity, breakage, or dissolution of the cementite and that the damage model is simple. The main reason for this research was to find a better way to predict and improve how railway materials resist fatigue cracks. The presented model investigates the interaction between the material microstructure, plastic deformation, and fatigue crack growth. The model helps to choose the right material and heat treatment to make components last longer and perform better. This may aid in the development of more fatigue-resistant rail steels.