In Situ Measurement and Mapping of Lubricant Film Temperature in Cylindrical Roller Thrust Bearings Using Thin-Film Sensors
Abstract
1. Introduction
1.1. State of the Art
| Author | Component | Measurement Type | Sensor Material | Coating | Key Findings/Conclusions |
|---|---|---|---|---|---|
| Peeken et al. [19] | Gear contact @ Oil: CLP 150 Full-film lubrication | Pressure | Mn | Al2O3 | Measured temperature and pressure while varying surface texture. Numerical calculations complemented experiments. |
| Temperature | Ti | ||||
| Kagerer [20] | Gear contact @ Oil: FVA 3 Full-film lubrication | Pressure | Mn | None | Investigated pressure, temperature, and film thickness up to 1600 MPa. Error analysis and comparison of the measurement data with the calculation tool developed by Oster [16]. |
| Temperature | Ti | ||||
| Tychsen [21] | Gear contact @ | Pressure | Mn | SiO2 | Contributed significantly to the ongoing efforts to compare thermal EHL data with real experimental results. |
| Kuhl and Holland [22] | Gear contact @ U: 1500 min−1 Slip: 50% Oil: FVA 3 Regime: full-film lubrication | Pressure | Cr | SiO2 | Extended the work initiated by Tychsen without protective layers to confirm their suitability; sensors demonstrated high accuracy, durability, and dynamic performance under extreme mechanical stress, matching the resilience of case-hardened gears. |
| Temperature | Ti | ||||
| Sperrfechter [24] | Twin-disc contact: Steel vs. Ceramic Disc @ U: 3600 min−1 Slip: 3 to 40% Oil: FVA 4 Regime: full-film lubrication | Pressure | Unknown | Al2O3 ZrO2 | Developed an iterative algorithm for error compensation in combined pressure–temperature sensors, providing an alternative to double-layer transducers by Baumann and Kuhl [8,9,15]. The method capacitively measured lubrication gap height while accounting for oil dielectric variations from temperature and pressure. |
| Temperature | Unknown | ||||
| Dauber [25] | Twin-disc contact: Steel vs. Ceramic Disc @ U:13.09 m/s Slip: 0 Oil: FVA 4 Regime: full-film lubrication | Pressure | Mn | Al2O3 ZrO2 | Focused on friction factors and lubricant film thickness. Studied non-Newtonian oil behaviour. |
| Temperature | Ti | ||||
| Kreil [26] | Twin-disc contact Steel with Al2O3, coating Load: 0.6 to 1 GPa U: 16 and 8 m/s Slip: 30% Oil: FVA 3A Regime: full-film lubrication | Pressure | Mn | -- | Reported thin-film sensor lifetime of 2 h without a protective layer, avoiding mixed friction. |
| Höhn et al. [27] | Twin-disc contact Load: 0.6 to 1 GPa U: 16 and 8 m/s Slip: 0% Oil: ISO VG 100 mineral Regime: full-film lubrication | Pressure | Mn | None | To protect the sensors, tests were limited to pure rolling with a 2.5–3.5 μm film thickness resulting in mixed lubrication. Provided valuable insights into surface roughness effects on pressure distribution under controlled conditions. |
| Miyata et al. [28] | Twin-disc contact Load: 0.98 to 1.5 GPa U: 5 to 12 m/s Slip = 0 to 4% Oil: Santotrac 50 Regime: full-film lubrication | Temperature | Pt | Al2O3 | Temperature rise in an elliptical contact area increases with slip, circumferential velocity, and pressure. Under low-slip conditions, spin motion causes significantly higher temperature rise than no-spin motion. However, as slip increases, the temperature difference between spin and no-spin motion diminishes. |
| Wilczek [29,30] | Twin-disc contact Load: 0.5 to 0.9 GPa U: 2.5 to 10 m/s Slip = 0 to 30% Oil: mineral gear oil (Transol 75). Regime: full-film lubrication | Pressure | Mn | SiO2 | Piezoelectric and self-induction effects were studied and found to be negligible with higher supply current. |
| Mayer [32] | Twin-disc contact Steel vs. Al2O3 Disc | Pressure | Mn | None | The sensor layer was directly coated on the surface. A focus on the influence of surface texture in the absence of a protective layer. |
| Temperature | Pt | ||||
| Ebner et al. [33] | Twin-disc Steel vs. AL2O3 and ZrO2 Ceramic Disc @ Load: 0.6 to 1 GPa U: 8 to 16 m/s Slip = 20 to 30% Oil: MIN100 (ISOVG100) Regime: full-film lubrication | Temperature | Pt | DLC | Results revealing differences in thermal inertia between two discs. Changing the sensor disc material highlighted the impact of thermal insulation on EHL temperature and fluid friction. TEHL simulations confirmed these findings, emphasizing the significance of sensor position and dimensions in capturing temperature variations across the film thickness. |
1.2. Goal of This Paper
2. Materials and Methods
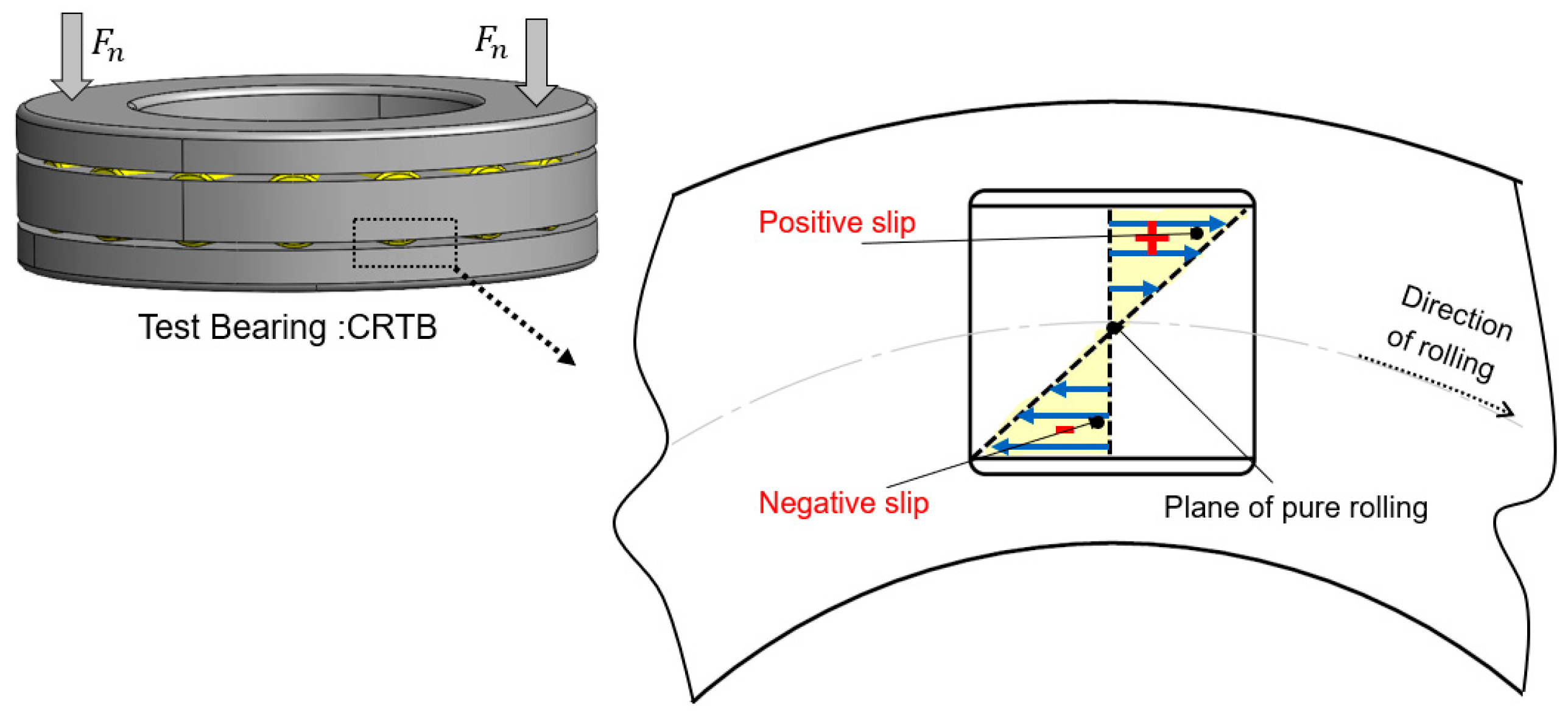
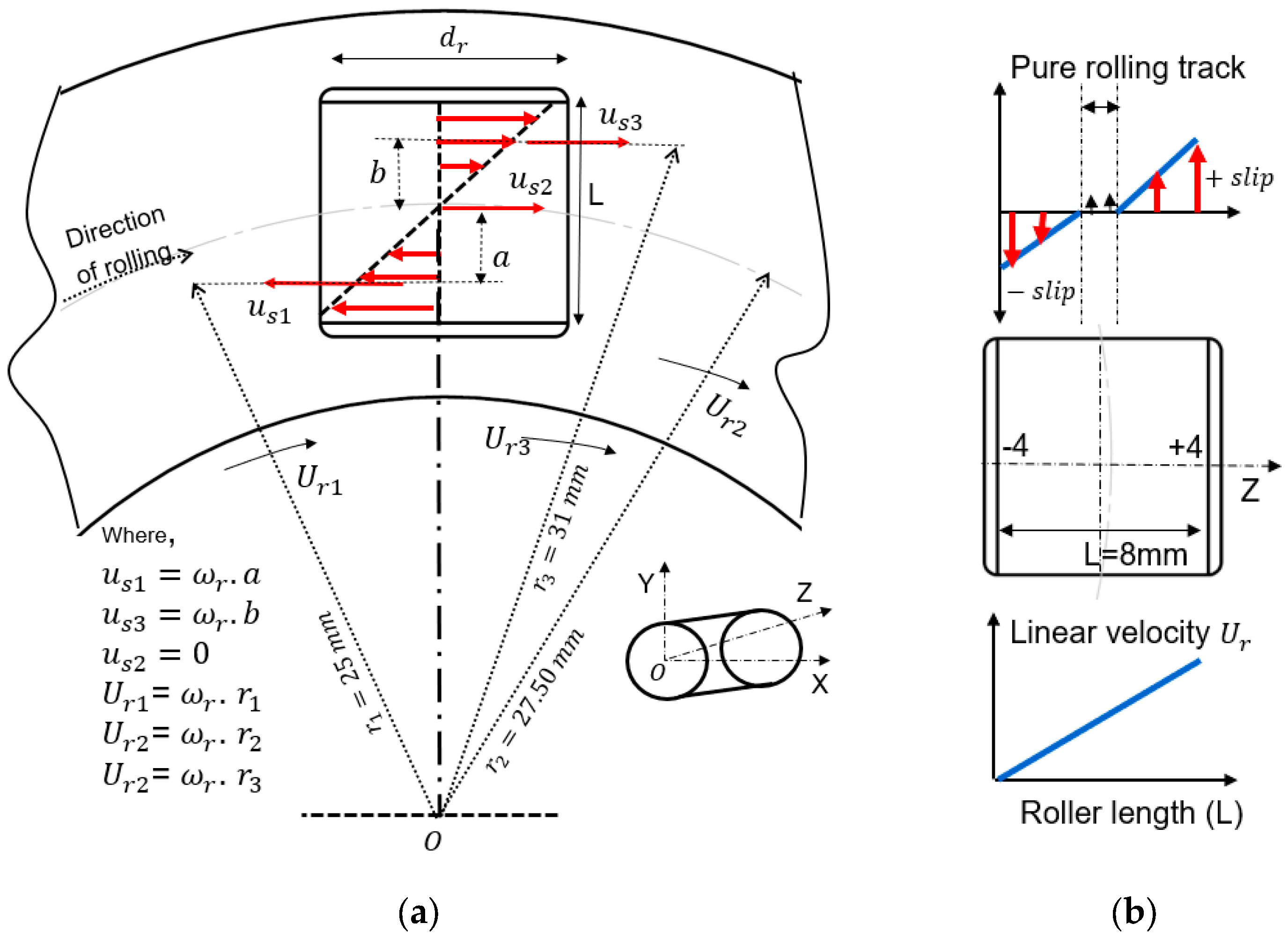
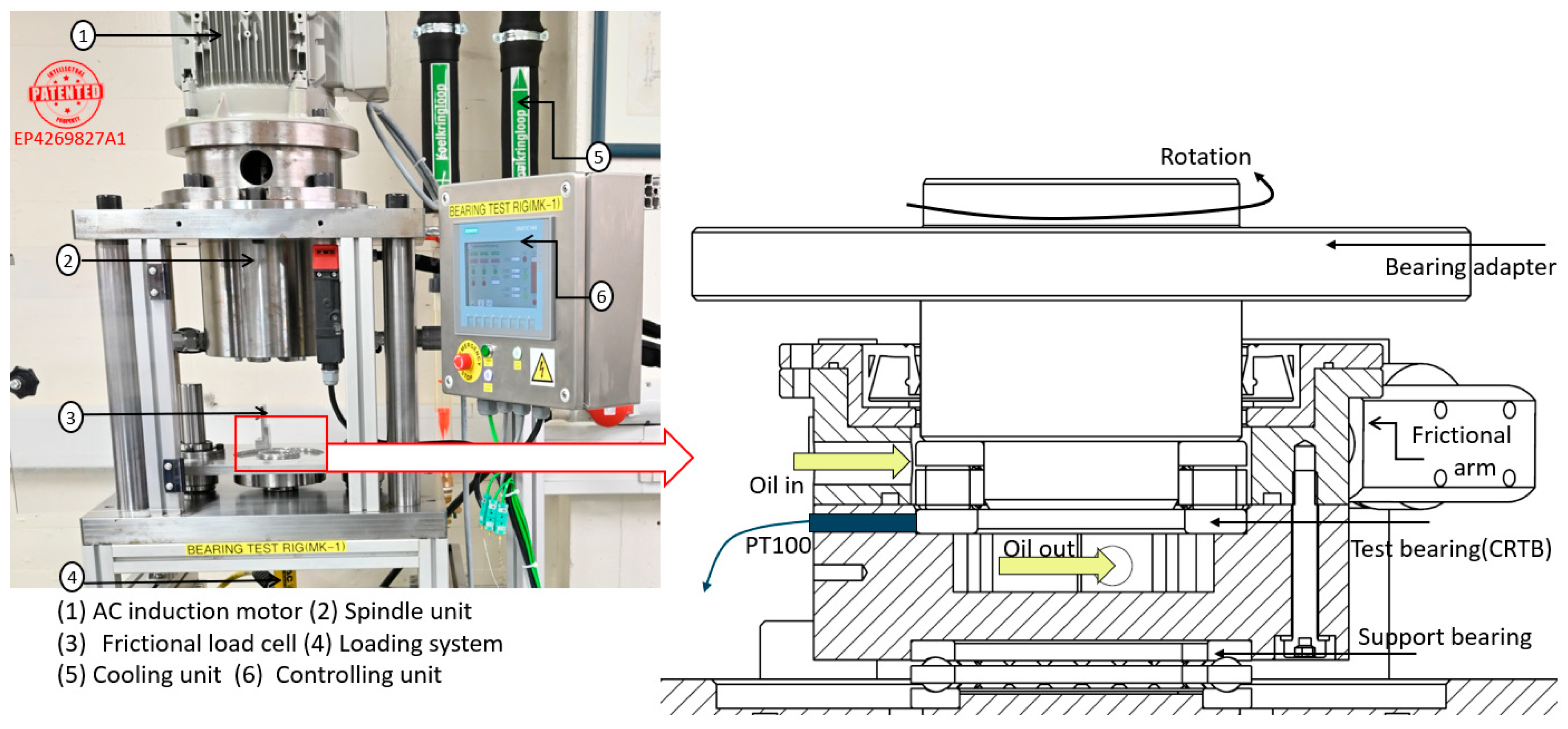
2.1. Characteristics of TEHL in CRTB
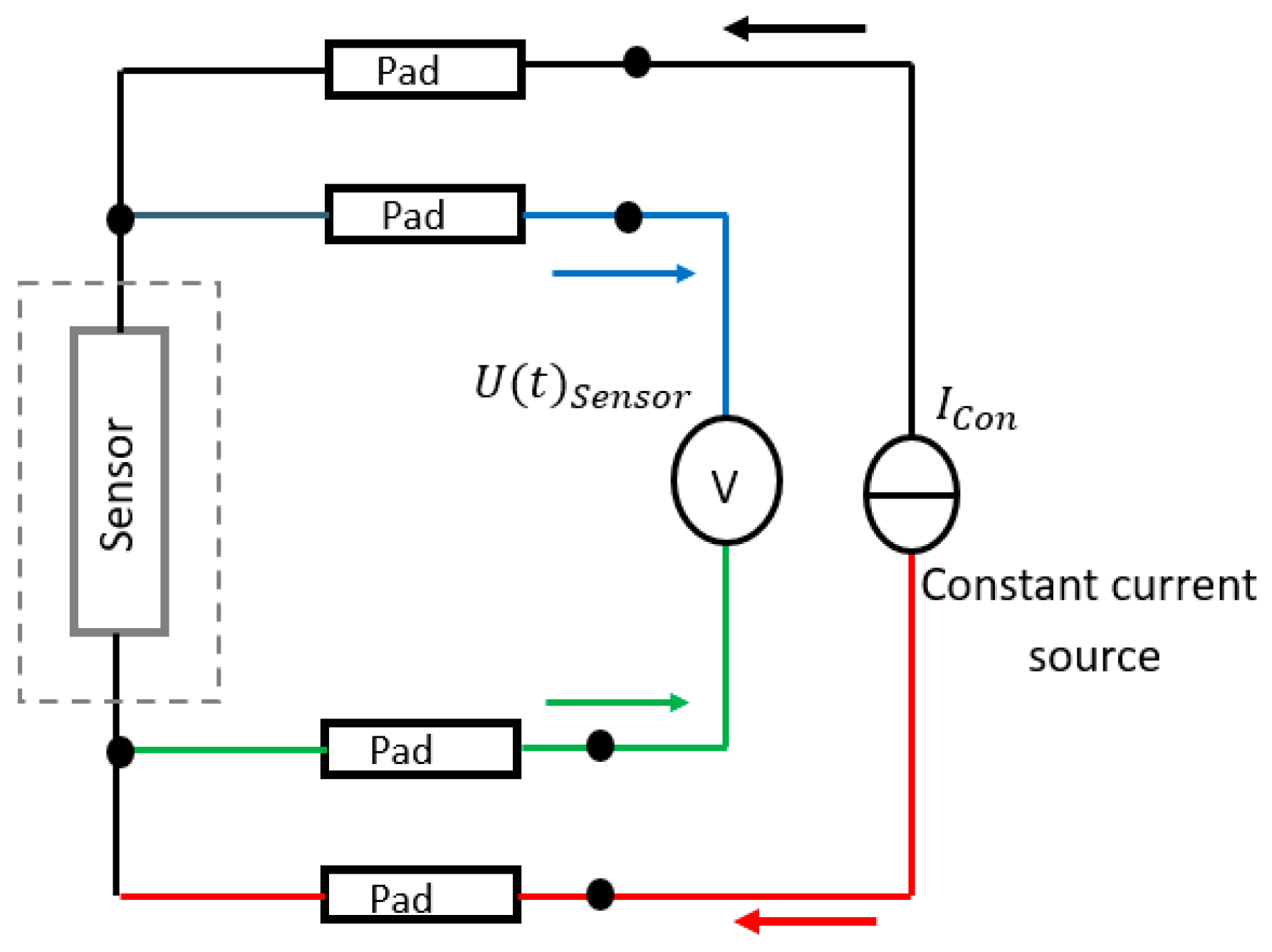
2.2. Thin-Film Sensor Measurement Principle
- An electrically insulating Al2O3 layer applied to the steel surface.
- A structured metallic sensor layer.
- A Diamond-Like Carbon (SICON®) coating for wear protection, preventing direct contact of the roller with the metallic sensor strip.
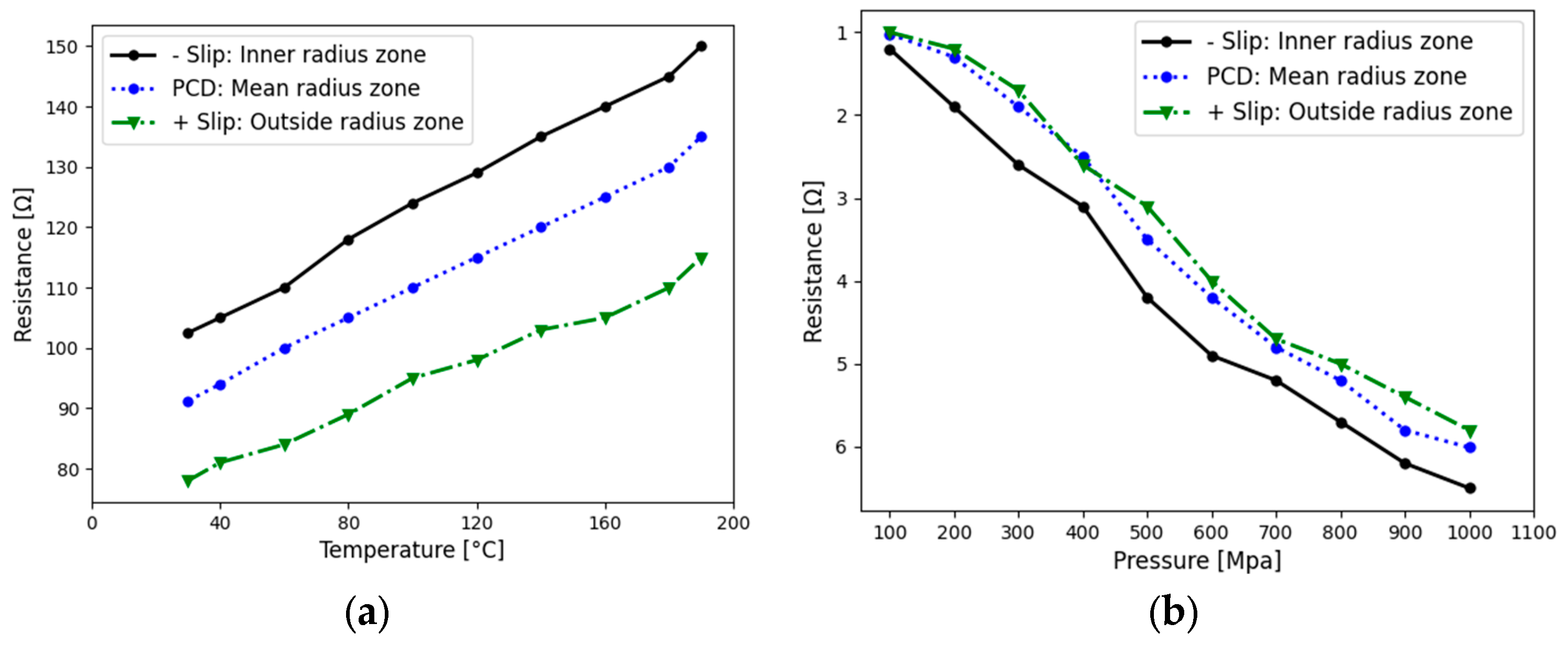
2.3. Thermo- and Piezo-Resistive Sensor Characterization
2.4. Experimental Setup
3. Design of Experiments
| Algorithm 1 measurement protocol |
| do determine the temperature and pressure coefficients and |
| for all U, G & W: |
|
If Mechanical and thermal equilibrium/steady-state do Supply a constant current of 4 mA for each sensor do 1. Measure: • Sensor output voltage @ • Total frictional torque • Temperatures , and |
| 2. Calculate the change in resistance using Equation (4) |
| 3. Calculate TEHL film temperature rise by rearranging Equation (3) |
4. Results and Discussion
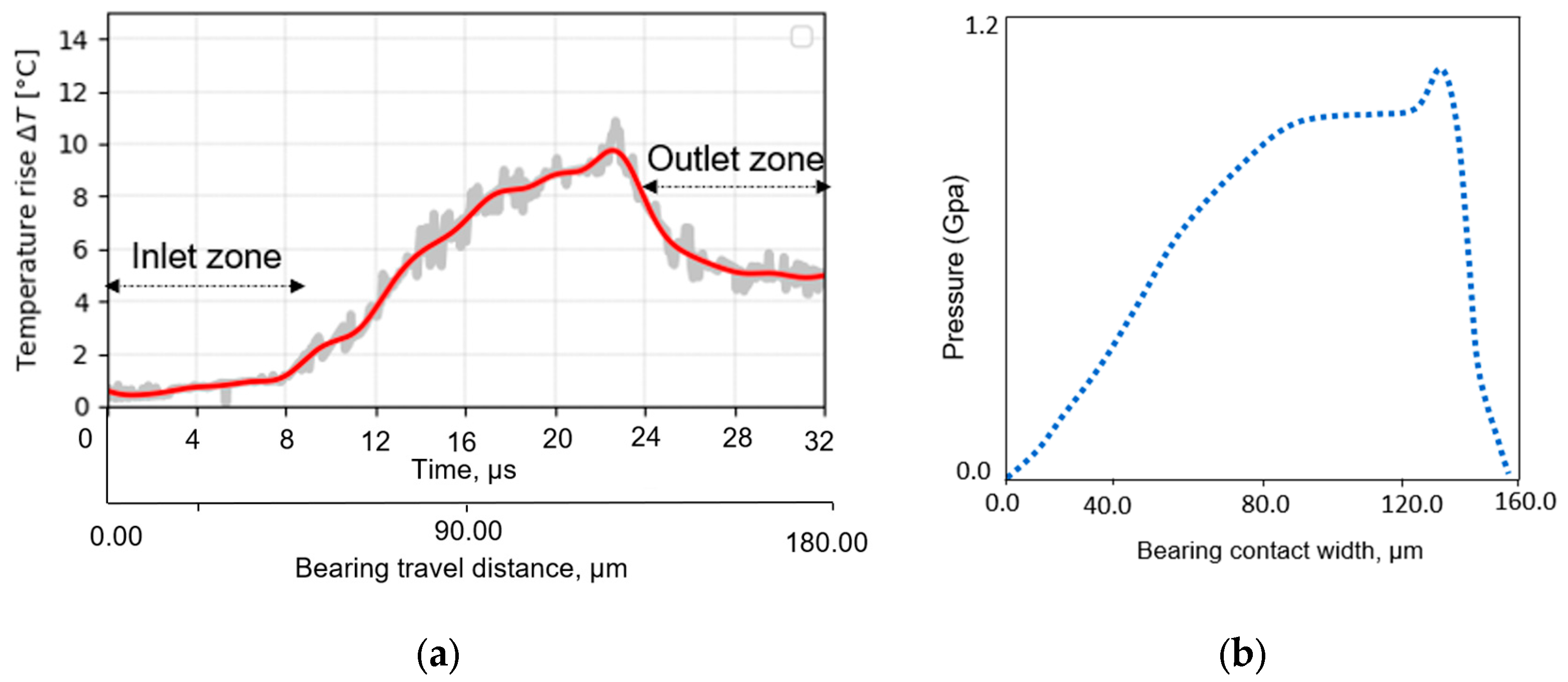
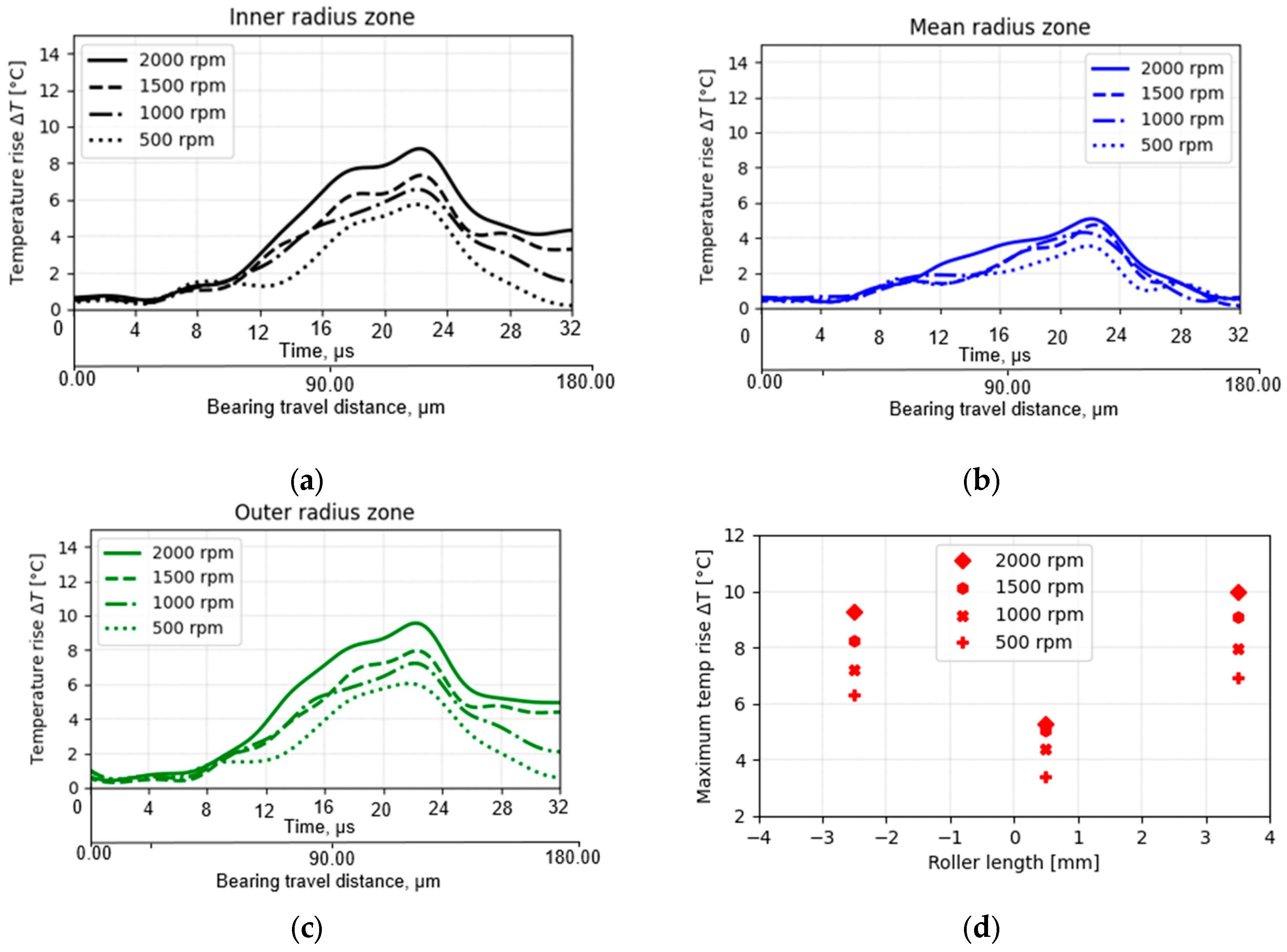
4.1. Measurement of TEHL Contact Temperature Distribution
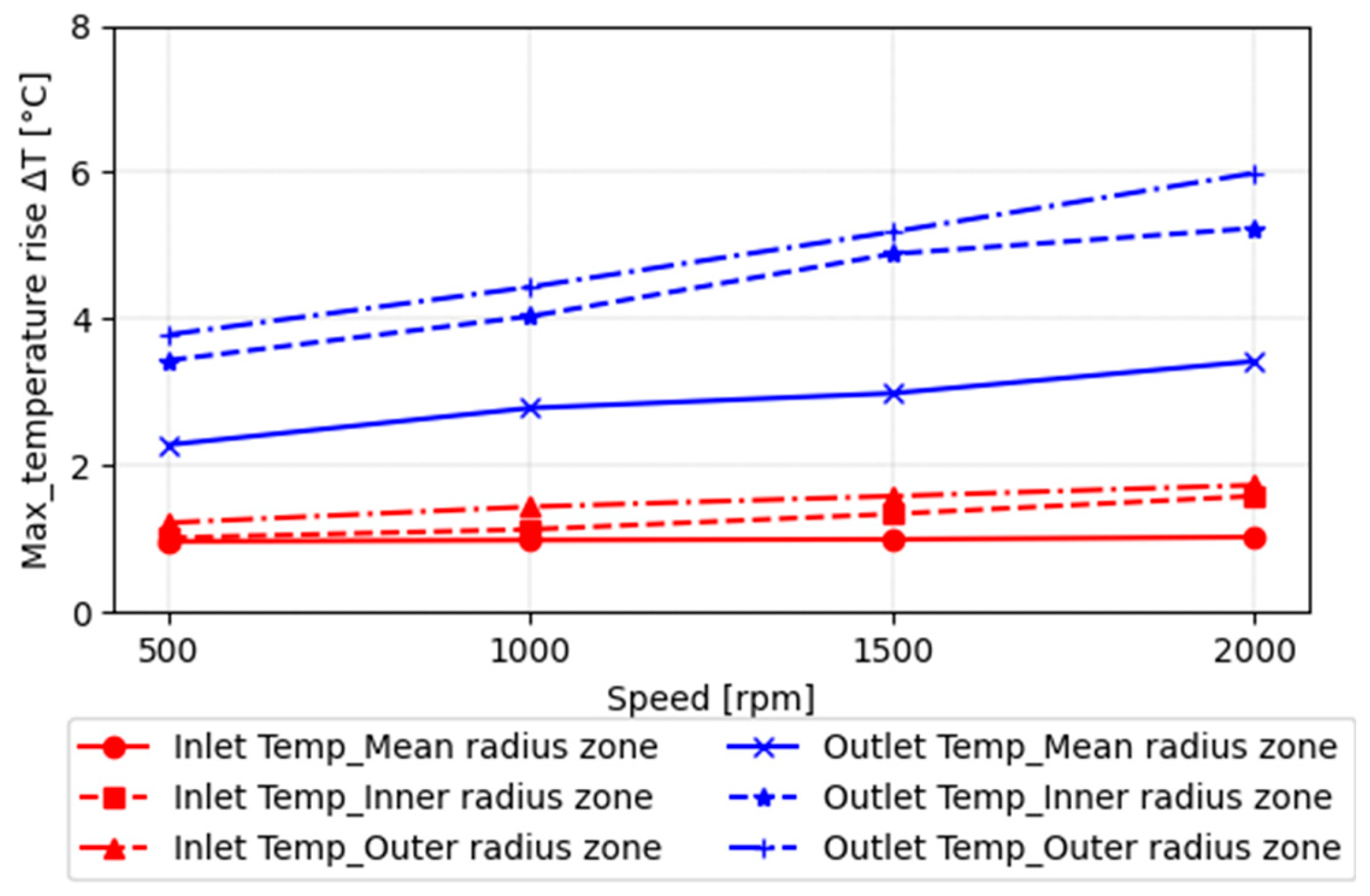
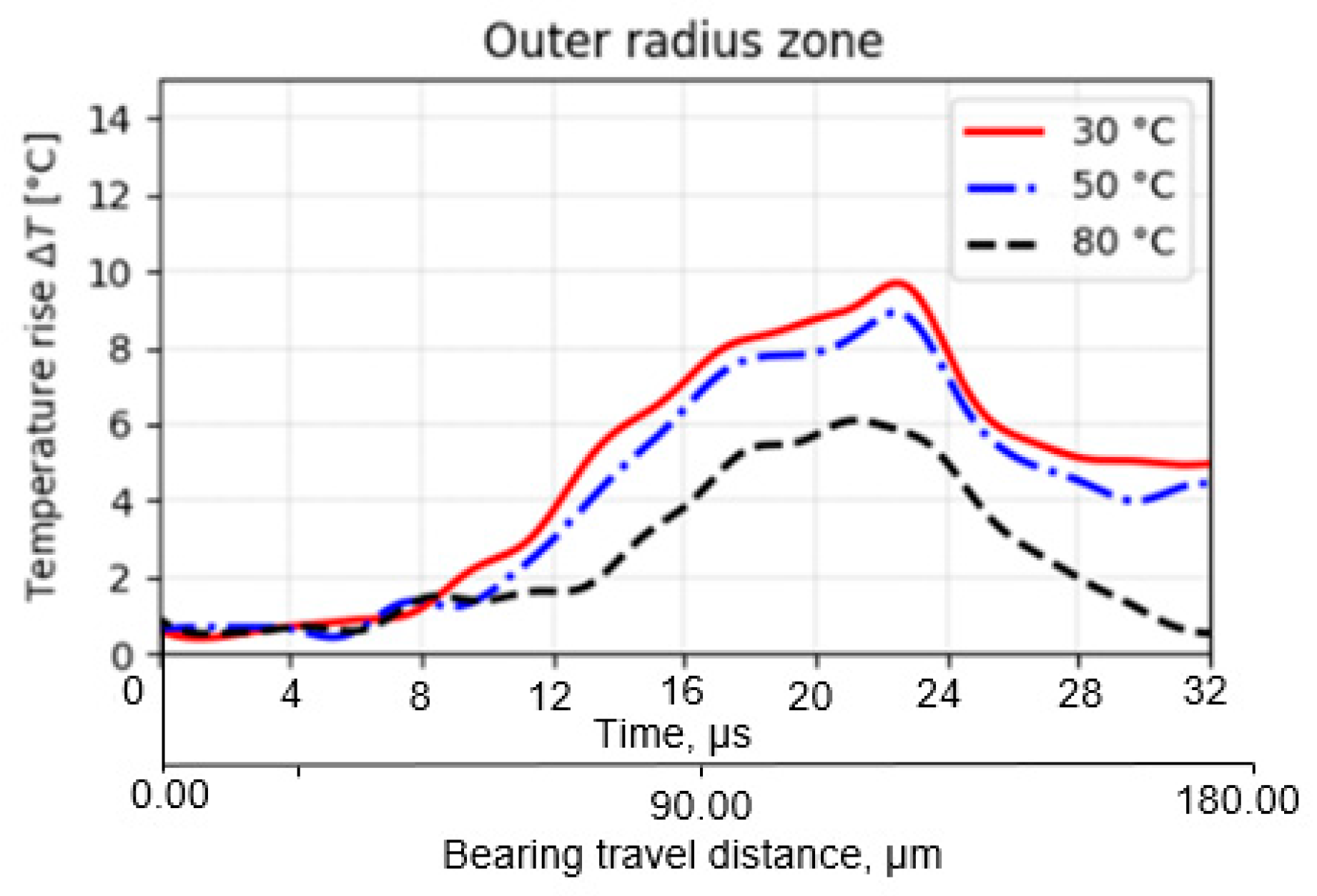
4.2. Influence of Operating Conditions on EHL Film Temperature Rise
5. Conclusions
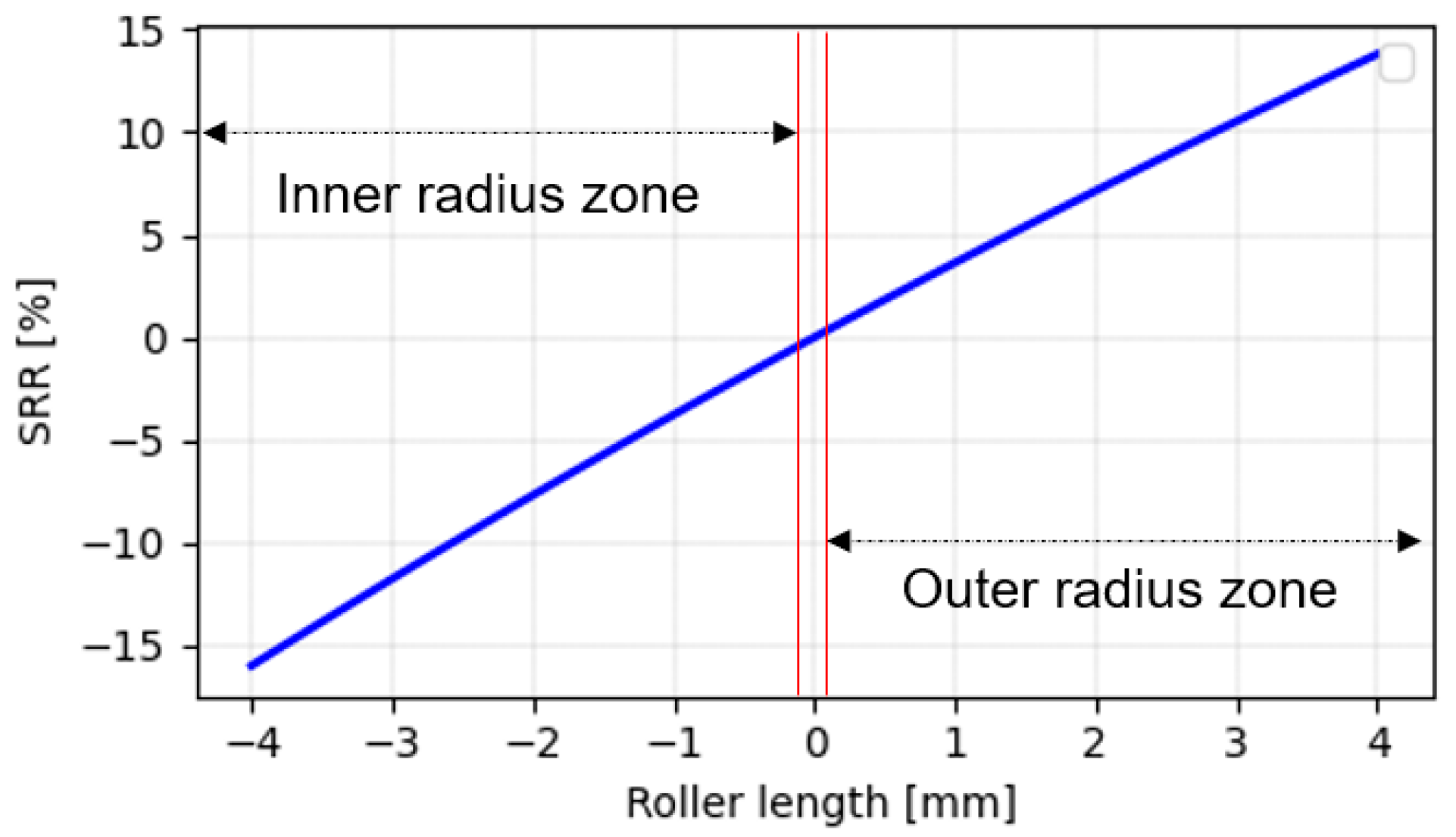
- Slip vs. temperature rise—The experiments confirmed a direct correlation between the slip-to-roll ratio (SRR) and the temperature rise. As the SRR increases, the temperature also increases. At the pitch radius (centre of the raceway, where pure rolling occurs), the measured temperature profiles were consistently lower compared to locations near the inner or outer radii of the bearing. The temperature decreased from the inner raceway zone towards the mean radius and similarly from the outer raceway zone towards the mean radius.
- Temperature spike—A small temperature spike was observed near the outlet region, approximately at the same location as the well-known Petrusevic spike for pressure, provided that sufficient film thickness existed for EHL operation. At lower rotational velocities or higher temperatures, leaning towards mixed lubrication, this spike tends to disappear as expected for Hertzian-like contacts. The results demonstrated that surface pressure, shear rates, sliding friction, and circumferential speed strongly influence the contact temperature.
- Inlet shear heating and Oil supply temperature—Using these thin-film sensors, it is possible to accurately measure the temperature rise in the inlet zone caused by viscous shear heating due to the recirculation of excess oil in front of the Hertzian contact area. Moreover, the contact temperature is significantly affected by the oil supply temperature, as expected. As lubricant viscosity decreases roughly exponentially with temperature, the film thickness reduces significantly at higher temperatures, as does the viscous shear heating, despite the higher shear rates. Consequently, this leads to a smaller temperature rise throughout the contact area.
6. Patents
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| b | Hertzian half-width contact (m) |
| Pitch diameter (m) | |
| Central film thickness of the oil (m) | |
| Sensors dimensions (µm) | |
| Sliding velocity (m/s) | |
| Raceway surface velocities (m/s) | |
| Roller surface velocities (m/s) | |
| t | Time |
| w | Load-per-unit length (Nm) |
| Distance from the pitch radius (m) | |
| CRTB | Cylindrical roller thrust bearing |
| Equivalent Young’s modulus (GPa) | |
| EHL | Elasto–hydrodynamic lubrication |
| Excitation current (A) | |
| F | Applied load (N) |
| L | Length of the roller (m) |
| Global frictional torque (Nm) | |
| N | Number of rolling elements |
| RBT | Roller-bearing tribometer |
| Root mean square of roller surface roughness | |
| Root mean square of raceway surface roughness | |
| Initial resistance of the sensor (Ohm) | |
| Change in resistance (Ohm) | |
| Power dissipation () | |
| Change in pressure (bar) | |
| Change in temperature (°C) | |
| Linear velocity (m/s) | |
| Measured voltage drop (V) | |
| SRR | Slip-to-roll ratio |
| TEHL | Thermo-elasto-hydrodynamic lubrication |
| Temperature of oil at the entry of the Hertzian contact (). | |
| Bearing temperature °C | |
| Oil inlet temperature °C | |
| Oil outlet temperature °C | |
| Bearing temperature °C | |
| Temperature coefficients 1/K | |
| Pressure coefficients 1/bar | |
| Strain rates |
References
- Manjunath, M.; Fauconnier, D.; Ost, W.; De Baets, P. Experimental Analysis of Rolling Torque and Thermal Inlet Shear Heating in Tapered Roller Bearings. Machines 2023, 11, 801. [Google Scholar] [CrossRef]
- Spikes, H. Basics of EHL for Practical Application. Lubr. Sci. 2015, 27, 45–67. [Google Scholar] [CrossRef]
- Stratmann, A.; Jacobs, G.; Hsu, C.J.; Gachot, C.; Burghardt, G. Antiwear Tribofilm Growth in Rolling Bearings under Boundary Lubrication Conditions. Tribol. Int. 2017, 113, 43–49. [Google Scholar] [CrossRef]
- Paladugu, M.; Lucas, D.R.; Scott Hyde, R. Effect of Lubricants on Bearing Damage in Rolling-Sliding Conditions: Evolution of White Etching Cracks. Wear 2018, 398–399, 165–177. [Google Scholar] [CrossRef]
- Dieter, F.; Manjunath, M.; Ost, W. Bearing Lubrication Monitoring Probe Device, System, Method and Assembly; European Patent Office: Paris, France, 2023. [Google Scholar]
- Fatourehchi, E.; Mohammadpour, M.; Theodossiades, S.; Rahnejat, H. Thermal Modelling of Mixed Non-Newtonian Thermo-Elastohydrodynamics in Dry Sump Lubrication Systems. In Proceedings of the 6th World Tribology Congress, Beijing, China, 17–22 September 2017. [Google Scholar]
- Albahrani, S.; Philippon, D.; Vergne, P.; Bluet, J. A Review of in Situ Methodologies for Studying Elastohydrodynamic Lubrication. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2016, 230, 86–110. [Google Scholar] [CrossRef]
- Kannel, J.W.; Bell, J.C.; Allen, C.M. Methods for Determining Pressure Distributions in Lubricated Rolling Contact. ASLE Trans. 2008, 8, 250–270. [Google Scholar] [CrossRef]
- Cheng, H.S.; Orcutt, F.K. Paper 13: A Correlation between the Theoretical and Experimental Results on the Elastohydrodynamic Lubrication of Rolling and Sliding Contacts. Proc. Inst. Mech. Eng. Conf. Proc. 1965, 180, 158–168. [Google Scholar] [CrossRef]
- Orcutt, F.K. Experimental Study of Elastohydrodynamic Lubrication. ASLE Trans. 2008, 8, 381–396. [Google Scholar] [CrossRef]
- Hamilton, G.M.; Moore, S.L. Deformation and Pressure in an Elastohydrodynamic Contact. Proc. R. Soc. London A Math. Phys. Sci. 1971, 322, 313–330. [Google Scholar] [CrossRef]
- Safa, M.M.A.; Anderson, J.C.; Leather, J.A. Transducers for Pressure, Temperature and Oil Film Thickness Measurement in Bearings. Sens. Actuators 1982, 3, 119–128. [Google Scholar] [CrossRef]
- Taranto, J.; Stromsta, R.R.; Weir, R.C. Application of Thin Film Head Technology to a high performance head/track disk file. IEEE Trans. Magn. 1978, 14, 188–190. [Google Scholar] [CrossRef]
- Köhler, A. Die Entwicklung von Aufgedampften Messwertaufnehmern und Deren Anwendung Zur Druck- und Temperaturmessung in Geschmierten Wälz- und Gleitkontakten. Ph.D. Thesis, Rheinisch-Westfälische Technische Hochschule Aachen, Aachen, Germany, 1981. [Google Scholar]
- Simon, M. Messung von Elasto-Hydrodynamischen Parametern und Ihre Auswirkung auf die Grübchentragfähigkeit Vergüteter Scheiben und Zahnräder. Ph.D. Thesis, Technische Universität München, Munich, Germany, 1984. [Google Scholar]
- Oster, P. Beanspruchung der Zahnflanken Unter Bedingungen der Elastohydrodynamik. Ph.D. Thesis, Technische Universität München, München, Germany, 1982. [Google Scholar]
- Baumann, H. Druck- und Temperaturmessungen Mittels Aufgedampfter Dünnschichtaufnehmer in Einem Elasthydrodynamischen. Ph.D. Thesis, Universität Karlsruhe, Karlsruhe, Germany, 1985. [Google Scholar]
- Baumann, H. Measuring Surface Temperatures between Rolling Steel Cylinders Using Double-Layer Transducers. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2016, 201, 263–270. [Google Scholar] [CrossRef]
- Peeken, H.; Ayanoglu, P.; Knoll, G.; Welsch, G. Measurement of Lubricating Film Thickness, Temperature and Pressure in Gear Contacts with Surface Topography as a Parameter. Lubr. Sci. 1990, 3, 33–42. [Google Scholar] [CrossRef]
- Kagerer, E. Messung von Elastohydrodynamischen Parametern Im Hochbelasteten Scheiben-und Zahnkontakt. Ph.D. Thesis, Technische Universität München, Munich, Germany, 1991. [Google Scholar]
- Tychsen, M. Zur Messung der Schmierspaltweite in Verzahnungen Mittels Dünnfilmsensoren. In VDI Fortschritt-Berichte, 31700; Ph.D. Thesis; VDI-Verlag: Düsseldorf, Germany, 1993; Volume 9, 171p. [Google Scholar]
- Holland, J.; Kühl, S. Dünnschicht-Sensoren Zur Gemeinsamen Resistiven Druck- und Temperaturmessung in Hochbelasteten Geschmierten Kontakten. Tech. Mess. 1998, 65, 48–52. [Google Scholar] [CrossRef]
- Mihara, Y. Measurement of Oil-Film Pressure and Strain Distribution in Engine and Machine Elements Using a Thin-Film Sensor. Tribol. Trans. 2008, 45, 11–20. [Google Scholar] [CrossRef]
- Sperrfechter, T.; Haller, R. Elastohydrodynamic Lubrication Between Rolling and Sliding Ceramic Cylinders: An Experimental Investigation. J. Tribol. 2000, 122, 721–724. [Google Scholar] [CrossRef]
- Dauber, O. Elastohydrodynamic Rolling Friction in Steel-Ceramic-Contacts. Ph.D. Thesis, Universität Karlsruhe, Karlsruhe, Germany, 2001. [Google Scholar]
- Kreil, O.; Schouten, M.J.W. Einfluss Der Oberflächenstruktur Auf Druckverteilung Und Schmierfilmdicke Im EHD-Kontakt. Ph.D. Thesis, Technischen Universität München, Munich, Germany, 2008. [Google Scholar]
- Höhn, B.R.; Michaelis, K.; Kreil, O. Influence of Surface Roughness on Pressure Distribution and Film Thickness in EHL-Contacts. Tribol. Int. 2006, 12, 1719–1725. [Google Scholar] [CrossRef]
- Miyata, S.; Höhn, B.R.; Michaelis, K.; Kreil, O. Experimental Investigation of Temperature Rise in Elliptical EHL Contacts. Tribol. Int. 2008, 41, 1074–1082. [Google Scholar] [CrossRef]
- Wilczek, A. Influence of Electrical Parameters of a Thin-Layer Sensor on the Accuracy of Pressure Measurement in an EHD Contact. J. Tribol. 2011, 133, 031504. [Google Scholar] [CrossRef]
- Wilczek, A. The Influence of Construction Features of a Thin-Layer Sensor on Pressure Distributions Recorded in an Elastohydrodynamic Contact. J. Tribol. 2012, 134, 011501. [Google Scholar] [CrossRef]
- Emmrich, S.; Plogmeyer, M.; Bartel, D.; Herrmann, C. Development of a Thin-Film Sensor for in Situ Measurement of the Temperature Rise in Rolling Contacts with Fluid Film and Mixed Lubrication. Sensors 2021, 21, 6787. [Google Scholar] [CrossRef] [PubMed]
- Mayer, J. Einfluss der Oberfläche und des Schmierstoffs auf das Reibungsverhalten im EHD-Kontakt. Ph.D. Thesis, Technische Universität München, Munich, Germany, 2014. [Google Scholar]
- Ebner, M.; Ziegltrum, A.; Lohner, T.; Michaelis, K.; Stahl, K. Measurement of EHL Temperature by Thin Film Sensors—Thermal Insulation Effects. Tribol. Int. 2020, 149, 105515. [Google Scholar] [CrossRef]
- Echávarri Otero, J.; de la Guerra Ochoa, E.; Chacón Tanarro, E.; Franco Martínez, F.; Contreras Urgiles, R.W. An Analytical Approach for Predicting EHL Friction: Usefulness and Limitations. Lubricants 2022, 10, 141. [Google Scholar] [CrossRef]
- Echávarri Otero, J.; De La Guerra Ochoa, E.; Chacón Tanarro, E.; Díaz Lantada, A.; Munoz-Guijosa, J.M. Analytical Model for Predicting Friction in Line Contacts. Lubr. Sci. 2016, 28, 189–205. [Google Scholar] [CrossRef]
- Manjunath, M.; Hausner, S.; Heine, A.; De Baets, P.; Fauconnier, D. Electrical Impedance Spectroscopy for Precise Film Thickness Assessment in Line Contacts. Lubricants 2024, 12, 51. [Google Scholar] [CrossRef]
- Havaej, P.; Degroote, J.; Fauconnier, D. Sensitivity of TEHL Simulations to the Use of Different Models for the Constitutive Behaviour of Lubricants. Lubricants 2023, 11, 151. [Google Scholar] [CrossRef]
- Havaej, P.; Degroote, J.; Fauconnier, D. A Quantitative Analysis of Double-Sided Surface Waviness on TEHL Line Contacts. Tribol. Int. 2023, 183, 108389. [Google Scholar] [CrossRef]
- Habchi, W. Finite Element Modelling of Elastohydrodynamic Lubrication Problems; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2018. [Google Scholar]
- Sui, P.C.; Sadeghi, F. Non-Newtonian Thermal Elastohydrodynamic Lubrication. J. Tribol. 1991, 113, 390–396. [Google Scholar] [CrossRef]
- Scott, S. Bair High Pressure Rheology for Quantitative Elastohydrodynamics; Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar]
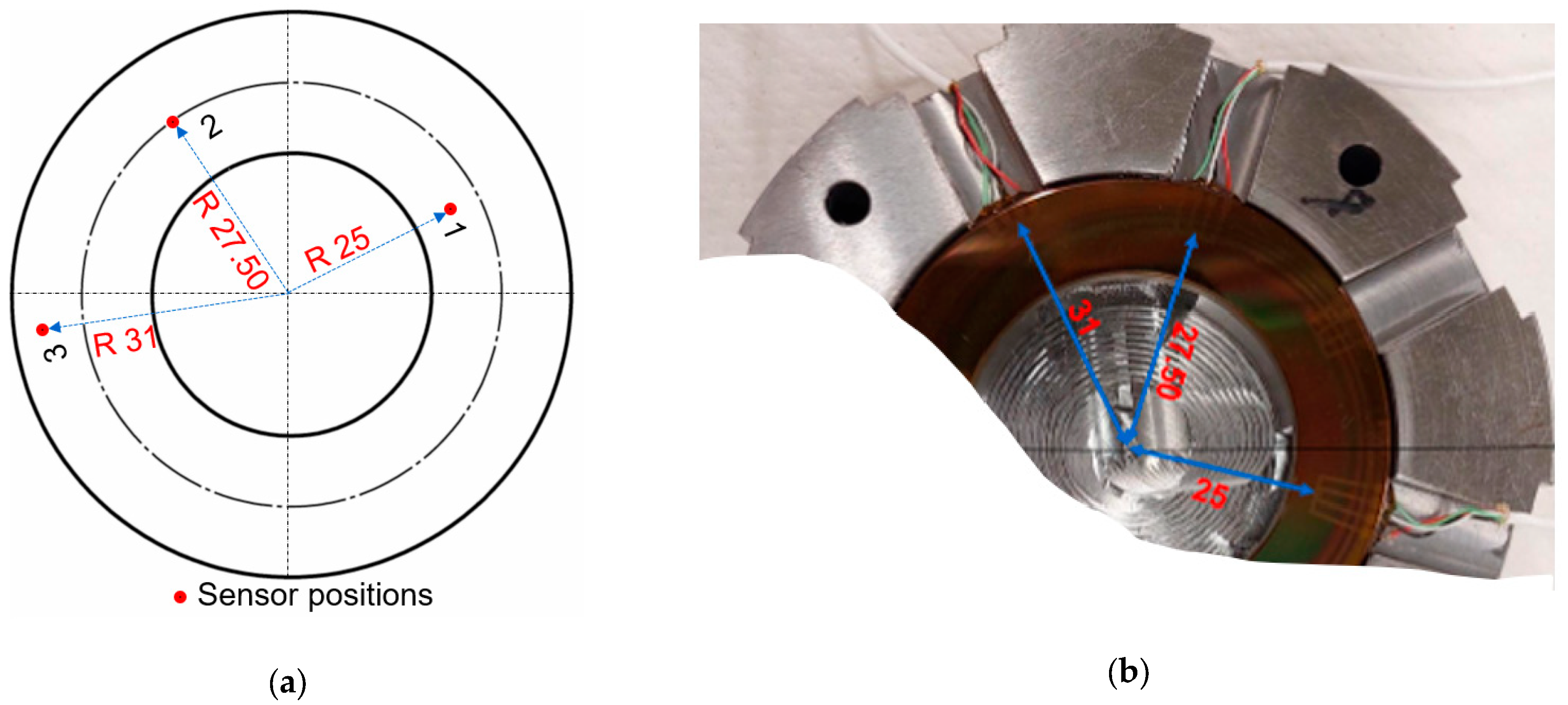




| Sensor Position | Temperature Coefficient1/K | Pressure Coefficient1/bar |
| −Slip zone, 1 | 3.24 × 10−3 | 0.908 × 10−6 |
| PCD zone, 2 | 3.19 × 10−3 | 0.918 × 10−6 |
| +Slip zone, 3 | 3.22 × 10−3 | 0.923 × 10−6 |
| FVA 3A | Units | |
|---|---|---|
| Oil type | Paraffin-based solvent raffinate | |
| Density | 884.1 | Kg/m3 |
| Viscosity at 40 °C | 90.02 | mm2/s |
| Viscosity at 100 °C | 10.41 | mm2/s |
| Viscosity–pressure coefficient (at 200 MPa) | 2.16 × 103 bar−1 @ 25 °C 1.58 × 103 bar−1 @ 80 °C |
| Hertzian pressure, MPa | 655 | 1028 | 1285 |
| Film thickness, µm | 1.08 | 0.944 | 0.880 |
| Shear rate, s−1 | 1.85 × 105 | 2.11 × 105 | 2.27 × 105 |
| Sliding frictional torque, Nm | 0.587 | 1.46 | 2.29 |
| Bearing temperature, °C | 54 | 59 | 61 |
| Supply oil temperature, °C | 30 °C | 50 °C | 80 °C |
| Viscosity, Cst | 103.28 | 76.77 | 36.95 |
| Film thickness, µm | 1.28 | 0.72 | 0.35 |
| Sliding friction, Nm | 1.32 | 1.46 | 1.65 |
| Bearing temperature, °C | 31.2 | 53.5 | 81.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Manjunath, M.; De Baets, P.; Fauconnier, D. In Situ Measurement and Mapping of Lubricant Film Temperature in Cylindrical Roller Thrust Bearings Using Thin-Film Sensors. Machines 2025, 13, 297. https://doi.org/10.3390/machines13040297
Manjunath M, De Baets P, Fauconnier D. In Situ Measurement and Mapping of Lubricant Film Temperature in Cylindrical Roller Thrust Bearings Using Thin-Film Sensors. Machines. 2025; 13(4):297. https://doi.org/10.3390/machines13040297
Chicago/Turabian StyleManjunath, Manjunath, Patrick De Baets, and Dieter Fauconnier. 2025. "In Situ Measurement and Mapping of Lubricant Film Temperature in Cylindrical Roller Thrust Bearings Using Thin-Film Sensors" Machines 13, no. 4: 297. https://doi.org/10.3390/machines13040297
APA StyleManjunath, M., De Baets, P., & Fauconnier, D. (2025). In Situ Measurement and Mapping of Lubricant Film Temperature in Cylindrical Roller Thrust Bearings Using Thin-Film Sensors. Machines, 13(4), 297. https://doi.org/10.3390/machines13040297







