Detecting Particle Contamination in Bearings of Inverter-Fed Induction Motors: A Comparative Evaluation of Monitoring Signals
Abstract
1. Introduction
2. Theoretical Background
2.1. Signatures in the Vibration Spectrum
2.2. Fault Signatures in the Stator Current Spectrum
2.3. Signatures in the Rotor Speed Spectrum
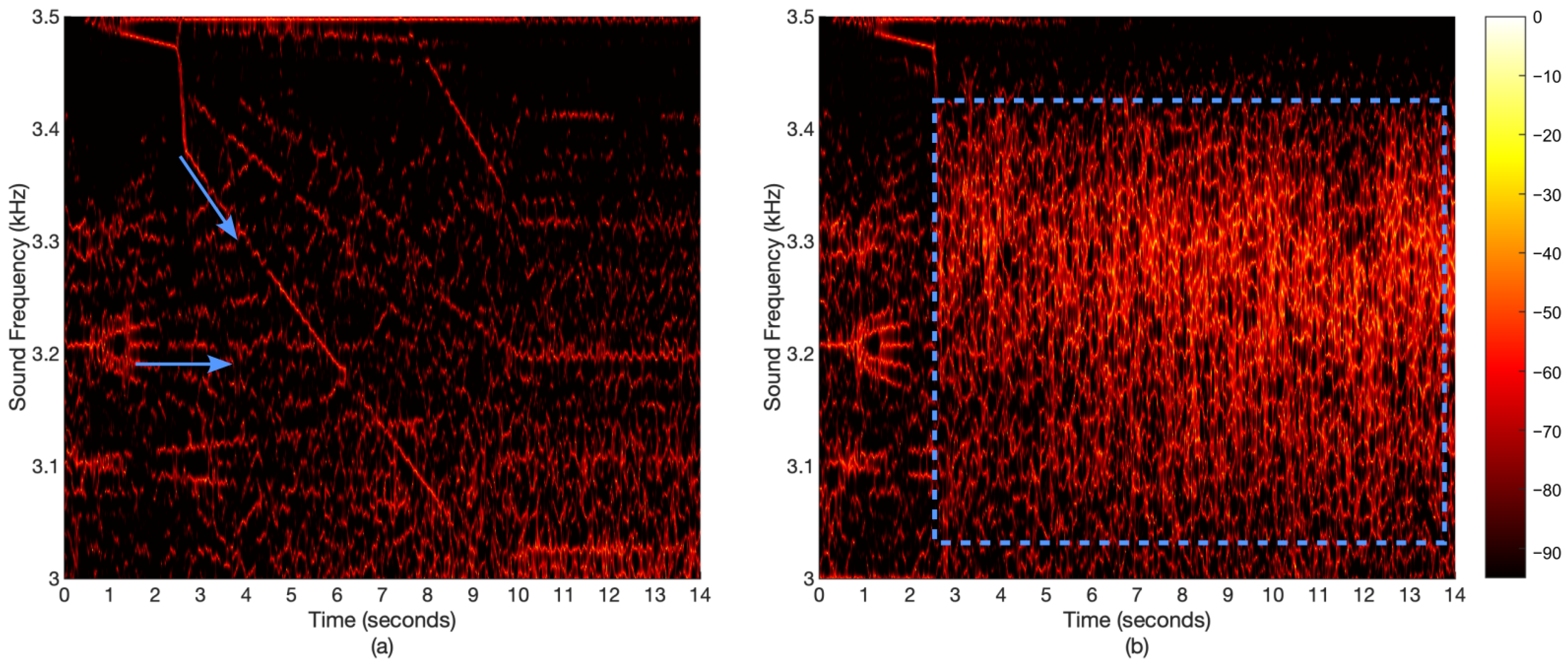
2.4. Signatures in the Sound Spectrum
2.5. Minimum Norm
2.6. Short-Time Minimum Norm
3. Experimental Setup
- Stator current was measured using a Hall-effect transducer by LEM, model LA25-P.
- Rotor speed was measured using an optical sensor from Datalogic, model S60-PA-5-W08-NH.
- Sound was measured using a directional microphone, model SG-108.
- Vibration signals were collected with a triaxial accelerometer by STMicroelectronics. The best results were obtained along the x-axis (see Figure 2a) because vibrations in induction motors are typically radial.
4. Experimental Results
4.1. Time-Domain Analysis
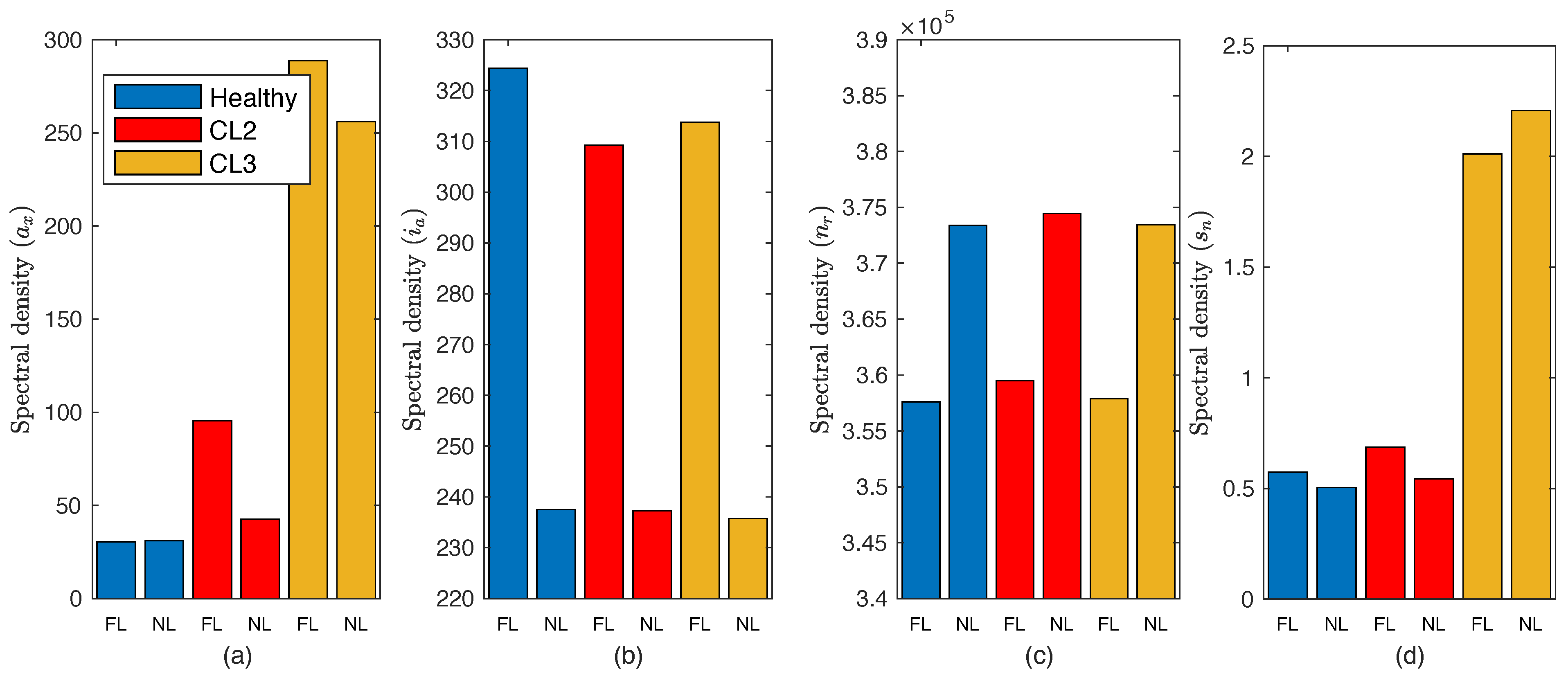
4.2. Frequency-Domain Analysis
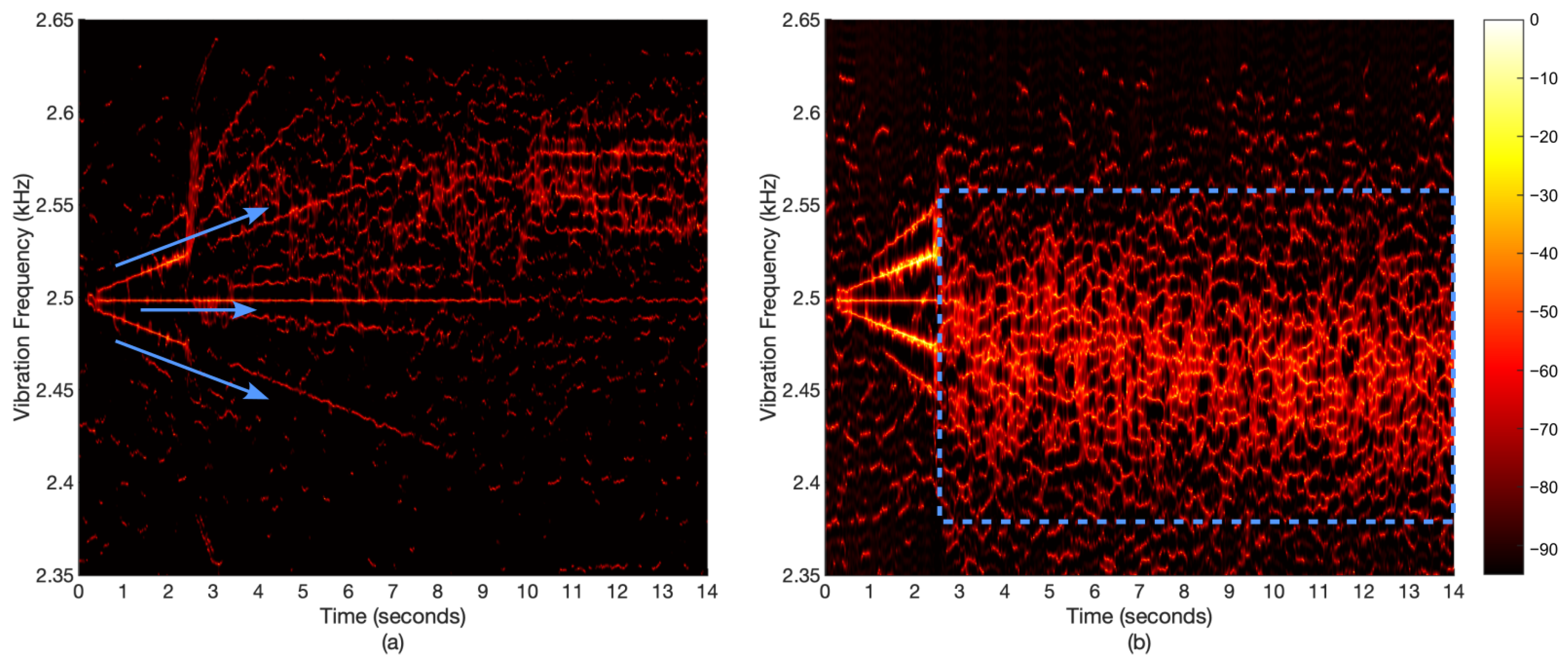
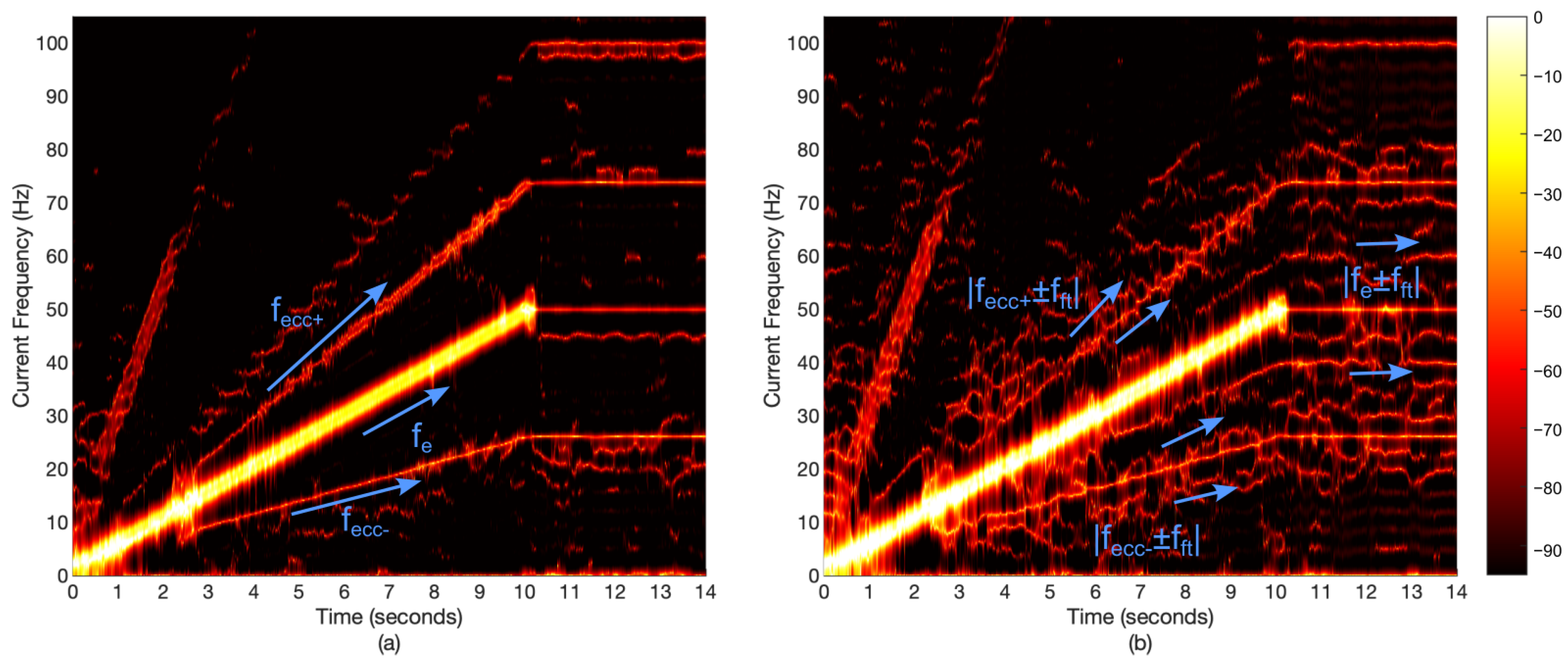
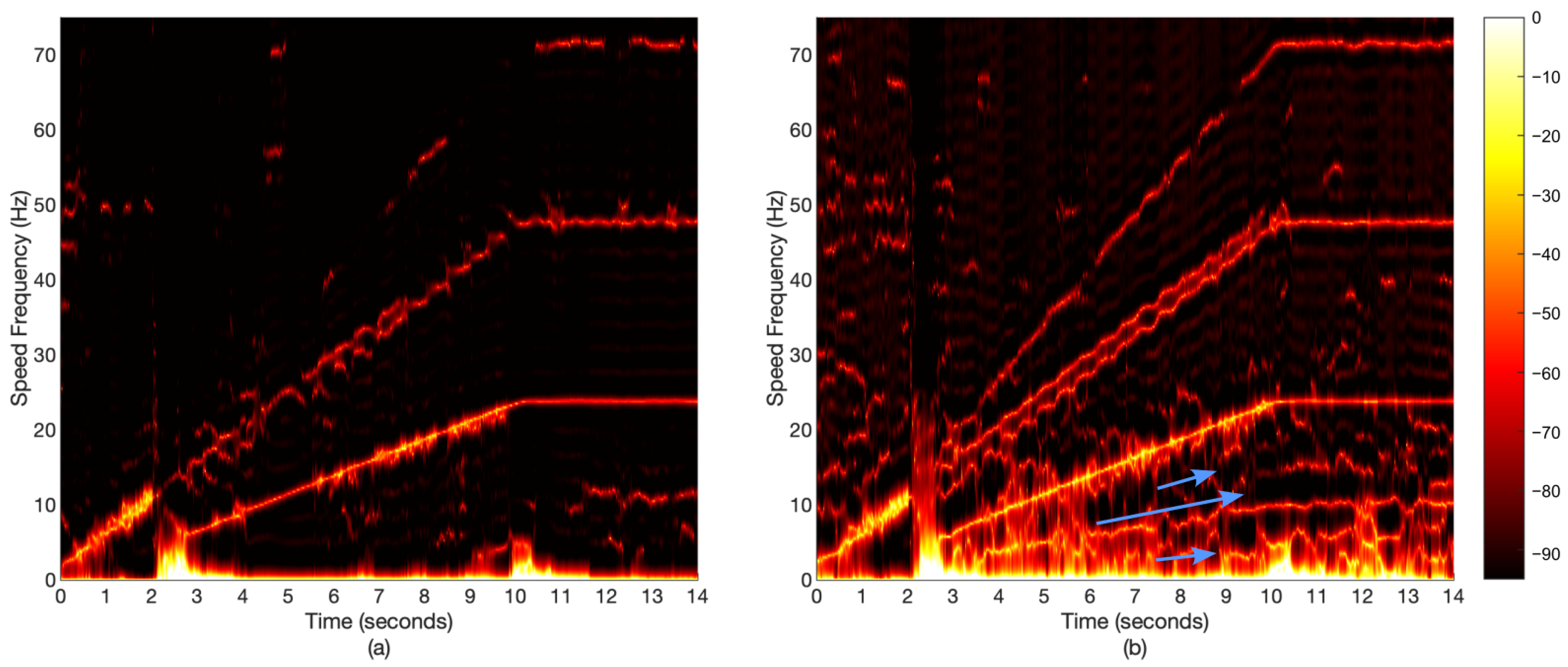
4.3. Time-Frequency Analysis
4.3.1. Motor Vibrations
4.3.2. Electrical Current
4.3.3. Rotor Speed
4.3.4. Sound
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CL | Contamination level |
| Supply rated frequency | |
| Bearing ball spin frequency | |
| Fundamental supply frequency | |
| Bearing fundamental train frequency | |
| Bearing ball pass inner frequency | |
| Bearing ball pass outer frequency | |
| Sampling frequency | |
| Switching frequency | |
| FL | Rated-load |
| IM | Induction motor |
| Min-Norm | Minimum norm |
| NL | No-load |
| PSD | Power spectral density |
| PWM | Pulse width modulation |
| SNR | Signal-to-noise ratio |
| STMN | Short-time minimum norm |
| VSI | Voltage source inverter |
References
- Kumar, S.; Mukherjee, D.; Guchhait, P.K.; Banerjee, R.; Srivastava, A.K.; Vishwakarma, D.; Saket, R.K. A comprehensive review of condition based prognostic maintenance (CBPM) for induction motor. IEEE Access 2019, 7, 90690–90704. [Google Scholar] [CrossRef]
- Javed, K.; Gouriveau, R.; Zerhouni, N.; Nectoux, P. Enabling health monitoring approach based on vibration data for accurate prognostics. IEEE Trans. Ind. Electron. 2014, 62, 647–656. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiao, X.; Han, Y. Abnormal Detection of Rolling Bearing Based on Multidimensional Feature Prediction. In Proceedings of the 2023 3rd Asia-Pacific Conference on Communications Technology and Computer Science (ACCTCS), Shenyang, China, 25–27 February 2023; pp. 542–546. [Google Scholar] [CrossRef]
- Palmer, C. Lubricant Contamination: The Prime Cause of Mechanical Machinery Failure. Available online: https://www.machinerylubrication.com/Read/32725/lubricant-contamination-prime-cause-of-mechanical-machinery-failure (accessed on 2 February 2025).
- GMN Bearing USA. 8 Common Ball Bearing Problems. Available online: https://www.gmnbt.com/resources/guides/ball-bearing/fixing-common-bearing-problems/ (accessed on 16 February 2025).
- Kulkarni, S.; Wadkar, S. Investigation for distributed defects in ball bearing using vibration signature analysis—A review. Int. J. Sci. Res. 2012, 2, 157–160. [Google Scholar] [CrossRef]
- Morales-Espejel, G.E.; Zhou, Y. Rolling Bearing Damage from Particle Contamination–Diagnosis via Inspection. Tribol. Online 2024, 19, 95–104. [Google Scholar] [CrossRef]
- Rameshkumar, K.; Nataraj, K.; Krishnakumar, P.; Saimurugan, M. Machine Learning Approach for Predicting the Solid Particle Lubricant Contamination in a Spherical Roller Bearing. IEEE Access 2024, 12, 78680–78700. [Google Scholar] [CrossRef]
- Stief, A.; Ottewill, J.R.; Baranowski, J.; Orkisz, M. A PCA and two-stage Bayesian sensor fusion approach for diagnosing electrical and mechanical faults in induction motors. IEEE Trans. Ind. Electron. 2019, 66, 9510–9520. [Google Scholar] [CrossRef]
- Zhu, J.; Hu, T.; Jiang, B.; Yang, X. Intelligent bearing fault diagnosis using PCA–DBN framework. Neural Comput. Appl. 2020, 32, 10773–10781. [Google Scholar] [CrossRef]
- Cui, H.; Hong, M.; Qiao, Y.; Yin, Y. Application of VPMCD method based on PLS for rolling bearing fault diagnosis. J. Vibroengineering 2017, 19, 160–175. [Google Scholar] [CrossRef]
- Huo, Z.; Zhang, Y.; Shu, L.; Gallimore, M. A new bearing fault diagnosis method based on fine-to-coarse multiscale permutation entropy, laplacian score and SVM. IEEE Access 2019, 7, 17050–17066. [Google Scholar] [CrossRef]
- Wang, H.; Xu, J.; Yan, R.; Gao, R.X. A new intelligent bearing fault diagnosis method using SDP representation and SE-CNN. IEEE Trans. Instrum. Meas. 2019, 69, 2377–2389. [Google Scholar] [CrossRef]
- Zhiyi, H.; Haidong, S.; Lin, J.; Junsheng, C.; Yu, Y. Transfer fault diagnosis of bearing installed in different machines using enhanced deep auto-encoder. Measurement 2020, 152, 107393. [Google Scholar] [CrossRef]
- Wen, L.; Li, X.; Gao, L.; Zhang, Y. A new convolutional neural network-based data-driven fault diagnosis method. IEEE Trans. Ind. Electron. 2017, 65, 5990–5998. [Google Scholar] [CrossRef]
- An, Z.; Li, S.; Wang, J.; Jiang, X. A novel bearing intelligent fault diagnosis framework under time-varying working conditions using recurrent neural network. ISA Trans. 2020, 100, 155–170. [Google Scholar] [CrossRef] [PubMed]
- Mao, W.; Liu, Y.; Ding, L.; Li, Y. Imbalanced fault diagnosis of rolling bearing based on generative adversarial network: A comparative study. IEEE Access 2019, 7, 9515–9530. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, S.; Wang, B.; Habetler, T.G. Deep learning algorithms for bearing fault diagnostics—A comprehensive review. IEEE Access 2020, 8, 29857–29881. [Google Scholar] [CrossRef]
- El Bouharrouti, N.; Koveshnikov, S.; Garcia-Calva, T.A.; Vehviläinen, M.; Kudelina, K.; Naseer, U.M.; Vaimann, T.; Belahcen, A. Multi-Rate Vibration Signal Analysis for Enhanced Data-Driven Monitoring of Bearing Faults in Induction Machines. In Proceedings of the 2024 International Conference on Electrical Machines (ICEM), Torino, Italy, 1–4 September 2024; pp. 1–7. [Google Scholar] [CrossRef]
- Gao, Z.; Cecati, C.; Ding, S.X. A survey of fault diagnosis and fault-tolerant techniques—Part I: Fault diagnosis with model-based and signal-based approaches. IEEE Trans. Ind. Electron. 2015, 62, 3757–3767. [Google Scholar] [CrossRef]
- El Bouharrouti, N.; Sitnikov, M.; Hemeida, A.; Martin, F.; Kudelina, K.; Naseer, M.U.; Belahcen, A. Co-simulations of induction machines coupled with a radial ball bearing for mechanical defects analysis. IET Electr. Power Appl. 2024, 1–13. [Google Scholar] [CrossRef]
- Martin-Diaz, I.; Garcia-Calva, T.; Duque-Perez, O.; Morinigo-Sotelo, D. Imbalanced Diagnosis Scheme for Incipient Rotor Faults in Inverter-Fed Induction Motors. Appl. Sci. 2024, 14, 7237. [Google Scholar] [CrossRef]
- Frosini, L.; Harlişca, C.; Szabó, L. Induction machine bearing fault detection by means of statistical processing of the stray flux measurement. IEEE Trans. Ind. Electron. 2014, 62, 1846–1854. [Google Scholar] [CrossRef]
- Aviña-Corral, V.; Rangel-Magdaleno, J.; Morales-Perez, C.; Hernandez, J. Bearing Fault Detection in Adjustable Speed Drive-Powered Induction Machine by Using Motor Current Signature Analysis and Goodness-of-Fit Tests. IEEE Trans. Ind. Inform. 2021, 17, 8265–8274. [Google Scholar] [CrossRef]
- Liu, C.; Gryllias, K. A semi-supervised Support Vector Data Description-based fault detection method for rolling element bearings based on cyclic spectral analysis. Mech. Syst. Signal Process. 2020, 140, 106682. [Google Scholar] [CrossRef]
- Sun, M.; Wang, H.; Liu, P.; Long, Z.; Yang, J.; Huang, S. A Novel Data-Driven Mechanical Fault Diagnosis Method for Induction Motors Using Stator Current Signals. IEEE Trans. Transp. Electrif. 2023, 9, 347–358. [Google Scholar] [CrossRef]
- Lee, S.B.; Stone, G.C.; Antonino-Daviu, J.; Gyftakis, K.N.; Strangas, E.G.; Maussion, P.; Platero, C.A. Condition Monitoring of Industrial Electric Machines: State of the Art and Future Challenges. IEEE Ind. Electron. Mag. 2020, 14, 158–167. [Google Scholar] [CrossRef]
- Antonino-Daviu, J. Electrical monitoring under transient conditions: A new paradigm in electric motors predictive maintenance. Appl. Sci. 2020, 10, 6137. [Google Scholar] [CrossRef]
- Frosini, L. Novel diagnostic techniques for rotating electrical machines—A review. Energies 2020, 13, 5066. [Google Scholar] [CrossRef]
- Chen, B.; Hai, Z.; Chen, X.; Chen, F.; Xiao, W.; Xiao, N.; Fu, W.; Liu, Q.; Tian, Z.; Li, G. A time-varying instantaneous frequency fault features extraction method of rolling bearing under variable speed. J. Sound Vib. 2023, 560, 117785. [Google Scholar] [CrossRef]
- Vitor, A.L.O.; Goedtel, A.; Castoldi, M.F.; Souza, W.A.; Bazan, G.H. Induction Machine Fault Diagnosis with Quadratic Time–Frequency Distributions: State of the Art. IEEE Trans. Instrum. Meas. 2023, 72, 1–16. [Google Scholar] [CrossRef]
- Feng, Z.; Yu, X.; Zhang, D.; Liang, M. Generalized adaptive mode decomposition for nonstationary signal analysis of rotating machinery: Principle and applications. Mech. Syst. Signal Process. 2020, 136, 106530. [Google Scholar] [CrossRef]
- Yu, G. A concentrated time–frequency analysis tool for bearing fault diagnosis. IEEE Trans. Instrum. Meas. 2019, 69, 371–381. [Google Scholar] [CrossRef]
- Inturi, V.; Sabareesh, G.; Supradeepan, K.; Penumakala, P. Integrated condition monitoring scheme for bearing fault diagnosis of a wind turbine gearbox. J. Vib. Control 2019, 25, 1852–1865. [Google Scholar] [CrossRef]
- Sahu, P.K.; Rai, R.N.; Kumar, T.C.A. Grease Contamination Detection in the RollingElement Bearing Using Deep Learning Technique. Int. J. Mech. Eng. Robot. Res. 2022, 11, 275–280. [Google Scholar] [CrossRef]
- Kulkarni, S.; Bewoor, A. Vibration Based Condition Assessment of Ball Bearing with Distributed Defects. J. Meas. Eng. 2016, 4, 87–94. [Google Scholar]
- Duque-Perez, O.; Del Pozo-Gallego, C.; Morinigo-Sotelo, D.; Fontes Godoy, W. Condition Monitoring of Bearing Faults Using the Stator Current and Shrinkage Methods. Energies 2019, 12, 3392. [Google Scholar] [CrossRef]
- Blodt, M.; Granjon, P.; Raison, B.; Rostaing, G. Models for bearing damage detection in induction motors using stator current monitoring. IEEE Trans. Ind. Electron. 2008, 55, 1813–1822. [Google Scholar] [CrossRef]
- Tsoumas, I.P.; Tischmacher, H. Influence of the Inverter’s Modulation Technique on the Audible Noise of Electric Motors. IEEE Trans. Ind. Appl. 2014, 50, 269–278. [Google Scholar] [CrossRef]
- Garcia-Calva, T.A.; Morinigo-Sotelo, D.; de Jesus Romero Troncoso, R. Fundamental Frequency Normalization for Reliable Detection of Rotor and Load Defects in VSD-Fed Induction Motors. IEEE Trans. Energy Convers. 2022, 37, 1467–1474. [Google Scholar] [CrossRef]
- Frini, M.; Choqueuse, V.; Auger, F. Parametric Tracking of Electrical Current Components Using Gradient Descent Algorithm. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2022, 236, 8834–8841. [Google Scholar] [CrossRef]
- Garcia-Calva, T.A.; Morinigo-Sotelo, D.; Duque-Perez, O.; Garcia-Perez, A.; Romero-Troncoso, R.d.J. Time-Frequency Analysis Based on Minimum-Norm Spectral Estimation to Detect Induction Motor Faults. Energies 2020, 13, 4102. [Google Scholar] [CrossRef]
- Jalali-Farahani, B.; Ismail, M. Adaptive Noise Cancellation Techniques in Sigma–Delta Analog-to-Digital Converters. IEEE Trans. Circuits Syst. Regul. Pap. 2007, 54, 1891–1899. [Google Scholar] [CrossRef]
- Nandi, S.; Toliyat, H.; Li, X. Condition Monitoring and Fault Diagnosis of Electrical Motors—A Review. IEEE Trans. Energy Convers. 2005, 20, 719–729. [Google Scholar] [CrossRef]


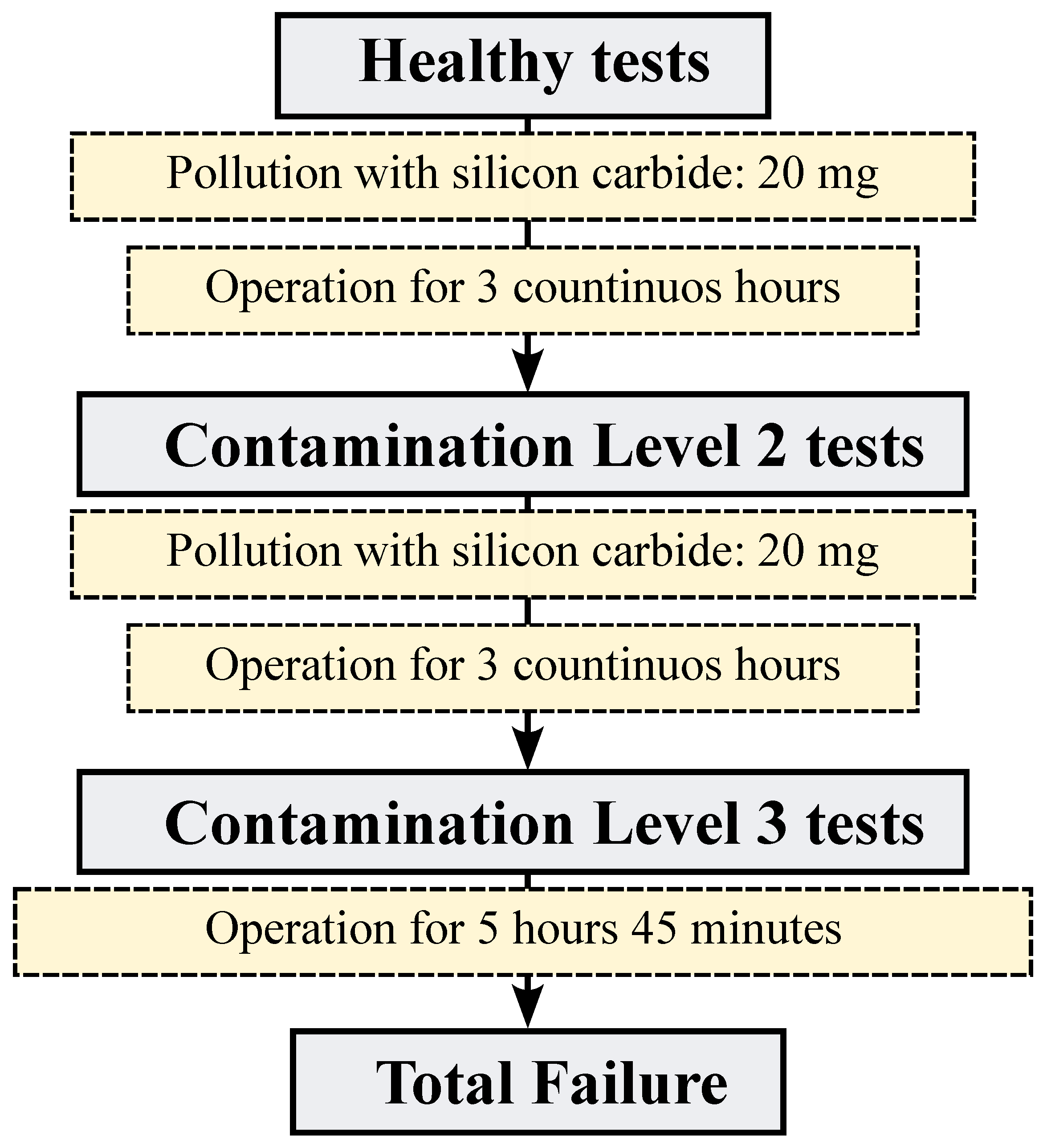

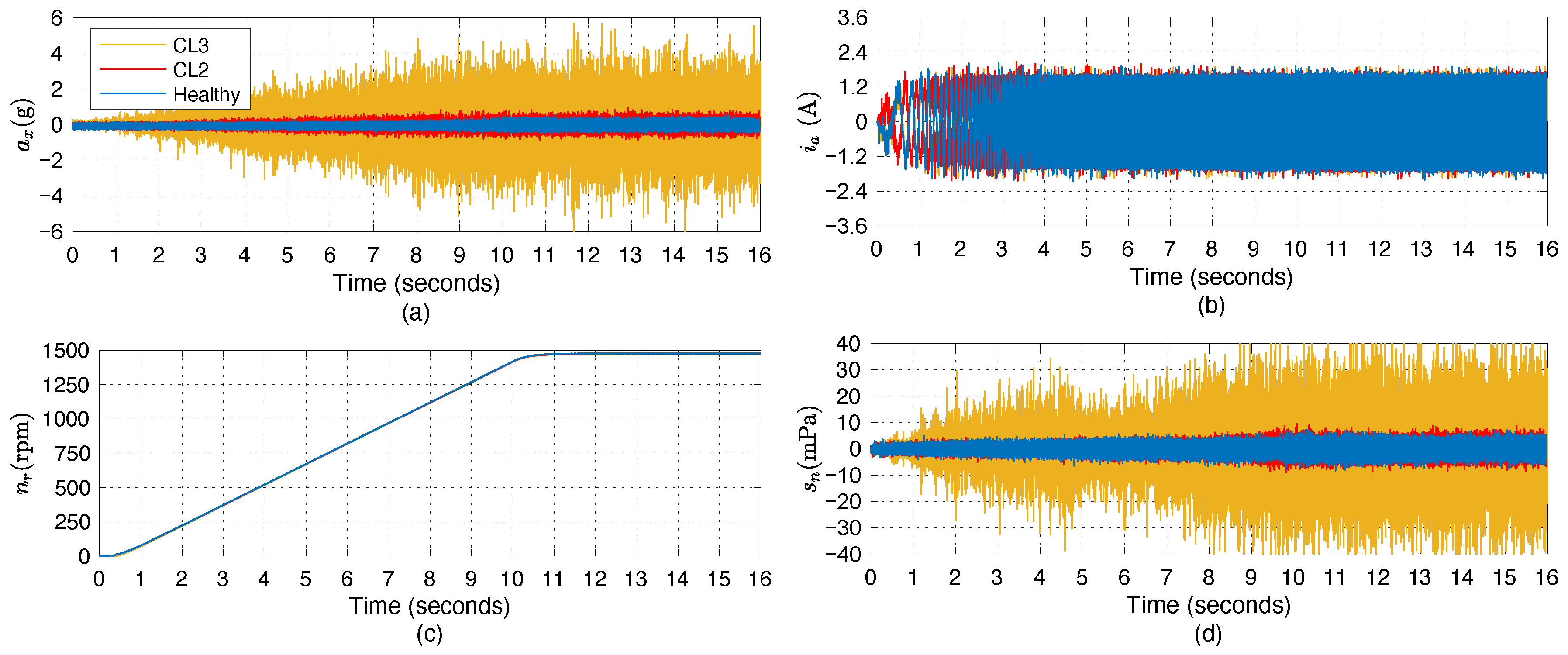
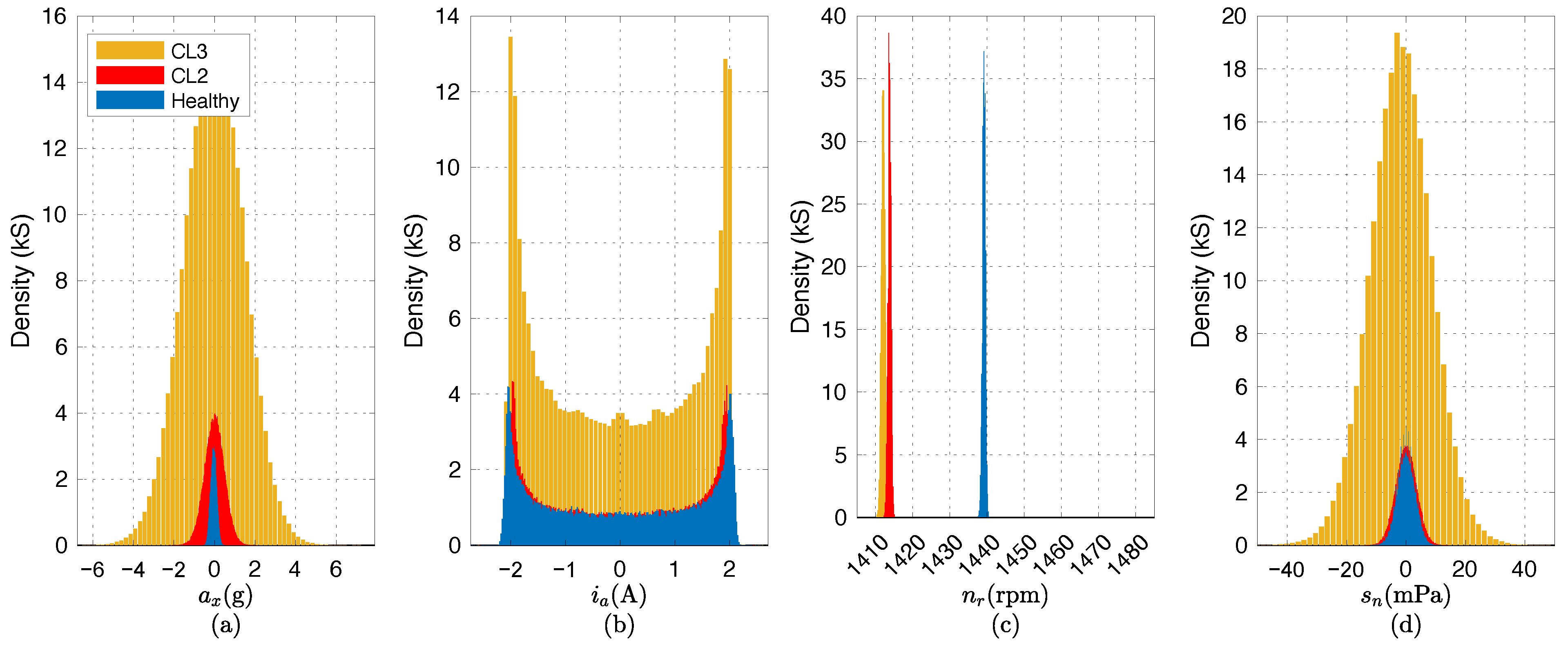

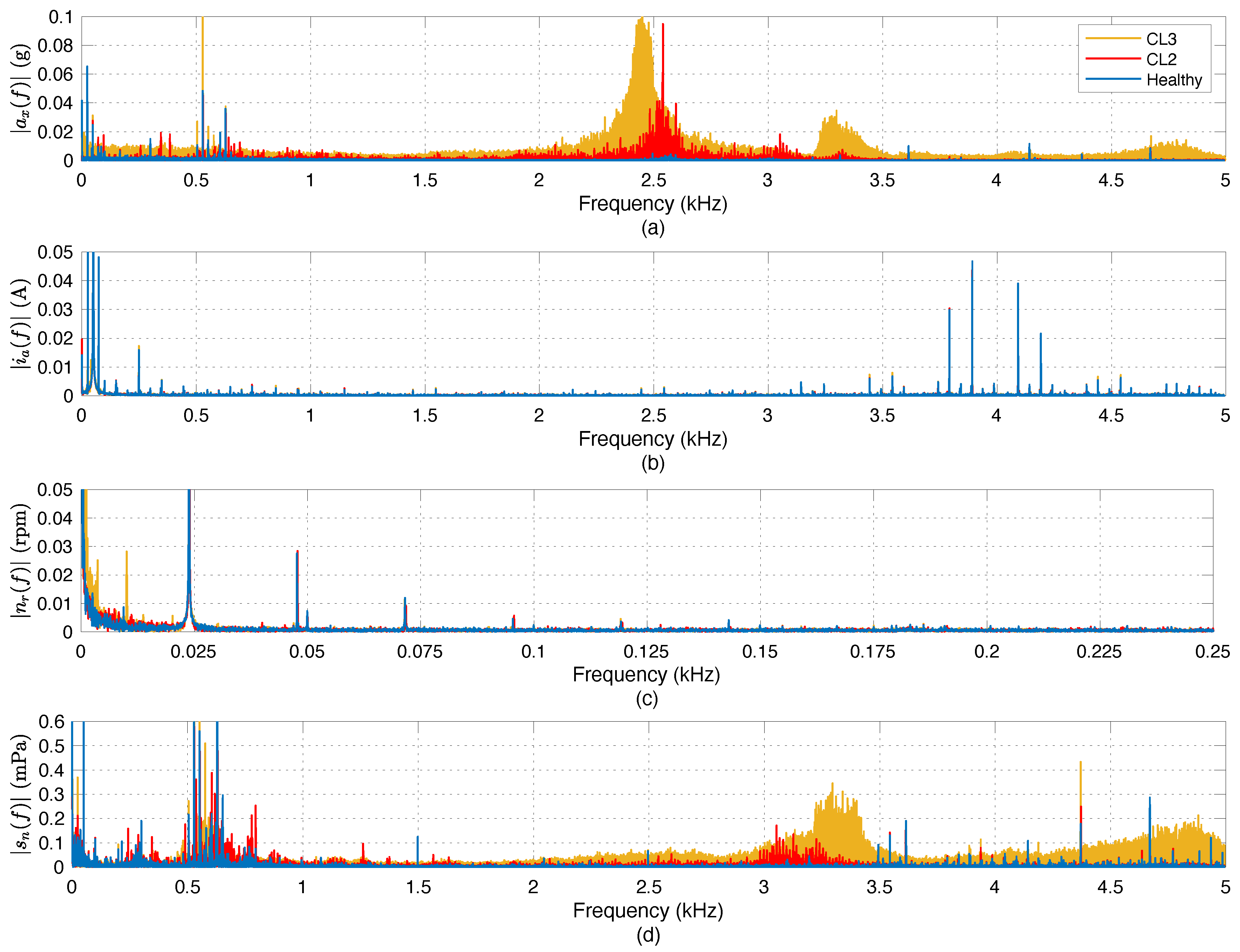

| Parameter | Specification |
|---|---|
| Number of balls | 9 |
| Ball diameter (mm) | 6.27 |
| Pitch diameter (mm) | 30.92 |
| External diameter (mm) | 42 |
| Internal diameter (mm) | 20 |
| Inner raceway diameter (mm) | 2.325 |
| Outer raceway diameter (mm) | 2.405 |
| Width (mm) | 12 |
| Dynamic load rating (kN) | 9.95 |
| Static load rating (kN) | 5 |
| Mass bearing (kg) | 0.069 |
| Healthy Bearing | Contamination Level 1 | Contamination Level 2 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 30.4 k | 324 k | 358 M | 0.57 k | 95.5 k | 309 k | 360 M | 686 | 289 k | 314 k | 358 M | 2.01 k | |
| −42 m | −16 m | 1.4 k | −0.21 m | −3.27 m | −241 | 1.46 k | −1.72 m | −1.62 m | −132 | 1.46 k | 0.99 m | |
| 21 m | 2.16 | 0.17 m | 0.8 m | 240 m | 1.96 | 18 m | 1.2 m | 2.17 | 2.02 | 24.1 | 10.8 m | |
| Healthy Bearing | Contamination Level 1 | Contamination Level 2 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 3.11 k | 238 k | 373 M | 5.04 k | 4.25 k | 237 k | 374 M | 5.45 k | 256 k | 236 k | 373 M | 2.21 k | |
| −47 m | −17.8 m | 1.43 k | −0.54 m | −27 m | −12.2 m | 1.42 k | 0.55 m | 12 m | −23.5 m | 1.41 k | 0.21 m | |
| 21 m | 1.15 | 0.181 | 6.5 m | 0.045 | 1.15 | 0.164 | 7.6 m | 1.70 | 1.13 | 0.201 | 13 m | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Garcia-Calva, T.; Duque-Perez, Ó.; Romero-Troncoso, R.J.; Morinigo-Sotelo, D.; Martin-Diaz, I. Detecting Particle Contamination in Bearings of Inverter-Fed Induction Motors: A Comparative Evaluation of Monitoring Signals. Machines 2025, 13, 269. https://doi.org/10.3390/machines13040269
Garcia-Calva T, Duque-Perez Ó, Romero-Troncoso RJ, Morinigo-Sotelo D, Martin-Diaz I. Detecting Particle Contamination in Bearings of Inverter-Fed Induction Motors: A Comparative Evaluation of Monitoring Signals. Machines. 2025; 13(4):269. https://doi.org/10.3390/machines13040269
Chicago/Turabian StyleGarcia-Calva, Tomas, Óscar Duque-Perez, Rene J. Romero-Troncoso, Daniel Morinigo-Sotelo, and Ignacio Martin-Diaz. 2025. "Detecting Particle Contamination in Bearings of Inverter-Fed Induction Motors: A Comparative Evaluation of Monitoring Signals" Machines 13, no. 4: 269. https://doi.org/10.3390/machines13040269
APA StyleGarcia-Calva, T., Duque-Perez, Ó., Romero-Troncoso, R. J., Morinigo-Sotelo, D., & Martin-Diaz, I. (2025). Detecting Particle Contamination in Bearings of Inverter-Fed Induction Motors: A Comparative Evaluation of Monitoring Signals. Machines, 13(4), 269. https://doi.org/10.3390/machines13040269










