A Composite Vision-Based Method for Post-Assembly Dimensional Inspection of Engine Oil Seals
Abstract
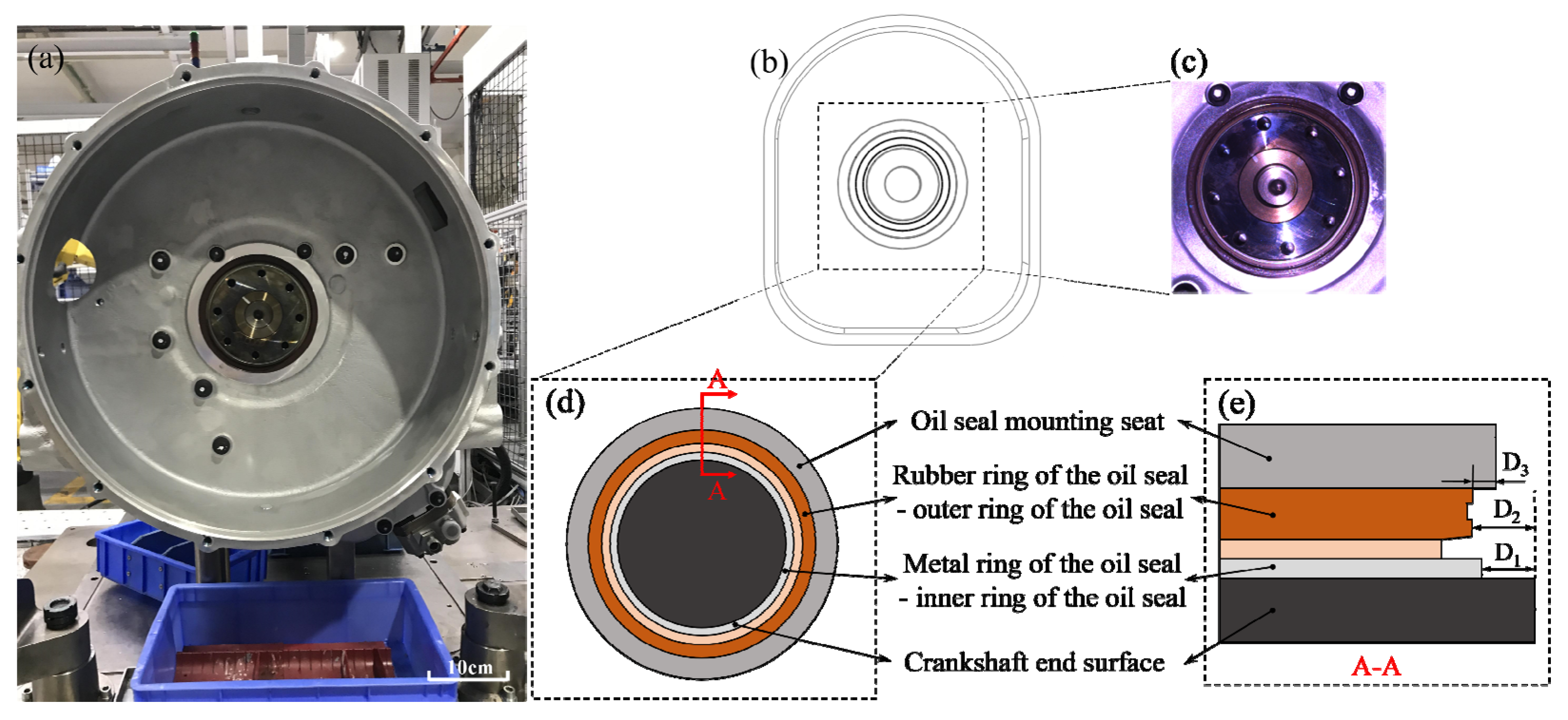
1. Introduction
2. Principle
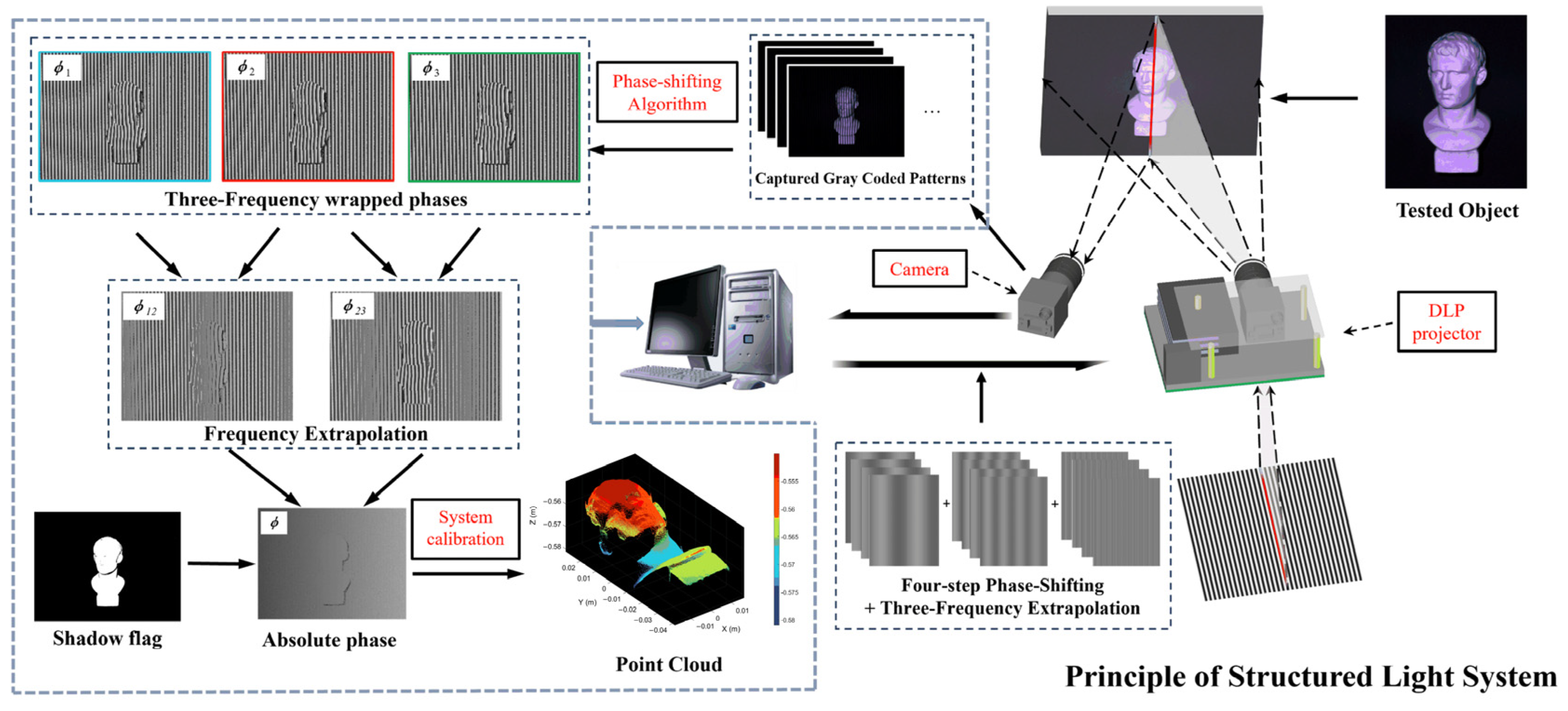
2.1. Basics of PSP
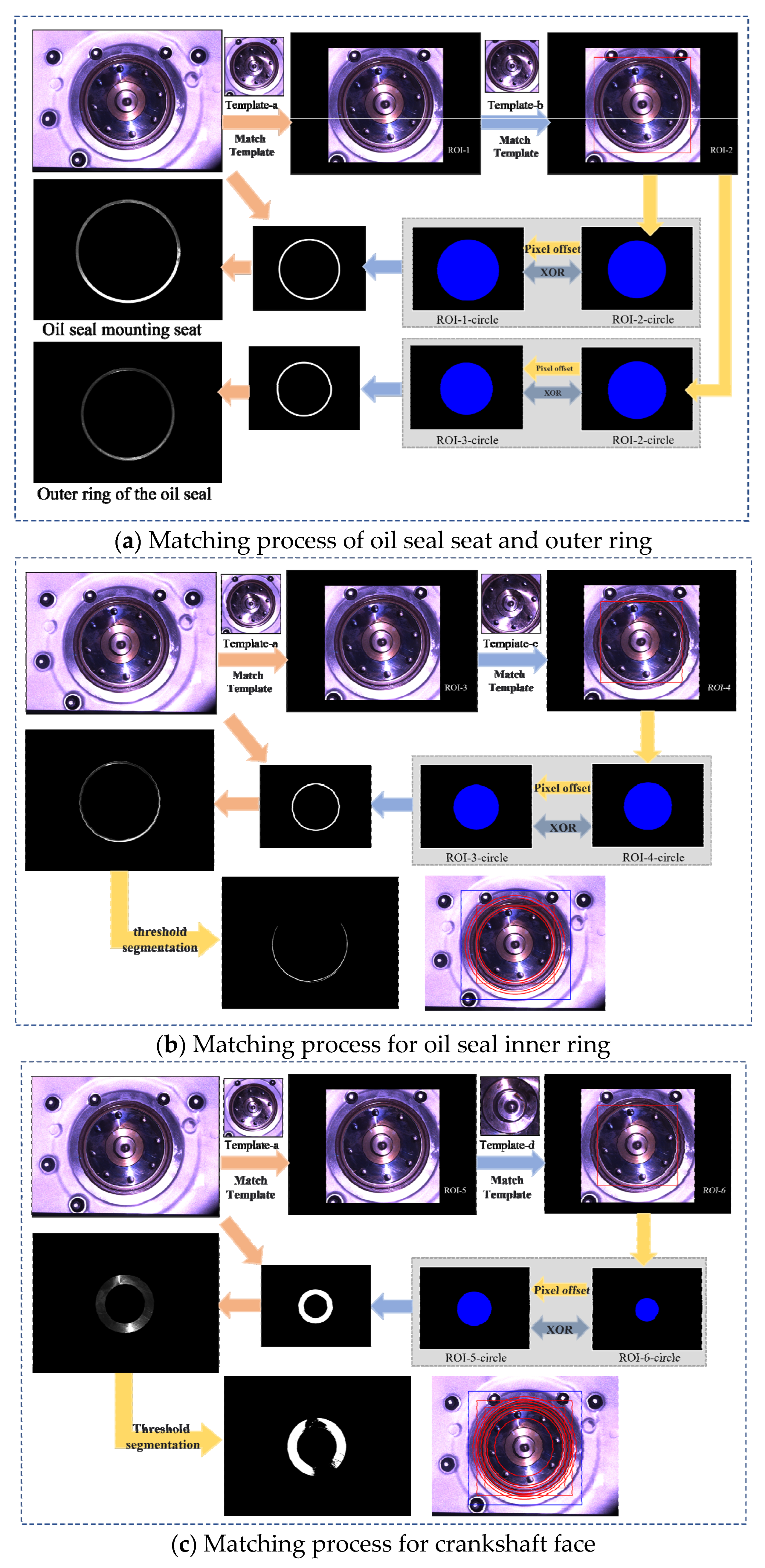
2.2. Multiple Progressive Template Matching Method
2.3. Three-Dimensional Reconstruction of Composite Vision
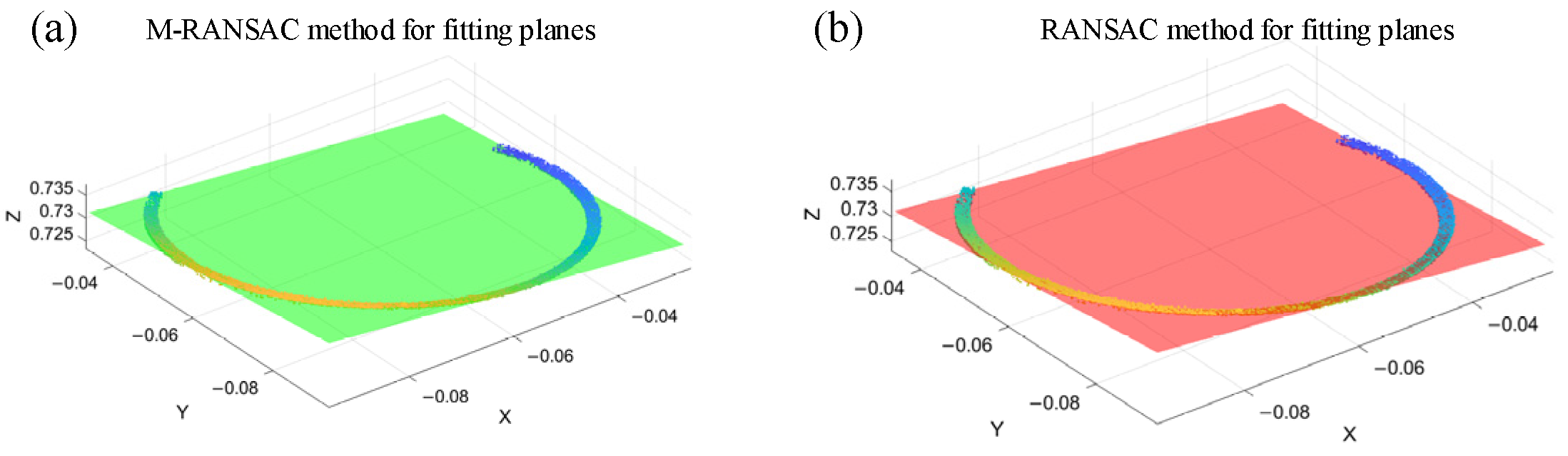
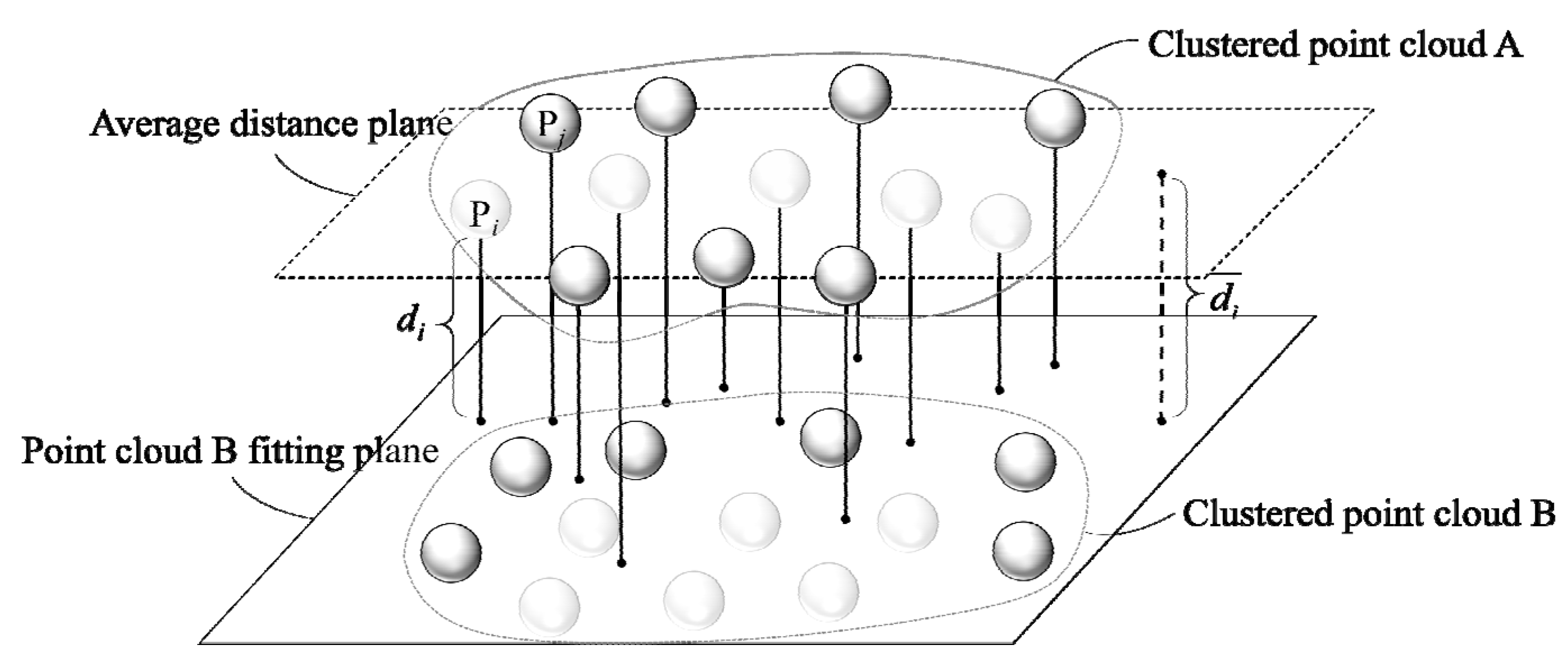
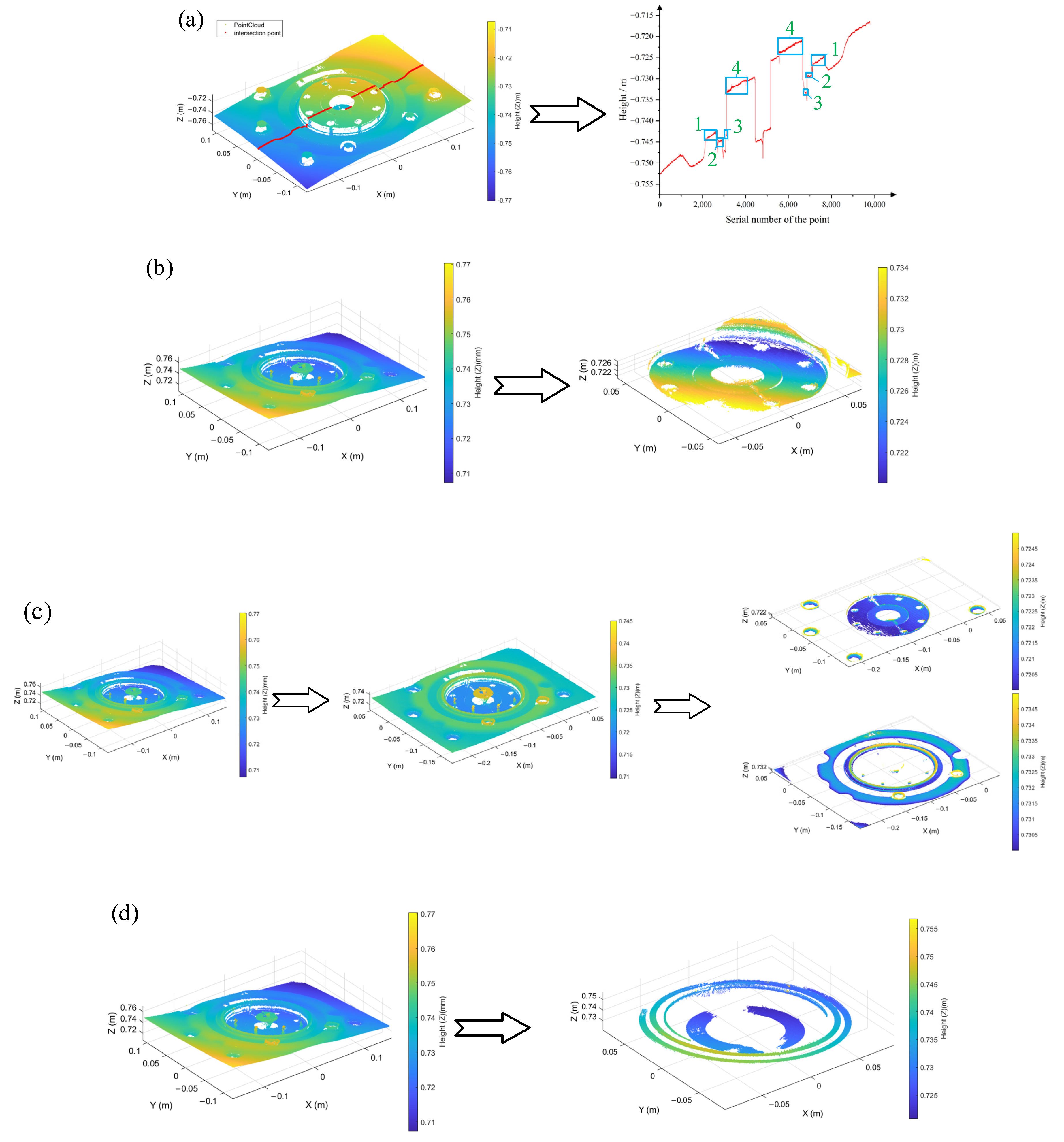
2.3.1. Modified RANSAC Plane Fitting Algorithm
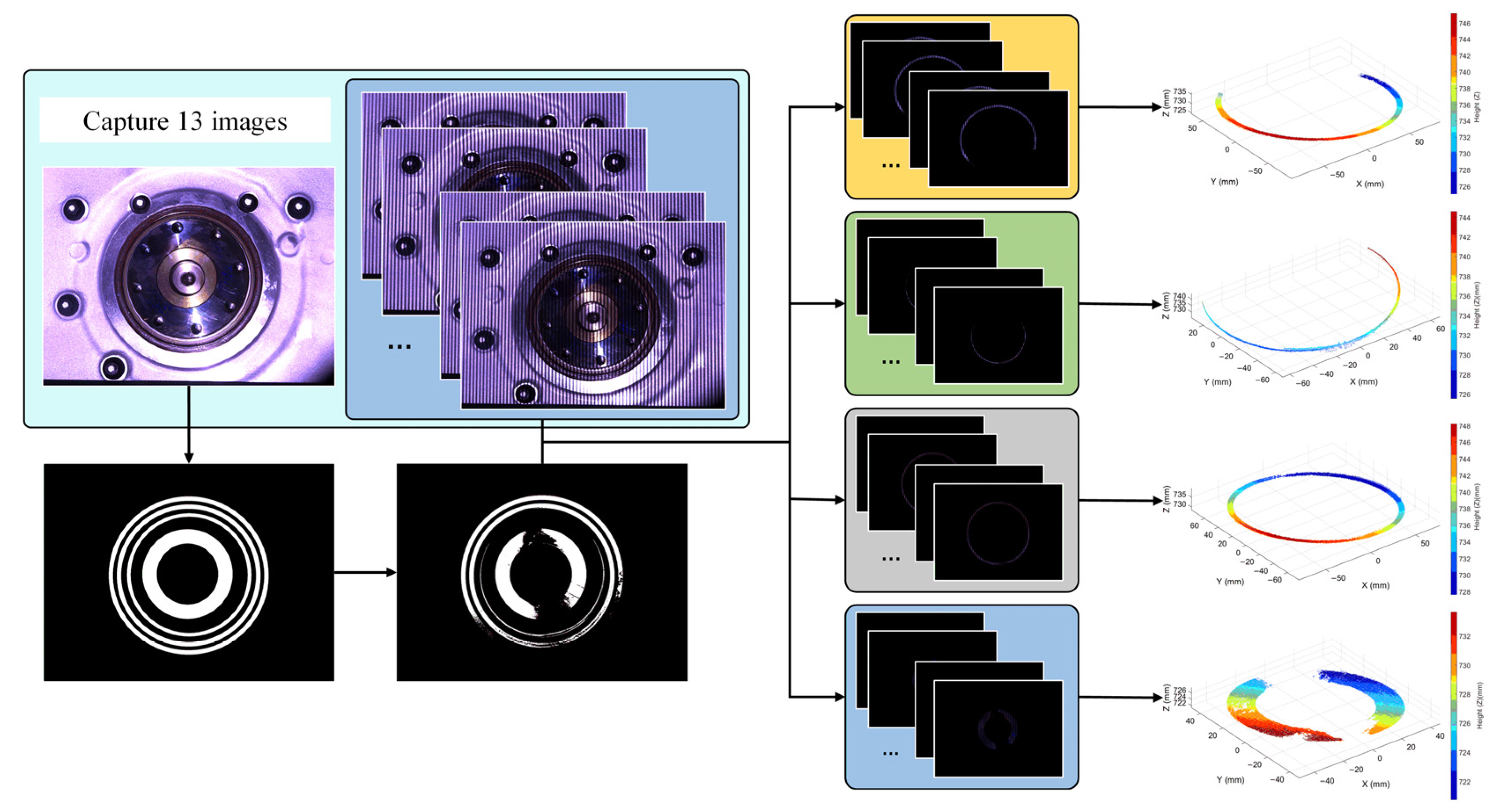
2.3.2. Distance Calculation
3. Experiments and Results
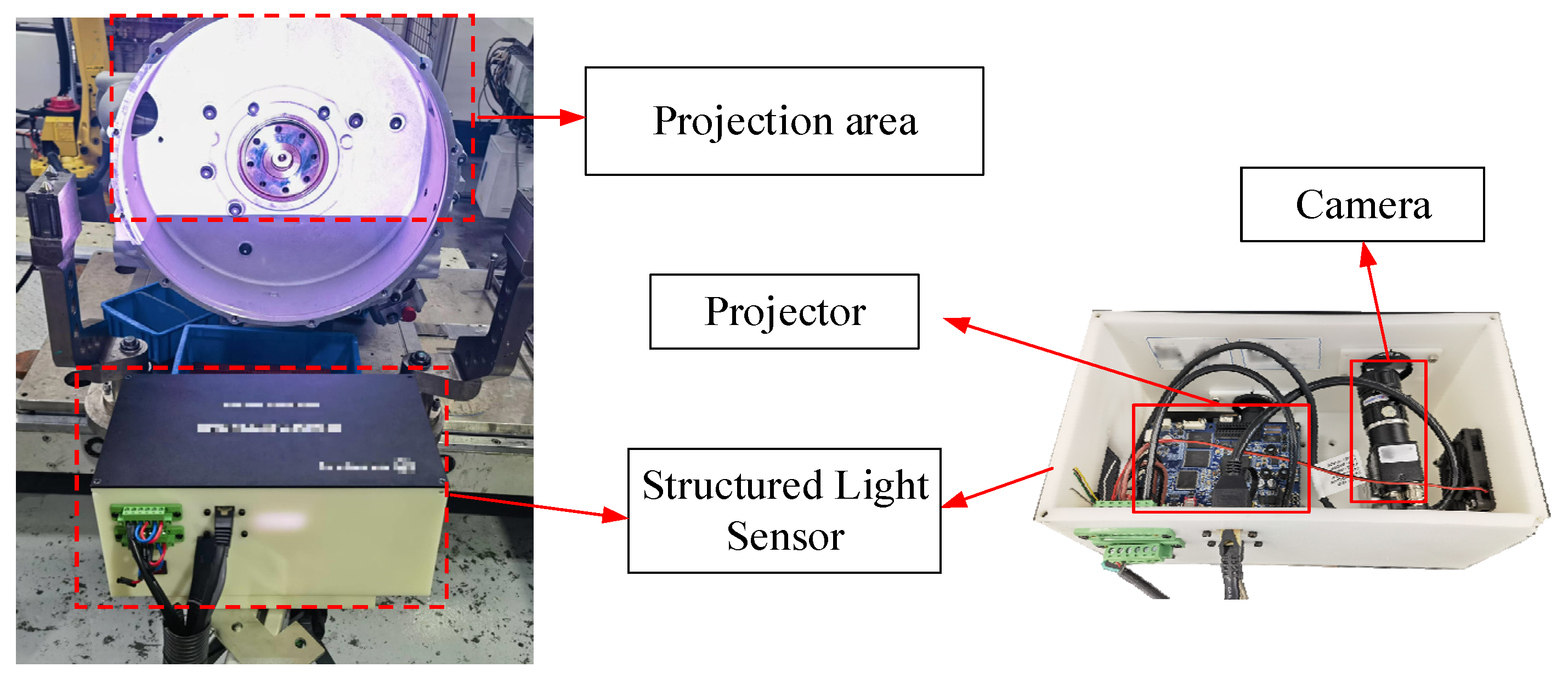
3.1. Experimental Setup
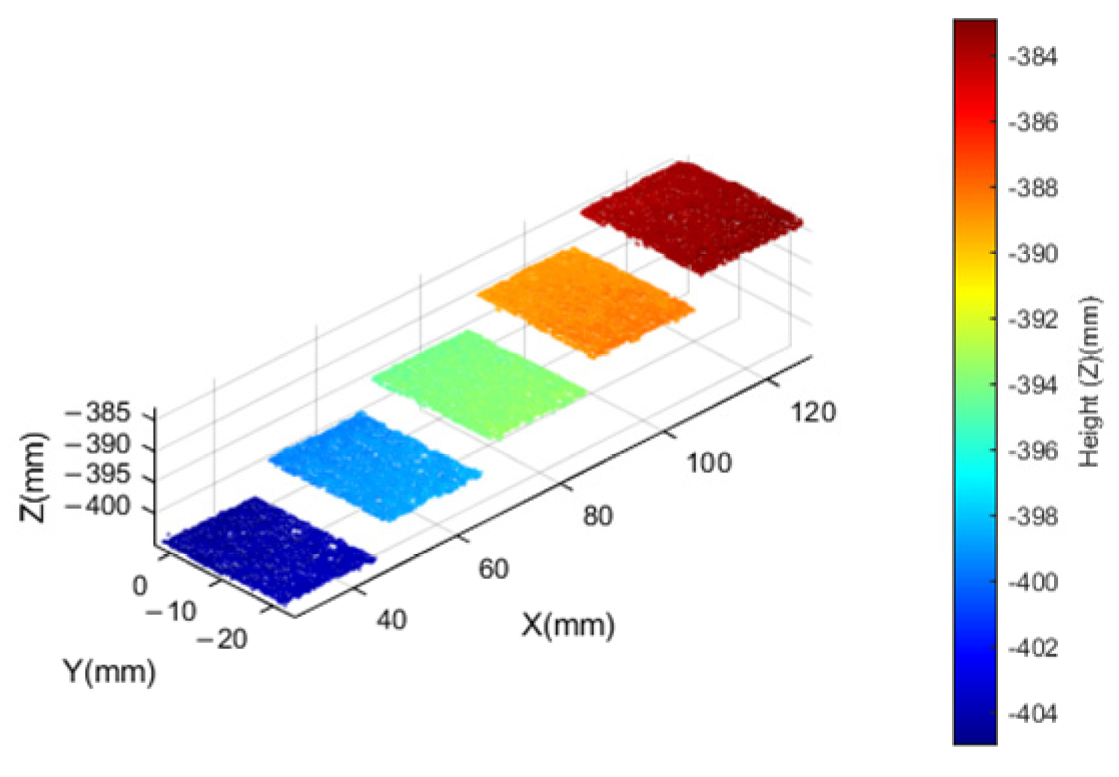
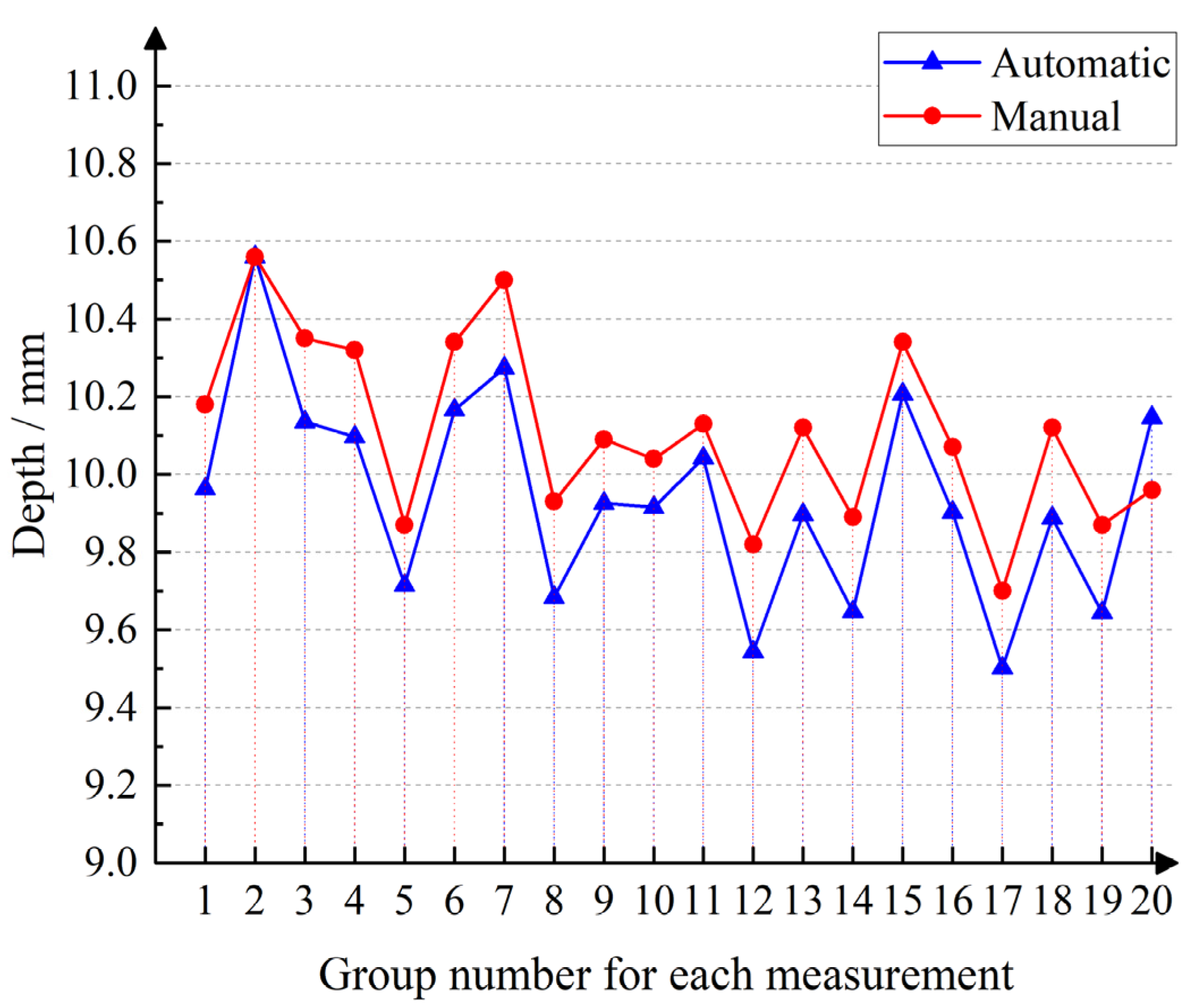
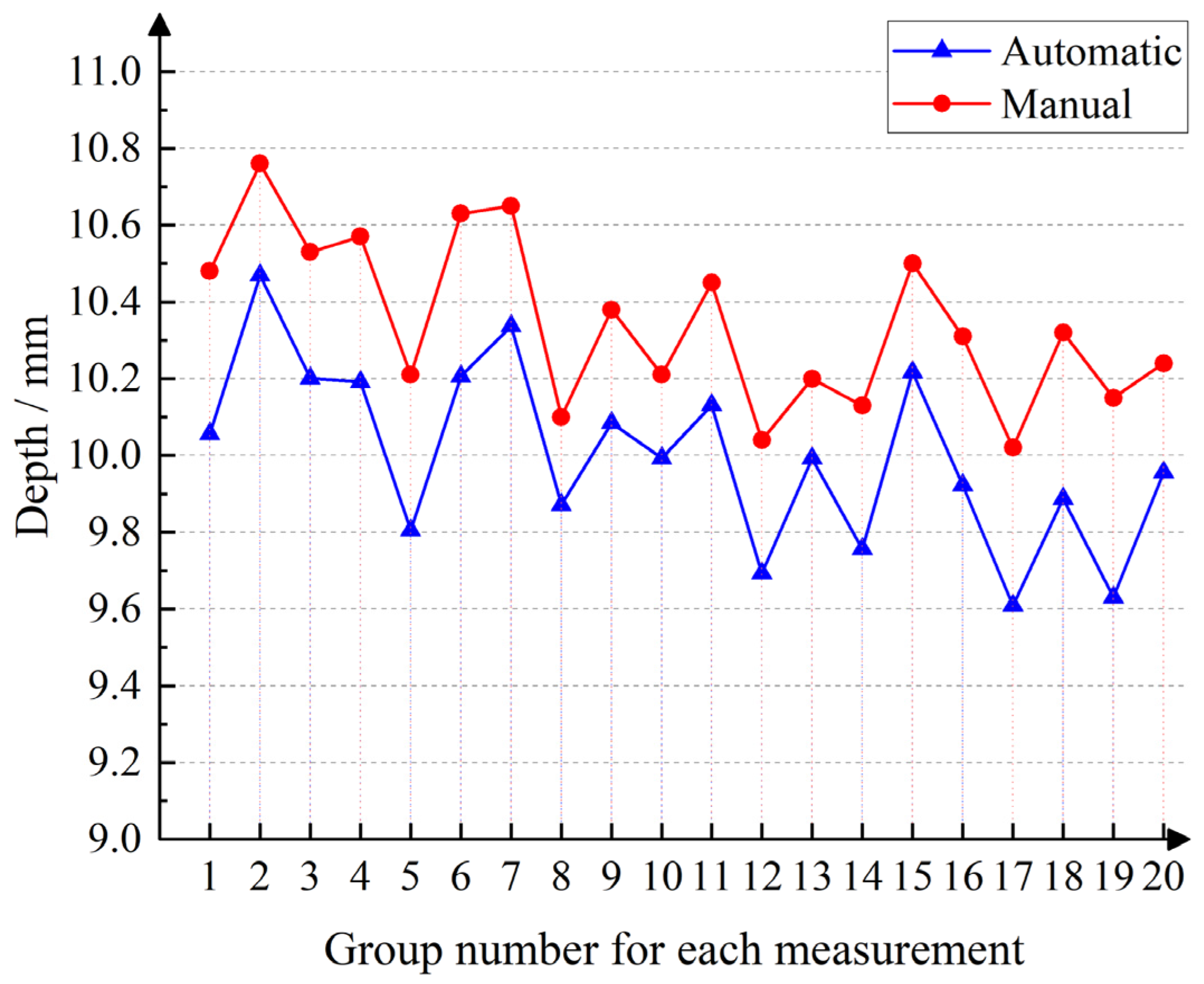
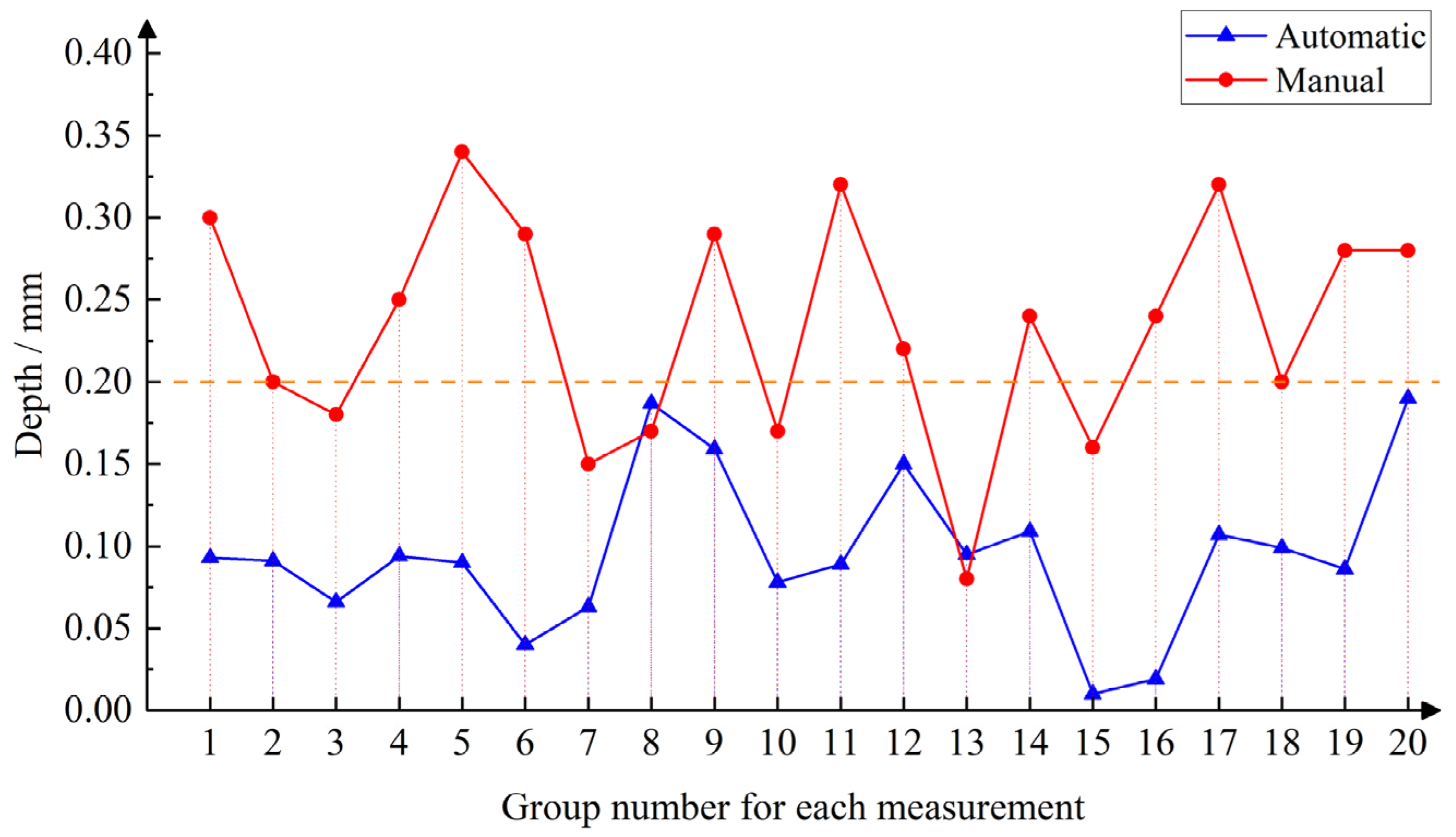
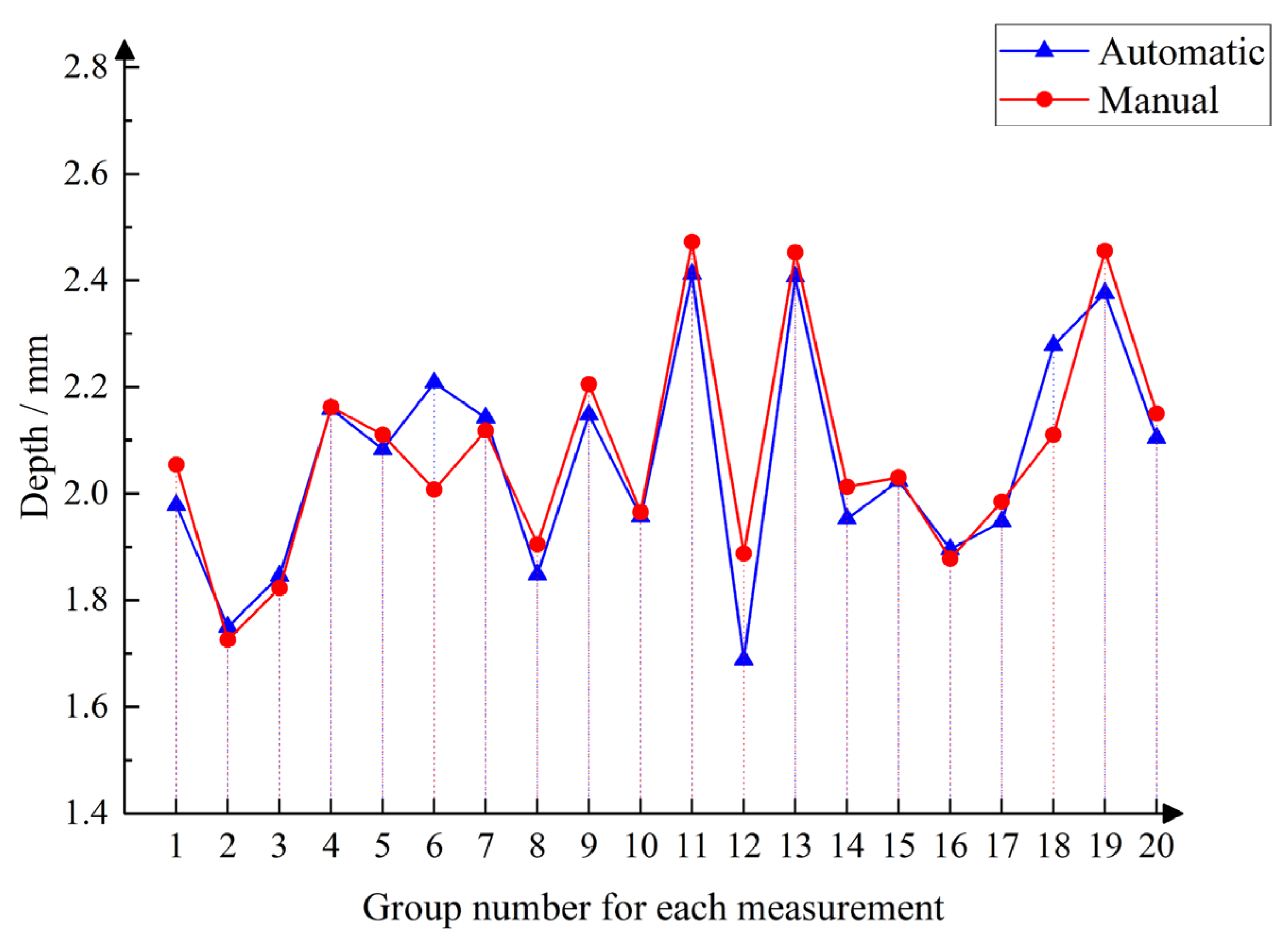
3.2. Oil Seal Actual Measurement Analysis
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| PSP | phase shift profilometry |
| FPP | fringe projection profilometry |
| ROI | region of interest |
| M-RANSAC | modified random sample consensus |
References
- Park, W.; Son, S.; Choi, D. Oil-Sealing Performance Evaluation of Labyrinth Seal Using Combined Finite Element Analysis and Computational Fluid Dynamics. Lubricants 2023, 11, 400. [Google Scholar] [CrossRef]
- Jiang, L.; Zhang, X. Inspection algorithm based on Gaussian filtering for oil seal spring. Opt. Eng. 2014, 53, 102–108. [Google Scholar] [CrossRef]
- Wu, Z.J.; Sun, C.K.; Liu, J. An Online Visual Inspection System for Oil-Seal Dimension. Appl. Mech. Mater. 2012, 130–134, 3548–3552. [Google Scholar] [CrossRef]
- Xia, G.F.; Yu, Z.L. Oil Seal Defect Detection Method Based on Deep Learning. J. Mech. Electr. Eng. 2023, 40, 69–75. [Google Scholar]
- Bzura, P. Diagnostic Model of Crankshaft Seals. Pol. Marit. Res. 2019, 26, 39–46. [Google Scholar] [CrossRef]
- Liu, J.; He, Z.D.; Lou, T.S.; Wang, C.D. Oil seal defect detection based on entropy rate clustering and ring-band differencing. Modul. Mach. Tool. Auto. Manu. Technol. 2018, 8, 90–92+96. [Google Scholar]
- Zhang, G.; Li, Y.; Xu, X.Y. Application of image processing technology in oil seal defect detection and identification. Inf. Technol. Informat. 2020, 11, 72–73. [Google Scholar]
- Shi, L.; Yu, Z.L. Research on oil seal defect detection method based on image processing. J. Changchun University Sci. Technol. 2021, 44, 48–54. [Google Scholar]
- Del Olmo, A.; De Lacalle, L.N.L.; De Pissón, G.M.; Pérez-Salinas, C.; Ealo, J.A.; Sastoque, L.; Fernandes, M.H. Tool wear monitoring of high-speed broaching process with carbide tools to reduce production errors. Mech. Syst. Signal Process. 2022, 172, 109003. [Google Scholar] [CrossRef]
- Aldekoa, I.; del Olmo, A.; Sastoque-Pinilla, L.; Sendino-Mouliet, S.; Lopez-Novoa, U.; de Lacalle, L.N.L. Early detection of tool wear in electromechanical broaching machines by monitoring main stroke servomotors. Mech. Syst. Signal Process. 2023, 204, 110773. [Google Scholar]
- Xu, L.; Pang, M. Research on tire tread depth measurement system based on structured light. Laser J. 2022, 43, 179–183. [Google Scholar]
- Xu, D.S.; Du, F.Z. Research on gap and step measurement technology of aircraft skin seams based on line structured light. Aerosp. Manuf. Technol. 2017, 5, 77–81. [Google Scholar]
- Yu, S.; Guo, H.; Yang, W.; Zhao, Y.; Wu, H.; Sun, X.; Yu, X. Depth Measurement Error Analysis and Structural Parameter Correction of Structured Light Depth Imager. Photonics 2024, 11, 396. [Google Scholar] [CrossRef]
- Zhao, H.; Hu, P.; Yang, S. Aircraft cabin door gap measurement technology and applications based on planar structured light. Sci. Technol. Eng. 2024, 24, 1045–1051. [Google Scholar]
- Li, S.Y.; Le, Y.S.; Gao, J.C.; Zhao, X.F. Bolt loosening angle measurement along full range of screw exposure length based on 3D point cloud. Automat. Constr. 2024, 168, 105785. [Google Scholar] [CrossRef]
- Zheng, Z.H.; Gao, Y.Q.; He, Z.B.; Wang, C.Y.; Xie, H.; Liu, G.H. Dimensional measurement of anti-stress cone of HV cable joints based on 3D point cloud. Meas. Sci. Technol. 2023, 34, 115009. [Google Scholar] [CrossRef]
- Wang, C.Y.; Zhou, Z.F.; Wang, Y.Q.; Wu, M.H. Measurement of concave polygon of automotive dashboard based on planar structured light. J. Appl. Opt. 2023, 43, 143–149. [Google Scholar]
- Wang, J.; Yang, Y.; Xu, P. Noise-induced phase error comparison in multi-frequency phase-shifting profilometry based on few fringes. Opt. Laser Technol. 2023, 159, 109034. [Google Scholar] [CrossRef]
- Yan, H.; Chen, Q.; Feng, S.J.; Zuo, C. Microscopic fringe projection profilometry: A review. Opt. Lasers Eng. 2020, 135, 106192. [Google Scholar]
- Tomislav, P.; Tomislav, P.; Damagoj, Z. Selection of optimal frequencies in multiple-frequency fringe projection profilometry. Opt. Lasers Eng. 2023, 163, 107455. [Google Scholar]
- Duan, S.S. Detection method of downhole belt conveyor deviation fault based on ROI edge image straight line feature. China Min. Mag. 2024, 33, 162–167. [Google Scholar]
- Han, Y. Reliable Template Matching for Image Detection in Vision Sensor Systems. Sensors 2021, 21, 8176. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.C.; Wang, H.; Zhou, Y.L.; Liu, J.B.; Dai, P.; Du, X.Y.; Wahab, M.A. Automatic laser profile recognition and fast tracking for structured light measurement using deep learning and template matching. Measurement 2021, 169, 108362. [Google Scholar]
- Zhang, Z.Y. A flexible new technique for camera calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1330–1334+472. [Google Scholar]
- Liu, Y.; Zhang, B.; Yuan, X. An Improved Projector Calibration Method by Phase Mapping Based on Fringe Projection Profilometry. Sensors 2023, 23, 1142. [Google Scholar] [CrossRef]
- Shui, W.Y.; Zhou, M.Q.; Maddock, S.; He, T.P.; Wang, X.C.; Deng, Q.Q. A PCA-Based method for determining craniofacial relationship and sexual dimorphism of facial shapes. Comput. Biol. Med. 2017, 90, 33–49. [Google Scholar]
- Huang, J.; Zhang, D.; Xu, B. Research on Fingerprint Precision Recognition Method Based on Structured Light. J. Appl. Opt. 2025, in press.






| Method | Matching Time | Matching Success Rate | Matching Success Rate After Adding Noise |
|---|---|---|---|
| Single-template matching | 0.542 s | 85% | 83% |
| Proposed method | 0.873 s | 97% | 96% |
| Parameters | Initial Value |
|---|---|
| Maximum number of iterations | 100 |
| Initial distance threshold | 0.001 mm |
| Voxel downsampling resolution | 0.001 mm |
| 0.3 | |
| 1.5 |
| Relevant Parameters | Running Time (s) | Mean Distance Average (mm) | RMSE |
|---|---|---|---|
| RANSAC [26] | 0.0024 | 0.3232 | 0.0214 |
| M-RANSAC | 0.0019 | 0.2747 | 0.0124 |
| No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Mean Error | 0.023 | 0.021 | 0.021 | 0.020 | 0.019 | 0.020 | 0.021 | 0.020 | 0.019 | 0.019 |
| RMSE | 0.022 | 0.020 | 0.021 | 0.020 | 0.020 | 0.020 | 0.018 | 0.020 | 0.019 | 0.018 |
| Matching Area | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 10 | 0 | −10 | 0 | |
| 35 | −20 | −35 | 80 | |
| Tmin | 0 | 60 | 0 | 60 |
| Tmax | 220 | 220 | 127 | 220 |
| Method | Advantages | Disadvantages | Applicable Scenarios |
|---|---|---|---|
| I | Based on the cross-section curve fracture characteristics, the gap size can be effectively extracted. | (1) The point cloud is not exactly parallel to the XOY plane, and there may be camera angle errors. (2) Large height error in local area, resulting in missing point cloud. | Suitable for large planar surfaces with localized height errors in the point cloud |
| II | Straight-through filtering preprocesses the point cloud data to simplify the data processing process and allows for coarse screening of the target area. | (1) Relying on spatial coordinate range screening, it is difficult to deal with complex background noise. (2) Cannot accurately distinguish the target area from noise. | Suitable for scenes where there are obvious spatial differences between the target area and the noise, but complex backgrounds are difficult to segment. |
| III | Able to rotate the point cloud to accommodate straight-through filtering And Cluster segmentation can effectively divide different regions. | (1) It is difficult to accurately distinguish the target area from the interference area when the local non-planar features are significant. (2) The clustering results are disturbed by noise and the plane fitting deviation is large. | Suitable for scenarios where planar features are present in the point cloud and are uniformly distributed. |
| Proposed method | Effectively segment the target area and avoid the defects of the above three methods and provide higher plane fitting accuracy and robustness. | Requires preprocessing, such as creating templates and adjusting matching parameters. | Suitable for scenes with complex backgrounds and noise, and where high-precision plane fitting is required, such as high-precision measurements or complex device inspections. |
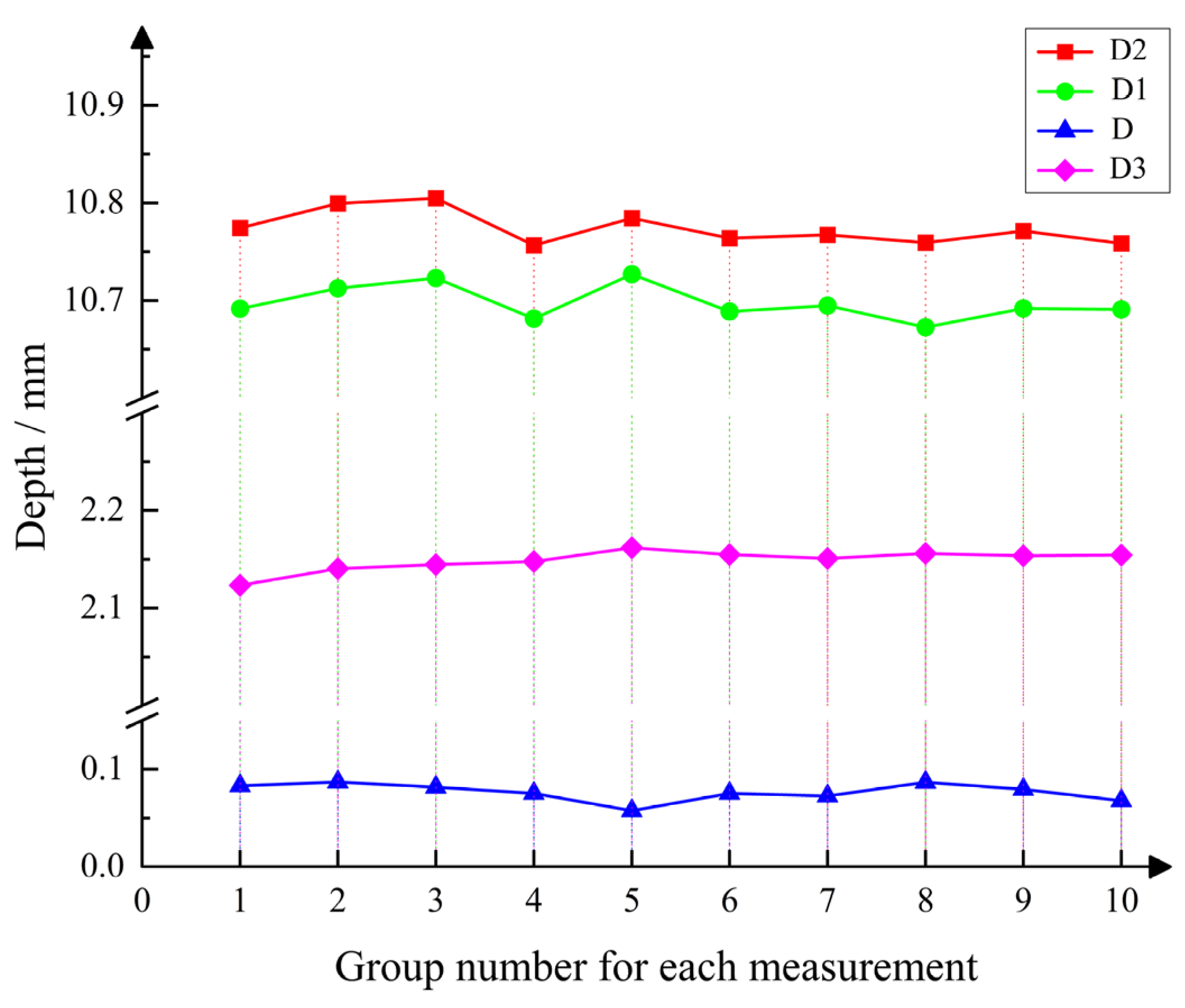
| D1 (mm) | D2 (mm) | D (mm) | D3 (mm) | |
|---|---|---|---|---|
| Average | 10.6873 | 10.7559 | 0.0685 | 2.1455 |
| Range | 0.0217 | 0.0355 | 0.025 | 0.031 |
| RMSE | 0.0562 | 0.0384 | 0.0201 | 0.0465 |
| D1 (mm) | D2 (mm) | D (mm) | D3 (mm) | |
|---|---|---|---|---|
| Average | 10.6974 | 10.7739 | 0.0764 | 2.1488 |
| Range | 0.0542 | 0.048 | 0.0293 | 0.0385 |
| RMSE | 0.0503 | 0.0757 | 0.02786 | 0.0498 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Zhao, J.; Gao, X.; Li, W.; Jin, R.; Tang, G.; Huang, Y.; Chen, S. A Composite Vision-Based Method for Post-Assembly Dimensional Inspection of Engine Oil Seals. Machines 2025, 13, 261. https://doi.org/10.3390/machines13040261
Li Y, Zhao J, Gao X, Li W, Jin R, Tang G, Huang Y, Chen S. A Composite Vision-Based Method for Post-Assembly Dimensional Inspection of Engine Oil Seals. Machines. 2025; 13(4):261. https://doi.org/10.3390/machines13040261
Chicago/Turabian StyleLi, Yu, Jing Zhao, Xingyu Gao, Weiming Li, Rongtong Jin, Guohao Tang, Yang Huang, and Shuibiao Chen. 2025. "A Composite Vision-Based Method for Post-Assembly Dimensional Inspection of Engine Oil Seals" Machines 13, no. 4: 261. https://doi.org/10.3390/machines13040261
APA StyleLi, Y., Zhao, J., Gao, X., Li, W., Jin, R., Tang, G., Huang, Y., & Chen, S. (2025). A Composite Vision-Based Method for Post-Assembly Dimensional Inspection of Engine Oil Seals. Machines, 13(4), 261. https://doi.org/10.3390/machines13040261






