Fault Diagnosis of Reciprocating Compressor Valve Based on Triplet Siamese Neural Network
Abstract
1. Introduction
2. Methodology
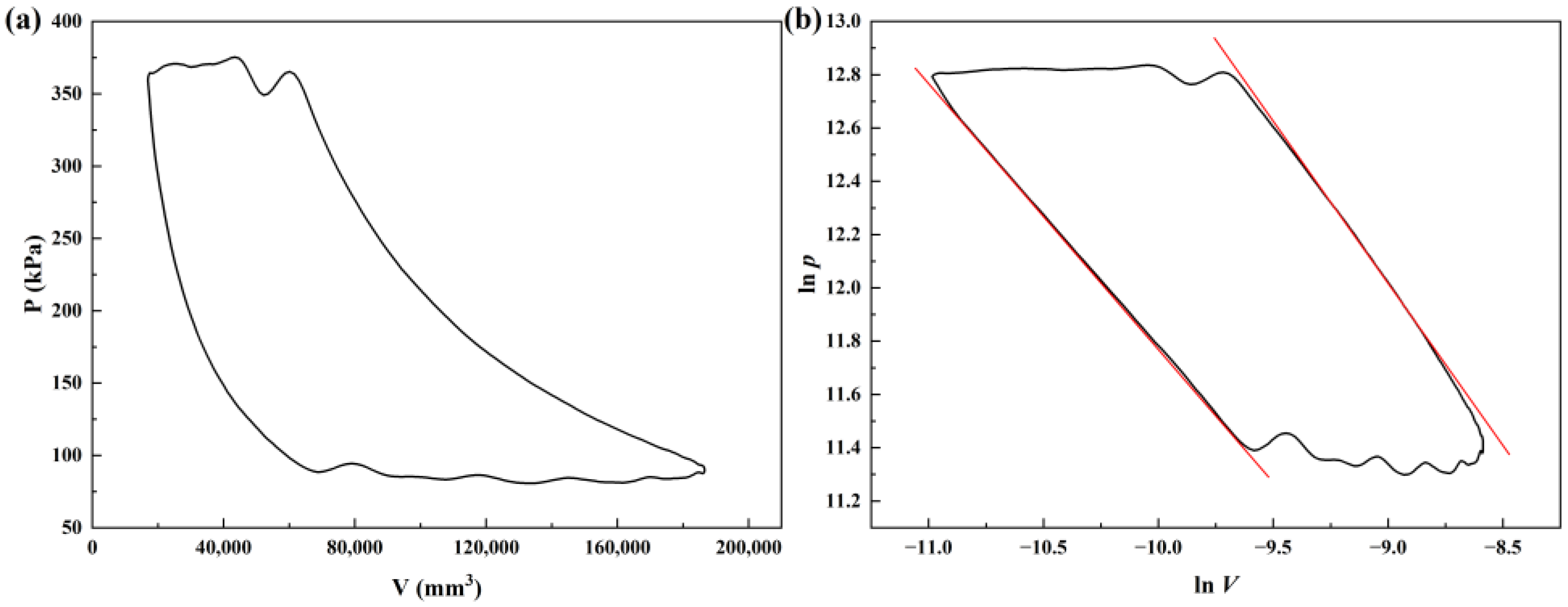
2.1. Establishment of Standard Reference for Logarithmic p-V Diagram
2.2. Preprocessing Method of Logarithmic p-V Diagram Difference
2.3. Feature Extraction for Logarithmic p-V Diagram Difference Sequence
2.4. Classification
3. Experimental Setup and Data Acquisition
4. Results and Discussion
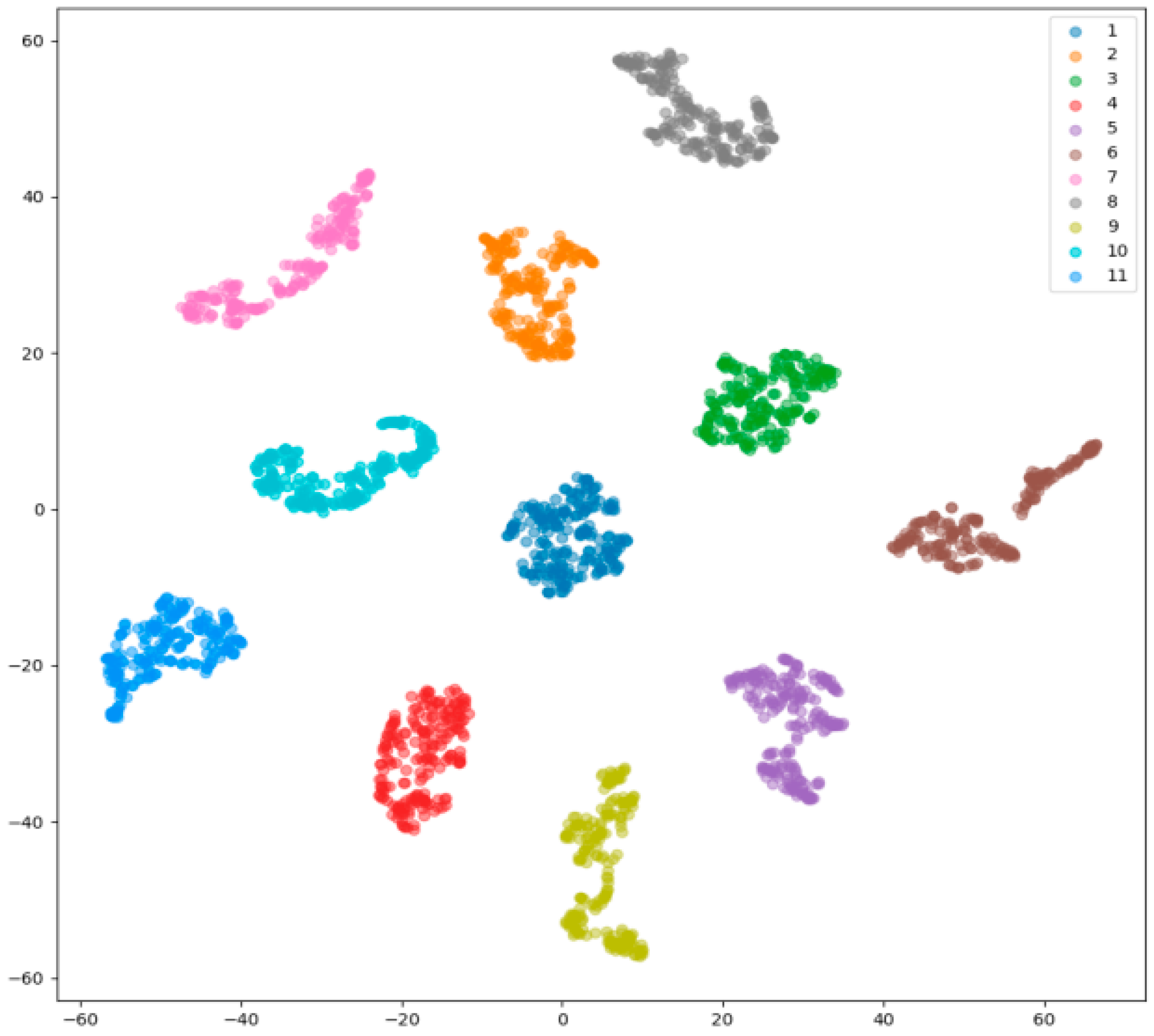
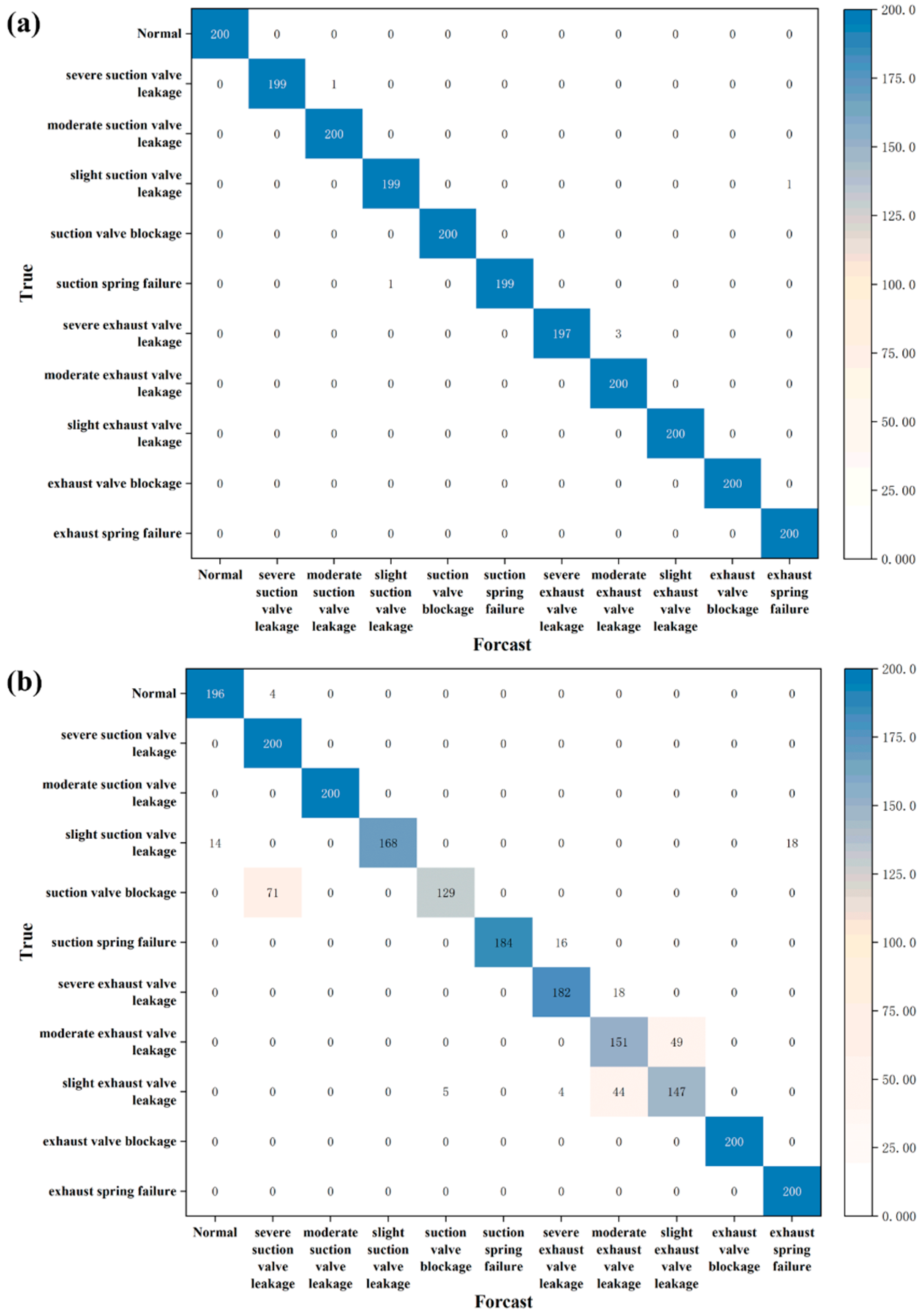
4.1. Fault Classification Effect
4.2. Comparisons with Other Methods
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pichler, K.; Lughofer, E.; Pichler, M.; Buchegger, T.; Klement, E.P.; Huschenbett, M. Detecting cracks in reciprocating compressor valves using pattern recognition in the pV diagram. Pattern Anal. Appl. 2015, 18, 461–472. [Google Scholar] [CrossRef]
- Pichler, K.; Lughofer, E.; Pichler, M.; Buchegger, T.; Klement, E.P.; Huschenbett, M. Fault detection in reciprocating compressor valves under varying load conditions. Mech. Syst. Signal Process. 2016, 70, 104–119. [Google Scholar] [CrossRef]
- Frankt, P.M. Fault Diagnosis in Dynamic Systems Using Analytical and Knowledge-Based Redundancy a Survey and Some New Results; Pergamon Press, Inc.: Oxford, UK, 1990. [Google Scholar]
- Luo, K.; Huang, J.; Sun, S.; Guo, J.J.; Wang, X. Research on a generic diagnostic model for reciprocating compressors in a data-driven mode. Equip. Manag. Maint. 2014, 6, 60–64. [Google Scholar] [CrossRef]
- Miao, Z.C.; Gao, S.Y.; He, Z.M.; Ou, Y. Single-objective tracking algorithm based on Siamese networks. Chin. J. Liq. Cryst. Disp. 2023, 38, 256–266. [Google Scholar] [CrossRef]
- Zhao, X.; Liu, Y.; Han, G. Cooperative Use of Recurrent Neural Network and Siamese Region Proposal Network for Robust Visual Tracking. IEEE Access 2021, 9, 57704–57715. [Google Scholar] [CrossRef]
- An, N.; Yan, W.Q. Multitarget Tracking Using Siamese Neural Networks. ACM Trans. Multimed. Comput. Commun. Appl. 2021, 17, 1–16. [Google Scholar] [CrossRef]
- Osiecka-Drewniak, N.; Deptuch, A.; Urbanska, M. A Siamese neural network framework for glass transition recognition. Soft matter 2024, 20, 2400–2406. [Google Scholar] [CrossRef]
- Xue, Z.; Zhu, T.; Zhou, Y.; Zhang, M. Bag-of-Features-Driven spectral-spatial Siamese neural network for hyperspectral image classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 1085–1099. [Google Scholar] [CrossRef]
- Zhan, T.; Song, B.; Xu, Y.; Wan, M.; Wang, X.; Yang, G.; Wu, Z. SSCNN-S: A Spectral-Spatial Convolution Neural Network with Siamese Architecture for Change Detection. Remote Sens. 2021, 13, 895. [Google Scholar] [CrossRef]
- Liu, B.; Yu, X.; Zhang, P.; Yu, A.; Fu, Q.; Wei, X. Supervised deep feature extraction for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2017, 56, 1909–1921. [Google Scholar] [CrossRef]
- Huang, Y.; Li, Y.; Heyes, T.; Jourjon, G.; Cheng, A.; Seneviratne, S.; Thilakarathna, K.; Webb, D.; Da Xu, R.Y. Task adaptive siamese neural networks for open-set recognition of encrypted network traffic with bidirectional dropout. Pattern Recognit. Lett. 2022, 159, 132–139. [Google Scholar] [CrossRef]
- Djamaluddin, M.; Munir, R.; Utama, N.P.; Kistijantoro, A.I. Open-Set profile-to-frontal face recognition on a very limited dataset. IEEE Access. 2023, 11, 65787–65797. [Google Scholar] [CrossRef]
- Liu, P.; Zhang, Y.; Ma, M.; He, Z.; Zhang, W. Open-Set Recognition Algorithm of Signal Modulation Based on Siamese Neural Network; Springer: Cham, Switzerland, 2022. [Google Scholar] [CrossRef]
- Tiboni, M.; Remino, C.; Bussola, R.; Amici, C. A review on vibration-based condition monitoring of rotating machinery. Appl. Sci. 2022, 12, 972. [Google Scholar] [CrossRef]
- Zhang, Y.; Ji, J.; Ma, B. Reciprocating compressor fault diagnosis using an optimized convolutional deep belief network. J. Vib. Control 2020, 26, 1538–1548. [Google Scholar] [CrossRef]
- Zhang, Y.; Ji, J. Intelligent fault diagnosis of a reciprocating compressor using mode isolation convolutional deep belief networks. IEEE/ASME Trans. Mechatron. 2020, 26, 1668–1677. [Google Scholar] [CrossRef]
- Yu, Z.; Zhang, B.; Hu, G.; Chen, Z. Early fault diagnosis model design of reciprocating compressor valve based on multiclass support vector machine and decision tree. Sci. Program. 2022, 2022, 1–7. [Google Scholar] [CrossRef]
- Medina, R.; Sánchez, R.-V.; Cabrera, D.; Cerrada, M.; Estupiñan, E.; Ao, W.; Vásquez, R.E. Scale-Fractal Detrended Fluctuation Analysis for Fault Diagnosis of a Centrifugal Pump and a Reciprocating Compressor. Sensors 2024, 24, 461. [Google Scholar] [CrossRef]
- Li, X.; Lin, T.; Yang, Y.; Mba, D.; Loukopoulos, P. Index similarity assisted particle filter for early failure time prediction with applications to turbofan engines and compressors. Expert Syst. Appl. 2022, 207, 118008. [Google Scholar] [CrossRef]
- Zhang, L.; Duan, L.; Hong, X.; Zhang, X. Fault diagnosis method of reciprocating compressor based on domain adaptation under multi-working conditions. In Proceedings of the 2021 IEEE International Conference on Mechatronics and Automation (ICMA), Takamatsu, Japan, 8–11 August 2021; pp. 588–593. [Google Scholar]
- Mondal, D.; Gu, F.; Ball, A.D. Condition Monitoring of a Reciprocating Air Compressor Using Vibro-Acoustic Measurements. In Proceedings of the IncoME-VI and TEPEN 2021: Performance Engineering and Maintenance Engineering; Springer International Publishing: Cham, Switzerland, 2022; pp. 615–628. [Google Scholar]
- Zhang, Z.; Chen, L.; Zhang, C.; Shi, H.; Li, H. GMA-DRSNs: A novel fault diagnosis method with global multi-attention deep residual shrinkage networks. Measurement 2022, 196, 111203. [Google Scholar] [CrossRef]
- Zhang, Y.; Ji, J.; Ma, B. Fault diagnosis of reciprocating compressor using a novel ensemble empirical mode decomposition-convolutional deep belief network. Measurement 2020, 156, 107619. [Google Scholar] [CrossRef]
- Zhang, J.; Duan, L.; Luo, S.; Li, K. Fault diagnosis of reciprocating machinery based on improved MEEMD-SqueezeNet. Measurement 2023, 217, 113026. [Google Scholar] [CrossRef]
- Lv, Q.; Cai, L.; Yu, X.; Ma, H.; Li, Y.; Shu, Y. An automatic fault diagnosis method for the reciprocating compressor based on HMT and ANN. Appl. Sci. 2022, 12, 5182. [Google Scholar] [CrossRef]
- Li, X.; Ren, P.; Zhang, Z.; Jia, X.; Peng, X. A p-V diagram based fault identification for compressor valve by means of linear discrimination analysis. Machines 2022, 10, 53. [Google Scholar] [CrossRef]
- Shen, W.D.; Tong, J.G. Thermodynamics of Engineering; Higher Education Press: Beijing, China, 2007; pp. 267–269. [Google Scholar]
- Dong, C.Q.; Liang, Z.; Tian, J.L.; Tian, F.; Li, X.R.; Li, S.S.; He, H.G. Determination of gas variability index for natural gas compressors. Compress. Technol. 2013, 4, 7–10. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–57. [Google Scholar] [CrossRef]
- Bromley, J.; Guyon, I.; LeCun, Y.; Säckinger, E.; Shah, R. Signature verification using a “Siamese” time delay neural network. Adv. Neural Inf. Process. Syst. 1993, 6, 737–744. [Google Scholar] [CrossRef]
- Serrano, N.; Bellogín, A. Siamese neural networks in recommendation. Neural Comput. Appl. 2023, 35, 13941–13953. [Google Scholar] [CrossRef]
- Hoffer, E.; Ailon, N. Deep metric learning using Triplet network. In Proceedings of the International Conference on Learning Representations, Banff, AB, Canada, 14–16 April 2014. [Google Scholar]
- Hadsell, R.; Chopra, S.; Lecun, Y. Dimensionality Reduction by Learning an Invariant Mapping. In Proceedings of the 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’06), New York, NY, USA, 17–22 June 2006. [Google Scholar] [CrossRef]
- Wang, J.; Song, Y.; Leung, T.; Rosenberg, C.; Wu, Y. Learning fine-grained image similarity with deep ranking. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 138–1393. [Google Scholar]
- Hinton, G.E.; Srivastava, N.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R.R. Improving neural networks by preventing co-adaptation of feature detectors. arXiv 2012, arXiv:1207.0580. [Google Scholar]











| Possible Cases | Characteristic | Schematic Diagram |
|---|---|---|
| Easy triplet | parameters cannot update |  |
| Hard triplet | parameters can update | |
| Semi-hard triplet | parameters can update |
| Layer | Kernel Number | Kernel Size | Activation Function |
|---|---|---|---|
| convolutional layer | 128 | 5 | PReLU |
| convolutional layer | 64 | 3 | PReLU |
| pooling layer | - | 2 | - |
| dropout layer | - | - | - |
| convolutional layer | 32 | 3 | PReLU |
| convolutional layer | 32 | 3 | PReLU |
| pooling layer | - | 2 | - |
| dropout layer | - | - | - |
| linear layer | - | 1024 | PReLU |
| linear layer | - | 512 | PReLU |
| linear layer | - | 11 | - |
| Name | Parameter |
|---|---|
| volume flow (m3/min) | 0.1 |
| speed (rpm) | 688 |
| inlet/outlet pressure (MPa) | 0/0.6 |
| volume flow (m3/min) | 0.1 |
| speed (rpm) | 688 |
| inlet/outlet pressure (MPa) | 0/0.6 |
| Failure Type | Simulation Measure | Detail | |
|---|---|---|---|
| leakage | valve plate trepanning | suction valve | rA * = 0.05% |
| rA = 0.17% | |||
| rA = 0.22% | |||
| exhaust valve | rA = 0.1% | ||
| rA = 0.15% | |||
| rA = 0.20% | |||
| blockage | catching adding | suction valve | add trepanning catching on valve seat |
| exhaust valve | add trepanning catching on lift limiter | ||
| spring failure | length changing | low elastic force | 10 mm spring truncated to 5 mm |
| high elastic force | 10 mm spring is replaced with an 18 mm spring of the same material and diameter | ||
| Valve Condition | Tag |
|---|---|
| normal | 1 |
| severe leaking suction valve | 2 |
| moderate leaking suction valve | 3 |
| slight leaking suction valve | 4 |
| blocked suction valve | 5 |
| spring failure suction valve | 6 |
| severe leaking exhaust valve | 7 |
| moderate leaking exhaust valve | 8 |
| slight leaking exhaust valve | 9 |
| blocked exhaust valve | 10 |
| spring failure exhaust valve | 11 |
| Number | Logarithmic p-V Diagram Difference Sequence | p-V Diagram | ||||
|---|---|---|---|---|---|---|
| SNN | CNN | SVM | SNN | CNN | SVM | |
| 1 | 100 | 100 | 99.86 | 95.81 | 85.59 | 74.27 |
| 2 | 100 | 100 | 99.86 | 99.40 | 79.68 | 74.27 |
| 3 | 100 | 100 | 99.86 | 99.72 | 88.95 | 74.27 |
| 4 | 100 | 100 | 99.86 | 95.72 | 83.23 | 74.27 |
| 5 | 100 | 100 | 99.86 | 94.00 | 88.09 | 74.27 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Wang, W.; Chen, W.; Xiao, Q.; Xu, W.; Li, Q.; Wang, J.; Liu, Z. Fault Diagnosis of Reciprocating Compressor Valve Based on Triplet Siamese Neural Network. Machines 2025, 13, 263. https://doi.org/10.3390/machines13040263
Zhang Z, Wang W, Chen W, Xiao Q, Xu W, Li Q, Wang J, Liu Z. Fault Diagnosis of Reciprocating Compressor Valve Based on Triplet Siamese Neural Network. Machines. 2025; 13(4):263. https://doi.org/10.3390/machines13040263
Chicago/Turabian StyleZhang, Zixuan, Wenbo Wang, Wenzheng Chen, Qiang Xiao, Weiwei Xu, Qiang Li, Jie Wang, and Zhaozeng Liu. 2025. "Fault Diagnosis of Reciprocating Compressor Valve Based on Triplet Siamese Neural Network" Machines 13, no. 4: 263. https://doi.org/10.3390/machines13040263
APA StyleZhang, Z., Wang, W., Chen, W., Xiao, Q., Xu, W., Li, Q., Wang, J., & Liu, Z. (2025). Fault Diagnosis of Reciprocating Compressor Valve Based on Triplet Siamese Neural Network. Machines, 13(4), 263. https://doi.org/10.3390/machines13040263






