Enhanced Seat Suspension Performance Through Positive Real Network Optimization and Skyhook Inertial Control
Abstract
1. Introduction
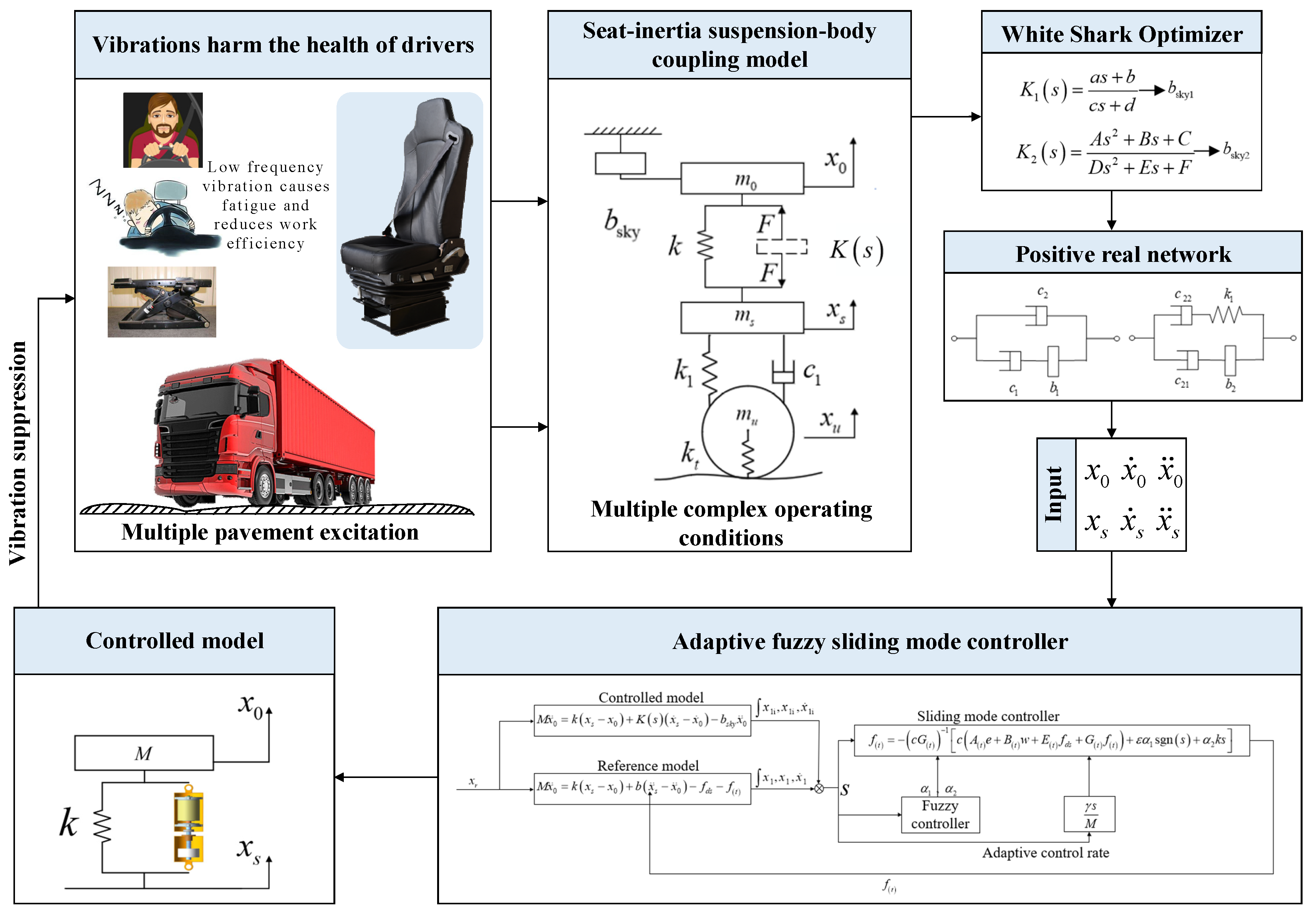
2. Seat Inertial Suspension Model
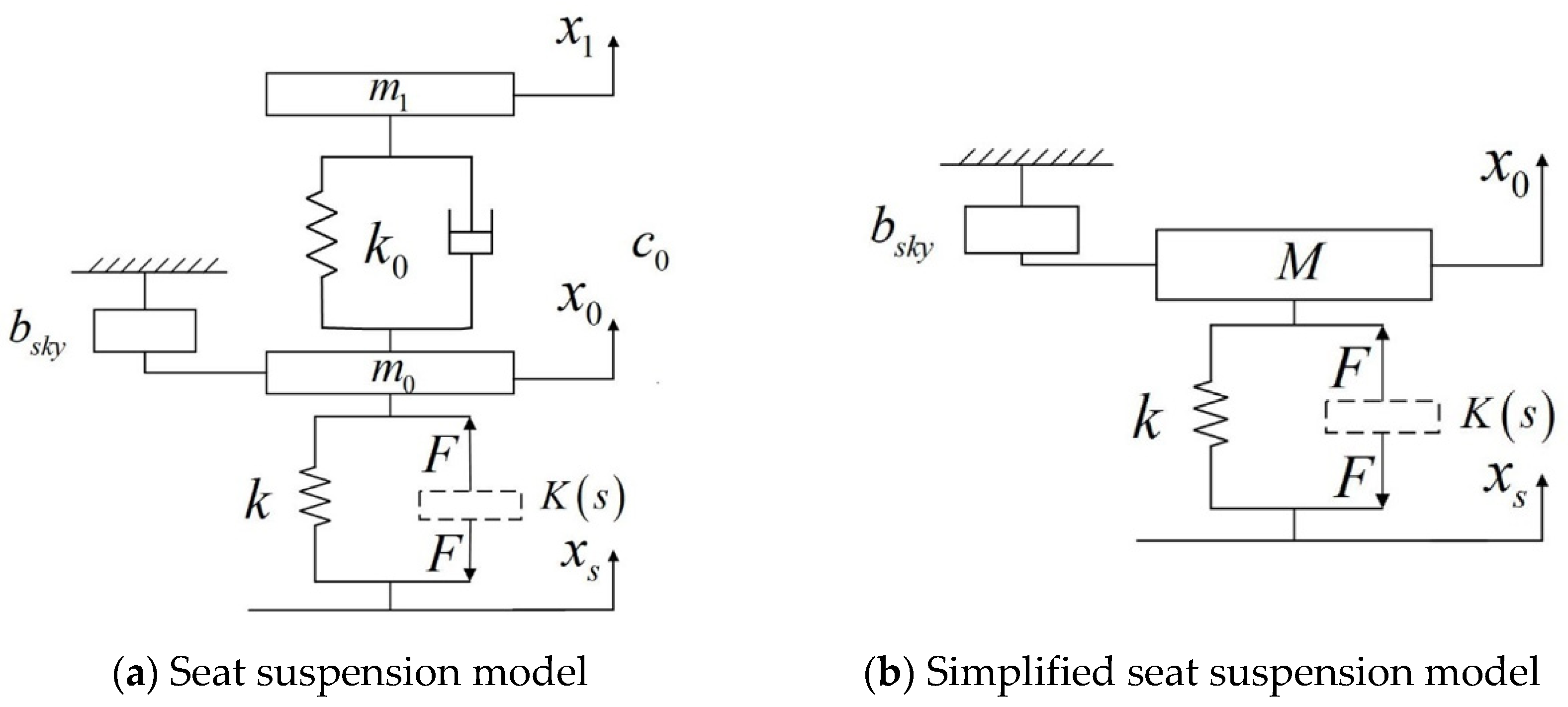
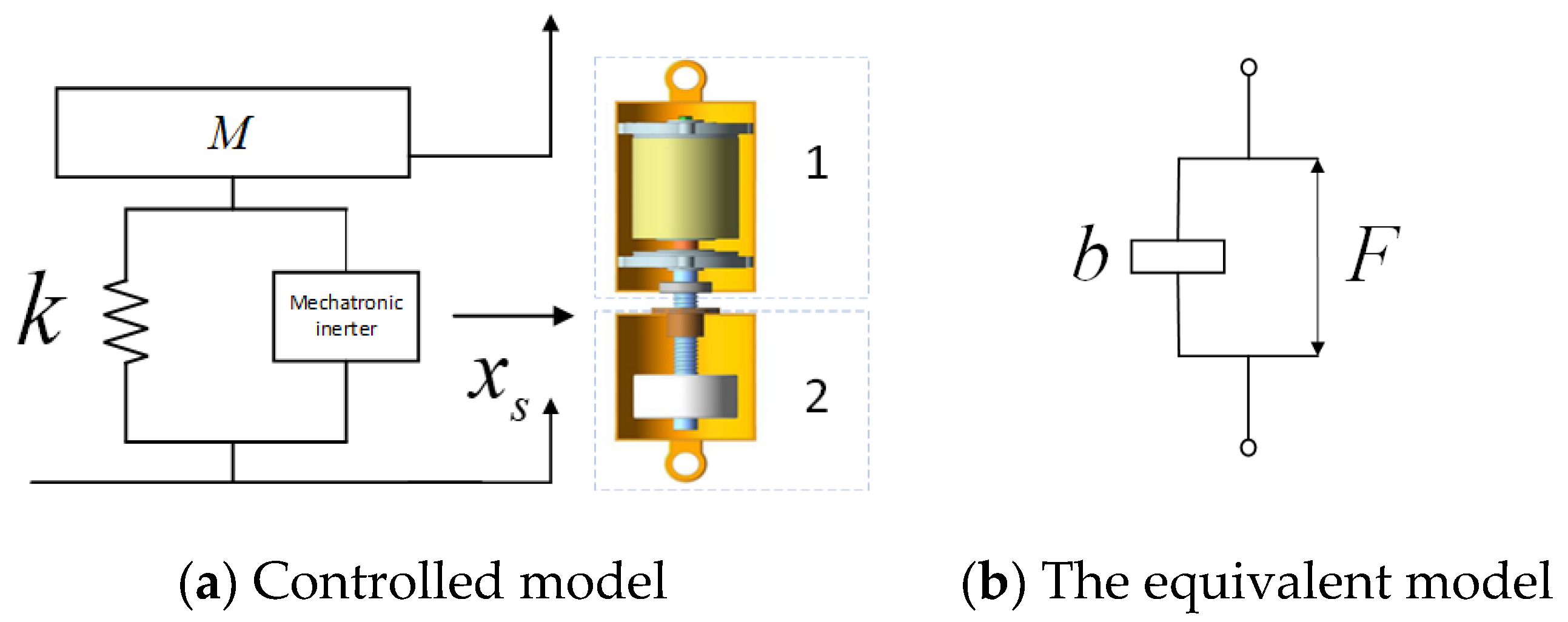
2.1. Heavy-Duty Vehicle Seat Inertial Suspension Model
2.2. Passive Network Synthesis
3. Seat Suspension Optimization Design
3.1. Selection of Optimization Objectives
3.2. Constrained Optimization
3.3. Solution of Seat Suspension Structure Based on Passive Network Synthesis
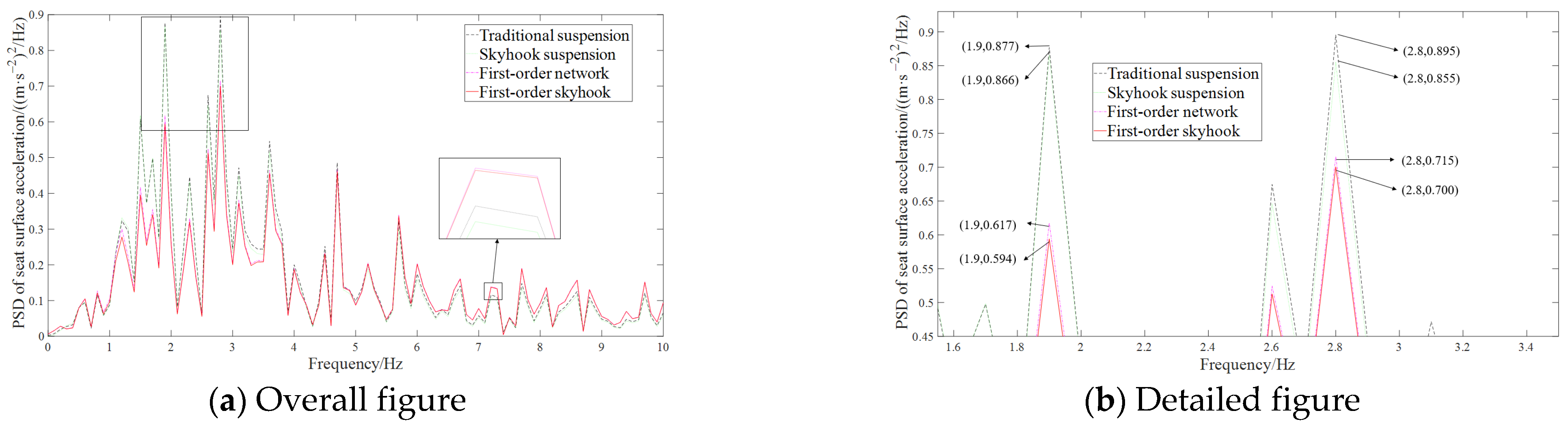
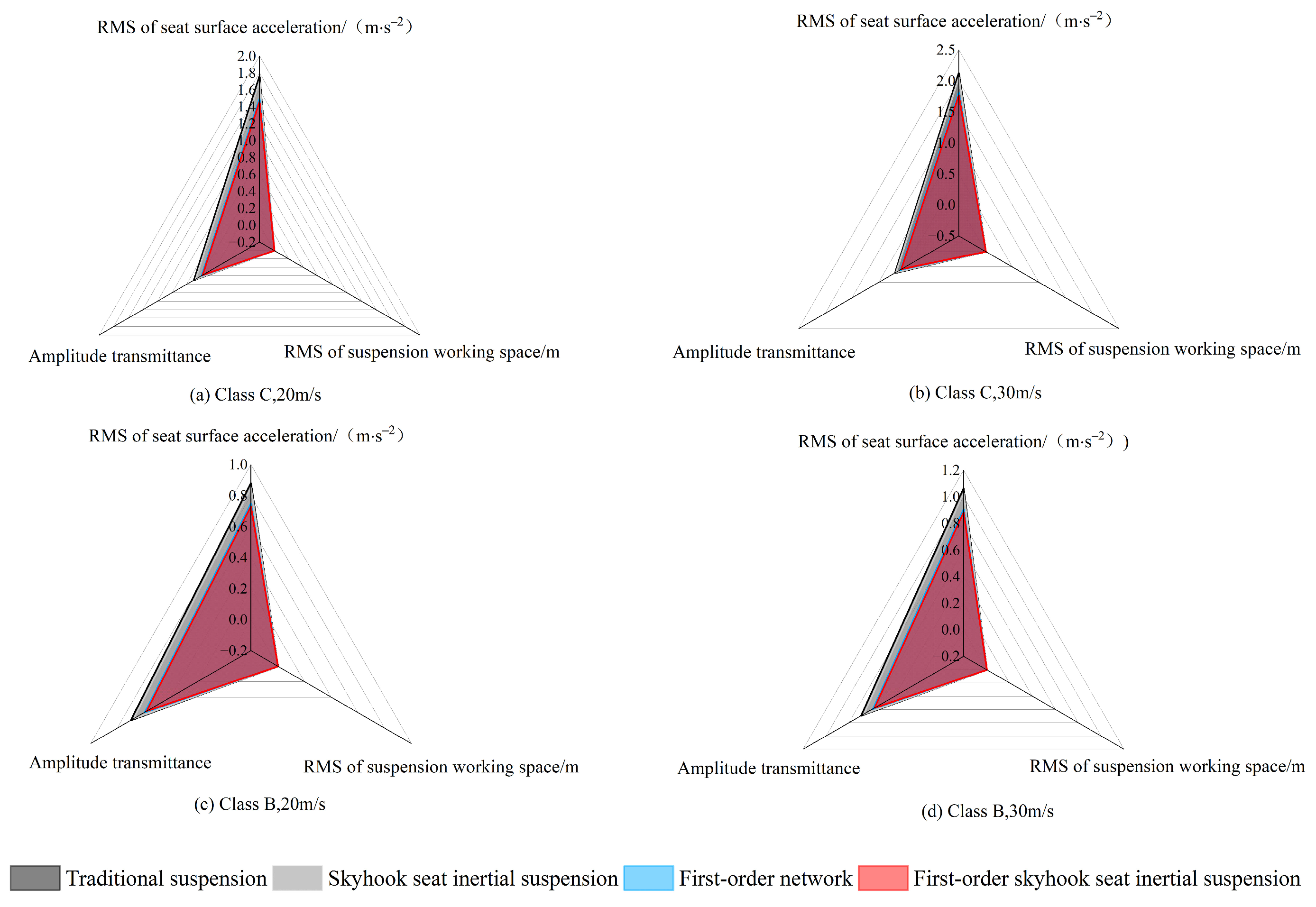
4. Performance Analysis of the Network Seat Suspension
4.1. First-Order Skyhook Seat Inertial Suspension Systems
4.2. Second-Order Skyhook Seat Inertial Suspension
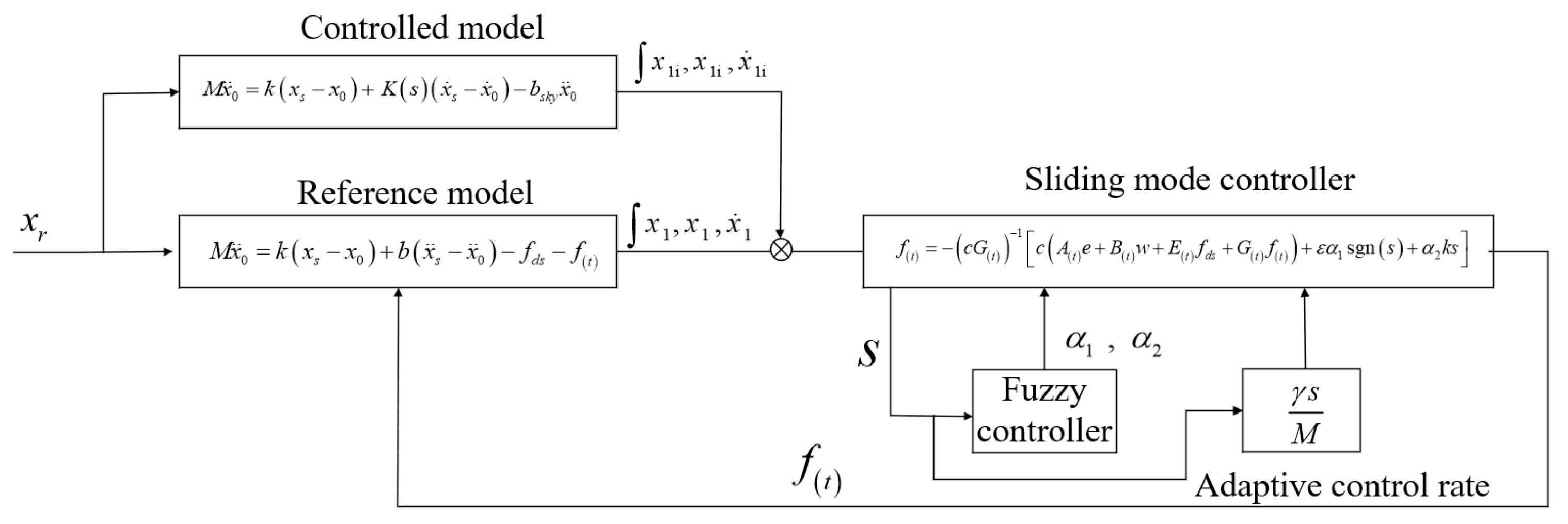
5. Design of Second-Order Skyhook Seat Inertial Suspension Control System
5.1. Fuzzy Sliding-Mode Controller Modeling and Approach Rate Design
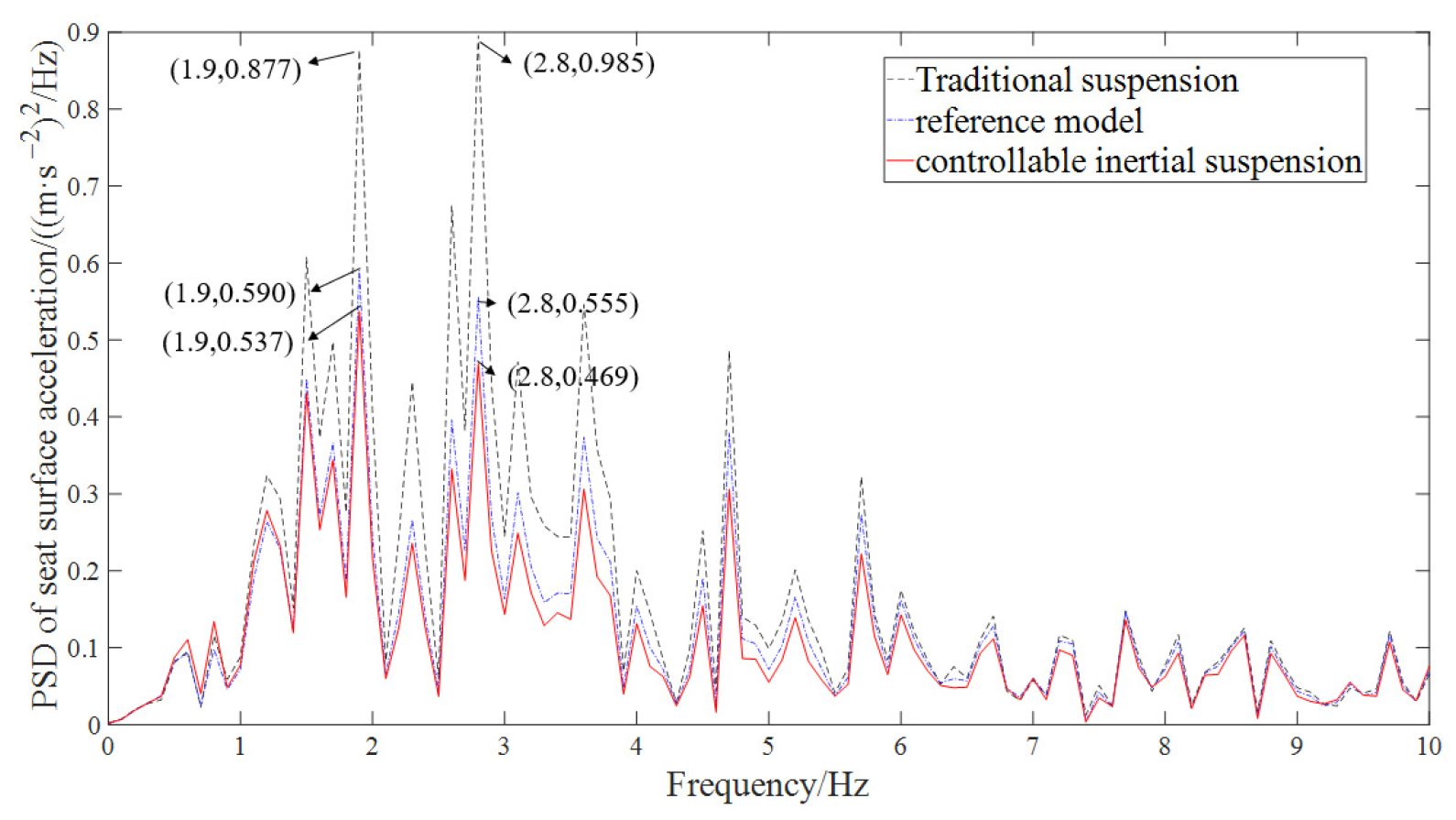
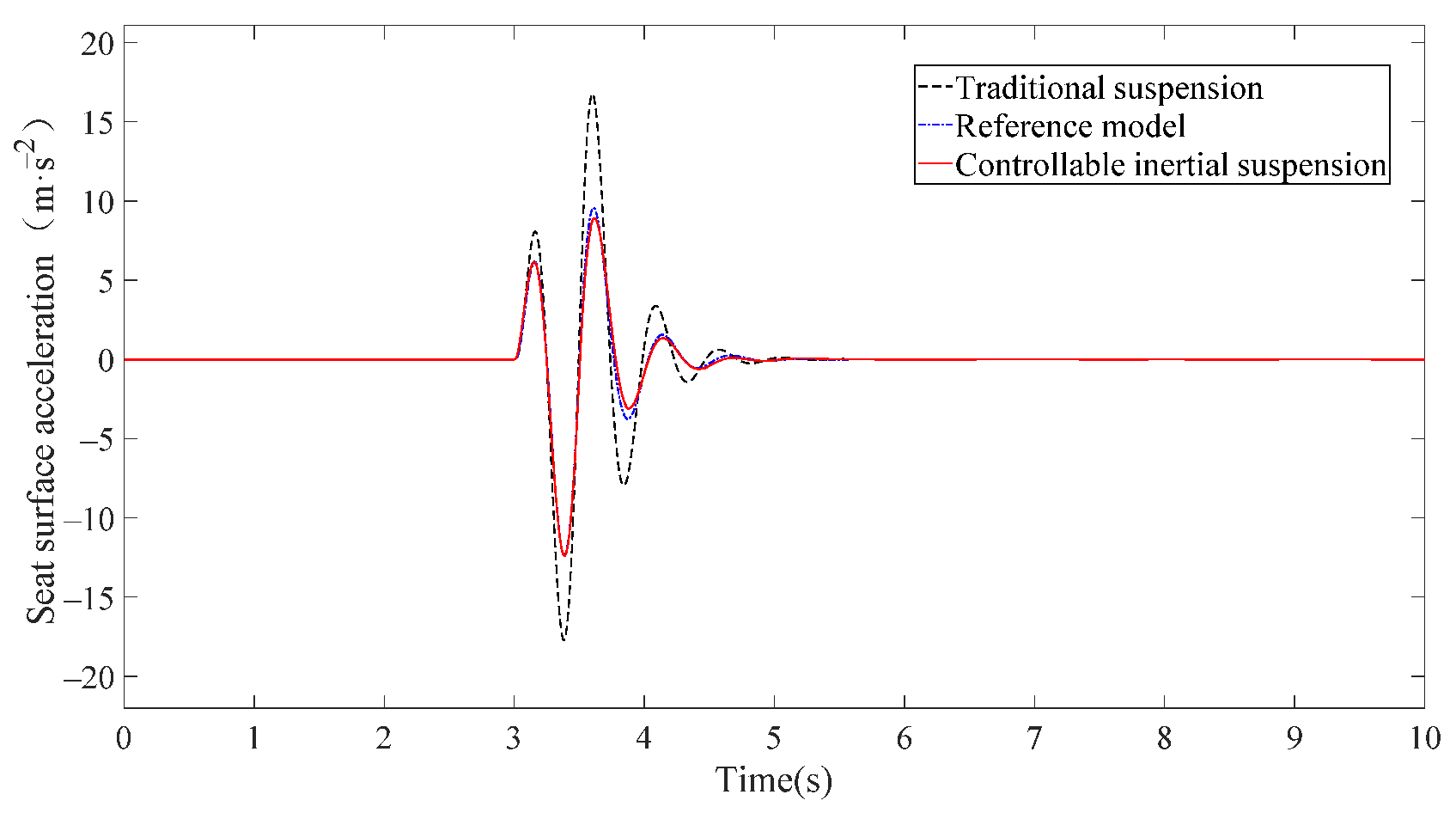
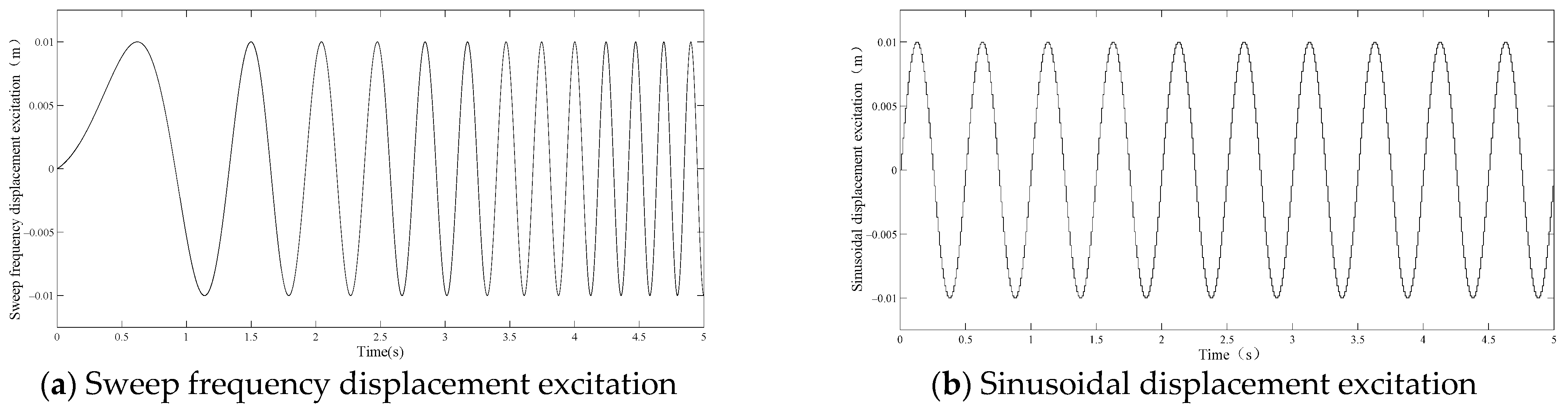
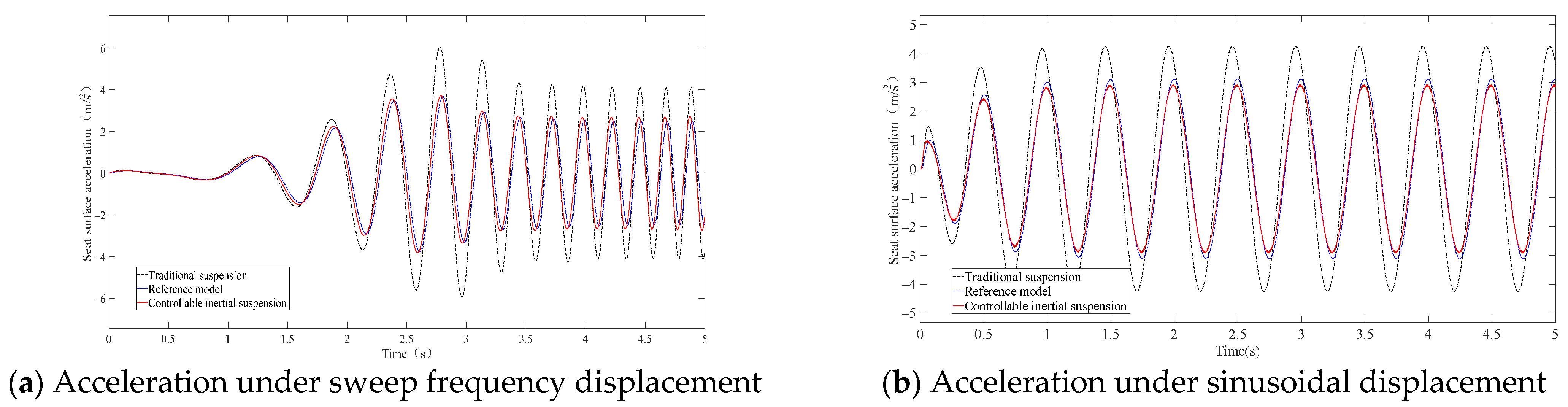
5.2. Performance Analysis of Seat-Controllable Inertial Suspension
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kuang, H.; Qiu, Y.; Liu, C.; Zheng, X. A nonlinear biodynamic model of seated human body exposed to vertical vibration with sensitivity analysis. Mech. Syst. Signal Process. 2023, 204, 110758. [Google Scholar] [CrossRef]
- Kia, K.; Johnson, P.W.; Kim, J.H. The effects of different seat suspension types on occupants’ physiologic responses and task performance: Implications for autonomous and conventional vehicles. Appl. Ergon. 2021, 93, 103380. [Google Scholar] [CrossRef] [PubMed]
- Stanczyk, T.L.; Zuska, A. Application of anthropodynamic dummies for evaluating the impact of vehicle seat vibrations upon human body. J. Theor. Appl. Mech. 2015, 53, 1029–1039. [Google Scholar] [CrossRef][Green Version]
- Zuska, A.N.D.R.Z.E.J.; Stanczyk, T.L. Review of anthropodynamic dummies used to evaluate the effect of vibrations on sitting human (vehicle driver). Archiwum Motoryzacji 2014, 65, 65–74. [Google Scholar]
- Zuska, A.; Stanczyk, T.L. Analysis of the impact of selected anthropometric parameters on the propagation of vertical vibration in the body of a seated person (driver). J. Vibroeng. 2015, 17, 3936–3948. [Google Scholar]
- Heidarian, A.; Wang, X. Review on Seat Suspension System Technology Development. Appl. Sci. 2019, 9, 2834. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, C.; Guo, K.; Sun, M.; Yao, Q. Dynamics modeling and characteristics analysis of scissor seat suspension. J. Vib. Control 2017, 23, 2819–2829. [Google Scholar] [CrossRef]
- Ning, D.; Sun, S.; Du, H.; Li, W. Integrated active and semi-active control for seat suspension of a heavy duty vehicle. J. Intell. Mater. Syst. Struct. 2018, 29, 91–100. [Google Scholar] [CrossRef]
- Du, H.; Li, W.; Zhang, N. Vibration control of vehicle seat integrating with chassis suspension and driver body model. Adv. Struct. Eng. 2013, 16, 1–9. [Google Scholar] [CrossRef]
- Zhao, L.; Zhou, C.; Yu, Y.; Yang, F. An analytical formula of driver RMS acceleration response for quarter-car considering cushion effects. Veh. Syst. Dyn. 2017, 55, 1283–1296. [Google Scholar] [CrossRef]
- Song, Y.; Chen, L.; Yang, T. Geometrically nonlinear inerter for vibration suppression. Appl. Math. Mech. 2023, 44, 1871–1886. [Google Scholar] [CrossRef]
- Yang, M.; Luo, X.; Zhang, X.; Ding, H.; Chen, L. Enhancing suspension vibration reduction by diagonal inerter. Appl. Math. Mech. 2022, 43, 1531–1542. [Google Scholar] [CrossRef]
- Ning, D.; Du, H.; Sun, S.; Li, W.; Li, W. An energy saving variable damping seat suspension system with regeneration capability. IEEE Trans. Ind. Electron. 2018, 65, 8080–8091. [Google Scholar] [CrossRef]
- Gad, S.; Metered, H.; Bassuiny, A.; Abdel Ghany, A.M. Multi-objective genetic algorithm fractional-order PID controller for semi-active magnetorheologically damped seat suspension. J. Vib. Control 2017, 23, 1248–1266. [Google Scholar] [CrossRef]
- Liu, P.; Ning, D.; LUO, L.; Zhang, N.; Du, H. An electromagnetic variable inertance and damping seat suspension with controllable circuits. IEEE Trans. Ind. Electron. 2021, 69, 2811–2821. [Google Scholar] [CrossRef]
- Cui, L.; Xue, X.; Le, F.; Mao, H.; Ding, S. Design and experiment of electro hydraulic active suspension for controlling the rolling motion of spray boom. Int. J. Agric. Biol. Eng. 2019, 12, 72–81. [Google Scholar] [CrossRef]
- Zhang, Y.; Ren, C.; Ma, K.; Xu, Z.; Zhou, P.; Chen, Y. Effect of delayed resonator on the vibration reduction performance of vehicle active seat suspension. J. Low Freq. Noise Vib. Act. Control 2022, 41, 387–404. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, X.; Sun, C. Research on a novel displacement-dependent semi-active valve damping control mechanism used in the seat suspension system. Adv. Mech. Eng. 2023, 15, 1–17. [Google Scholar] [CrossRef]
- Smith, M.C. Synthesis of mechanical networks: The inerter. IEEE Trans. Autom. Control 2002, 47, 1648–1662. [Google Scholar] [CrossRef]
- Dai, J.; Gai, P.P.; Xu, Z.D.; Huang, X.H. Inerter location effect on the generalized tuned mass damper inerter control. Structures 2023, 58, 105517. [Google Scholar] [CrossRef]
- Shen, Y.; Qiu, D.; Yang, X.; Chen, J.; Guo, Y.; Zhang, T. Vibration isolation performance analysis of a nonlinear fluid inerter-based hydro-pneumatic suspension. Int. J. Struct. Stability Dyn. 2024. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, C.; Lai, S.K.; Chen, Z.; Chen, L. Frequency-dependent equivalent impedance analysis for optimizing vehicle inertial suspensions. Nonlinear Dyn. 2024, 1–26. [Google Scholar] [CrossRef]
- Desai, R.; Guha, A.; Seshu, P. Modelling and simulation of active and passive seat suspensions for vibration attenuation of vehicle occupants. Int. J. Dynam. Control 2021, 9, 1423–1443. [Google Scholar] [CrossRef]
- Patel, C.C. Shared mass damper linking adjacent structures subjected to random excitation. Structures 2023, 56, 104869. [Google Scholar] [CrossRef]
- Zhang, Y.; Hu, N.; Cheng, Z.; Zhang, L.; Chen, H. Dynamic Modeling of the Aircraft Landing Gear Based on ISD Mechanism. In Proceedings of the 2018 Prognostics and System Health Management Conference PHM-Chongqing, Chongqing, China, 26–28 October 2018; pp. 344–349. [Google Scholar] [CrossRef]
- Li, Y.; Jiang, J.Z.; Sartor, P.; Neild, S.A.; Wang, H. Including inerters in aircraft landing gear shock strut to improve the touch-down performance. Procedia Eng. 2017, 199, 1689–1694. [Google Scholar] [CrossRef]
- Wu, H.; Gong, N.; Yang, J.; Gong, L.; Li, W.; Sun, S. Investigation of a semi-active suspension system for high-speed trains based on magnetorheological isolator with negative stiffness characteristics. Mech. Syst. Signal Process. 2024, 208, 111085. [Google Scholar] [CrossRef]
- Chen, X.; Shen, L.; Hu, X.; Li, G.; Yao, Y. Suspension parameter optimal design to enhance stability and wheel wear in high-speed trains. Veh. Syst. Dyn. 2024, 62, 1230–1252. [Google Scholar] [CrossRef]
- Zhang, H.; Ling, L.; Zhai, W.; Wang, K. An active suspension system for enhancing running safety of high-speed trains under strong crosswind. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2024, 238, 544–558. [Google Scholar] [CrossRef]
- Ali, S.A.; Metered, H.; Bassiuny, A.M.; Ghany, A.A. Theoretical investigation of the rail vehicle suspension system using different optimised controllers by harmony search algorithm incorporating magnetorheological dampers. Int. J. Veh. Perform. 2024, 10, 144–176. [Google Scholar] [CrossRef]
- Shen, W.; Long, Z.; Cai, L.; Niyitangamahoro, A.; Zhu, H.; Li, Y.; Qiu, C. An inerter-based electromagnetic damper for civil structures: Modeling, testing, and seismic performance. Mech. Syst. Signal Process. 2022, 173, 109070. [Google Scholar] [CrossRef]
- Ma, R.; Bi, K.; Hao, H. Inerter-based structural vibration control: A state-of-the-art review. Eng. Struct. 2021, 243, 112655. [Google Scholar] [CrossRef]
- Liu, C.; Chen, L.; Lee, H.P.; Yang, Y.; Zhang, X. A review of the inerter and inerter-based vibration isolation: Theory, devices, and applications. J. Frankl. Inst. 2022, 359, 7677–7707. [Google Scholar] [CrossRef]
- Jereczek, B.; Maciejewski, I.; Krzyzynski, T.; Krolikowski, T. Implementation of the SMC control strategy to an active horizontal seat suspension system. Procedia Comput. Sci. 2023, 225, 3527–3535. [Google Scholar] [CrossRef]
- Li, Y.; Yang, X.; Shen, Y.; Liu, Y.; Wang, W. Optimal design and dynamic control of the HMDV inertial suspension based on the ground-hook positive real network. Adv. Eng. Softw. 2022, 171, 103171. [Google Scholar] [CrossRef]
- Jeong, Y.; Yim, S. Design of Active Suspension Controllers for 8 × 8 Armored Combat Vehicles. Machines 2024, 12, 931. [Google Scholar] [CrossRef]
- Esmaeial, J.S.; Akbari, A.; Farnam, A.; Azad, N.L.; Crevecoeur, G. Adaptive Neuro-Fuzzy Control of Active Vehicle Suspension Based on H2 and H∞ Synthesis. Machines 2023, 11, 1022. [Google Scholar] [CrossRef]
- Deng, L.; Sun, S.; Christie, M.; Ning, D.; Jin, S.; Du, H.; Li, W. Investigation of a seat suspension installed with compact variable stiffness and damping rotary magnetorheological dampers. Mech. Syst. Signal Process. 2022, 171, 108802. [Google Scholar] [CrossRef]
- Wang, S.; Hui, Y.; Sun, X.; Shi, D. Neural network sliding mode control of intelligent vehicle longitudinal dynamics. IEEE Access 2019, 7, 162333–162342. [Google Scholar] [CrossRef]
- Jereczek, B.; Maciejewski, I.; Krzyżyński, T.; Królikowski, T. Modeling and simulation of the horizontal seat suspension system under random vibration. Procedia Comput. Sci. 2022, 207, 858–866. [Google Scholar] [CrossRef]
- Jiang, J.Z.; Smith, M.C. Regular positive-real functions and five-element network synthesis for electrical and mechanical networks. IEEE Trans. Autom. Control 2011, 56, 1275–1290. [Google Scholar] [CrossRef]
- Čakmak, D.; Tomičević, Z.; Wolf, H.; Božić, Ž.; Semenski, D.; Trapić, I. Vibration fatigue study of the helical spring in the base-excited inerter-based isolation system. Eng. Fail. Anal. 2019, 103, 44–56. [Google Scholar] [CrossRef]




| Parameter | Value |
|---|---|
| Human body mass | 70 |
| Seat mass | 30 |
| Seat suspension damping coefficient | 1.906 |
| Seat spring stiffness | 15 |
| Torso stiffness coefficient | 49.34 |
| Trunk damping coefficient | 2.475 |
| 326 | |
| Damping coefficient of body suspension | 14 |
| Tire stiffness coefficient | 1300 |
| Sprung mass | 1396 |
| Unsprung mass | 150 |
| Parameter | Value | |
|---|---|---|
| First-order network | a | 3873 |
| b | 1046 | |
| c | 1 | |
| d | 3 | |
| Second-order network | A | 1,259,122 |
| B | 8,854,718 | |
| C | 111,376,300 | |
| D | 986 | |
| E | 7225 | |
| F | 18,725 | |
| Parameter | Value | |
|---|---|---|
| First-order network | 1317 | |
| 3490 | ||
| 383 | ||
| 64 | ||
| Second-order network | 18,725 | |
| 5948 | ||
| 1277 | ||
| 986 | ||
| 199 | ||
| Conditions | Performance Index | Traditional Suspension | Skyhook Seat Inertial Suspension | First-Order Network | First-Order Skyhook Seat Inertial Suspension |
|---|---|---|---|---|---|
| Class C, 20 m/s | RMS of seat surface acceleration/ | 1.7626 | 1.7009 | 1.4987 | 1.4618 |
| RMS of suspension working space/ | 0.0053 | 0.0058 | 0.0056 | 0.0053 | |
| Amplitude transmittance | 0.7001 | 0.6755 | 0.5952 | 0.5806 |
| Conditions | Performance Index | Traditional Suspension | Skyhook Inertial Suspension | Second-Order Network | Second-Order Skyhook Seat Inertial Suspension |
|---|---|---|---|---|---|
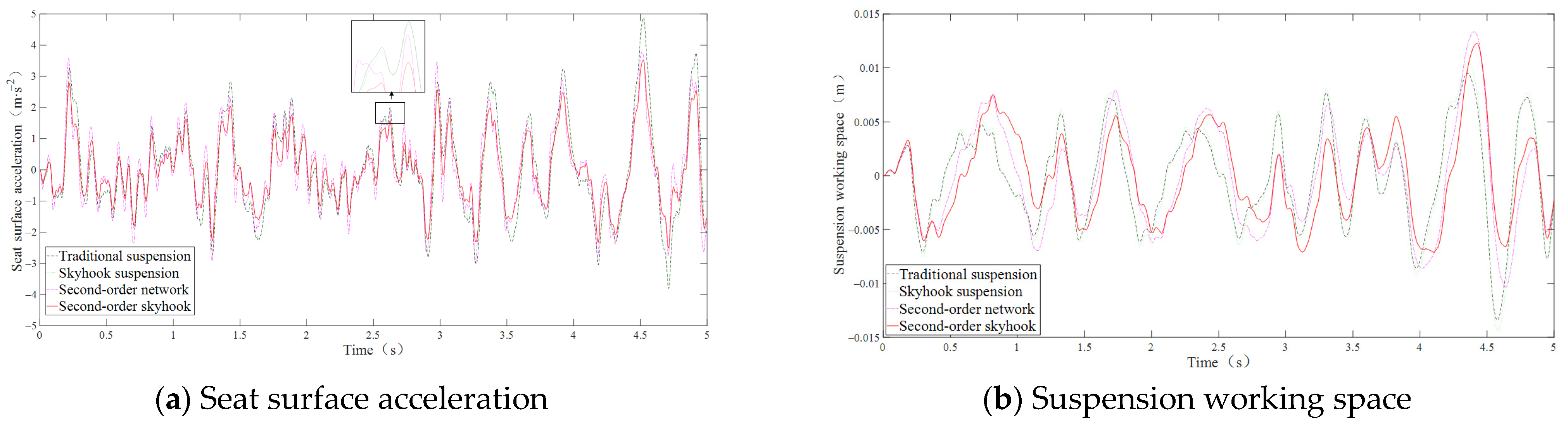
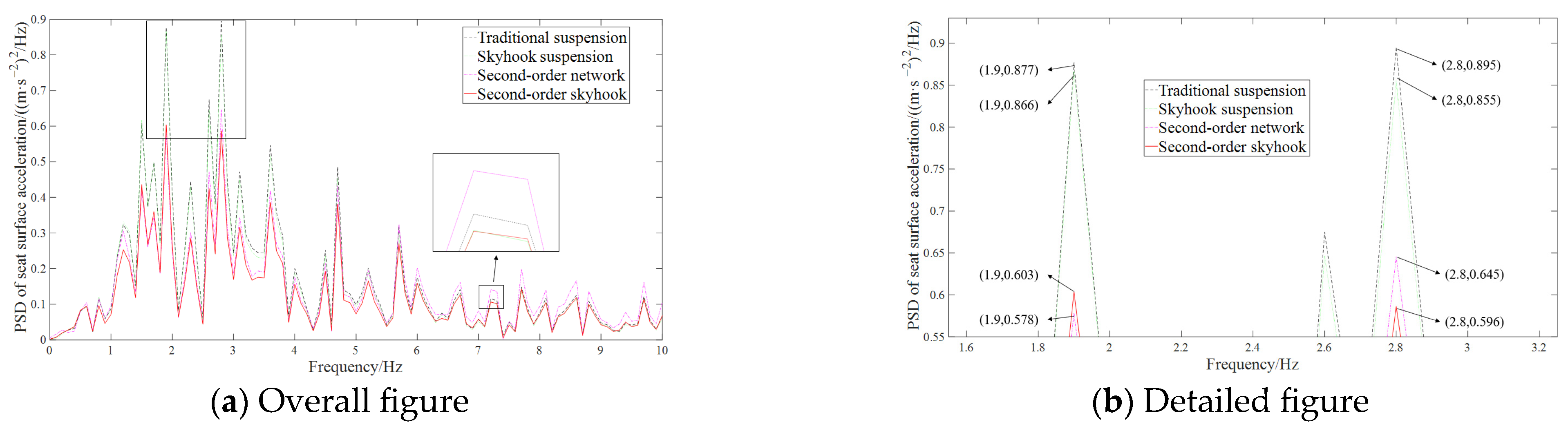
| Class C, 20 m/s | RMS of seat surface acceleration/(m·s−2) | 1.7626 | 1.7009 | 1.4326 | 1.2693 |
| RMS of suspension working space/ | 0.0053 | 0.0058 | 0.0056 | 0.0053 | |
| Amplitude transmittance | 0.7001 | 0.6755 | 0.5690 | 0.5302 |
| ZO | PS | PM | PB | NS | NM | NB | |
|---|---|---|---|---|---|---|---|
| ZO | PS | PM | PB | PS | PM | PB | |
| PM | PM | PS | ZO | PB | PS | ZO |
| Conditions | Performance Index | Traditional Suspension | Second-Order Skyhook Seat Inertial Suspension | Controllable Inertial Seat Suspension |
|---|---|---|---|---|
| Class C, 20 m/s | RMS of seat surface acceleration/(m·s−2) | 1.7626 | 1.2693 | 1.2348 |
| RMS of suspension working space/m | 0.0053 | 0.0053 | 0.0057 |
| Conditions | Performance Index | Traditional Suspension | Second-Order Skyhook Seat Inertial Suspension | Controllable Inertial Seat Suspension |
|---|---|---|---|---|
| Road excitation: Figure 15b | RMS of seat surface acceleration/(m·s−2) | 2.613 | 1.5247 | 1.6654 |
| reduction | 41.70% | 36% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Sun, R.; Yang, Y.; Liu, Y.; Hong, J.; Liu, C. Enhanced Seat Suspension Performance Through Positive Real Network Optimization and Skyhook Inertial Control. Machines 2025, 13, 222. https://doi.org/10.3390/machines13030222
Yang X, Sun R, Yang Y, Liu Y, Hong J, Liu C. Enhanced Seat Suspension Performance Through Positive Real Network Optimization and Skyhook Inertial Control. Machines. 2025; 13(3):222. https://doi.org/10.3390/machines13030222
Chicago/Turabian StyleYang, Xiaofeng, Rui Sun, Yi Yang, Yanling Liu, Jingchen Hong, and Changning Liu. 2025. "Enhanced Seat Suspension Performance Through Positive Real Network Optimization and Skyhook Inertial Control" Machines 13, no. 3: 222. https://doi.org/10.3390/machines13030222
APA StyleYang, X., Sun, R., Yang, Y., Liu, Y., Hong, J., & Liu, C. (2025). Enhanced Seat Suspension Performance Through Positive Real Network Optimization and Skyhook Inertial Control. Machines, 13(3), 222. https://doi.org/10.3390/machines13030222







