A Novel Bearing Fault Diagnosis Method Based on Improved Convolutional Neural Network and Multi-Sensor Fusion
Abstract
1. Introduction
2. Theoretical Background
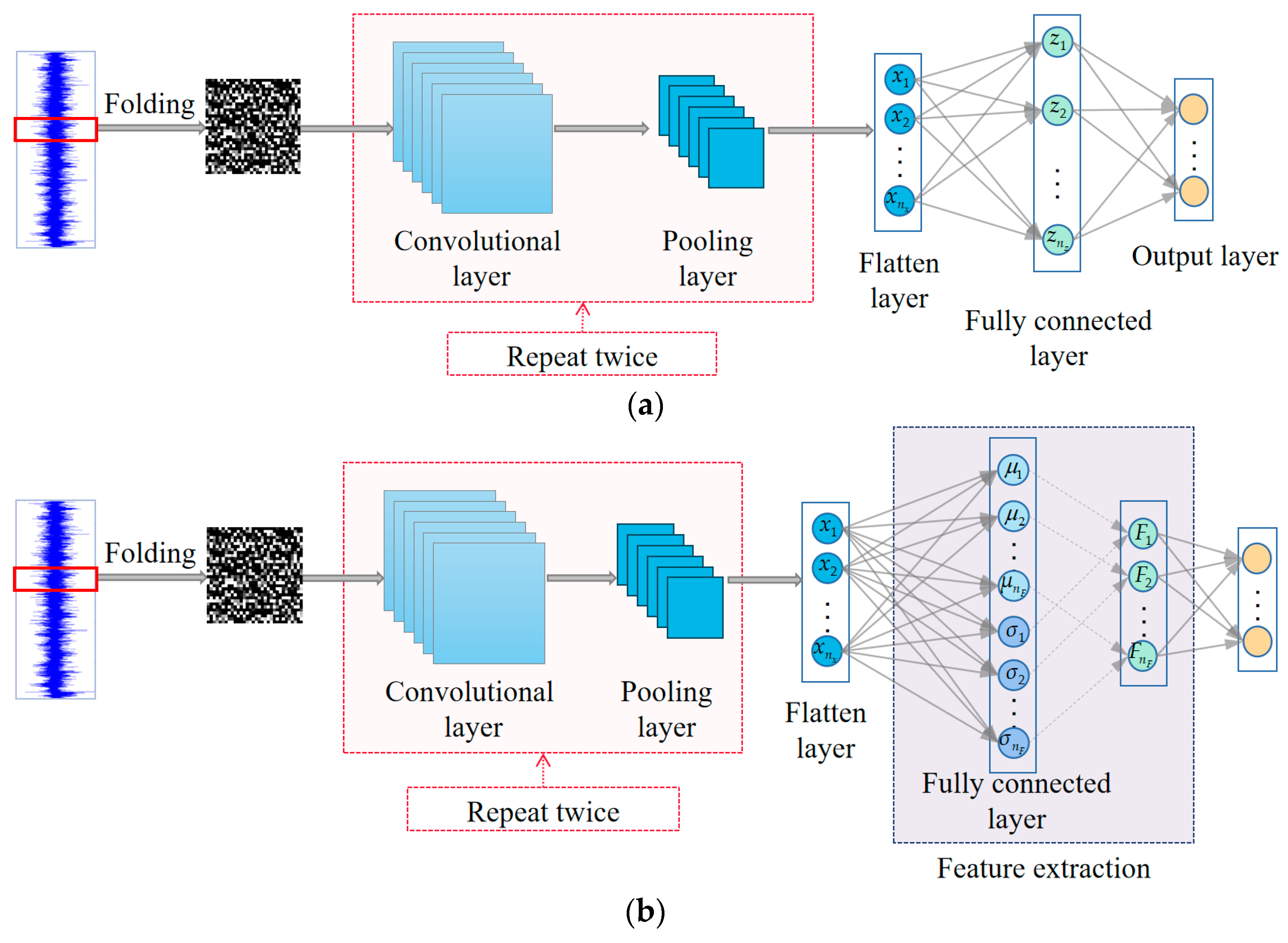
2.1. Convolutional Neural Network
2.2. Variational Bayesian Inference
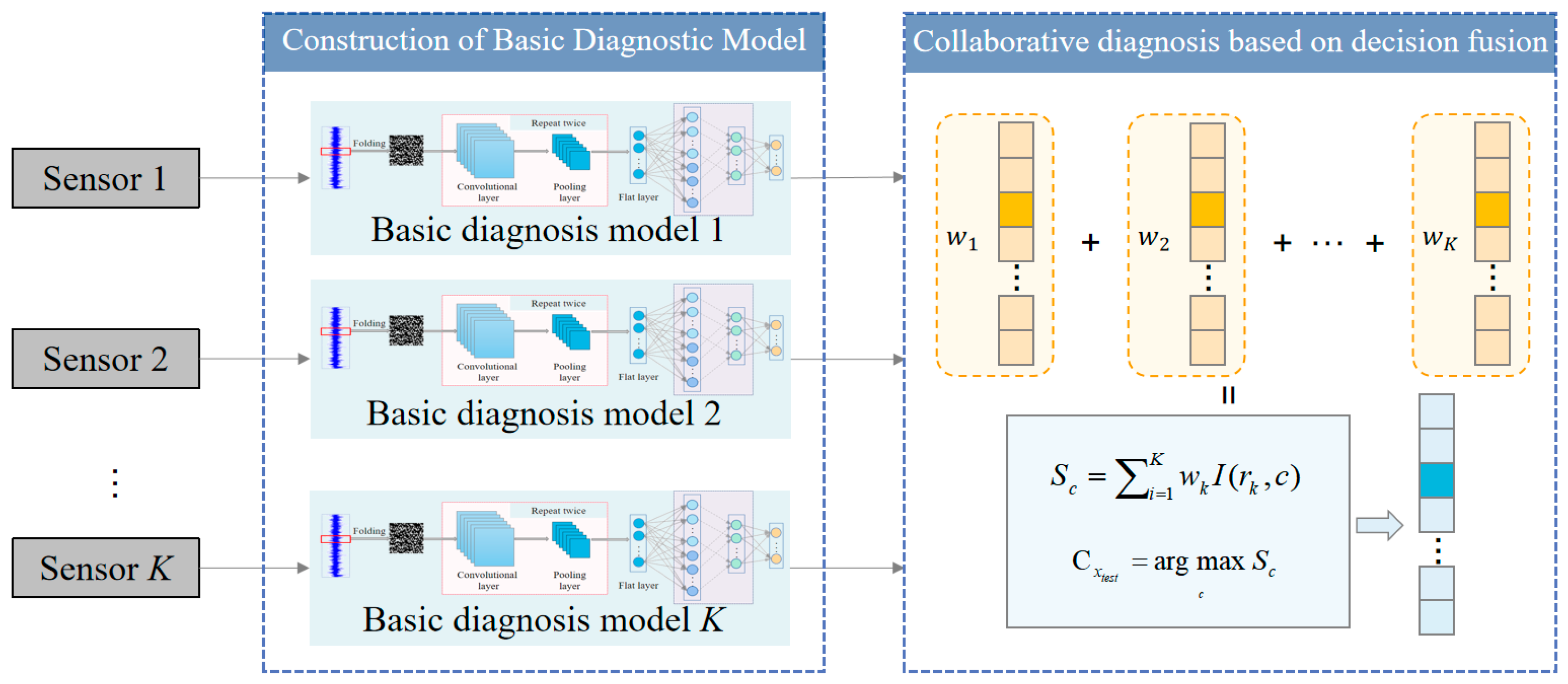
3. Proposed Method
3.1. VBICNN
3.2. Decision-Level Fusion Method Based on Weighted Fusion Strategy
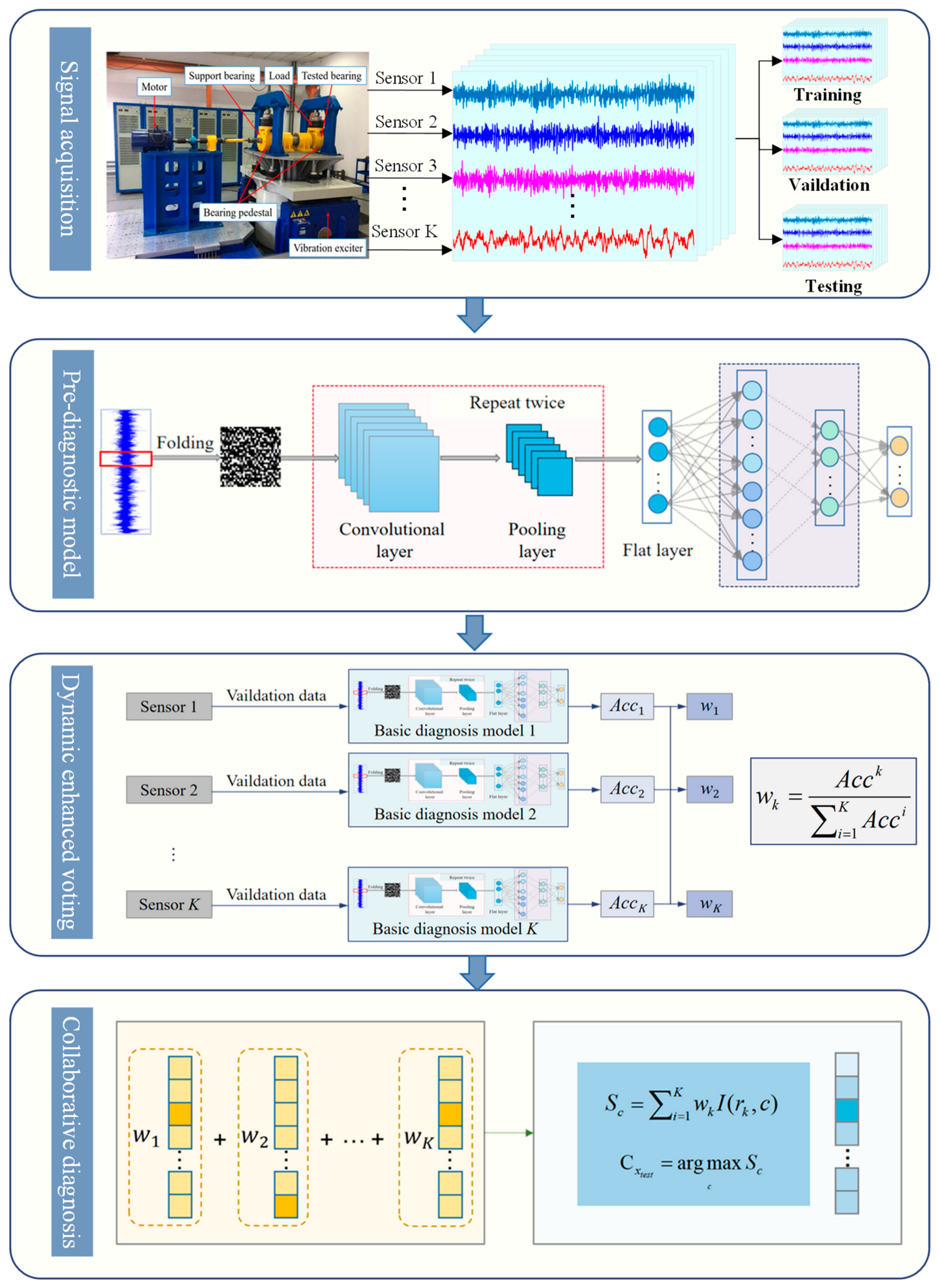
3.3. Flow of the Proposed Method
4. Experimental Study
4.1. Experimental Setup
4.2. Structural Design of the Model
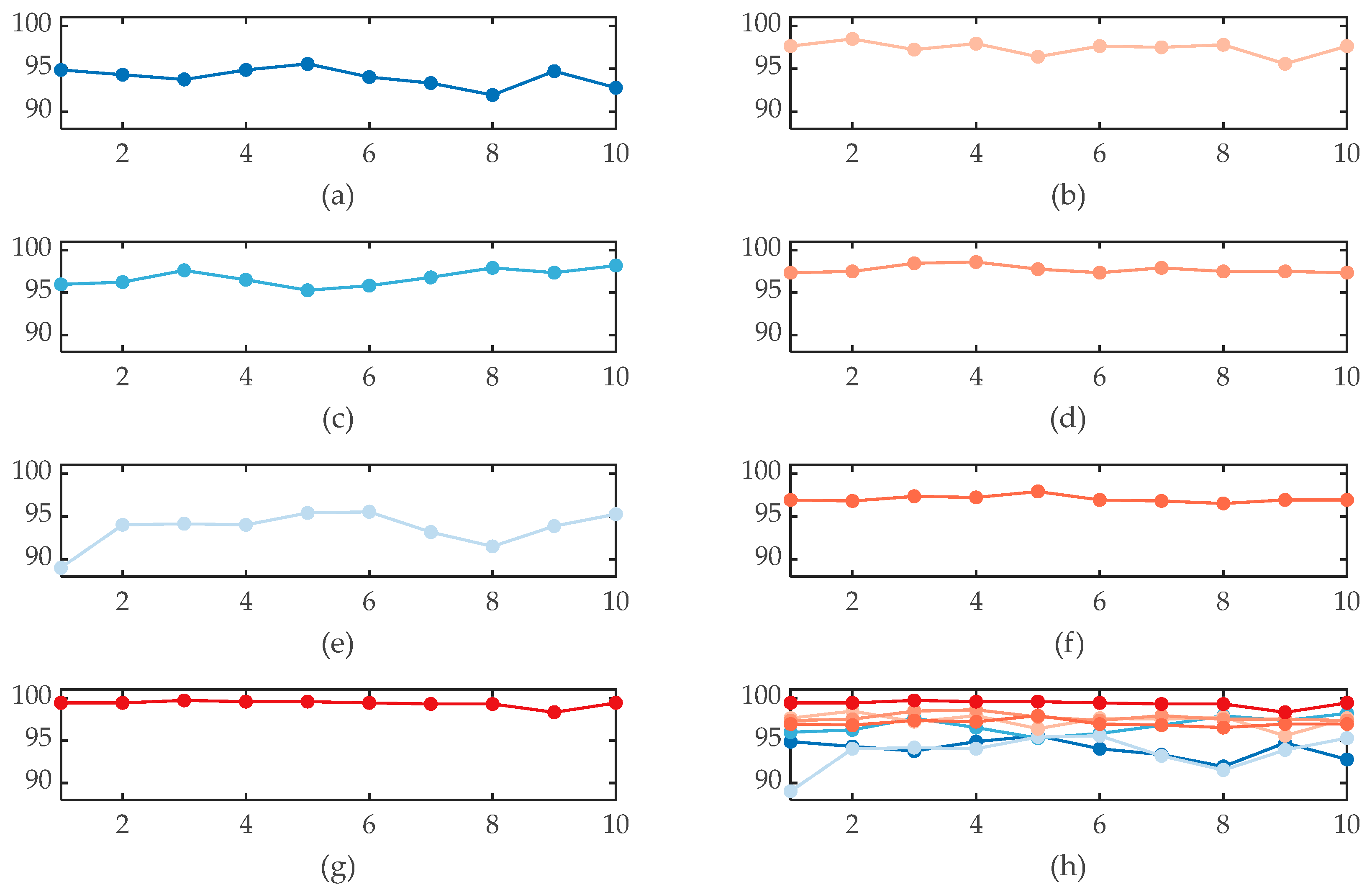
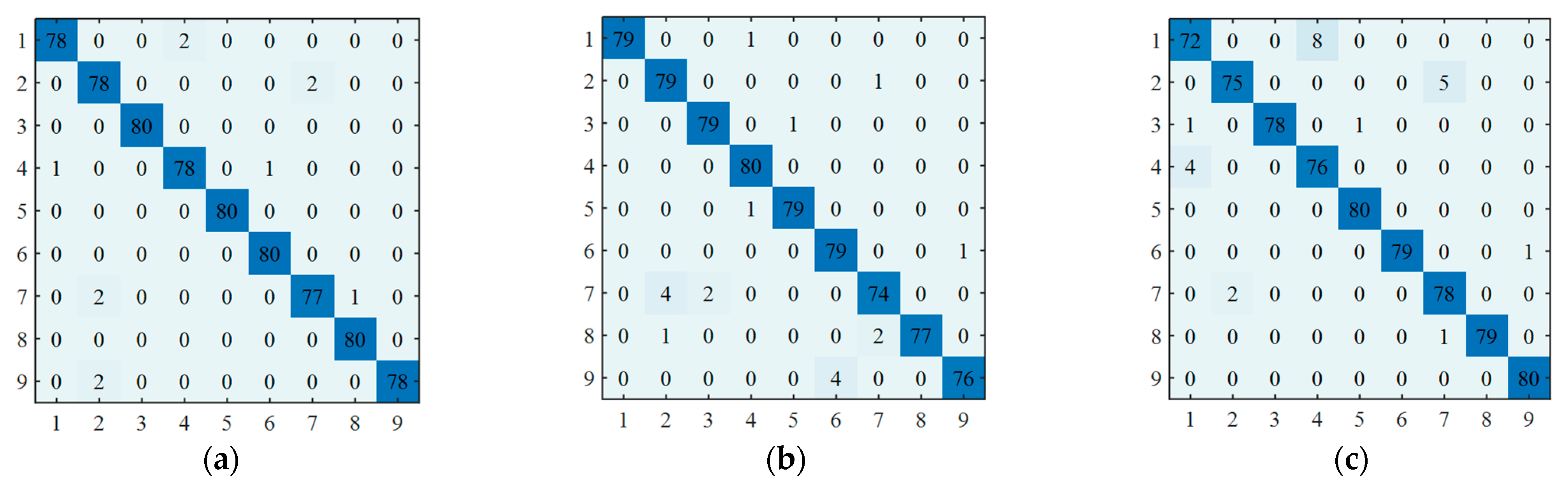
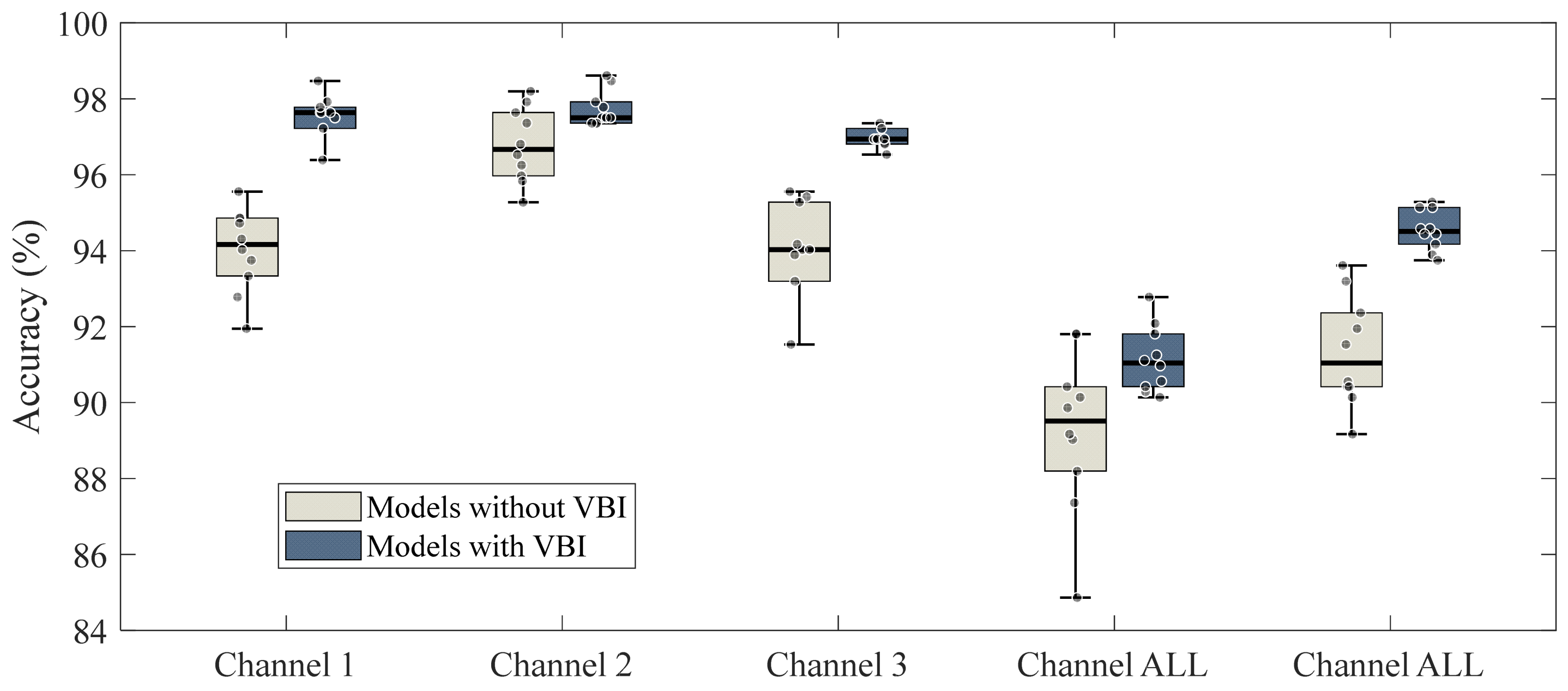
4.3. Ablation Experiment and Results
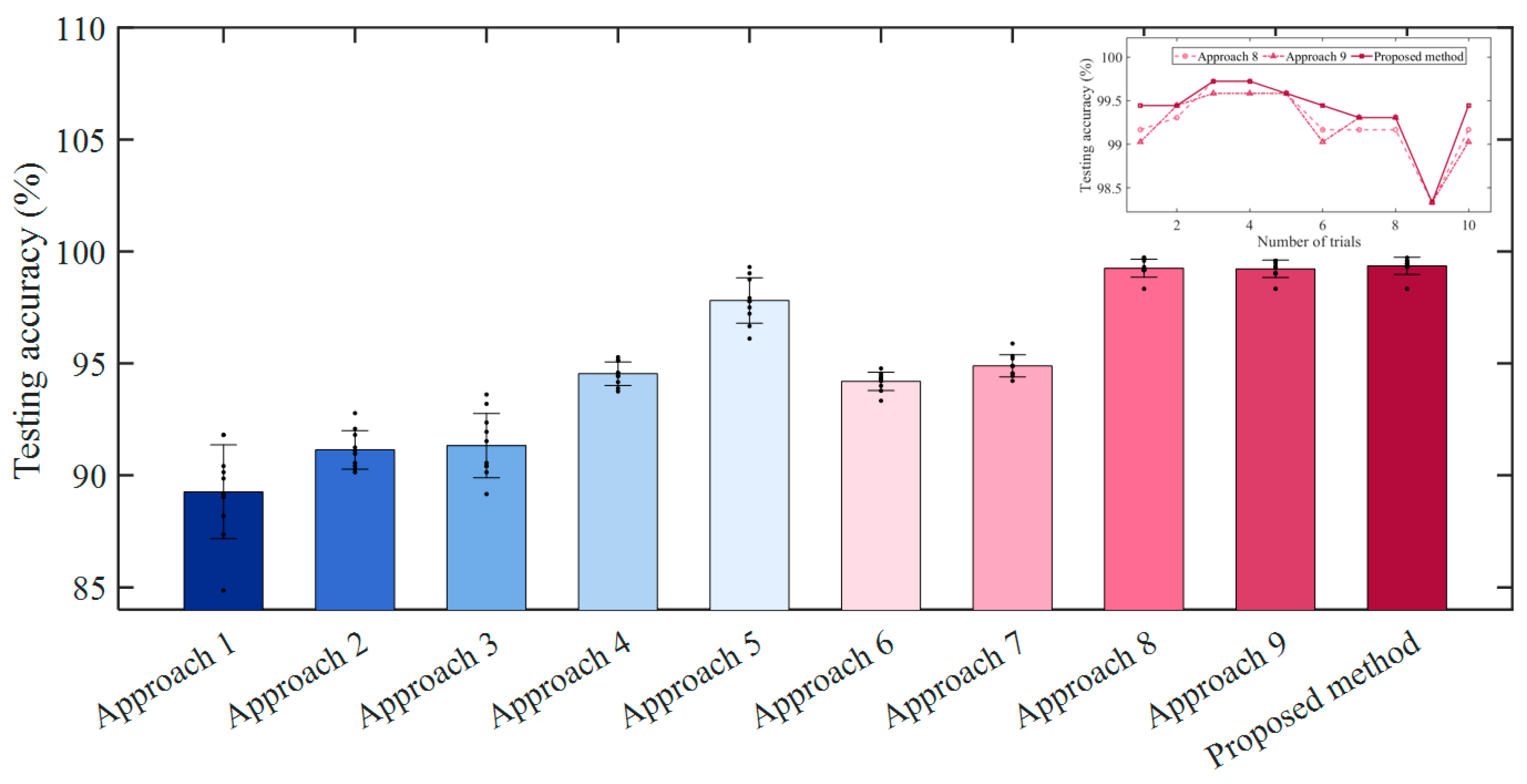
4.4. Comparative Experiments and Results
- Approach 1: A fault diagnosis approach based on the data-level fusion driven by principal component analysis (PCA) and CNN. Fuse the signals of all channels by PCA. And input the fusion result into CNN for classification.
- Approach 2: A fault diagnosis approach based on the data-level fusion driven by PCA and VBICNN. Input the fused signals of Approach 1 into VBICNN for classification.
- Approach 3: A fault diagnosis approach based on the data-level fusion driven by linear weighting and CNN. Fuse the signals of all channels by a similarity-based linear weighting method. And input the fusion result into CNN for classification.
- Approach 4: A fault diagnosis approach based on the data-level fusion driven by linear weighting and VBICNN. Input the fused signals of Approach 3 into VBICNN for classification.
- Approach 5: A diagnosis approach based on statistical feature fusion. Extract the statistical features of the signals of each channel. The features of all channels were combined with the Softmax classifier for classification. The statistical features used are consistent with the reference [41].
- Approach 6: A fault diagnosis approach based on the feature-level fusion driven by sparse auto-encoder (SAE). Extract the features of each channel signal by using SAE. The features of all channels were combined with the Softmax classifier for classification.
- Approach 7: A fault diagnosis approach based on the feature-level fusion driven by variational auto-encoder (VAE). Extract the features of each channel signal by using VAE. The features of all channels were combined with the Softmax classifier for classification.
- Approach 8: A decision-level fusion method based on the average voting. Based on the pre-diagnosis results of each channel obtained by VBICNN, use the average voting to assign the weights of each VBICNN for fusion.
- Approach 9: A decision-level fusion method based on weighted voting. Adopt the second fusion strategy proposed in the reference [40] to assign the weights of each VBICNN for fusion.
5. Discussion
5.1. The Necessity of Multi-Channel Information Fusion Diagnosis
5.2. The Effectiveness of Variational Bayesian Inference
6. Conclusions
- (1)
- The comparison with the diagnosis method based on a single-channel signal confirmed that multi-channel signals contain complementary information, which enables the acquisition of more accurate and stable results.
- (2)
- The comparison with the models without variational Bayesian inference confirms that variational Bayesian inference has the advantage of dealing with high-dimensional uncertain data, which could improve the classification performance of CNN.
- (3)
- Comparison with other multichannel fusion approaches confirms that the proposed approach has better performance in multi-channel vibration signal fusion diagnosis. The comparison approaches include several data-level fusion methods, feature-level fusion methods, and decision-level fusion methods.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Alshorman, O.; Irfan, M.; Abdelrahman, R.B.; Abdelrahman, B.; Masadeh, M.; Alshorman, A.; Sheikh, M.A.; Saad, N.; Rahman, S. Advancements in condition monitoring and fault diagnosis of rotating machinery: A comprehensive review of image-based intelligent techniques for induction motors. Eng. Appl. Artif. Intell. 2024, 130, 107724. [Google Scholar] [CrossRef]
- Liu, L.; Cheng, Y.; Song, D.; Zhang, W.; Tang, G.; Luo, Y. A lightweight network with adaptive input and adaptive channel pruning strategy for bearing fault diagnosis. IEEE Trans. Instrum. Meas. 2024, 73, 3510911. [Google Scholar] [CrossRef]
- Peng, D.; Wang, H.; Liu, Z.; Zhang, W.; Zuo, M.; Chen, J. Multibranch and multiscale CNN for fault diagnosis of wheelset bearings under strong noise and variable load condition. IEEE Trans. Ind. Inform. 2017, 16, 4949–4960. [Google Scholar] [CrossRef]
- Strombergsson, D.; Marklund, P.; Berglund, K.; Larsson, P.E. Bearing monitoring in the wind turbine drivetrain: A comparative study of the FFT and wavelet transforms. Wind Energy 2020, 23, 1380–1393. [Google Scholar] [CrossRef]
- Sahraoui, M.A.; Rahmoune, C.; Meddour, I.; Bettahar, T.; Zair, M. New criteria for wrapper feature selection to enhance bearing fault classification. Adv. Mech. Eng. 2023, 15, 16878132231183862. [Google Scholar] [CrossRef]
- Kumar, D.; Mehran, S.; Shaikh, M.Z.; Hussain, M.; Chowdhry, B.S.; Hussain, T. Triaxial bearing vibration dataset of induction motor under varying load conditions. Data Brief 2022, 42, 108315. [Google Scholar] [CrossRef]
- Chen, B.; Cheng, Y.; Allen, P.; Wang, S.; Gu, F.; Zhang, W.; Ball, A.D. A product envelope spectrum generated from spectral correlation/coherence for railway axle-box bearing fault diagnosis. Mech. Syst. Signal Proc. 2025, 225, 112262. [Google Scholar] [CrossRef]
- Igba, J.; Alemzadeh, K.; Durugbo, C.; Eiriksson, E.T. Analysing RMS and peak values of vibration signals for condition monitoring of wind turbine gearboxes. Renew. Energy 2016, 91, 90–106. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, W.; Xiong, Q.; Lu, T.; Mei, G. A novel fault diagnosis model for bearing of railway vehicles using vibration signals based on symmetric alpha-stable distribution feature extraction. Shock Vib. 2016, 2016, 5714195. [Google Scholar] [CrossRef]
- Chen, B.; Song, D.; Zhang, W.; Cheng, Y. A novel spectral coherence-based envelope spectrum for railway axle-box bearing damage identification. Struct. Health Monit. 2023, 22, 879–896. [Google Scholar] [CrossRef]
- Hou, H.; Zhang, X.; Wang, X.; Wan, Y.; Shi, H.; Liu, W.; Wang, P. Location of underground multilayer media based on BP neural network and near-field electromagnetic signal. IEEE Sens. J. 2025, 25, 725–736. [Google Scholar] [CrossRef]
- Wang, X.; Jiang, H. Gearbox fault diagnosis based on refined time-shift multiscale reverse dispersion entropy and optimised support vector machine. Machines 2023, 11, 646. [Google Scholar] [CrossRef]
- Ziani, R.; Felkaoui, A.; Zegadi, R. Bearing fault diagnosis using multiclass support vector machines with binary particle swarm optimization and regularized Fisher’s criterion. J. Intell. Manuf. 2017, 28, 405–417. [Google Scholar] [CrossRef]
- Yao, C.; Li, N.; Feng, Z.; Chen, D. Fault diagnosis based on rough set attribute reduction and bayesian classifier. China Mech. Eng. 2015, 26, 1969–1977. [Google Scholar]
- Dong, S.; Wang, P.; Abbas, K. A survey on deep learning and its applications. Comput. Sci. Rev. 2021, 40, 100379. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Janssens, O.; Slavkovikj, V.; Vervisch, B.; Stockman, K.; Loccufier, M.; Verstockt, S.; Van de Wallk, R.; Van Hoecke, S. Convolutional neural network based fault detection for rotating machinery. J. Sound Vibr. 2016, 377, 331–345. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, Z.; Chen, X.; Zhai, Z.; Liu, Y. Interpretability discussion on convolutional neural network in bearing fault diagnosis. Bearing 2020, 7, 54–60. [Google Scholar]
- Mohiuddin, M.; Islam, M.S.; Islam, S.; Miah, M.S.; Niu, M. Intelligent Fault Diagnosis of Rolling Element Bearings Based on Modified AlexNet. Sensors 2023, 23, 7764. [Google Scholar] [CrossRef]
- Ruan, D.; Wang, J.; Yan, J.; Gühmann, C. CNN parameter design based on fault signal analysis and its application in bearing fault diagnosis. Adv. Eng. Inform. 2023, 55, 101877. [Google Scholar] [CrossRef]
- Salunkhe, V.G.; Khot, S.M.; Jadhav, P.S.; Yelve, N.P.; Kumbhar, M.B. Experimental Investigation Using Robust Deep VMD-ICA and 1D-CNN for Condition Monitoring of Roller Element Bearing. J. Comput. Inf. Sci. Eng. 2024, 24, 124501. [Google Scholar] [CrossRef]
- Xu, Y.; Feng, K.; Yan, X.; Sheng, X.; Sun, B.; Liu, Z.; Yan, R. Cross-modal fusion convolutional neural networks with online soft-label training strategy for mechanical fault diagnosis. IEEE Trans. Ind. Inform. 2024, 20, 73–84. [Google Scholar] [CrossRef]
- Yang, S.; Wang, Y.; Li, C. Wind turbine gearbox fault diagnosis based on an improved supervised autoencoder using vibration and motor current signals. Meas. Sci. Technol. 2021, 32, 114003. [Google Scholar] [CrossRef]
- Xie, T.; Huang, X.; Choi, S. Intelligent mechanical fault diagnosis using multisensor fusion and convolution neural network. IEEE Trans. Ind. Inform. 2022, 18, 3213–3223. [Google Scholar] [CrossRef]
- Chen, X.; Shao, H.; Xiao, Y.; Yan, S.; Cai, B.; Liu, B. Collaborative fault diagnosis of rotating machinery via dual adversarial guided unsupervised multi-domain adaptation network. Mech. Syst. Signal Proc. 2023, 198, 119427. [Google Scholar] [CrossRef]
- Stief, A.; Ottewill, J.; Baranowski, J.; Orkisz, M. A PCA and two-stage bayesian sensor fusion approach for diagnosing electrical and mechanical faults in induction motors. IEEE Trans. Ind. Electron. 2019, 66, 9510–9520. [Google Scholar] [CrossRef]
- Wang, C.; Xin, C.; Xu, Z.; Qin, M.; He, M. Mix-VAEs: A novel multisensor information fusion model for intelligent fault diagnosis. Neurocomputing 2022, 492, 234–244. [Google Scholar] [CrossRef]
- Mejbel, B.G.; Sarow, S.A.; Al-Sharify, M.T.; Al-Haddad, L.A.; Ogaili, A.A.F.; Al-Sharify, Z.T. A Data Fusion Analysis and Random Forest Learning for Enhanced Control and Failure Diagnosis in Rotating Machinery. J. Fail. Anal. Prev. 2024, 24, 2979–2989. [Google Scholar] [CrossRef]
- Huo, Z.; Martinez-Garcia, M.; Zhang, Y.; Shu, L. A Multisensor Information Fusion Method for High-Reliability Fault Diagnosis of Rotating Machinery. IEEE Trans. Instrum. Meas. 2022, 71, 3500421. [Google Scholar] [CrossRef]
- Li, X.; Jiang, H.; Niu, M.; Wang, R. An enhanced selective ensemble deep learning method for rolling bearing fault diagnosis with beetle antennae search algorithm. Mech. Syst. Signal Proc. 2020, 142, 106752. [Google Scholar] [CrossRef]
- Xu, X.; Song, D.; Wang, Z.; Zheng, Z. A novel collaborative bearing fault diagnosis method based on multisignal decision-level dynamically enhanced fusion. IEEE Sens. J. 2024, 24, 34766. [Google Scholar] [CrossRef]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Zhao, X.; Wang, L.; Zhang, Y.; Han, X.; Deveci, M.; Parmar, M. A review of convolutional neural networks in computer vision. Artif. Intell. Rev. 2024, 57, 99. [Google Scholar] [CrossRef]
- Yasin, M.; Sarigül, M.; Avci, M. Logarithmic Learning Differential Convolutional Neural Network. Neural Netw. 2024, 172, 106114. [Google Scholar] [CrossRef]
- Momeny, M.; Latif, A.M.; Sarram, M.A.; Sheikhpour, R.; Zhang, Y. A noise robust convolutional neural network for image classification. Results Eng. 2021, 10, 100225. [Google Scholar] [CrossRef]
- Fox, C.; Roberts, S. A tutorial on variational Bayesian inference. Artif. Intell. Rev. 2012, 38, 85–95. [Google Scholar] [CrossRef]
- Zhang, C.; Bütepage, J.; Kjellström, H.; Mandt, S. Advances in Variational Inference. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 41, 2008–2026. [Google Scholar] [CrossRef]
- Cao, Y.; Jan, N.M.; Huang, B.; Wang, Y.; Pan, Z.; Gui, W. No-delay multimodal process monitoring using Kullback-Leibler divergence-based statistics in probabilistic mixture models. IEEE Trans. Autom. Sci. Eng. 2023, 20, 167–178. [Google Scholar] [CrossRef]
- Lin, H.; Hu, C. Variational inference based distributed noise adaptive Bayesian filter. Signal Process. 2021, 178, 107775. [Google Scholar] [CrossRef]
- Chao, Q.; Gao, H.; Tao, J.; Wang, Y.; Zhou, J.; Liu, C. Adaptive decision-level fusion strategy for the fault diagnosis of axial piston pumps using multiple channels of vibration signals. Sci. China-Technol. Sci. 2022, 65, 470–480. [Google Scholar] [CrossRef]
- Chen, Z.; Li, W. Multisensor feature fusion for bearing fault diagnosis using sparse autoencoder and deep belief network. IEEE Trans. Instrum. Meas. 2017, 66, 1693–1702. [Google Scholar] [CrossRef]
- Ohta, H.; Sugimoto, N. Vibration characteristics of tapered roller bearings. J. Sound Vibr. 1996, 190, 137–147. [Google Scholar] [CrossRef]
- Li, N.; Zhang, J.; Meng, X.; Han, Q.; Zhai, J. Dynamic response and failure analysis of bearing under the impact of vibration excitation. Eng. Fail. Anal. 2023, 154, 107640. [Google Scholar] [CrossRef]
- Zhang, J.; Han, D.; Xie, Z.; Huang, C.; Rao, Z.; Song, M.; Su, Z. Nonlinear behaviors analysis of high-speed rotor system supported by aerostatic bearings. Tribol. Int. 2022, 170, 107111. [Google Scholar] [CrossRef]



| Inner race Diameter | Pitch Circle Diameter | Roller Diameter | Roller Number | Contact Angle (°) |
|---|---|---|---|---|
| 130 mm | 184 mm | 27 mm | 17 | 0 |
| Description | Number of Nodes | Config |
|---|---|---|
| Input layer | 32 × 32 × 1 | - |
| The first convolutional layer | 32 × 32 × 8 | 5@8/Stride(1,1)/Relu |
| The first pooling layer | 8 × 8 × 8 | Stride(4,4) |
| The second convolutional layer | 8 × 8 × 16 | 5@16/Stride(1,1)/Relu |
| The second pooling layer | 2 × 2 × 16 | Stride(2,2) |
| Flatten layer | 64 | - |
| feature extraction layer | 32 | Tahn |
| Output layer | 9 | - |
| Model | Fusion Strategy | Testing Accuracy | |
|---|---|---|---|
| Average Accuracy | Standard Deviations | ||
| CNN | Channel 1 | 94.01% | 1.0925 |
| Channel 2 | 96.78% | 0.9729 | |
| Channel 3 | 93.61% | 2.0020 | |
| VBCNN | Channel 1 | 97.38% | 0.8283 |
| Channel 2 | 97.74% | 0.4630 | |
| Channel 3 | 97.04% | 0.3823 | |
| Proposed method | Channel All | 99.37% | 0.3829 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Xu, X.; Song, D.; Zheng, Z.; Li, W. A Novel Bearing Fault Diagnosis Method Based on Improved Convolutional Neural Network and Multi-Sensor Fusion. Machines 2025, 13, 216. https://doi.org/10.3390/machines13030216
Wang Z, Xu X, Song D, Zheng Z, Li W. A Novel Bearing Fault Diagnosis Method Based on Improved Convolutional Neural Network and Multi-Sensor Fusion. Machines. 2025; 13(3):216. https://doi.org/10.3390/machines13030216
Chicago/Turabian StyleWang, Zhongyao, Xiao Xu, Dongli Song, Zejun Zheng, and Weidong Li. 2025. "A Novel Bearing Fault Diagnosis Method Based on Improved Convolutional Neural Network and Multi-Sensor Fusion" Machines 13, no. 3: 216. https://doi.org/10.3390/machines13030216
APA StyleWang, Z., Xu, X., Song, D., Zheng, Z., & Li, W. (2025). A Novel Bearing Fault Diagnosis Method Based on Improved Convolutional Neural Network and Multi-Sensor Fusion. Machines, 13(3), 216. https://doi.org/10.3390/machines13030216






