Unraveling the Vibration Mechanism in Robotic Harmonic Drive: Coupled Dynamics Under Cyclic Inertial Loading and Installation Errors
Abstract
1. Introduction
- The system is equated as a combination of primary components, among which the contact mechanism and interaction force are modeled to establish the system dynamic model. This model characterizes the coupled vibration response of the entire harmonic drive, enabling comprehensive dynamic performance analysis.
- Installation errors and cyclic inertial loading are considered in the proposed model, allowing the model to capture key vibration responses observed in field applications.
- The sideband distribution of the harmonic drive has been revealed through simulation analysis and compared with experiment signals. The results have verified the fidelity of the proposed dynamic harmonic drive model and experimental measurements.
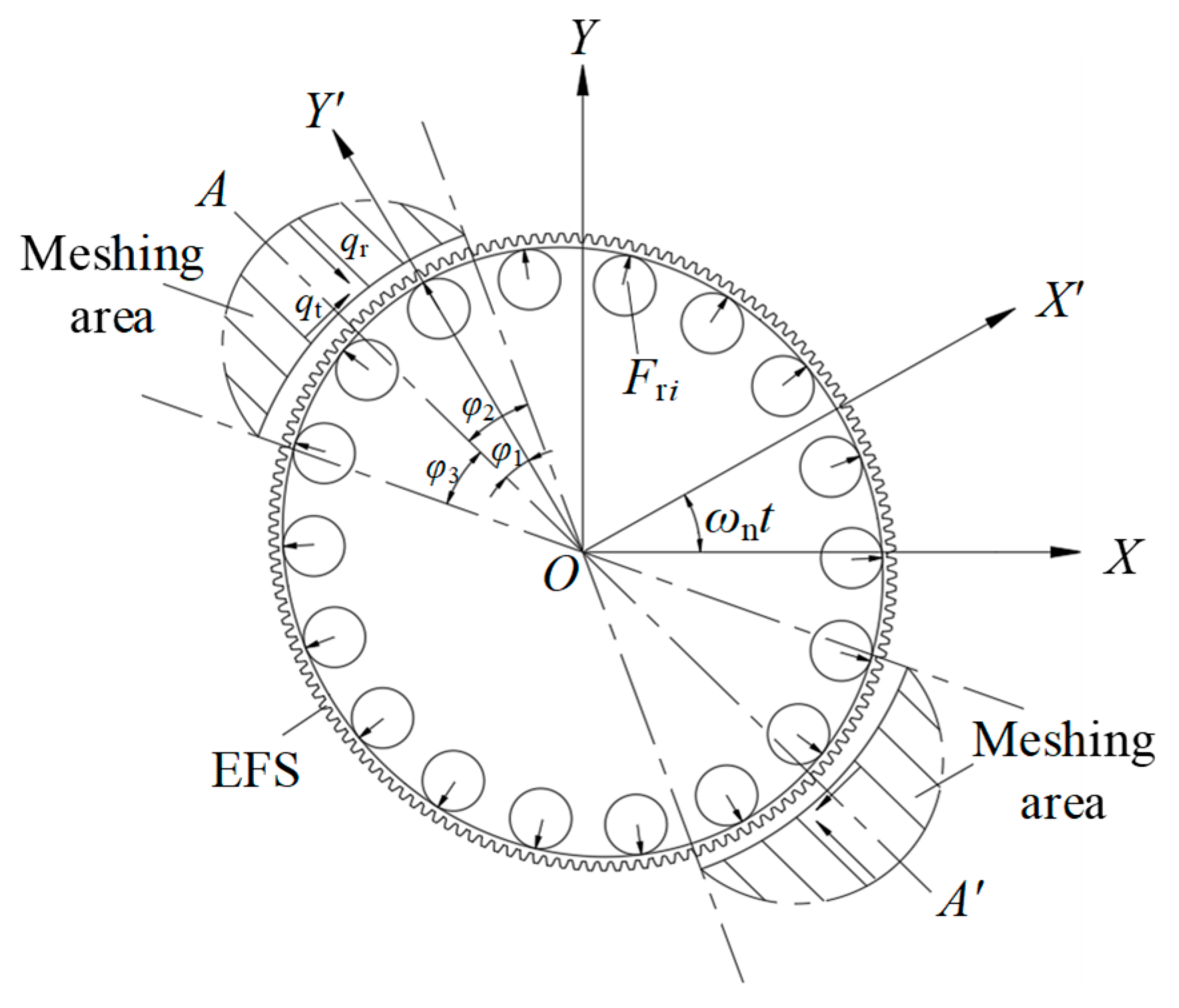
2. Framework of the Novel Harmonic Drive Model
2.1. Kinematic Relation
2.2. Equivalence of the Harmonic Drive
3. Contact Mechanics Modeling
3.1. Model of Meshing Force
3.1.1. Derivation of Continuously Distributed Meshing Force
3.1.2. Composition of Discretely Distributed Meshing Forces
3.1.3. Equivalent Meshing Stiffness Between EFS and CS
3.2. Model of Roller Contact Forces
3.2.1. Contact Force Derivation of One Roller
3.2.2. Contact Force Composition of Rollers
3.2.3. Equivalent Stiffness of Roller Contact Between EFS and EC
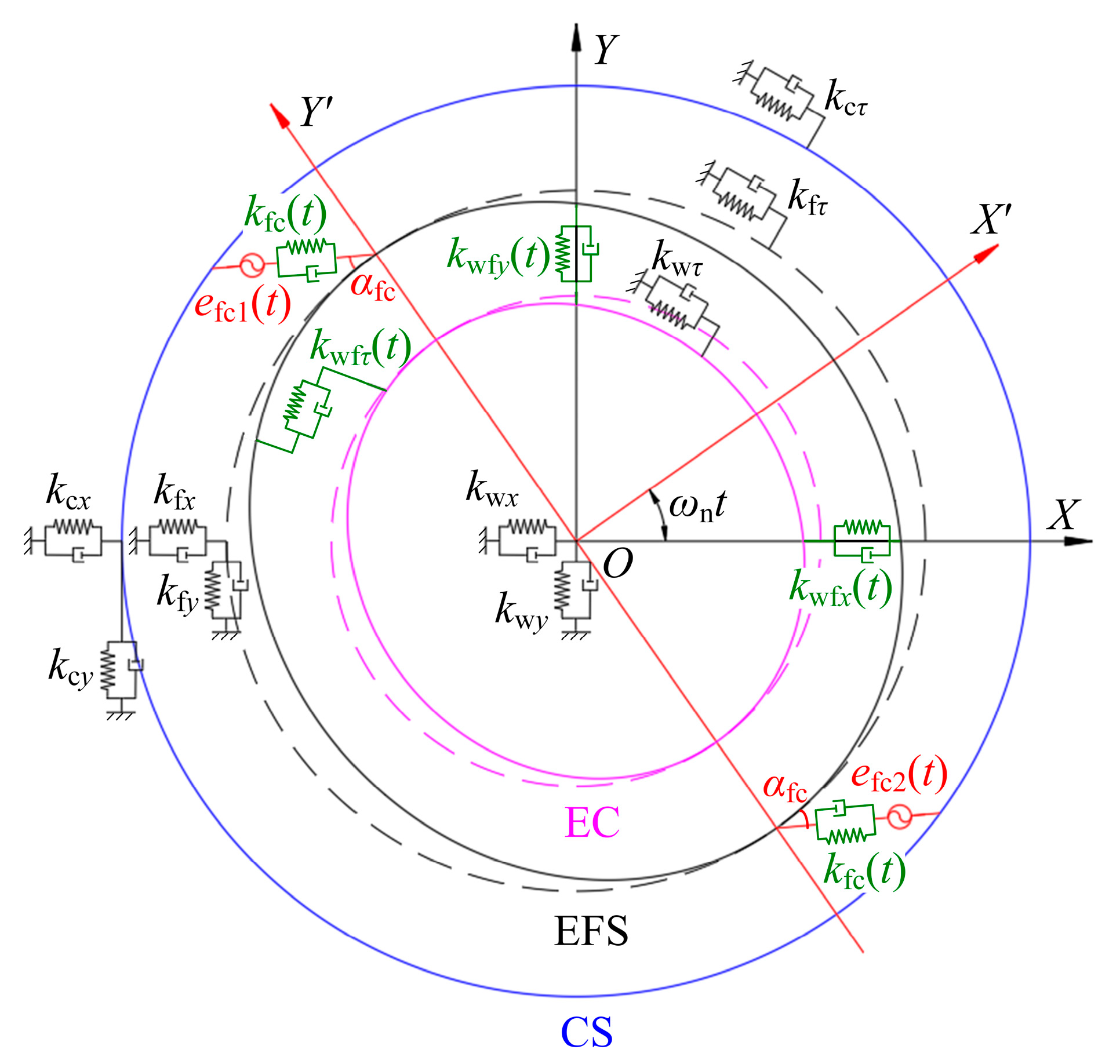
4. Dynamic Model of the Harmonic Drive
4.1. Excitation Analysis on Installation Errors
- (1)
- Case 1: installation error induced by eccentric EFS
- (2)
- Case 2: installation error induced by eccentric CS
4.2. Dynamics Differential Equation
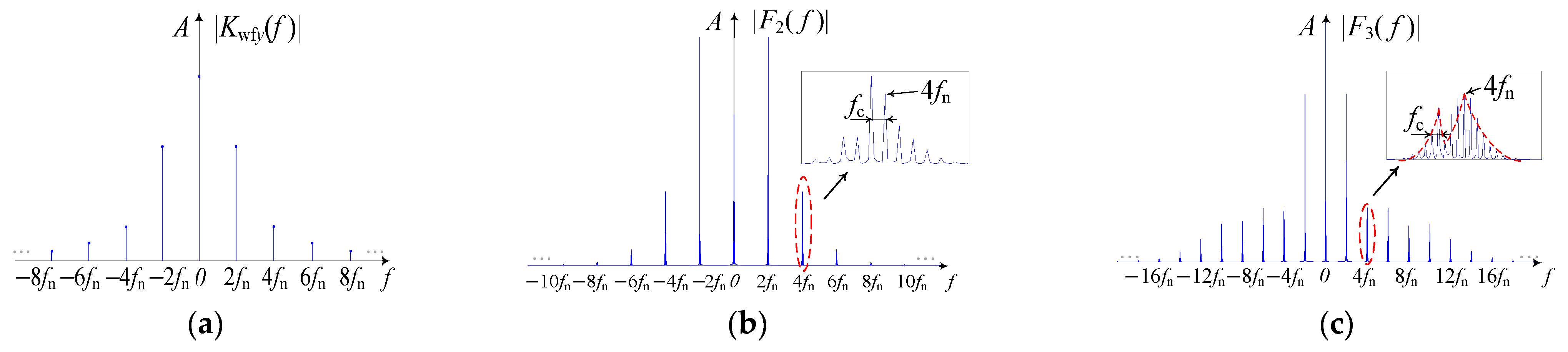
4.3. Characteristics of Vibration Response
4.3.1. Cyclic Load and Eccentricity Excitation
4.3.2. Feedback Excitation
5. Simulation
5.1. Parameter Settings of the Proposed Dynamic Model
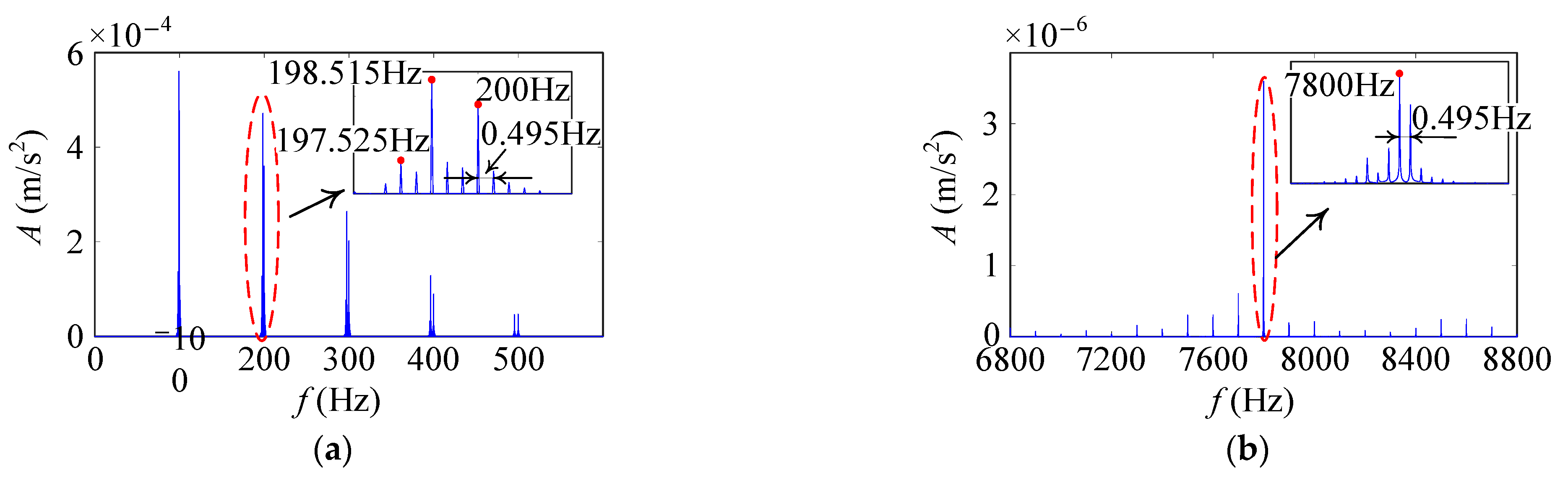
5.2. Result Analysis
- (i)
- the carrier frequencies of nfn, nfn − (n − 1)fc and nfn − (n + 1)fc;
- (ii)
- the modulation frequencies of integer multiple orders of fc.
6. Experiment
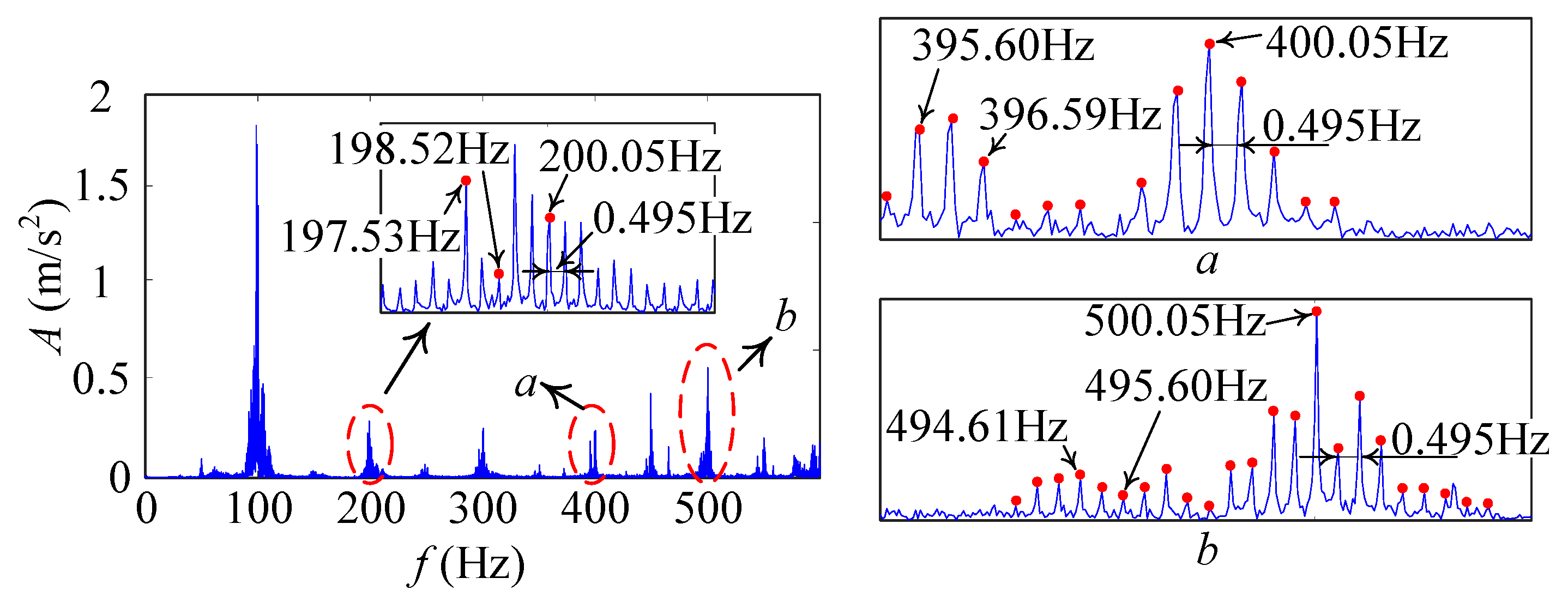
6.1. Vibration Signal Analysis
- (1)
- Vibration response in Exp. 1
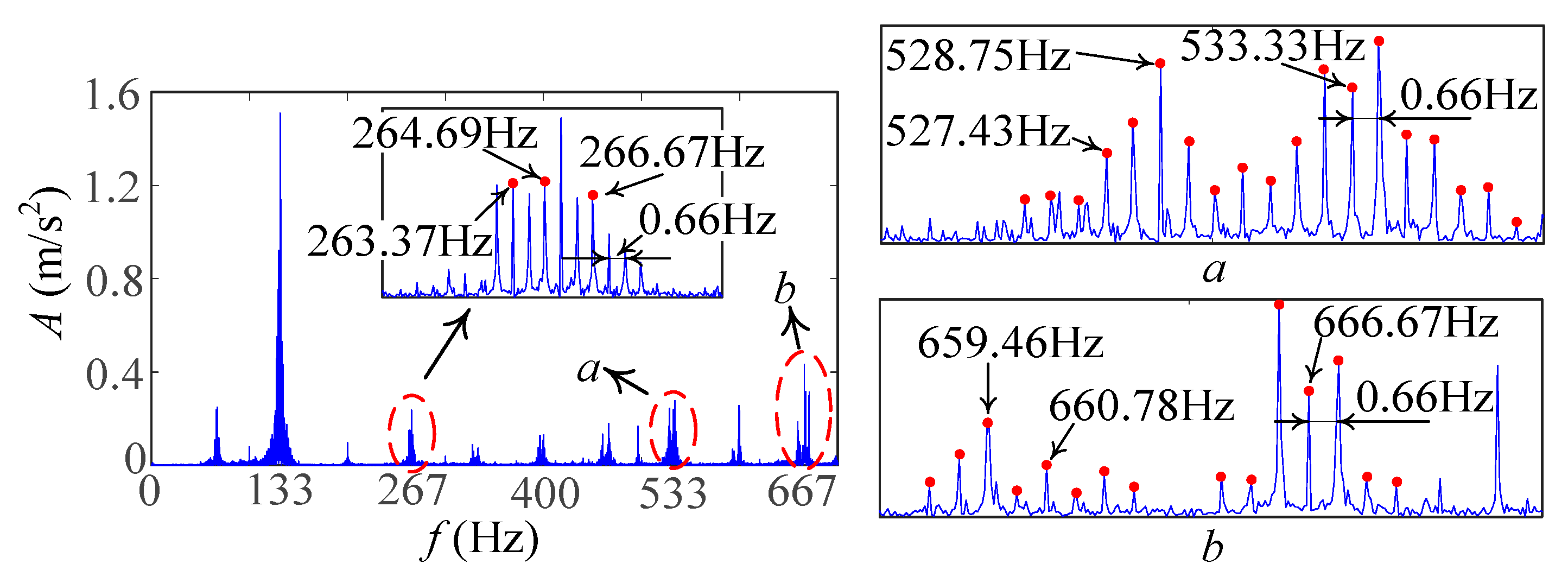
- (2)
- Vibration response in Exp. 2
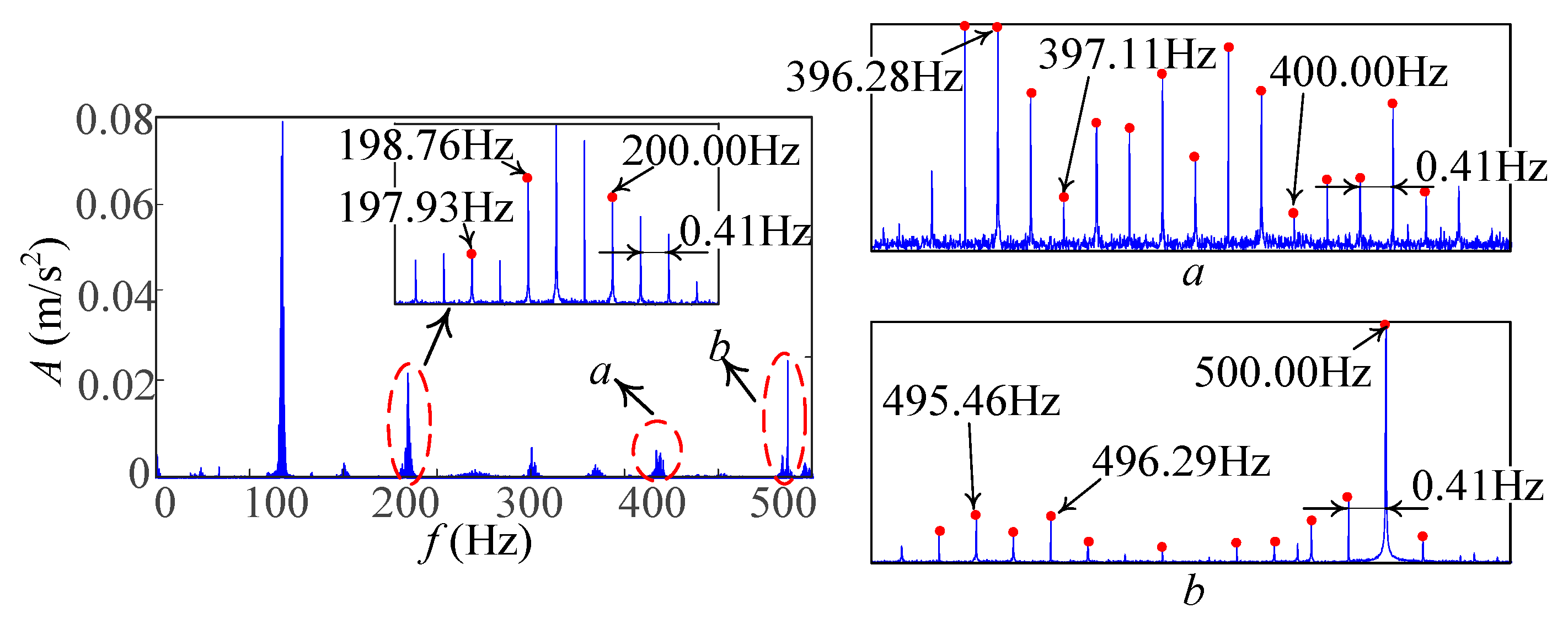
- (3)
- Vibration responses in Exp. 3 and Exp. 4
6.2. Discussion
7. Conclusions
- (1)
- There is little meshing component in the vibration response of the harmonic drive. The reason is that many teeth participate in the meshing process, and the meshing stiffness changes little as the tooth alternates.
- (2)
- Under time-varying load, the vibration response contains the carrier frequency located at nfn, nfn − (n − 1)fc, and nfn − (n + 1)fc, as well as the modulation frequency of multiple output frequencies.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| FS | flexspline |
| WG | wave generator |
| CS | circular spline |
| DoF | degrees of freedom |
| EC | equivalent cam |
| EFS | equivalent flexspline |
Nomenclature
| ωn | Angular velocity of the wave generator (WG). |
| nf, nc | Tooth numbers of the flexspline (FS) and circular spline (CS). |
| a, b | Half-lengths of the major and minor axes of the flexspline ellipse. |
| R | Radius of the undeformed equivalent flexspline (EFS). |
| OXY | Absolute coordinate system fixed to the ground. |
| OX’Y’ | Rotating coordinate system whose Y’-axis coincides with the major axis of the equivalent cam (EC). |
| θi, ϕi | Angular positions of the i-th roller or tooth in the coordinate system. |
| hi | Slope of the tangent at the i-th contact point on the EFS. |
| xp, yp, θp | Translational and rotational displacements of component p (p = w, f, c: EC, EFS, CS). |
| rwf, rfc | Effective radii of roller contact and meshing contact. |
| α | Pressure angle of the tooth profile. |
| qt, qr, qz | Tangential, radial, and normal components of distributed meshing force. |
| qt,max | Maximum tangential component of distributed meshing force. |
| fi | Meshing force acting on the i-th tooth. |
| Fx1, Fy1 | Equivalent force components along the X’- and Y’-axes. |
| M1 | Equivalent torque generated by discretely distributed meshing forces. |
| Fri(t) | Radial contact force on the i-th roller between the EFS and EC. |
| Fμi(t) | Tangential friction force on the i-th roller. |
| Fx(t), Fy(t), M(t) | Resultant forces and torque obtained by superimposing all roller forces. |
| ∆ρi(t) | Radial deformation of the EFS at the i-th roller. |
| Average deformation of the circumferential points of the EFS. | |
| μ | Friction coefficient between the roller and the EFS. |
| kf | Elastic stiffness of the EFS material. |
| kfc(t) | Time-varying meshing stiffness between EFS and CS. |
| kwfx(t), kwfy(t), kwfτ(t) | Equivalent stiffnesses of the roller contact between EFS and EC in X, Y, and torsional directions. |
| kpl | Support stiffness of component p (p = w, f, c) in direction l (l = x, y, τ). |
| cpl | Damping coefficient of the support damper for component p in direction l. |
| δpl | Displacement along the direction of the equivalent meshing stiffness. |
| km, ψm | Fourier coefficient and phase of the m-th harmonic of meshing stiffness. |
| kln, ψl | Fourier coefficient and phase of the n-th harmonic for stiffness kwfl(t) (l = x, y, τ). |
| mp | Mass of component p (p = w, f, c). |
| Ip | Rotational inertia of component p (p = w, f, c) about the Z-axis. |
| fn | Input frequency of the wave generator (rotation frequency). |
| fc | Output frequency of the circular spline. |
| fs | Sampling frequency of the experimental data acquisition system. |
| T(t) | Time-varying transmitted torque or cyclic inertial load. |
| e(t) | Installation error or eccentric displacement along the meshing direction. |
| efc1(t), efc2(t) | Periodic installation errors on both ends of the major axis. |
| efn, ecn | Fourier coefficients of installation error harmonics. |
| ϕn | Phase angles of the n-th harmonic in Fourier series expansions. |
| Kfc(f) | Frequency-domain expression of time-varying meshing stiffness. |
| Kfc(f), E(f) | Fourier transforms of excitation displacement and installation error. |
| F1(f), F2(f), F3(f) | Frequency spectra of cyclic load, nonlinear feedback, and overall excitation. |
| rwf | Effective radius of roller contact. |
| bR | Tooth width of the circular spline. |
| dg | Pitch diameter of the circular spline. |
References
- Wang, J.; Wan, Z.; Dong, Z.; Li, Z. Research on Performance Test System of Space Harmonic Reducer in High Vacuum and Low Temperature Environment. Machines 2020, 9, 1. [Google Scholar] [CrossRef]
- Li, F.; Li, X.; Guo, Y.; Shang, D. Analysis of Contact Mechanical Characteristics of Flexible Parts in Harmonic Gear Reducer. Shock. Vib. 2021, 2021, 5521320. [Google Scholar] [CrossRef]
- Mongia, C.; Goyal, D.; Sehgal, S. Vibration Response-Based Condition Monitoring and Fault Diagnosis of Rotary Machinery. Mater. Today Proc. 2022, 50, 679–683. [Google Scholar] [CrossRef]
- Jia, H.; Li, J.; Xiang, G.; Wang, J.; Xiao, K.; Han, Y. Modeling and Analysis of Pure Kinematic Error in Harmonic Drive. Mech. Mach. Theory 2021, 155, 104122. [Google Scholar] [CrossRef]
- Understanding and Modeling the Behavior of a Harmonic Drive Gear Transmission. Available online: https://dspace.mit.edu/handle/1721.1/6803 (accessed on 2 January 2025).
- Li, X.; Song, C.; Zhu, C.; Song, H. Load Analysis of Thin-Walled Flexible Bearing in Harmonic Reducer Considering Assembly with Flexspline and Cam. Mech. Mach. Theory 2023, 180, 105154. [Google Scholar] [CrossRef]
- Trang, T.; Pham, T.; Hu, Y.; Li, W.; Lin, S. A Quick Stress Calculation Method for Flexspline in Harmonic Actuators Based on the Finite Element Method. Cogent Eng. 2022, 9, 2138123. [Google Scholar] [CrossRef]
- Hu, Q.; Li, H.; Wang, G.; Li, L. Research on Torsional Stiffness of Flexspline-Flexible Bearing Contact Pair in Harmonic Drive Based on Macro-Micro Scale Modeling. Front. Mater. 2023, 10, 1211019. [Google Scholar] [CrossRef]
- Li, R.; Zhou, G.; Li, D. Structural Design of Flexible Wheel of Harmonic Reducer Based on Efficiency Improvement. Mech. Syst. Signal Process. 2023, 201, 110677. [Google Scholar] [CrossRef]
- Ghorbel, F.H.; Gandhi, P.S.; Alpeter, F. On the Kinematic Error in Harmonic Drive Gears. J. Mech. Des. 2001, 123, 90–97. [Google Scholar] [CrossRef]
- Xiong, Y.; Zhu, Y.; Yan, K. Load Analysis of Flexible Ball Bearing in a Harmonic Reducer. J. Mech. Des. 2020, 142, 022302. [Google Scholar] [CrossRef]
- Yague-Spaude, E.; Gonzalez-Perez, I.; Fuentes-Aznar, A. Stress Analysis of Strain Wave Gear Drives with Four Different Geometries of Wave Generator. Meccanica 2020, 55, 2285–2304. [Google Scholar] [CrossRef]
- Song, C.; Li, X.; Yang, Y.; Sun, J. Parameter Design of Double-Circular-Arc Tooth Profile and Its Influence on Meshing Characteristics of Harmonic Drive. Mech. Mach. Theory 2022, 167, 104567. [Google Scholar] [CrossRef]
- Ma, J.; Li, C.; Luo, Y.; Cui, L. Simulation of Meshing Characteristics of Harmonic Reducer and Experimental Verification. Adv. Mech. Eng. 2018, 10, 1687814018767494. [Google Scholar] [CrossRef]
- Zhang, Y.; Pan, X.; Li, Y.; Wang, G.; Wu, G. Meshing Stiffness Calculation of Disposable Harmonic Drive under Full Load. Machines 2022, 10, 271. [Google Scholar] [CrossRef]
- Tang, T.; Li, J.; Wang, J.; Xiao, K.; Han, Y. Double-Circular-Arc Tooth Profile Design and Parametric Analysis on the Comprehensive Performance of the Harmonic Drive. Proc. Inst. Mech. Eng. Part. J. J. Eng. Tribol. 2022, 236, 480–498. [Google Scholar] [CrossRef]
- Raviola, A.; De Martin, A.; Guida, R.; Jacazio, G.; Mauro, S.; Sorli, M. Harmonic Drive Gear Failures in Industrial Robots Applications: An Overview. PHM Soc. Eur. Conf. 2021, 6, 11. [Google Scholar] [CrossRef]
- Zhao, J.; Yan, S. Coupling Vibration Analysis for Harmonic Drive in Joint and Flexible Arm Undergoing Large Range Motion. In Proceedings of the 2016 International Symposium on Flexible Automation (ISFA), Cleveland, OH, USA, 1–3 August 2016; IEEE: Cleveland, OH, USA; pp. 442–449. [Google Scholar]
- Masoumi, M.; Alimohammadi, H. An Investigation into the Vibration of Harmonic Drive Systems. Front. Mech. Eng. 2013, 8, 409–419. [Google Scholar] [CrossRef]
- Hu, R.; Zhou, G.; Li, J. A Nonlinear Torsional Vibration Model of Harmonic Gear Reducer and the Effect of Various Factors on Torsional Vibration during Start and Stop. J. Vib. Control 2022, 28, 1536–1549. [Google Scholar] [CrossRef]
- Zhao, X.Z.; Guo, Y.Y.; Li, Z.; Ye, B.Y.; Chen, T.J. Injury Characteristic Frequency Analysis of Flexible Thin-Wall Bearing. J. Vib. Eng. 2020, 33, 1313–1323. [Google Scholar]
- Zhang, X.; Tao, T.; Jiang, G.; Mei, X.; Zou, C. A Refined Dynamic Model of Harmonic Drive and Its Dynamic Response Analysis. Shock. Vib. 2020, 2020, 1841724. [Google Scholar] [CrossRef]
- Yang, X.; Qiang, D.; Chen, Z.; Wang, H.; Zhou, Z.; Zhang, X. Dynamic Modeling and Digital Twin of a Harmonic Drive Based Collaborative Robot Joint. In Proceedings of the 2022 International Conference on Robotics and Automation (ICRA), Philadelphia, PA, USA, 23 May 2022; IEEE: Philadelphia, PA, USA; pp. 4862–4868. [Google Scholar]
- Gu, J.; Tong, T.; Huang, D.; Li, M. Study on Torsional Vibration of a Harmonic Driver Based on Time-Varying Stiffness Caused by Manufacturing Error. J. Vibroengineering 2021, 23, 619–631. [Google Scholar] [CrossRef]
- Shi, J.F.; Han, C.; Chen, L.X.; Jin, W.Y. Investigating Wear-Induced Health-Instability Dynamics in Spur Gear Systems with Installation Error. Nonlinear Dyn. 2025, 113, 22701–22722. [Google Scholar] [CrossRef]
- Ivanov, M.N. The Harmonic Drive; National Defense Industry Press: Beijing, China, 1987. [Google Scholar]
- Zhang, X.; Zhang, C.; Wang, P.; Yang, F.; Peng, C. Stiffness Reliability Analysis of Harmonic Drive Considering Contact Pairs Wear. Eng. Comput. 2024, 41, 1327–1352. [Google Scholar] [CrossRef]
- Li, Y.; Ding, K.; He, G.; Lin, H. Vibration Mechanisms of Spur Gear Pair in Healthy and Fault States. Mech. Syst. Signal Process. 2016, 81, 183–201. [Google Scholar] [CrossRef]








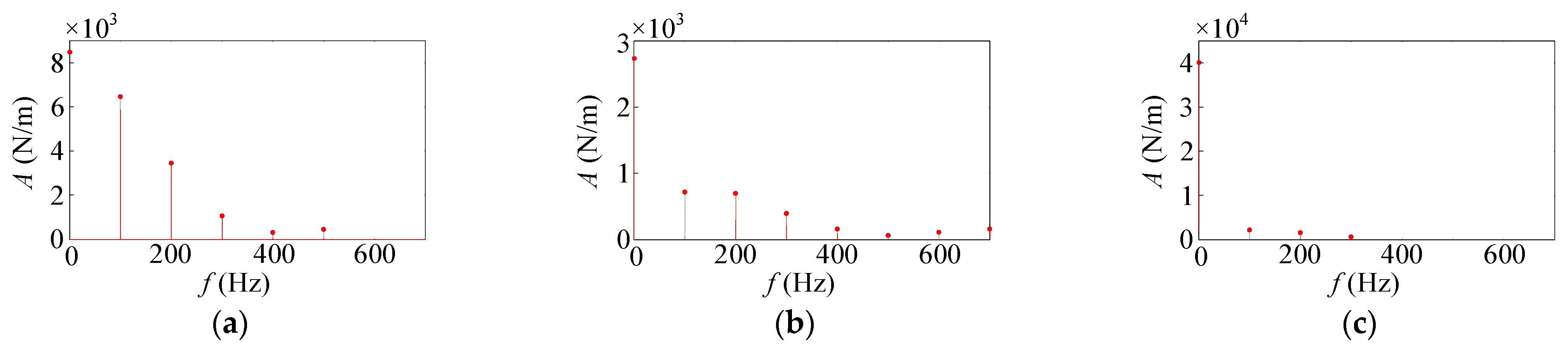






| Component | Mass (kg) | Rotational Inertia About the z-Axis (kg·m2) |
|---|---|---|
| Cam | 0.601 | 6.695 × 10−4 |
| FS | 0.416 | 9.189 × 10−4 |
| CS | 0.735 | 4.000 × 10−3 |
| Order | Coefficient | Order | Coefficient | Order | Coefficient |
|---|---|---|---|---|---|
| 0 | 1.000 × 10−4 | 4 | 6.250 × 10−7 | 8 | 3.910 × 10−8 |
| 1 | 5.000 × 10−6 | 5 | 3.125 × 10−7 | 9 | 1.950 × 10−8 |
| 2 | 2.500 × 10−6 | 6 | 1.563 × 10−7 | 10 | 9.800 × 10−9 |
| Component | kpx (N/m) | kpy (N/m) | kpt (N/m) |
|---|---|---|---|
| EC (p = w) | 9.971 × 108 | 9.971 × 108 | 6.130 × 104 |
| EFS (p = f) | 1.000 × 109 | 1.000 × 109 | 1.700 × 107 |
| CS (p = c) | 1.084 × 109 | 1.084 × 109 | 1.500 × 108 |
| Component | cpx (N·s/m) | cpy (N·s/m) | cpt (N·s/m) |
|---|---|---|---|
| EC (p = w) | 101 | 101 | 5.233 |
| EFS (p = f) | 90 | 90 | 8.0 |
| CS (p = c) | 75 | 75 | 0.9 |
| Exp. 1 * | Exp. 2 | Exp. 3 | Exp. 4 | |
|---|---|---|---|---|
| Input speed (rpm) | 3000 | 4000 | 3000 | 3000 |
| Transmission ratio | 101:1 | 101:1 | 51:1 | 121:1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, G.; Zhou, B.; Zheng, Y.; Lin, H.; Xu, L.; Zheng, Z. Unraveling the Vibration Mechanism in Robotic Harmonic Drive: Coupled Dynamics Under Cyclic Inertial Loading and Installation Errors. Machines 2025, 13, 1083. https://doi.org/10.3390/machines13121083
He G, Zhou B, Zheng Y, Lin H, Xu L, Zheng Z. Unraveling the Vibration Mechanism in Robotic Harmonic Drive: Coupled Dynamics Under Cyclic Inertial Loading and Installation Errors. Machines. 2025; 13(12):1083. https://doi.org/10.3390/machines13121083
Chicago/Turabian StyleHe, Guolin, Bin Zhou, Yuan Zheng, Huibin Lin, Lei Xu, and Ziheng Zheng. 2025. "Unraveling the Vibration Mechanism in Robotic Harmonic Drive: Coupled Dynamics Under Cyclic Inertial Loading and Installation Errors" Machines 13, no. 12: 1083. https://doi.org/10.3390/machines13121083
APA StyleHe, G., Zhou, B., Zheng, Y., Lin, H., Xu, L., & Zheng, Z. (2025). Unraveling the Vibration Mechanism in Robotic Harmonic Drive: Coupled Dynamics Under Cyclic Inertial Loading and Installation Errors. Machines, 13(12), 1083. https://doi.org/10.3390/machines13121083





