Research on Vibration-Damping and Deflection Correction of BTA Deep Hole Drilling Tool Systems Based on Dynamic Pressure Lubrication and Squeeze Film Theory
Abstract
1. Introduction
2. Theory of Vibration-Damping and Deviation Correction for BTA Deep Hole Drilling Tool Systems
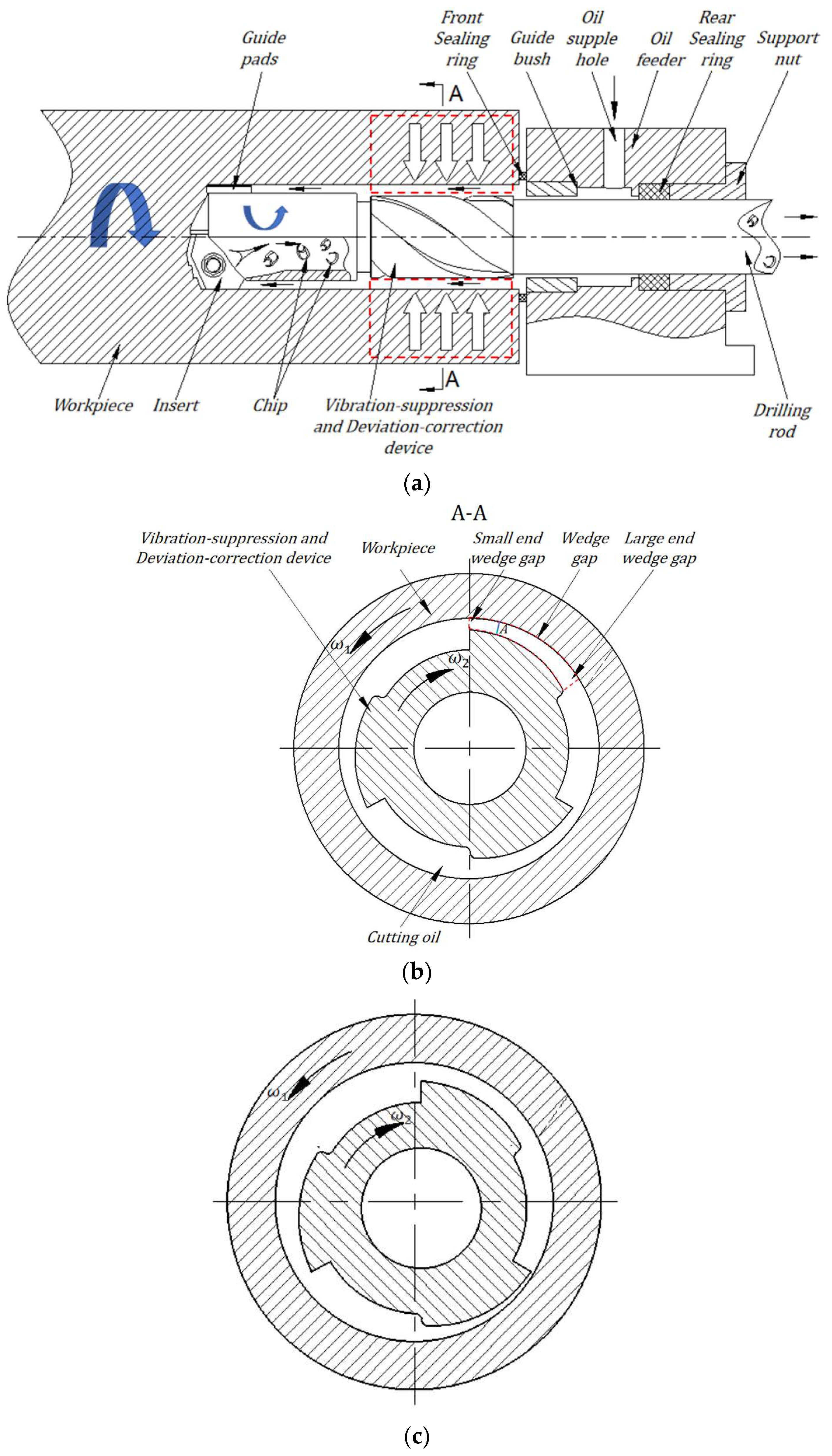
2.1. Vibration-Damping and Deviation Correction Mechanism
2.2. Theoretical Analysis of Oil Film Pressure Distribution in Devices
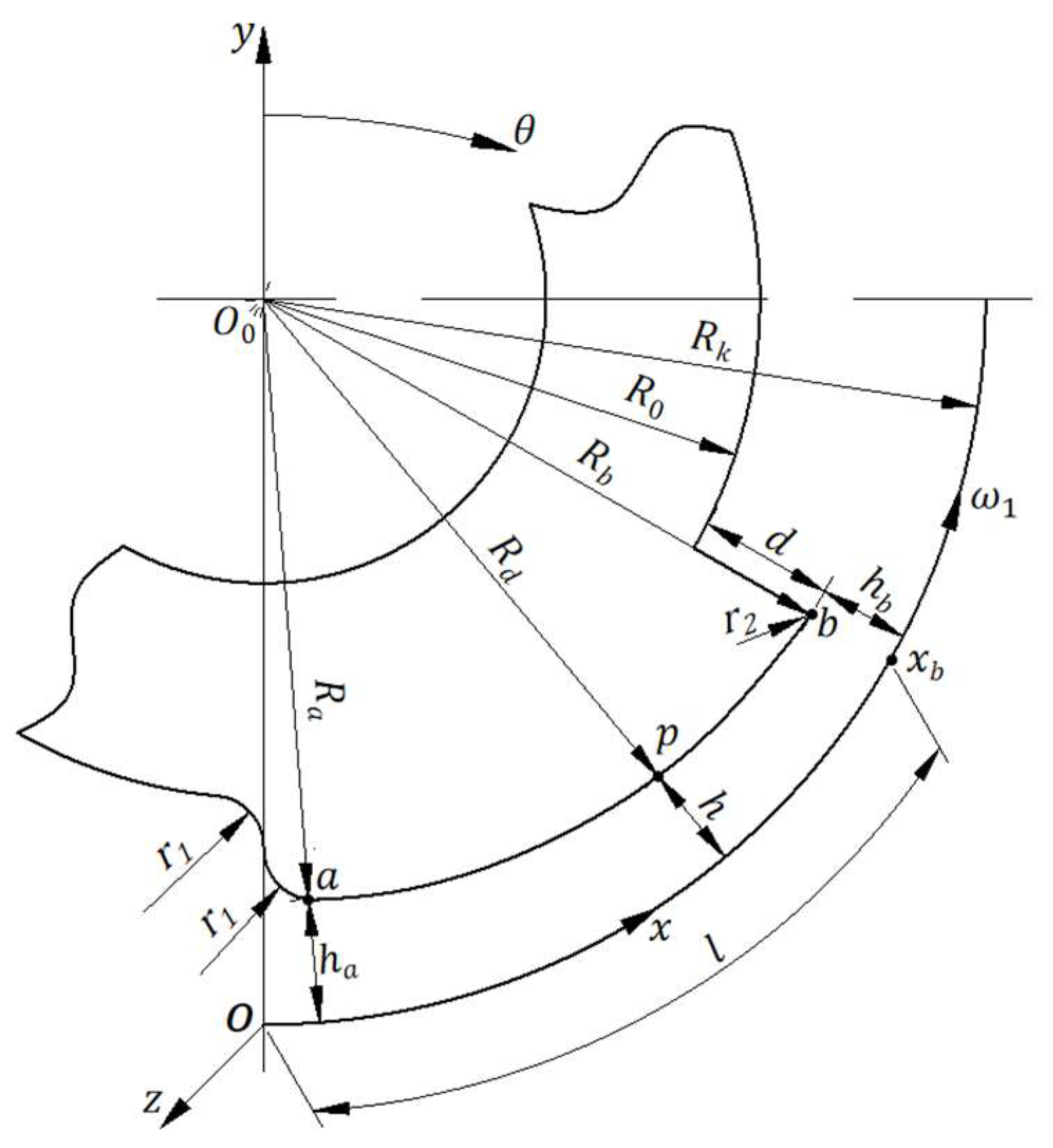
2.2.1. Thickness of the Wedge-Shaped Oil Film in the Device
2.2.2. Analysis and Calculation of Pressure Distribution Within Wedge-Shaped Oil Film for Device
2.3. Key Dimension Design for Vibration-Damping and Deflection Correction Device in Deep Hole Drilling
2.3.1. Helix Angle
2.3.2. Minimum Oil Film Thickness
2.3.3. Film Thickness Ratio
2.3.4. Oil Passage Groove
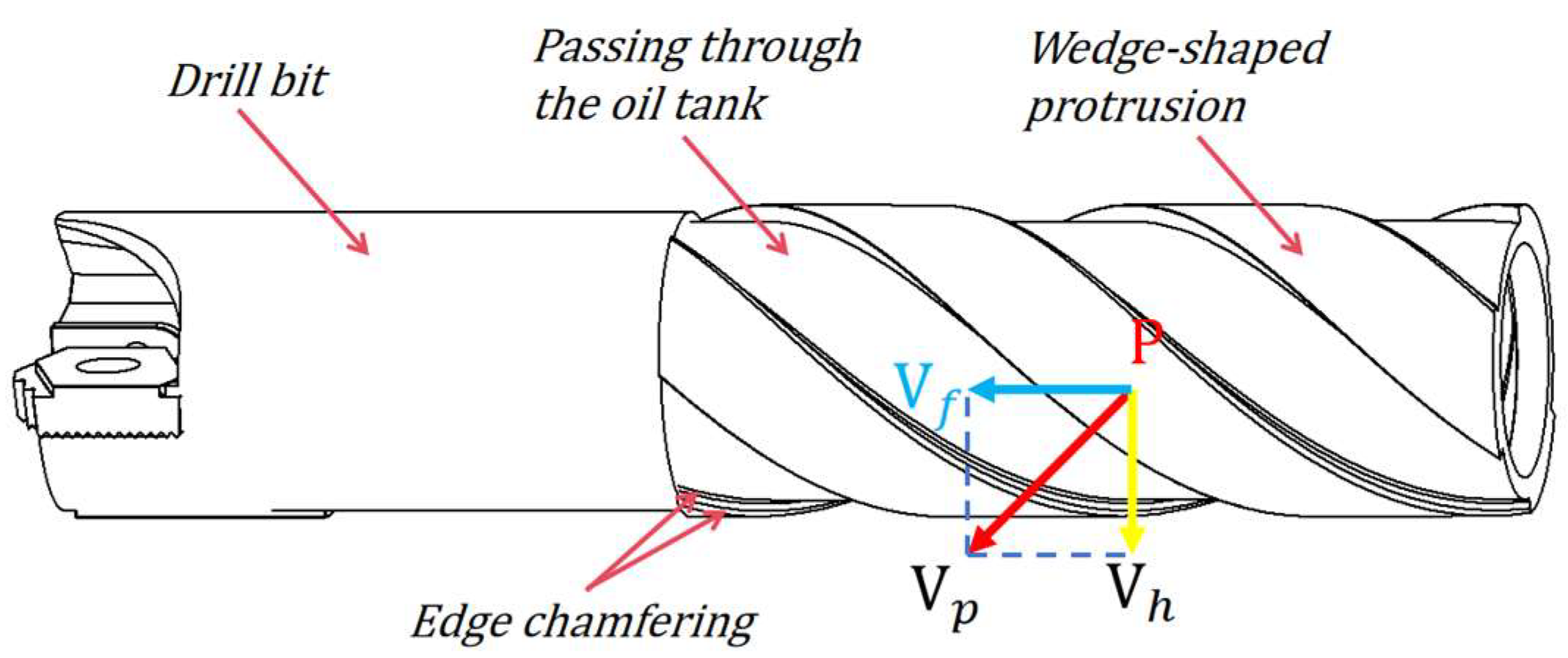
2.3.5. Edge Chamfering
2.3.6. Aspect Ratio
3. Experimental Analysis
3.1. Laboratory Bench Design and Construction
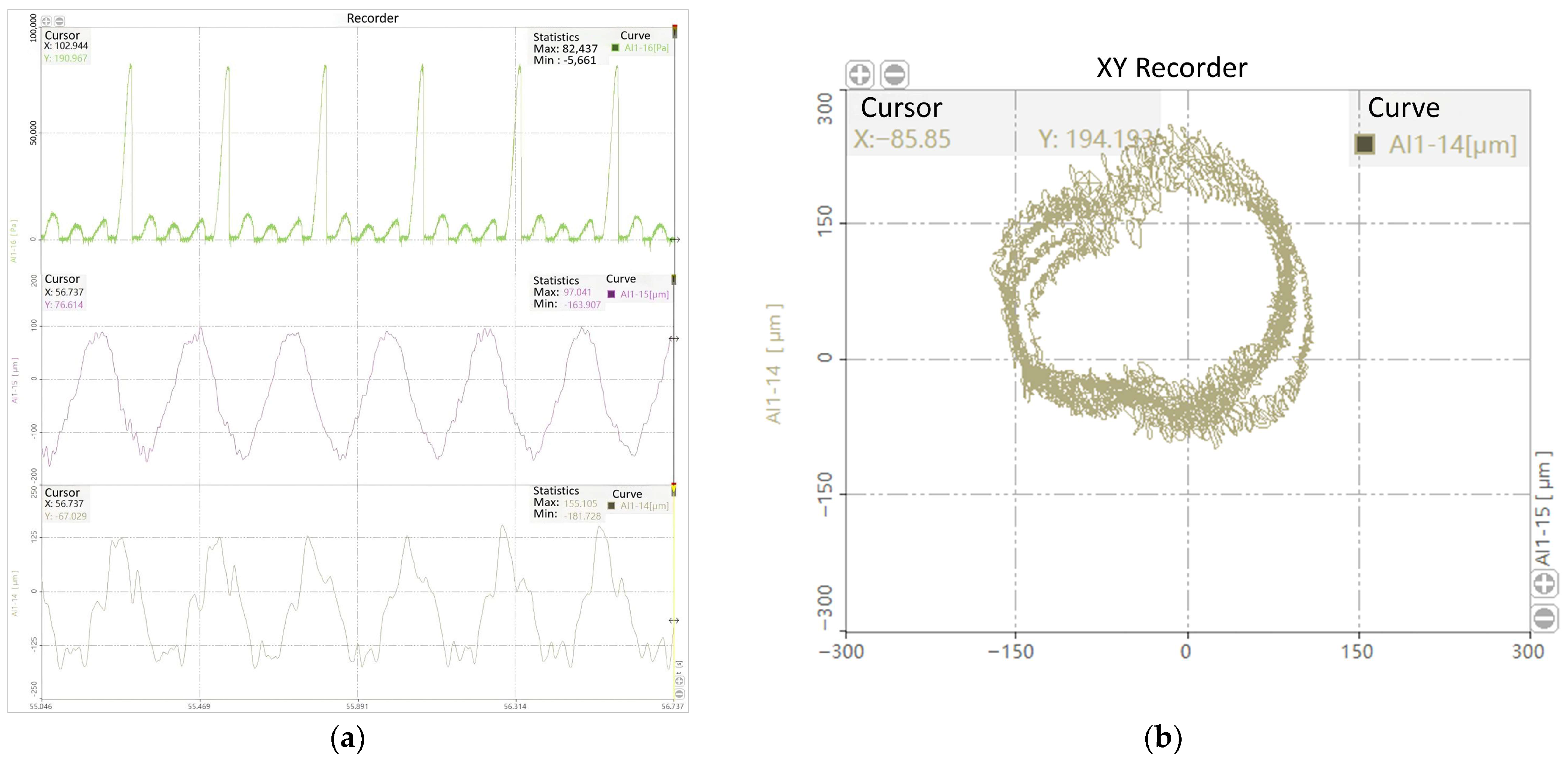
3.2. Measurement and Analysis of Oil Film Pressure Distribution and Stability
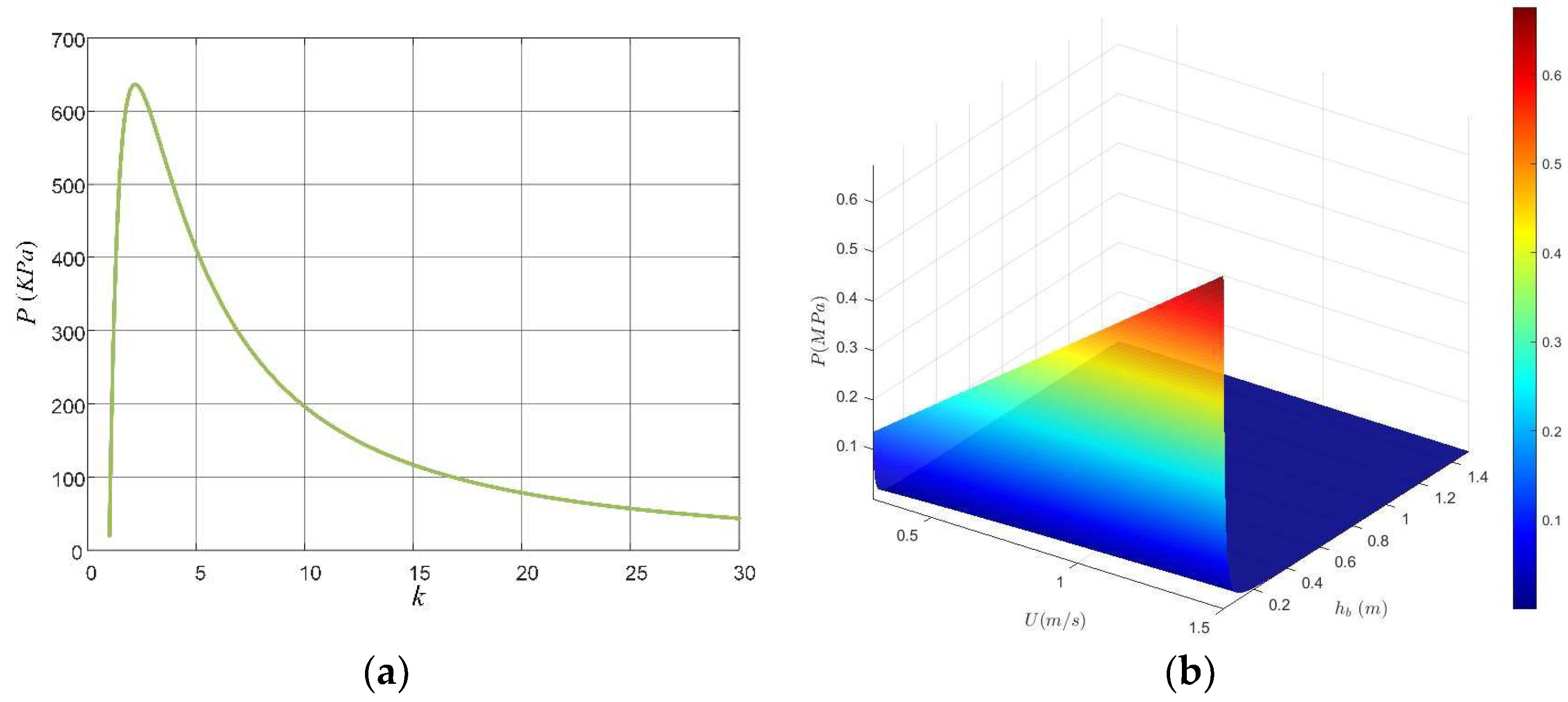
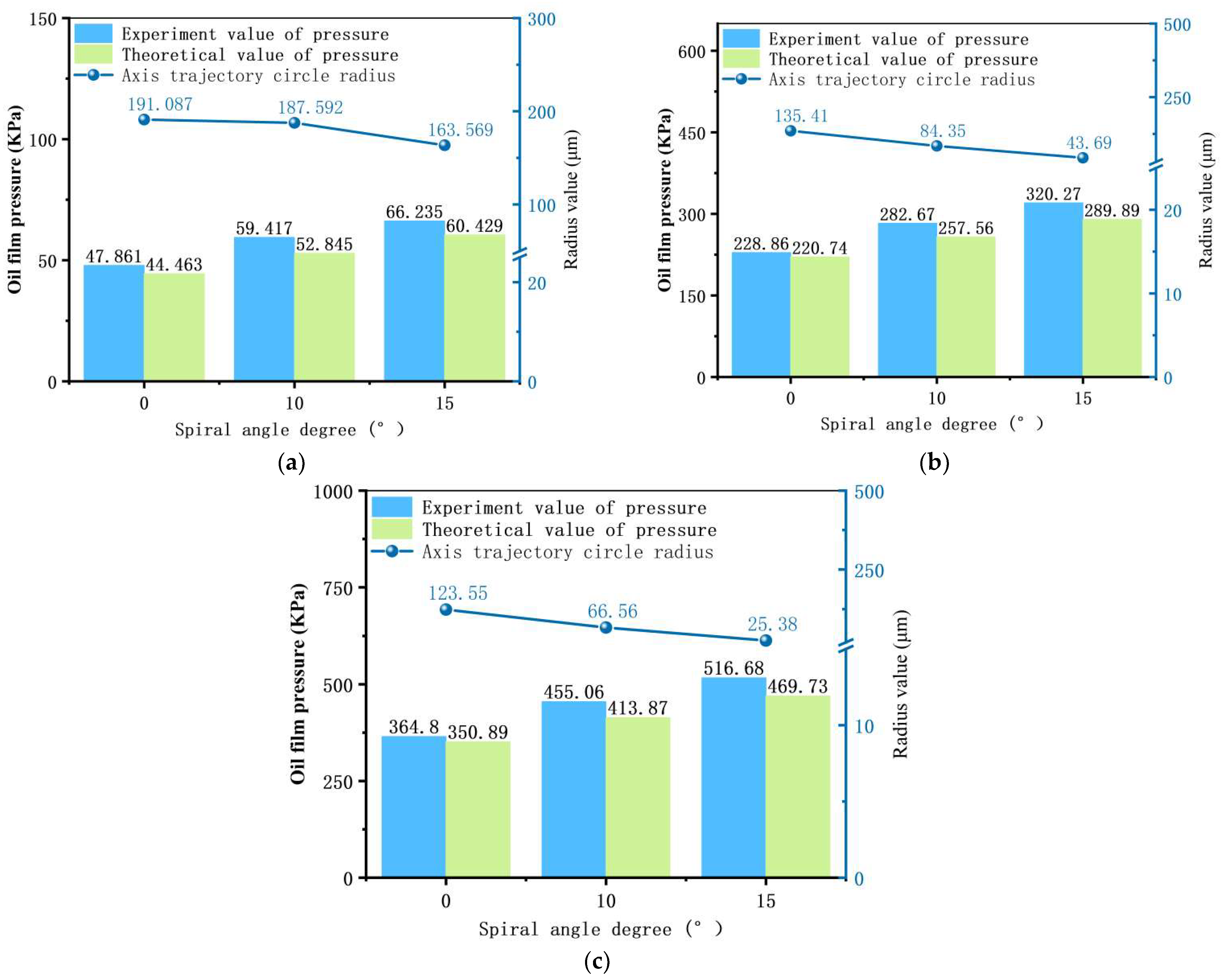
3.2.1. The Influence of Structure on the Distribution and Stability of Oil Film Pressure in the Device
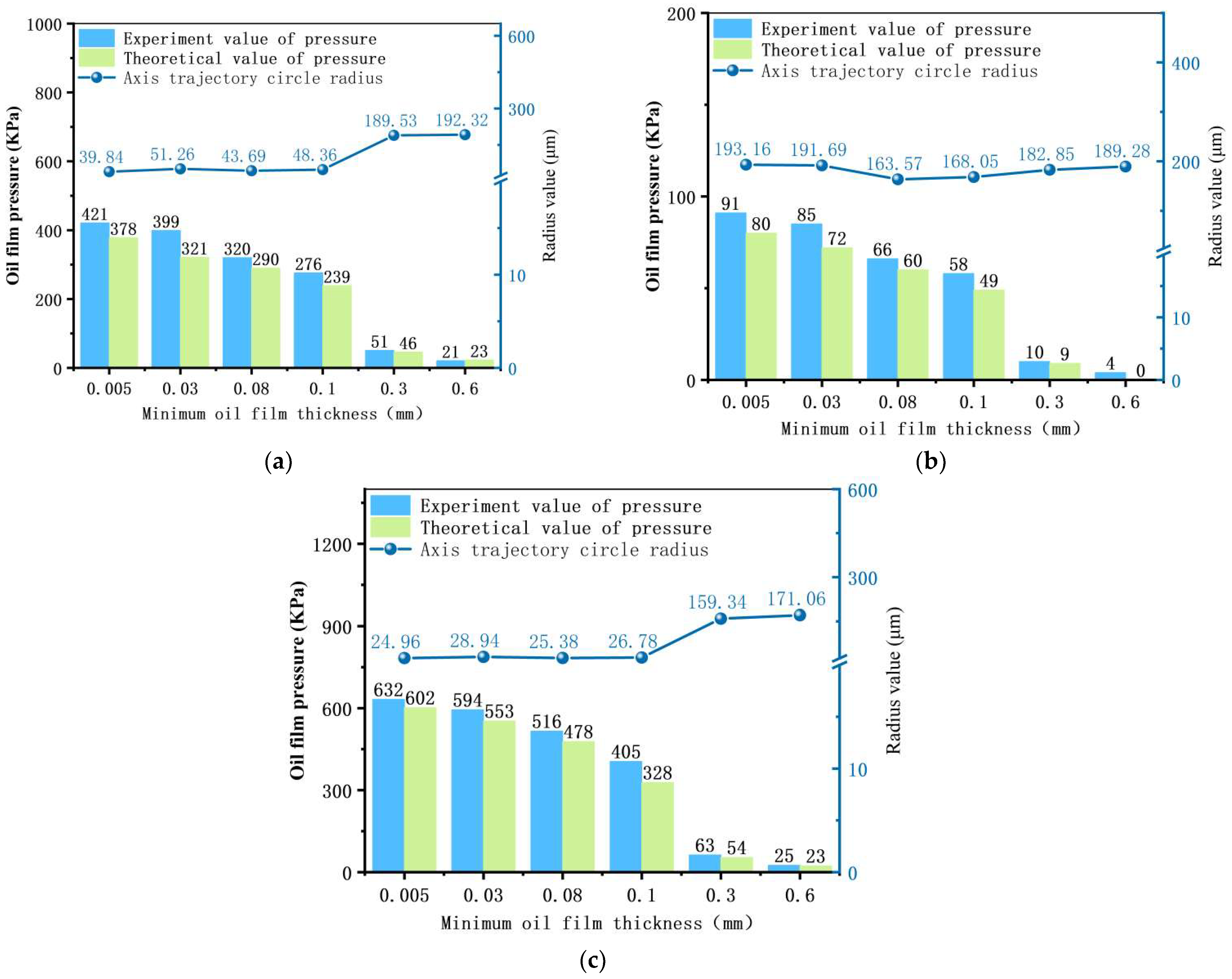
3.2.2. The Effect of Minimum Oil Film Thickness on the Oil Film Pressure Distribution and Stability of the Equipment
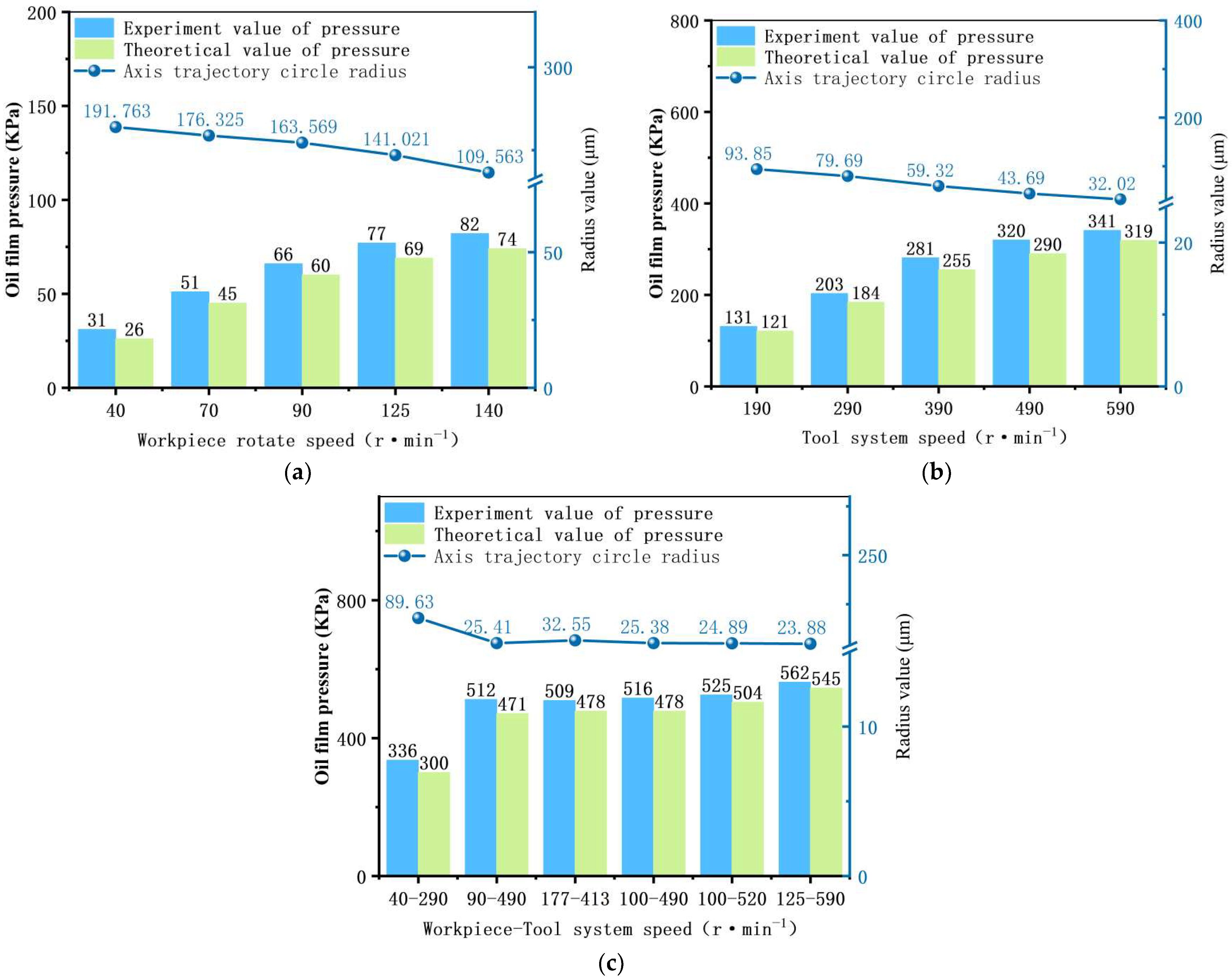
3.2.3. Effect of Rotational Speed on Oil Film Pressure Distribution and Stability in the Device
- (1)
- Tool system stationary; workpiece rotation at 40 , 70 , 90 , 125 , and 140
- (2)
- Workpiece stationary; tool system rotation at 190 , 290 , 390 , 490 , and 590
- (3)
- Both workpiece and tool system rotating: 40–290 , 90–490 , 177–413 , 100–490 , 100–520 , and 125–590 . The average values of oil film pressure and the radius of the shaft center’s trajectory are recorded, as shown in Figure 14.
3.3. ϕ29.35 Deep Hole Drilling Test
4. Conclusions
- A novel vibration-damping and deflection correction method for deep hole machining based on dynamic pressure lubrication and squeeze film damping theory is proposed, with a detailed elaboration on its operational principles. A Vibration-Damping and Deflection Correction Device for BTA deep hole drilling is designed. This device generates oil film pressure during drilling, exerting vibration-damping and deviation correction effects on the tool system. Consequently, it reduces exit deviation in deep hole machining and suppresses chatter.
- Through theoretical analysis and experimental validation of the Vibration-Damping and Deflection Correction Device, the influence patterns of structural dimensions, minimum oil film thickness, rotational speed, and other factors on oil film pressure distribution and stability were established. Design criteria for the key dimensions of the Vibration-Damping and Deflection Correction Device were derived. Experimental validation: The calculated results from the constructed oil film pressure mathematical model exhibit consistent trends with the experimental measurements. The numerical deviation between the two falls within ±15%. Beyond considering sensor measurement accuracy, the underlying causes warrant further investigation. Research indicates that, when drilling ordinary gun steel workpieces, designing the device with a minimum oil film thickness of 0.08 a helix angle of 15°, and a length of 50 can form a large and stable oil film, achieving the device’s vibration-damping and deviation correction performance.
- This vibration-damping and deviation correction theory has been applied in drilling , , and deep holes, such as and . The axial deviation of deep holes after drilling was reduced by an average of 50% to 70%, while the roundness error decreased by an average of 28%. The axial deviation of deep holes after boring was reduced by an average of 25% to 50%, while the roundness error decreased by an average of 15%. The roundness error is directly related to the amplitude of the tool system vibration. Therefore, research on the dynamic characteristics (stiffness coefficient and damping coefficient) of the wedge-shaped pressure oil film, both through calculation and experimental determination, is of great significance for the optimized design of this device.
- To facilitate inspection of the Vibration-Damping and Deflection Correction Device’s machining quality, the device can be designed with four wedge-shaped protrusions evenly distributed around the circumference—a structure symmetrical about the axis origin. The wedge dimensions can be directly measured using a tilt meter and micrometer.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wan, B.Y.; Peng, F.; Jin, Y.; Peng, Y.; Liu, D. Drilling Technology Status and Development Trends of Deep-sea Seafloor Drill. J. Mech. Eng. 2024, 60, 385–402. [Google Scholar]
- Wang, S.Q. Deep Hole Machining Technology, 3rd ed.; Northwestern Polytechnical University Press: Xi’an, China, 2003; pp. 1–10. [Google Scholar]
- Chandar, J.B.; Nagarajan, L.; Kumar, M.S. Recent Research Progress in Deep Hole Drilling Process: A Review. Surf. Rev. Lett. 2021, 28, 213003. [Google Scholar] [CrossRef]
- Richardson, R.; Bhatti, R. A review of research into the role of guide pads in BTA deep-hole machining. J. Mater. Process. Technol. 2001, 110, 61–69. [Google Scholar] [CrossRef]
- Li, X.; Zheng, J.; Yu, B.; Du, Y.; Zhou, Y. Analytical Model of Hole Diameter and Self-Guiding Machining Mechanism of BTA Deep Hole Drilling. Materials 2022, 15, 5329. [Google Scholar] [CrossRef] [PubMed]
- Zhang, R.; Liang, Z.; Yi, L.; Hu, J.; Du, Y.; Ma, Y.; Zhao, Q.; Xiong, L.; Zhao, Y. Research on the mechanism of single-tooth BTA deep hole processing under the condition of a weakly rigid slender drill rod. Eng. Fail. Anal. 2025, 170, 109302. [Google Scholar] [CrossRef]
- Summa, J.; Michel, S.; Kurkowski, M.; Biermann, D.; Stommel, M.; Herrmann, H.-G. Process Monitoring of a Vibration Dampening CFRP Drill Tube in BTA deep hole drilling using Fibre-Bragg-Grating Sensors. Procedia CIRP 2022, 115, 119–124. [Google Scholar] [CrossRef]
- Atsutoshi, H.; Hiromitsu, G.; Takayuki, T. Effect of Electrode Shape on High Aspect Ratio Deep Hole Drilling by EDM. Procedia CIRP 2022, 113, 262–266. [Google Scholar] [CrossRef]
- Afzaal, A.; Jibin, B.; Mustafizur, R. Novel EDM deep hole drilling strategy using tubular electrode with orifice. CIRP Ann. Manuf. Technol. 2021, 70, 151–154. [Google Scholar]
- Wang, P.; Hu, J.; Hu, H.; Yu, D.; Yin, Z.; Zou, H.; Lai, T. Debris motion and taper suppression in EDM deep hole machining assisted by longitudinal/torsional ultrasonic vibration. J. Manuf. Process. 2025, 133, 798–810. [Google Scholar] [CrossRef]
- Jibin, B.; Afzaal, A.; Ashwani, A. Effect of recirculation zone on debris evacuation during EDM deep hole drilling. Procedia CIRP 2021, 102, 393–398. [Google Scholar] [CrossRef]
- Fan, R.; Mei, X.; Cui, J. Process in laser drilling of deep microholes without taper on metal materials. Sci. China Technol. Sci. 2024, 67, 37–59. [Google Scholar] [CrossRef]
- Zhanwen, A.; Zou, G.; Li, W.; You, Y.; Feng, B.; Sheng, Z.; Du, C.; Xiao, Y.; Huo, J.; Liu, L. Deep learning driven multifeature extraction for quality evaluation of ultrafast laser drilled microhole arrays. J. Laser Appl. 2023, 35, 042006. [Google Scholar] [CrossRef]
- Maghami, A.; Salehi, M.; Khoshdarregi, M. A 3D deep learning model for rapid prediction of structural dynamics of workpieces during machining. Procedia CIRP 2021, 104, 1753–1758. [Google Scholar] [CrossRef]
- Robert, S.; Simon, S.; Frank, W.; Biermann, D.; Zabel, A. Tool design for the integration of piezoelectric and micro magnetic sensors to realize in-process measurements in BTA deep hole drilling. Procedia CIRP 2023, 119, 408–413. [Google Scholar] [CrossRef]
- Sun, J.; Sun, C.; Yan, Z.; Yang, W.; Zhou, C.; Zhang, P.; Shu, L. State-of-art, challenges, and outlook on deep hole boring: Chatter suppression, tool wear monitoring, and error measurement. Int. J. Adv. Manuf. Technol. 2025, 136, 2075–2105. [Google Scholar] [CrossRef]
- Gerken, J.F.; Klages, N.; Biermann, D.; Denkena, B. Development and analysis of a mechatronic system for in-process monitoring and compensation of straightness deviation in BTA deep hole drilling. Mech. Syst. Signal Process. 2022, 170, 108838. [Google Scholar] [CrossRef]
- Gerken, J.F.; Biermann, D. Concept of a Mechatronic System for Targeted Drill Head Direction and Angular Alignment Control in BTA Deep Hole Drilling//Congress of the German Academic Association for Production Technology; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Kong, L.F.; Niu, H.; Hou, X.; Wang, Q. Whirling vibration of drilling shaft in minimal quantity lubrication deep hole drilling using theoretical and experimental investigation. J. Mech. Eng. Sci. 2015, 229, 2433–2442. [Google Scholar] [CrossRef]
- Ma, G.H. Investigation on Dynamic Characteristics of BTA Deep-Hole Drilling Shaft System; North University of China: Taiyuan, China, 2018. [Google Scholar]
- Robert, S.; Simon, S.; Frank, W.; Biermann, D.; Zabel, A. Influence of the process parameters and forces on the bore sub-surface zone in BTA deep-hole drilling of AISI 4140 and AISI 304 L. Procedia CIRP 2020, 87, 41–46. [Google Scholar]
- Yu, X.; Lin, Y.; Wang, P.; Yang, X.; Lan, Z.; Shao, M.; Li, L.; Li, E.; Dai, R.; Jia, W.; et al. Analysis of lubrication characteristics of dynamic-static pressure hybrid thrust bearing considering key factors under eccentric loads. Tribol. Int. 2024, 194, 109471. [Google Scholar] [CrossRef]








| Oil Film Pressure | |
| Relative Speed | |
| Minimum Oil Film Thickness | |
| Wedge-Shaped Oil Film Thickness Ratio | |
| Hole Diameter | |
| Dynamic Viscosity of Cutting Oil |
| Workpiece–Tool Speed | Params | Mean | Standard Deviation | 95% Confidence Interval |
|---|---|---|---|---|
| 90—0 | * | 47.861 | 3.211 | [41.567,54.155] |
| * | 59.417 | 3.102 | [53.337,65.497] | |
| * | 66.235 | 3.128 | [60.104,72.366] | |
| * | 191.087 | 24.363 | [143.336,238.838] | |
| * | 187.592 | 13.962 | [160.226,214.958] | |
| * | 163.569 | 22.103 | [120.247,206.891] | |
| 0—490 | 228.86 | 2.732 | [223.508,234.218] | |
| 282.67 | 2.491 | [277.786,287.550] | ||
| 320.27 | 2.293 | [315.778,324.766] | ||
| 135.41 | 17.687 | [100.743,170.077] | ||
| 84.35 | 8.659 | [67.380,101.324] | ||
| 43.69 | 5.663 | [32.589,54.787] | ||
| 100—490 | 364.8 | 2.172 | [360.545,369.059] | |
| 455.06 | 1.752 | [451.629,458.497] | ||
| 516.68 | 1.585 | [513.571,519.785] | ||
| 123.55 | 16.596 | [91.018,156.074] | ||
| 66.56 | 7.302 | [52.245,80.869] | ||
| 25.38 | 4.695 | [16.181,34.585] |
| Workpiece–Tool Speed | Params | Mean | Standard Deviation | 95% Confidence Interval |
|---|---|---|---|---|
| * | 421.362 | 1.881 | [417.675,425.049] | |
| * | 398.952 | 1.912 | [395.204,402.700] | |
| * | 319.664 | 2.311 | [315.134,324.194] | |
| * | 276.032 | 2.568 | [270.999,281.065] | |
| * | 50.910 | 3.150 | [44.736,57.084] | |
| * | 21.007 | 3.254 | [14.629,27.385] | |
| * | 39.838 | 5.676 | [28.713,50.963] | |
| * | 51.257 | 6.775 | [37.978,64.536] | |
| * | 43.686 | 5.901 | [32.120,55.252] | |
| * | 48.363 | 5.210 | [38.151,58.575] | |
| * | 189.532 | 23.941 | [142.608,236.456] | |
| * | 192.319 | 24.110 | [145.063,239.575] | |
| 91.332 | 3.029 | [85.395,97.269] | ||
| 84.754 | 3.106 | [78.666,90.842] | ||
| 66.235 | 3.128 | [60.104,72.366] | ||
| 57.921 | 3.151 | [51.745,64.097] | ||
| 9.772 | 3.322 | [3.261,16.283] | ||
| 3.799 | 3.436 | [−2.936,10.534] | ||
| 193.160 | 25.056 | [144.050,242.270] | ||
| 191.689 | 24.137 | [144.380,238.998] | ||
| 163.569 | 22.103 | [120.247,206.891] | ||
| 168.051 | 22.109 | [124.717,211.385] | ||
| 182.848 | 23.444 | [136.898,228.798] | ||
| 189.276 | 23.000 | [144.196,234.356] | ||
| 631.824 | 1.193 | [629.486,634.162] | ||
| 594.027 | 1.335 | [591.410,596.644] | ||
| 515.739 | 1.524 | [512.752,518.726] | ||
| 405.023 | 1.867 | [401.364,408.682] | ||
| 62.935 | 3.167 | [56.728,69.142] | ||
| 24.791 | 3.223 | [18.474,31.108] | ||
| 24.962 | 2.945 | [19.190,30.734] | ||
| 28.937 | 4.395 | [20.323,37.551] | ||
| 25.382 | 3.221 | [19.069,31.695] | ||
| 26.778 | 3.305 | [20.300,33.256] | ||
| 159.341 | 20.963 | [118.254,200.428] | ||
| 171.062 | 23.665 | [124.679,217.445] |
| Workpiece–Tool Speed | Params | Mean | Standard Deviation | 95% Confidence Interval |
|---|---|---|---|---|
| 40—0 | * | 30.756 | 3.215 | [24.455,37.057] |
| * | 191.763 | 24.241 | [144.251,239.275] | |
| 70—0 | * | 50.564 | 3.159 | [44.372,56.756] |
| * | 176.325 | 23.482 | [130.300,222.350] | |
| 90—0 | * | 66.235 | 3.128 | [60.104,72.366] |
| * | 163.569 | 22.103 | [120.247,206.891] | |
| 125—0 | * | 76.763 | 3.165 | [70.560,82.966] |
| * | 141.021 | 20.276 | [101.280,180.762] | |
| 140—0 | * | 82.429 | 3.099 | [76.355,88.503] |
| * | 109.563 | 11.218 | [87.576,131.550] | |
| 0—190 | 130.819 | 2.951 | [125.035,136.603] | |
| 93.852 | 10.264 | [73.735,113.969] | ||
| 0—290 | 203.080 | 2.789 | [197.614,208.546] | |
| 79.688 | 9.684 | [60.707,98.669] | ||
| 0—390 | 280.903 | 2.552 | [275.901,285.905] | |
| 59.323 | 7.998 | [43.647,74.999] | ||
| 0—490 | 319.867 | 2.313 | [315.334,324.400] | |
| 43.692 | 6.001 | [31.930,55.454] | ||
| 0—590 | 341.086 | 2.164 | [336.845,345.327] | |
| 32.024 | 4.739 | [22.736,41.312] | ||
| 40–290 | 336.331 | 2.235 | [331.950,340.712] | |
| 89.631 | 8.985 | [72.020,107.242] | ||
| 90–490 | 511.779 | 1.578 | [508.686,514.872] | |
| 25.414 | 3.332 | [18.883,31.945] | ||
| 177–413 | 509.069 | 1.621 | [505.892,512.246] | |
| 32.547 | 4.862 | [23.017,42.077] | ||
| 100–490 | 516.029 | 1.581 | [512.930,519.128] | |
| 25.384 | 3.335 | [18.847,31.921] | ||
| 100–520 | 525.119 | 1.522 | [522.136,528.102] | |
| 24.886 | 2.867 | [19.267,30.505] | ||
| 125–590 | * | 561.872 | 1.463 | [559.005,564.739] |
| * | 23.878 | 2.245 | [19.478,28.278] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Chen, T.; Yu, D. Research on Vibration-Damping and Deflection Correction of BTA Deep Hole Drilling Tool Systems Based on Dynamic Pressure Lubrication and Squeeze Film Theory. Machines 2025, 13, 986. https://doi.org/10.3390/machines13110986
Wang Y, Chen T, Yu D. Research on Vibration-Damping and Deflection Correction of BTA Deep Hole Drilling Tool Systems Based on Dynamic Pressure Lubrication and Squeeze Film Theory. Machines. 2025; 13(11):986. https://doi.org/10.3390/machines13110986
Chicago/Turabian StyleWang, Yu, Tong Chen, and Daguo Yu. 2025. "Research on Vibration-Damping and Deflection Correction of BTA Deep Hole Drilling Tool Systems Based on Dynamic Pressure Lubrication and Squeeze Film Theory" Machines 13, no. 11: 986. https://doi.org/10.3390/machines13110986
APA StyleWang, Y., Chen, T., & Yu, D. (2025). Research on Vibration-Damping and Deflection Correction of BTA Deep Hole Drilling Tool Systems Based on Dynamic Pressure Lubrication and Squeeze Film Theory. Machines, 13(11), 986. https://doi.org/10.3390/machines13110986






