Analysis of Flexible Bearing Load Under Various Torque Conditions

Abstract

This paper aims to develop a model for calculating the ball load of the thin-walled flexible bearing (FB) in a harmonic drive under various external torque conditions. The effect of the flexspline (FS) on the FB ball load is considered, and the equivalent ring is improved to calculate the ball load of the FB. Then, the accuracy of the proposed model in calculating the ball load is verified using a finite element analysis model. Finally, a fitting formula is obtained to rapidly evaluate the FB ball load via the geometrical parameters of the FB and the FS under various external torques. The results show that the FB ball load is mainly affected by the FB maximum radial deformation under low external torque. When subjected to heavy external torque, the maximum ball load is mainly affected by the FS’s geometric parameters.

1. Introduction

The harmonic drive (HD) has been widely used in robot joints, and has advantages such as small transmission error, large load capacity, and compact size [1,2,3]. As a complex rigid-flexible coupled transmission mechanism, shown in Figure 1, an HD is composed of flexible (flexspline (FS) and flexible bearing (FB)) and rigid (circular spline (CS) and cam) components [4,5]. FB is deformed by the action of the cam and then forms an interference fit with the FS. It is the core component of an HD. Experiments show that the wear of the FB can lead to HD failure [6,7]. Meanwhile, the ball load distribution is a key factor in determining the fatigue and wear of the FB [8,9]. However, it is difficult to directly observe and measure the deformation and force on the inside of an HD using an experiment. Therefore, the accurate calculation of the FB ball load is extremely important as a reference for analyzing subsequent wear and accuracy degradation.

The current research on the theoretical calculation of the FB ball load is mainly based on the Thin-walled Ring Theory [10,11,12]. The FB outer race is usually simplified as an equivalent ring with equal thickness. Then, the FB ball load is solved by establishing its relationship with the deformation of the equivalent ring. Some studies focus on the deformation of the equivalent ring under the action of the cam [13,14]. The FS is in contact with the FB outer race under the action of the cam. Thus, some scholars optimize an equivalent ring by simplifying the ring instead of the FS and consider the FS and FB outer race as a whole to improve the solution accuracy for FB ball load [15,16]. The FS is regarded as a ring in preceding studies, and the effect of the FS tooth is not considered. However, relevant studies show that the FS bending stiffness, which affects the deformation of the equivalent ring, is determined by the FS tooth [17,18,19]. Therefore, the effect of the FS tooth cannot be neglected when calculating the FB ball load.

The current literature has extensively studied the FB ball load under no and low torque, but the HD is subjected to various speeds and external torque conditions throughout operation [20]. According to previous studies, the FS is detached from FB under heavy external torque [21,22]. Therefore, based on earlier studies, it is critical to reflect the separation between the FS and FB under heavy external torque when analyzing the deformation of the equivalent ring. Additionally, the correction of the geometric parameters of the HD is required for the analysis of bearing wear [23,24]. It is necessary to establish the exact relationship between ball load and geometric parameters efficiently for subsequently analyzing FB wear.

This investigation primarily aims to calculate the ball load of FB accurately and efficiently. The equivalent ring is improved for representing the partial contact between the FS and FB under various external torques. On this basis, the effect of the FS tooth on the deformation of the equivalent ring is studied. The sensitivity analysis of the FB and FS geometric parameters on FB ball load is investigated. Subsequently, the fitting formulae of the FB ball load and the geometrical parameters of FB and FS which accord with the orthogonal simulation results are summarized. Ultimately, based on the above fitting formula, the FB ball load can be quickly evaluated.

The study is structured as follows. An equivalent ring is improved and a static analysis model for the FB ball load is developed in Section 2. In Section 3, the influence of the FB and FS’s geometric parameters on the FB ball load is studied. In Section 4, orthogonal simulations of the geometric parameters of the FB and FS are discussed, and the fitting formulae are established under various external torques. Finally, the conclusions are drawn in Section 5.

2. Model and Methodology for FB Ball Load

The FS and FB outer race are considered as a whole, and an equivalent ring is improved according to the partial contact between the FS and FB. The deformation of the equivalent ring is determined by the meshing force applied to the FS and ball load applied to the FB outer face. Therefore, in this section, its deformation is calculated by superposing the action of ball load and meshing force. Then, the FB ball load distribution can be solved according to the deformation coordination equation.

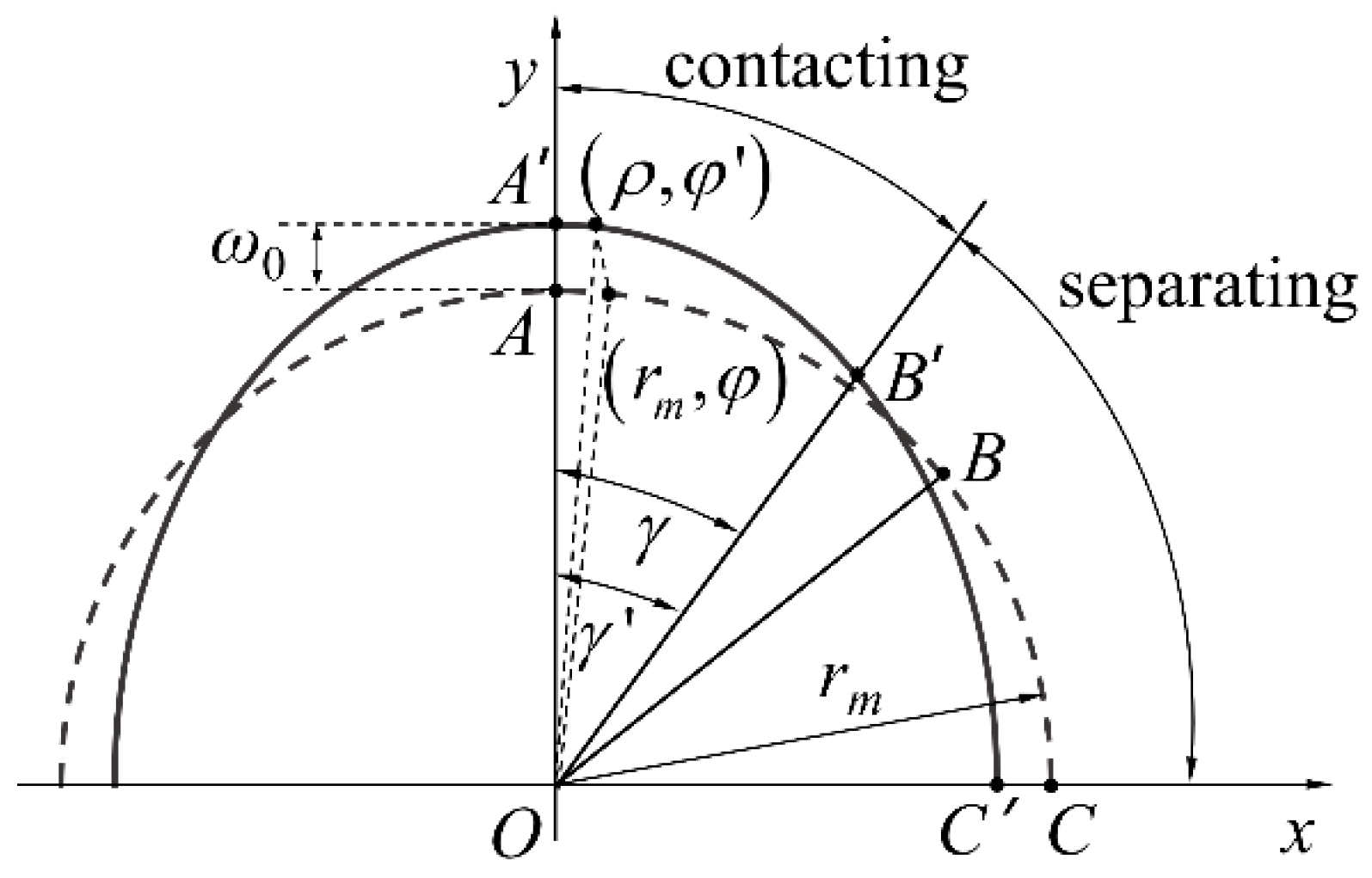
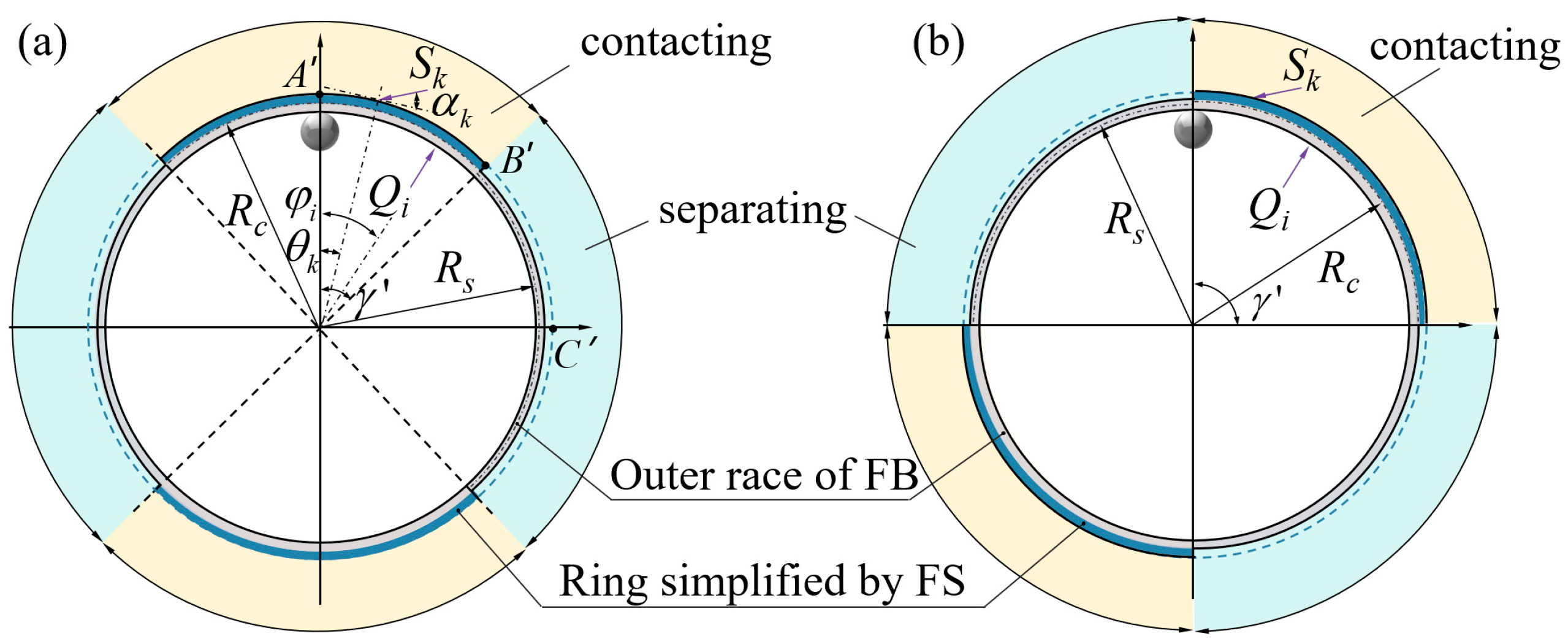
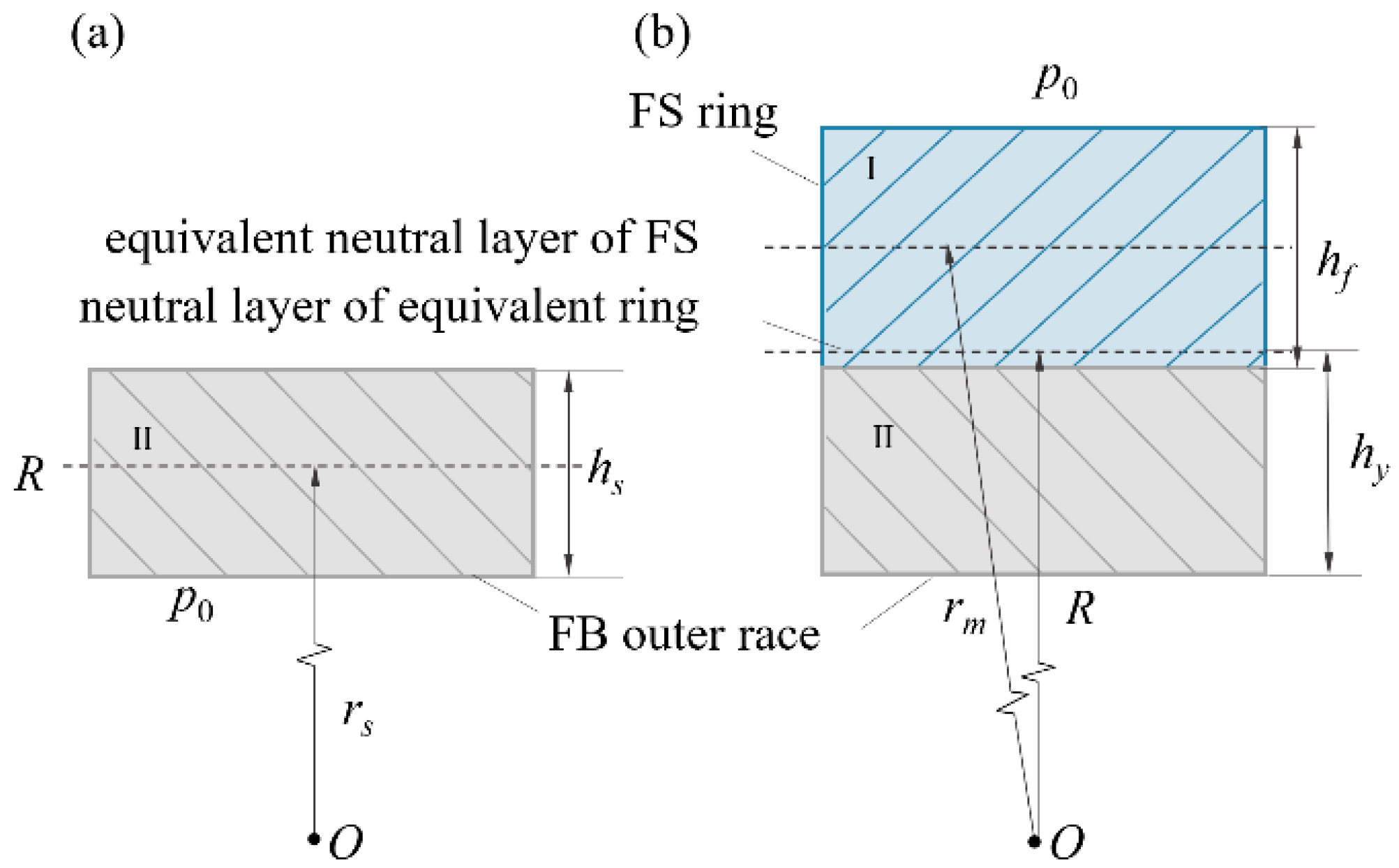
2.1. Improved Equivalent Ring

Based on the contact condition between the FS and FB, the equivalent ring is established. When the FS and FB are in contact, they are integrated as an entity. When no contact occurs, the equivalent ring is composed of the FB. The contact between the FB and FS after assembly is shown in Figure 2.

As shown in Figure 2, the FS is divided by wrapping angle γ into arc AB and arc BC before deformation. Arc AB is deformed to curve A′B′ in close contact with the FB, and arc BC is deformed to curve B′C′. Arc B′C′ separates with the FS, when the WG is assembled with FS. γ′ is the wrapping angle after FS deformation. According to the geometric constraint and equilibrium equations of the ring with continuous conditions [25], γ′ can be calculated as follows:

$$\begin{array}{l}{\displaystyle {\int }_0^{{\gamma }^{\prime }}(\rho -r_m)\mathrm{d}}\phi \prime +{\displaystyle \frac{\ddot{\rho }{|}_{{\phi }^{\prime }={\gamma }^{\prime }}\left[4{\cos }^2\gamma +\left(2\gamma -\pi -2\cos \gamma \sin \gamma \right)\left(\raisebox{1ex}{$\pi $}\!\left/ \!\raisebox{-1ex}{$2$}\right.-\gamma \right)\right]}{2\gamma -\pi +2\cos \gamma \sin \gamma }}+\\ \dot{\rho }{|}_{{\phi }^{\prime }={\gamma }^{\prime }}\left[{\displaystyle \frac{{\cos }^2\gamma \left(2\pi -4\gamma \right)}{2\gamma -\pi +2\cos \gamma \sin \gamma }}+3\right]+\left[\rho (\gamma \prime )-r_m\right]\left({\displaystyle \frac{\pi }{2}}-\gamma \right)=0\end{array},$$

(1)

where the point at polar angle φ to the y-axis on the ring is moved to polar point (ρ, φ′) after FS deformed, r_m is the FS neutral line radius. ρ is the polar diameter of the FS and can be calculated:

$$\rho ={\displaystyle \frac{r_a{r}_b}{\sqrt{{r_a}^2\sin \phi {\prime }^2+{r_b}^2\cos \phi {’}^2}}}.$$

(2)

In Equation (2), r_a and r_b are the major and minor axis of the ellipse, while r_a is the sum of the FS neutral line radius r_m and ω₀ is the maximum radial deformation of the FS and FB outer race.

According to the assumption of non-elongation on the mid-layer, the relationship between γ′ and γ can be determined by the following equation:

$$r_m\gamma ={\displaystyle {\int }_0^{\gamma ’}\sqrt{{\rho }^2+{\dot{\rho }}^2}}\mathrm{d}\phi ’,$$

(3)

where γ′ can be determined by Equation (1), based on the numerical approximation method.

When the FS contacts the FB, it is represented as a ring without tooth features for computational simplicity, as illustrated in Figure 3. According to previous research [19], the tooth effect on the FS bending stiffness can be replaced by the FS bending stiffness coefficient C_tr. C_tr is mainly reflected in root thickness s_f, dedendum arc radius r_f, and tooth rack thickness h₀. The characteristic formula of the C_tr can be fitted as shown in Equation (4):

$$C_{tr}={\displaystyle \frac{0.477s_f+0.522r_f}{h_0}}+0.692.$$

(4)

The bending strain energy of tooth unit and beam unit is identical after simplification. The bending stiffness of the ring E_fI_f can be calculated:

$$E_f{I}_f=C_{tr}{E}_0{I}_0,$$

(5)

where E₀I₀ is the bending stiffness of the beam with length p₀, and E₀ is the elastic modulus of the beam, and its section moment of inertia I₀ can be calculated:

$$I_0={\displaystyle \frac{b_0{h_0}^3}{12}},$$

(6)

where b₀ is the width of the beam, and h₀ is its thickness.

Based on the simplified ring of the FS and its contact condition with the FB, an equivalent ring model is established, as depicted in Figure 4. The wrap angle γ′ is determined by Equation (1) under no or low external torque. According to Ivanov′s experiment [21], the wrapping angle is 90° in the first and third quadrants and 0° in the second and fourth quadrants when the FS is subjected to heavy external torque.

In Figure 4, Q_i denotes the ball load of the ith ball and φ_i is the angular position of the ball. S_k denotes the meshing force of the kth tooth. θ_k is the angular position of the tooth, and α_k is the meshing angle. The sum of moments generated by meshing forces relative to the center O is balanced with the external torque.

Referring to the cross section of the equivalent ring within a pitch as shown in Figure 5, the neutral line radius R of a point on the equivalent ring can be expressed in segments as follows:

(1)

If the point on the equivalent ring exceeds the range of the wrapping angle, then

$$R=r_s,$$

(7)

where r_s is the neutral line radius of the FB outer race.

(2)

If the point on the equivalent ring does not exceed the range of the wrapping angle, then

$$R=h_y+r_s-\raisebox{1ex}{$h_s$}\!\left/ \!\raisebox{-1ex}{$2$}\right.,$$

(8)

where h_s is the thickness of the FB outer race.

The thicknesses of the FS and the FB outer race are too small for the radius R, so it can be assumed that the curvatures of the FS ring and the FB outer race are equal. Then, h_y can be determined by the integral method,

$$h_y={\displaystyle \frac{E_s{h_s}^2+E_f{h}_f\left(2h_s+h_f\right)}{2E_s{h}_s+2E_f{h}_f}},$$

(9)

where E_s is the elastic modulus of the outer race and h_f is the equivalent thickness of the FS ring under the influence of the FS tooth, which can be calculated by the formula proposed by Yao [26].

The bending stiffness W of the equivalent ring is also segmented by the wrapping angle and is expressed as follows:

(1)

If the point on the equivalent ring exceeds the range of the wrapping angle, then

$$W=E_s{I}_s,$$

(10)

where I_s is the inertia moment of the outer race section.

(2)

If the point on the equivalent ring does not exceed the range of the wrapping angle, then

$$W=E_s{I}_s+E_f{I}_f.$$

(11)

Combining Equations (1) and (3) into Equation (11), the bending stiffness W can be written as:

$$W=E_s{I}_s+({\displaystyle \frac{0.477s_f+0.522r_f}{h_0}}+0.692)E_0{I}_0.$$

(12)

Equation (12) can be used to reflect the influence of the FS’s geometric parameters on the bending stiffness W, which further affects the FB ball load.

2.2. Superposition Method for FB Ball Load

Due to the flexibility feature, the equivalent ring is deformed by the action of all unknown ball loads and meshing forces. The deformation coordination equation can be constructed using the superposition method:

$$\left[{\delta }_i\right]=C_S\left[S_k\sin {\alpha }_k\right]+C_Q[Q_i],$$

(13)

where δ_i is the radial deformation on the equivalent ring at the angular position of the ith ball. C_S and C_Q are the influence coefficient matrixes consisting of unit radial deformations produced by meshing forces and ball load, and can be specifically expressed as:

$$C_S=\left[\begin{array}{cccc}{c}_{S11}& c_{S12}& \dots & c_{S1z}\\ c_{S21}& c_{S22}& \dots & c_{S2z}\\ \dots & \dots & c_{Sik}& \dots \\ c_{Sn1}& c_{Sn2}& \dots & c_{Snz}\end{array}\right], C_Q=\left[\begin{array}{cccc}{c}_{Q11}& c_{Q12}& \dots & c_{Q1n}\\ c_{Q21}& c_{Q22}& \dots & c_{Q2n}\\ \dots & \dots & c_{Qij}& \dots \\ c_{Qn1}& c_{Qn2}& \dots & c_{Qnn}\end{array}\right],$$

(14)

where n is the ball number and z is the FS tooth number.

Due to the thickness of the equivalent ring being too small for its radius, the change in the equivalent ring curvature is approximately equal when a force is applied on the point within or outside the wrapping angle. Thus, the deformation of the equivalent ring, which is segmented by the wrapping angle, still satisfies Thin-walled Ring Theory. The symbol c_Sik is used to represent the influence coefficient of the meshing force S_k on the equivalent ring at the angular position of the kth tooth, and it can be expressed in segments as follows:

$$c_{Sik}=\left\{\begin{array}{l}{\displaystyle \frac{R^3}{4W}}\left[-({\theta }_k-{\phi }_i)\sin ({\theta }_k-{\phi }_i)+\left({\displaystyle \frac{({\theta }_k-{\phi }_i)}{2}}-\pi \right)({\theta }_k-{\phi }_i)\cos ({\theta }_k-{\phi }_i)-2\right],{\theta }_k-{\phi }_i\ge 0\\ {\displaystyle \frac{R^3}{4W}}\left[-\left({\theta }_k-{\phi }_i+2\pi \right)\sin ({\theta }_k-{\phi }_i)+{\displaystyle \frac{({\theta }_k-{\phi }_i)}{2}}\left({\theta }_k-{\phi }_i+2\pi \right)\cos ({\theta }_k-{\phi }_i)-2\right],{\theta }_k-{\phi }_i<0\end{array}\right..$$

(15)

Similarly, c_Qij is used to represent the influence coefficient of the ball load Q_j on the equivalent ring at the angular position of the ith ball, and c_Qij can be expressed in segments as follows:

$$c_{Qij}=\left\{\begin{array}{l}{\displaystyle \frac{R^3}{4W}}\left[\left({\phi }_j-{\phi }_i\right)\sin \left({\phi }_j-{\phi }_i\right)-\left({\displaystyle \frac{\left({\phi }_j-{\phi }_i\right)}{2}}-\pi \right){\phi }_{ij}\cos \left({\phi }_j-{\phi }_i\right)+2\right],{\phi }_j-{\phi }_i\ge 0\\ {\displaystyle \frac{R^3}{4W}}\left[\left({\phi }_j-{\phi }_i+2\pi \right)\sin \left({\phi }_j-{\phi }_i\right)-{\displaystyle \frac{{\left({\phi }_j-{\phi }_i\right)}^2}{2}}\cos \left({\phi }_j-{\phi }_i\right)+2\right],{\phi }_j-{\phi }_i<0\end{array}\right..$$

(16)

Equations (15) and (16) can be used to determine the influence coefficient matrixes in Equation (13). The meshing force S_k can be calculated iteratively using the meshing flexibility matrix, when the external torque of the HD is determined [27]. The ball load Q_i can be expressed by Hertzian Contact Theory:

$$Q_i=k{u}^{3/2},$$

(17)

where k is the contact stiffness between the outer race and ball, u represents the contact deformation, which is the result of subtraction between the deformation δ_i and the initial radial clearance δ_i0. If the subtraction is less than zero, it means that the ball is not in contact with the equivalent ring, and u can be expressed as:

$$u=\left\{\begin{array}{l}{\delta }_i-{\delta }_{i0},{\delta }_i\ge {\delta }_{i0}\\ 0,{\delta }_i<{\delta }_{i0}\end{array}\right..$$

(18)

In Equation (18), ${\delta }_{i0}=\raisebox{1ex}{$P_d$}\!\left/ \!\raisebox{-1ex}{$2$}\right.+r_m-\rho$. Where P_d denotes the internal radial clearance of the ball before the cam is inserted into an FB.

Combining Equation (18) into Equation (17), the ball load Q_i in contact can be written as:

$$Q_i=k{\left[{\delta }_i-\left(\raisebox{1ex}{$P_d$}\!\left/ \!\raisebox{-1ex}{$2$}\right.+r_m-\rho \right)\right]}^{3/2}.$$

(19)

In summary, the radial deformation δ_i in Equation (13) is influenced by all ball loads, which are currently unknown. The relationship between the ith ball load Q_i and the deformation δ_i can be established by Equation (19). A set of n nonlinear simultaneous equations can be constituted by substituting Equation (19) into Equation (13), and can be solved iteratively using the Newton–Raphson method. The flowchart for programming the computation of the ball load is shown in Figure 6.

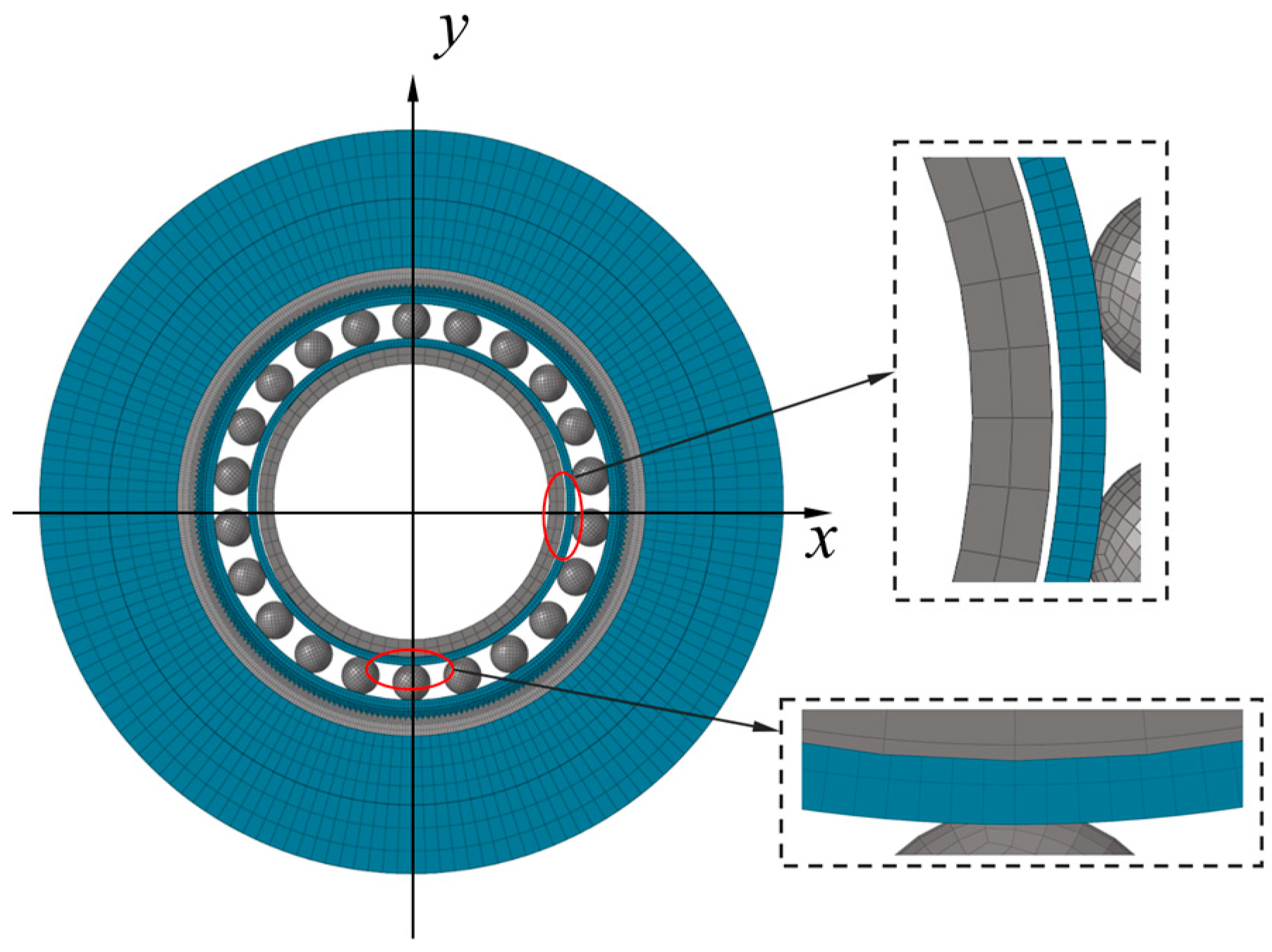
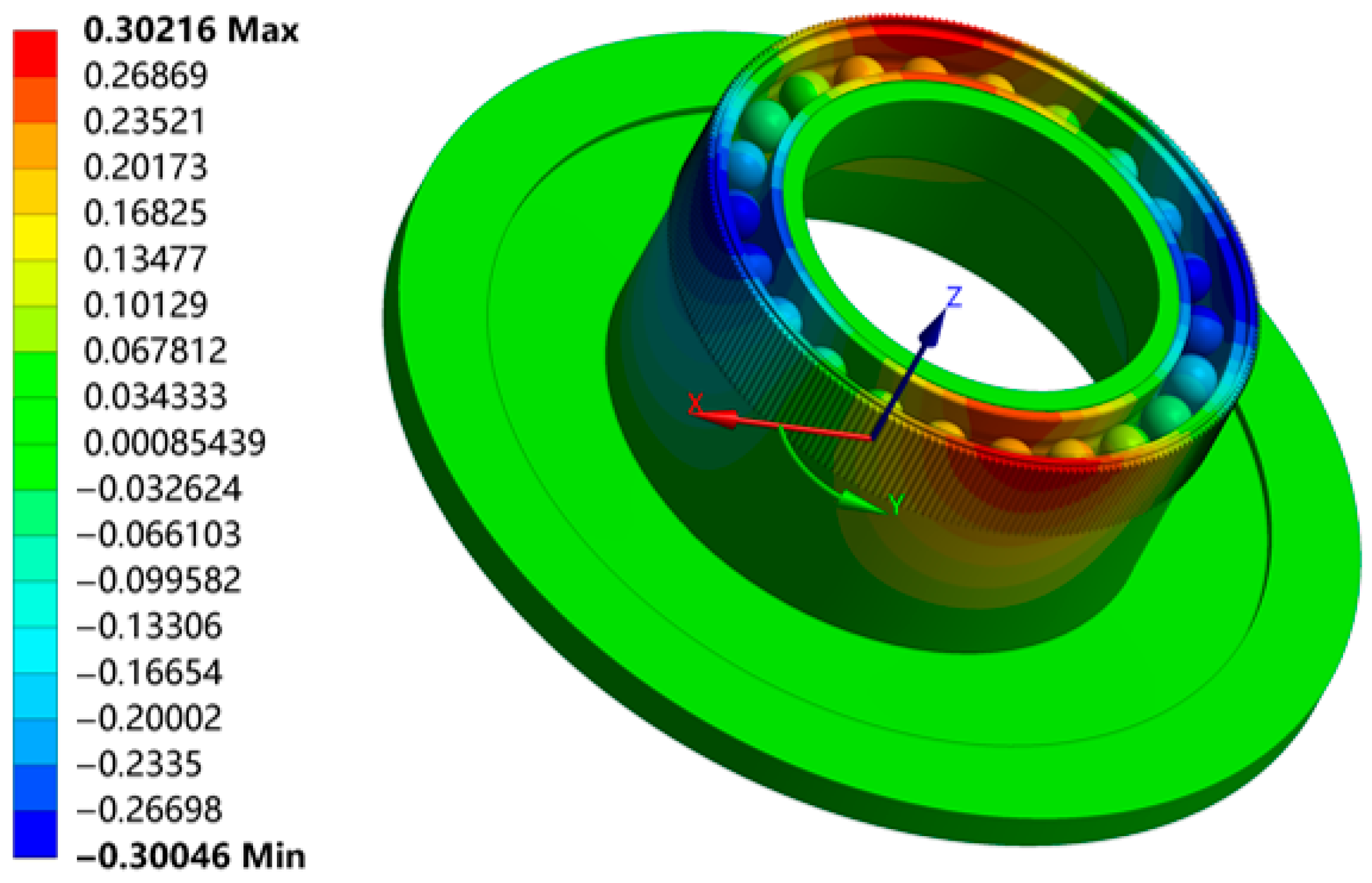
2.3. Validation of FB Ball Load

The simulation model of the HD (SHG-20-100) is built as shown in Figure 7, which refers to the geometric and material parameters in

Table 1. Geometric parameters of HD.

Parameter	Description	Value	Units
n	Number of balls	22	/
z	Number of FS teeth	200	/
rm	FS neutral line radius	24.450	mm
rs	neutral line radius of FB outer race	18.850	mm
hs	thickness of FB outer race	1.000	mm
ω0	The maximum radial deformation	0.300	mm
Pd	Radial clearance	0.001	mm
sf	root thickness of FS tooth	0.410	mm
rf	dedendum arc radius of FS tooth	0.300	mm
h0	tooth rack thickness	0.690	mm

and

Table 2. Material parameters of HD.

Part	Material	Elastic Modulus (MPa)	Poisson’s Ratio
FS	40CrNiMoA	209,000	0.295
FB	GCr15	219,000	0.300
Cam	42CrMo	212,000	0.280

. The model is developed using a C3D8R element, a mesh number of 1,332,712, and a size of 0.25 mm. The element mass of the model is 0.97, its Jacobian ratio is 1.10, and its aspect ratio is 1.21. The model contact type is friction contact.

Simulation modeling of HD deformation and forces under loaded conditions in Ansys Workbench 2021 R2. The simulation consists of two steps. At the assembly stage, the gap between the FB and the FS is eliminated after the cam is inserted into the FB. Then, the external load T (14 Nm) is applied to the bottom of the FS at the loading stage. The radial deformation of the FS and the FB at the assembly stage is shown in Figure 8. The maximum radial deformation in the simulation is 0.302 mm, which occurs along the major axis. It is greater than the theoretical maximum radial deformation (ω₀) of 0.72%. This shows that the simulation result of the deformation above matches the actual deformation, which confirms the reliability of the simulation model.

The variation of the FB ball load for the first ball at different angular positions is obtained using different calculation methods and is shown in Figure 9. According to the theoretical and simulation results, the number of balls in the contact state is the same. The maximum ball load occurs at the angular position of the first and twelfth balls according to all methods. The value of the maximum ball load in this study is 44.48 N, which is approximately 4.8% less than its simulation result (46.72 N). The maximum error of the ball load in this study is 6.09%, compared with 15.07% for the method proposed by Xiong [14]. These results show that the FB ball load calculated in this study is more consistent with the FEM, which indicates that the improved equivalent ring presented in Section 2.1 is more reliable.

3. Analyses of Influence on FB Ball Load

As described in Section 2, the FB ball load is relevant to the external torque and the geometric parameters of the FB and the FS, while the FB maximum radial deformation ω₀ and the FS bending stiffness coefficient C_tr are selected to study their effects.

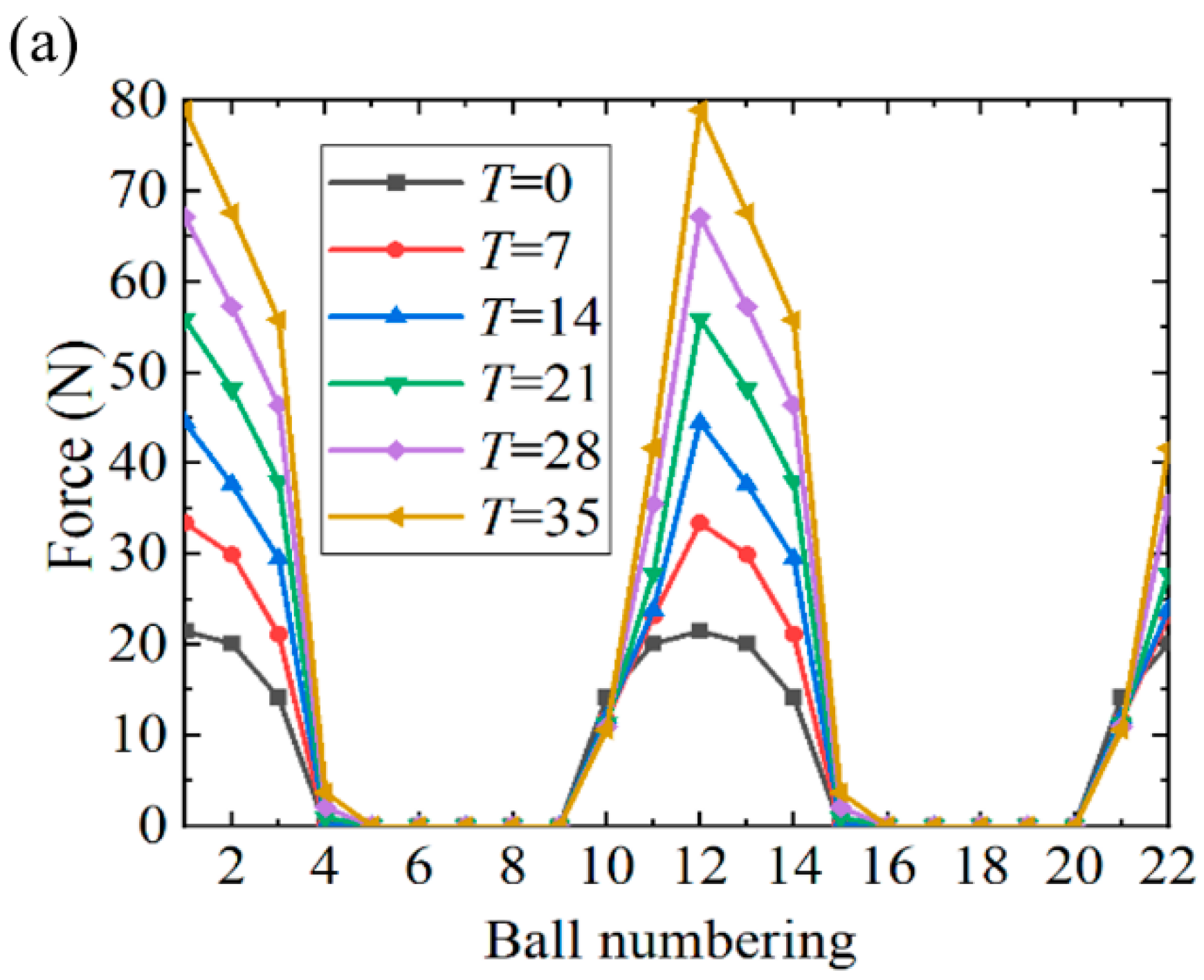
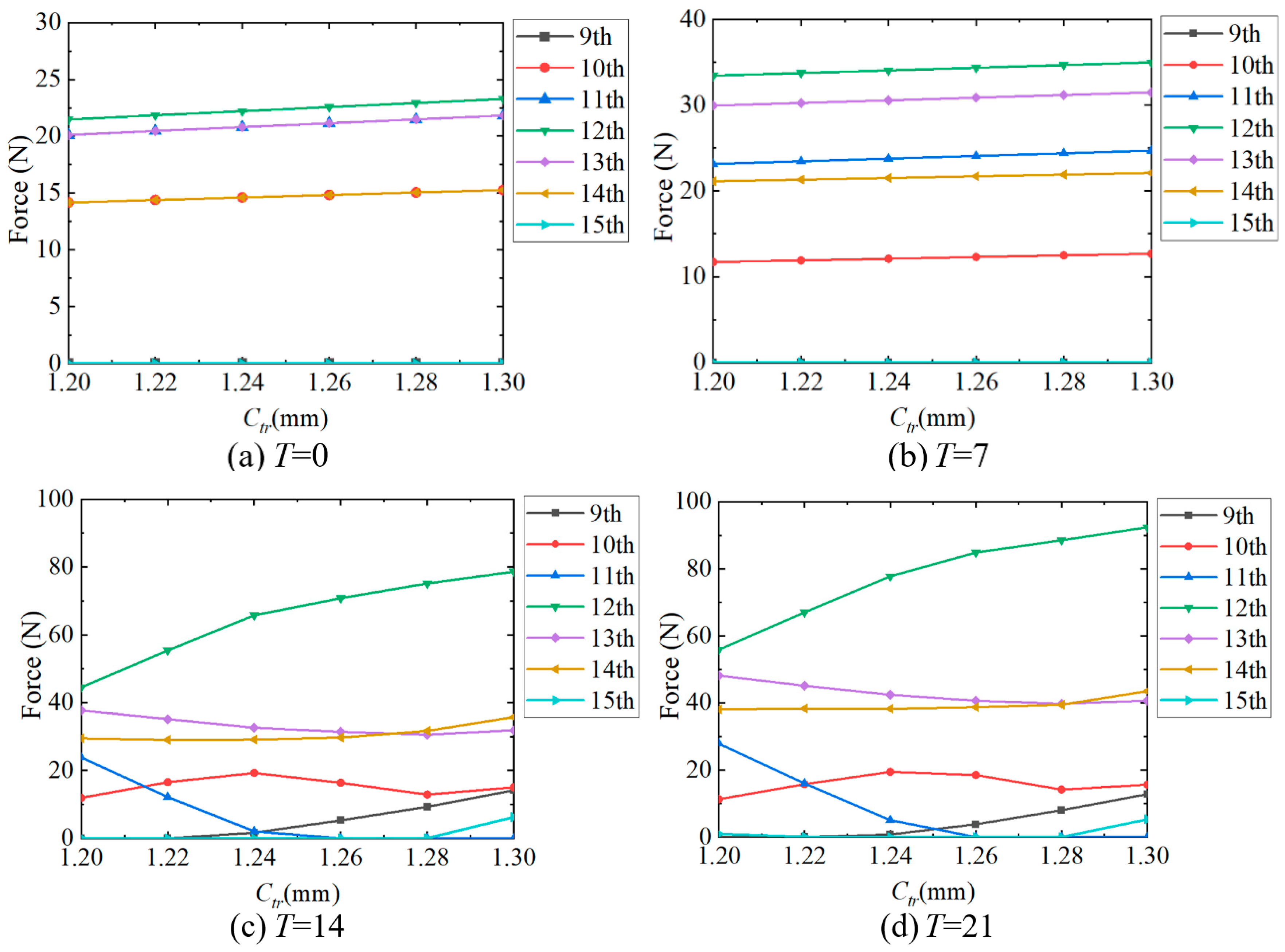
3.1. Influence of External Torque T

The rated torque of the HD (SHG-20-100) is 35 Nm. The external torque can be considered low when it is less than 30% of the rated load, while the heavy external torque exceeds 30% of the rated load. The FB ball load is calculated under various external torques (7 Nm, 14 Nm, 21 Nm, 28 Nm, and 35 Nm), as shown in Figure 10a. According to the results presented in the figure, the distribution of the FB ball load is no longer symmetrical with respect to the major axis due to the influence of the external torque, but is centrosymmetric. Therefore, only half of the balls engaged in contact (from the ninth to the fifteenth ball) are analyzed, as shown in Figure 10b. As the external torque T increases, the number of balls engaged in contact changes slightly, with 10 and 12 under low and heavy external torque, respectively. With the exception of the 10th ball, the FB ball load shows an increasing relationship with the external torque.

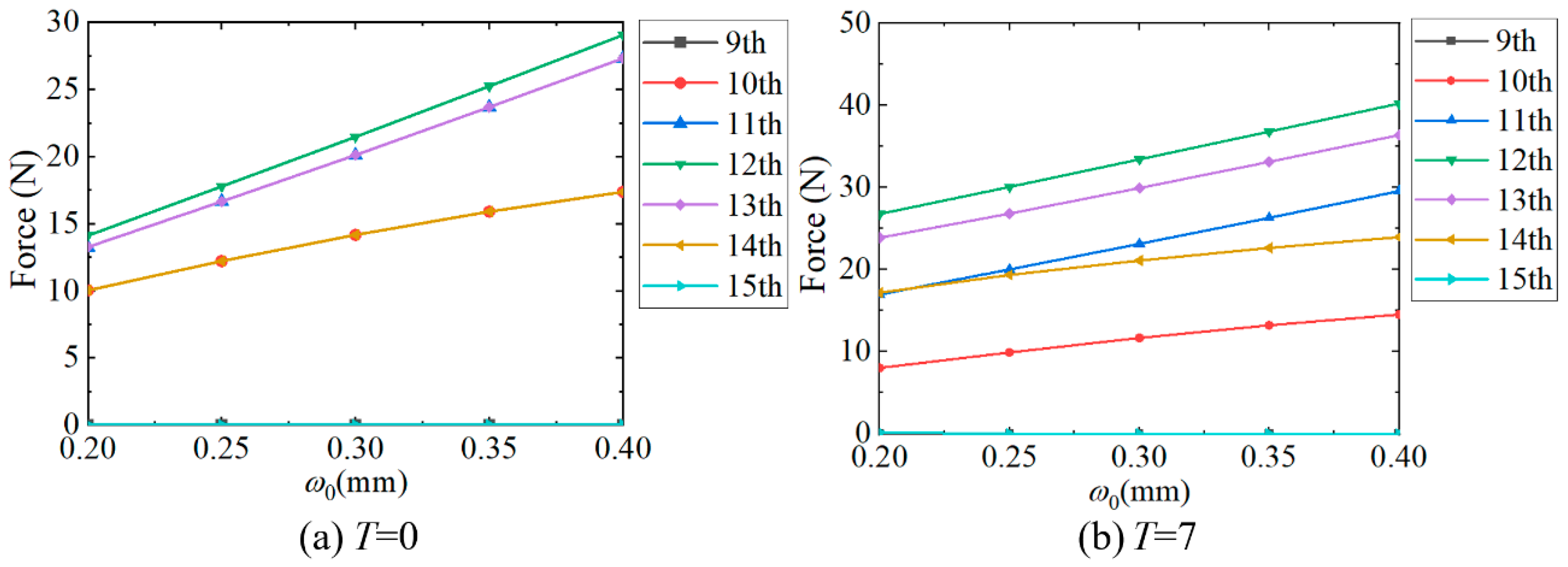
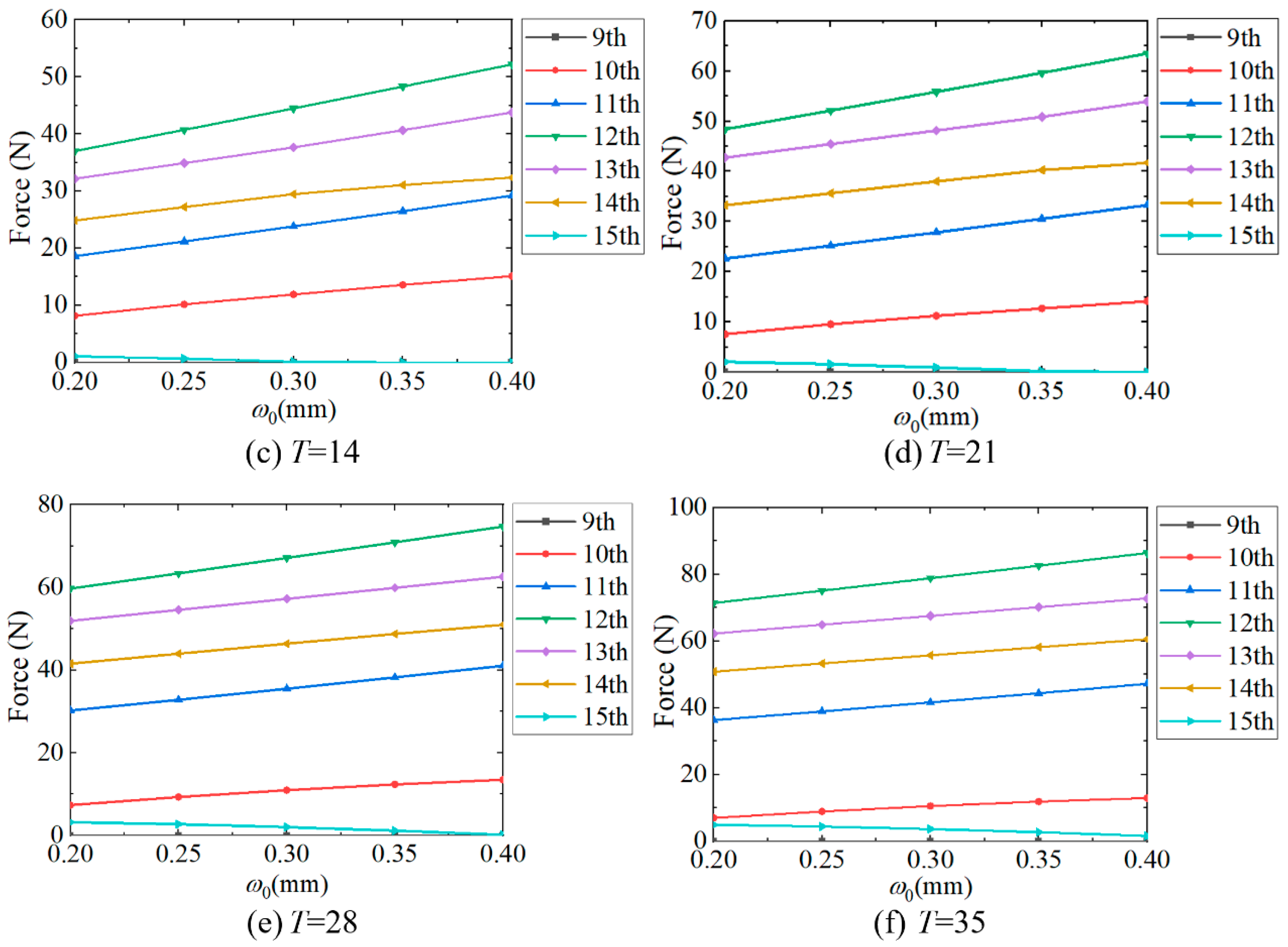
3.2. Influence of the Maximum Radial Deformation ω₀

To analyze whether the influence of the maximum radial deformation ω₀ on the ball load is affected by the external torque T, the FB ball load from the ninth to the fifteenth balls are calculated under various external torques. As shown in Figure 11, when the ω₀ increases, the number of balls engaged in contact does not change under low external torque, but decreases under heavy external torque. As ω₀ increases, the major contact ball loads (from the 10th to the 14th balls) show an approximately linear relationship with the ω₀ under various external torque. The change rate of the major contact ball loads is calculated when ω₀ increases from 0.2 mm to 0.4 mm, as shown in Figure 12. The result reveals that the ball loads exhibit higher sensitivity to ω₀ under low torque, except for Ball 10, whereas the influence diminishes significantly near the rated torque. This demonstrates that external torque is critical when analyzing factors affecting the ball load. Consequently, prior studies concluding that ω₀ dominates the ball load without external torque reveal significant limitations.

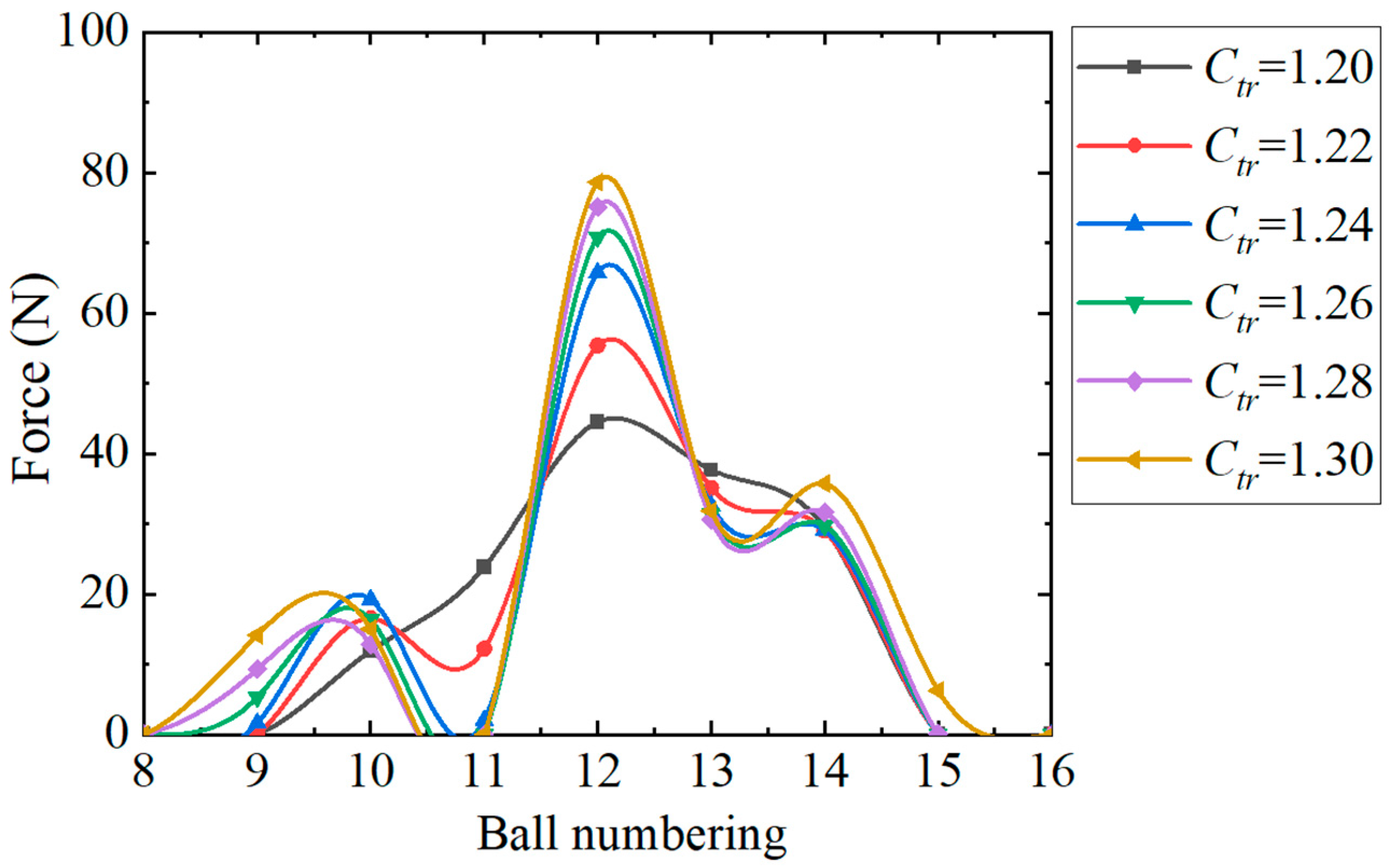
3.3. Influence of the FS Bending Stiffness Coefficient C_tr

Since the FS bending stiffness coefficient C_tr has an identified relationship with the root thickness s_f, the dedendum arc radius r_f, and the tooth rack thickness h₀ in Equation (3), the influence of the FS tooth geometric parameter on the ball load can be replaced by C_tr. As can be seen in Figure 13, the geometric parameters of the FS tooth have an obvious effect on the ball load. When the bending stiffness coefficient C_tr increases from 1.2 to 1.3, the maximum ball load increases from 44.48 N to 78.61 N with a growth rate of 76.7%. It further proves that the influence of the FS tooth on the FB ball load cannot be ignored. When C_tr is greater than 1.24, three peaks appear in the distribution of the ball load. This may cause the FB to be subjected to more impacts, and its wear will be aggravated. However, the stress of the FS increases rapidly as C_tr decreases, which leads to fatigue failure of the FS [26]. Therefore, the minimum value of C_tr is suggested to be preferentially adopted when the maximum stress design requirement is met.

In order to analyze whether the influence of C_tr on the ball load is affected by the external torque T, the FB ball load from the ninth to the fifteenth balls are calculated under various external torques. As shown in Figure 14, the FS bending stiffness coefficient C_tr has little effect on the ball load under low external toque. However, the ball load reflects the complex non-linear change under heavy torque as C_tr varies. Therefore, the ball load is analyzed separately for low and heavy torque conditions.

4. Orthogonal Simulations and Fitting Formulae

Rapidly constructing the relationship between the FB ball load and the geometric parameters of the HD is of great significance for the study of wear. When the external torque is determined, the FB ball load is relevant to the maximum radial deformation of the FB ω₀ and the bending stiffness coefficient C_tr. In this section, a variety of ball load distributions with different ω₀ and C_tr are calculated, which are designed by orthogonal simulations. The formulas for solving the ball load in the major contact zone are fitted under low torque (7 Nm) and rated torque (35 Nm).

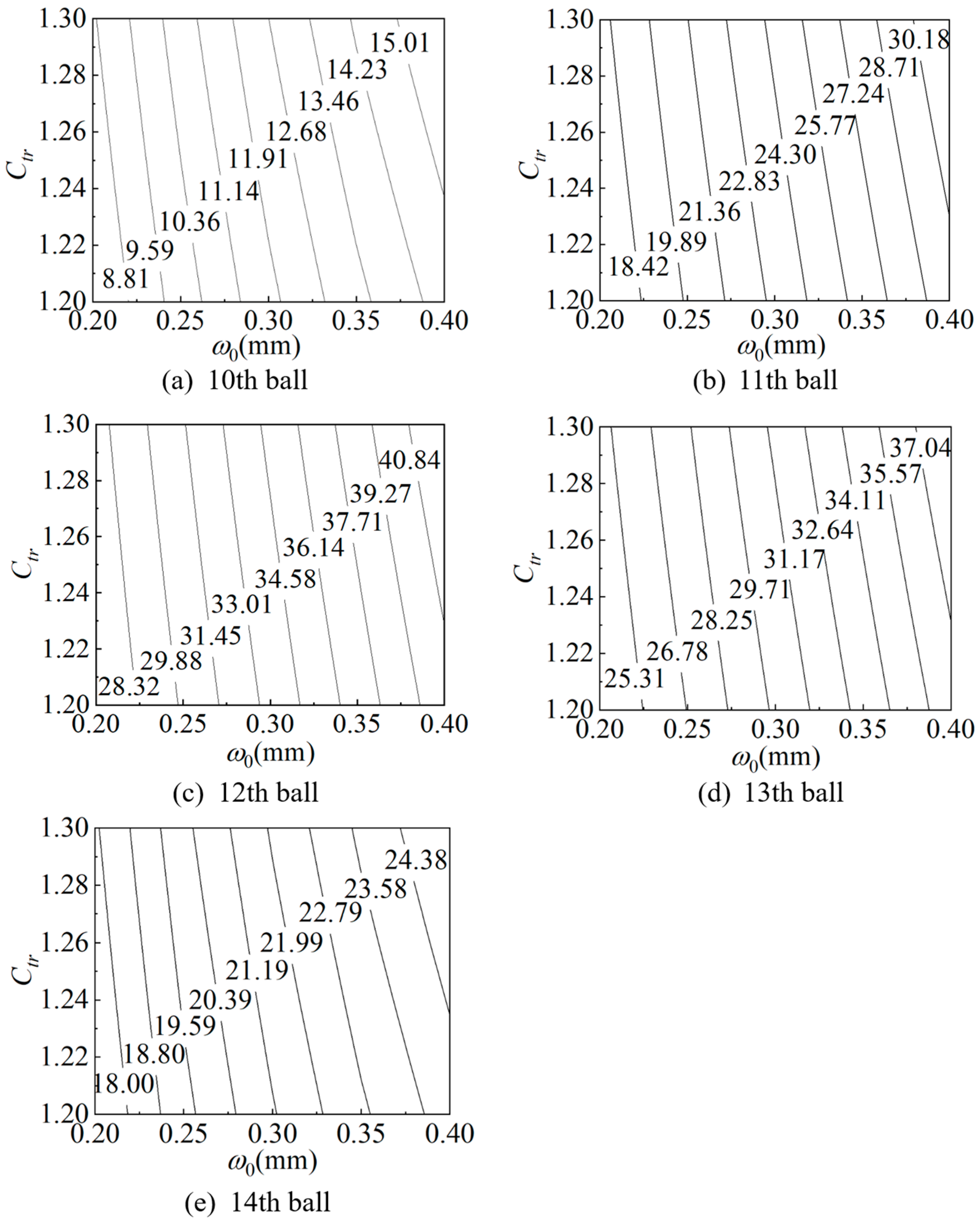
4.1. Orthogonal Simulation Under Low Torque

When the external torque T is 7 Nm, the results of the orthogonal simulation of the ω₀ and C_tr of the FB ball load within the major contact zone are illustrated as a contour map in Figure 15. The ball load shows linear monotonic increasing trends with ω₀ and C_tr. Then, a linear surface equation, as shown in Equation (20), is constructed to fit the FB ball load in Figure 15. The fitting results are illustrated in

Table 3. The parameters of the fitted surface.

The ith Ball Load Qi	A1	A2	A3
10	33.9602	9.6640	−10.2891
11	65.4500	15.5663	−15.1118
12	70.0736	15.5621	−6.2371
13	65.2366	15.5269	−8.1775
14	34.9527	9.6516	−1.2101

.

$$Q_i=A_1{\omega }_0+A_2{C}_{tr}+A_3.$$

(20)

Obviously, the maximum ball load is directly proportional to both ω₀ and C_tr under low torque. The maximum radial deformation ω₀ has a more significant impact on the FB ball load than the bending stiffness coefficient C_tr. The effect of the FB wear on the clearance can be equated to a reduction in ω₀, which means that when the HD is working under low torque, the coupled relationship between the FB wear and the FB ball load should be focused on. The variation of the FS geometric parameters on the ball load can be neglected, and the geometric parameters of the FB should be corrected for the investigation on wear.

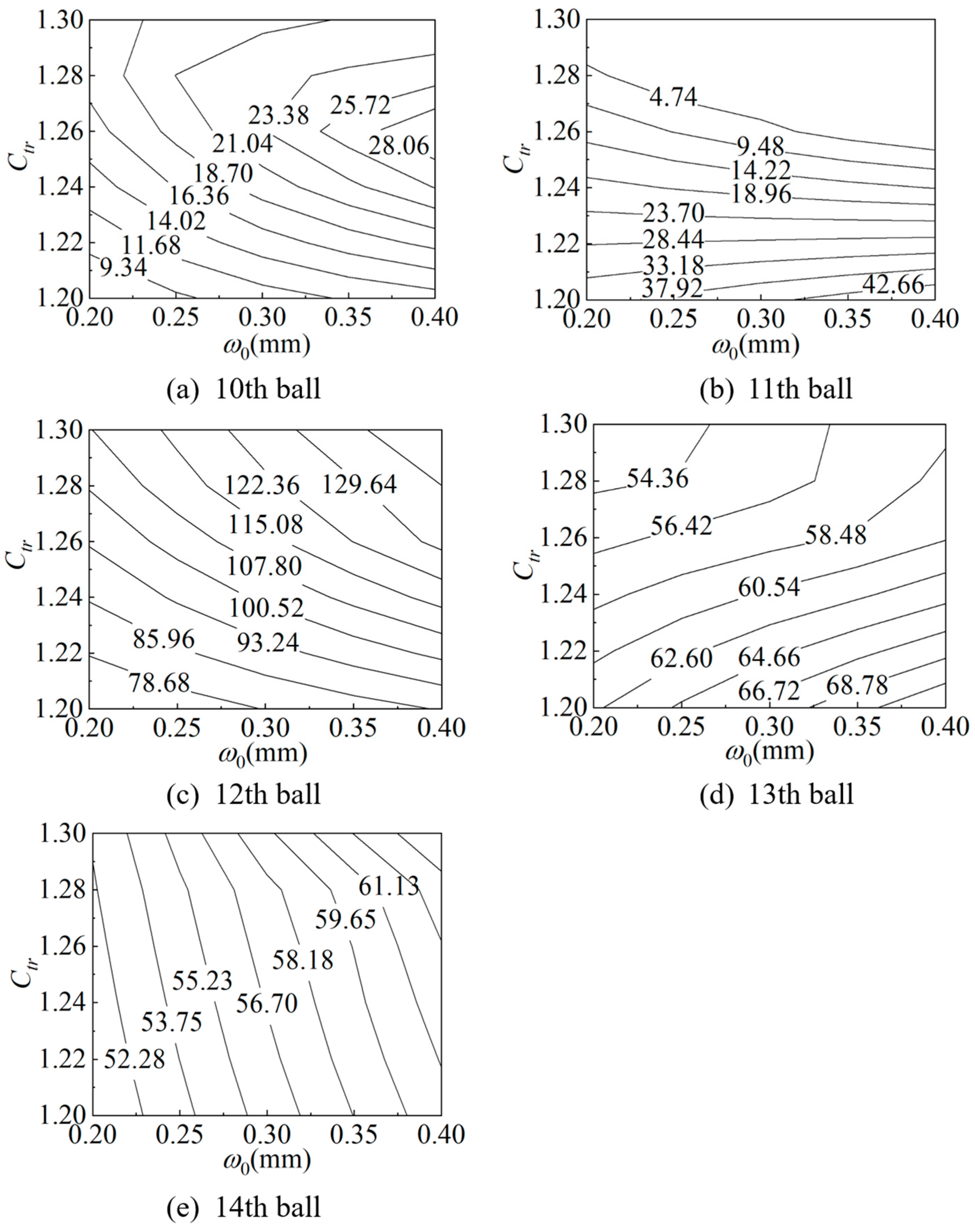
4.2. Orthogonal Simulation Under Rated Torque

The results of the orthogonal simulation of the ω₀ and C_tr of the FB ball load under rated torque are illustrated as a contour map in Figure 16. It can be noted that the ball load varies significantly with changing ω₀ and C_tr.

Surface equations, as shown in Equations (21)–(25), are constructed to fit the FB ball load within the major contact zone in Figure 16. Based on Section 3, the 10th ball load is changed parabolically with C_tr. The surface equation can then be constructed:

$$Q_{10}=42.0258{\omega }_0-2491.4189{(C_{tr}+0.02673{\omega }_0-1.2789)}^2+9.7033.$$

(21)

The 11th ball load is changed exponentially with C_tr. The surface equation can be constructed:

$$Q_{11}=-35.4051{\omega }_0+9804.9620e^{-3.7059C_{tr}}-71.1757.$$

(22)

The 12th ball load is changed in a power function with C_tr. The surface equation can then be constructed:

$$Q_{12}=250.8662{\omega }_0-1497.6177{\left(C_{tr}-{\displaystyle \frac{0.0175}{{\omega }_0}}\right)}^{-12.8433}+79.1926.$$

(23)

The 13th ball load is changed parabolically with C_tr. The surface equation can then be constructed:

$$Q_{13}=15.2763{\omega }_0+861.1740{(C_{tr}-0.1423{\omega }_0-1.28073)}^2+49.98569.$$

(24)

The 14th ball load is changed in a power function with C_tr. The surface equation can then be constructed:

$$Q_{14}=47.17326{\omega }_0+{(0.16317{\omega }_0+0.76556C_{tr})}^{28.51751}+41.38361.$$

(25)

The relationship between the FB ball load and the geometric parameters of the FB and the FS can be rapidly established via Equations (21)–(25). Taking the maximum ball load as an example, combining Equation (3) and Equation (23), the maximum ball load can be written as:

$$Q_{12}=250.8662{\omega }_0-1497.6177{\left({\displaystyle \frac{0.477s_f+0.522r_f}{h_0}}+0.692+{\displaystyle \frac{0.0175}{{\omega }_0}}\right)}^{-12.8433}+79.1926$$

(26)

It can be seen in Equation (26) that, under rated torque, the geometric parameters of the FS are the main factors in the maximum ball load. When the FS is worn, the tooth rack thickness h₀ is reduced. Then, the maximum ball load increases, which leads to severe wear on the FB and the FS. Therefore, in subsequent analyses of the FB wear, under rated external torque, the geometric parameter of the FS must be corrected.

5. Conclusions

Aiming to address the limitation of theoretical ball load calculations and their influence on factor analysis without external torque, an equivalent ring model is improved to calculate the FB ball load under various torques in this paper. The effects of the geometric parameters of the FB and the FS on the FB ball load are investigated. In addition, the fitting formulae are obtained to rapidly evaluate the FB ball load in a major contact zone. The conclusions are summarized as follows:

(1)

The ball load solution model is established under various external torques by analyzing the contact and deformation of the FS and the FB. The calculation of the FB ball load is more consistent with that of the FEM model. The maximum error of the ball load engaged in contact is 6.09%, and the accuracy was improved by 59.58% compared to the original equivalent ring model.

(2)

The FB ball load is greatly affected by the geometric parameters of the FS tooth. As the root thickness and the dedendum arc radius increase, the maximum ball load increases, and when the tooth rack thickness increases, the maximum ball load decreases. With the bending stiffness coefficient increasing from 1.2 to 1.3, the maximum ball load increases by 76.7%.

(3)

The geometric parameters that mainly affect the ball load vary under different external torques. The maximum radial deformation is the main factor under low external torque, while the bending stiffness coefficient is the main factor under rated external torque. This provides a basis for selecting the correction of the geometric parameters in subsequent wear analysis.