On the Use of the Detectivity Parameter for the Condition Monitoring of Wind Turbines
Abstract
1. Introduction
1.1. Motivation and Background
1.2. Literature Review
1.3. Present Study Overview
2. Theory of Hjorth’s Parameters and Detectivity
2.1. Synopsis
2.2. Time-Domain Hjorth’s Parameters Definition
- Activity (Act): as a measure of variance, reflects the overall energy or intensity of the signal:In practical terms, it is sensitive to amplitude fluctuations and can be used to detect changes in signal power due to external perturbations, noise, or the dynamics of the underlying system. For example, in mechanical systems, an increase in Activity may indicate the onset of wear or imbalance.
- Mobility (Mob): measures the standard deviation of the signal’s frequency content,It is particularly useful for identifying transitions in operating regimes or shifts in dominant frequency components. Since it is normalized via Activity, Mobility is invariant to amplitude scaling, making it robust for a comparative analysis across different signal magnitudes.
- Complexity (Comp): quantifies the variation in frequency, indicating how similar the signal is to a pure sine wave,It serves as a higher-order descriptor, capturing the intricacy of the waveform, and it is sensitive to the presence of fine-grained structures, such as modulations, transients, or irregular oscillations. A signal with high complexity may exhibit non-stationary behavior, multi-frequency content, or structural irregularities that are not evident from Activity or Mobility alone.
2.3. Frequency-Domain Interpretation of Hjorth’s Parameters
- Activity is associated with the zeroth-order spectral moment:This represents the total power of the signal and corresponds to its variance in the time domain, as established by Parseval’s theorem.
- Mobility is related to the second-order spectral moment and is defined as follows:where the integration bounds ( to ) are omitted to avoid overloading the notation (this simplification will be used hereafter). The given expression reflects the spread of the spectral energy around the origin and can be interpreted as the standard deviation of the frequency content. Signals with higher Mobility exhibit more rapid fluctuations or higher dominant frequencies.
- Complexity involves a normalized combination of the fourth, second, and zeroth-order moments:This parameter quantifies the deviation of the signal from a pure sinusoid. A Complexity value close to 1 indicates a narrow-band, regular waveform (e.g., a sine wave), while higher values suggest richer spectral content, broader bandwidth, or structural irregularity in the signal.
- : Total signal power (area under the PSD curve).
- : Frequency-weighted power, emphasizing higher frequencies.
- : Sensitivity to bandwidth and sharpness of spectral peaks.
2.4. Definition of Detectivity
- Activity increases with signal energy, often associated with fault onset or increased dynamic excitation.
- Mobility tends to decrease when the signal becomes more irregular or lower in frequency content.
- Complexity increases with waveform irregularity and spectral density.
3. LTU Wind Turbines Dataset
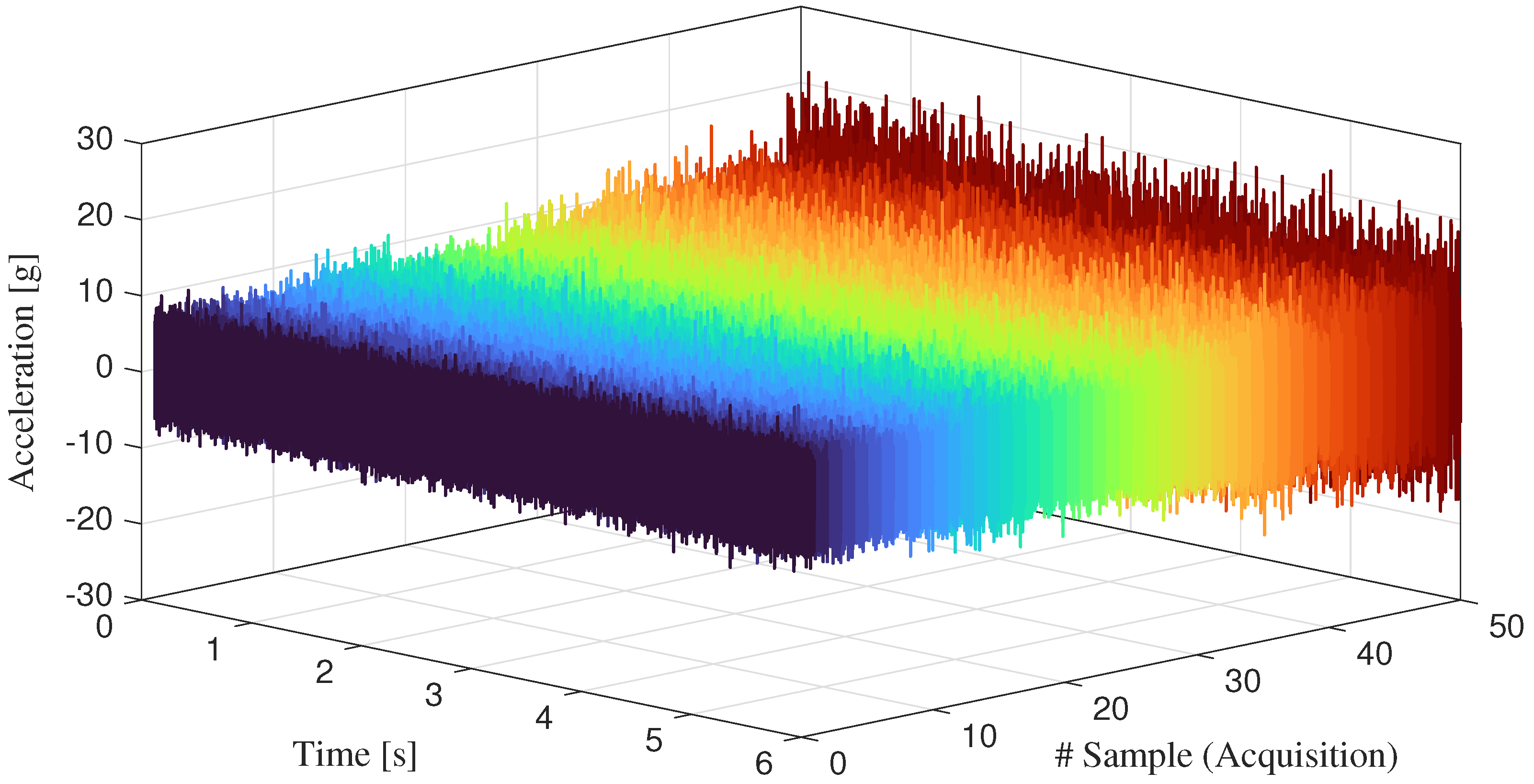
3.1. Dataset Description
- Inner raceway failure on a four-point ball bearing on the output shaft: the output shaft bearing was replaced after 1.2 years in operation.
- Inner raceway failure in one of the four cylindrical roller bearings that support one of the planets in the first planetary gear: the entire gearbox was replaced after 2 years in operation.
3.2. Analysis Methodology
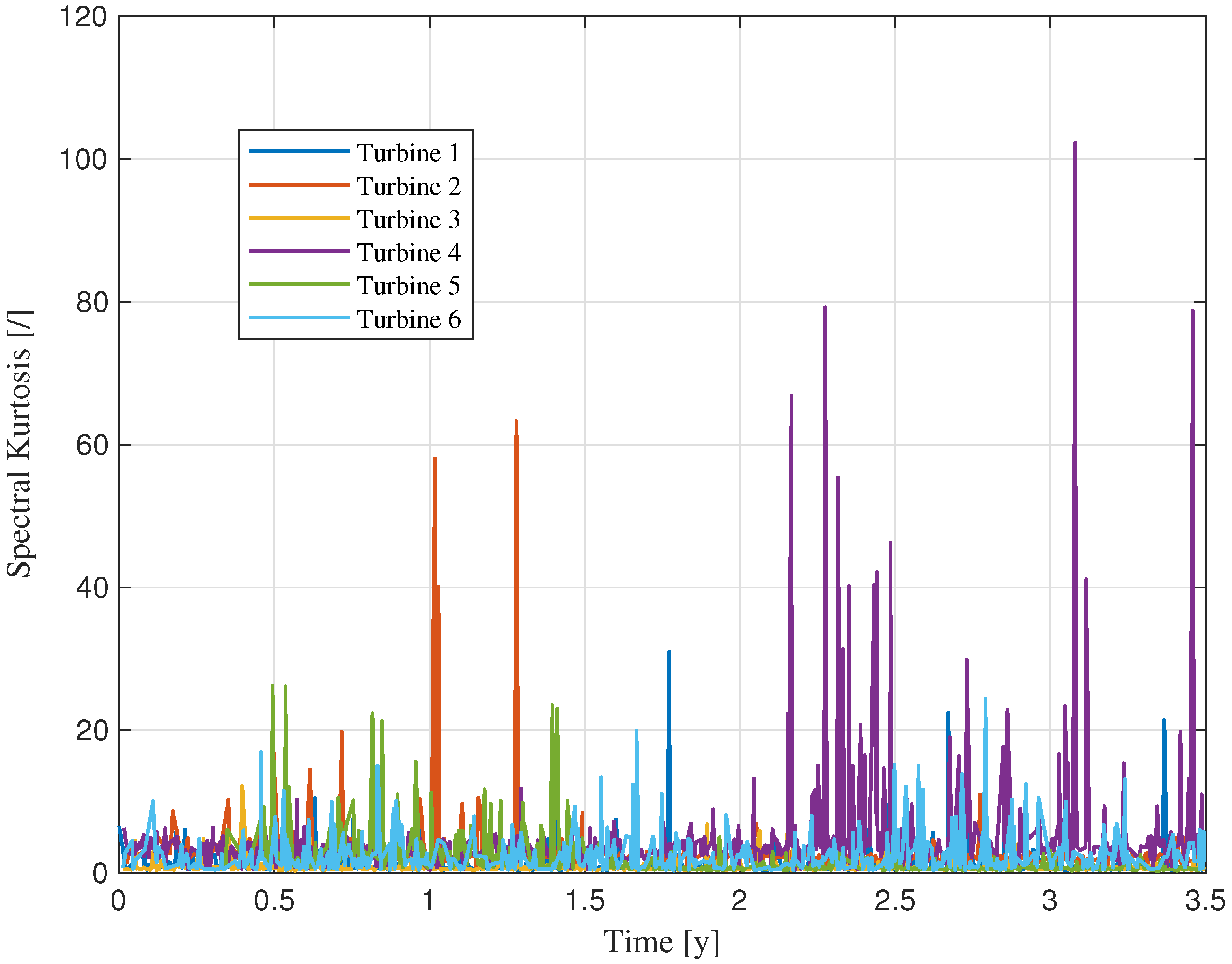
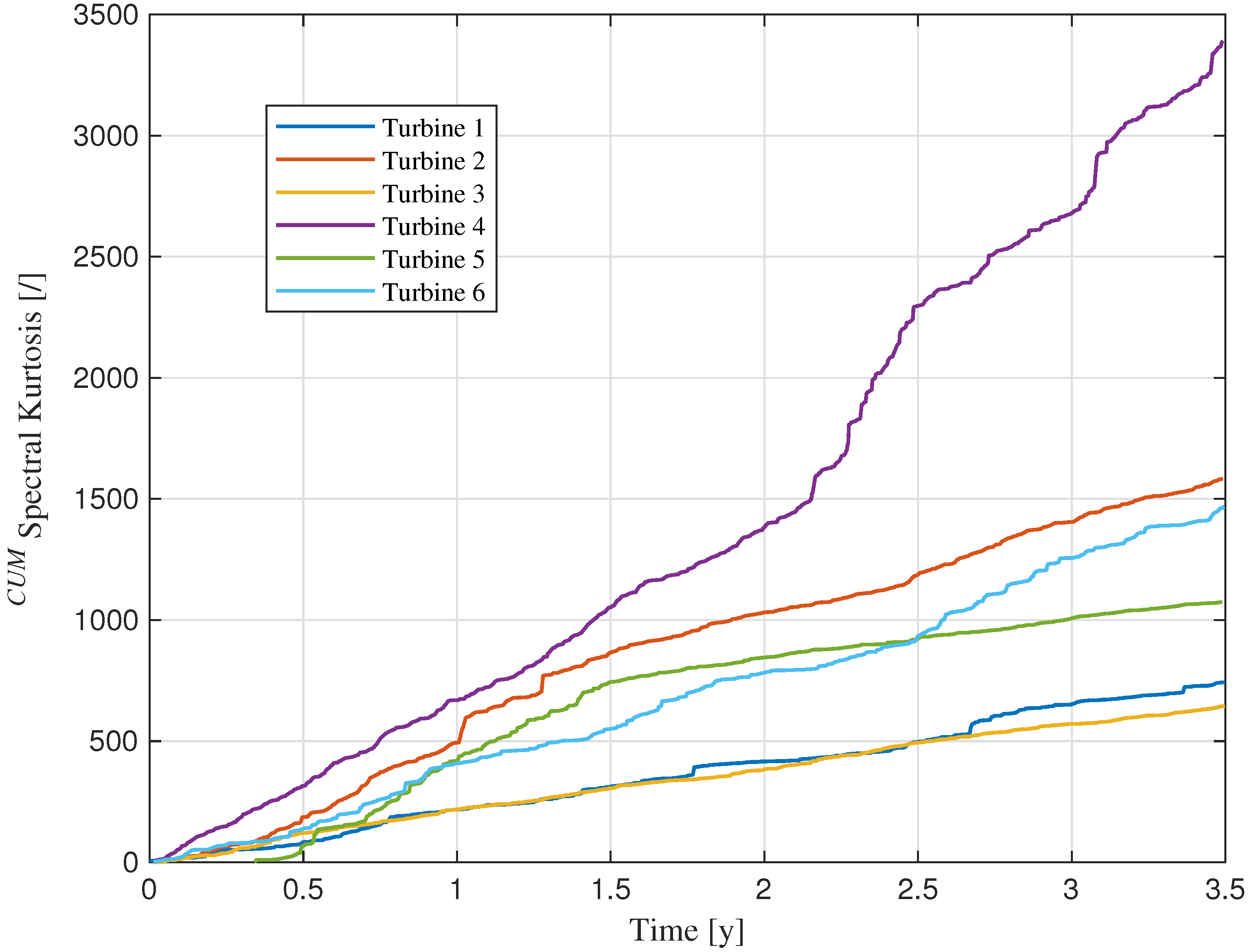
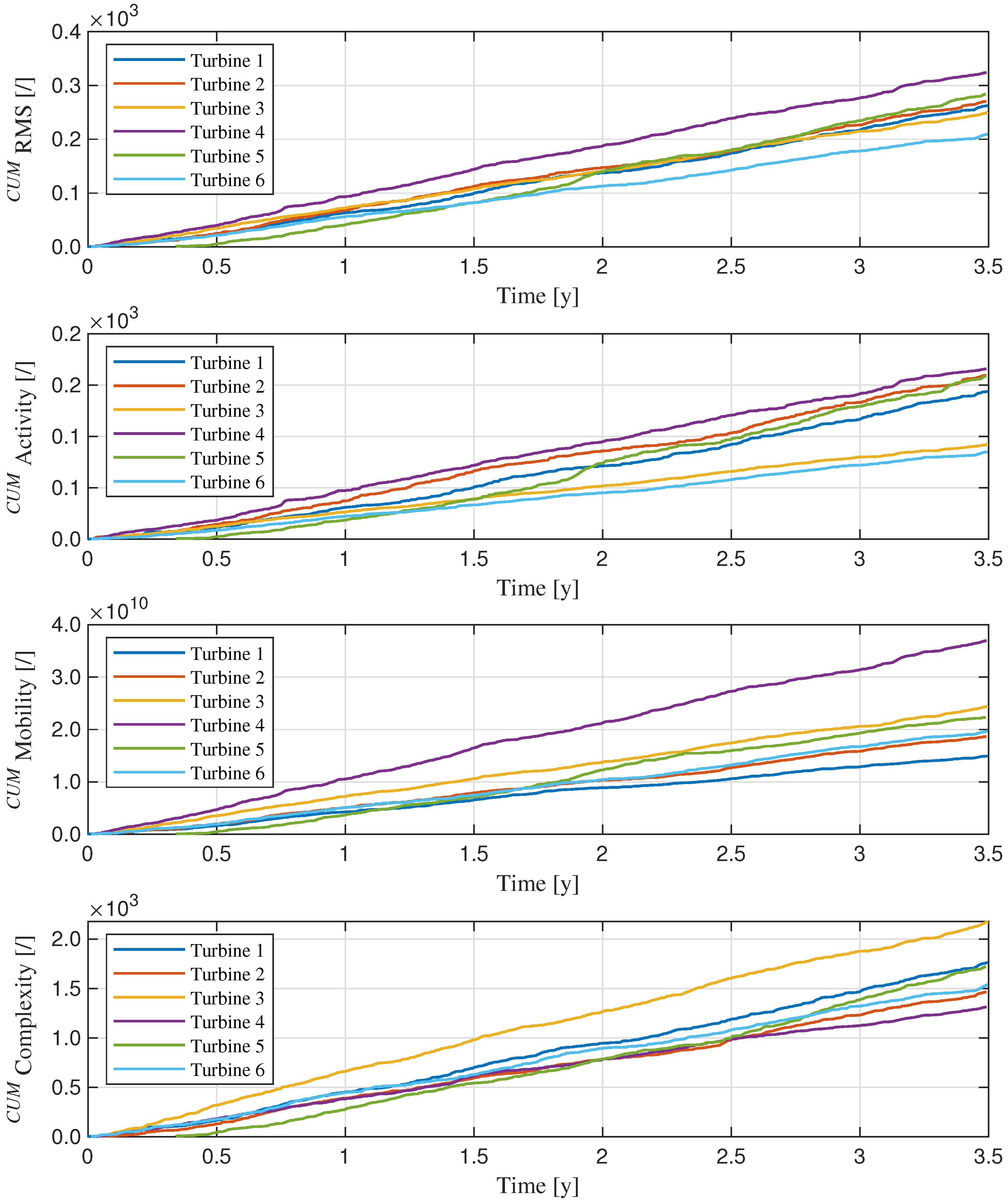
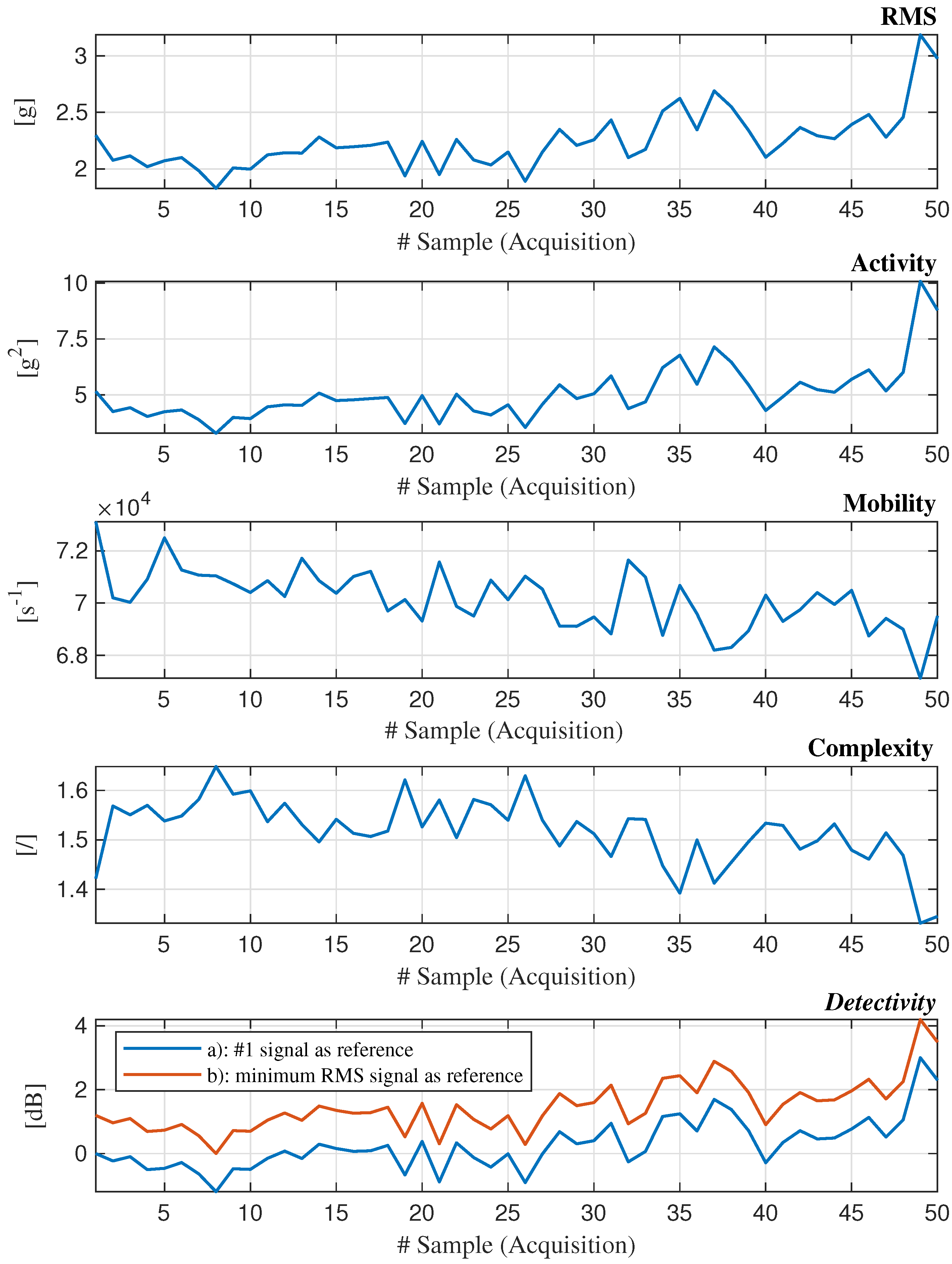
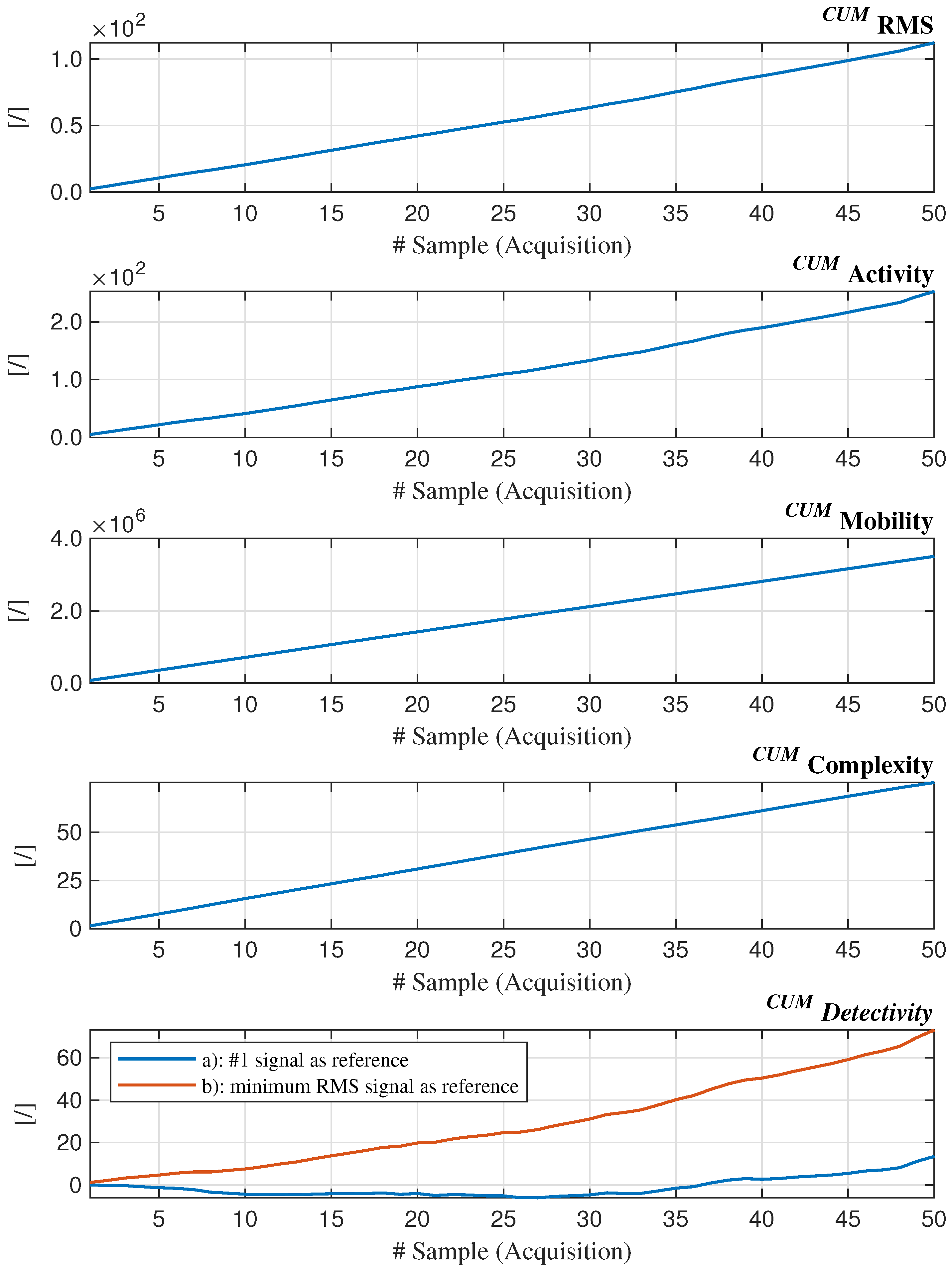
3.3. Results
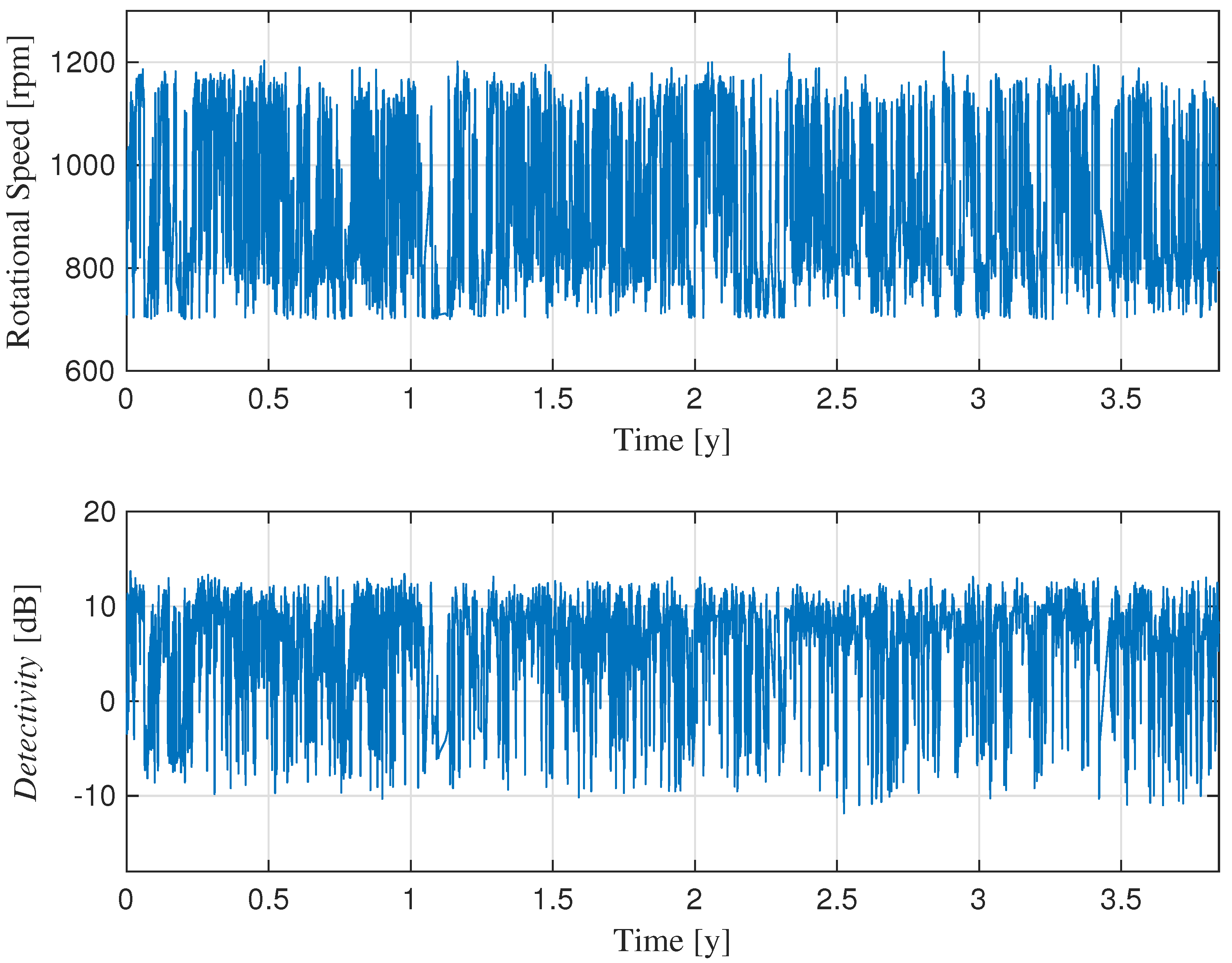
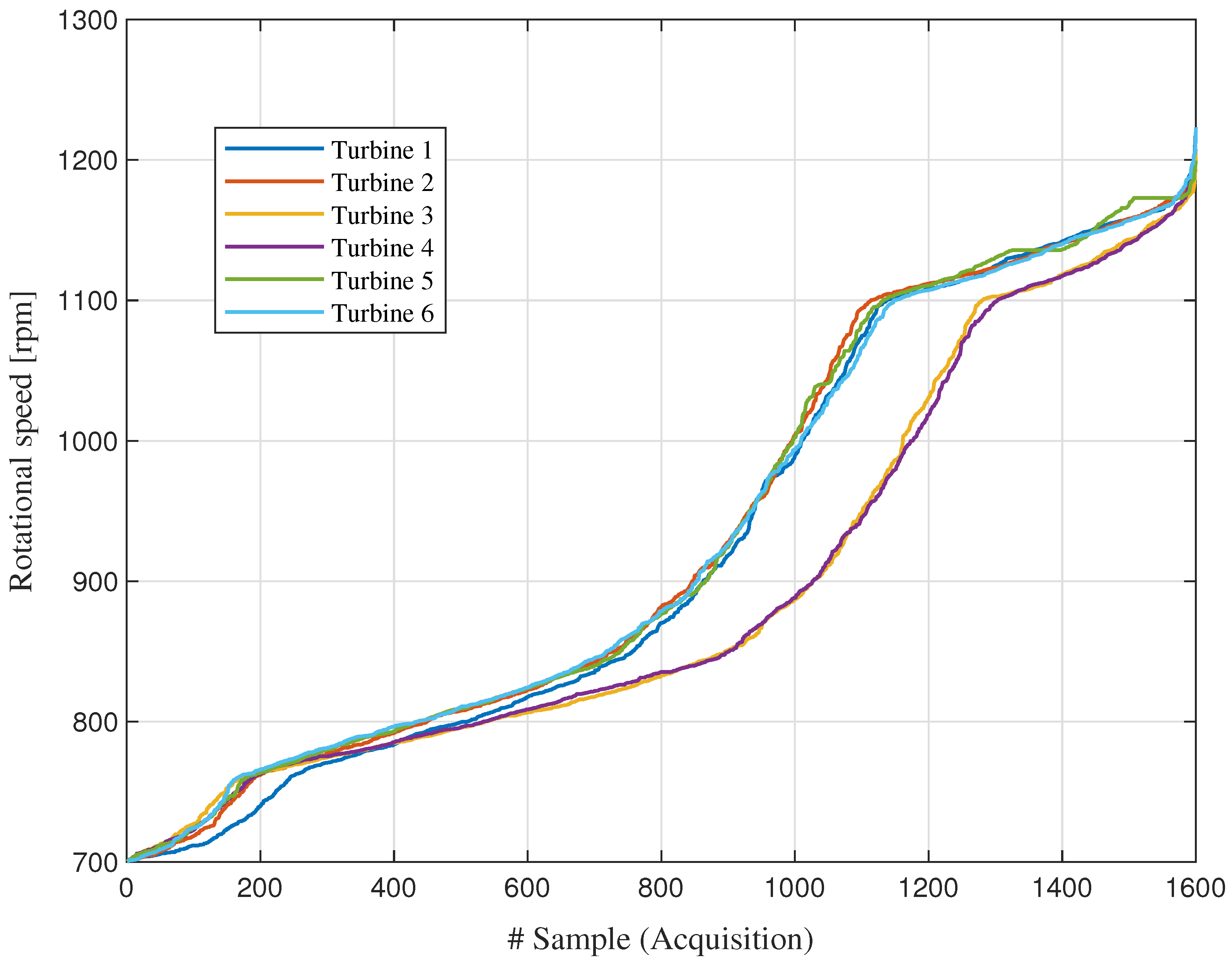
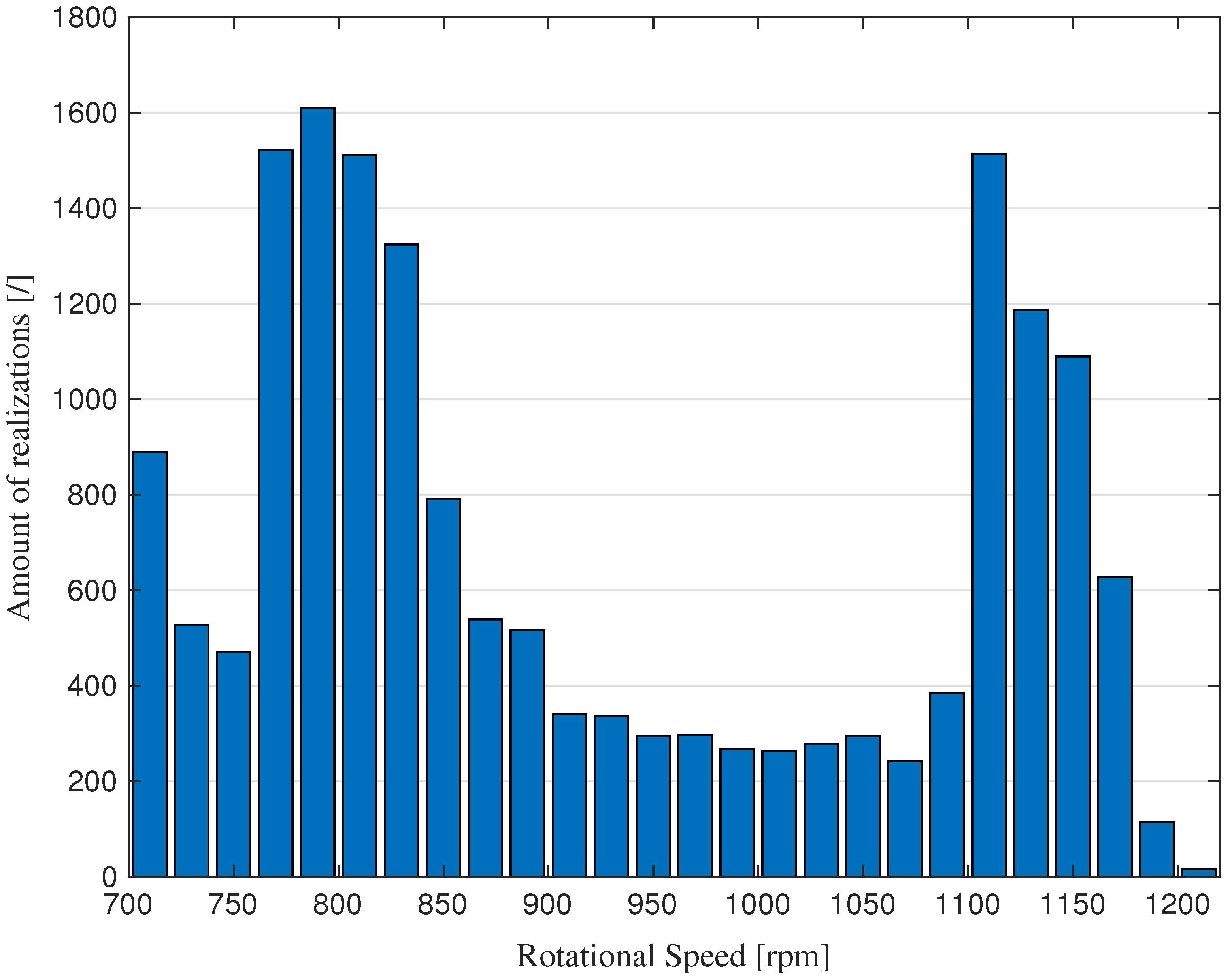
4. Utility-Scale Wind Turbine Dataset
4.1. Dataset Description
- FTF: 0.42 × (shaft speed)
- BPFO: 6.72 × (shaft speed)
- BPFI: 9.47 × (shaft speed)
- BSF: 1.435 × (shaft speed)
4.2. Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Act | Activity |
| Mob | Mobility |
| Com | Complexity |
| Dtc | Detectivity |
| Generic metric expressed in dB | |
| Generic metric obtained by applying the reference signal | |
| Gs | Gaussian signal |
| SK | Spectral Kurtosis |
| Cumulant of a generic metric | |
| k-th element of the cumulative vector of a generic metric | |
| FTF | Fundamental train frequency |
| BPFO | Ball pass frequency outer race |
| BPFI | Ball pass frequency inner race |
| BSF | Ball spin frequency |
References
- Taylor, J.I. The Gear Analysis Handbook; Vibration Consultants: Tampa, FL, USA, 2000. [Google Scholar]
- Taylor, J.I.; Kirkland, D.W. The Bearing Analysis Handbook; Vibration Consultants: Tampa, FL, USA, 2004. [Google Scholar]
- Taylor, J.I. The Vibration Analysis Handbook; Vibration Consultants: Tampa, FL, USA, 2003. [Google Scholar]
- Randall, R.B. Vibration-Based Condition Monitoring; John Wiley & Sons: Chichester, UK, 2003. [Google Scholar]
- Randall, R.B.; Antoni, J. Rolling element bearing diagnostics—A tutorial. Mech. Syst. Signal Process. 2011, 25, 485–520. [Google Scholar] [CrossRef]
- El-Thalji, I.; Jantunen, E. A summary of fault modelling and predictive health monitoring of rolling element bearings. Mech. Syst. Signal Process. 2015, 60, 252–272. [Google Scholar] [CrossRef]
- Moshrefzadeh, A.; Fasana, A. Planetary gearbox with localised bearings and gears faults: Simulation and time/frequency analysis. Meccanica 2017, 52, 3759–3779. [Google Scholar] [CrossRef]
- D’Elia, G.; Delvecchio, S.; Cocconcelli, M.; Dalpiaz, G. Application of cyclostationary indicators for the diagnostics of distributed faults in ball bearings. In Proceedings of the ASME Design Engineering Technical Conference, Portland, OR, USA, 4–7 August 2013; Volume 8. [Google Scholar]
- D’Elia, G.; Cocconcelli, M.; Mucchi, E. An algorithm for the simulation of faulted bearings in non-stationary conditions. Meccanica 2018, 53, 1147–1166. [Google Scholar] [CrossRef]
- Hurley, N.; Rickard, S. Comparing measures of sparsity. IEEE Trans. Inf. Theory 2009, 55, 4723–4741. [Google Scholar] [CrossRef]
- Wang, D. Some further thoughts about spectral kurtosis, spectral L2/L1 norm, spectral smoothness index and spectral Gini index for characterizing repetitive transients. Mech. Syst. Signal Process. 2018, 108, 360–368. [Google Scholar] [CrossRef]
- Wang, D.; Peng, Z.; Xi, L. The sum of weighted normalized square envelope: A unified framework for kurtosis, negative entropy, Gini index and smoothness index for machine health monitoring. Mech. Syst. Signal Process. 2020, 140, 106725. [Google Scholar] [CrossRef]
- Albezzawy, M.N.; Nassef, M.G.; Sawalhi, N. Rolling element bearing fault identification using a novel three-step adaptive and automated filtration scheme based on Gini index. ISA Trans. 2020, 101, 453–460. [Google Scholar] [CrossRef]
- Antoni, J. The spectral kurtosis: A useful tool for characterising non-stationary signals. Mech. Syst. Signal Process. 2006, 20, 282–307. [Google Scholar] [CrossRef]
- Miao, Y.; Zhao, M.; Hua, J. Research on sparsity indexes for fault diagnosis of rotating machinery. Measurement 2020, 158, 107735. [Google Scholar] [CrossRef]
- Stewart, R.M. Some Useful Data Analysis Techniques for Gearbox Diagnostics; Report MHM/R/10/77; Machine Health Monitoring Group, Institute of Sound and Vibration Research, University of Southampton: Southampton, UK, 1977. [Google Scholar]
- Sharma, V.; Parey, A. A review of gear fault diagnosis using various condition indicators. Procedia Eng. 2016, 144, 253–263. [Google Scholar] [CrossRef]
- Antoni, J.; Borghesani, P. A statistical methodology for the design of condition indicators. Mech. Syst. Signal Process. 2019, 114, 290–327. [Google Scholar] [CrossRef]
- Cerrada, M.; Sánchez, R.V.; Li, C.; Pacheco, F.; Cabrera, D.; Valente de Oliveira, J.; Vásquez, R.E. A review on data-driven fault severity assessment in rolling bearings. Mech. Syst. Signal Process. 2018, 99, 169–196. [Google Scholar] [CrossRef]
- Cocconcelli, M.; Capelli, L.; Camargo Molano, J.C.; Borghi, D. Development of a methodology for condition-based maintenance in a large-scale application field. Machines 2018, 6, 17. [Google Scholar] [CrossRef]
- Li, X.; Yu, T.; Wang, X.; Li, D.; Xie, Z.; Kong, X. Fusing joint distribution and adversarial networks: A new transfer learning method for intelligent fault diagnosis. Appl. Acoust. 2024, 216, 109767. [Google Scholar] [CrossRef]
- Zhi, S.; Su, K.; Yu, J.; Li, X.; Shen, H. An unsupervised transfer learning bearing fault diagnosis method based on multi-channel calibrated Transformer with shiftable window. Struct. Health Monit. 2025, 28, 1–18. [Google Scholar] [CrossRef]
- Li, X.; Xiao, S.; Li, Q.; Zhu, L.; Wang, T.; Chu, F. The bearing multi-sensor fault diagnosis method based on a multi-branch parallel perception network and feature fusion strategy. Reliab. Eng. Syst. Saf. 2025, 261, 111122. [Google Scholar] [CrossRef]
- Zhi, S.; Niu, Y.; Ma, L.; Wu, H.; Shen, H.; Wang, T. Local entropy selection scaling-extracting Chirplet transform for enhanced time-frequency analysis and precise state estimation in reliability-focused fault diagnosis of non-stationary signals. Eksploat. Niezawodn. Maint. Reliab. 2026, 28, 1–18. [Google Scholar] [CrossRef]
- Hjorth, B.; Elema-Schönander, A.B. EEG analysis based on time domain properties. Electroencephalogr. Clin. Neurophysiol. 1970, 29, 306–310. [Google Scholar] [CrossRef]
- Cocconcelli, M.; Strozzi, M.; Camargo Molano, J.C.; Rubini, R. Detectivity: A combination of Hjorth’s parameters for condition monitoring of ball bearings. Mech. Syst. Signal Process. 2022, 160, 108247. [Google Scholar] [CrossRef]
- Cocconcelli, M.; d’Elia, G.; Strozzi, M.; Rubini, R. Diagnostics of Wind Turbine by Detectivity. In Proceedings of the 5th International Conference of the International Federation for the Promotion of Mechanism and Machine Science (IFToMM Italy 2024), Turin, Italy, 11–13 September 2024; pp. 319–326. [Google Scholar]
- LTU Wind Dataset Homepage. Available online: https://ltu.diva-portal.org/smash/record.jsf?pid=diva2%3A1244889&dswid=-7062 (accessed on 4 July 2024).
- Martin-del-Campo, S.; Sandin, F.; Strömbergsson, D. Dictionary Learning Approach to Monitoring of Wind Turbine Drivetrain Bearings. Int. J. Comput. Intell. Syst. 2021, 14, 1–10. [Google Scholar] [CrossRef]
- Github—Wind Turbine High-Speed Bearing Prognosis Data. Available online: https://github.com/mathworks/WindTurbineHighSpeedBearingPrognosis-Data (accessed on 4 July 2025).
- Bechhoefer, E.; Van Hecke, B.; He, D. Processing for Improved Spectral Analysis. In Proceedings of the Annual Conference of the Prognostics and Health Management Society, New Orleans, LA, USA, 14–17 October 2013. [Google Scholar]
- D’Elia, G.; Cocconcelli, M.; Daga, A.P.; Garibaldi, L.; Rubini, R. Bearing diagnostics based on a Spectral combination of Hjorth’s parameters. In Proceedings of the SURVISHNO 2023—International Conference on Surveillance, Vibration and Signal Processing for Fault Detection, Trondheim, Norway, 20–22 June 2023. [Google Scholar]
- Antoni, J. Fast computation of the kurtogram for the detection of transient faults. Mech. Syst. Signal Process. 2007, 21, 108–124. [Google Scholar] [CrossRef]
- MathWorks—Wind Turbine High-Speed Bearing Prognosis. Available online: https://it.mathworks.com/help/predmaint/ug/wind-turbine-high-speed-bearing-prognosis.html (accessed on 4 July 2025).
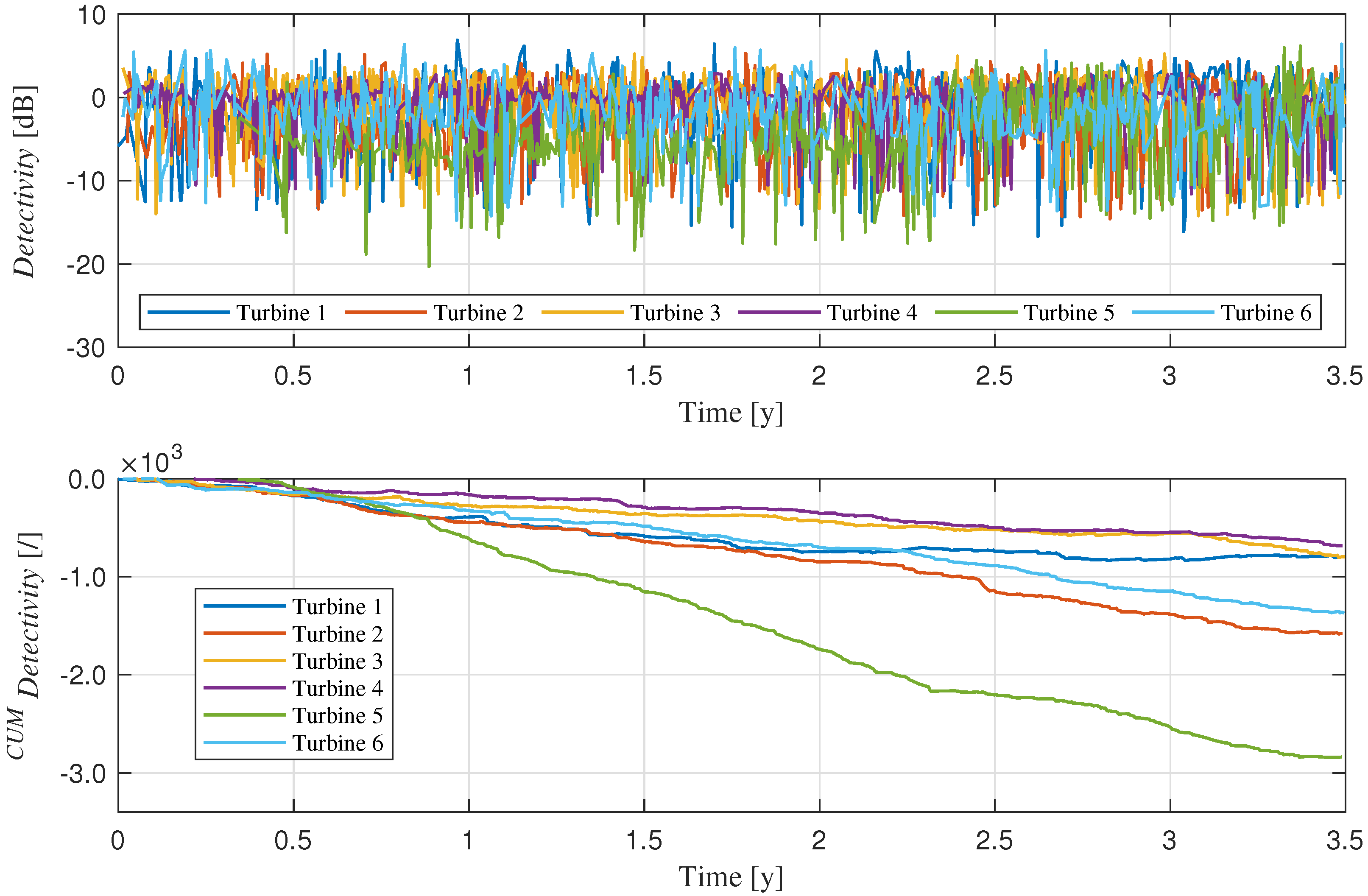


| Tested Turbine | |||||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | ||
| Turbine taken as reference | 1 | 0 | 49.2 | 60.9 | 63.4 | 69.6 | 59.9 |
| 2 | 49.2 | 0 | 54.8 | 56.6 | 63.5 | 53.6 | |
| 3 | 60.9 | 54.8 | 0 | 20.7 | 63.1 | 54.5 | |
| 4 | 63.4 | 56.6 | 20.7 | 0 | 66.9 | 55.8 | |
| 5 | 69.6 | 63.5 | 63.1 | 66.9 | 0 | 63.3 | |
| 6 | 59.9 | 53.6 | 54.5 | 55.8 | 63.3 | 0 | |
| Zero-mean Gs as reference | 6.15 | 2.32 | 1.17 | 1.09 | 6.13 | 1.47 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grosso, P.; D’Elia, G.; Strozzi, M.; Rubini, R.; Cocconcelli, M. On the Use of the Detectivity Parameter for the Condition Monitoring of Wind Turbines. Machines 2025, 13, 980. https://doi.org/10.3390/machines13110980
Grosso P, D’Elia G, Strozzi M, Rubini R, Cocconcelli M. On the Use of the Detectivity Parameter for the Condition Monitoring of Wind Turbines. Machines. 2025; 13(11):980. https://doi.org/10.3390/machines13110980
Chicago/Turabian StyleGrosso, Pasquale, Gianluca D’Elia, Matteo Strozzi, Riccardo Rubini, and Marco Cocconcelli. 2025. "On the Use of the Detectivity Parameter for the Condition Monitoring of Wind Turbines" Machines 13, no. 11: 980. https://doi.org/10.3390/machines13110980
APA StyleGrosso, P., D’Elia, G., Strozzi, M., Rubini, R., & Cocconcelli, M. (2025). On the Use of the Detectivity Parameter for the Condition Monitoring of Wind Turbines. Machines, 13(11), 980. https://doi.org/10.3390/machines13110980








