Integrated Error Compensation for Robotic Arm Polishing of Cylindrical Aspheric Optical Components
Abstract
1. Introduction
2. Related Research
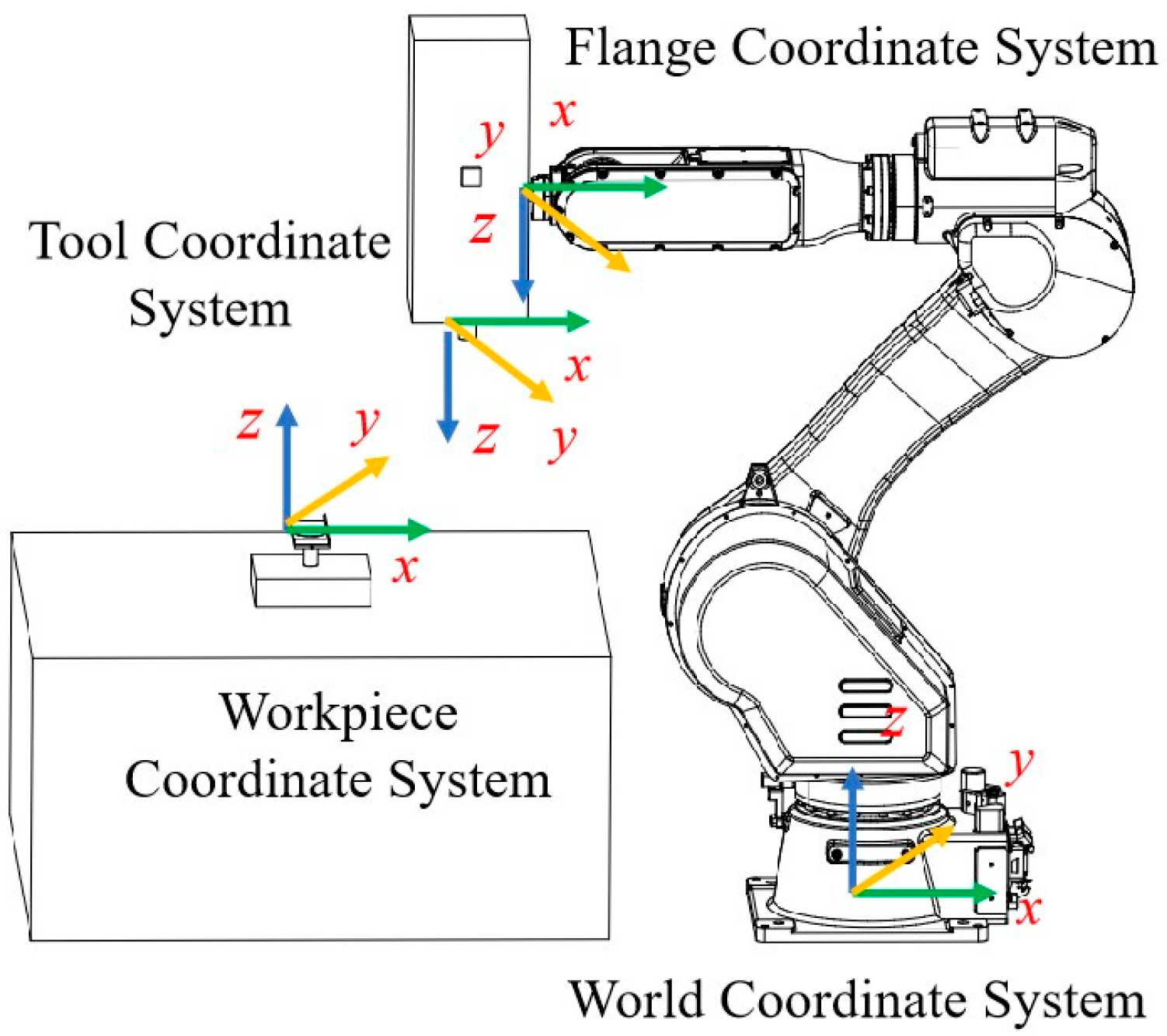
3. Curvature-Driven Trajectory Design for Robotic Arm Polishing
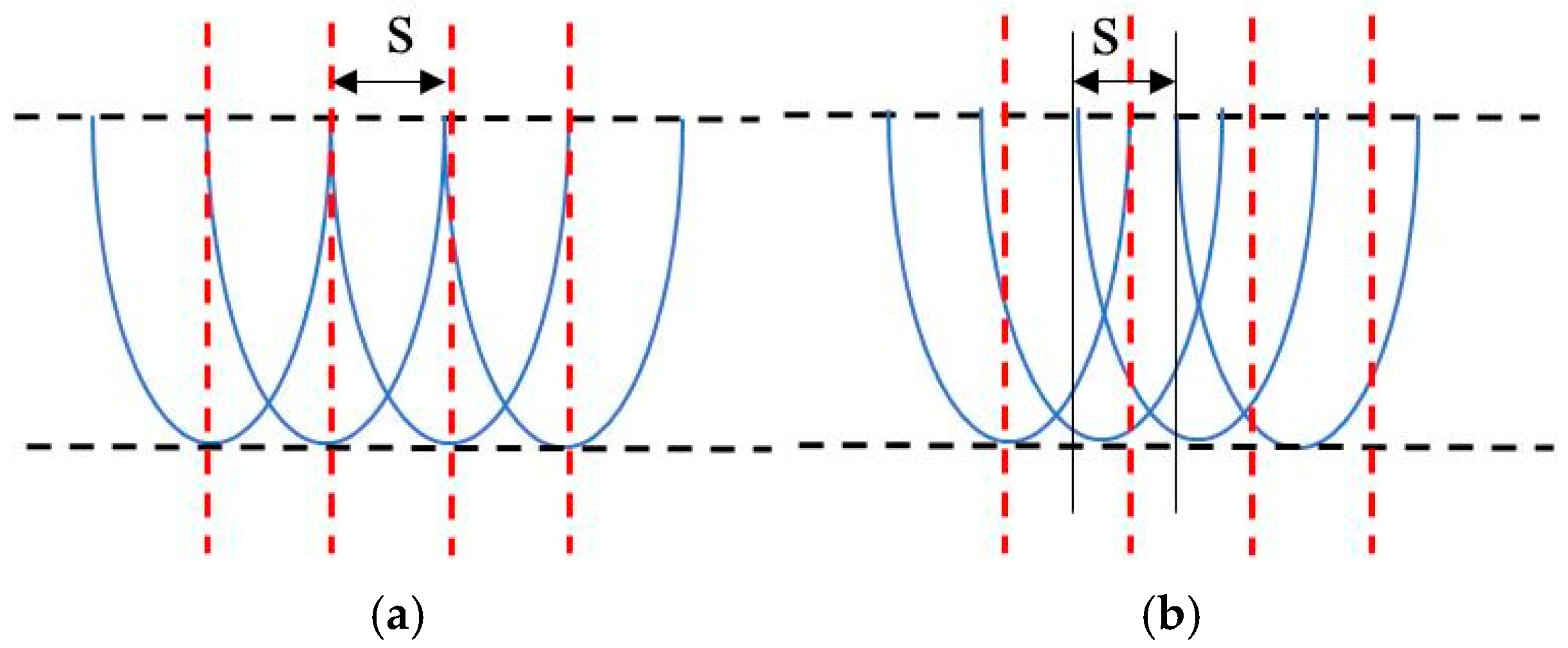
3.1. Grating Trajectory Removal Profile Modeling
- (a)
- When m = 2k + 1, hm achieves its maximum at X = ks, as show in Equation (3).
- (b)
- When m = 2k, hm achieves its maximum at X = (k − 1) s + s/2, as shown in Equation (4).
3.2. Curvature-Driven Variable-Spacing Trajectory Design for Complex Curvature Surfaces
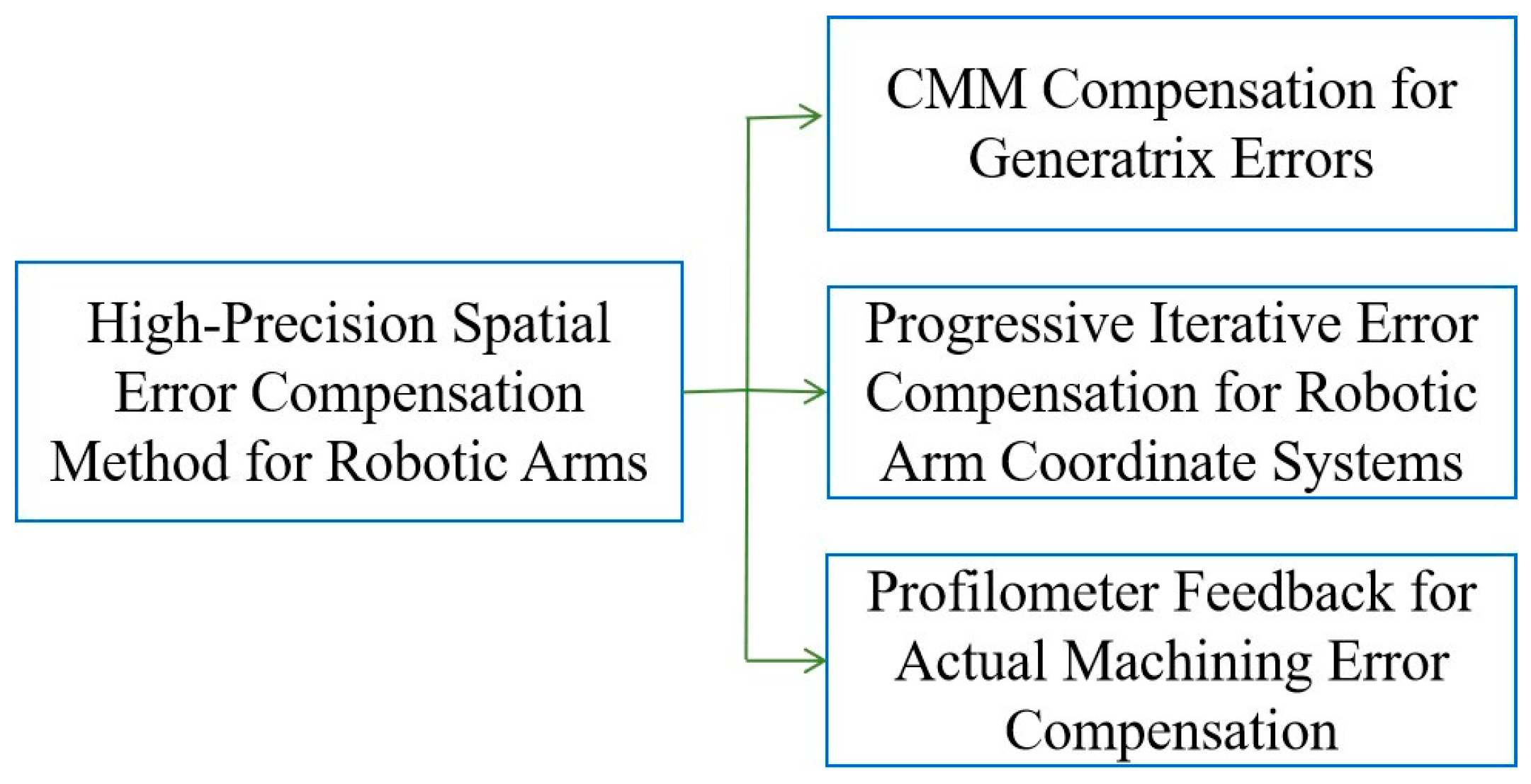
4. Error Compensation Research in Robotic Arm Polishing Processes
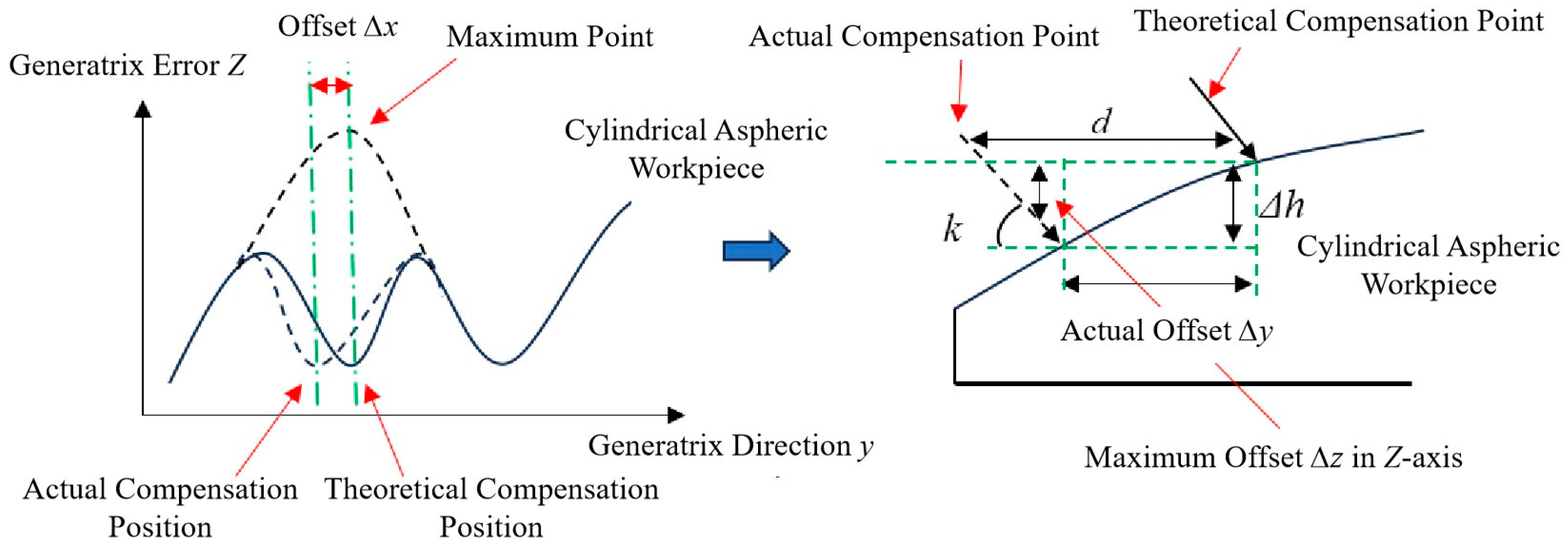
4.1. Cylindrical Generatrix Offset Compensation Based on CMM
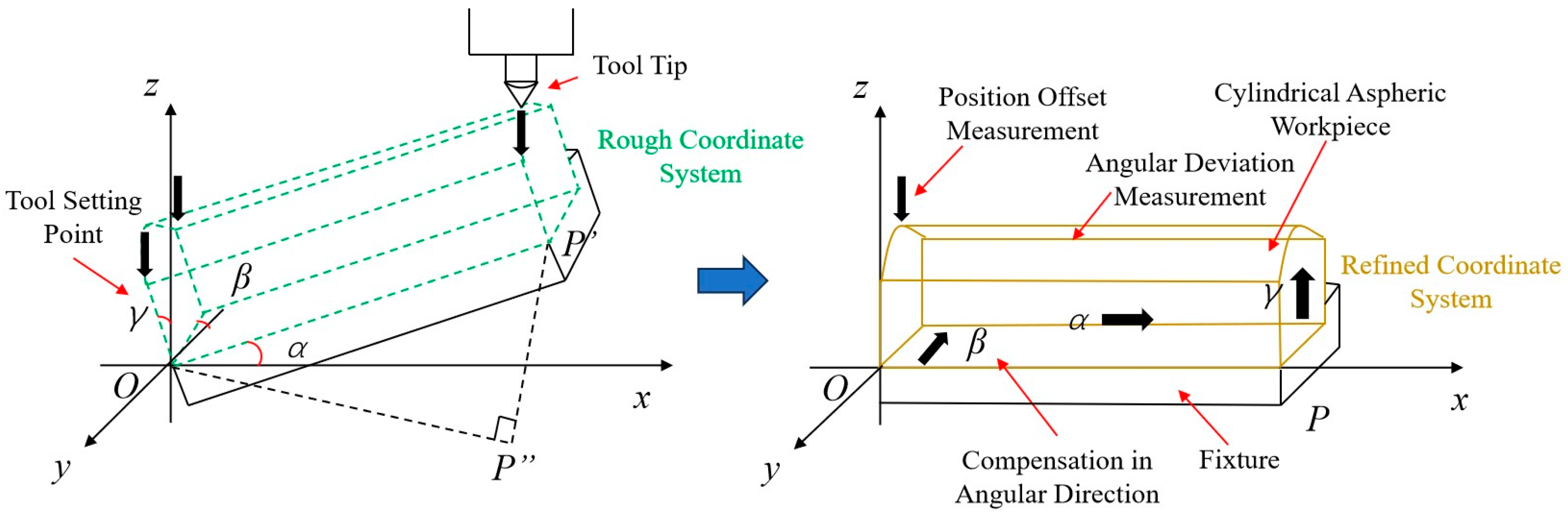
4.2. High-Precision Robotic Arm Coordinate System Progressive Error Compensation
- (a)
- First, the end-effector of the robotic arm approximately establishes the workpiece coordinate system. This initial step incurs an error ranging from 20 to 30 μm due to limited positioning accuracy, which encompasses deviations in three spatial directions and positions.
- (b)
- Second, a dial gauge is employed to accurately measure deviations in three dimensions, thereby maintaining error control at the micrometer level.
- (c)
- Finally, a laser tracker is employed to calibrate the relative position between the end-effector of the robotic arm and the workpiece, thereby obtaining deviations at three distinct positions. Subsequently, it plans for point cloud calibration to refine both the directional and positional errors within the spatial coordinate system. Following three progressive iterations, a high-precision workpiece coordinate system is established.
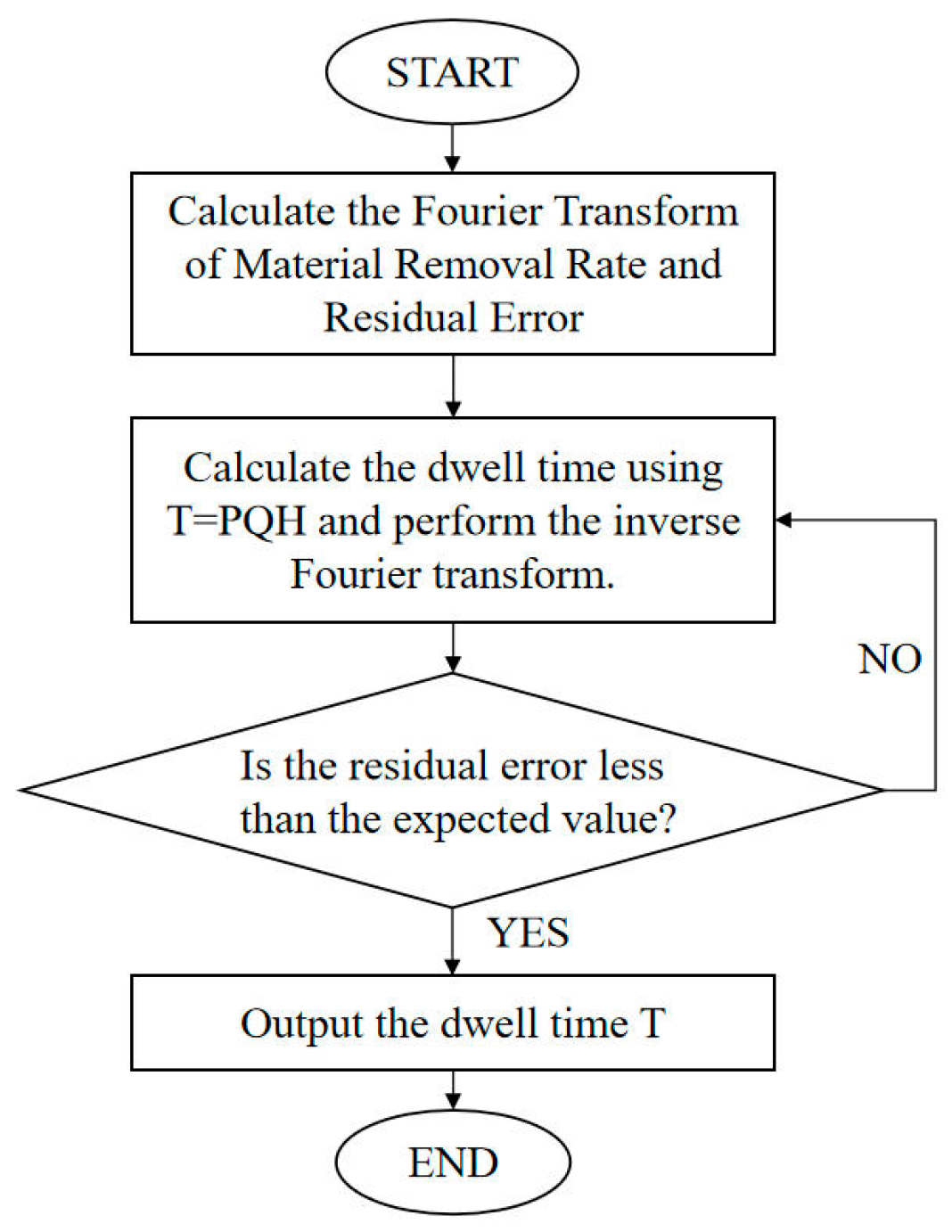
4.3. Error Feedback Compensation Based on Profilometry
5. Robotic Arm Polishing Experiment on Cylindrical Aspheric Workpiece
5.1. Experimental Equipment
5.2. Experimental Environmental Control
5.3. Fixture and Tool Setting Error Compensation
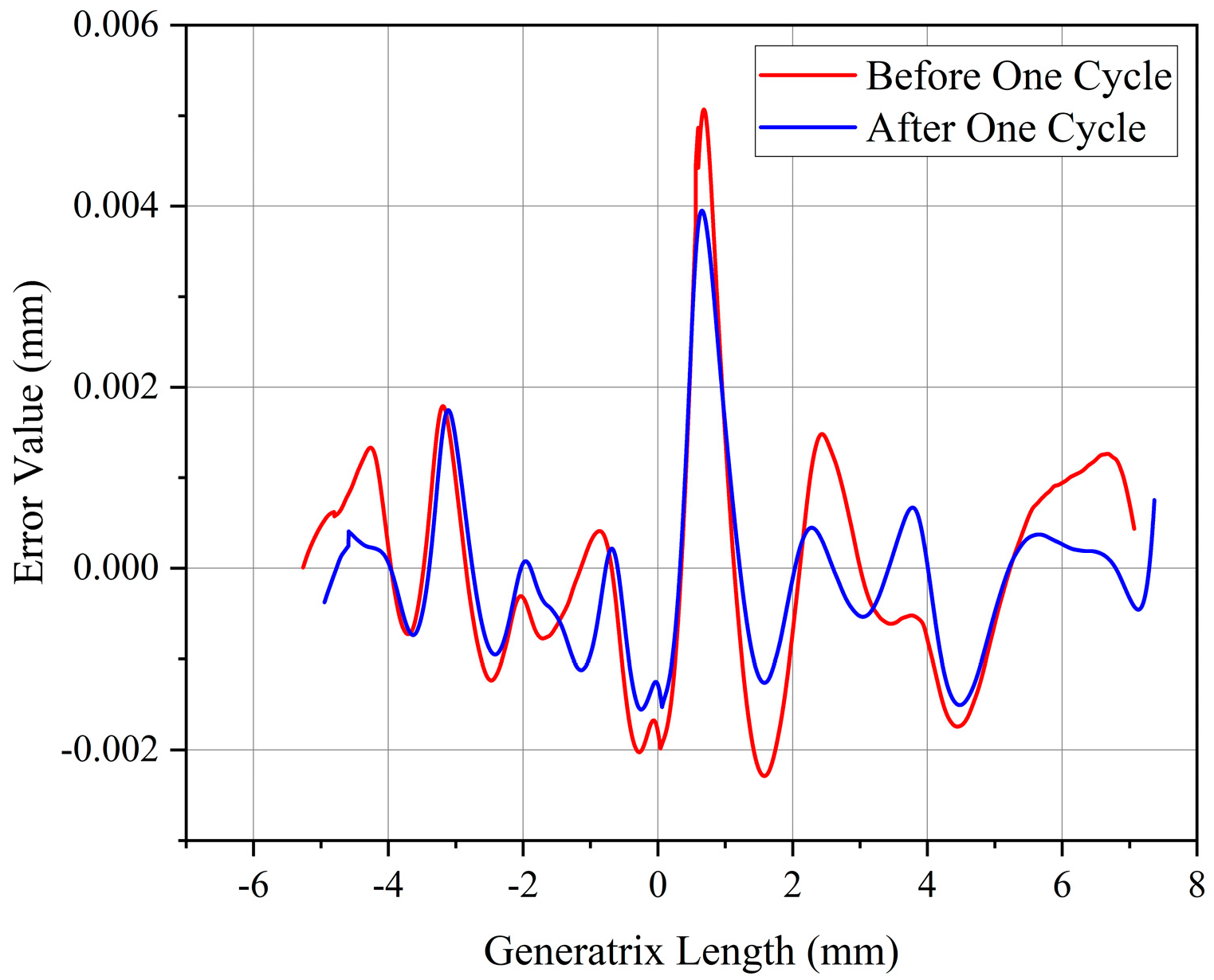
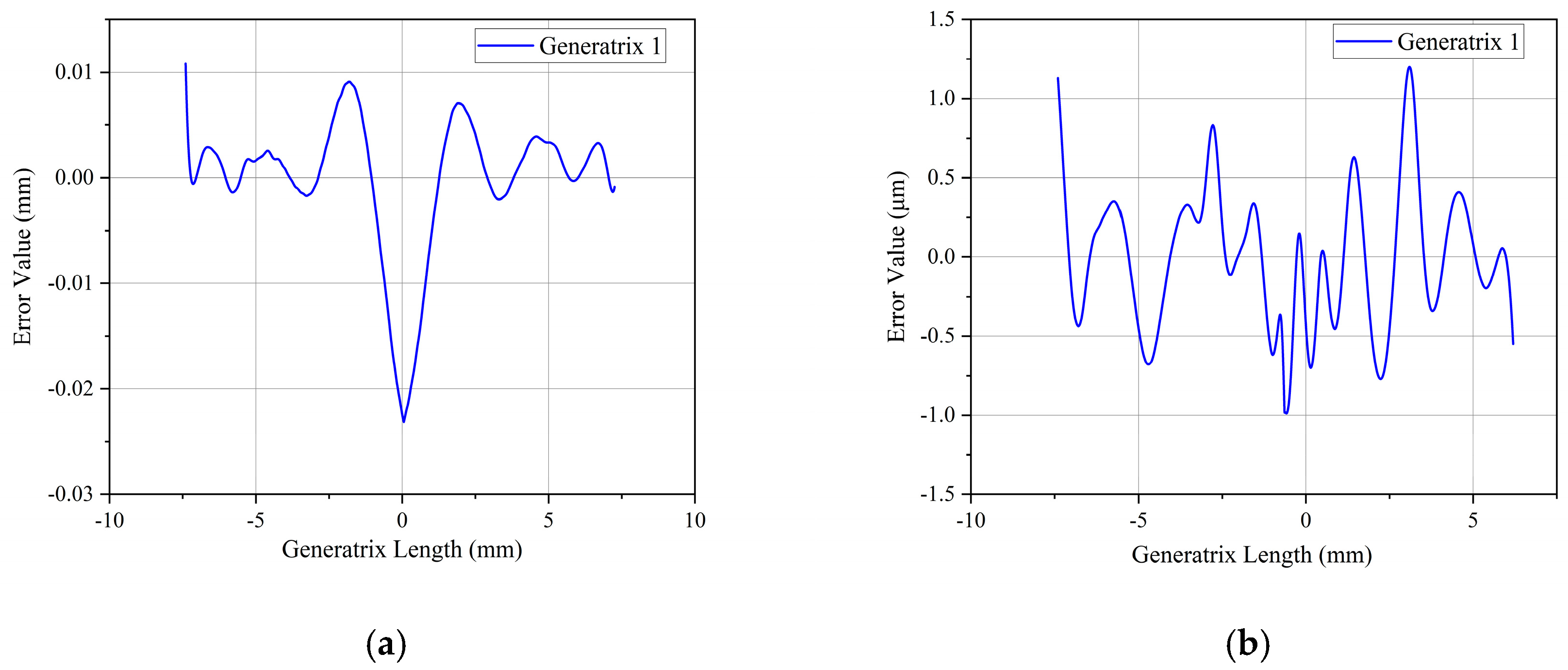
5.4. Experimental Results and Discussion
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yuan, J.; Lyu, B.; Hang, W.; Deng, Q. Review on the progress of ultra-precision machining technologies. Front. Mech. Eng. 2017, 12, 158–180. [Google Scholar] [CrossRef]
- Wang, Z.; Shi, C.; Zhang, P.; Yang, Z.; Chen, Y.; Guo, J. Recent Progress of Advanced Optical Manufacturing Technology. J. Mech. Eng. 2021, 57, 23–56. [Google Scholar]
- Deng, Y.; Wang, G.; Yue, X.; Zhou, K. A Review of Robot Grinding and Polishing Force Control Mode. In Proceedings of the 19th IEEE International Conference on Mechatronics and Automation (IEEE ICMA), Guilin, China, 7–10 August 2022; Electronic Network: West Yorkshire, UK, 2022; pp. 1413–1418. [Google Scholar]
- Muruganantham, V.R.; Thirumalaimuthukumaran, M.; Akila, K.; Bhuvanesh, D.; Praveen, R. Implementation of an Automatic Polishing Process with a Conveyor Mechanism. Appl. Mech. Mater. 2024, 920, 129–139. [Google Scholar] [CrossRef]
- Li, Z.-L.; Wang, R.; Zhang, X.-Q.; Zhu, L.M. B-spline surface approximation method for achieving optimum dwell time in deterministic polishing. J. Mater. Process. Technol. 2023, 318, 118031. [Google Scholar] [CrossRef]
- Huang, T.; Zhao, D.; Cao, Z.-C. Trajectory planning of optical polishing based on optimized implementation of dwell time. Precis. Eng.-J. Int. Soc. Precis. Eng. Nanotechnol. 2020, 62, 223–231. [Google Scholar] [CrossRef]
- Peng, Y.; Shen, B.; Wang, Z.; Yang, P.; Yang, W.; Bi, G. Review on polishing technology of small-scale aspheric optics. Int. J. Adv. Manuf. Technol. 2021, 115, 965–987. [Google Scholar] [CrossRef]
- Fan, C.; Xu, K.; Zhang, L.; Yuan, Q.; Wang, Q.; Wanga, K.; Sun, L. Kinematic Planning and In-Situ Measurement of Seven-Axis Five-Linkage Grinding and Polishing Machine Tool for Complex Curved Surface. Mach. Sci. Technol. 2022, 26, 203–228. [Google Scholar] [CrossRef]
- Kordonski, W.I.; Jacobs, S.D. Magnetorheological finishing. Int. J. Mod. Phys. B 1996, 10, 2837–2848. [Google Scholar] [CrossRef]
- Wang, Y.; Dai, C.; Li, W.; Meng, X.; Dong, H.; Wang, P. Polishing an off-axis aspheric mirror by ion beam figuring. In Proceedings of the 8th International Symposium on Advanced Optical Manufacturing and Testing Technologies—Advanced Optical Manufac-turing Technologies, Suzhou, China, 26–29 April 2016. [Google Scholar]
- Chen, X.; Yu, H.; Pan, H.; Chen, L.; Liang, X.; You, H. A Layered Split Polishing Path Planning Method Used in AWJP Based on Optical Glass Surface Morphology. Int. J. Precis. Eng. Manuf. 2025, 26, 269–282. [Google Scholar] [CrossRef]
- Bouland, C.; Urlea, V.; Beaubier, K.; Samoilenko, M.; Brailovski, V. Abrasive flow machining of laser powder bed-fused parts: Numerical modeling and experimental validation. J. Mater. Process. Technol. 2019, 273, 116262. [Google Scholar] [CrossRef]
- Feng, Y.; Cheng, H.; Wang, T.; Dong, Z.; Tam, H.-Y. Optimal strategy for fabrication of large aperture aspheric surfaces. Appl. Opt. 2014, 53, 147–155. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Q.; Zhang, L.; Han, Y.; Fan, C. Polishing path generation for physical uniform coverage of the aspheric surface based on the Archimedes spiral in bonnet polishing. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2019, 233, 2251–2263. [Google Scholar] [CrossRef]
- Mao, J.; Ni, L.; Xiang, B.; Shu, L. Position Error Modeling and Compensation for Robot Bonnet Polishing. Mech. Sci. Technol. Aerosp. Eng. 2023, 42, 724–729. [Google Scholar]
- Tam, H.Y.; Zhang, L.; Hua, M. Material removal by fixed abrasives following curved paths. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2004, 218, 713–720. [Google Scholar] [CrossRef]
- Guo, J.; Wang, D.; Fan, R.; Chen, W.; Zhao, G. Kinematic calibration and error compensation of a hexaglide parallel manipulator. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2019, 233, 215–225. [Google Scholar] [CrossRef]
- Sun, T.; Zhai, Y.; Song, Y.; Zhang, J. Kinematic calibration of a 3-DoF rotational parallel manipulator using laser tracker. Robot. Comput. Integr. Manuf. 2016, 41, 78–91. [Google Scholar] [CrossRef]
- Shao, X.; Ji, L.; Zou, H.; Xie, Y. Parameter calibration method for manipulators based on laser displacement measurement. J. Beijing Univ. Aeronaut. Astronaut. 2022, 48, 2281–2288. [Google Scholar]
- Wan, Y.; Shi, C.; Yuan, J.; Wu, F. Control method of polishing errors by dwell time compensation. High Power Laser Part. Beams 2011, 23, 97–100. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, H. Generic model of time-variant tool influence function and dwell-time algorithm for deterministic polishing. Int. J. Mech. Sci. 2021, 211, 106795. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, Y.; Kang, R.; Ji, F. An Elementary Approximation of Dwell Time Algorithm for Ultra-Precision Computer-Controlled Optical Surfacing. Micromachines 2021, 12, 471. [Google Scholar] [CrossRef]
- Wang, B.; Tie, G.; Shi, F.; Song, C.; Guo, S. Research on the influence of the non-stationary effect of the magnetorheological finishing removal function on mid-frequency errors of optical component surfaces. Opt. Express 2023, 31, 35016–35031. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Wan, Y.; Zeng, Z.; Xu, L.; Zhao, H.; Fang, K. Freeform surface grinding and polishing by CCOS based on industrial robot. In Proceedings of the 8th International Symposium on Advanced Optical Manufacturing and Testing Technologies—Advanced Optical Manufacturing Technologies, Suzhou, China, 6–29 April 2016. [Google Scholar]














| Equation Variables | Variable Values |
|---|---|
| R | 8.364 |
| K | −1.004811 |
| A4 | 0.000153225 |
| A6 | −1.40 × 10−6 |
| A8 | 4.24 × 10−8 |
| A10 | −3.02 × 10−10 |
| A12 | −6.84 × 10−13 |
| A14 | −1.10 × 10−15 |
| Direction of Movement | Dial Gauge Reading Difference Δh/(mm) | Angular Deviation/(°) |
|---|---|---|
| X-direction | 0.331 | 0.189 |
| Y-direction | 0.098 | 0.374 |
| Z-direction | 0.298 | 0.171 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Li, R.; Xie, J.; Wang, Y.; Sun, L. Integrated Error Compensation for Robotic Arm Polishing of Cylindrical Aspheric Optical Components. Machines 2025, 13, 979. https://doi.org/10.3390/machines13110979
Liu Y, Li R, Xie J, Wang Y, Sun L. Integrated Error Compensation for Robotic Arm Polishing of Cylindrical Aspheric Optical Components. Machines. 2025; 13(11):979. https://doi.org/10.3390/machines13110979
Chicago/Turabian StyleLiu, Yao, Ruiliang Li, Jingjing Xie, Yiming Wang, and Lin Sun. 2025. "Integrated Error Compensation for Robotic Arm Polishing of Cylindrical Aspheric Optical Components" Machines 13, no. 11: 979. https://doi.org/10.3390/machines13110979
APA StyleLiu, Y., Li, R., Xie, J., Wang, Y., & Sun, L. (2025). Integrated Error Compensation for Robotic Arm Polishing of Cylindrical Aspheric Optical Components. Machines, 13(11), 979. https://doi.org/10.3390/machines13110979




