Graded Evaluation and Optimal Scheme Selection of Mine Rock Diggability Based on the Multidimensional Cloud Model
Abstract
1. Introduction
2. Data Sources and Evaluation Framework
2.1. Data Description
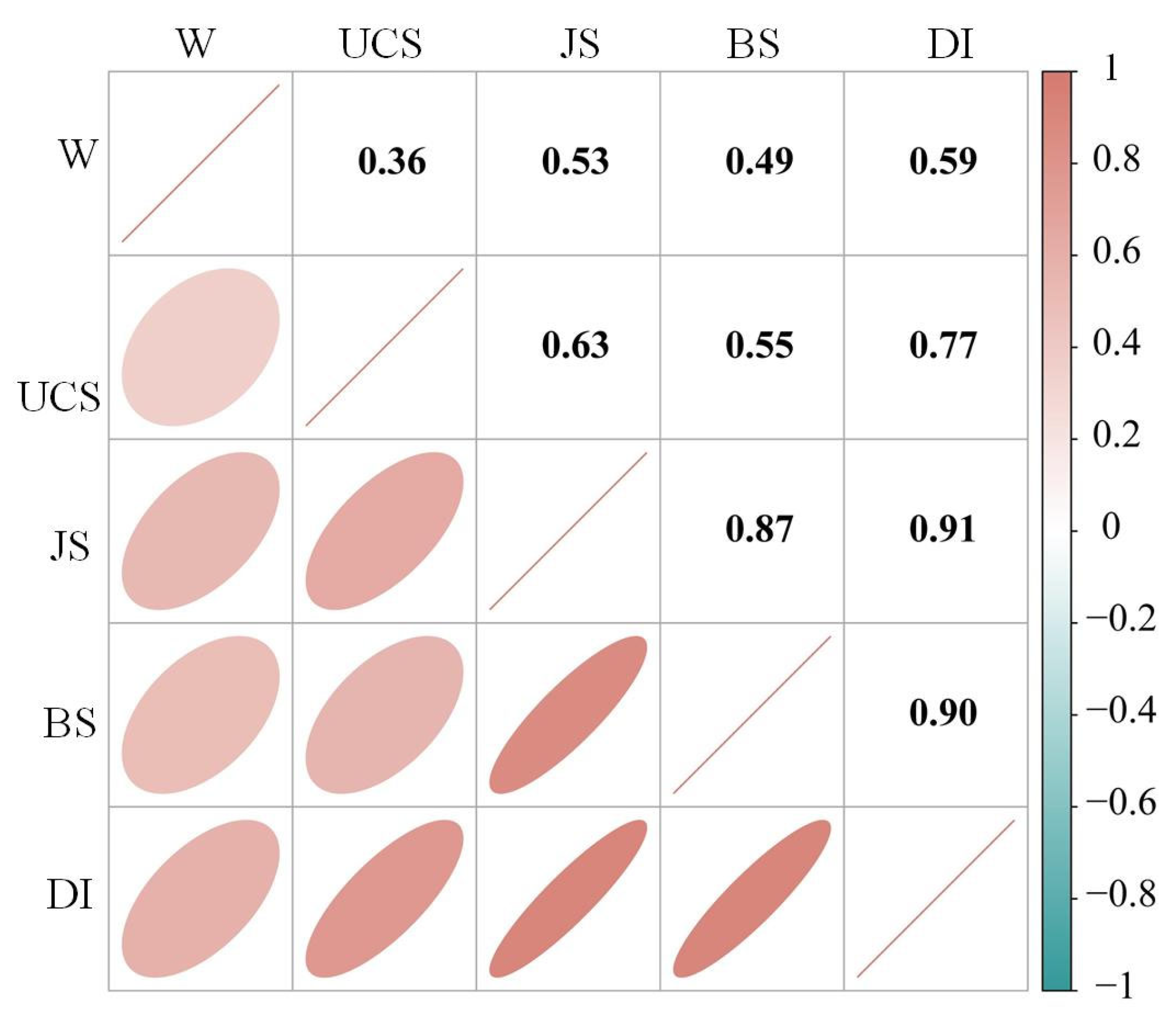
2.2. Data Analysis
2.3. Rock Diggability Evaluation Framework
3. Methodology
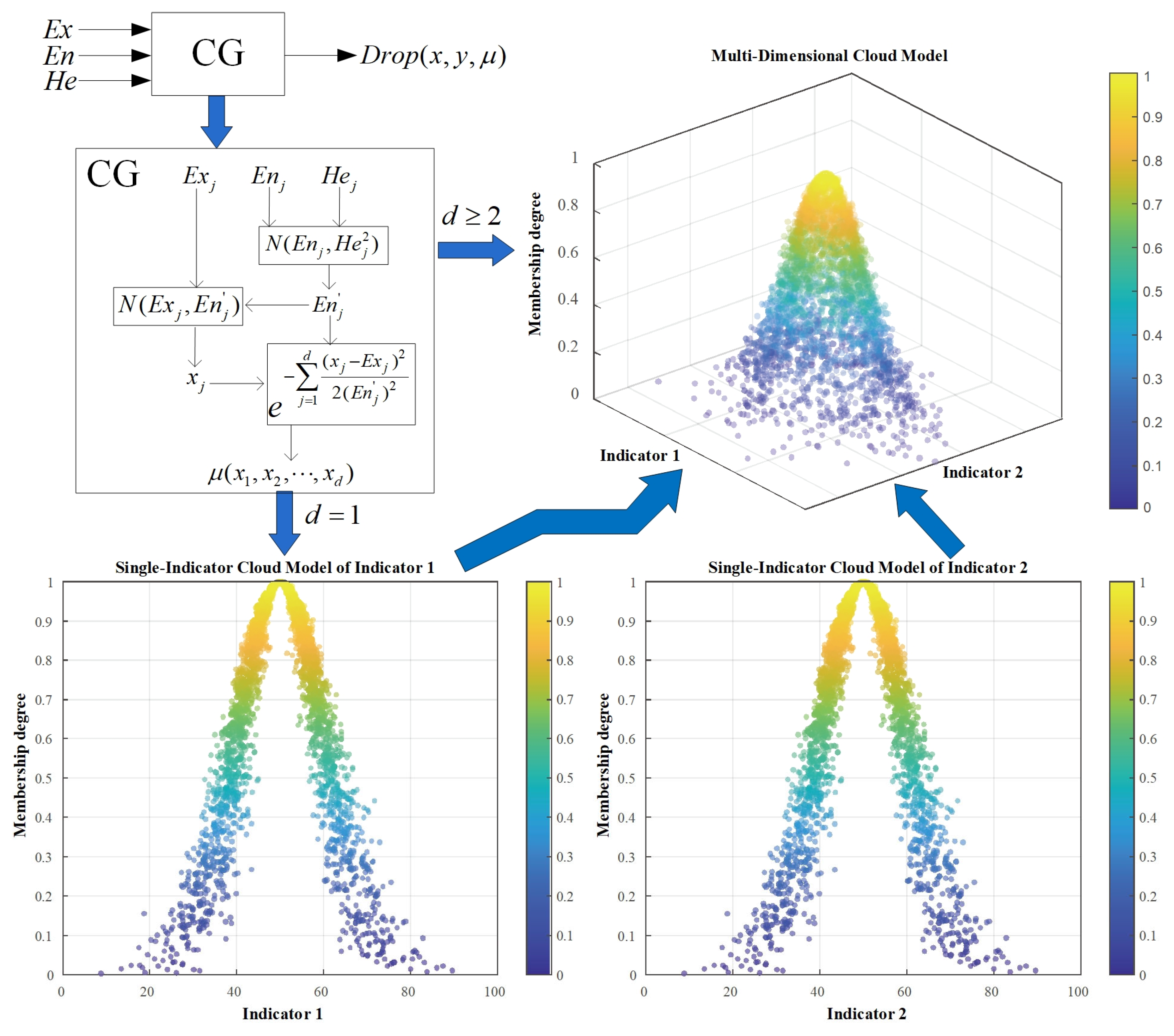
3.1. Multidimensional Cloud Model
- (1)
- Generate perturbed entropy
- (2)
- Determine the positions of cloud drops
- (3)
- Membership calculation
3.2. Subjective Weights (Expert Evaluation)
- (1)
- Expert evaluation
- (2)
- Construction of the judgment matrix
- (3)
- Weight calculation
- (4)
- Consistency test
3.3. Objective Weight
3.3.1. Entropy Weight Method (EW)
- (1)
- Standardization
- (2)
- Calculation of proportions
- (3)
- Calculation of entropy
- (4)
- Calculation of the difference coefficient
- (5)
- Weight calculation
3.3.2. Coefficient of Variation Method (CV)
- (1)
- Calculation of standard deviation
- (2)
- Calculation of the coefficient of variation
- (3)
- Weight calculation
3.3.3. CRITIC Method
- (1)
- Calculation of correlation
- (2)
- Calculation of information quantity
- (3)
- Weight calculation
3.3.4. Principal Component Analysis (PCA)
- (1)
- Construction of the covariance matrix
- (2)
- Solve for eigenvalues and eigenvectors
- (3)
- Calculation of contribution rate and cumulative contribution rate
- (4)
- Calculation of indicator weights
3.3.5. Factor Analysis Method (FA)
- (1)
- Establishment of the factor model
- (2)
- Extraction of factors and loading matrix
- (3)
- Calculation of weights
3.4. Comprehensive Weights (Combination of Subjective and Objective Weights)
4. Rock Excavatability Modeling and Evaluation
4.1. Comprehensive Weights
4.1.1. Subjective Wights (Expert Evaluation)
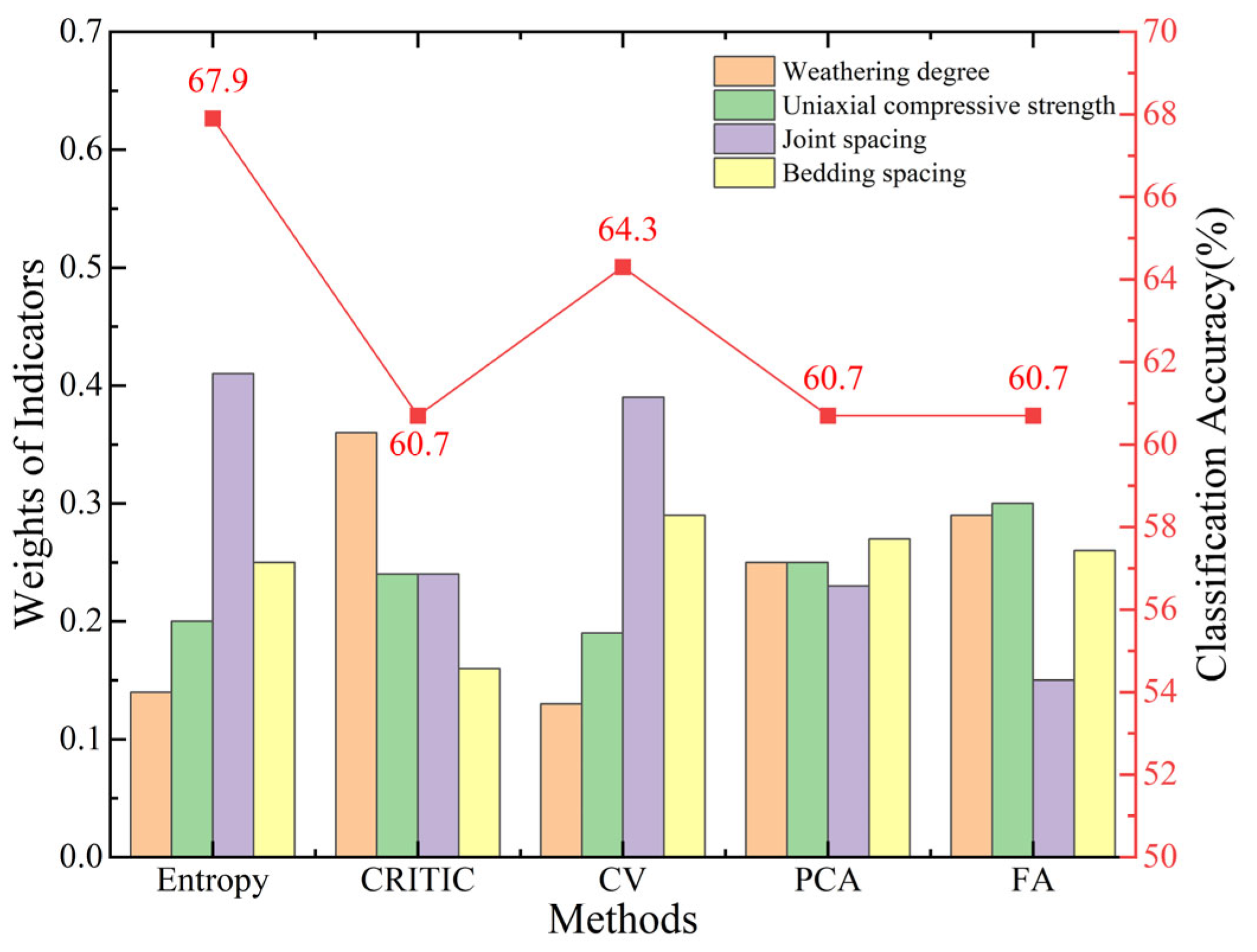
4.1.2. Objective Weights
4.1.3. Optimal Weights
4.2. Cloud Model
4.2.1. Single-Indicator Benchmark Cloud Model
4.2.2. Multi-Dimensional Benchmark Cloud Model
4.3. Diggability Evaluation Based on Multi-Dimensional Cloud Model
4.3.1. Diggability Evaluation Results Based on Multi-Dimensional Cloud Model
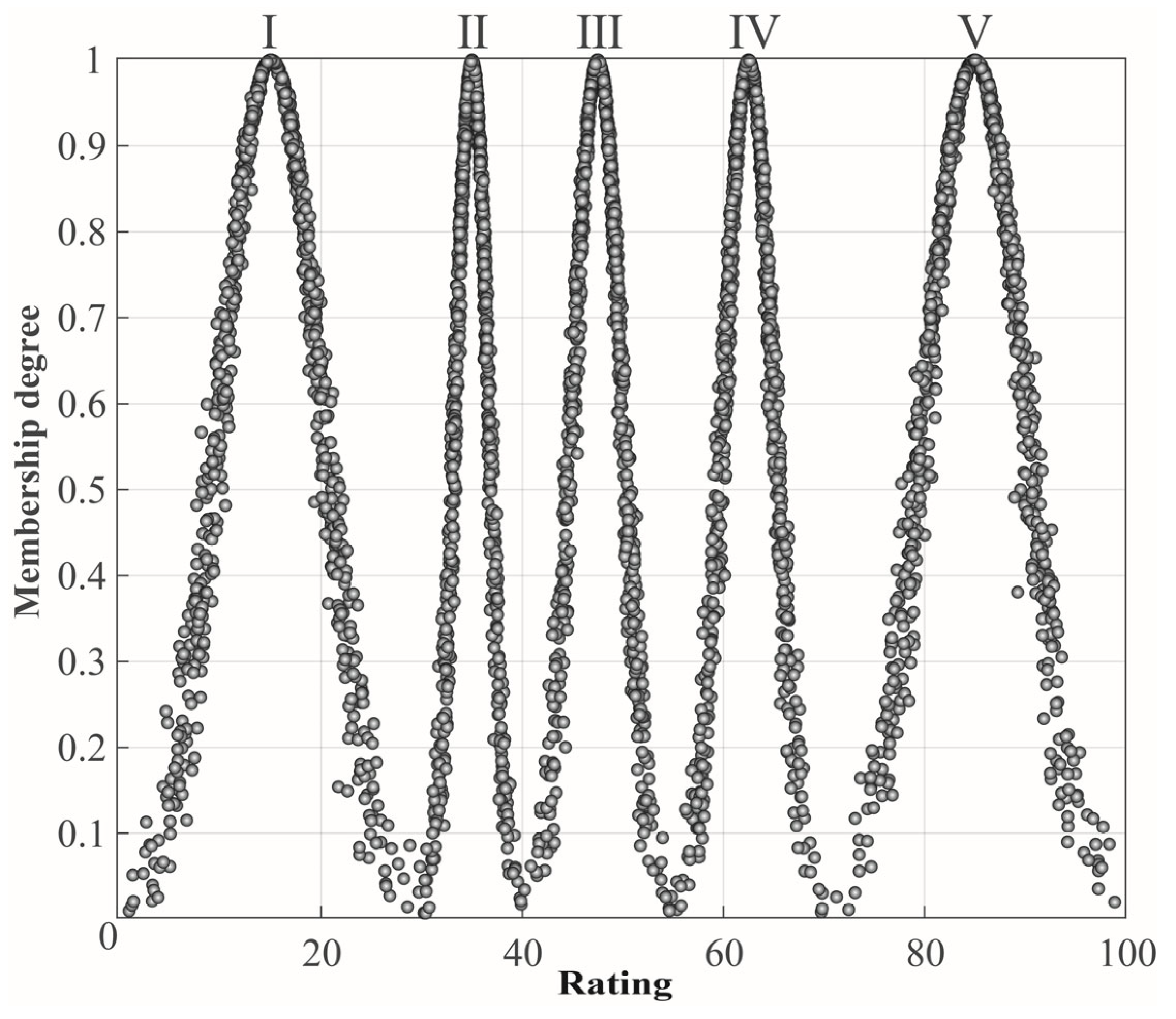
4.3.2. Diggability Evaluation Analysis Based on Single-Indicator Cloud Model
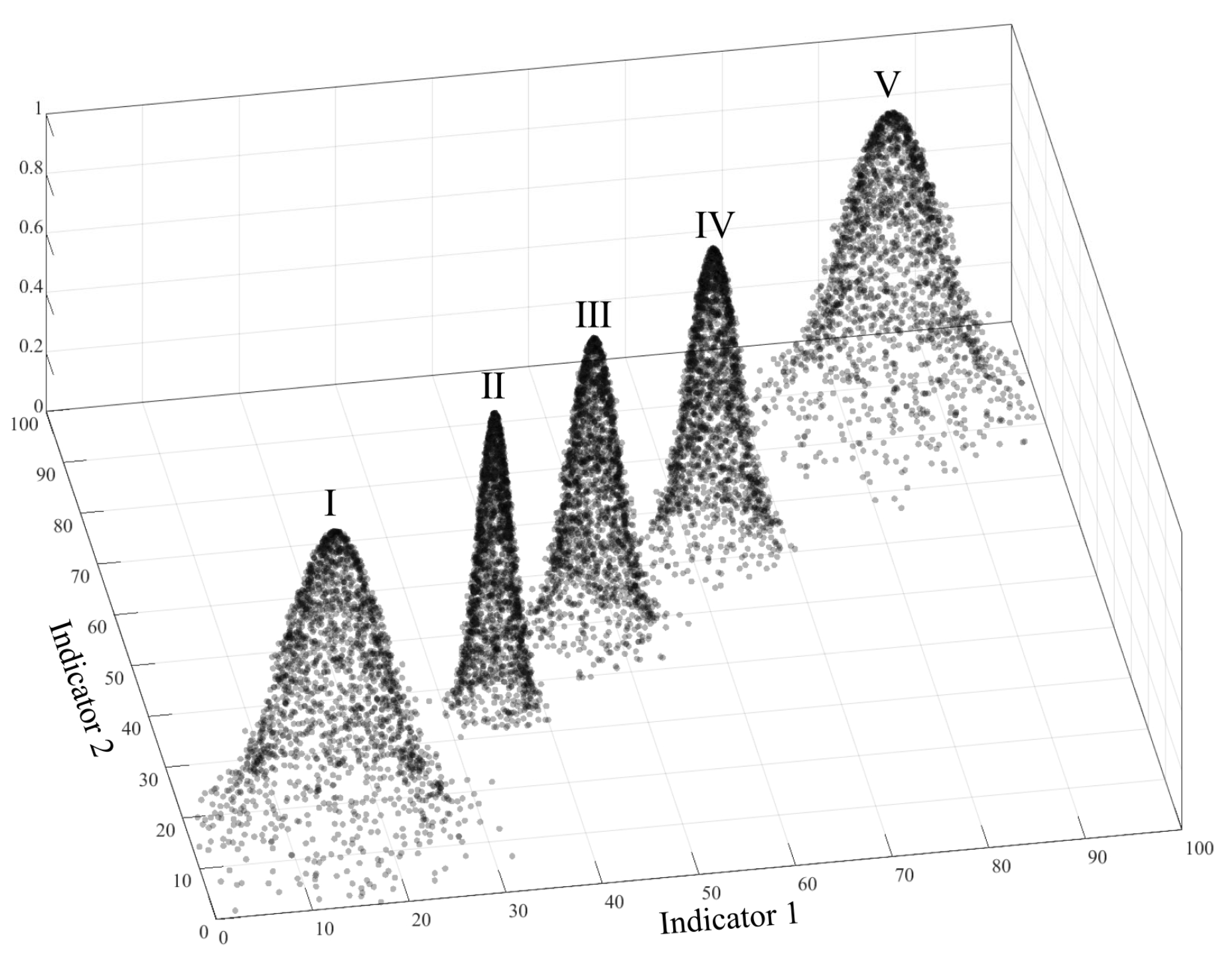
4.3.3. Analysis of Diggability Evaluation Based on Multi-Dimensional Cloud Model
5. Conclusions
- (1)
- A diggability evaluation system for rock masses was established, and diggability grade criteria under different conditions were defined.
- (2)
- Indicator weights were determined using a combination of subjective and objective methods, with the final optimal weights being WD (0.16), UCS (0.18), JS (0.34), and BS (0.32), balancing expert experience and data characteristics.
- (3)
- Visualization using single-indicator cloud models effectively mitigated the issue of transitional intervals, addressing the difficulty of grading transitional values.
- (4)
- Multi-dimensional cloud models considered interactions among indicators, optimizing indicator interactions and enhancing the interpretability of diggability grades.
- (5)
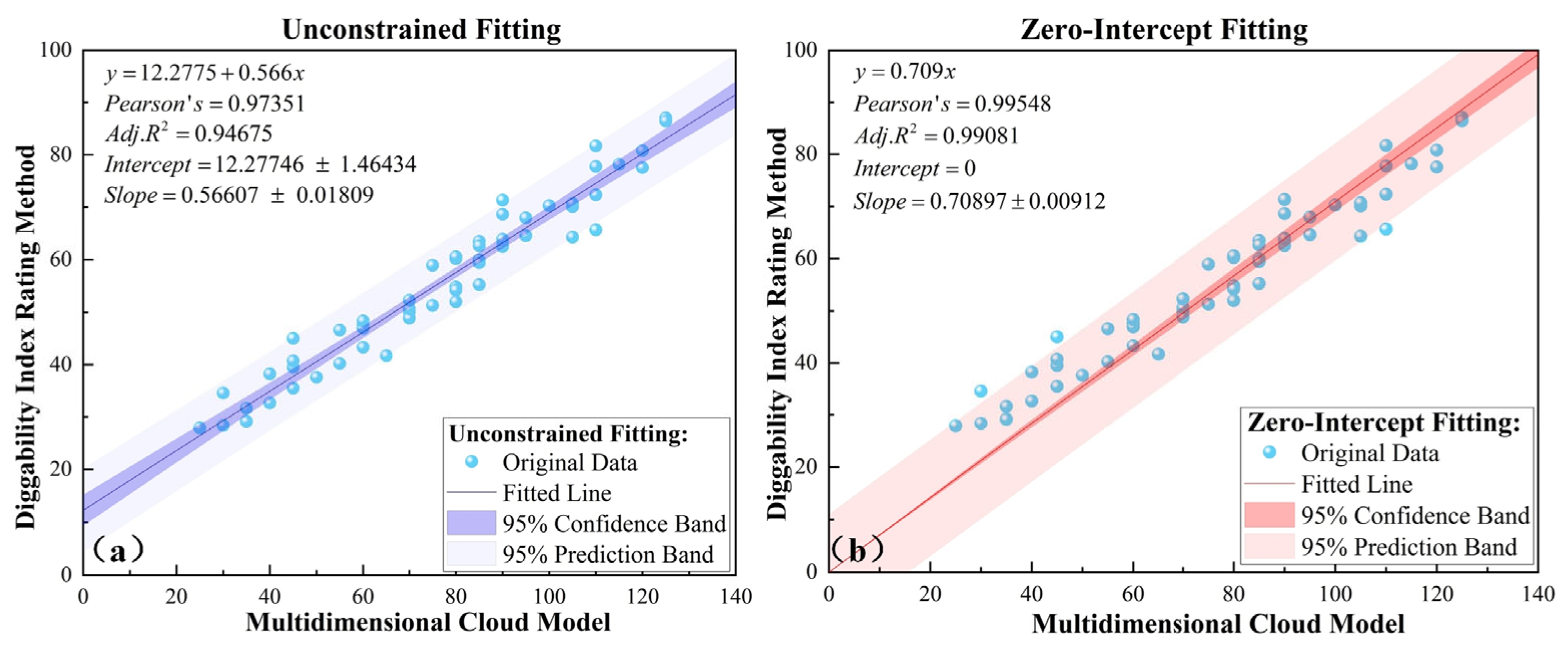
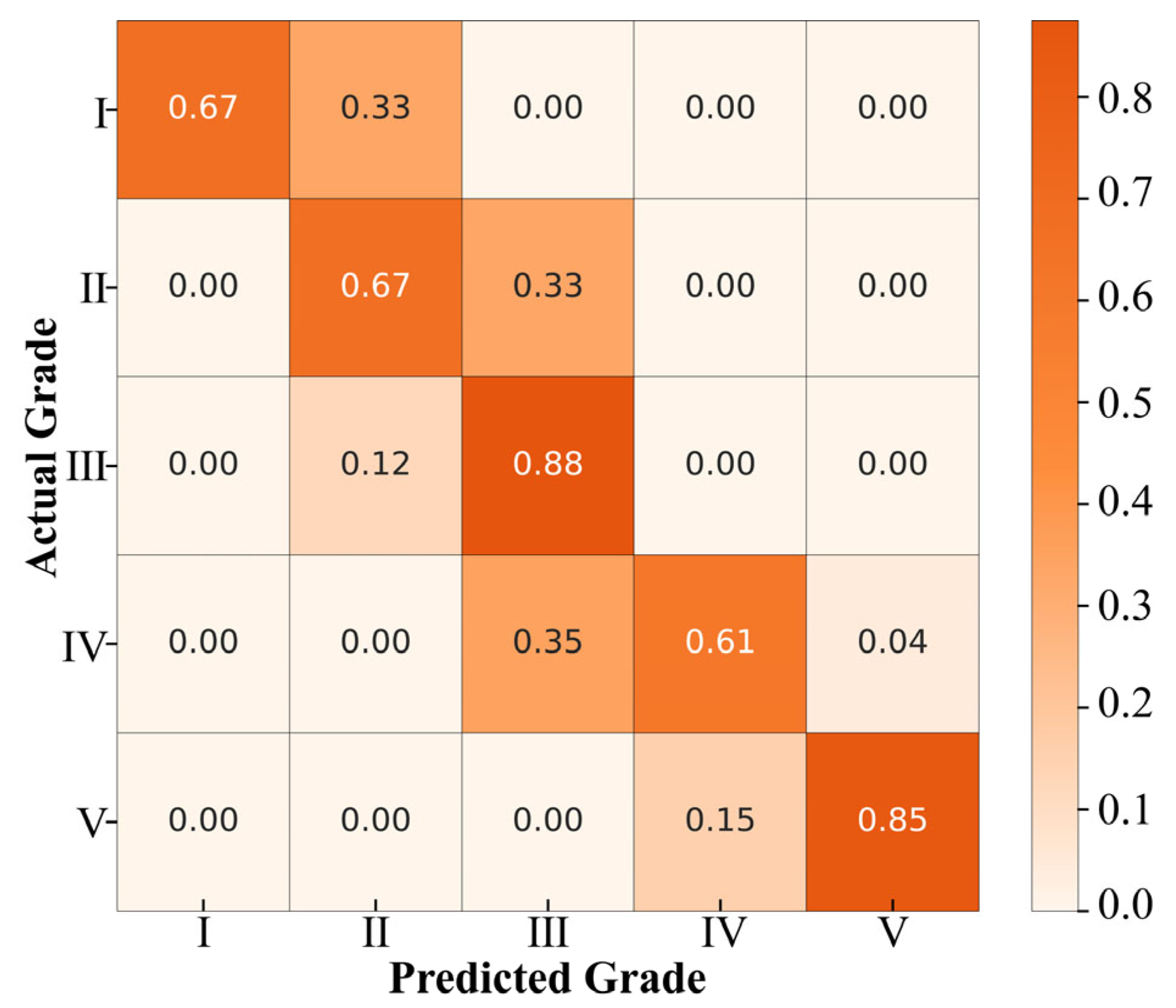
- Evaluation results from multi-dimensional cloud models were highly consistent with the Diggability Index method (R2 = 0.991), with an absolute level accuracy of 74% and a cloud-model-based accuracy of 100%, validating the reliability and applicability of the proposed method.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Stille, H.; Palmström, A. Practical Use of the Concept of Geotechnical Categories in Rock Engineering. Tunn. Undergr. Space Technol. 2018, 79, 1–11. [Google Scholar] [CrossRef]
- Goktan, R.M.; Eskikaya, S. Prediction of Ripping Machine Performance in Terms of Rockmass Properties: Technical Paper. Civ. Eng. S. Afr. 1991, 1991, 13–14. [Google Scholar]
- Karpuz, C. A Classification System for Excavation of Surface Coal Measures. Min. Sci. Technol. 1990, 11, 157–163. [Google Scholar] [CrossRef]
- Howarth, D.F. Mechanical Rock Excavation—Assessment of Cuttability and Borability. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1989, 26, A197. [Google Scholar] [CrossRef]
- Bilim, N. Determination of Drillability of Some Natural Stones and Their Association with Rock Properties. Sci. Res. Essays 2011, 6, 382–387. [Google Scholar]
- Scoble, M.J.; Muftuoglu, Y.V. Derivation of a Diggability Index for Surface Mine Equipment Selection. Min. Sci. Technol. 1984, 1, 305–322. [Google Scholar] [CrossRef]
- Santos, V.; Da Silva, P.F.; Brito, M.G. Estimating RMR Values for Underground Excavations in a Rock Mass. Minerals 2018, 8, 78. [Google Scholar] [CrossRef]
- Rusydy, I.; Al-Huda, N. New Rock Mass Classifications for Limestone of the Woyla Group and Its Empirical Relationship in Aceh Province, Indonesia. Carbonates Evaporites 2021, 36, 15. [Google Scholar] [CrossRef]
- Xu, J.; Luo, S.; Xiao, X. Review of the Experimental Studies of the Cracking Behaviors of Fractured Rocks under Compression. Geohazard Mech. 2024, 2, 59–82. [Google Scholar] [CrossRef]
- Hekmatnejad, A.; Rojas, E.; Saavedra, C.; Crespin, B. Presentation of the Universal Discontinuity Index (UDi) System and Its Application to Predict the Geometry of over-Excavation along a Tunnel at New El Teniente Mine. Eng. Geol. 2022, 311, 106901. [Google Scholar] [CrossRef]
- Meng, Y.; Jing, H.; Liu, X.; Yin, Q.; Zhang, L.; Liu, H. Experimental and Numerical Investigation on the Effect of Bedding Plane Properties on Fracture Behaviour of Sandy Mudstone. Theor. Appl. Fract. Mech. 2021, 114, 102989. [Google Scholar] [CrossRef]
- Rotimi, O.J.; Atunbi, J.F.; Enaworu, E.; Ameliko, A.A. Rippability Potential of the Near Surface Deposits of Jubilee Homes Parkland, Southwest, Nigeria. J. Environ. Earth Sci. 2015, 5, 85. [Google Scholar]
- Ismail, M.A.M.; Kumar, N.S.; Abidin, M.H.Z.; Madun, A. Rippability Assessment of Weathered Sedimentary Rock Mass Using Seismic Refraction Methods. J. Phys. Conf. Ser. 2018, 995, 012105. [Google Scholar] [CrossRef]
- Iphar, M.; Goktan, R.M. An Application of Fuzzy Sets to the Diggability Index Rating Method for Surface Mine Equipment Selection. Int. J. Rock Mech. Min. Sci. 2006, 43, 253–266. [Google Scholar] [CrossRef]
- Zhou, J.; Chen, C.; Armaghani, D.J.; Ma, S. Developing a Hybrid Model of Information Entropy and Unascertained Measurement Theory for Evaluation of the Excavatability in Rock Mass. Eng. Comput. 2022, 38, 247–270. [Google Scholar] [CrossRef]
- Bendezu, M.; Romanel, C.; Roehl, D. Finite Element Analysis of Blast-Induced Fracture Propagation in Hard Rocks. Comput. Struct. 2017, 182, 1–13. [Google Scholar] [CrossRef]
- Pinheiro, M.; Emery, X.; Miranda, T.; Lamas, L.; Espada, M. Modelling Geotechnical Heterogeneities Using Geostatistical Simulation and Finite Differences Analysis. Minerals 2018, 8, 52. [Google Scholar] [CrossRef]
- Zhang, X.; Xia, X.; Li, H.; Fu, S. Damage Mechanism and Parameter Optimization of Rock Mass Blasting Under High In-Situ Stress. In Proceedings of the 58th U.S. Rock Mechanics/Geomechanics Symposium, Golden, CO, USA, 23–26 June 2024; OnePetro: Richardson, TX, USA, 2024. [Google Scholar]
- Yaghoubi, E.; Yaghoubi, E.; Khamees, A.; Vakili, A.H. A Systematic Review and Meta-Analysis of Artificial Neural Network, Machine Learning, Deep Learning, and Ensemble Learning Approaches in Field of Geotechnical Engineering. Neural Comput. Appl. 2024, 36, 12655–12699. [Google Scholar] [CrossRef]
- Tiryaki, B. Application of Artificial Neural Networks for Predicting the Cuttability of Rocks by Drag Tools. Tunn. Undergr. Space Technol. 2008, 23, 273–280. [Google Scholar] [CrossRef]
- Huang, S.; Zhou, J. Cutting—Edge Soft Computing Technologies for Rock Mass Excavatability: Transforming Prediction with Hybrid GA—MLP and GEP—Based Criteria. Rock Mech. Rock Eng. 2025. [Google Scholar] [CrossRef]
- Kuznetsova, N.; Zhgun, D.; Golovanevskiy, V. Plasma Blasting of Rocks and Rocks-like Materials: An Analytical Model. Int. J. Rock Mech. Min. Sci. 2022, 150, 104986. [Google Scholar] [CrossRef]
- Niu, G.; He, X.; Xu, H.; Dai, S. Development of Rock Classification Systems: A Comprehensive Review with Emphasis on Artificial Intelligence Techniques. Eng 2024, 5, 217–245. [Google Scholar] [CrossRef]
- Hartlieb, P.; Bock, S. Theoretical Investigations on the Influence of Artificially Altered Rock Mass Properties on Mechanical Excavation. Rock Mech. Rock Eng. 2018, 51, 801–809. [Google Scholar] [CrossRef]
- Zhao, H.; Chen, B.; Li, S.; Li, Z.; Zhu, C. Updating the Models and Uncertainty of Mechanical Parameters for Rock Tunnels Using Bayesian Inference. Geosci. Front. 2021, 12, 101198. [Google Scholar] [CrossRef]
- Liu, G.; Zhou, C.; Feng, K.; Jiang, Q.; Li, S.; Bao, H.; Li, A. Probabilistic Evaluation Method for the Stability of Large Underground Cavern Considering the Uncertainty of Rock Mass Mechanical Parameters: A Case Study of Baihetan Underground Powerhouse Project. Eng. Geol. 2024, 340, 107660. [Google Scholar] [CrossRef]
- Alipenhani, B.; Bakhshandeh Amnieh, H.; Majdi, A. Evaluation of Effective Geomechanical Parameters in Rock Mass Cavability Using Different Intelligent Techniques. Int. J. Min. Geo-Eng. 2024, 58, 307–313. [Google Scholar] [CrossRef]
- Yao, S.; Zhou, J.; Khandelwal, M.; Lawal, A.I.; Li, C.; Onifade, M.; Kwon, S. Intelligent Decision Framework for Booster Fan Optimization in Underground Coal Mines: Hybrid Spherical Fuzzy-Cloud Model Approach Enhancing Ventilation Safety and Operational Efficiency. Machines 2025, 13, 367. [Google Scholar] [CrossRef]
- Zhou, J.; Chen, C.; Wei, C.; Du, K. An Improved Connection Cloud Model of an Updated Database: A Multicriteria Uncertainty Model for Coal Burst Liability Evaluation. Nat. Resour. Res. 2022, 31, 1687–1704. [Google Scholar] [CrossRef]
- Guo, D.-S.; Meng, F.-Y.; Wu, H.-N.; Yang, X.-X.; Liu, Z. Risk Assessment of Shield Tunneling Crossing Building Based on Variable Weight Theory and Cloud Model. Tunn. Undergr. Space Technol. 2024, 145, 105593. [Google Scholar] [CrossRef]
- Barton, N. Suggested Methods for the Quantitative Description of Discontinuities in Rock Masses: International Society for Rock Mechanics. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1978, 16, 22. [Google Scholar]
- Li, D.; Liu, C.; Gan, W. A New Cognitive Model: Cloud Model. Int. J. Intell. Syst. 2009, 24, 357–375. [Google Scholar] [CrossRef]
- Li, S.; Wang, G.; Yang, J. Survey on Cloud Model Based Similarity Measure of Uncertain Concepts. CAAI Trans. Intell. Technol. 2019, 4, 223–230. [Google Scholar] [CrossRef]
- Gong, S.; Yao, S.; Xi, F.; Liu, J.; Ren, X.; Niu, D.; Ding, J.; Zhang, H.; Wang, J.; Wang, S. A Comparison of Research Methods to Determine the Sustainability of Mineral Resources in Henan Province Based on Cloud Analysis. Sustainability 2022, 14, 15834. [Google Scholar] [CrossRef]
- Yang, J.; Han, J.; Wan, Q.; Xing, S.; Chen, F. A Novel Similarity Measurement for Triangular Cloud Models Based on Dual Consideration of Shape and Distance. PeerJ Comput. Sci. 2023, 9, e1506. [Google Scholar] [CrossRef]
- Deng, Y.; Liu, S.; Zhang, W.; Wang, L.; Wang, J. General Multidimensional Cloud Model and Its Application on Spatial Clustering in Zhanjiang, Guangdong. J. Geogr. Sci. 2010, 20, 787–798. [Google Scholar] [CrossRef]
- Wang, M.; Wang, X.; Liu, Q.; Shen, F.; Jin, J. A Novel Multi-Dimensional Cloud Model Coupled with Connection Numbers Theory for Evaluation of Slope Stability. Appl. Math. Model. 2020, 77, 426–438. [Google Scholar] [CrossRef]
- Zheng, Y.; Shi, Z.; Peng, X.; Li, J.; Feng, X. Multidimensional Generalized Normal Cloud Model for Uncertainty Propagation. Comp. Appl. Math. 2025, 44, 272. [Google Scholar] [CrossRef]
- Vidal, L.-A.; Marle, F.; Bocquet, J.-C. Using a Delphi Process and the Analytic Hierarchy Process (AHP) to Evaluate the Complexity of Projects. Expert. Syst. Appl. 2011, 38, 5388–5405. [Google Scholar] [CrossRef]
- Saaty, T.L. The Analytic Hierarchy Process: Planning, Priority Setting, Resource Allocation; McGraw-Hill: New York, NY, USA, 1980; ISBN 978-0-07-054371-3. [Google Scholar]
- Pant, S.; Kumar, A.; Ram, M.; Klochkov, Y.; Sharma, H.K. Consistency Indices in Analytic Hierarchy Process: A Review. Mathematics 2022, 10, 1206. [Google Scholar] [CrossRef]
- Zhou, K.; Lin, Y.; Deng, H.; Li, J.; Liu, C. Prediction of Rock Burst Classification Using Cloud Model with Entropy Weight. Trans. Nonferrous Met. Soc. China 2016, 26, 1995–2002. [Google Scholar] [CrossRef]
- Qiao, C.; Wang, Y.; Li, C.; Yan, B. Application of Extension Theory Based on Improved Entropy Weight Method to Rock Slope Analysis in Cold Regions. Geotech. Geol. Eng. 2021, 39, 4315–4327. [Google Scholar] [CrossRef]
- Wang, N.; Zhang, Y. Research on Evaluation of Wuhan Air Pollution Emission Level Based on Entropy Weight Method. Sci. Rep. 2024, 14, 5012. [Google Scholar] [CrossRef]
- Ghorbani, S. A Hybrid Quantitative Approach for Assessment of Geotechnical Hazards in Rock Tunnels Using Finite Element and Variation Coefficient Methods. Sci. Rep. 2025, 15, 28802. [Google Scholar] [CrossRef]
- Ecer, F.; Haseli, G.; Krishankumar, R.; Hajiaghaei-Keshteli, M. Evaluation of Sustainable Cold Chain Suppliers Using a Combined Multi-Criteria Group Decision-Making Framework under Fuzzy ZE-Numbers. Expert Syst. Appl. 2024, 245, 123063. [Google Scholar] [CrossRef]
- Jolliffe, I.T.; Cadima, J. Principal Component Analysis: A Review and Recent Developments. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2016, 374, 2065. [Google Scholar] [CrossRef]
- Tripathi, M.; Singal, S.K. Allocation of Weights Using Factor Analysis for Development of a Novel Water Quality Index. Ecotoxicol. Environ. Saf. 2019, 183, 109510. [Google Scholar] [CrossRef]




| Transformed Score | 0–20 | 20–40 | 40–60 | 60–80 | 80–100 | |
|---|---|---|---|---|---|---|
| Indicators | ||||||
| Weathering degree | Completely | Highly | Moderately | Slightly | Unweathered | |
| 10 | 30 | 50 | 70 | 90 | ||
| Uniaxial compressive strength (MPa) | 0–20 | 20–40 | 40–60 | 60–100 | >100 | |
| Joint spacing (m) | 0–0.3 | 0.3–0.6 | 0.6–1.5 | 1.5–2 | >2 | |
| Bedding spacing (m) | 0–0.1 | 0.1–0.3 | 0.3–0.6 | 0.6–1.5 | >1.5 | |
| Diggability Level | I | II | III | IV | V |
|---|---|---|---|---|---|
| Fuzzy score | 0–30 | 30–40 | 40–55 | 55–70 | 70–100 |
| Index | 0–40 | 40–50 | 50–70 | 70–100 | >100 |
| Ease of digging | Very Easy | Easy | Difficult | Very Difficult | Marginal Without Blasting |
| Excavation method | 1. Ripping 2. Dragline 3. Shovel digging | 1. Ripping 2. Dragline 3. Shovel digging | 1. Ripping 2. Shovel digging | Shovel digging | Shovel digging |
| Indicators | Expert 1 | Expert 2 | Expert 3 | Expert 4 | Expert 5 | |
|---|---|---|---|---|---|---|
| Weathering degree | 0.135 | 0.120 | 0.202 | 0.279 | 0.158 | |
| Uniaxial compressive strength | 0.151 | 0.166 | 0.163 | 0.216 | 0.111 | |
| Joint spacing | 0.398 | 0.344 | 0.237 | 0.188 | 0.180 | |
| Bedding spacing | 0.316 | 0.370 | 0.398 | 0.317 | 0.552 | |
| Consistency test | CI | 0.046 | 0.016 | 0.061 | 0.02 | 0.017 |
| RI | 0.900 | 0.900 | 0.900 | 0.900 | 0.900 | |
| CR | 0.051 | 0.018 | 0.068 | 0.022 | 0.019 | |
| Indicators | EWM | CRITIC | CV | PCA | FA |
|---|---|---|---|---|---|
| Weathering degree | 0.14 | 0.36 | 0.13 | 0.25 | 0.29 |
| Uniaxial compressive strength | 0.20 | 0.24 | 0.19 | 0.25 | 0.30 |
| Joint spacing | 0.41 | 0.24 | 0.39 | 0.23 | 0.15 |
| Bedding spacing | 0.25 | 0.16 | 0.29 | 0.27 | 0.26 |
| Classification accuracy (%) | 67.90 | 60.70 | 64.30 | 60.70 | 60.70 |
| Level | I | II | III | IV | V |
|---|---|---|---|---|---|
| 15 | 35 | 47.5 | 62.5 | 85 | |
| 5 | 1.67 | 2.5 | 2.5 | 5 | |
| 0.5 | 0.167 | 0.25 | 0.25 | 0.5 |
| Site | Diggability Index Rating Method | Multidimensional Cloud Model | ||
|---|---|---|---|---|
| Rating | Ease of Digging Classification | Rating | Ease of Digging Classification | |
| 1 | 90 | Very Difficult | 62.49 | Very Difficult |
| 2 | 85 | Very Difficult | 63.48 | Very Difficult |
| 3 | 95 | Very Difficult | 64.57 | Very Difficult |
| 4 | 90 | Very Difficult | 63.63 | Very Difficult |
| 5 | 90 | Very Difficult | 71.34 | Marginal Without Blasting |
| 6 | 70 | Very Difficult | 50.01 | Difficult |
| 7 | 85 | Very Difficult | 59.98 | Very Difficult |
| 8 | 60 | Difficult | 43.33 | Difficult |
| 9 | 90 | Very Difficult | 68.63 | Very Difficult |
| 10 | 50 | Difficult | 37.59 | Easy |
| 11 | 110 | Marginal Without Blasting | 65.67 | Very Difficult |
| 12 | 80 | Very Difficult | 60.21 | Very Difficult |
| 13 | 70 | Very Difficult | 48.87 | Difficult |
| 14 | 85 | Very Difficult | 55.24 | Very Difficult |
| 15 | 105 | Marginal Without Blasting | 70.08 | Marginal Without Blasting |
| 16 | 30 | Very Easy | 34.57 | Easy |
| 17 | 80 | Very Difficult | 54.82 | Difficult |
| 18 | 85 | Very Difficult | 59.42 | Very Difficult |
| 19 | 80 | Very Difficult | 60.54 | Very Difficult |
| 20 | 125 | Marginal Without Blasting | 87.07 | Marginal Without Blasting |
| 21 | 45 | Easy | 45.04 | Difficult |
| 22 | 45 | Easy | 39.48 | Easy |
| 23 | 45 | Easy | 40.73 | Difficult |
| 24 | 70 | Very Difficult | 50.66 | Difficult |
| 25 | 70 | Very Difficult | 52.32 | Difficult |
| 26 | 60 | Difficult | 47.62 | Difficult |
| 27 | 80 | Very Difficult | 52.01 | Difficult |
| 28 | 100 | Marginal Without Blasting | 70.27 | Marginal Without Blasting |
| 29 | 110 | Marginal Without Blasting | 72.31 | Marginal Without Blasting |
| 30 | 75 | Very Difficult | 58.93 | Very Difficult |
| 31 | 60 | Difficult | 46.94 | Difficult |
| 32 | 90 | Very Difficult | 63.87 | Very Difficult |
| 33 | 75 | Very Difficult | 51.31 | Difficult |
| 34 | 80 | Very Difficult | 54.23 | Difficult |
| 35 | 120 | Marginal Without Blasting | 80.79 | Marginal Without Blasting |
| 36 | 60 | Difficult | 48.36 | Difficult |
| 37 | 40 | Easy | 38.25 | Easy |
| 38 | 35 | Very Easy | 29.18 | Very Easy |
| 39 | 45 | Easy | 35.49 | Easy |
| 40 | 65 | Difficult | 41.71 | Difficult |
| 41 | 35 | Very Easy | 31.65 | Easy |
| 42 | 40 | Easy | 32.65 | Easy |
| 43 | 55 | Difficult | 46.62 | Difficult |
| 44 | 35 | Very Easy | 29.11 | Very Easy |
| 45 | 30 | Very Easy | 28.35 | Very Easy |
| 46 | 25 | Very Easy | 27.87 | Very Easy |
| 47 | 110 | Marginal Without Blasting | 77.74 | Marginal Without Blasting |
| 48 | 105 | Marginal Without Blasting | 64.29 | Very Difficult |
| 49 | 115 | Marginal Without Blasting | 78.16 | Marginal Without Blasting |
| 50 | 120 | Marginal Without Blasting | 77.53 | Marginal Without Blasting |
| 51 | 55 | Difficult | 40.21 | Difficult |
| 52 | 110 | Marginal Without Blasting | 81.70 | Marginal Without Blasting |
| 53 | 105 | Marginal Without Blasting | 70.69 | Marginal Without Blasting |
| 54 | 85 | Very Difficult | 62.63 | Very Difficult |
| 55 | 95 | Very Difficult | 67.97 | Very Difficult |
| 56 | 125 | Marginal Without Blasting | 86.43 | Marginal Without Blasting |
| Site | Diggability Index Rating Method | Multidimensional Cloud Model Distribution | ||
|---|---|---|---|---|
| Rating | Ease of Digging Classification | Rating | Ease of Digging Classification | |
| 5 | 90 | Very Difficult | 71.34 | Marginal Without Blasting *—Marginal Without Blasting |
| 6 | 70 | Very Difficult | 50.01 | Difficult *—Very Difficult |
| 10 | 50 | Difficult | 37.59 | Easy *—Difficult |
| 11 | 110 | Marginal Without Blasting | 65.67 | Very Difficult *—Marginal Without Blasting |
| 13 | 70 | Very Difficult | 48.87 | Difficult *—Very Difficult |
| 16 | 30 | Very Easy | 34.57 | Very Easy—Easy * |
| 17 | 80 | Very Difficult | 54.82 | Difficult *—Very Difficult |
| 21 | 45 | Easy | 45.04 | Easy—Difficult * |
| 23 | 45 | Easy | 40.73 | Easy—Difficult * |
| 24 | 70 | Very Difficult | 50.66 | Difficult *—Very Difficult |
| 25 | 70 | Very Difficult | 52.32 | Difficult *—Very Difficult |
| 27 | 80 | Very Difficult | 52.01 | Difficult *—Very Difficult |
| 33 | 75 | Very Difficult | 51.31 | Difficult *—Very Difficult |
| 34 | 80 | Very Difficult | 54.23 | Difficult *—Very Difficult |
| 41 | 35 | Very Easy | 31.65 | Very Easy —Easy * |
| 48 | 105 | Marginal Without Blasting | 64.29 | Very Difficult *—Marginal Without Blasting |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, S.; Li, X.; Zhou, J.; Khandelwal, M. Graded Evaluation and Optimal Scheme Selection of Mine Rock Diggability Based on the Multidimensional Cloud Model. Machines 2025, 13, 1019. https://doi.org/10.3390/machines13111019
Yao S, Li X, Zhou J, Khandelwal M. Graded Evaluation and Optimal Scheme Selection of Mine Rock Diggability Based on the Multidimensional Cloud Model. Machines. 2025; 13(11):1019. https://doi.org/10.3390/machines13111019
Chicago/Turabian StyleYao, Shibin, Xiaoyuan Li, Jian Zhou, and Manoj Khandelwal. 2025. "Graded Evaluation and Optimal Scheme Selection of Mine Rock Diggability Based on the Multidimensional Cloud Model" Machines 13, no. 11: 1019. https://doi.org/10.3390/machines13111019
APA StyleYao, S., Li, X., Zhou, J., & Khandelwal, M. (2025). Graded Evaluation and Optimal Scheme Selection of Mine Rock Diggability Based on the Multidimensional Cloud Model. Machines, 13(11), 1019. https://doi.org/10.3390/machines13111019








