Non-Line-of-Sight Error Compensation Method for Ultra-Wideband Positioning System

Abstract

Existing Ultra-Wideband (UWB) positioning methods are poorly suited for underground mobile devices and have limited positioning effectiveness in complex scenarios such as narrow tunnels, high dust levels, metallic structures, moving personnel, and machinery. To address this, we propose a UWB positioning method for non-line-of-sight (NLOS) error compensation, significantly improving the positioning accuracy of mobile equipment in coal mine tunnels. First, the characteristics of the impulse response waveform channel of the dataset are extracted, and the AdaBoost-based ensemble learning method is used to identify the mixture propagation channel. Then, combined with the UWB range noise model, the extended Kalman filter (EKF) algorithm is used to compensate for UWB NLOS errors. Finally, a mobile tag is used in conjunction with four positioning base stations to obtain positioning data, and the positioning effect in coal mine tunnels is simulated using a ranging noise model. The experimental results show that the EKF error compensation algorithm has good positioning accuracy and algorithm stability in different motion states in a noisy environment.

1. Introduction

With the continuous development in intelligent mining technology, high-precision positioning in coal mine tunnels has become a critical factor in achieving unmanned or minimally manned operations underground [1]. Precise positioning not only improves coal mining efficiency but also enhances safety by reducing human involvement in hazardous underground environments. However, despite the widespread application of automation technologies, reliable underground positioning remains challenging due to the limited availability of Global Navigation Satellite System (GNSS) signals [2,3]. Coal-mine tunnels are characterized by poor visibility, frequent signal blockage, and strong multipath propagation, which require positioning systems to maintain robustness under highly dynamic and variable conditions [4].

Among various localization technologies, UWB has drawn increasing attention because of its high ranging precision, strong anti-multipath capability, and obstacle penetration [5,6]. Nevertheless, UWB positioning systems continue to face significant challenges due to NLOS effects. In underground environments, NLOS propagation is a common issue that causes substantial errors in positioning. Addressing these errors is crucial for improving the accuracy and robustness of UWB systems in complex environments. To overcome the limitations of standalone systems, this study proposes a method for compensating NLOS errors in UWB positioning, aimed at enhancing the accuracy of mobile equipment positioning in coal mine tunnels. A public dataset is used to extract channel impulse response (CIR) features, with comparisons made between two feature selection methods: filter and wrapper. An AdaBoost ensemble classifier is used for LOS/NLOS identification, and its results are integrated into an EKF framework to compensate for NLOS errors. Finally, experiments are conducted to validate the effectiveness of the proposed EKF approach in reducing NLOS errors and improving positioning accuracy.

2. Related Research

Several studies have focused on improving the performance of UWB positioning systems in underground environments. For instance, Sun et al. [7] proposed an angle residual weighted adaptive Kalman filtering (ARWAKF) approach for UWB/Inertial Navigation System (INS)-based positioning of mine-used underground monorail cranes, which shows improvements in positioning accuracy. Similarly, Li et al. [8] developed a two-stage fusion positioning algorithm that combines UWB/INS/Magnetometer and incorporates fuzzy comprehensive evaluation (FCE) and a robust extended Kalman filter (IREKF) to improve robustness in NLOS environments.

However, UWB systems continue to struggle with NLOS propagation effects. Wang et al. [9] introduced a robust EKF approach with variance expansion to adjust NLOS measurements, while Zhang et al. [10] proposed Neyman–Pearson and Bayesian sequential detection methods for improved measurement classification. Additionally, several machine learning approaches, such as Fan et al. [11]’s improved particle swarm optimization and Yan et al. [12]’s proposed Bayesian sequential testing methods, have been explored to compensate for NLOS errors.

In parallel, diverse NLOS recognition techniques have been explored: Li et al. [13] used multidimensional scaling; Diao et al. [14] relied on the Cayley–Menger determinant; Wu et al. [15] analyzed distance correlations through machine learning; and Cui et al. [16] introduced a Morlet wavelet–Convolutional Neural Network (CNN) hybrid model effective mainly in static scenes. Despite their merits, these algorithms often lack universality across different tunnel environments. Statistical methods require threshold tuning, while machine learning methods depend heavily on kernel design and retraining in new conditions [17,18,19]. To further improve robustness, several hybrid or adaptive strategies have been reported, including voting- and clustering-based NLOS correction [20], generalized robust UKF approaches [21,22], and fingerprint-based NLOS suppression schemes [23,24,25].

3. Analysis of Positioning Error Sources in UWB Systems

The narrow space of underground mine tunnels and the wide variety of mining machinery and equipment make high-precision positioning extremely difficult to implement underground. In a typical NLOS environment, most positioning signals experience reflection and refraction along their propagation paths in the tunnels, resulting in signal energy attenuation. The complex waveforms of the acquired impulse response signals directly affect the positioning accuracy of UWB signals, as shown in Figure 1. The sources of error in UWB positioning in coal mine tunnels are analyzed as follows:

(1)

Multi-path effect: UWB positioning signals are blocked by various mining equipment, tunnel walls, underground personnel, or other obstacles along the track, causing refraction and scattering along the propagation path, which results in attenuation of the received signal energy and phase delay at the base station.

(2)

Multiple access interference: When performing precise positioning of multiple electric locomotives or multiple sets of mobile tags within the positioning range of the same group of base stations in a tunnel, interference between positioning signals of the same frequency or adjacent frequencies generated by multiple signal sources can cause an increase in the time delay characteristics of the positioning signal waveform and a decrease in positioning accuracy.

(3)

Other factors: In addition to the above error factors, positioning errors can also be affected by electromagnetic interference and environmental factors, such as humidity and temperature in tunnels. The impact of these interference factors cannot be ignored.

4. Enhancing Ultra-Wideband Positioning with Channel Impulse Response and Extended Kalman Filter

4.1. CIR Feature Extraction, Dataset, and Normalization

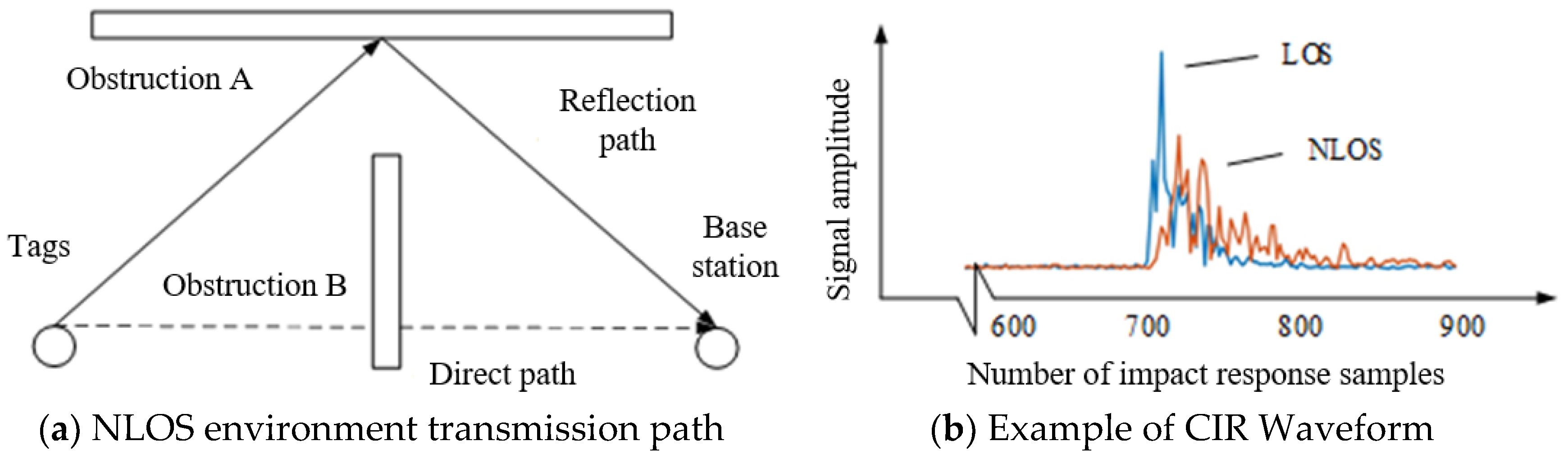
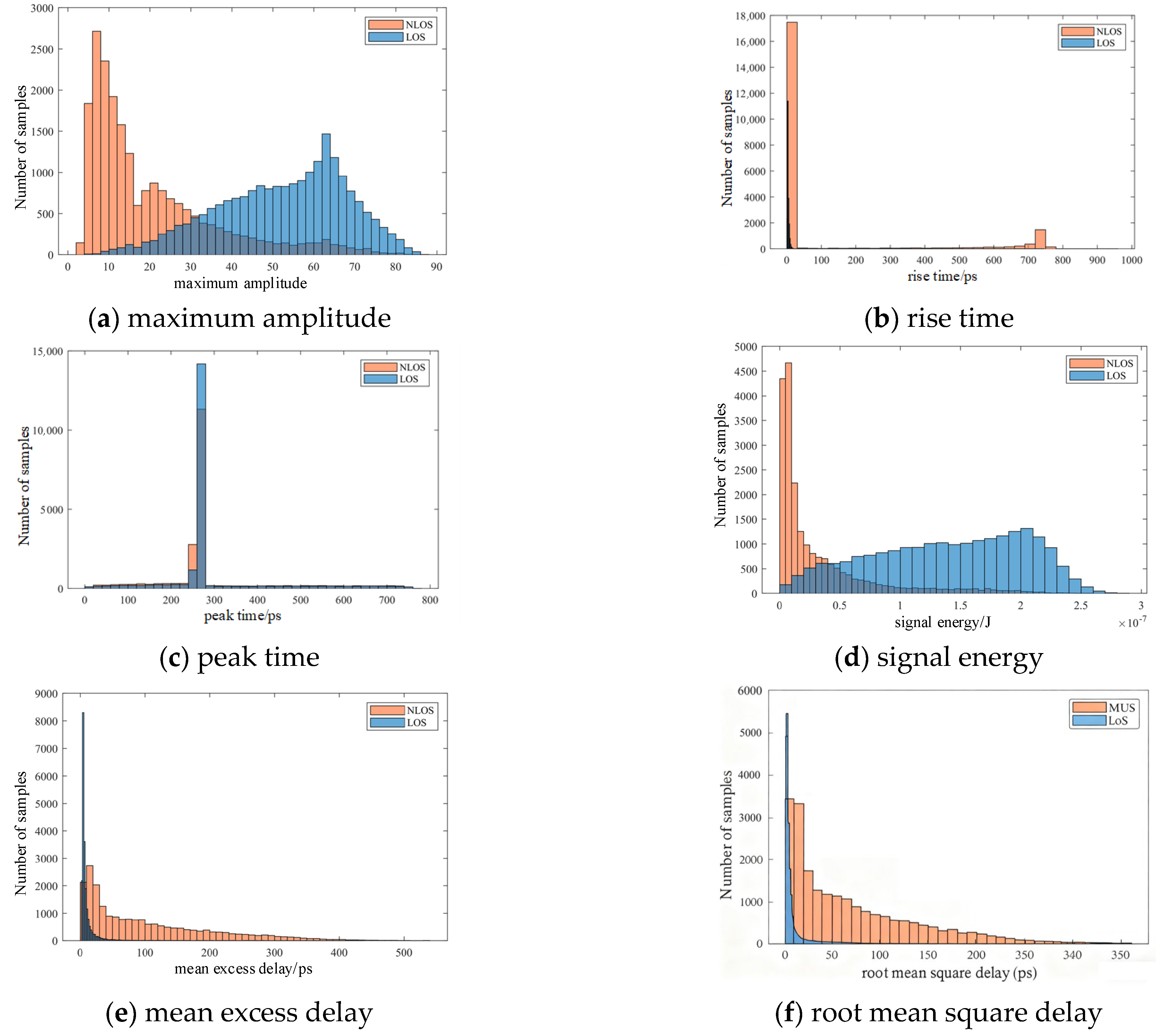
In underground mine tunnel environments, obstacles affecting UWB signals through absorption or reflection of propagation paths manifest their influence accurately in the corresponding CIR waveform. Consequently, data mining techniques enable extraction of characteristic parameters from CIR waveforms. Analysis of these channel waveform features facilitates differentiation between LOS and NLOS propagation conditions. Characteristic parameters of CIR waveforms commonly employed for this purpose are summarized in

Table 1. Characteristic parameters of CIR waveforms.

Symbol	Description	Expression
rmax	maximum amplitude	$r_{\max }=\max \left|r(t_i)\right|$
trise	rise time	$t_{rise}=t_H-t_L$
tp	peak time	$t_p=t_{pt}-t_0$
εr	signal energy	${\epsilon }_r={\displaystyle \underset{T}{\int }\left|r{(t_i)}^2\right|}dt$
τmed	mean excess delay	${\tau }_{med}={\displaystyle \frac{{\displaystyle {\int }_{-\infty }^{\infty }t{\left|r(t_i)\right|}^{2}dt}}{{\displaystyle {\int }_{-\infty }^{\infty }{\left|r(t_i)\right|}^{2}dt}}}$
τrmsd	root mean square delay	${\tau }_{rmsd}={\displaystyle \frac{{{\displaystyle \int }}_{-\mathsf{\infty }}^{\mathsf{\infty }}{(t_i-{\tau }_m)}^2|r(t_i){|}^{2}dt}{{{\displaystyle \int }}_{-\mathsf{\infty }}^{\mathsf{\infty }}|r(t_i){|}^{2}dt}}$
κ	kurtosis	$\kappa ={\displaystyle \frac{{\mu }^4}{{\sigma }^4}}={\displaystyle \frac{E[{(r(t_i)-{\mu }_{\left|r\right|})}^4]}{{(E[{(r(t_i)-{\mu }_{\left|r\right|})}^2])}^2}}$
ske	skewness	$ske={\displaystyle \frac{E{[|r(t_i)|-{\mu }_{\left|r\right|})}^3]}{E{[{(|r(t_i)|-{\mu }_{\left|r\right|})}^2]}^{3/2}}}$

.

Statistical distributions and characteristics of key parameters were analyzed using a publicly available dataset [26], which contains approximately 42,000 processed samples of UWB channel impulse responses under both LOS and NLOS conditions. The samples were obtained by segmenting and overlapping the original records from four indoor environments to enhance data diversity and balance between LOS and NLOS cases. Each record includes tag and anchor coordinates, range measurements, received signal strength (RSS), first-path index, and LOS/NLOS label. The dataset is split into training (70%), validation (10%), and testing (20%) subsets. In addition, nine data groups with different NLOS ratios (10–90%) are constructed to evaluate classifier robustness under varying propagation conditions. The results are shown in Figure 2.

As illustrated in Figure 2, eight characteristic parameters are extracted from the CIR. Under NLOS conditions, delayed and attenuated multipath components lead to smaller rₘₐₓ and εᵣ, while τ_med and τ_rmsd become larger. Moreover, higher-order statistical parameters such as κ and ske change markedly because of asymmetric and heavy-tailed signal shapes.

To mitigate the impact of dimensional and unit disparities among distinct CIR characterization parameters on data analysis outcomes, all the parameters undergo normalization processing. This procedure addresses comparability issues across heterogeneous feature parameters.

To address poor NLOS identification accuracy caused by single-feature dependency, this study employs multiple waveform characteristics for NLOS recognition, necessitating optimal feature selection. As a critical preprocessing step, feature selection identifies optimal feature subsets by eliminating irrelevant or weakly relevant parameters from the original set. This dimensionality reduction directly enhances model generalization, mitigates overfitting, and reduces algorithmic complexity.

Wrapper methods iteratively derive optimal feature subsets by evaluating feature combinations against learner performance. Given the constrained feature dimensions and stringent accuracy requirements inherent to this study on LOS/NLOS classification of UWB signals, the wrapper method constitutes the optimal feature selection approach under these operational conditions.

4.2. LOS/NLOS Recognition with Wrapper-Selected Features

The AdaBoost ensemble method integrates multiple base classifiers trained on an identical dataset into a strong classifier to perform LOS/NLOS classification of UWB signals. This integrated strong learner achieves a synergistic combination of constituent models, effectively mitigating the inherent limitations in base classifier accuracy.

As shown in Figure 3, the AdaBoost iterative algorithm undergoes a three-step process. Firstly, initialization of training data weight distribution assigns equal initial weights 1/N to each sample. Secondly, training multiple weak classifiers involves reducing weights of correctly classified samples for the next iteration’s training set, updating sample weights iteratively. Finally, combining weak classifiers into a strong classifier adjusts each base classifier’s weight in the final classifier by modifying the classification function based on error rates.

For initial training samples denoted as T = {(x₁, y₁),(x₂, y₂),…,(x_m, y_m)}, the output weight for the k-th base classifier is updated to D(k) = (w_k1,w_k2,…,w_km) according to the results from the (k−1)-th classifier, where w_i = 1/m (i = 1,2,…,m). For binary classification like LOS/NLOS with output classes {−1,1}, the error rate e_k of the k-th weak classifier G_k(x) on the training set is given by Equation (1) and its weight coefficient α_k by Equation (2).

$$e_k=P(G_k(x_i)\ne y_i)={\displaystyle \sum }_{i=1}^m{W}_{ki,}I(G_k(x_i)\ne y_i)$$

(1)

$${\alpha }_k={\displaystyle \frac{1}{2}}\log {\displaystyle \frac{1-e_k}{e_k}}$$

(2)

where larger e_k results in smaller α_k. The weight coefficient D(k) = (w_k1,w_k2,…,w_km) for the first k base classifiers updates the (k + 1)-th classifier’s weights per Equations (3) and (4), where Z_k is the normalization factor.

$${\omega }_{k+1,i}={\displaystyle \frac{{\omega }_{ki}}{Z_k}}exp(-{\alpha }_k{y}_i{G}_k(x_i))$$

(3)

$$Z_k={\displaystyle \sum }_{i=1}^m{\omega }_{ki}exp(-{\alpha }_k{y}_i{G}_k(x_i))$$

(4)

The w_k+1,I calculation shows that misclassified samples (y_iG_k(x_i) < 0) receive increased weights for the next weak classifier, while correctly classified samples have reduced weights. Adaboost employs a weighted averaging strategy to output the strong classifier as in Equation (5).

$$f(x)=sign({\displaystyle \sum }_{k=1}^K{\alpha }_k{G}_k(x))$$

(5)

We employed the public dataset to validate the recognition algorithm’s performance. Evaluation metrics for the LOS/NLOS binary classification, including accuracy, precision, recall, F1-score, and Matthews correlation coefficient (MCC), are presented in

Table 2. Comparison of machine learning algorithms for NLOS recognition.

Algorithm	Accuracy	Precision	Recall	F1	MCC
KNN	0.9484	0.9318	0.9765	0.9536	0.7977
SVM	0.9488	0.9318	0.9774	0.9540	0.7984
CNN	0.9545	0.9333	0.9893	0.9604	0.8104
AdaBoost	0.9562	0.9366	0.9884	0.9617	0.8137

. All the models were implemented in Python 3.9 using the scikit-learn and TensorFlow libraries. As shown, we implemented multiple machine learning algorithms, namely k-Nearest Neighbors (KNN), Support Vector Machine (SVM), CNN, and Adaptive Boosting (AdaBoost). The algorithms were implemented using retained default hyperparameter values during pre-training. All the algorithms achieved comparable recognition accuracy exceeding 94.84%, while the AdaBoost-based ensemble exhibited the most stable and robust performance, particularly when the LOS/NLOS ratio was balanced.

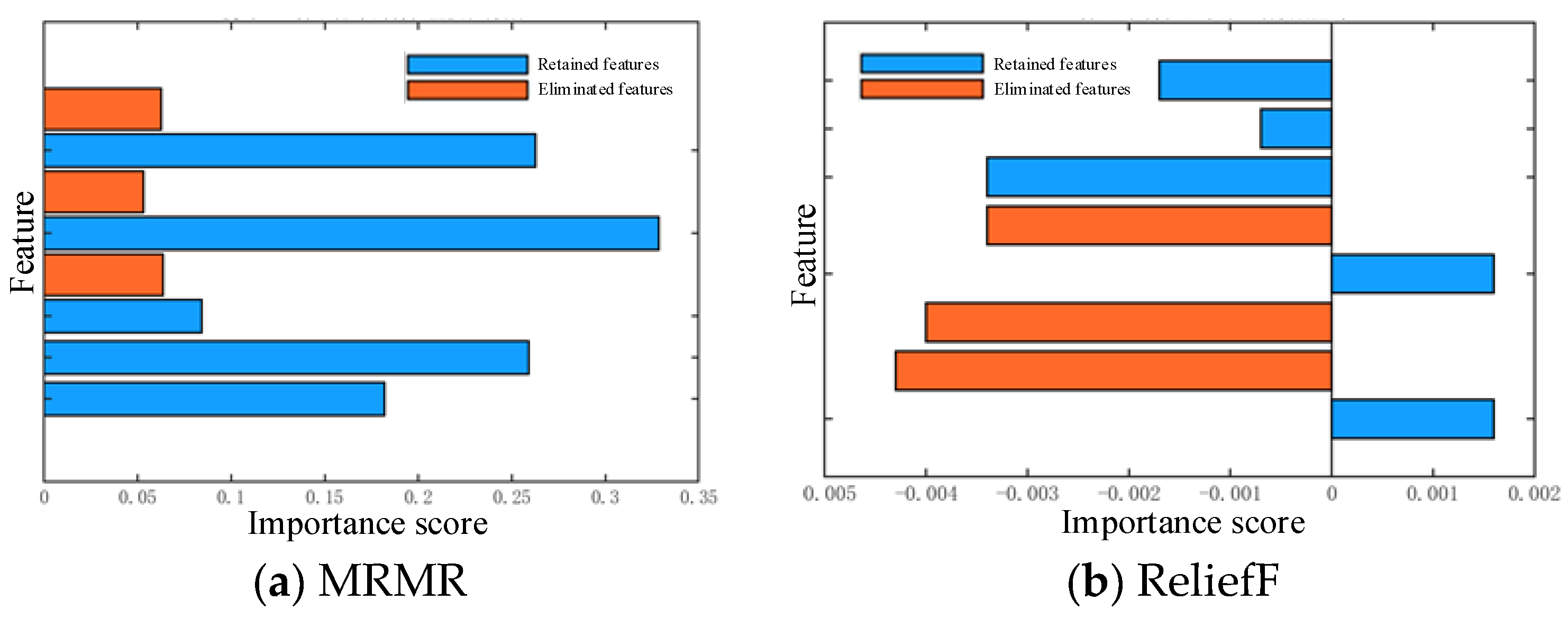
To validate the recognition performance of filter-based feature selection algorithms, this experiment extracted 6000 positioning data groups from the dataset. The MRMR and ReliefF algorithms were employed to compute important scores for each feature parameter, as illustrated in Figure 4. The MRMR algorithm simultaneously satisfied minimum redundancy among features and maximum relevance between features and the target variable. Here, MRMR scores ranged between (0, 0.35). Features were prioritized by importance score as follows: τ_rmsd < ske < ε_r < t_p < r_max < κ < t_rise < τ_m. The ReliefF algorithm evaluated feature-target correlations by updating feature weights based on their ability to distinguish neighboring samples. The final average weight scores ranged from (−0.005, 0.002). Features were prioritized as t_rise < t_p < ε_r < τ_rmsd < ske < κ < r_max < τ_m. The optimal feature subset could then be determined by specifying the number of retained features.

As shown in

Table 3. Comparison of feature parameters and accuracy under each feature selection algorithm.

Algorithm		Feature Parameters	Accuracy
wrapper-based	Initial	$r_{\max }+t_{rise}+t_p+{\mathrm{\epsilon }}_r+{\mathrm{\tau }}_m+{\mathrm{\tau }}_{rmsd}+\mathrm{\kappa }+ske{r}_{\max }+t_{rise}+t_p+\mathrm{\epsilon }\mathrm{\tau }\mathrm{\tau }\mathrm{\kappa }$	95.5%
	Round 1	$r_{\max }+t_{rise}+t_p+{\mathrm{\epsilon }}_r+{\mathrm{\tau }}_m+{\mathrm{\tau }}_{rmsd}+\mathrm{\kappa }+ske$	96.1%
	Round 2	$r_{\max }+t_{rise}+{\mathrm{\epsilon }}_r+{\mathrm{\tau }}_m+{\mathrm{\tau }}_{rmsd}+\mathrm{\kappa }+ske$	96.3%
	Round 3	$r_{\max }+t_{rise}+{\mathrm{\epsilon }}_r+{\mathrm{\tau }}_m+{\mathrm{\tau }}_{rmsd}$	96.4%
	Round 4	$r_{\max }+{\mathrm{\epsilon }}_r+{\mathrm{\tau }}_m+{\mathrm{\tau }}_{rmsd}$	92.6%
Filter-based	MRMR	$r_{\max }+t_{rise}+t_p+{\mathrm{\tau }}_m+\mathrm{\kappa }$	95.8%
	ReliefF	$r_{\max }+{\mathrm{\tau }}_m+{\mathrm{\tau }}_{rmsd}+\mathrm{\kappa }+ske$	95.7%

, the wrapper-based feature selection demonstrated monotonically increasing accuracy in the first three iterations, followed by decreased accuracy in the fourth iteration. Thus, the optimal feature subset for the wrapper method was {r_max, t_rise, ε_r, τ_m, τ_rmsd}. Compared with the MRMR and ReliefF algorithms, which retained five feature parameters and shared common features {r_max, τ_m}, the wrapper method achieved superior performance. Consequently, the wrapper-derived feature subset {r_max, t_rise, ε_r, τ_m, τ_rmsd} was adopted as the optimal feature selection configuration.

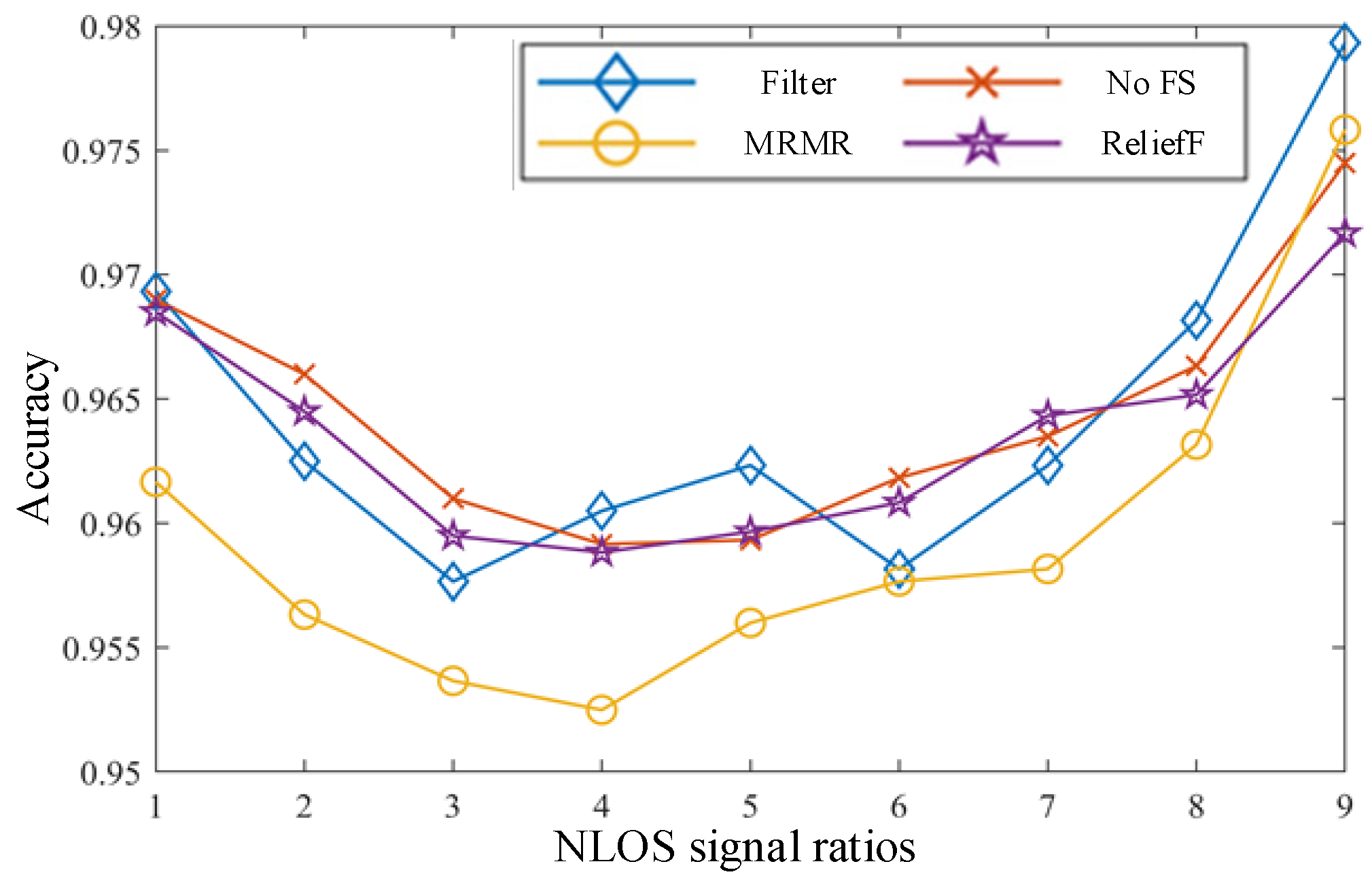
Figure 5 illustrates the experimental framework where 9 groups of 6000 signal segments were extracted from the dataset, each with distinct NLOS proportions ranging from 10% to 90%. This comparative analysis evaluated the accuracy of the AdaBoost-based recognition algorithm across different NLOS signal ratios scenarios.

The experimental results indicate that the AdaBoost-based ensemble classifier effectively identifies NLOS signals across different NLOS signal ratios scenarios, achieving recognition rates above 85%. In environments with the two extreme regions, all feature selection methods produce subsets with similarly high recognition accuracy. When LOS and NLOS signals occur in near-equal proportions, the wrapper-derived feature subset demonstrates superior recognition accuracy. Consequently, this study adopts the wrapper method for feature selection and employs the AdaBoost-based ensemble classifier as the final LOS/NLOS recognition algorithm.

4.3. EKF-Based NLOS Error Suppression

Under LOS conditions, UWB errors originate from multiple contributing factors, including signal attenuation, multipath effects, multi-user interference, and clock drift. The noise model can be effectively approximated as Gaussian, where UWB positioning measurements represent the summation of true range values and Gaussian noise, as expressed in Equation (6):

$$R_{LOS}=R_{true}+GM{M}_{error}$$

(6)

where the GMM_error probability density function is given by Equation (7), and this effectively characterizes the statistical properties of LOS noise. This is achieved by weighting and combining Gaussian-distributed noise components generated from multipath signals in LOS propagation.

$$p(x)={\displaystyle \sum }_{j=1}^K{\pi }_{j}N(x|u_j,{\epsilon }_j)$$

(7)

Under NLOS conditions, UWB signals undergo extensive reflections and scattering from obstacles, including tunnel walls, mechanical equipment, and personnel within underground mines. These interactions cause rapid signal attenuation accompanied by substantial delay spread, resulting in heavy-tailed amplitude distributions. Stable distributions are employed to model NLOS noise due to their inherent properties of self-similarity, heavy-tailed characteristics, and shape adaptability, with the probability density function formalized in Equation (8).

$$\begin{array}{l}f(x;\alpha ,\beta ,\gamma ,\delta )={\displaystyle \frac{1}{2\pi }}{{\displaystyle \int }}_{-\mathsf{\infty }}^{\mathsf{\infty }}{e}^{-jtx}M(t;\alpha ,\beta ,\gamma ,\delta )dt\\ M(t;\alpha ,\beta ,\gamma ,\delta )=e^{jt\delta }\left\{\begin{array}{cc}{e}^{-{\gamma }^{\alpha }|t{|}^{\alpha }}& \alpha \ne 1\\ e^{-\gamma |t|}(\beta +jsign(t)\tan (\pi \beta /2))& \alpha =1\end{array}\right.\end{array}$$

(8)

where the parameter α, bounded between 0 and 2, determines the heaviness of the distribution tail. The symmetry parameter β indicates distribution skewness when β ≠ 0. The parameter γ indicates distribution width and height, while δ indicates the distribution skew value.

UWB NLOS noise models exhibit inherent complexity, as their statistical properties vary with channel environments and transmission distances. Consequently, practical implementations require context-specific model selection and optimization. Thus, UWB positioning measurements can be formally expressed as follows:

$$R_{UWB}=R_{true}+G{M}_{error}+S{D}_{error}$$

(9)

The EKF [27] is a widely adopted state estimation algorithm designed to address significant deviations between estimated and true states in nonlinear systems with non-Gaussian distributions. This study employs the EKF algorithm to mitigate NLOS positioning errors in UWB systems. For nonlinear systems, the state and observation models are formalized in Equation (10).

$$\left\{\begin{array}{c}{X}_k=F(X_{k-1})+{\omega }_k\hfill \\ Y_k=H(X_k)+{\Delta }_k\hfill \end{array}\right.$$

(10)

where the state vectors at time steps k−1 and k are denoted as X_k−1 and X_k, respectively. The observation matrix at time k is represented by Y_k. The F(⋅) and H(⋅) denote the state transition function and nonlinear observation function, respectively. ω_k denotes process noise and Δ_k denotes observation noise during state evolution.

For an n-dimensional variable x with mean $\overline{x}$ and covariance P_x, the objective is to predict an m-dimensional variable y with mean $\overline{y}$ and covariance P_y. The relationship between y and x is governed by the following nonlinear transformation:

$$y=f(x)$$

(11)

Performing a Taylor series expansion of Equation (12) at point $\overline{x}$ yields the following:

$$y=f(\overline{x}+e)=f(\overline{x})+f^{(1)}{e}^1+{\displaystyle \frac{f^{(2)}{e}^2}{2!}}+{\displaystyle \frac{f^{(3)}{e}^3}{3!}}+\cdots$$

(12)

In Equation (12), f⁽ⁱ⁾(⋅) denotes the i-th order partial derivative of x at point $\overline{x}$, and e represents the neighborhood deviation of x at point $\overline{x}$. The mean $\overline{y}$ and covariance P_y of y are derived as shown in Equation (13) and Equation (14):

$$\overline{y}=E[y]=E[f(\overline{x})+f^{(1)}{e}^1+{\displaystyle \frac{f^{(2)}{e}^2}{2!}}+{\displaystyle \frac{f^{(3)}{e}^3}{3!}}+\cdots ]$$

(13)

$$P_y=E[(y-\overline{y}){(y-\overline{y})}^T]$$

(14)

In this study, the EKF is applied to compensate for NLOS ranging errors in the UWB positioning system. The system state vector is defined as

$$X_k={\left[x_k,y_k\right]}^T$$

(15)

The process model assumes a constant-velocity motion:

$$z_k=h\left(X_k\right)+v_k=\sqrt{{\left(x_k-x_i\right)}^2+{\left(y_k-y_i\right)}^2}+v_k$$

(16)

where $\left(x_i,y_i\right)$ denotes the anchor coordinates and $v_k$ represents the measurement noise.

To optimize computational efficiency while maintaining acceptable engineering error margins in practical applications, only the first two statistical moments of f⁽ⁱ⁾(⋅) are computed to approximate $\overline{y}$ and P_y. The mathematical representation of the EKF for nonlinear systems is formalized in Equation (1):

$$\left\{\begin{array}{c}{X}_k={\mathrm{\Phi }}_{k/k-1}{X}_{k-1}+{\omega }_k\\ Y_k=H_k{X}_k+{\Delta }_k\end{array}\right.$$

(17)

where the ${\mathrm{\Phi }}_{k/k-1}$ and $H_k$ are denoted state transition matrix and observation model matrix, respectively. Therefore, the EKF state prediction and covariance prediction are computed as follows in Equation (18):

$$\left\{\begin{array}{c}{\widehat{X}}_k={\mathrm{\Phi }}_{k/k-1}{\widehat{X}}_{k-1}\\ P_k={\mathrm{\Phi }}_{k/k-1}{P}_{k/k-1}{\mathrm{\Phi }}_{k/k-1}^T+Q_{k-1}\end{array}\right.$$

(18)

where ${\widehat{X}}_k$ denotes the predicted state vector; $P_k$ and $P_{k/k-1}$ represent the a priori and posterior error covariance matrices, respectively; and $Q_{k-1}$ represents the process noise covariance matrix.

The state gain and state estimation error covariance are given by Equation (19), while the EKF gain is computed in Equation (20):

$$\left\{\begin{array}{c}\widehat{X}={\widehat{X}}_{k/k-1}+K_k(Y_k-H_k{\widehat{X}}_{k/k-1})\\ P_k=(I-K_k{H}_k)P_{k/k-1}\end{array}\right.$$

(19)

$$K_k=P_{k/k-1}{H}_k^T{(H_k{P}_{k/k-1}{H}_k^T+R_k)}^{-1}$$

(20)

5. Experimental Analysis

To ensure experimental reproducibility, all data were collected using DW1000 UWB modules operating at a center frequency of 6.5 GHz with a 500 MHz bandwidth. The four anchors were synchronized via cable connection, and the mobile tag was mounted on a trolley moving along the designed trajectory. Each experiment was repeated three times, and all range data were logged at 10 Hz for offline processing in MATLAB (r2021b). Before EKF filtering, the raw UWB range measurements were denoised using a 5-point median filter to remove impulsive outliers.

To verify the effectiveness and stability of the proposed NLOS error compensation method for UWB positioning, as shown in Figure 6, this experiment employs one mobile tag with four anchor nodes to collect positioning data, simulating mine tunnel localization using ranging noise models. Given that LOS and NLOS ranging errors in confined spaces follow Gaussian mixture and stable distributions, respectively, and considering UWB ranging module accuracy ranges from 10 to 30 cm, LOS noise error was set as Gaussian distribution {μ, σ} = {0, 0.1}, while stable distribution {α, β, γ, δ} = {(0,2], [−1,1], (0,∞), (-∞,∞)} was introduced as NLOS error noise. The sampling period was t = 0.1 s with a total experiment duration of 80 s. Performance was evaluated by comparing ranging accuracy, algorithm stability, and positioning precision of the EKF error compensation algorithm under different NLOS noise environments.

The experimental site measured 15 m × 9.5 m. As illustrated in Figure 7, the anchor coordinates were (−3.5, −1), (11.5, −1), (11.5, 8.5), and (−3.5, 8.5). The target initiated closed-loop motion from the starting position (0, 0), with an initial velocity of 0.5 m/s along the x-axis and zero initial velocity along the y-axis. Several metallic pillars and moving personnel were intentionally positioned along the tunnel to introduce NLOS conditions. During turning phases, the target underwent uniform deceleration along the x-axis and uniform acceleration along the y-axis. The ideal trajectory comprised four segments of uniform linear motion and four turning segments.

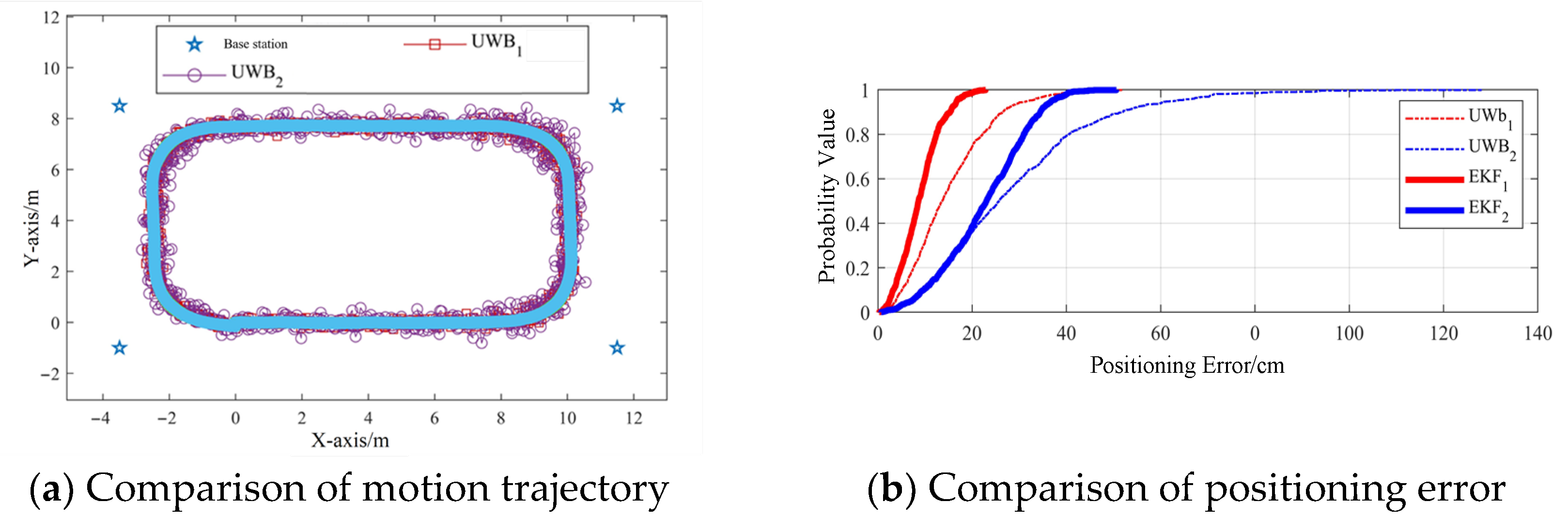
Under different observation noise conditions, the UWB measurements and optimized trajectories obtained using the time difference in arrival positioning algorithm and EKF error compensation algorithm are shown in Figure 8a. After EKF filtering, the optimized trajectory exhibited significantly reduced fluctuations and smoother motion compared to raw UWB trajectories under identical noise conditions. The EKF effectively mitigated NLOS noise impacts. Additionally, the optimized trajectories better approximated the ideal path during straight-line motion than during turns.

The cumulative distribution functions of errors under both noise conditions are presented in Figure 8b. For observation noise R = 0.01, the maximum errors of the UWB measurements and EKF-compensated results within the simulated range were 50 cm and 23 cm, respectively. At R = 0.1, these values increased to 125 cm and 50 cm. These results demonstrate the EKF’s robust error compensation capability for UWB positioning systems.

To compare positioning errors of different motion states, this paper uses segments 3 and 6 under observation noise R = 0.01 after trajectory optimization. These non-adjacent segments represent uniform linear motion and turning motion, respectively, with 100 measurement points over 10 s. Positioning errors are shown in

Table 4. Data analysis of positioning errors.

	UWB Maximum Error (cm)		RMSE (cm)			EKF Maximum Error (cm)		RMSE (cm)
	UWBX	UWBY	UWBX	UWBY	2D	EKFX	EKFY	EKFX	EKFY	2D
linear	25.13	52.34	1.05	1.99	2.26	8.42	8.38	0.56	0.58	0.81
turning	26.15	24.23	1.12	1.33	1.73	18.95	9.95	0.52	0.56	0.76

and Figure 9.

At observation noise R = 0.01, the maximum UWB measurement errors in the x-axis for uniform linear motion and turning motion were 25 cm and 26 cm, respectively, while in the y-axis they were 52 cm and 34 cm, respectively. After EKF error compensation processing, the maximum errors in the x-axis were corrected to 8 cm and 19 cm, and the maximum errors in the x-axis were corrected to 8 cm and 10 cm.

The root mean square error (RMSE) is calculated as the square root of the average squared difference between the estimated and true positions along both axes, and is expressed as follows:

$$RMSE=\sqrt{{\displaystyle \frac{1}{N}}{\displaystyle \sum _{i=1}^N\left[{\left(x_i-{\widehat{x}}_i\right)}^2+{\left(y_i-{\widehat{y}}_i\right)}^2\right]}}$$

(21)

where $x_i$ and $y_i$ denote the ground truth, ${\widehat{x}}_i$ and ${\widehat{y}}_i$ are the corresponding estimated positions, and N is the total number of samples.

Comparison of the RMSE results before and after error compensation shows that the UWB measurements exhibit larger errors in the y-axis compared to the x-axis; the EKF-compensated results demonstrate comparable magnitudes in both the x-axis and y-axis; meanwhile, the y-axis deviation from ground truth is greater in turning motion than in uniform linear motion, indicating EKF has certain limitations in compensating complex maneuvers such as turning motion.

The experimental results indicate that the EKF-based error compensation method significantly improves the positioning accuracy of UWB systems under NLOS conditions. As shown in Figure 8, the EKF effectively reduced measurement fluctuations, especially during straight-line motion, and outperformed raw UWB measurements. However, the EKF-compensated results showed higher errors in the y-axis during turning motion, as observed in Figure 9, suggesting that the EKF method might have limitations in compensating for more complex maneuvers, such as rapid direction changes.

6. Conclusions

This paper analyzes error sources in underground UWB positioning, establishing LOS/NLOS signal identification and NLOS error compensation algorithms as research priorities. Initially, characteristics are extracted from CIR waveform channels in public datasets. Subsequent comparison of filter-based and wrapper-based feature selection methods determines the optimal approach. An AdaBoost-based ensemble learning method is then implemented for LOS/NLOS channel identification. The simulation results demonstrate that the recognition algorithm with wrapper-based feature selection outperforms conventional methods. Furthermore, a UWB ranging noise model is proposed, with NLOS errors compensated via EKF algorithms. The experimental results ultimately confirm that the EKF error compensation algorithm achieves robust positioning accuracy and algorithmic stability across varying motion states under dual noise environments. However, it should be noted that the current evaluation is based on simulated NLOS data derived from public indoor datasets, which may not fully represent the propagation characteristics of underground tunnels. In future work, more attention will be given to positioning performance under sparse anchor configurations and degraded network geometry, with the proposed method being extended to real-world data integration and multi-sensor fusion for improved robustness.