Design Optimization of Sensor-Embedded Bearing Rings in Heavy-Duty Electric Shovel Applications via Multi-Physics Coupling Analysis and Experimental Validation
Abstract
1. Introduction
2. Theoretical Modeling Framework
2.1. Heat Generation Formula
2.2. Heat Transfer Formula
- 1.
- Natural Convection Coefficient
- 2.
- Forced Convection Coefficient
2.3. Thermal–Mechanical Coupling Model
- 1.
- Thermal Load Transferred to Structural Domain
- 2.
- Thermally Driven Mechanical Boundary Loading
- 3.
- Thermomechanical Coupled Modeling and Simulation Strategy
2.4. Geometry and Slotting Model
3. Finite Element Simulation
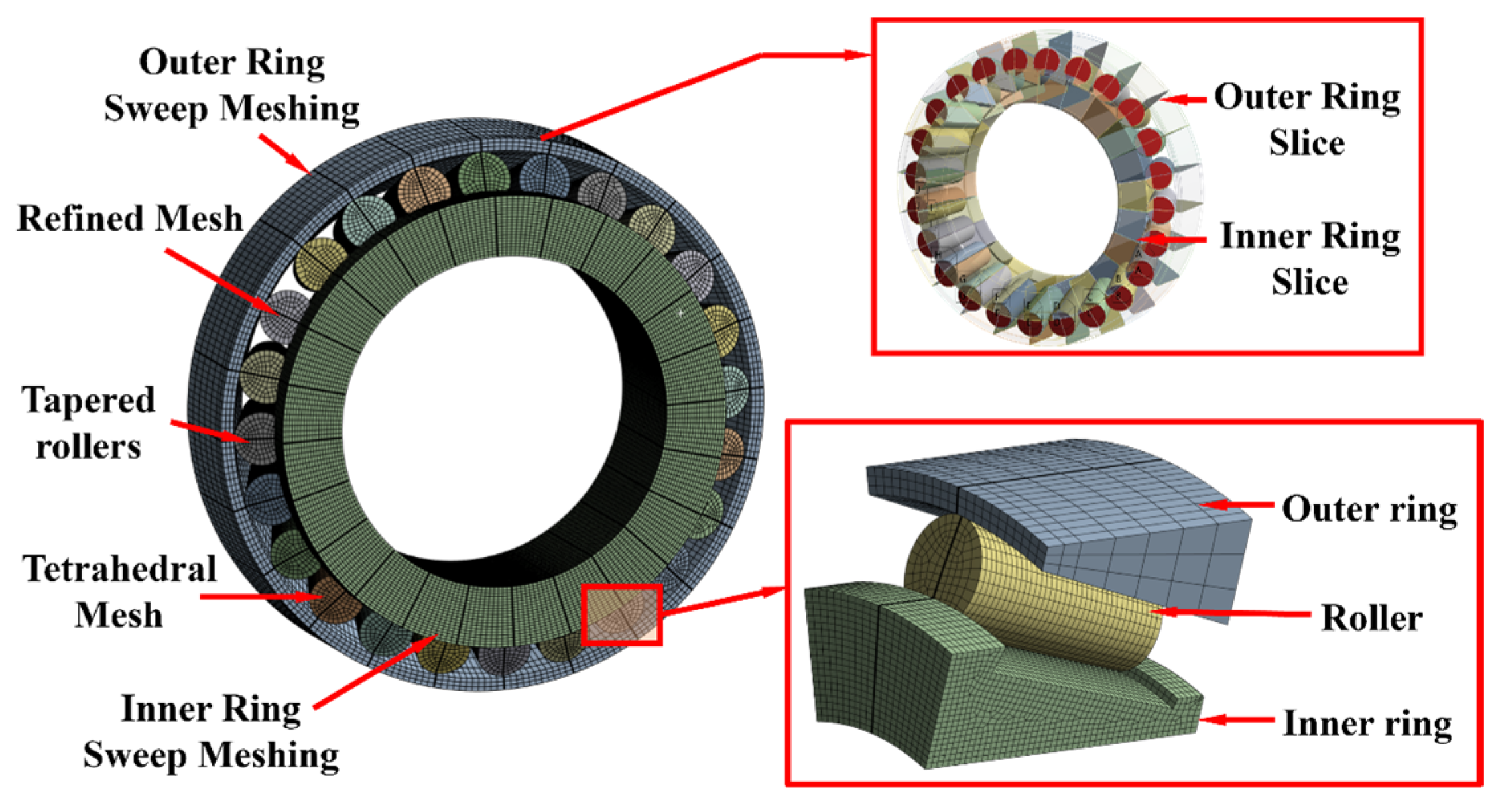
3.1. Model Setup
- 1.
- Contact Definition
- 2.
- Finite Element Meshing Strategy
- 3.
- Load and Boundary Condition Setting
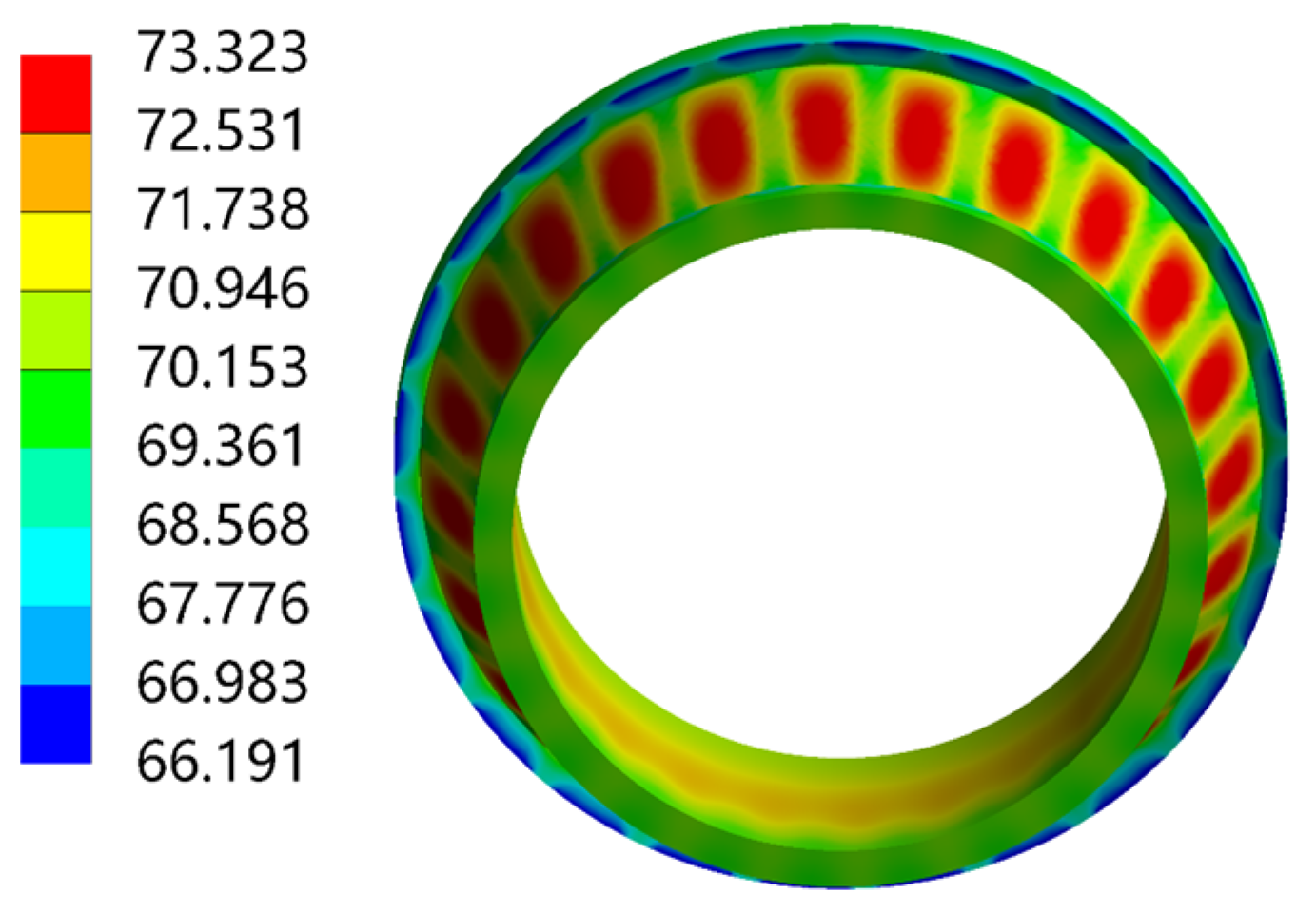
3.2. Validation of Simulation Model
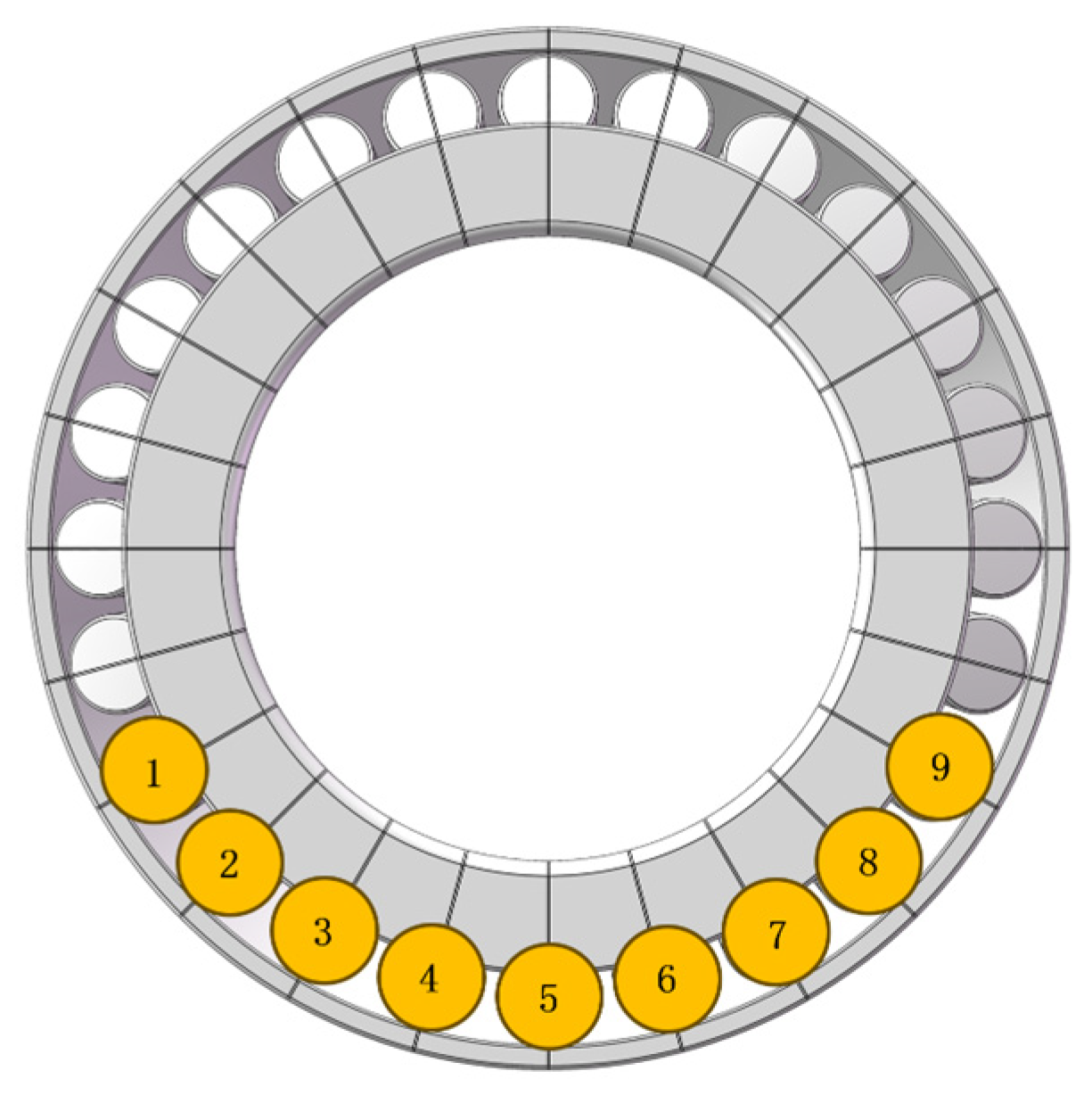
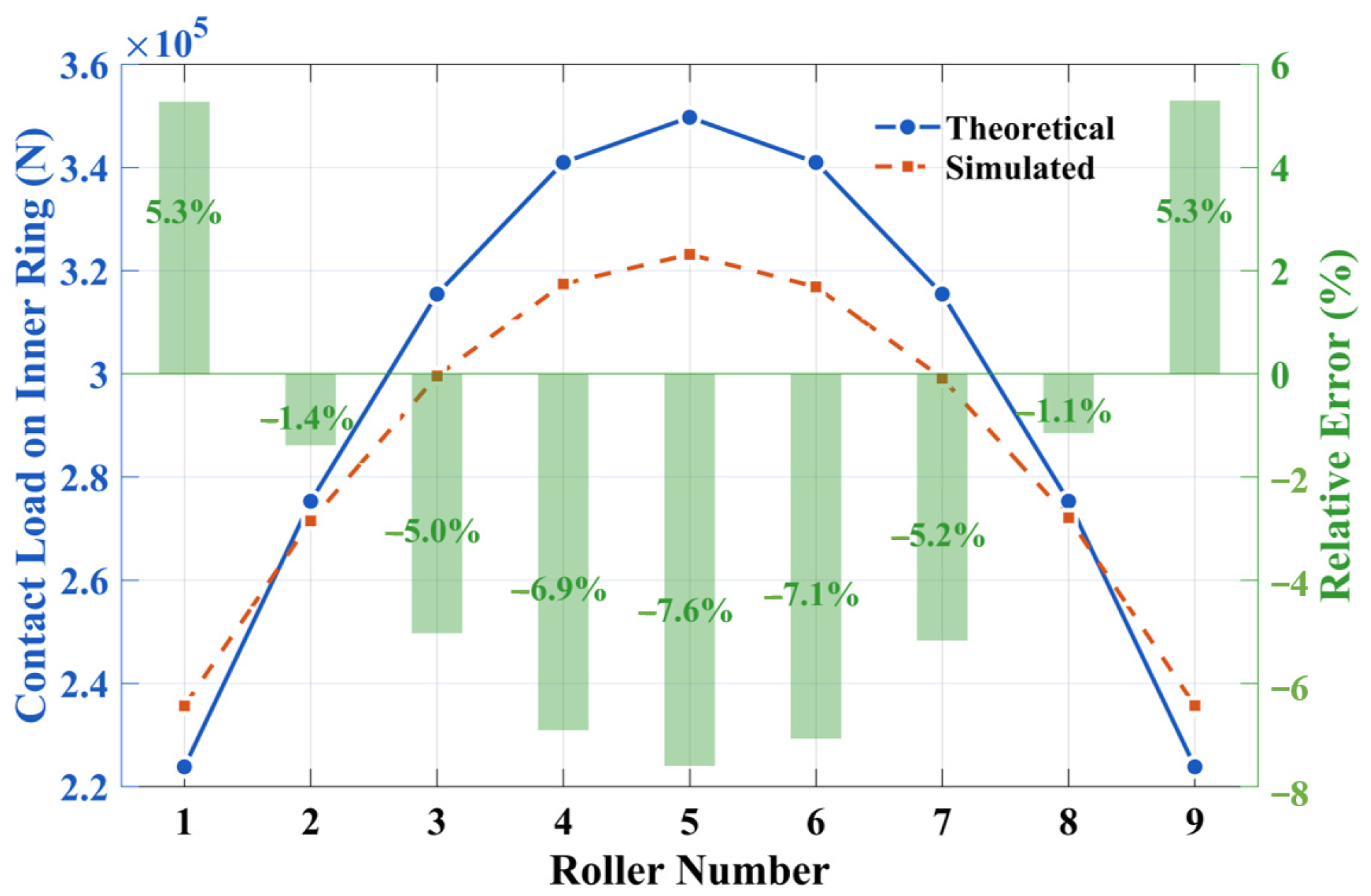
- 1.
- Contact Load Distribution Verification
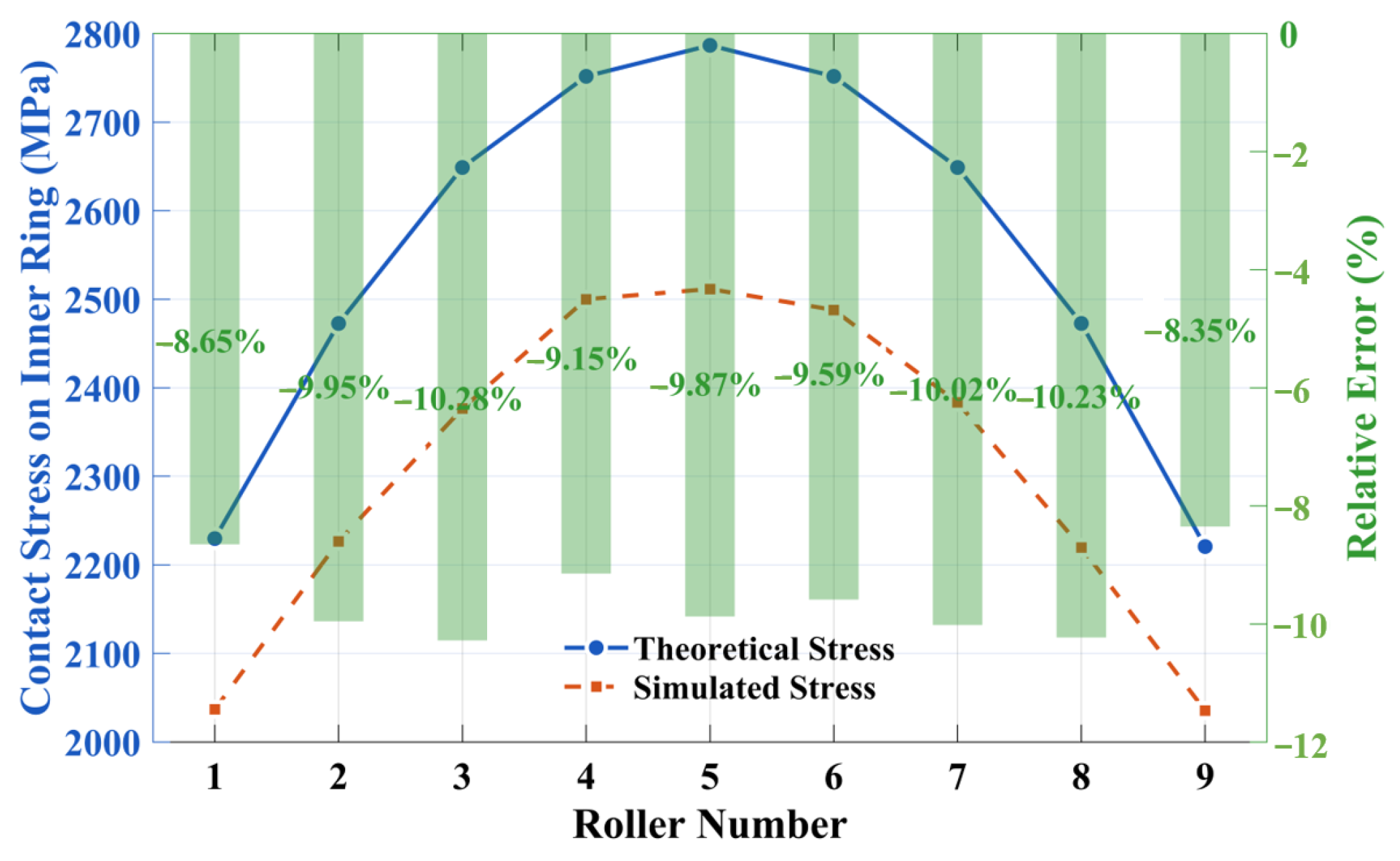
- 2.
- Contact Stress Verification
4. Experimental Verification
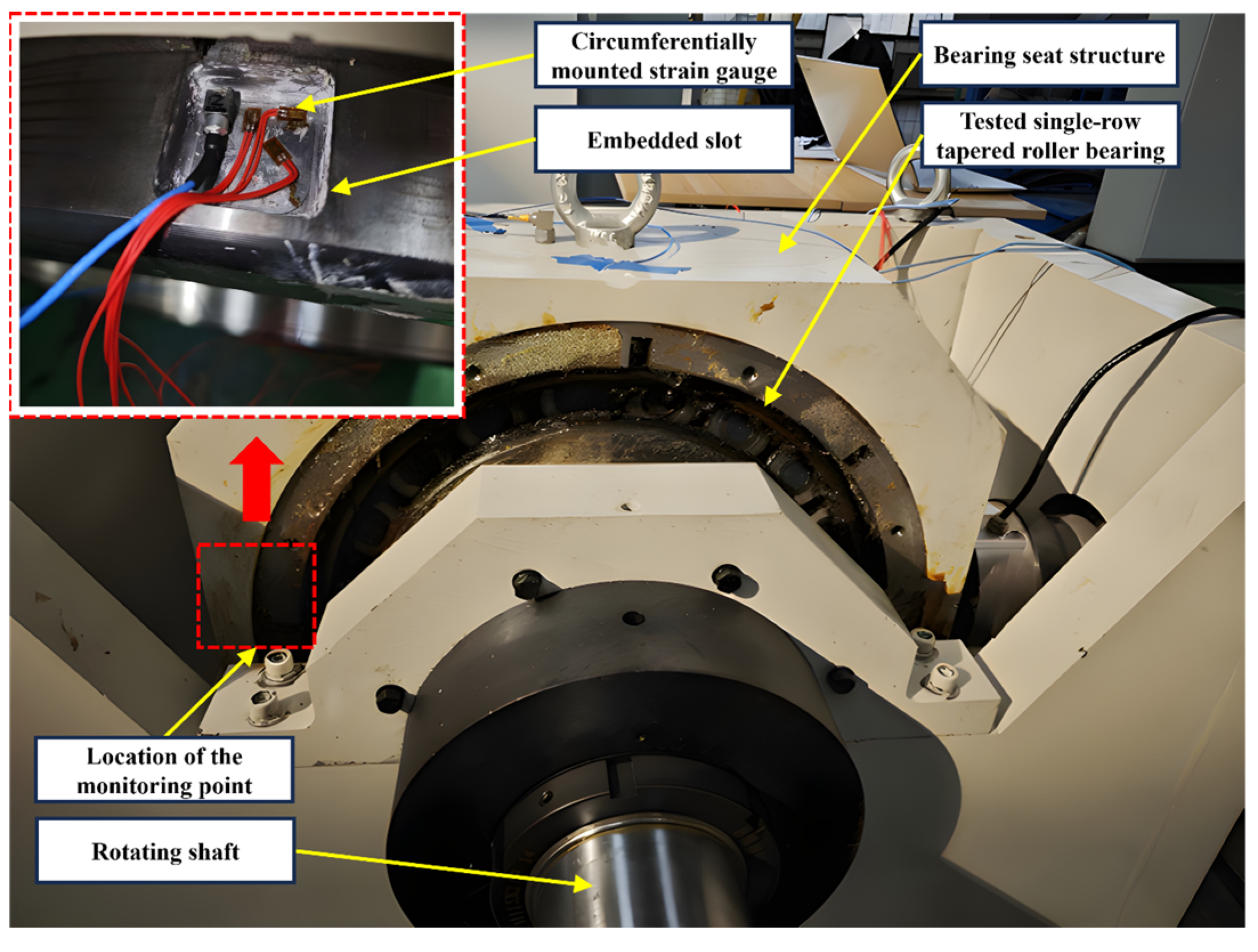
4.1. Experimental Platform and Sensor Layout
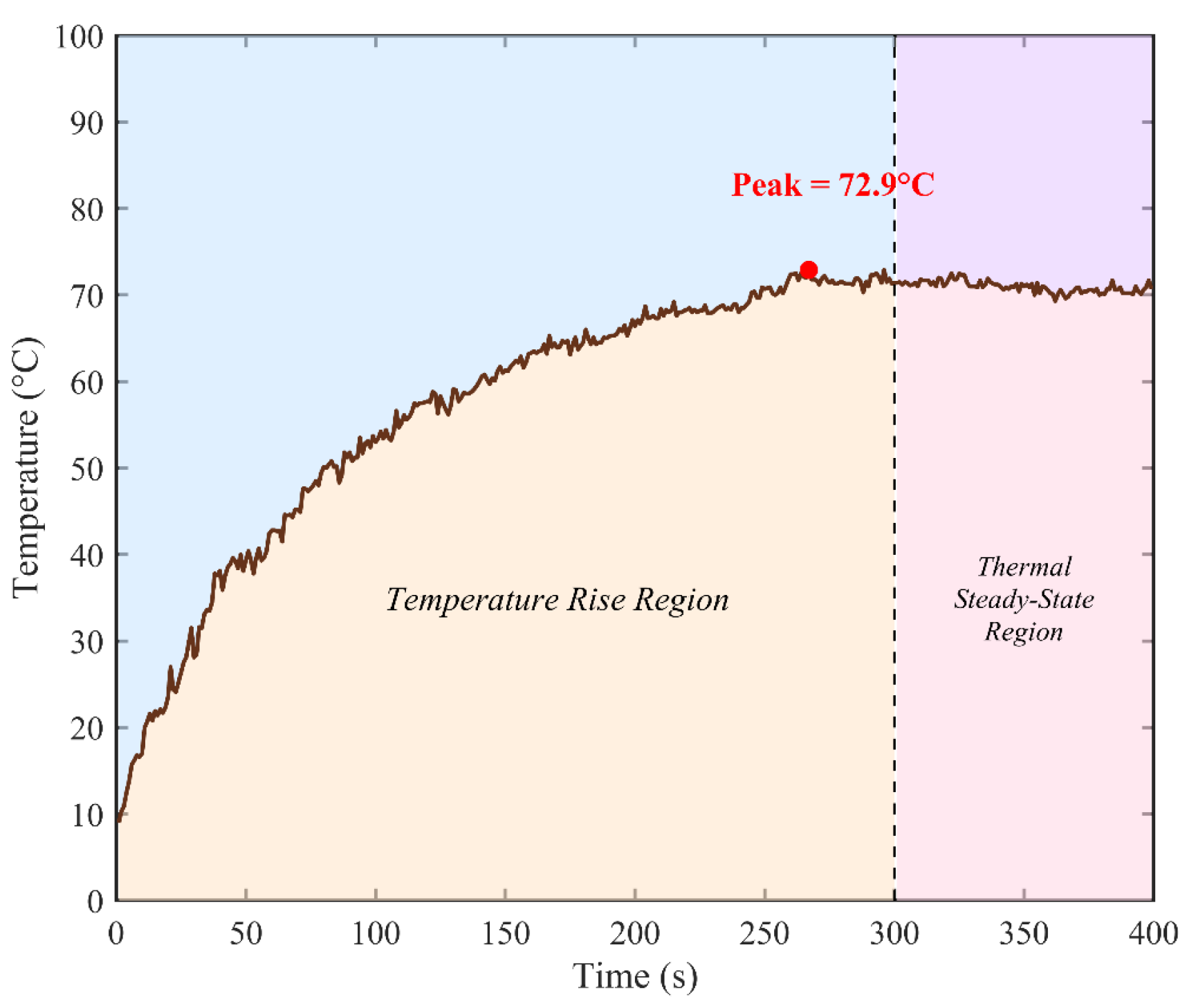
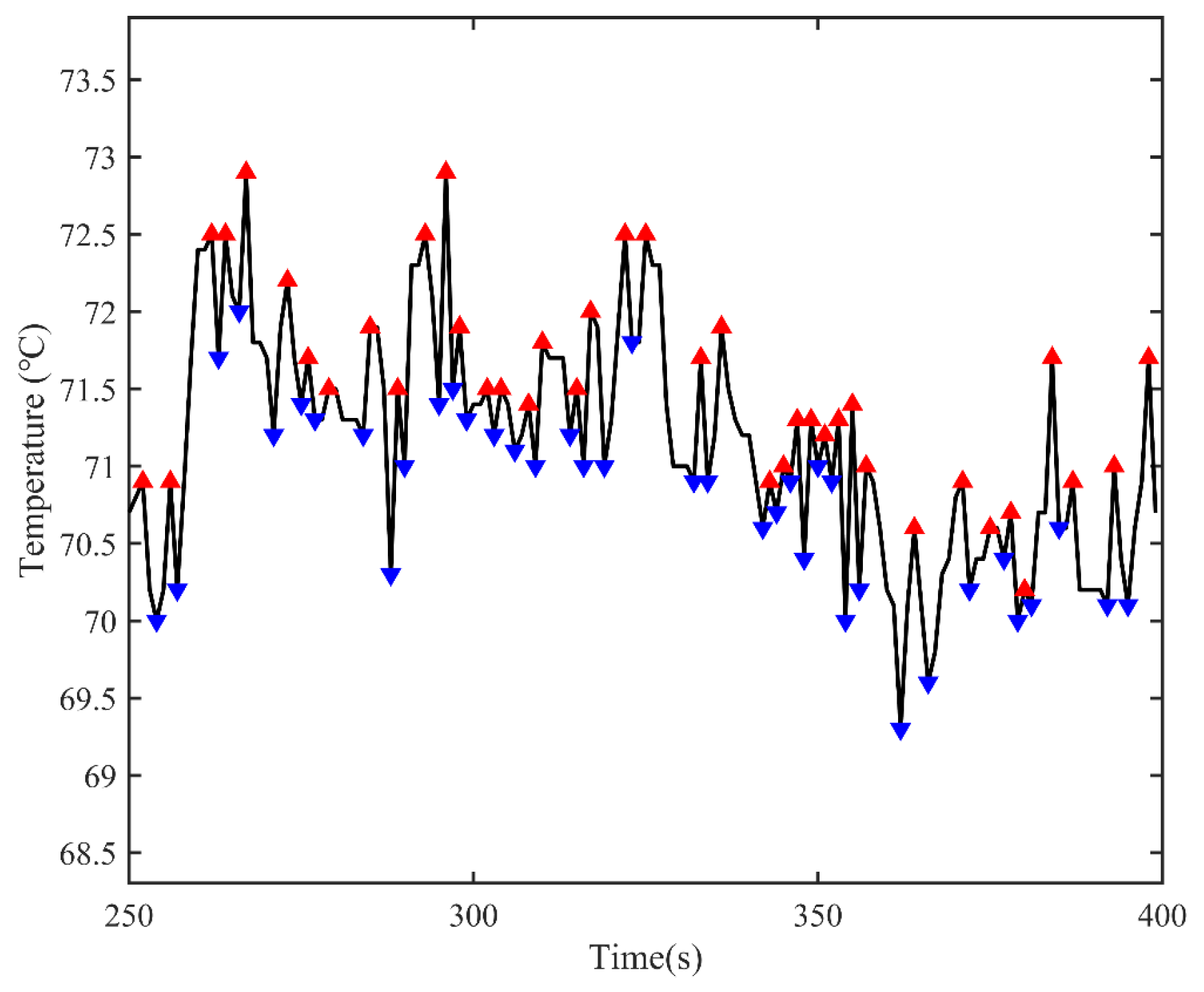
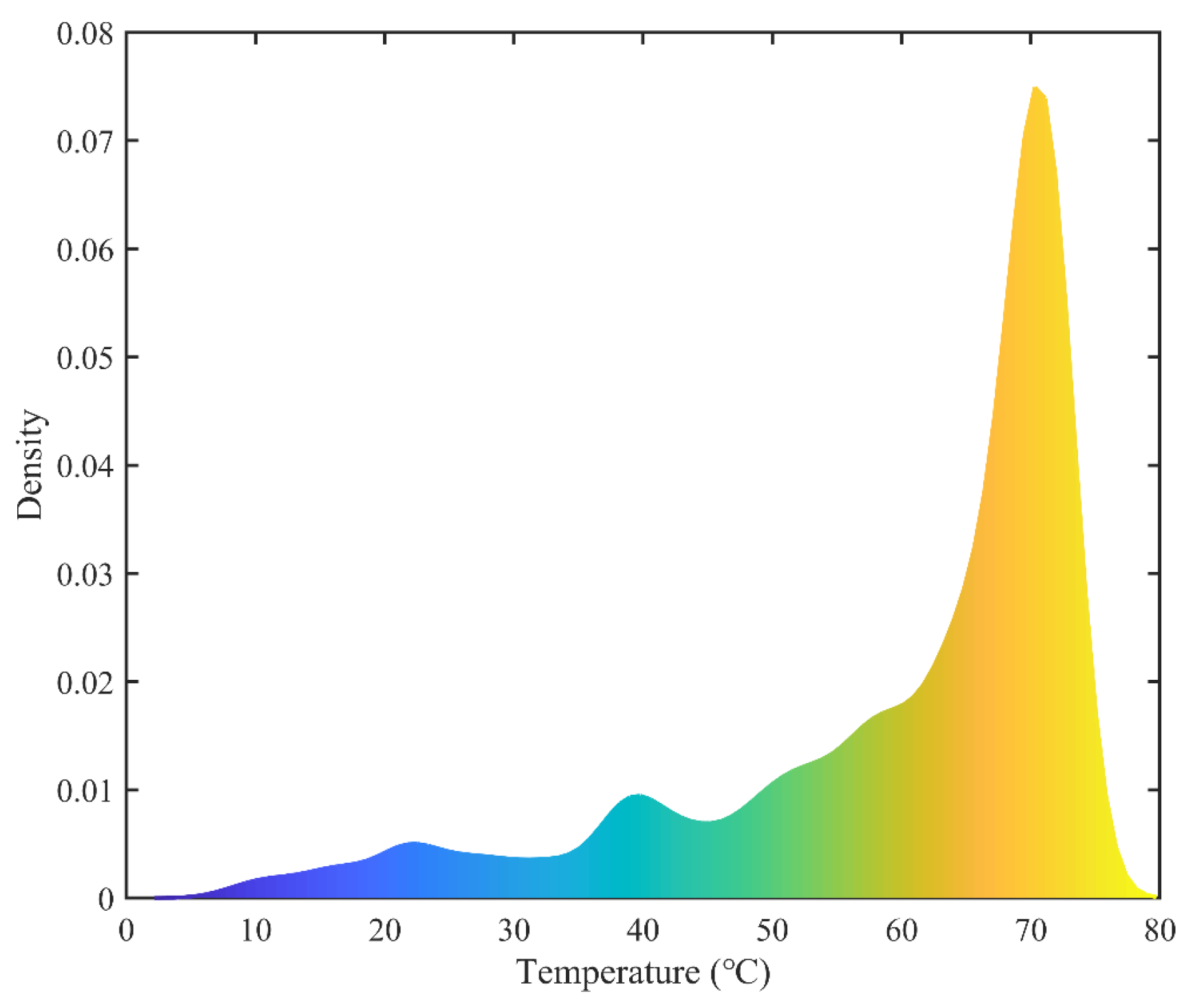
4.2. Thermal Response Experiment
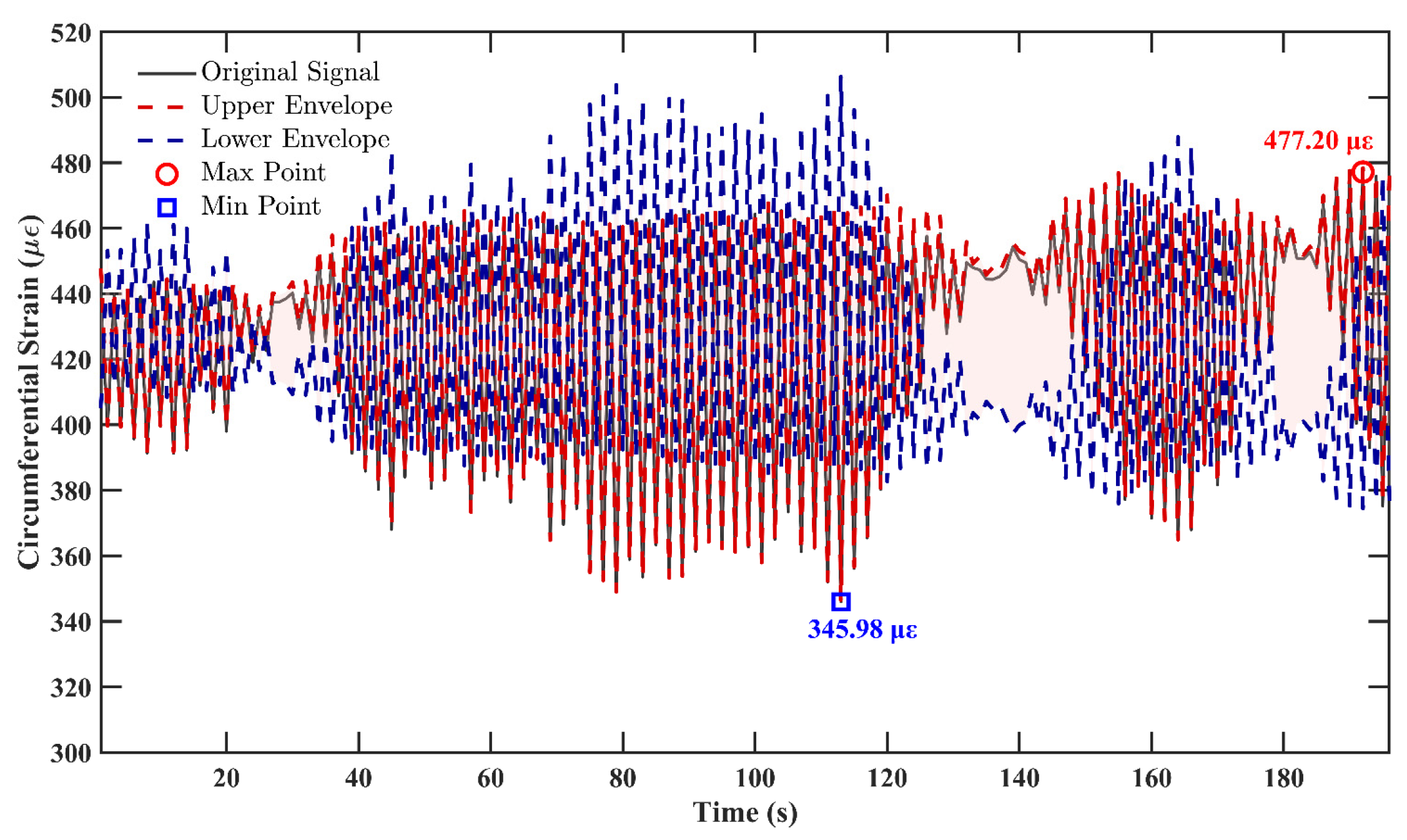
4.3. Strain Response Experiment
4.4. Comprehensive Analysis
5. Structural Optimization and Design Recommendations
5.1. Performance Metrics and Composite Evaluation Function
- 1.
- Thermal response indicator: Maximum steady-state temperature, which reflects internal heat accumulation. Higher temperatures indicate poorer heat dissipation. All configurations are normalised against the reference case without a groove.
- 2.
- Structural response indicator: The ratio of maximum equivalent stress to material yield strength, which reflects the safety margin. A smaller ratio indicates higher structural integrity.
- 3.
- Sensing response indicator: Maximum principal strain in the embedded groove region, representing strain sensitivity. Within acceptable strain limits, higher strain values are favourable for signal acquisition.
5.2. Actual Operating Condition Settings
5.3. Parametric Analysis Methodology
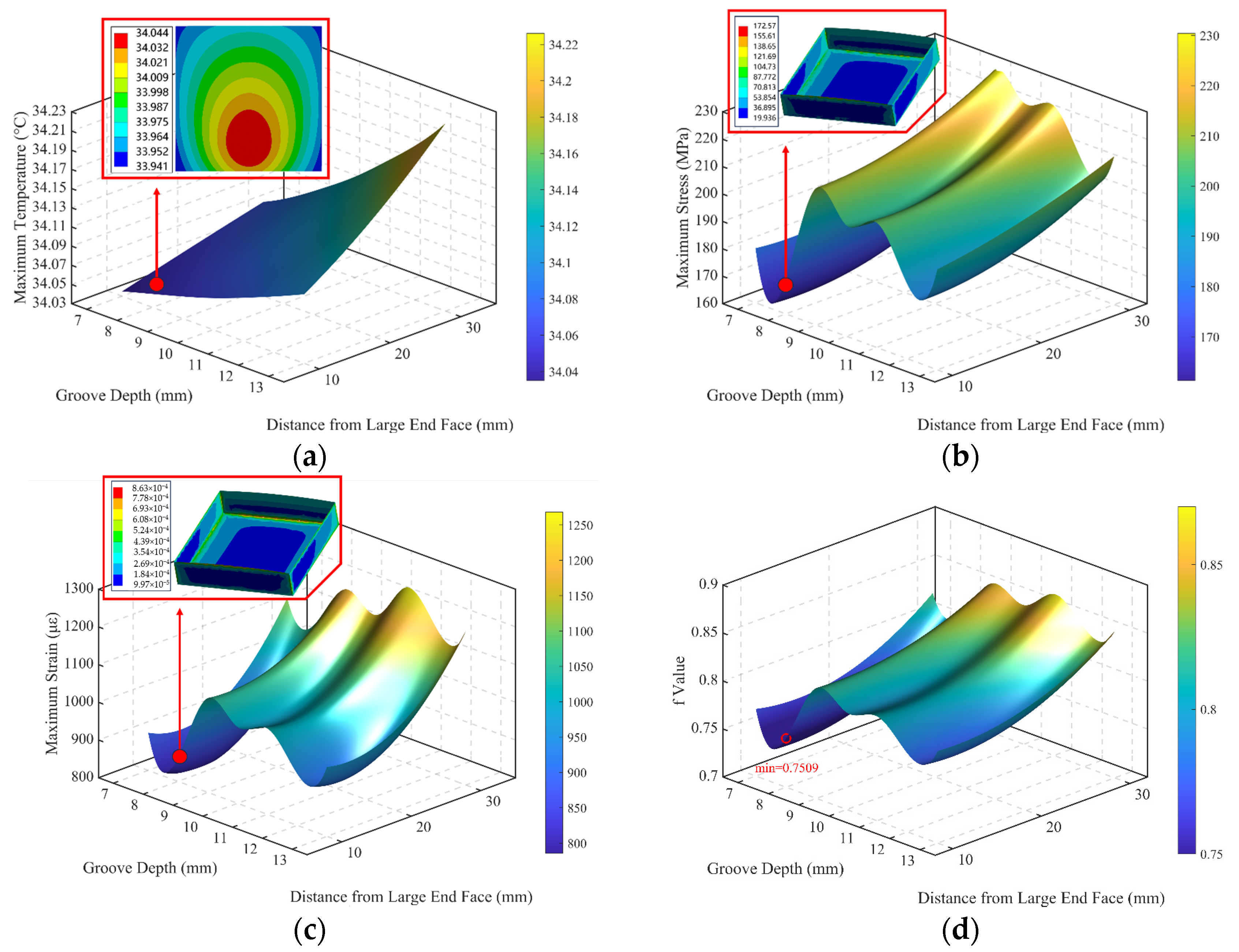
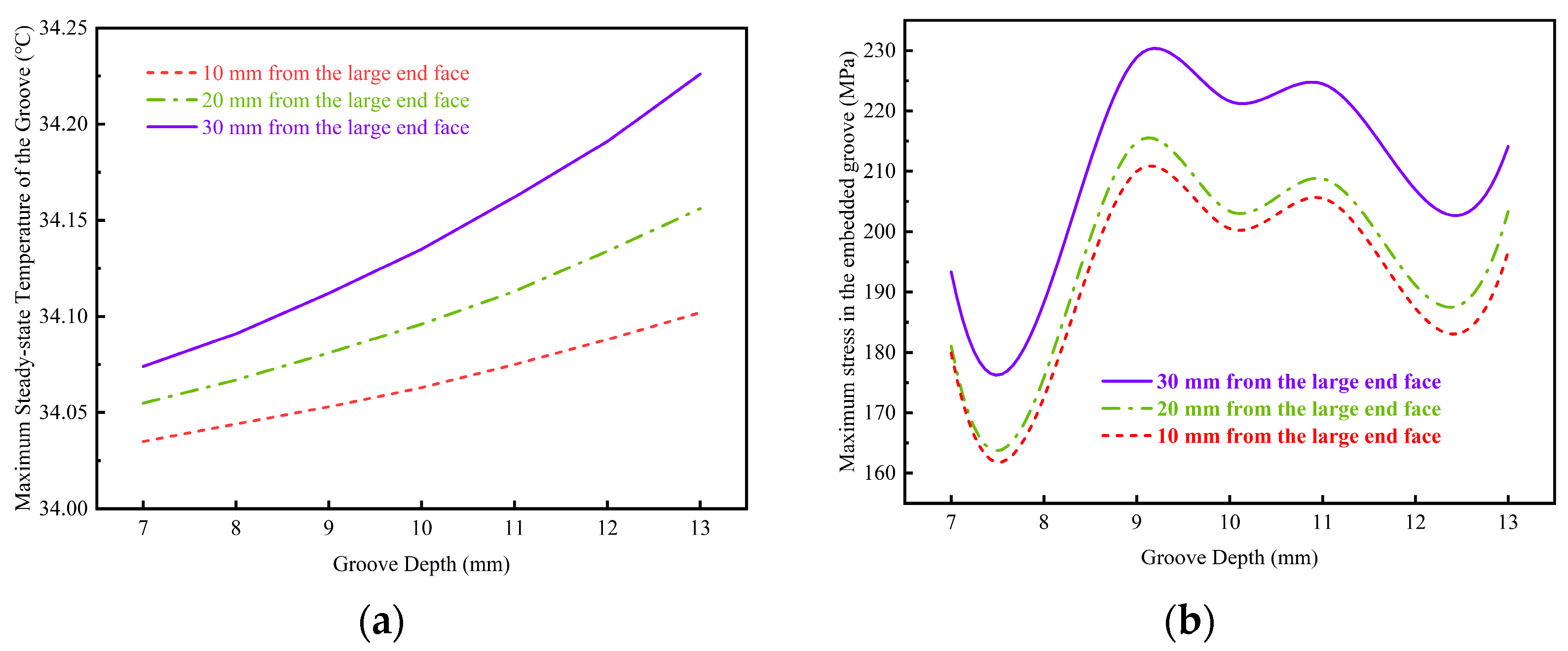
5.4. Influence of Groove Structure on Thermo-Mechanical Responses
- (1)
- Thermal Response Analysis:
- (2)
- Structural Stress Analysis:
- (3)
- Strain Sensing Analysis:
- (4)
- Comprehensive Performance Evaluation:
6. Conclusions
- (1)
- A multi-physics coupling model tailored to sensor-embedded bearing rings with embedded grooves was developed and verified by experiments. The model incorporates frictional heat generation, complex heat transfer boundaries, and contact stress distribution. A sequentially coupled thermo-mechanical simulation strategy, along with local slicing and mesh refinement, enables detailed analysis of interactions among rollers, raceways, and grooves, providing a foundation for performance evaluation.
- (2)
- The proposed model was validated through thermal and strain response experiments. The results show high consistency between simulation and experimental measurements, confirming the model’s accuracy.
- (3)
- A multi-objective performance function was proposed to evaluate the synergy of thermal–mechanical responses. The function integrates maximum steady-state temperature, equivalent stress, and principal strain with weighting coefficients, allowing for quantitative ranking of design configurations.
- (4)
- A relatively optimal groove configuration was identified. Among 21 tested parameter combinations, the configuration with an 8 mm groove depth and a 20 mm axial position achieved the best overall performance in thermal dissipation, structural safety, and strain sensitivity. This confirms the feasibility of the integrated structure–sensing design strategy in intelligent bearing applications.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Fa | Axial load (N) |
| Fr | Radial load (N) |
| Nu | Nusselt number |
| Gr | Grashof number |
| Pr | Prandtl number |
References
- Jirigala; Sun, J.L. Comparative study on critical mineral resources policies of China and foreign countries. World Scitech RD 2025, 47, 94–106. [Google Scholar] [CrossRef]
- Wang, H.N. Intelligent Structural Design and Research of Rolling Bearings. Master’s Thesis, North University of China, Taiyuan, China, 2023. [Google Scholar]
- Wang, Y.P. Development status and trends of informationization and intelligence of large electric shovel at home and abroad. Mech. Manag. Dev. 2021, 36, 283–285. [Google Scholar] [CrossRef]
- Li, X.D.; Liu, C.; Li, J.M.; Baghdadi, M.; Liu, Y.C. A multi-sensor environmental perception system for an automatic electric shovel platform. Sensors 2021, 21, 4355. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.C.; Shao, A.L.; Qu, F.M.; Yue, X.T.; Wang, H.Y.; Zhang, X.F.; Liu, X.B. Current status and prospects of mining technology in metal mines. Chin. J. Eng. 2025, 47, 971–983. [Google Scholar] [CrossRef]
- Chang, H. Research on Multiple Mechanism Cooperative Control System of Intelligent Large Mining Electric Shovel. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2021. [Google Scholar] [CrossRef]
- Qian, L.; Xu, Q.F.; Wang, J.X.; Zhang, S. Design of fault diagnosis and maintenance system of mechanical and electrical equipment in open-pit coal mines. Mod. Manuf. Technol. Equip. 2024, 60, 52–54. [Google Scholar] [CrossRef]
- El-Thalji, I.; Jantunen, E. A summary of fault modeling and predictive health monitoring of rolling element bearings. Mech. Syst. Signal Process. 2015, 60, 252–272. [Google Scholar] [CrossRef]
- Jin, X.; Chen, Y.M.; Wang, L.; Han, H.L.; Chen, P. Failure prediction, monitoring and diagnosis methods for slewing bearings of large-scale wind turbine: A review. Measurement 2021, 172, 108855. [Google Scholar] [CrossRef]
- Ma, J.P.; Zhuo, S.; Li, C.W.; Zhan, L.W.; Zhang, G.Z. Study on noncontact aviation bearing faults and speed monitoring. IEEE Trans. Instrum. Meas. 2021, 70, 1–21. [Google Scholar] [CrossRef]
- Cocconcelli, M.; Strozzi, M.; Molano, J.C.C.; Rubini, R. Detectivity: A combination of Hjorth’s parameters for condition monitoring of ball bearings. Mech. Syst. Signal Process. 2022, 164, 108247. [Google Scholar] [CrossRef]
- Zmarzly, P. Analysis of Technological Heredity in the Production of Rolling Bearing Rings Made of AISI 52100 Steel Based on Waviness Measurements. Materials 2022, 15, 3959. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Yang, S.P.; Liu, Y.Q.; Chen, Y.H.; Zhang, K. Establishment of the thermo-mechanical coupling model of axle box bearings with track irregularity excitation and analysis of its temperature characteristics. Appl. Math. Mech. 2024, 45, 1965–1986. [Google Scholar] [CrossRef]
- Jing, H.B.; Wang, N.; Li, D.H.; Zhao, D.Y.; Wang, P.; Zhang, C.M. Analysis on lubrication characteristics of a novel strain sensor-embedded water-lubricated bearing. Lubr. Eng. 2025, 1–10. Available online: https://link.cnki.net/urlid/44.1260.th.20250317.1100.028 (accessed on 18 March 2025).
- Yuan, Z.K. Development of a Self-Powered Sensing System for Intelligent Bearing. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2023. [Google Scholar] [CrossRef]
- Russell, T.; Shafiee, A.; Conley, B.; Sadeghi, F. Evaluating load distribution at the bearing-housing interface using thin film pressure sensors. Tribol. Int. 2022, 165, 107293. [Google Scholar] [CrossRef]
- Alian, H.; Konforty, S.; Ben-Simon, U.; Klein, R.; Tur, M.; Bortman, J. Bearing fault detection and fault size estimation using fiber-optic sensors. Mech. Syst. Signal Process. 2019, 120, 392–407. [Google Scholar] [CrossRef]
- Wang, N.; Wei, Y.J.; Zhang, N.; Wang, D.D.; Wang, M.W.; Zhang, C.M. Wireless sensor monitoring method for film pressure of embedded water-lubricated bearings. J. Electron. Meas. Instrum. 2024, 38, 38–46. [Google Scholar]
- Shao, Y.M.; Tu, W.B.; Zhou, X.J.; Ge, L. Smart bearing based on embedded multi-parameter sensors. Chin. J. Mech. Eng. 2010, 21, 2527–2531. [Google Scholar]
- Zhang, W.Y.; Chen, J.H.; Hua, G.R.; Wang, H. Research on embedded smart bearing structure analysis and vibration monitoring system design. J. Mech. Strength 2022, 44, 1293–1299. [Google Scholar] [CrossRef]
- Kang, K.; Kim, S.-W.; Yoon, K.; Choi, D.-H. Robust design optimization of an angular contact ball bearing under manufacturing tolerance. Struct. Multidiscip. Optim. 2019, 60, 1645–1665. [Google Scholar] [CrossRef]
- Zhao, H.; Fu, C.; Zhang, Y.C.; Wan, Z.Q.; Lu, K. A non-probabilistic reliability-based design optimization method via dimensional decomposition-aided Chebyshev metamodel. Reliab. Eng. Syst. Saf. 2025, 262, 111208. [Google Scholar] [CrossRef]
- Xiao, J.W.; Zhang, Y.C.; Chen, S.; Ding, X.X.; Shao, Y.M. Optimization method for information sensing measuring points of embedded smart bearing. Bearing 2023, 2, 12–18. [Google Scholar] [CrossRef]
- Bhat, J.A.; Harmain, G.A.; Najar, F.A. Alleviating thermal challenges in hydrodynamic bearings: A novel approach through thrust bearing pads with embedded cooling circuitry and deep recess. Tribol. Int. 2024, 194, 109438. [Google Scholar] [CrossRef]
- Luan, W.L.; Liu, Y.; Wang, Y.L.; Xu, F.C. Effect of herringbone groove structure parameters on the static performance of gas foil herringbone groove thrust bearings. Tribol. Int. 2023, 177, 107979. [Google Scholar] [CrossRef]
- Brito, F.P.; Miranda, A.S.; Claro, J.C.P.; Fillon, M. Experimental comparison of the performance of a journal bearing with a single and a twin axial groove configuration. Tribol. Int. 2012, 54, 1–8. [Google Scholar] [CrossRef]
- Brito, F.P.; Miranda, A.S.; Fillon, M. Analysis of the effect of grooves in single and twin axial groove journal bearings under varying load direction. Tribol. Int. 2016, 103, 609–619. [Google Scholar] [CrossRef]
- Ren, L.J.; Yan, W.J.; Chen, K.; Li, K.; Wang, Q.; Zhang, G.P. Modeling method and experimental study on thermal force coupling characteristics of grinding machine. Mach. Tool Hydraul. 2024, 52, 62–67. [Google Scholar] [CrossRef]
- Chang, Z.Y.; Hou, L.; Masarati, P.; Linn, R.Z.; Li, Z.G.; Chen, Y.S. Modeling and nonlinear analysis of a coupled thermo-mechanical dual-rotor system. Nonlinear Dyn. 2024, 112, 17811–17842. [Google Scholar] [CrossRef]
- Tan, Y.Q.; Dang, J.; Igarashi, A.; Himeno, T.; Hamada, Y. Hysteretic restoring force model of high damping rubber bearings including thermo-mechanical coupled effect. Eng. Struct. 2023, 277, 115449. [Google Scholar] [CrossRef]
- Yang, R.Z. Analysis on Slip Characteristics of Double-Row Angle Contact Ball Bearings Based on Heat-Mechanical Coupling. Master’s Thesis, Anhui Polytechnic University, Wuhu, China, 2024. [Google Scholar] [CrossRef]
- Su, C.; Chen, W.F. An improved model of motorized spindle for forecasting temperature rise based on thermal network method. Int. J. Adv. Manuf. Technol. 2022, 119, 5969–5991. [Google Scholar] [CrossRef]
- Zhan, Z.Q.; Wan, S.K.; Li, X.H.; Fang, B. Thermal behavior prediction of the spindle-bearing system based on the adaptive thermal network modeling method. Eng. Appl. Artif. Intell. 2025, 145, 110199. [Google Scholar] [CrossRef]
- Gao, Z.; Qi, X.Y.; Chang, L.; Ding, C. Thermal structure coupling calculation of motorized spindle based on thermal network method. Mod. Manuf. Eng. 2021, 6, 75–82. [Google Scholar] [CrossRef]
- Wang, L.K.; Hu, C.; Liu, F.Y.; Tang, H.B. Thermo-mechanical coupled characteristics for the non-axisymmetric outer ring of the high-speed rail axle box bearing with embedded intelligent sensor slots. Symmetry. 2025, 17, 1667. [Google Scholar] [CrossRef]
- Zhao, W.Y. Thermal Coupling Analysis of FAG Axle Box Bearing in High Speed EMU. Master’s Thesis, North China University of Technology, Beijing, China, 2024. [Google Scholar] [CrossRef]
- Zhang, J.H.; Yu, Y.J.; Xue, Y.J.; Li, J.S. Transient thermal-mechanical coupling analysis of high-speed cylindrical roller bearing. Manuf. Autom. 2024, 46, 161–165. [Google Scholar] [CrossRef]
- An, J.Q. Thermal Structure Coupling Analysis of Angular Contact Ball Bearings. Master’s Thesis, Shenyang University of Chemical Technology, Shenyang, China, 2020. [Google Scholar] [CrossRef]
- Song, D.L.; Li, X.Y.; Zheng, Z.J.; Dong, J.X.; He, P. Design of high speed train bogie bearing test-bed based on multi-physical field coupling monitoring. Exp. Technol. Manag. 2022, 39, 16–22. [Google Scholar] [CrossRef]
- Wang, L.K.; Hu, C.; Hu, L.; Liu, F.Y.; Tang, H.B. An investigation on the mechanical characteristics of railway locomotive axle box bearings with sensor-embedded slots. Machines 2025, 13, 358. [Google Scholar] [CrossRef]
- Deng, S.E.; Jia, Q.Y. Design Principles of Rolling Bearings; China Standards Press: Beijing, China, 2008. [Google Scholar]
- Tao, W.Q. Heat Transfer, 5th ed.; Higher Education Press: Beijing, China, 2019. [Google Scholar]

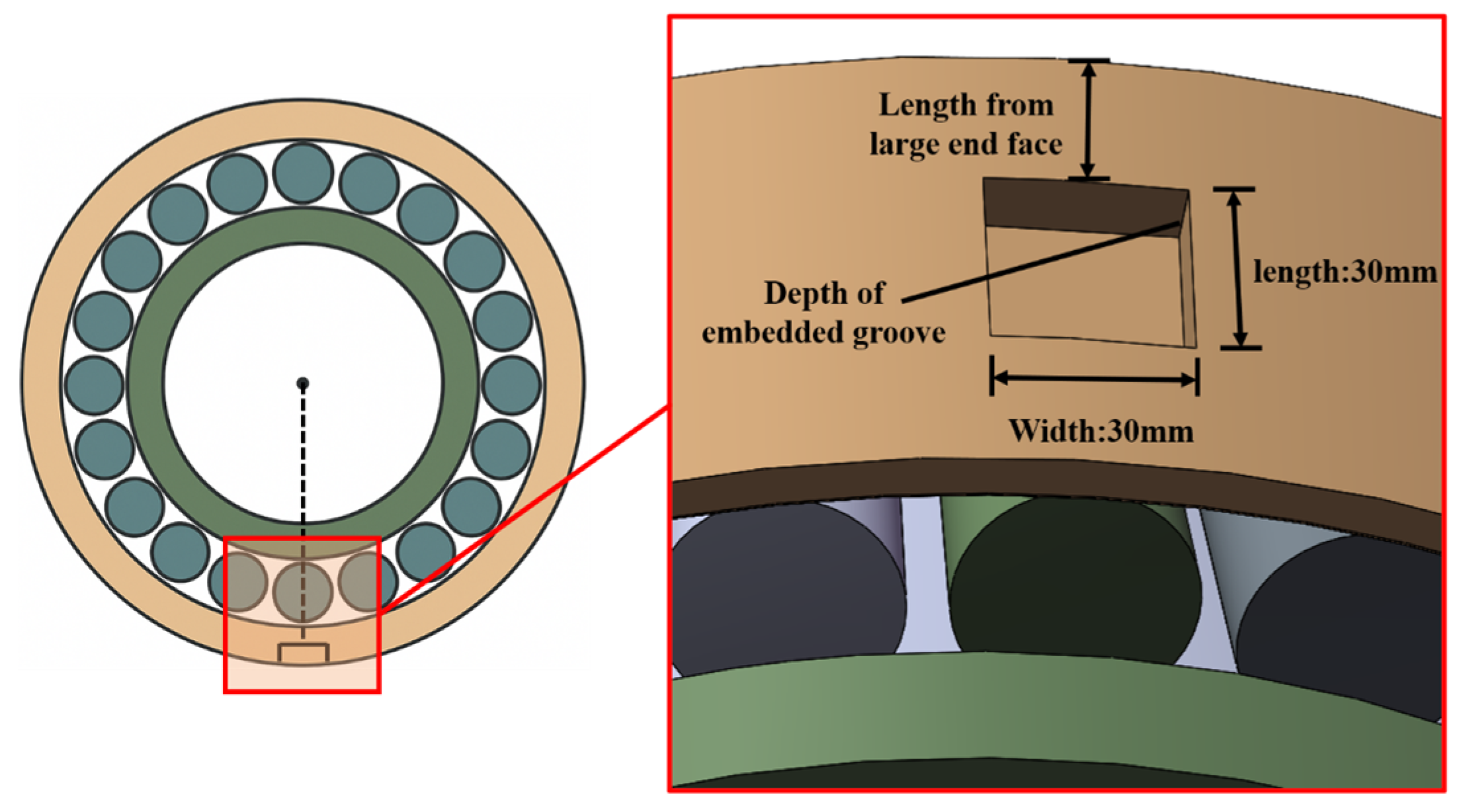


| Parameter | Value (mm) | Parameter | Value (mm) |
|---|---|---|---|
| Bearing outer diameter | 444.5 | Bearing bore diameter | 266.7 |
| Inner ring width | 117.48 | Outer ring width | 88.9 |
| Outer raceway diameter | 357.56–423.66 | Inner raceway diameter | 290.15–342 |
| Effective roller length | 85 | Roller length | 88 |
| Roller diameter | 36.44–42.52 | Bearing width | 120.65 |
| Operating Parameters | Value |
|---|---|
| Rotational Speed | 210 r/min |
| Radial Load | 120 kN |
| Axial Load | 50 kN |
| Operating Parameters | Value |
|---|---|
| Rotational Speed | 90 r/min |
| Radial Load | 120 kN |
| Axial Load | 50 kN |
| Operating Parameters | Value |
|---|---|
| Frictional heat generation | 1632.608 W |
| Radial Load | 684.0922 kN |
| Axial Load | 95.831 kN |
| Parameter | Value | ||||||
|---|---|---|---|---|---|---|---|
| Distance from the large end face | 10 mm | 20 mm | 30 mm | ||||
| Groove depth | 7 mm | 8 mm | 9 mm | 10 mm | 11 mm | 12 mm | 13 mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Liu, F.; Hu, C.; Tang, H. Design Optimization of Sensor-Embedded Bearing Rings in Heavy-Duty Electric Shovel Applications via Multi-Physics Coupling Analysis and Experimental Validation. Machines 2025, 13, 1008. https://doi.org/10.3390/machines13111008
Wang L, Liu F, Hu C, Tang H. Design Optimization of Sensor-Embedded Bearing Rings in Heavy-Duty Electric Shovel Applications via Multi-Physics Coupling Analysis and Experimental Validation. Machines. 2025; 13(11):1008. https://doi.org/10.3390/machines13111008
Chicago/Turabian StyleWang, Longkai, Fengyuan Liu, Can Hu, and Hongbin Tang. 2025. "Design Optimization of Sensor-Embedded Bearing Rings in Heavy-Duty Electric Shovel Applications via Multi-Physics Coupling Analysis and Experimental Validation" Machines 13, no. 11: 1008. https://doi.org/10.3390/machines13111008
APA StyleWang, L., Liu, F., Hu, C., & Tang, H. (2025). Design Optimization of Sensor-Embedded Bearing Rings in Heavy-Duty Electric Shovel Applications via Multi-Physics Coupling Analysis and Experimental Validation. Machines, 13(11), 1008. https://doi.org/10.3390/machines13111008






