A Multi-Constraint Assembly Registration Method Based on Actual Machined Surfaces
Abstract
1. Introduction
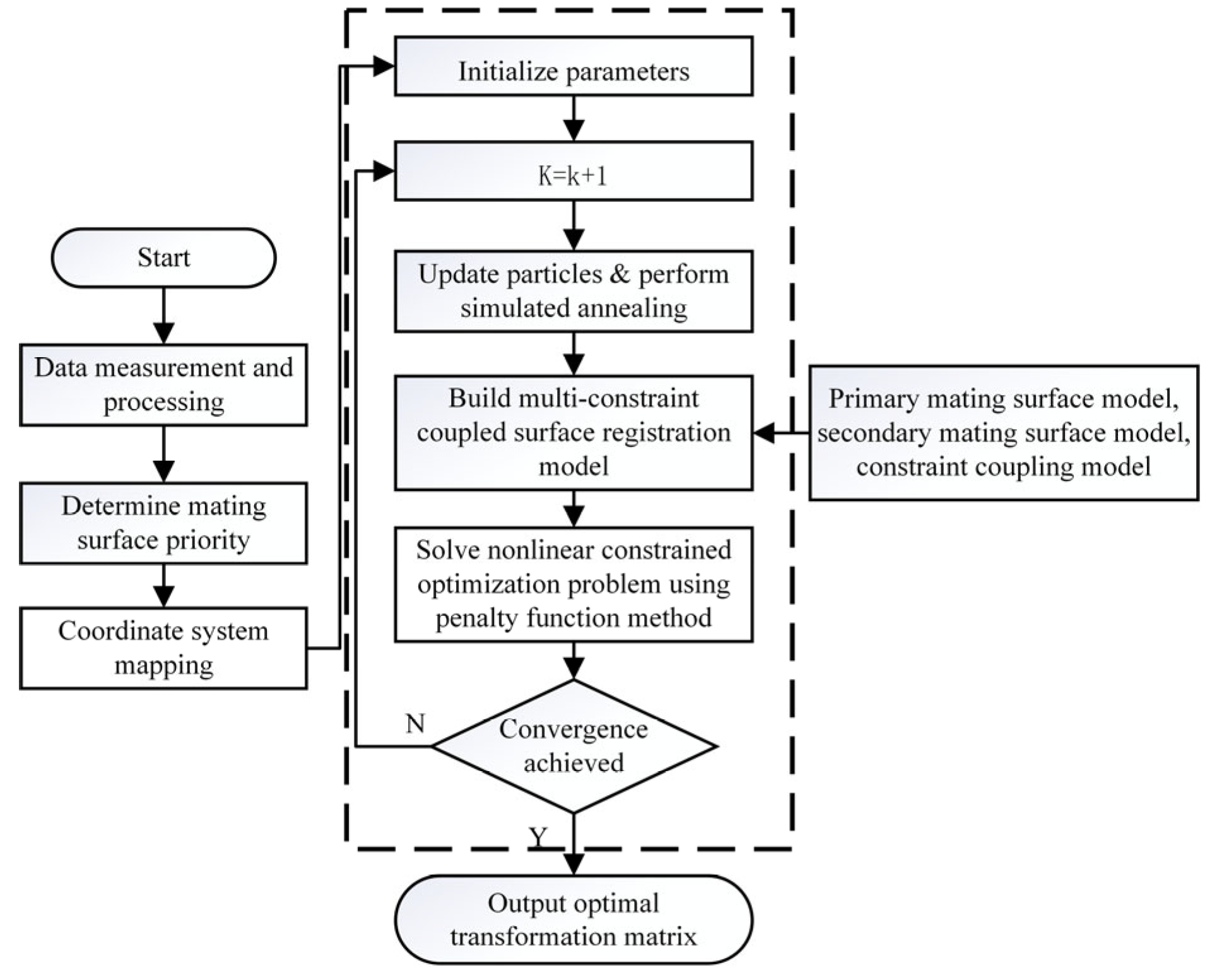
2. Multi-Constraint Coupled Registration Method
2.1. Modeling of Coupled Multi-Constraints
- Primary Mating Surface Model
- 2.
- Secondary Mating Surface Model
- 3.
- The Constraint Relationship Model
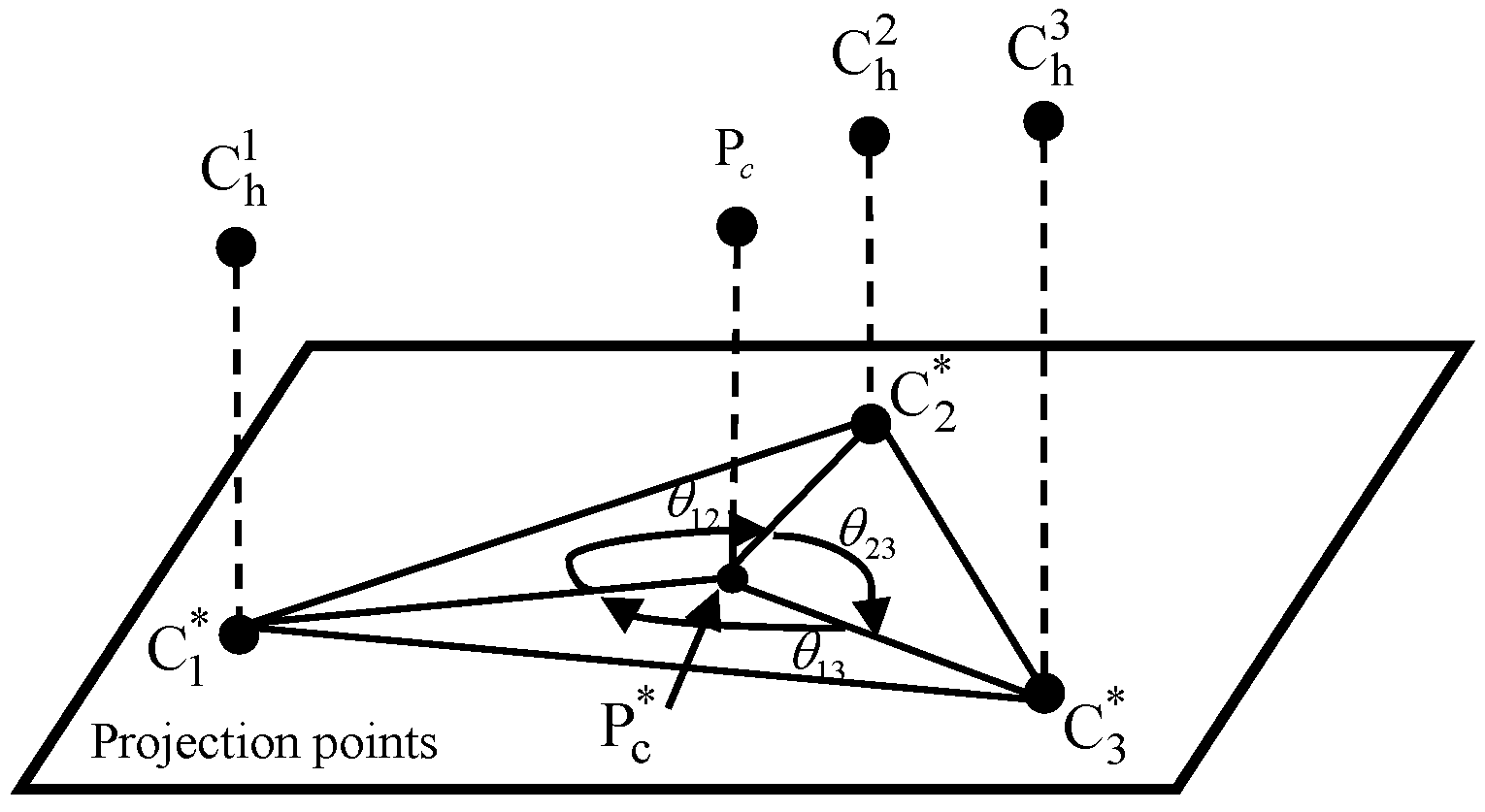
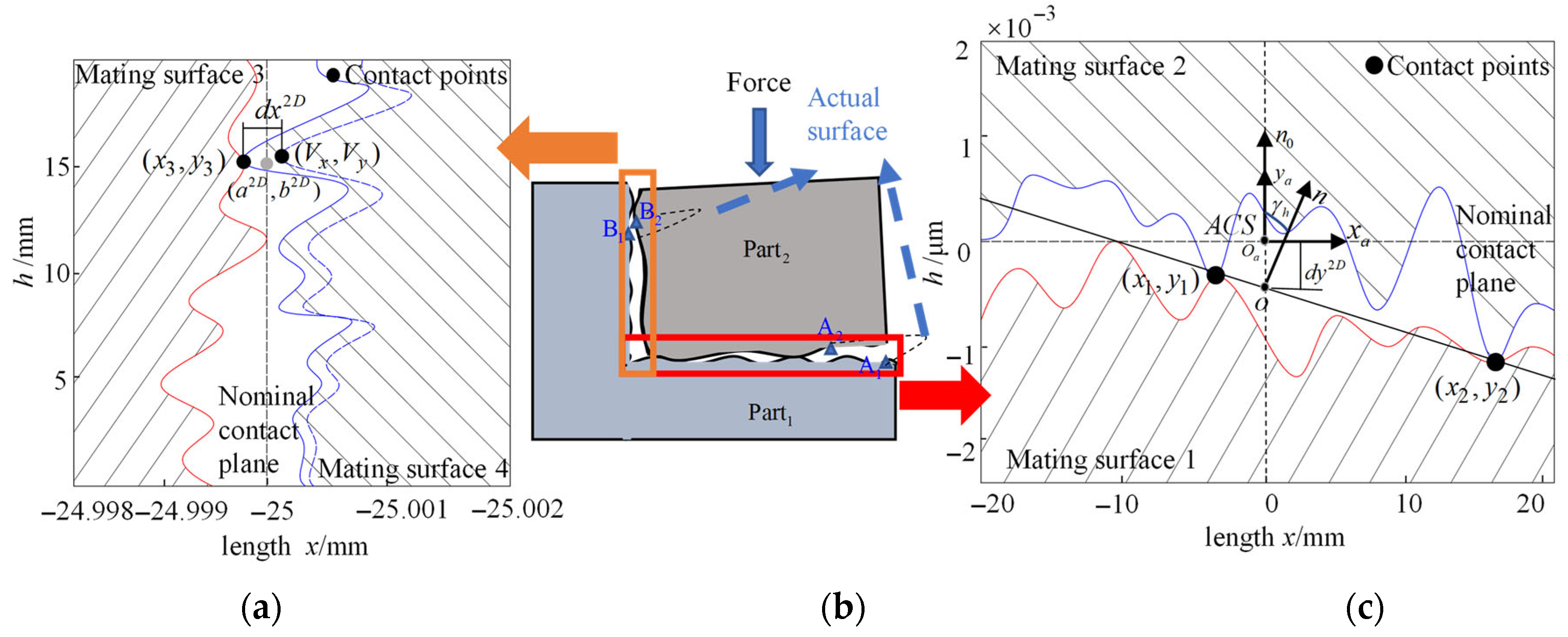
2.2. Determination of Primary and Secondary Contact Points
2.3. Assembly Pose Calculation Method with Multi-Constraint Coupled Registration
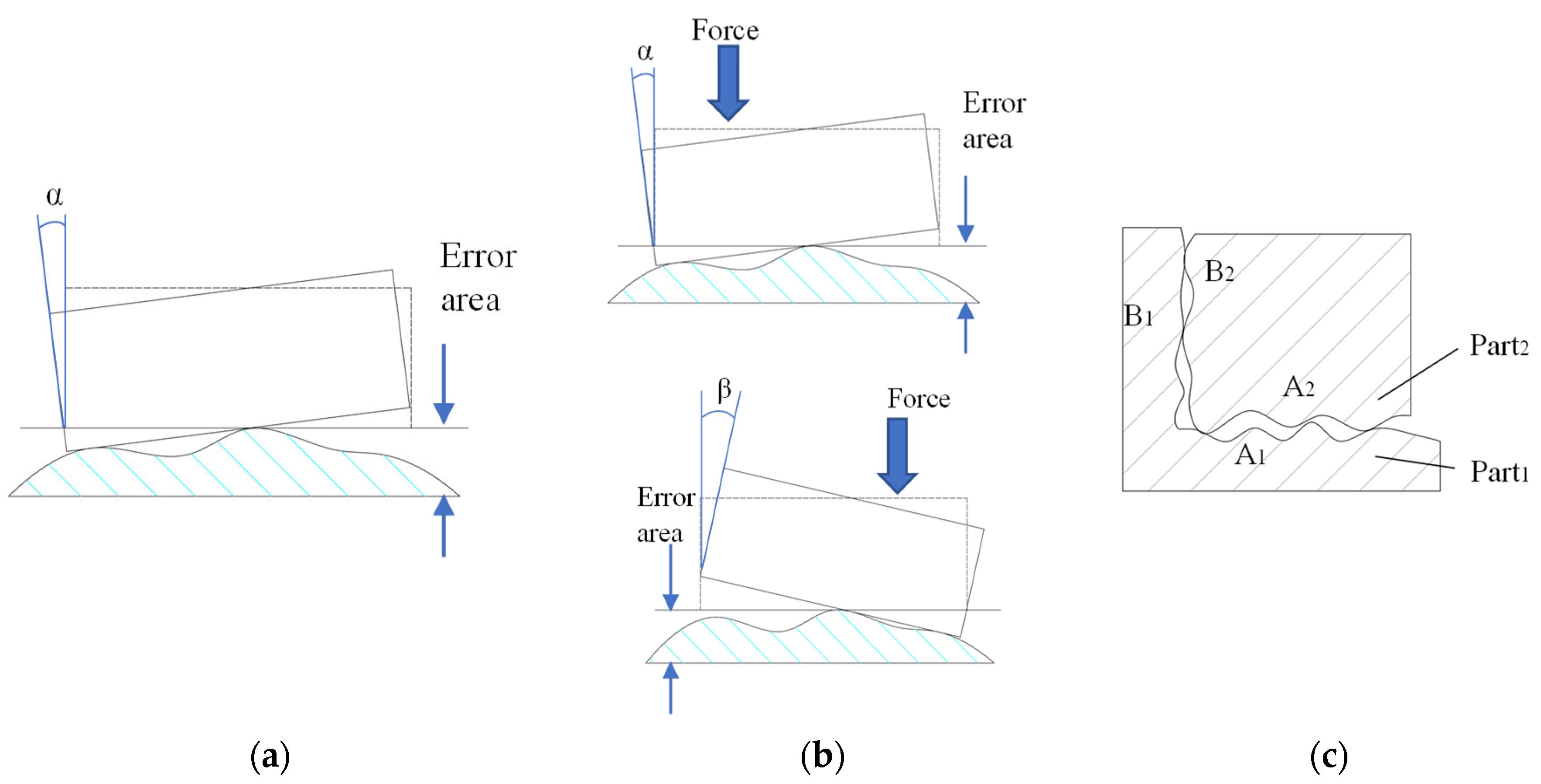
2.3.1. Two-Dimensional Assembly Case
- Constraint Analysis of Primary Mating Surfaces
- 2.
- Constraint Analysis of Secondary Mating Surfaces
- 3
- Relative Pose Representation
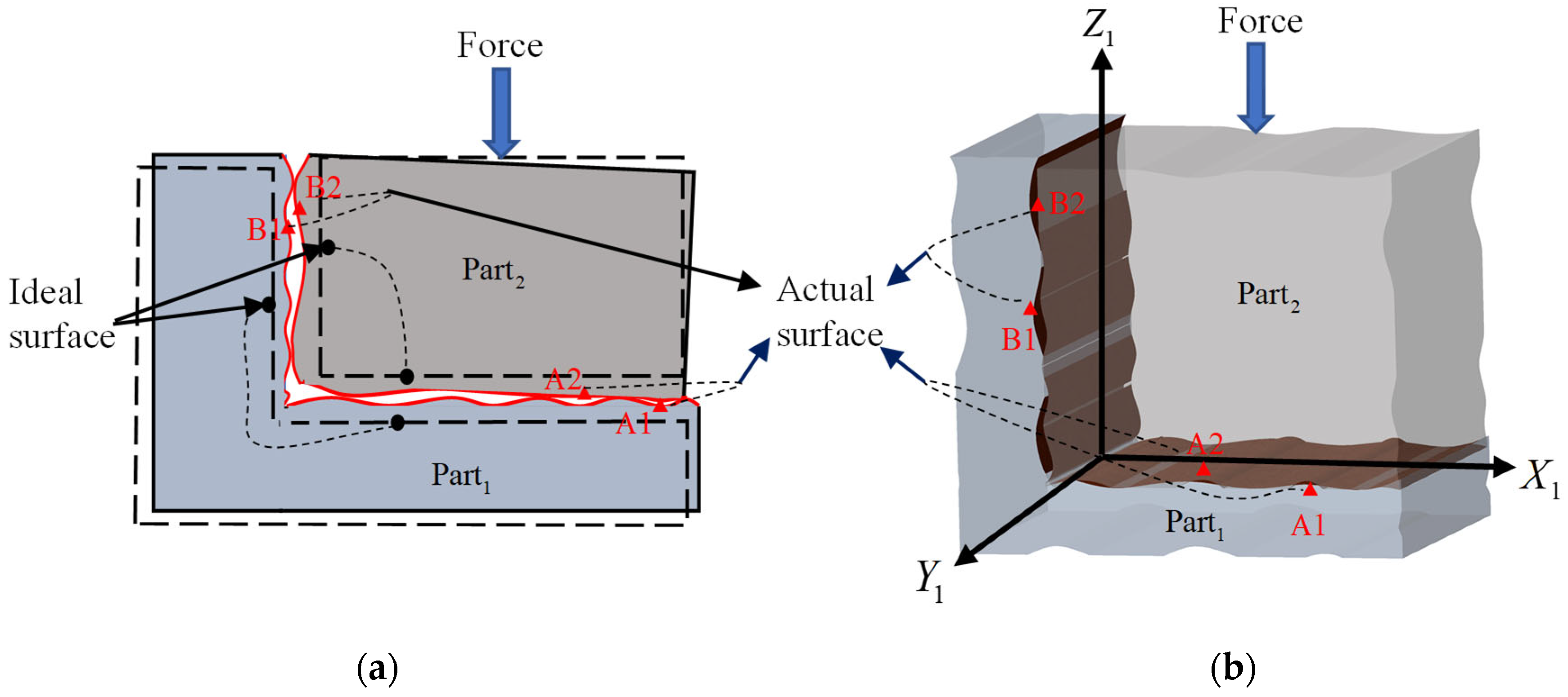
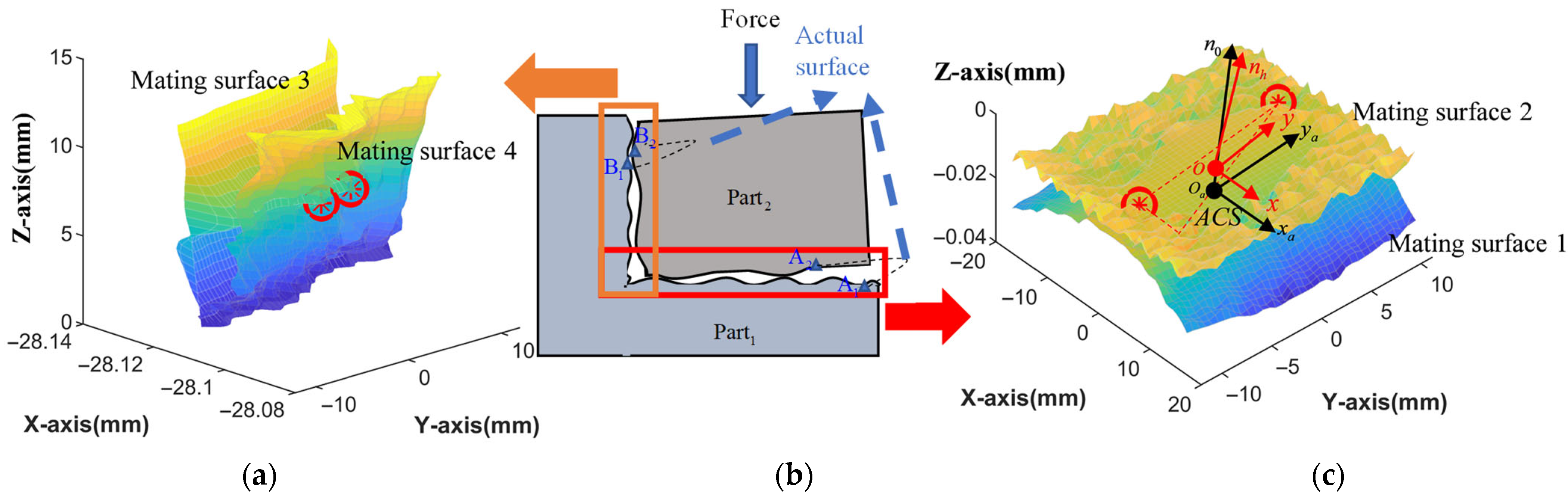
2.3.2. Three-Dimensional Assembly Case
- 1.
- Constraint Analysis of Primary Mating Surfaces
- 2
- Constraint Analysis of Secondary Mating Surfaces
- 3.
- Relative Pose Representation
3. Analysis of Registration States in 2D Assembly
3.1. Assembly Under a Vertical Applied External Force
3.2. Assembly with a Horizontal Applied External Force
4. Three-Dimensional Surface Registration Experiment
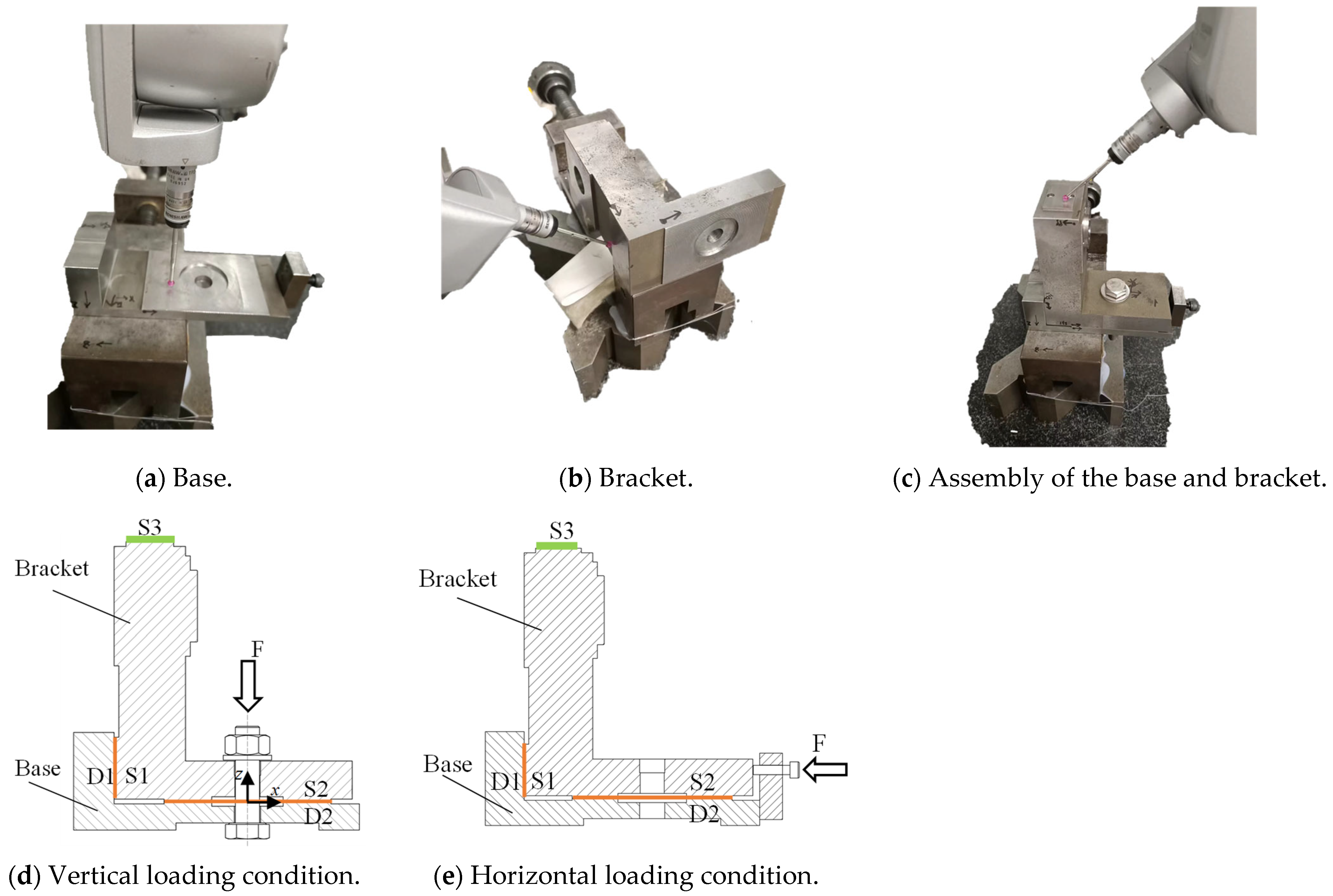
4.1. Experimental Setup
4.2. Experimental Scheme
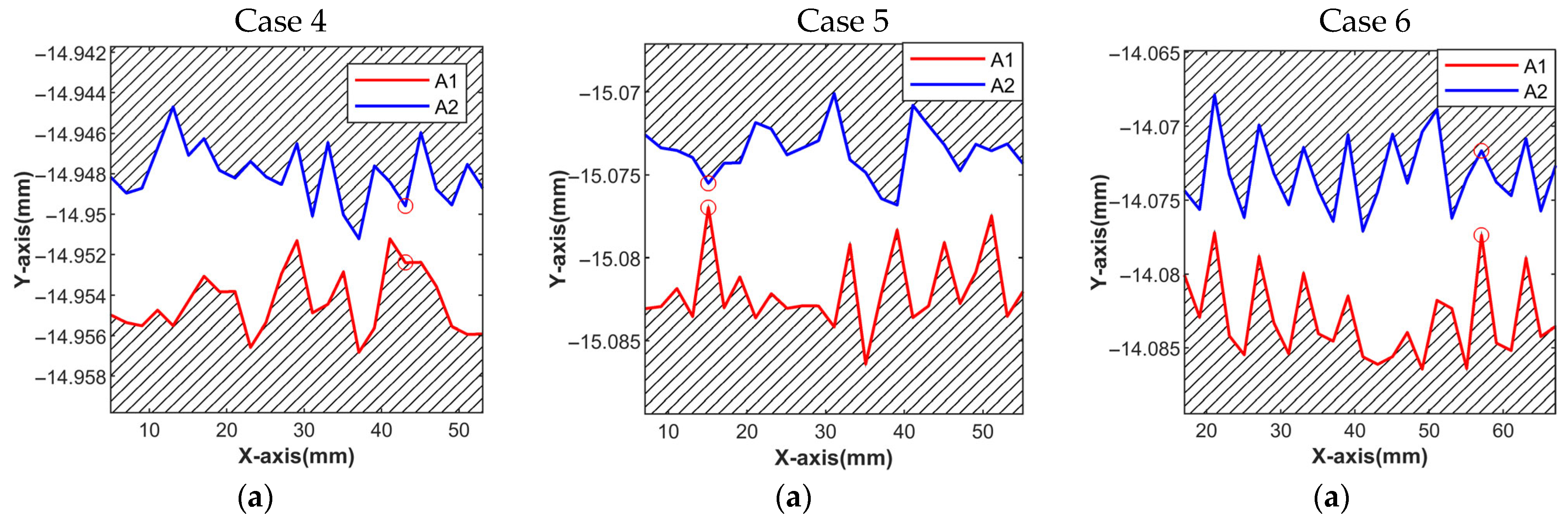
4.3. Analysis of 3D Surface Registration States
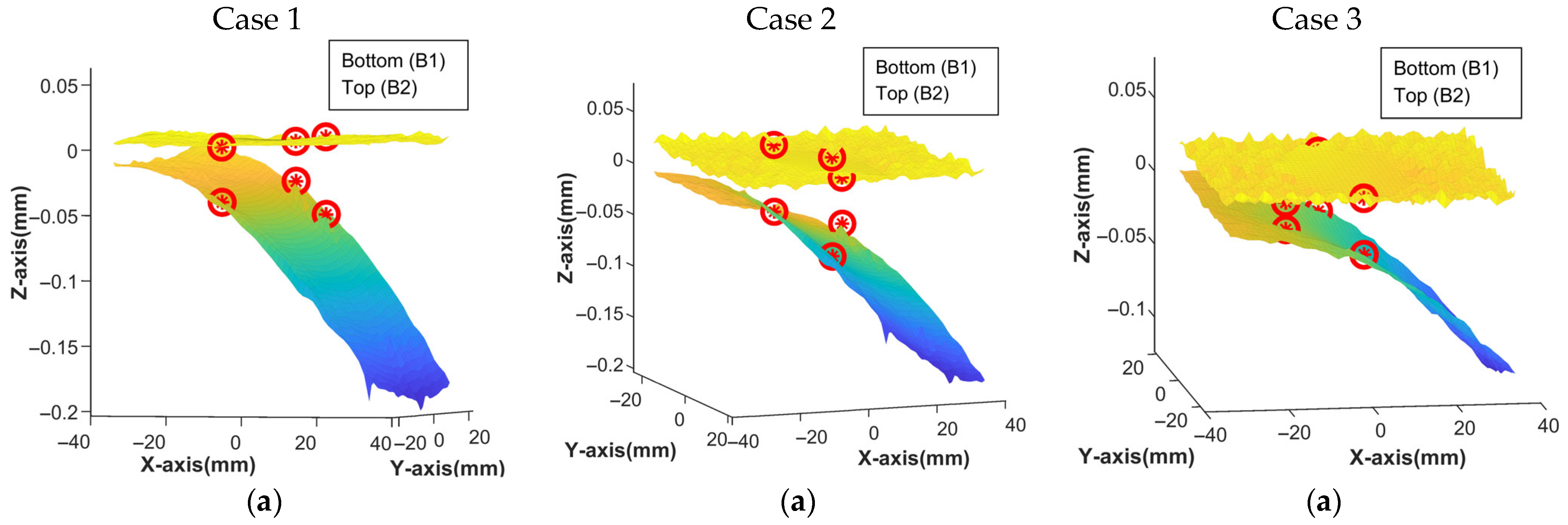
4.3.1. Registration Under Vertical Applied External Force
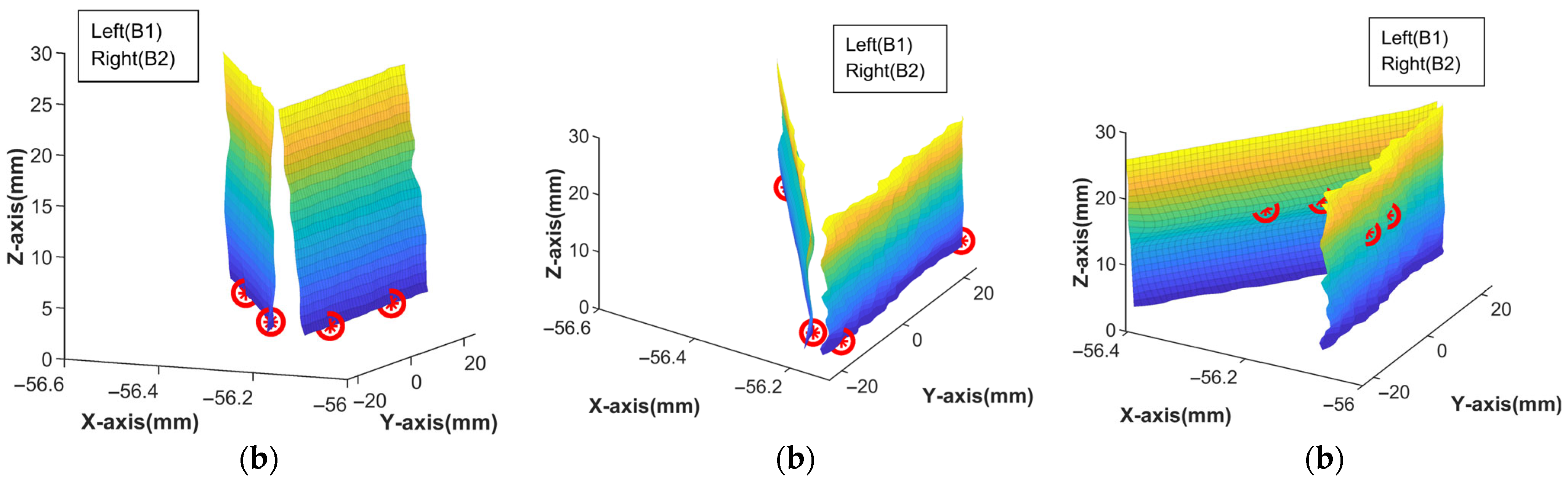
4.3.2. Registration Under Horizontal Applied External Force
4.4. Experimental Results
4.5. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Case (3D-Case) | Mapping Matrix M | Contact Points of the Assembly Coordinate System D1 and D2 | SDT | |
|---|---|---|---|---|
| Horizontal Mating Surfaces A1 and A2; Side Surfaces B1 and B2 | ||||
| 1 | A1 | (−3.9990, 15.9993, −0.0276) | ||
| (−5.9988, −22.0010, −0.0394) (4.0006, 15.9989, −0.0528) | ||||
| B1 | (−56.4066, 9.9989, 4.0006) (−56.2184, −14.0006, 4.0012) | |||
| A2 | (−4.1066, 16.0010, 0.0030) (−6.1066, −21.9992, 0.0028) (3.8933, 16.0009, 0.0066) | |||
| B2 | (−56.0979, 9.9989, 4.0007) (−56.0931, −14.0007, 4.0013) | |||
| 2 | A1 | (−3.9990, 15.9993, −0.0276) (0.0009, −22.0015, −0.0535) (12.0016, −14.0010, −0.0917) | ||
| B1 | (−56.1899, −18.0005, 4.0102) (−56.5116, 23.9998, 4.0099) | |||
| A2 | (−4.1233, 15.9963, 0.0174) (−0.1218, −22.0024, 0.0117) (11.8787, −14.0026, 0.0048) | |||
| B2 | (−56.1308, −18.0005, 4.0102) (−56.1484, 23.9998, 4.0099) | |||
| 3 | A1 | (−7.9985, 16.0005, −0.0145) (0.0016, −16.0001, −0.0262) (−15.9982, −5.9998, −0.0167) | ||
| B1 | (−56.1897, 2.0002, 16.0107) (−56.2479, −6.0002, 16.0103) | |||
| A2 | (−2.0607, 17.9965, 0.0141) (−0.0599, −16.0028, 0.0125) (−16.0603, −6.0033, 0.002) | |||
| B2 | (−56.0777, 2.0002, 16.0107) (−56.0749, −6.0002, 16.0103) | |||
| 4 | A1 | (−0.0839, −10.0002, 1.0230) (−0.3464, 23.9989, 1.0236) (−0.1286, −6.0009, 11.0485) | ||
| B1 | (40.1562, −24.0009, −15.0786) (40.1563, 19.9992, −15.0731) | |||
| A2 | (0.0314, −10.0002, 1.023) (0.0206, 23.9989, 1.0236) (0.0061, −6.0009, 11.0485) | |||
| B2 | (40.0493, −23.9815, −14.987) (40.0488, 20.0175, −14.9663) | |||
| 5 | A1 | (−0.0711, −11.9999, 0.9542) (−0.2694, 14.0002, 0.9539) (−0.0348, −18.0005, −11.0463) | ||
| B1 | (34.1562, 13.9988, −15.0622) (34.1561, −14.0012, −15.0731) | |||
| A2 | (0.0152, −11.9999, 0.9542) (0.0051, 14.0002, 0.9539) (0.0243, −18.0005, −11.0463) | |||
| B2 | (34.0328, 13.9977, −15.0402) (34.0331, −14.003, −15.0446) | |||
| 6 | A1 | (−0.286, −24.0002, −10.7048) (−0.0978, 2.0002, 1.2955) (−0.2324, −15.9998, 3.2949) | ||
| B1 | (40.0939, −5.9998, −14.7811) (48.0936, 16.0005, −14.7789) | |||
| A2 | (0.0237, −24.0002, −10.7048) (0.0145, 2.0002, 1.2955) (0.0128, −15.9998, 3.2949) | |||
| B2 | (40.0318, −5.9876, −14.7164) (48.0325, 16.0123, −14.6902) | |||
References
- Guo, H.; Zhang, Z.; Xiao, M.; Liu, H.; Zhang, Q. Tolerance optimization method based on flatness error distribution. Int. J. Adv. Manuf. Tech. 2021, 113, 279. [Google Scholar] [CrossRef]
- Saren, Q.; Zhang, Z.; Xiong, J.; Chen, X.; Zhu, D.; Wu, W.; Jin, X.; Shang, K. An accuracy and performance-oriented accurate digital twin modeling method for precision microstructures. J. Intell. Manuf. 2024, 35, 2887–2911. [Google Scholar] [CrossRef]
- Jiang, Q.; Feng, H.; Wang, Y.; Fang, C. Batch circular form error characterization and evaluation. Precis. Eng. 2017, 47, 223–230. [Google Scholar] [CrossRef]
- Mantripragada, R.; Whitney, D.D.E. The Datum Flow Chain: A Systematic Approach to Assembly Design and Modeling. Res. Eng. Des. 1998, 10, 150–165. [Google Scholar] [CrossRef]
- Camelio, J.; Hu, S.J.; Ceglarek, D. Modeling Variation Propagation of Multi-Station Assembly Systems with Compliant Parts. J. Mech. Des. 2003, 125, 673–681. [Google Scholar] [CrossRef]
- Anselmetti, B.; Mejbri, H.; Mawussi, K. Coupling experimental design—Digital simulation of junctions for the development of complex tolerance chains. Comput. Ind. 2003, 50, 277–292. [Google Scholar] [CrossRef]
- Anselmetti, B. Generation of functional tolerancing based on positioning features. Comput. Aided Des. 2006, 38, 902–919. [Google Scholar] [CrossRef]
- Lyu, C.; Liu, Z.; Ai, Y.; Yu, Z. Assembly Joint Surface Error Modeling and Tolerance Optimization in the Case of Coupled Tolerance. J. Mech. Eng. 2015, 51, 108–118. [Google Scholar] [CrossRef]
- Ke, J.; Jianhua, L.; Ruxin, N.; Chongying, G. Variation Analysis and Assembly Success Rate Computation for Clearance Fit under Constraint of Location Priority. J. Mech. Eng. 2014, 50, 136. [Google Scholar] [CrossRef]
- Hu, M.; Lai, X.M.; Lin, Z.Q.; Cheng, G.L.; Gan, P.; Zhu, J.H.; Zhou, L.B. Variation Analysis for Multi-Flexible Autobody Assembly. J. Shanghai Jiaotong Univ. 2000, 34, 1365–1368. [Google Scholar] [CrossRef]
- Mansuy, M.; Giordano, M.; Hernandez, P. A Generic Method for the Worst Case and Statistical Tridimensional Tolerancing Analysis. Procedia CIRP 2013, 10, 276–282. [Google Scholar] [CrossRef]
- Ding, S.; Zheng, X.; Bao, J.; Zhang, J. An improved Jacobian-Torsor model for statistical variation solution in aero-engine rotors assembly. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2021, 235, 466–483. [Google Scholar] [CrossRef]
- Zeng, W.; Rao, Y.; Wang, P.; Yi, W. A solution of worst-case tolerance analysis for partial parallel chains based on the Unified Jacobian-Torsor model. Precis. Eng. 2017, 47, 276–291. [Google Scholar] [CrossRef]
- Sun, J.; Siyi, D.; Zhimin, L.; Fuyong, Y.; Xun, M. Point-based solution using Jacobian-Torsor theory into partial parallel chains for revolving components assembly. J. Manuf. Syst. 2018, 46, 46–58. [Google Scholar] [CrossRef]
- Ding, S.; Zheng, X. Variation Analysis Considering the Partial Parallel Connection in Aero-Engine Rotor Assembly. Energies 2022, 15, 4451. [Google Scholar] [CrossRef]
- Besl, P.; McKay, N.D. Method for Registration of 3-D Shapes. In Proceedings of the Sensor Fusion IV: Control Paradigms and Data Structures, Boston, MA, USA, 12–15 November 1991; pp. 586–606. [Google Scholar] [CrossRef]
- Hu, X.; Zhao, Q.; Yang, Y.; Wan, S.; Sun, Y.; Hong, J. Accuracy analysis for machine tool spindles considering full parallel connections and form errors based on skin model shapes. J. Comput. Des. Eng. 2023, 10, 1970–1987. [Google Scholar] [CrossRef]
- Shen, T.; Lu, C. An assembly accuracy analysis approach of mechanical assembly involving parallel and serial connections considering form defects and local surface deformations. Precis. Eng. 2024, 88, 44–64. [Google Scholar] [CrossRef]
- Sangnui, S.; Peters, F. The Impact of Surface Errors on the Location and Orientation of a Cylindrical Workpiece in a Fixture. J. Manuf. Sci. Eng. 2001, 123, 325–330. [Google Scholar] [CrossRef]
- Lee, N.K.S.; Yu, G.H.; Chen, J.Y.; Joneja, A. Effect of Mechanical Alignment System on Assembly Accuracy. J. Manuf. Sci. Eng. 2003, 125, 595–608. [Google Scholar] [CrossRef]
- Lee, N.K.S.; Chen, J.Y.; Joneja, A. Effects of surface roughness on multi-station mechanical alignment processes. J. Manuf. Sci. Eng. 2001, 123, 433–444. [Google Scholar] [CrossRef]
- Lee, N.K.S.; Yu, G.; Joneja, A.; Ceglarek, D. The modeling and analysis of a butting assembly in the presence of workpiece surface roughness and part dimensional error. Int. J. Adv. Manuf. Tech. 2006, 31, 528–538. [Google Scholar] [CrossRef]
- Pierce, R.S.; Rosen, D. A Method for Integrating Form Errors Into Geometric Tolerance Analysis. J. Mech. Des. 2008, 130, 467–478. [Google Scholar] [CrossRef]
- Shang, K.; Wu, T.; Jin, X.; Zhang, Z.; Li, C.; Liu, R.; Wang, M.; Dai, W.; Liu, J. Coaxiality prediction for aeroengines precision assembly based on geometric distribution error model and point cloud deep learning. J. Manuf. Syst. 2023, 71, 681–694. [Google Scholar] [CrossRef]
- Zhang, J.; Qiao, L. Research on computing position and orientation deviations caused by mating two non-ideal planes. Procedia CIRP 2018, 75, 309–313. [Google Scholar] [CrossRef]
- Schleich, B.; Wartzack, S. Novel approaches for the assembly simulation of rigid Skin Model Shapes in tolerance analysis. Comput. Aided Des. 2018, 101, 1–11. [Google Scholar] [CrossRef]
- Wang, J.W.J.; Duan, L.D.L. A Direct Calculating Method and Experiment of Absolute Orientation for Unmanned Aerial Vehicle Photograph. Appl. Mech. Mater. 2013, 353–356, 3468. [Google Scholar] [CrossRef]
- Samper, S.; Adragna, P.; Favreliere, H.; Pillet, M. Modeling of 2D and 3D Assemblies Taking into Account Form Errors of Plane Surfaces. J. Comput. Inf. Sci. Eng. 2009, 9, 41005. [Google Scholar] [CrossRef]
- Daniel, F.; Weill, R.; Bourdet, P. Computer Aided Tolerancing and Dimensioning in Process Planning. ClRP Ann. 1986, 3511, 381–386. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, Z.; Jin, X.; Zhang, Q. A novel modelling method of geometric errors for precision assembly. Int. J. Adv. Manuf. Tech. 2018, 94, 1139–1160. [Google Scholar] [CrossRef]
- Liu, X.L.; Zhang, X.D.; Fang, F.Z.; Liu, S.G. Identification and compensation of main machining errors on surface form accuracy in ultra-precision diamond turning. Int. J. Mach. Tools Manuf. 2016, 105, 45–57. [Google Scholar] [CrossRef]
- Chen, H.; Jin, S.; Li, Z.; Lai, X. A solution of partial parallel connections for the unified Jacobian-Torsor model. Mech. Mach. Theory 2015, 91, 39–49. [Google Scholar] [CrossRef]



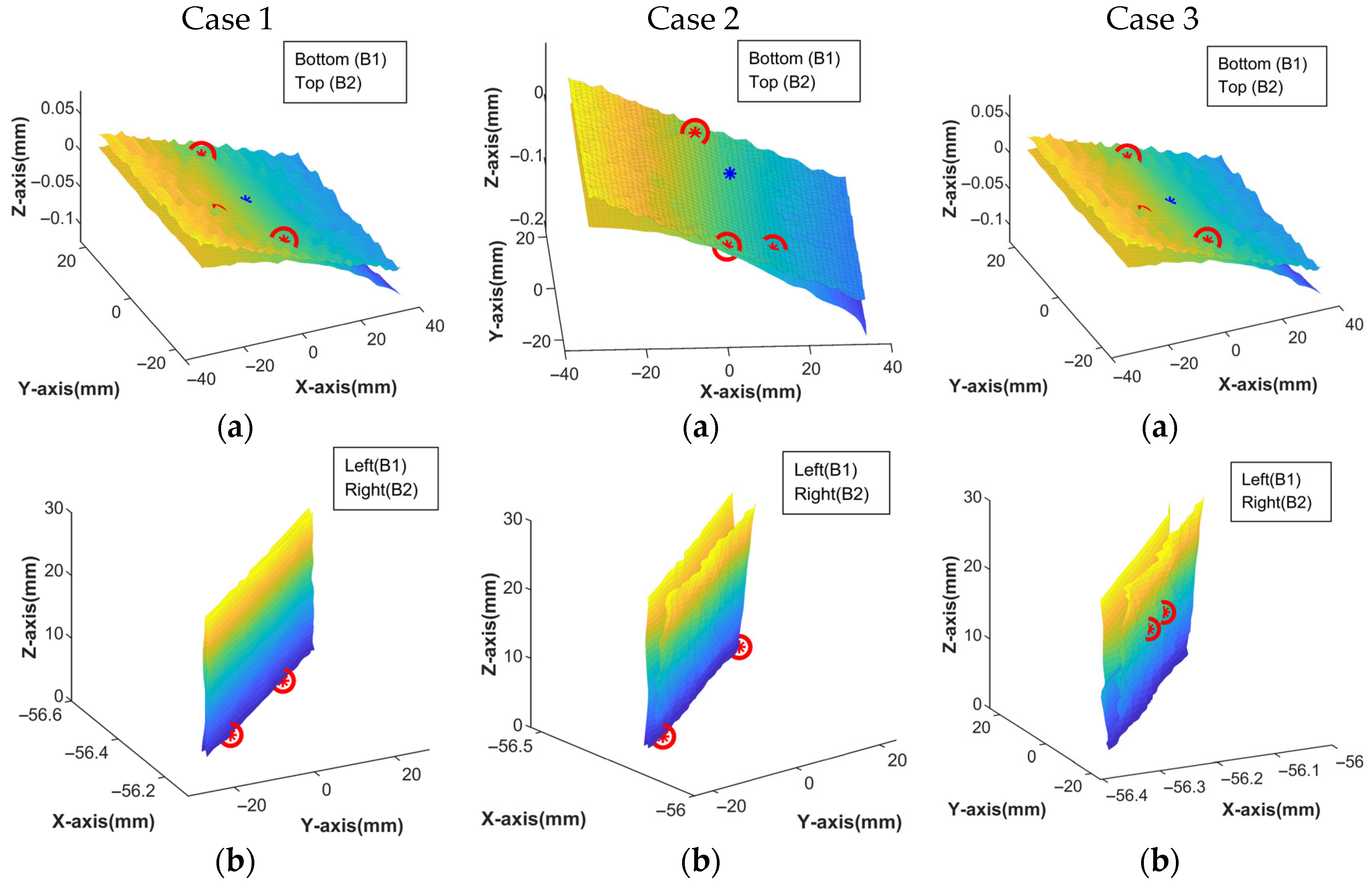

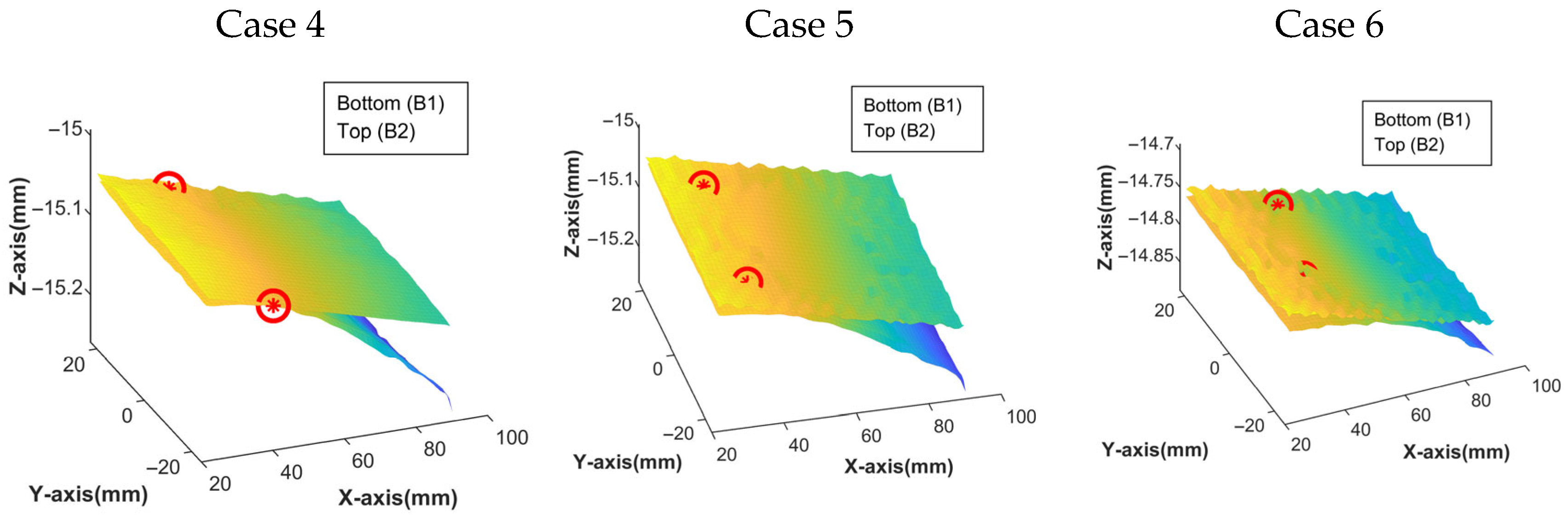
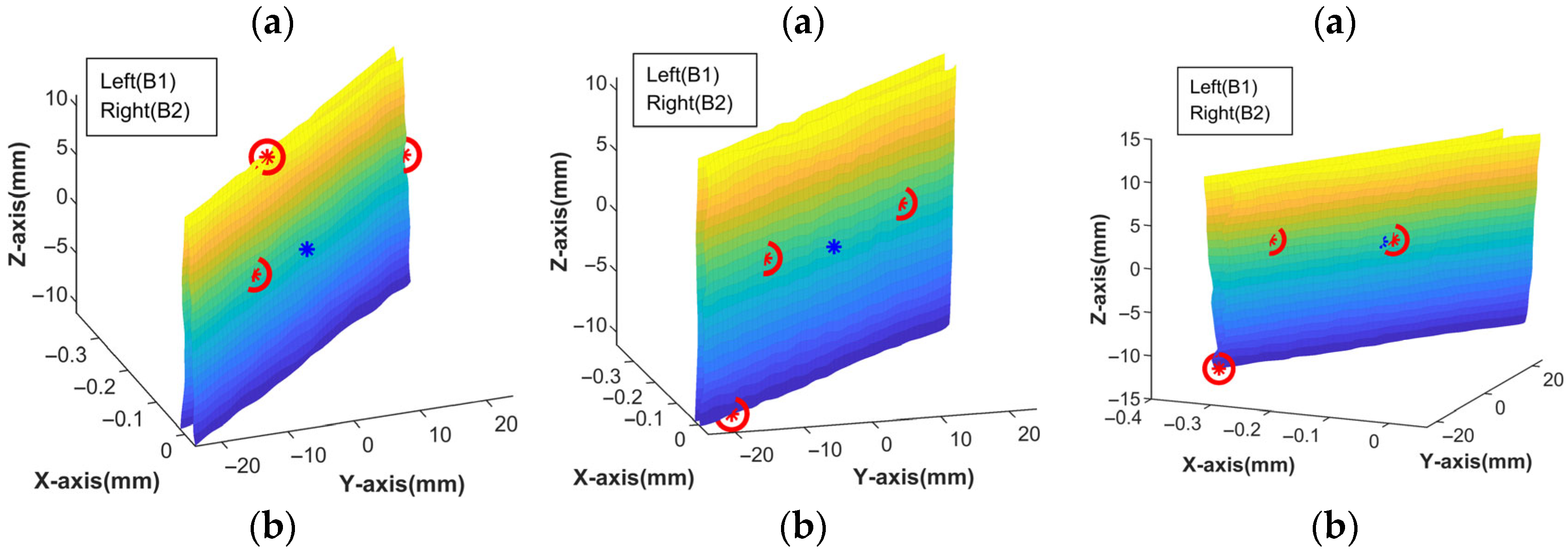
| Case (2D-Case) | Mapping Matrix M | Contact Points of the Assembly Coordinate System | SDT | |||
|---|---|---|---|---|---|---|
| Horizontal Mating Surfaces A1 and A2 | Vertical Mating Surfaces B1 and B2 | |||||
| 1 | A1 | (−0.1052, −0.0017) (25.8950, −0.00058) | B1 | (−33.0016, 13.9946) | ||
| A2 | (−0.1052, 0.00004) (25.8950, 0.0012) | B2 | (−33.0002, 13.9955) | |||
| 2 | A1 | (3.8969, −0.0019) (−10.1033, −0.0043) | B1 | (−39.1795, 26.0174) | ||
| A2 | (3.8969, 0.0016) (−10.1033, 0) | B2 | (−39.1776, 26.0210) | |||
| 3 | A1 | (19.8806, −0.0038) (−10.1204, −0.0030) | B1 | (−39.1889, 8.0650) | ||
| A2 | (19.8806, 0.0031) (−10.1204, 0.00070) | B2 | (−39.1885, 8.0727) | |||
| 4 | A1 | (43.0756, −14.9524) | B1 | (0, 8.9904) (−0.00184, −7.0136) | ||
| A2 | (43.0756, −14.9496) | B2 | (0.00064, 9.0662) (0.00002, −6.9341) | |||
| 5 | A1 | (15.0889, −15.0755) | B1 | (0.0006, 0.9407); (0.00019, −7.0593); | ||
| A2 | (15.0889, −15.0770) | B2 | (−0.00078, 0.9873); (−0.00033, −7.0127); | |||
| 6 | A1 | (57.0745, −14.0774) | B1 | (−0.0019, 9.9882) (−0.00024, −2.0125) | ||
| A2 | (57.0745, −14.0717) | B2 | (0, 9.9919) (0.0030, −2.0075) | |||
| No. | Part | Machining Method | Material |
|---|---|---|---|
| 1 | Base 1 | Milling machine 1 | grade 45 steel |
| 2 | Base 2 | Milling machine 2 | |
| 3 | Bracket 1 | Milling machine 1 | |
| 4 | Bracket 2 | Milling machine 2 |
| Case | Contact Surfaces | Pair of Assembled Samples | Force | |
|---|---|---|---|---|
| 1 | D1–S1; D2–S2 | Base 1 | Bracket 1 | vertical applied force |
| 2 | D1–S1; D2–S2 | Base 1 | Bracket 2 | |
| 3 | D1–S1; D2–S2 | Base 2 | Bracket 2 | |
| 4 | D1–S1; D2–S2 | Base 1 | Bracket 1 | horizontal applied force |
| 5 | D1–S1; D2–S2 | Base 1 | Bracket 2 | |
| 6 | D1–S1; D2–S2 | Base 2 | Bracket 2 | |
| Case (3D-Case) | 1 (%) | 2 (%) | 3 (%) | 4 (%) | 5 (%) | 6 (%) |
|---|---|---|---|---|---|---|
| RMSE | 1.6 | 1.4 | 1.5 | 1.2 | 1.3 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Jin, X.; Guo, H.; Li, C. A Multi-Constraint Assembly Registration Method Based on Actual Machined Surfaces. Machines 2025, 13, 1009. https://doi.org/10.3390/machines13111009
Liu L, Jin X, Guo H, Li C. A Multi-Constraint Assembly Registration Method Based on Actual Machined Surfaces. Machines. 2025; 13(11):1009. https://doi.org/10.3390/machines13111009
Chicago/Turabian StyleLiu, Lu, Xin Jin, Huan Guo, and Chaojiang Li. 2025. "A Multi-Constraint Assembly Registration Method Based on Actual Machined Surfaces" Machines 13, no. 11: 1009. https://doi.org/10.3390/machines13111009
APA StyleLiu, L., Jin, X., Guo, H., & Li, C. (2025). A Multi-Constraint Assembly Registration Method Based on Actual Machined Surfaces. Machines, 13(11), 1009. https://doi.org/10.3390/machines13111009







